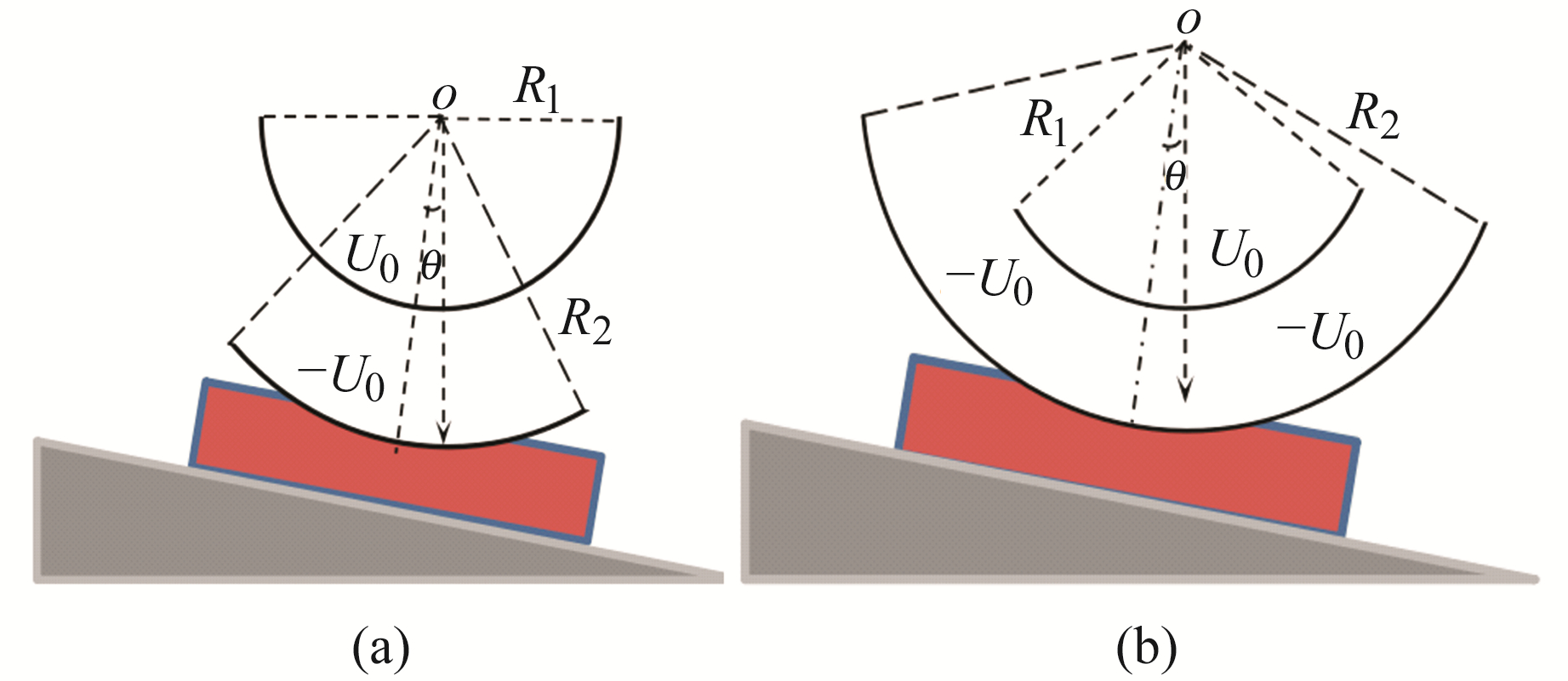
电容式角位移传感器的工作原理是将被测物体的角度变化转换为电容器电容的变化,具有高精度、高分辨率和可靠性,在角度等非电量测量和自动检测中应用广泛。在以往关于变面积型电容角位移传感器的研究[1-4]中没有计及传感器极板边缘效应对测量结果的影响,从而导致测量结果出现误差,精确度变低。为提高大地测量、高层建筑倾角测量及底盘悬挂系统倾角测量等的水平检测和倾角测量的精确度,本文给出一种变面积型圆柱面电容式倾角传感器(图 1),该传感器的探头由上、下两块圆柱面形的极板组成,其中下极板与底板固定,上极板可绕一固定轴转动并因重力作用在测量过程保持其竖直位置不变。当测量的倾角变化时,下极板与上极板的相对位置发生变化,导致传感器探头的电容发生变化。为利用格林函数法消除传感器极板的横向边缘效应所引起的测量误差,提高电容角位移传感器的测量精确度,本文针对电容式倾角传感器的结构,首先建立与之对应的复平面z上的二维静电场边值问题的数学模型,利用保角变换函数ζ=f(z)将z平面上的边值问题变换为位于ζ上半平面的二维边值问题,由格林函数法求得ζ平面上半平面的电势分布;再通过函数变换关系将上半平面的电势分布变换为电容传感器内的电势分布,继而得到场强分布;然后积分得到传感器极板的带电量及其电容量,给出传感器输出量C(θ)的数学表达式;最后利用MATLAB软件绘制出输出特性曲线,以分析传感器在不同区域的灵敏度及线性度,通过数值模拟分析给出提高电容传感器输出性能的途径。
|
图 1 变面积型圆柱面电容式倾角传感器结构示意图 Fig. 1 Structural diagram of variable area cylindrical capactive tilt sensor |
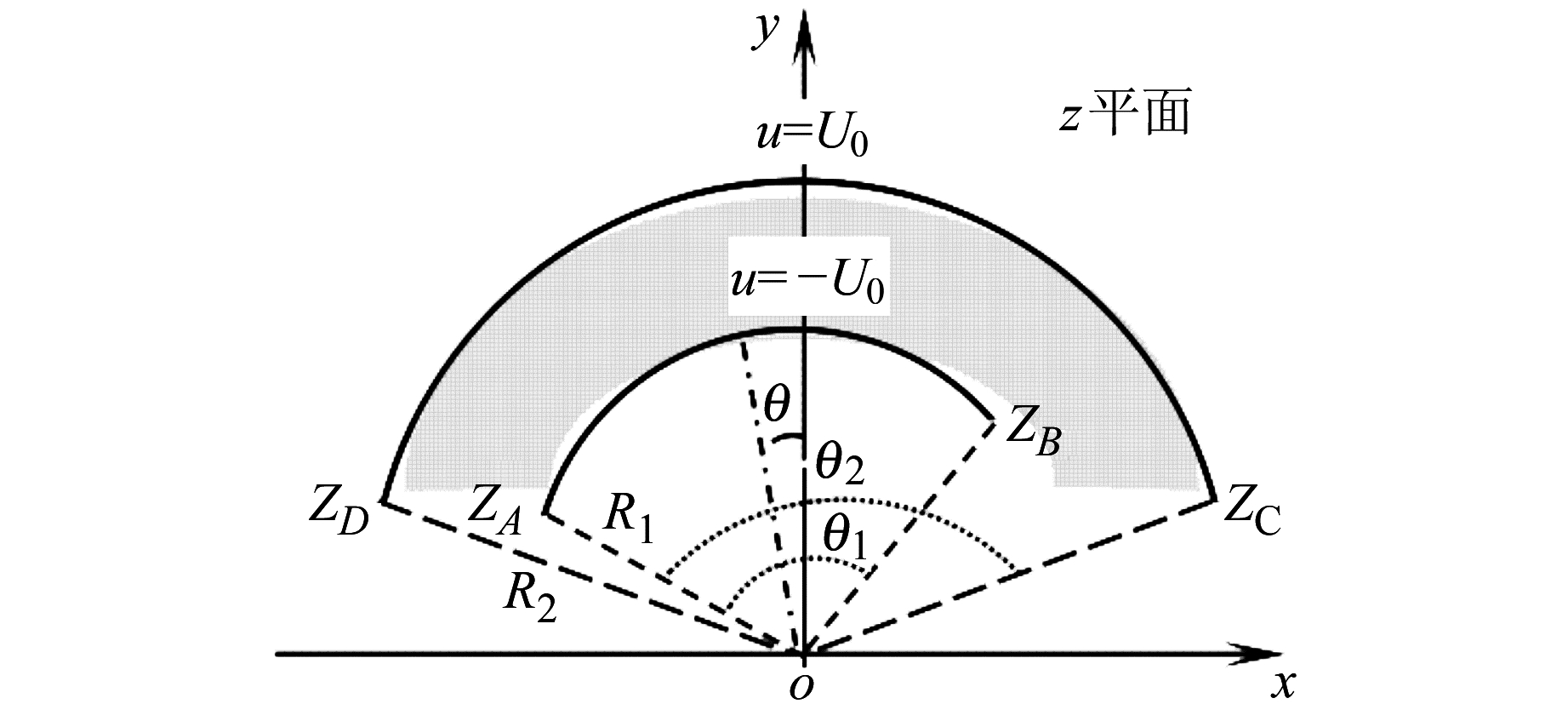
根据图 1变面积型圆柱面电容式倾角传感器建立图 2所示的坐标系,来研究该传感器的电场及其电容量随倾角变化的关系。在图 2中,内、外圆柱面的半径分别为R1、R2,其所对应的圆心角分别为θ1和θ2,电势分别为-U0和U0,内极板相对于初始位置(上极板关于y轴对称的位置)逆时针转过θ角度(θ即为图 1中的倾角)。当两个圆柱面的长度远大于其半径时,该传感器可视为无限长。因而在垂直于圆柱面轴线的所有截面中的电势和场强的分布都相同,则其内部的电场为平行平面场,取其中一个截面为z平面。
|
图 2 变面积型圆柱面电容式倾角传感器的横截面 Fig. 2 Cross section of variable area cylindrical capactive tilt sensor |
为求得变面积型圆柱面电容式倾角传感器内部的电场分布,首先作保角变换:
| $ w_1=i \ln (z) $ | (1) |
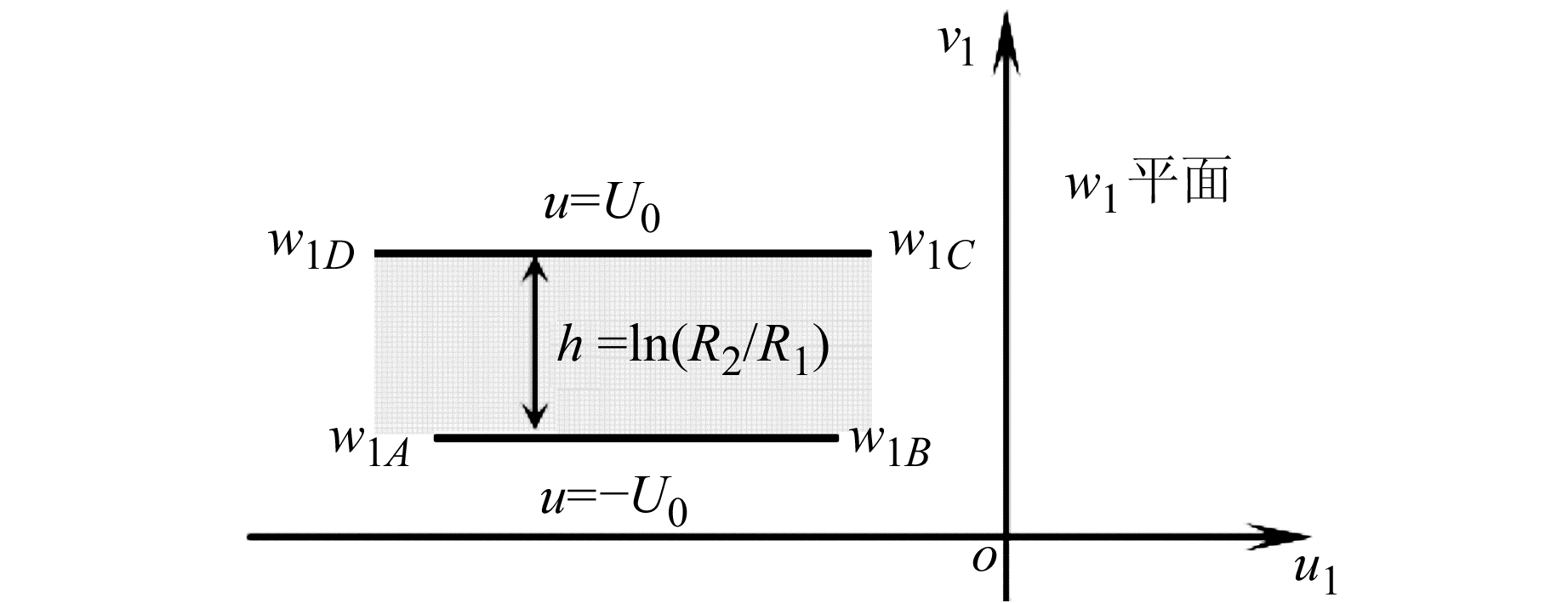
式(1)将z平面上半径分别为R1和R1的圆弧变换为w1平面上两平行线段AB和CD,AB和CD的间距为h=ln(R2/R1),如图 3所示。w1平面上两线段的起点和终点位置由该传感器的横截面在z平面上的圆弧位置zA、zB、zC、zD通过式(1)来确定,其位置分别为w1A、w1B、w1C和w1D,这8个点的位置及关系由以下公式给出:
| $ \left\{\begin{array}{l} z_A=-R_1 \sin \left(\theta_1 / 2+\theta\right)+i R_1 \cos \left(\theta_1 / 2+\theta\right) \\ z_B=R_1 \sin \left(\theta_1 / 2-\theta\right)+i R_1 \cos \left(\theta_1 / 2-\theta\right) \\ z_C=R_2 \sin \left(\theta_2 / 2\right)+i R_2 \cos \left(\theta_2 / 2\right) \\ z_D=-R_2 \sin \left(\theta_2 / 2\right)+i R_2 \cos \left(\theta_2 / 2\right) \end{array}\right. $ | (2) |
| $ \left\{\begin{array}{l} w_{1 A}=i \ln \left(z_A\right), w_B=i \ln \left(z_B\right) \\ w_C=i \ln \left(z_C\right), w_D=i \ln \left(z_D\right) \end{array}\right. $ | (3) |
|
图 3 变换后的带形区域 Fig. 3 Transformed ribbon region |
再作平移变换:
| $ w_2=w_1-i v_{1 A} $ | (4) |
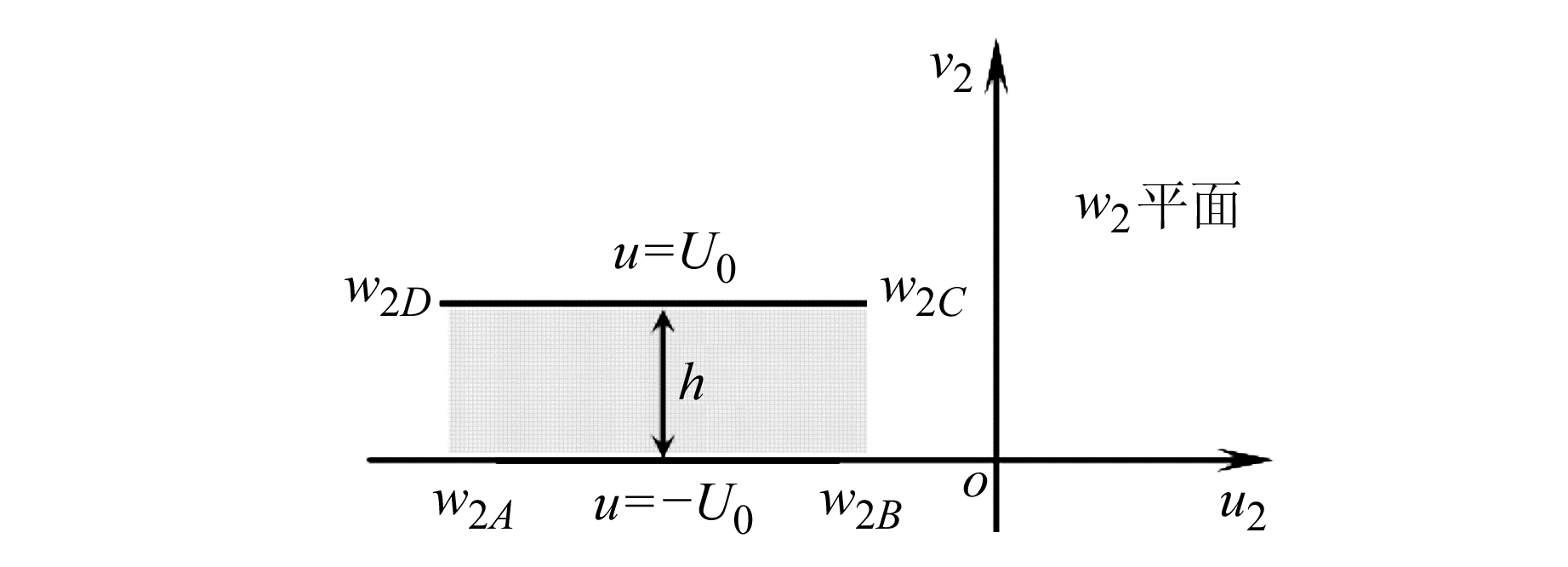
式中,v1A=Im(w1A)=ln(R1)。变换后的圆柱面电容式倾角传感器的横截面如图 4所示。
|
图 4 再变换后的带形区域 Fig. 4 Retransformed ribbon region |
为应用格林函数法求得圆柱面电容式倾角传感器内部的电势分布,需再进行保角变换[5]:
| $ \zeta=\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h} w_2} $ | (5) |
式(5)将w2上半平面的平行于实轴且与实轴间距为h的两条线段映射为位于ζ平面实轴上的两条线段,其带形域则映射为上半平面,如图 5所示。

|
图 5 再变换后的上半平面 Fig. 5 Retransformed upper half plane |
经式(1)、式(4)及式(5)变换后,z平面上传感器内的电势分布就变换为ζ上半平面的边值问题:
| $ \left\{\begin{array}{l} \nabla^2 u=0 \\ u=-U_0, \eta=0, \xi_A \leqslant \xi \leqslant \xi_B \\ u=U_0, \eta=0, \xi_C \leqslant \xi \leqslant \xi_D \end{array}\right. $ | (6) |
对于ζ平面上的边值问题,应用格林函数法[6]可得其电势分布为:
| $ \begin{gathered} u(\xi, \eta)=\frac{\eta}{{\rm{ \mathsf{ π}}}} \int_{-\infty}^{+\infty} \frac{f\left(\xi^{\prime}\right) \mathrm{d} \xi^{\prime}}{\left(\xi^{\prime}-\xi\right)^2+\eta^2}= \\ \frac{\eta}{{\rm{ \mathsf{ π}}}} \int_{\xi_C}^{\xi_D} \frac{U_0 \mathrm{~d} \xi^{\prime}}{\left(\xi^{\prime}-\xi\right)^2+\eta^2}+\frac{\eta}{{\rm{ \mathsf{ π}}}} \int_{\xi_A}^{\xi_B} \frac{\left(-U_0\right) \mathrm{d} \xi^{\prime}}{\left(\xi^{\prime}-\xi\right)^2+\eta^2}= \\ \frac{U_0}{{\rm{ \mathsf{ π}}}}\left(\arctan \frac{\xi_D-\xi}{\eta}-\arctan \frac{\xi_C-\xi}{\eta}\right)- \\ \frac{U_0}{{\rm{ \mathsf{ π}}}}\left(\arctan \frac{\xi_B-\xi}{\eta}-\arctan \frac{\xi_A-\xi}{\eta}\right) \end{gathered} $ | (7) |
| $ \begin{gathered} w_2=i \ln (z)-i \ln \left(R_1\right)= \\ i \ln \left(\sqrt{x^2+y^2} \cdot \mathrm{e}^{i \arctan \frac{y}{x}}\right)-i \ln \left(R_1\right)= \\ i\left[\frac{1}{2} \ln \left(x^2+y^2\right)+i \arctan \frac{y}{x}\right]-i \ln \left(R_1\right)= \\ \frac{i}{2} \ln \left(x^2+y^2\right)-\arctan \frac{y}{x}-i \ln \left(R_1\right) \\ \zeta=\xi+i \eta=\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h} w_2}=\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left[\frac{i}{2} \ln \left(x^2+y^2\right)-\arctan \frac{y}{x}-i \ln \left(R_1\right)\right]}= \\ \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot\left\{\cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]+\right. \\ \left.i \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]\right\} \end{gathered} $ | (8) |
将式(2)代入式(8),得:
| $ \left\{ \begin{array}{l} \xi_A=\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \left[\cot \left(\frac{\theta_1}{2}+\theta\right)\right]} , \\ \ \ \ \ \xi_B=\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \left[\cot \left(\frac{\theta_1}{2}-\theta\right)\right]}\\ \xi_C=-\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \left[\cot \left(\frac{\theta_2}{2}\right)\right]}, \\ \xi_D=-\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \left[\cot \left(\frac{\theta_2}{2}\right)\right]} \end{array} \right. $ | (9) |
将式(8)中的ξ、η及式(9)代入式(7),得:
| $\begin{array}{c} u(x, y)=\frac{U_0}{{\rm{ \mathsf{ π}}}}\left\{\arctan \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]}-\right. \\ \left.\arctan \frac{\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]}\right\}- \\ \frac{U_0}{{\rm{ \mathsf{ π}}}}\left\{\arctan \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta}{2}+\theta\right)}-\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]}-\right. \\ \left.\arctan \frac{\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}-\theta\right)}-\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \arctan \frac{y}{x}} \cdot \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{1}{2} \ln \left(x^2+y^2\right)-\ln \left(R_1\right)\right)\right]}\right\} \end{array} $ | (10) |
式(10)即为变面积型圆柱面电容式倾角传感器内部的电势分布函数,其极坐标形式为:
| $ \begin{gathered} u(\rho, \varphi)= \\ \frac{U_0}{{\rm{ \mathsf{ π}}}}\left\{\arctan \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cdot \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cdot \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}-\arctan \frac{\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cdot \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cdot \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}\right\}+ \\ \frac{U_0}{{\rm{ \mathsf{ π}}}}\left\{\arctan \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)}-\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cdot \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cdot \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}-\arctan \frac{\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}-\theta\right)}-\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cdot \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cdot \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}\right\} \end{gathered} $ | (11) |
其中,
由场强与电势的微分关系
| $\begin{array}{c} \boldsymbol{E}=-\left(\frac{\partial u}{\partial \rho} \boldsymbol{e}_\rho+\frac{1}{\rho} \frac{\partial u}{\partial \varphi} \boldsymbol{e}_{\varphi}\right)=\frac{U_0}{h}\left\{\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\rho} \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left[2\left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)\right]+\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\rho_2}{2}\right)} \cos \left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)}{\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h} \varphi}+\mathrm{e}^{2 \frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\rho_2}{2}\right)}+2 \mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\rho_2}{2}\right)} \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)}-\right. \\ \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\rho} \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left[2\left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)\right]+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)} \cos \left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)}{\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h} \varphi}+\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}+2 \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)} \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)}+ \\ \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\rho} \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left[2\left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)\right]-\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)} \cos \left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)}{\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h} \varphi}+\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)}-2 \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)} \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)}- \\ \left.\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\rho} \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left[2\left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)\right]-\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}-\theta\right)} \cos \left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)}{\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h} \varphi}+\mathrm{e}^{2 \frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}-\theta\right)}-2 \mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}-\theta\right)} \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left(\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right)}\right\}\boldsymbol{e}_{\rho}- \\ \frac{U_0}{{\rm{ \mathsf{ π}}}}\left\{-\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\rho} \frac{\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)} \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}{\mathrm{e}^{\frac{2 {\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}+\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h} \varphi}+2 \mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)} \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}+\right. \\ \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\rho} \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)} \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}{\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}+\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h} \varphi}+2 \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)} \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}- \\ \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\rho} \frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)} \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}{\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{-2 \frac{{\rm{ \mathsf{ π}}}}{h} \varphi}-2 \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)} \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi} \cos \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}+ \\ \left.\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\rho} \frac{\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}-\theta\right)} \sin \left[\frac{{\rm{ \mathsf{ π}}}}{h}\left(\ln \rho-\ln R_1\right)\right]}{{{\rm{e}}^{2\frac{{\rm{ \mathsf{ π}}} }{h}\left( {\frac{{\rm{ \mathsf{ π}}} }{2} - \frac{{{\theta _1}}}{2} - \theta } \right)}} + {{\rm{e}}^{ - 2\frac{{\rm{ \mathsf{ π}}} }{h}\varphi }} - 2{{\rm{e}}^{\frac{{\rm{ \mathsf{ π}}} }{h}\left( {\frac{{\rm{ \mathsf{ π}}} }{2} - \frac{{{\theta _1}}}{2} - \theta } \right)}}{{\rm{e}}^{ - \frac{{\rm{ \mathsf{ π}}} }{h}\varphi }}\cos \left[ {\frac{{\rm{ \mathsf{ π}}} }{h}\left( {\ln \rho - \ln {R_1}} \right)} \right]}\right\} \boldsymbol{e}_{\varphi} \end{array} $ | (12) |
为给出变面积型圆柱面电容式倾角传感器内部电场分布的直观图像,以验证本文所得结论的正确性,利用MATLAB软件对其电场分布进行数值模拟,得到电场线和等势线的分布见图 6。由图可知,该传感器内部的电场线与等势线及导体边界均垂直,场线分布正确,为预期结果。

|
图 6 圆柱面电容倾角传感器的电场 Fig. 6 Electric field of cylindrical capactive tilt sensor |
为计算简便,可假设变面积型圆柱面电容式倾角传感器的两个极板间的电压为U0(外极板的电势为U0,内极板的电势为0),取式(12)中ρ=R1,可得其内极板上的电荷面密度为:
| $ \begin{gathered} \sigma=\left|-\varepsilon_0 \varepsilon_r E_\rho\right|_{\rho=R_1} \mid=\varepsilon_0 \varepsilon_r \frac{U_0}{h R_1} \cdot \\ {\left[\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}+\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\partial_2}{2}\right)}}-\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h} \varphi}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\partial_2}{2}\right)}}\right]} \end{gathered} $ | (13) |
变面积型圆柱面电容式倾角传感器极板的带电量为:
| $ \begin{gathered} Q=\int_{\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)}^{\left(\frac{{\rm{ \mathsf{ π}}}}{2}+\frac{\theta_1}{2}+\theta\right)} \sigma \cdot R_1 \cdot L \mathrm{~d} \varphi= \\ \varepsilon_0 \varepsilon_r \frac{U_0 L \ln \left(R_1\right)}{2 {\rm{ \mathsf{ π}}} h}\left\{\ln \left[\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}+\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}}\right]-\right.\\ \left.\ln \left[\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}+\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}}\right]\right\} \end{gathered} $ | (14) |
由式(14)得变面积型圆柱面电容式倾角传感器的电容量为:
| $ \begin{array}{c} C=\frac{Q}{\Delta U}=\frac{Q}{U_0}= \\ \varepsilon_0 \varepsilon_r \frac{L \ln \left(R_1\right)}{2 {\rm{ \mathsf{ π}}} \ln \left(R_2 / R_1\right)}\left\{\ln \left[\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}+\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}}\right]-\right. \\ \left.\ln \left[\frac{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}+\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}}{\mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_1}{2}+\theta\right)}+\mathrm{e}^{\frac{{\rm{ \mathsf{ π}}}}{h}\left(\frac{{\rm{ \mathsf{ π}}}}{2}-\frac{\theta_2}{2}\right)}}\right]\right\} \\ \end{array} $ | (15) |
因为该传感器内的场强分布是通过格林函数法得到的,已经考虑了传感器极板横向的边缘效应,所以式(15)具有较高的精确度。
可以看出,在电容传感器电场分布较复杂及考虑边缘效应的的情况下,当动极板旋转时,两个极板的相对位置发生变化,极板间的电场分布也在发生变化,导致极板上的电荷分布发生变化,极板的带电量也发生变化,而两个极板间的电势差是恒定的,则传感器的电容量必然发生变化;再者,极板相对位置的变化还会影响到边缘效应的变化,引起两个极板边缘散射电场线宽度发生改变,从而引起边缘附加电容的变化。此为改变传感器电容量变化的两个因素。也就是说,该传感器不能由公式C=ε0S/d通过极板正对面积的变化来判定其电容量是否改变,当传感器动极板向外旋转(即θ增大)时,内外两个极板作为两个带电体的相对位置远离,才是导致传感器电容量减小的物理机制。
2.2 圆柱面电容式倾角传感器的输出特性曲线利用MATLAB软件的数值模拟功能,通过式(15)绘制出变面积型圆柱面电容式倾角传感器的电容量C随其角位移θ变化的输出特性曲线,结果见图 7。

|
图 7 变面积型圆柱面电容式倾角传感器的输出特性曲线 Fig. 7 Output characteristic curve of variable area cylindrical capactive tilt sensor |
MATLAB软件的数值模拟结果表明:1)当θ1≠θ2且θ1<θ2时,该传感器的线性度和灵敏度均较差(图 8(a));2)θ1=θ2时,该传感器的平均灵敏度及线性度均有较大幅度的提高(图 8(b));3)当θ1≠θ2且θ1>θ2时,该传感器具有较好的线性度和灵敏度,输出性特性比较理想(图(c)~(d)),且在一定的范围内随着θ2和θ1差值的增大,该传感器灵敏度和线性度均得到提高,输出特性得到改善。
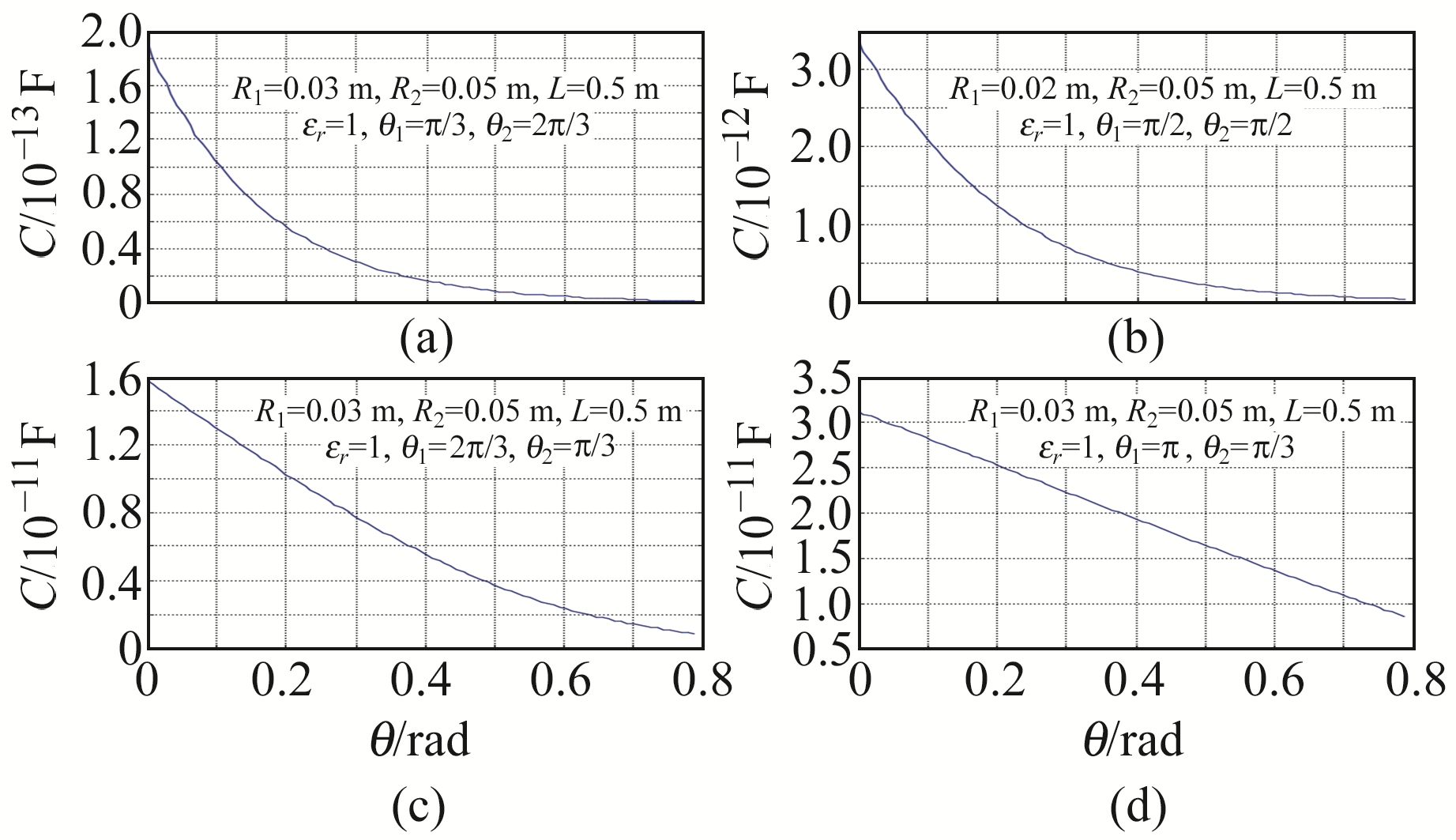
|
图 8 圆柱面电容倾角传感器的输出特性曲线 Fig. 8 Output characteristic curve of cylindrical capactive tilt sensor |
1) θ1<θ2。MATLAB软件的数值模拟结果表明,当θ1和θ2保持不变且θ1<θ2时,随着传感器内、外半径差的减小,传感器的输出特性变差(图 9)。
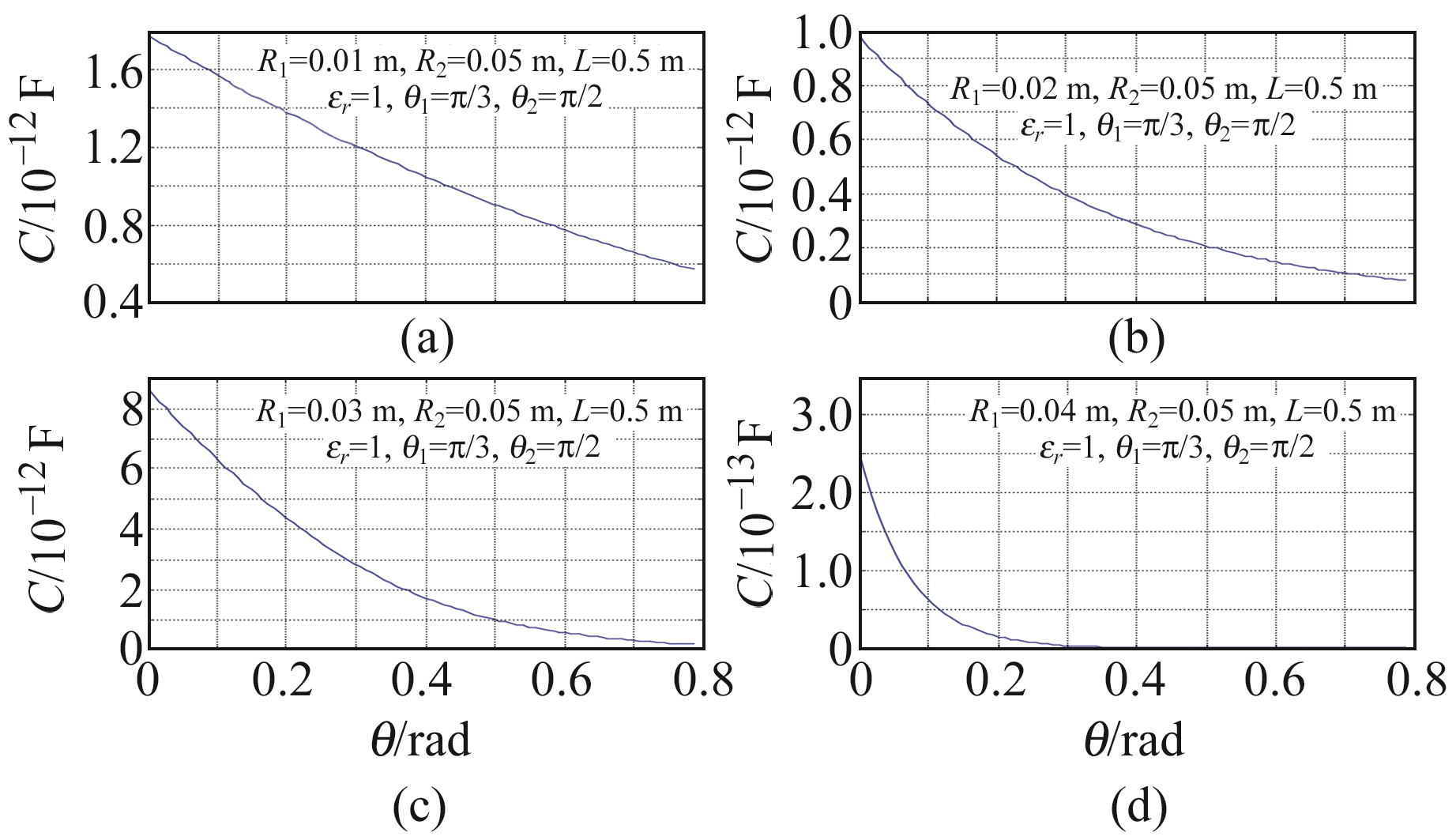
|
图 9 圆柱面电容倾角传感器的输出特性曲线 Fig. 9 Output characteristic curve of cylindrical capactive tilt sensor |
2) θ1=θ2。数值模拟结果表明,当θ1和θ2保持不变且θ1=θ2时,随着传感器内、外半径差的减小,传感器的输出特性变差(图 10)。
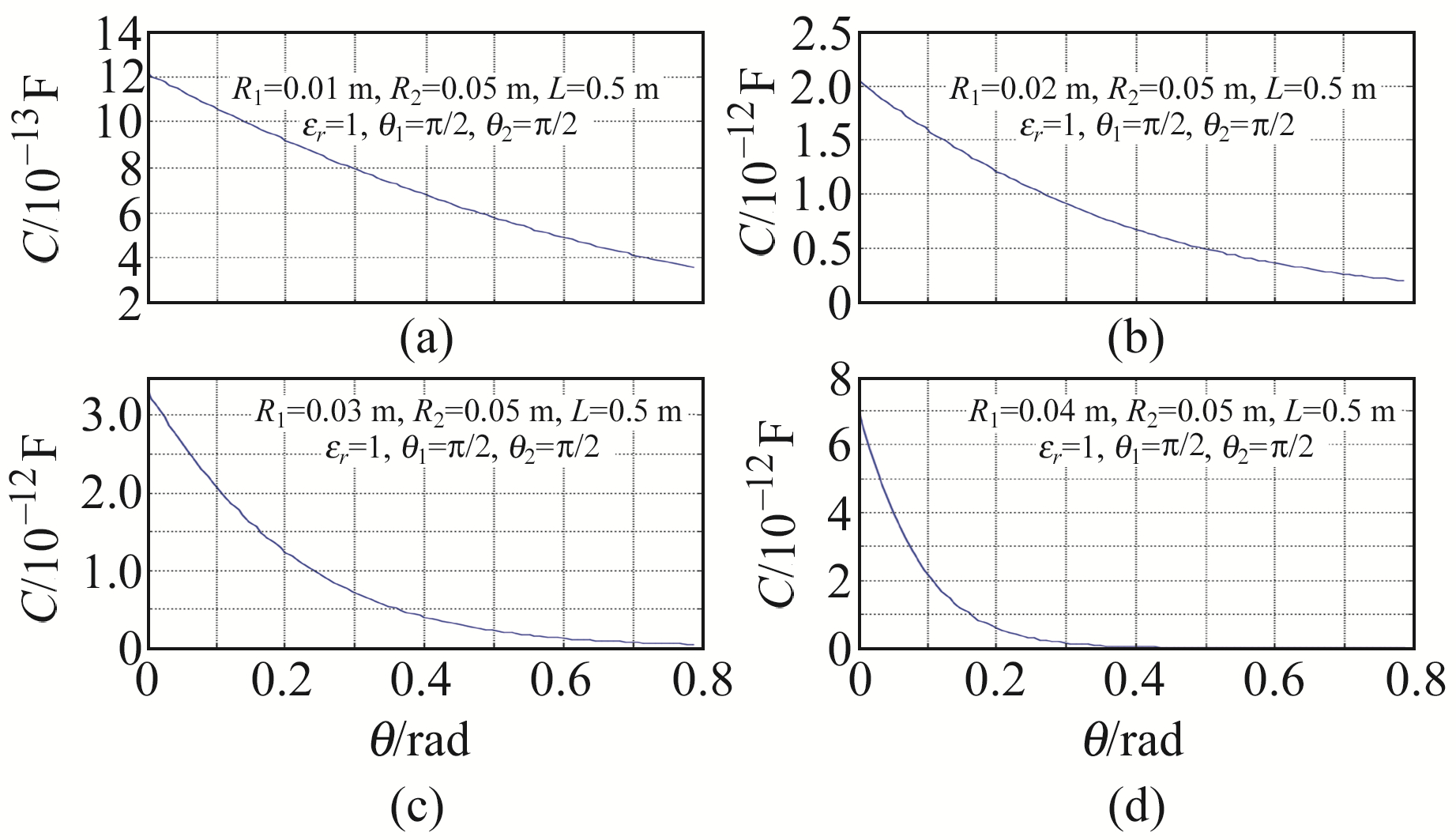
|
图 10 圆柱面电容倾角传感器的输出特性曲线 Fig. 10 Output characteristic curve of cylindrical capactive tilt sensor |
3) θ1>θ2。数值模拟结果表明,当θ1和θ2保持不变且θ1>θ2时,在θ1和θ2取值合适的情况下,随着传感器内、外半径差的减小,传感器的灵敏度和线性度均提高,输出特性得以改善(图 11)。

|
图 11 圆柱面电容倾角传感器的输出特性曲线 Fig. 11 Output characteristic curve of cylindrical capactive tilt sensor |
综合数值模拟结果(表 1,参数设置:R1=0.04 m, R2=0.05 m, L=0.5 m, εr=1, θ1=π, θ2=π/2)可以看出,在一定测量范围内,改善变面积型圆柱面电容式角位移传感器输出特性的途径有两个:1)减小两个极板圆柱面的半径差;2)使内圆柱面对应的圆心角大于外圆柱面对应的圆心角。二者都能在一定测量范围内提高传感器的敏度和线性度(图 6(b), 图 11(b)、(c)),如图 1(a)中所示结构的传感器,具有良好的输出特性。
|
|
表 1 变面积型圆柱面电容式倾角传感器的输出特性数据 Tab. 1 Output characteristic data of variable area cylindrical capacitive tilt sensor |
由于电容传感器的边缘效应使其极板存在边缘附加电容,而本文传感器内的场强分布是通过格林函数法得到的,已经考虑了传感器极板的横向边缘效应,故由式(13)给出的电容值要大于传感器在不计边缘效应时的电容值,式(13)具有较高的精确度。调整该传感器的几何尺寸还可以得到较好的输出特性。表 1中对于给定的传感器的几何尺寸,在30°测量范围内,每1°倾角对应的电容量变化量均为0.247×10-11 F左右,此时传感器具有良好的线性度和较高的灵敏度,输出特性良好。与表 1中传感器尺寸对应的30°测量范围,能满足倾角测量的实际需要,数值计算结果验证了该款传感器设计的可行性。
3 结语计算机数值模拟研究方法已成为继实验研究和理论分析之外的第3种研究手段。本文将理论分析与计算机数值模拟相结合,研究变面积型圆柱面电容式倾角传感器的输出特性,消除传感器极板的横向边缘效应对测量结果的影响,并指出提高该传感器灵敏度的途径。本文所讨论的变面积型圆柱面角位移电容式传感器具有结构简单、操作方便、可控性强等优点,且适当地选取上、下极板的圆心角和极板间距,具有较高的灵敏度和线性度。本文结论为传感器的设计与研究提供了一种新方法,在科研上具有一定的理论意义和实用价值。
| [1] |
Fan X C, Yu Z C, Peng K, et al. A Compact and High-Precision Capacitive Absolute Angular Displacement Sensor[J]. IEEE Sensors Journal, 2020, 20(19): 11 173-11 182 DOI:10.1109/JSEN.2020.2996257
(  0) 0) |
| [2] |
Yu Z C, Peng K, Liu X K, et al. A High-Precision Absolute Angular-Displacement Capacitive Sensor Using Three-Stagetime-Gratingin Conjunction with a Remodulation Scheme[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7 376-7 385 DOI:10.1109/TIE.2018.2881947
(  0) 0) |
| [3] |
Anil Kumar A S, Anandan N, George B, et al. Improved Capacitive Sensor for Combined Angular and Linear Displacement Sensing[J]. IEEE Sensors Journal, 2019, 19(22): 10 253-10 261 DOI:10.1109/JSEN.2019.2929538
(  0) 0) |
| [4] |
张文昭, 刘志壮, 王林惠, 等. 基于柱面差分电容的倾角传感器探头的研究[J]. 传感技术学报, 2022, 35(3): 325-327 (Zhang Wenzhao, Liu Zhizhuang, Wang Linhui, et al. Research of Tilt Sensor Probe Based on Differential Capacitance of Cylinder[J]. Chinese Journal of Sensors and Actuators, 2022, 35(3): 325-327)
(  0) 0) |
| [5] |
Görür A, Karpuz C. Analytic Formulas for Conductor-Backed Asymmetric CPW with One Lateral Ground Plane[J]. Microwave and Optical Technology Letters, 1999, 22(2): 123-126 DOI:10.1002/(SICI)1098-2760(19990720)22:2<123::AID-MOP13>3.0.CO;2-1
(  0) 0) |
| [6] |
王福谦, 殷勇, 刘伟歧. 基于保角映射的格林函数法及其应用[J]. 大学物理, 2018, 37(7): 15-18 (Wang Fuqian, Yin Yong, Liu Weiqi. The Green's Function Method Based on Conformal Mapping and Its Application[J]. College Physics, 2018, 37(7): 15-18)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

