2. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077;
3. 中国地震局第一监测中心,天津市耐火路7号,300180
通过圣杯(gravity recovery and interior laboratory, GRAIL)月球探测任务可以求解高精度的球谐系数月球重力场模型,为研究月球内部结构提供可靠的基础资料。在探索月球的地下结构时,通常需要消除近地表高频地形信号。由于地形起伏扰动是重力场的重要组成部分,其正演计算一直是重力学研究中的重要课题之一[1]。由于暂时缺乏具体的月球局部坐标系转换系统,为了获得月球深部重力异常,通常采用球坐标系法。Neumann等[2]通过与地形相关的球谐系数计算得出月球布格异常,其用于地形校正的有限功率地形法也可以称为Tesseroid的谱域正演法。Tesseroid单元体[3]是在传统直角坐标系的立方体元素上拓展的一种更适于表达大尺度计算的单元体。Wieczorek等[4]认为,扰动质量体产生的重力(引力)其精确表达式需要无限级数展开。但通过截断阶数,有限级数的求和也可以达到很高的精度,从而满足实际计算需求,如Tsoulis等[5]认为三次项的展开可以满足计算需求。Šprlák等[6]讨论球谐系数展开方法在月球重力场建模(包含地形影响)的适用性,就月球而言,谱域球谐系数法可以应用于平均半径球面10.2 km以上的空间。
本文首先通过月球重力场位系数和球谐合成技术获取GRAIL卫星高度的全球自由空气扰动重力梯度;然后在Wieczorek等[4]以及Neumann等[2]采用的基于标量重力地形校正的有限功率法的基础上,将其扩展到月球地形重力梯度的相关计算中;最后通过扣除地形影响后的全重力梯度异常进行结果分析及解释。
1 研究方法 1.1 月球自由空气扰动重力梯度获取全球重力场模型通常以球谐系数形式存储和发布。为了获得全球或局部扰动重力梯度值,通常可以通过球谐合成的方法进行恢复计算。扰动位的基本数学表达式为[7]:
| $ \begin{gathered} T(r, \theta, \lambda)=\frac{G M}{R} \sum\limits_{n=N_{\min }}^{N_{\max }} \sum\limits_{m=0}^n\left(\frac{R}{r}\right)^{n+1} \cdot \\ \left(\bar{C}_{n m} \cos (m \lambda)+\bar{S}_{n m} \sin (m \lambda)\right) \bar{P}_{n m}(\cos \theta) \end{gathered} $ | (1) |
式中,GM=4.902 8×1012 m3/s2为月球的地心引力常数,R=1 737×103 m为平均月球半径,r为地心半径,θ和λ分别为球面坐标下的余纬和经度,Cnm和Snm为通过减去月球正常重力场系数得到的完全归一化球谐系数,Pnm为(完全正则化)连带Legendre函数,Nmin和Nmax分别为球谐展开的最小和最大阶数。如果要把计算扩展到重力梯度(重力位二阶导数),通常需要使用以下的数学表达式[6, 8]:
| $ \begin{aligned} & T_{x x}=\frac{1}{r^2}\left(T_{\theta \theta}+r T_r\right) \\ & T_{x y}=T_{y x}=\frac{1}{r^2 \sin \theta}\left(T_{\lambda \theta}-\frac{\cos \theta}{\sin \theta} T_\lambda\right) \\ & T_{x z}=T_{z x}=\frac{1}{r}\left(\frac{1}{r} T_\theta-T_{r \theta}\right) \\ & T_{y y}=\frac{1}{r^2 \sin ^2 \theta}\left(T_{\lambda\lambda}+r \sin ^2 \theta T_r+\right. \\ &\left.\cos \theta \sin \theta T_\theta\right) \\ & T_{y z}=T_{z y}=\frac{1}{r \sin \theta}\left(T_{\lambda r}-\frac{1}{r} T_\lambda\right) \\ & T_{z z}=T_{r r} \end{aligned} $ | (2) |
式中,Tr、Tθ和Tλ分别为经度、纬度和地心方向上的重力位一阶导数,Tθθ、Trθ、Tλθ、Tλλ、Tλr和Trr分别为其相应的重力位二阶导数。
1.2 地形高程获取由于本文使用的原始地形模型数据也由球谐系数表示,因此同样需要采用类似的系数合成方法恢复计算得到月球数字地形模型(DTM)。从系数模型恢复地形数据的表达式为[9]:
| $ \begin{gathered} H(\theta, \lambda)=\sum\limits_{n=0}^{N_{\max }^{\mathrm{DTM}}} \sum\limits_{m=0}^n\left(\overline{\mathrm{HC}}_{n m} \cos (m \lambda)+\right. \\ \left.\overline{\mathrm{HS}}_{n m} \sin (m \lambda)\right) \bar{P}_{n m}(\cos \theta) \end{gathered} $ | (3) |
式中,NmaxDTM为DTM的最大阶数,HCnm和HSnm为地形模型的完全归一化球谐系数。
1.3 基于有限功率地形法的地形重力梯度改正本文使用的地形正演模型是球坐标系下由经纬度网格和地心半径组成的Tesseroid球形棱柱体。该单元体参考平面棱柱体模型,行星的表面形貌被分成类似的长度、宽度和高度单元。每个球形棱柱体的长度和宽度由2对角度组成:λ1、λ2(在经度方向)和φ1、φ2(在纬度方向),棱柱体的高度由到球体中心的距离r1、r2组成。
由于地形引起的重力效应也是重力场的组成部分,如果使用球谐系数展开来表示Tesseroid单元体产生的重力场,则球谐展开与式(1)和式(2)的表达形式是一致的,需要替换的是地形产生的球谐系数。通常认为三次项的级数展开可以满足计算精度[5]。在具体应用中,式(1)和式(2)中的相关系数可以用式(4)进行计算:
| $ C_{m m}^\beta=\left\{\begin{array}{l} \bar{C}_{n m} \\ \bar{S}_{n m} \end{array}\right\}=\frac{3}{2 n+1} \frac{1}{\bar{\rho}}\left(\frac{H_{n m}^1}{R}+\frac{(n+2) H_{n m}^2}{2 R^2}+\right. \\ \quad\quad\quad\quad\quad \left.\frac{(n+2)(n+1) H_{n m}^3}{6 R^3}\right) $ | (4) |
其中,
| $ \begin{gathered} H_{n m}^i=\frac{1}{4 \pi} \int_{\lambda_1=0}^{\lambda_2=2 \pi} \int_{\theta_1=0}^{\theta_2=\pi}\left(h_2^i-h_1^i\right) \cdot \\ \rho\left(r^{\prime}, \theta^{\prime}, \lambda^{\prime}\right) Y_{m m}^\beta\left(r^{\prime}, \theta^{\prime}, \lambda^{\prime}\right) \sin \theta^{\prime} \mathrm{d} \theta^{\prime} \mathrm{d} \lambda^{\prime} \end{gathered} $ | (5) |
| $ Y_{n m}^\beta(\theta, \lambda)=\bar{P}_{m m}(\cos \theta)\left\{\begin{array}{l} \cos m \lambda, \beta=0 \\ \sin m \lambda, \beta=1 \end{array}\right. $ | (6) |
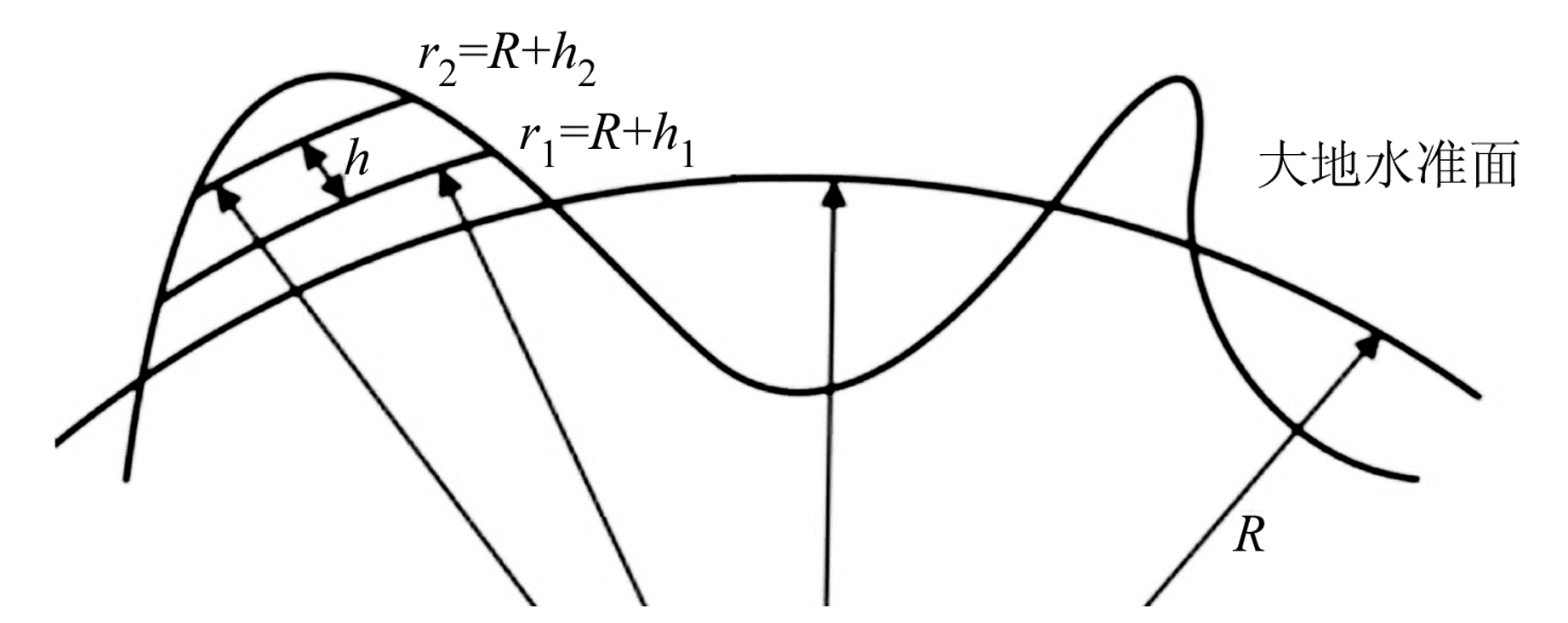
式中,θ=90°-φ,ρ=3 340 kg/m3为月球平均密度,h1和h2分别为地形起伏的上限和下限(图 1)。地形起伏的参考面通常取星球平均半径面或大地水准面,基准面以上为正值,以下为负值。因此,联合式(2)和式(4)可计算由地形引起的重力梯度效应。
|
图 1 地形起伏示意图 Fig. 1 Schematic view of topography |
采用Grazlgm420b模型计算自由空气扰动重力梯度[10],其模型位系数最高为420级,空间分辨率约为13 km,模型精度与GRAIL团队正式发布的产品精度相当。根据前文公式,在距离月球平均半径表面30 km的观测高度(卫星高度)上,以13 km分辨率恢复计算自由空气扰动重力梯度。同时,选择Moontopo720模型计算地形起伏引起的重力梯度效应[11]。该模型采用Runge-Krarup定理和向下迭代延拓方法,从而避免了发散效应,保留了月球表面高频信息。本文计算过程所涉及的原始数据均可在德国地学研究中心(GFZ)下载。
由于月球缺乏特定的大地水准面,本文使用Liang等[12]的卫星地形校正解决方案,使用半径为1 737 km的球面作为地形校正基准面[12],地形密度设定为2 550 kg/m3[13]。同时,扣除高于基准面的地形影响,并填充基准面下方的地形亏损。因此,校正后的最终异常反映的是相对于基准面的变化分布。为了保持重力信号频段的一致性,地形和重力场的球谐展开均在420阶。
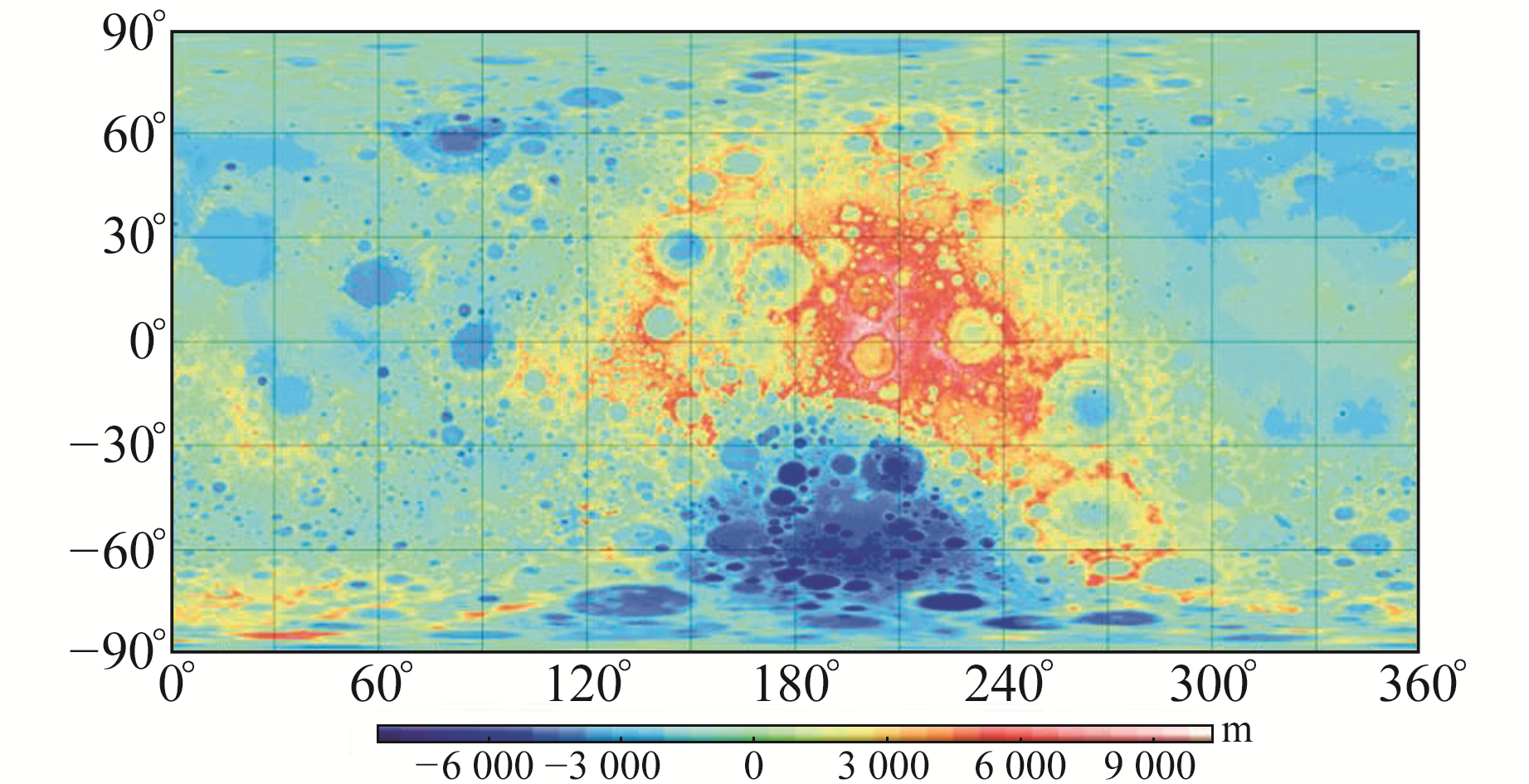
如表 1(单位E,1 E=10-9/s2)所示,月球自由空气扰动重力梯度(平均半径表面以上30 km高度)分布的数值变化的绝对值在100 E范围以内,以垂直重力梯度为例,其范围为-68.2~81.9 E,其他分量的分布范围都小于垂直分量。图 2和图 3表示的是月球自由空气扰动重力梯度和地形起伏的图形分布。图 2(f)垂直重力梯度揭示了局部正负异常交替的环形或圆形异常,这些异常分布和图 3中的月球地形起伏存在较强的图形相关性。重力和地形的图形相关性验证了Zuber等[13]的研究结果:98.5%的月球重力信号可归因于地形模型80°(68 km)和320° (17 km)之间的地形贡献。表 2(单位E)和图 4展示的是从自由空气重力梯度数据中减去地表地形影响后的异常分布。表 2所示的垂直重力梯度范围为-26.9~65.4 E,且与原始张量图相比,校正后的数据明显更平滑,但出现了一些显著的圆形或条形异常。其中圆形异常分布可能与质量瘤、火山或撞击坑有关[14],条形异常可能与断裂有关[15-16]。
|
|
表 1 原始扰动重力梯度 Tab. 1 Original disturbing gravity gradient |

|
图 2 原始扰动重力梯度 Fig. 2 Original disturbing gravity gradient |
|
图 3 月球地形起伏 Fig. 3 Lunar topographic relief |
|
|
表 2 地形校正后重力梯度异常 Tab. 2 Gravity gradient anomaly after terrain correction |

|
图 4 地形校正后重力梯度异常 Fig. 4 Gravity gradient anomaly after terrain correction |
根据重力梯度(重力位二阶导)的定义,它可以确定异常体的三维空间边界。通常,标量重力异常或其垂直梯度反映了异常体的中心位置;由于在物体的边缘处,水平梯度会发生明显的正负异常变化,从而通过水平分量可以估计异常体的平面空间分布[17]。基于这一原理,利用水平梯度的图形分布估算已确定的主要质量瘤的水平空间分布边界,具体结果如表 3所示。以盆地半径约为740 km的澄海质量瘤(Serentitas mascon)为例,依据图 4(a)和4(d)直接从图形进行解释,其南北(NS) 和东西(EW)边界约为18°。根据月球的空间参数进行距离换算,其在经度和纬度方向的平面最大空间分布约为540 km,与Zhao等[18]的三维空间反演结果接近。
|
|
表 3 质量瘤地下分布范围 Tab. 3 Underground range distribution of main mascons |
除了上述明显的圆形异常分布,在各个异常图上也呈现了标量重力中难以发现的大规模线性异常。在地球上,这些异常带图形通常被解释为与断层构造有关[19]。虽然目前普遍认为月球的地质构造活动已基本停止,但在其演化或撞击过程中会形成一些裂缝,故月球的垂直重力梯度异常带也被解释为与断裂构造有关[15-16]。在重力梯度的现有解释中,垂直梯度分量Tzz以比标量重力更为显著的方式反映梯度带断裂走向;由于地下构造复杂,其他分量也可以反映断裂走向,梯度分量Txx、Tyy等也可以通过正负极值间的梯度带反映断裂走向[5]。综合月球全张量异常图可以发现:1) 不同梯度分量对月球深部断裂的识别能力不同,其中,Tzz对断裂识别能力较强;Txx对东西(EW)方向断裂识别能力较强;Tyy和Tyz对南北(NS)方向断裂识别能力较强;除在南北极地区出现条状异常梯度带,Txy和Tzx呈现条状异常较少。例如,在150°~200° E和60°~70° S附近,有一条长达50°的细长异常断裂分布,这在Txx和Tzz分量的图形中均有所体现,但是其他分量中体现较弱或没有体现;在风暴洋周围270°~300° E和0°~60° S附近出现的竖向断裂在Tzz、Tyy和Tyz分量图形里都有明显体现。2) 南北极地区呈现水平横向分布的异常梯度带较多,赤道附近呈现竖向分布的异常梯度带较多。Melosh[20]推断在月球演化过程中,潮汐重力可能是其形成的动力源之一,并导致了月球深部的断层。在他的理论中,月球将形成3个主要构造带:极地正断层带,大致呈东西(EW)走向;赤道地区逆冲断层带,大致呈南北(NS)走向;中纬度滑动断裂带,大致呈NE60°或NW60°走向。根据全张量梯度图分析可知,其赤道和极地附近的断层走向与本文解算的图像分布基本一致。3)多梯度分量图形可以发现潜在断层,如320°~360° E和75° S附近有一条水平异常梯度带,这在Txx和Txz分量图形里有明显体现,但是在Tzz分量结果中体现较弱。在陆天启等[16]通过垂直梯度异常识别的结果中没有将其列为断裂带,但根据水平梯度异常带和断裂走向的图形相关性,此处可能是暂时未被发现的深部断裂。
3 结语本文将球谐谱域地形校正方法应用到月球的梯度异常计算中,首先使用满足精度要求的球谐阶次展开式,并在允许的高度范围内进行地形校正;其次通过直接从原始自由空气扰动重力梯度中减去地形影响来提供全张量异常结果,并与已知文献结果进行对比验证;最后通过月球全张量重力梯度异常进行相关结果分析和初步解释。通过这些异常结果,本文估算了月球主要质量瘤(mascon)异常的边界分布,同时,综合全张量重力梯度异常图,通过异常梯度带和断裂带的图形相关性初步验证潮汐重力引起的月球主要断层结构。但由于月球的地下构造复杂,如何更加准确地从重力梯度的角度进行解译研究仍需要开展更多的后续工作。
| [1] |
Hirt C, Yang M, Kuhn M, et al. SRTM2 Gravity: An Ultrahigh Resolution Global Model of Gravimetric Terrain Corrections[J]. Geophysical Research Letters, 2019, 46(9): 4 618-4 627 DOI:10.1029/2019GL082521
(  0) 0) |
| [2] |
Neumann G A, Zuber M T, Smith D E, et al. The Lunar Crust: Global Structure and Signature of Major Basins[J]. Journal of Geophysical Research: Planets, 1996, 101(E7): 16 841-16 863 DOI:10.1029/96JE01246
(  0) 0) |
| [3] |
Heck B, Seitz K. A Comparison of the Tesseroid, Prism and Point-Mass Approaches for Mass Reductions in Gravity Field Modelling[J]. Journal of Geodesy, 2007, 81(2): 121-136 DOI:10.1007/s00190-006-0094-0
(  0) 0) |
| [4] |
Wieczorek M A, Phillips R J. Potential Anomalies on A Sphere: Applications to the Thickness of the Lunar Crust[J]. Journal of Geophysical Research: Planets, 1998, 103(E1): 1 715-1 724 DOI:10.1029/97JE03136
(  0) 0) |
| [5] |
Tsoulis D, Stary B. An Isostatically Compensated Gravity Model Using Spherical Layer Distributions[J]. Journal of Geodesy, 2004, 78(7-8): 418-424 DOI:10.1007/s00190-004-0404-3
(  0) 0) |
| [6] |
Šprlák M, Han S C. On the Use of Spherical Harmonic Series Inside the Minimum Brillouin Sphere: Theoretical Review and Evaluation by GRAIL and LOLA Satellite Data[J]. Earth-Science Reviews, 2021, 222
(  0) 0) |
| [7] |
Heiskanen W A, Moritz H. Physical Geodesy[M]. Beijing: Surveing and Mapping Press, 1979
(  0) 0) |
| [8] |
Zhu L Z, Jekeli C. Gravity Gradient Modeling Using Gravity and DEM[J]. Journal of Geodesy, 2009, 83(6): 557-567 DOI:10.1007/s00190-008-0273-2
(  0) 0) |
| [9] |
Pavlis N K, Holmes S A, Kenyon S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B4)
(  0) 0) |
| [10] |
Wirnsberger H, Krauss S, Mayer-Gürr T. First Independent Graz Lunar Gravity Model Derived from GRAIL[J]. Icarus, 2019, 317: 324-336 DOI:10.1016/j.icarus.2018.08.011
(  0) 0) |
| [11] |
Bucha B, Hirt C, Kuhn M. Divergence-Free Spherical Harmonic Gravity Field Modeling Based on the Runge-Krarup Theorem: A Case Study for the Moon[J]. Journal of Geodesy, 2019, 93(4): 489-513 DOI:10.1007/s00190-018-1177-4
(  0) 0) |
| [12] |
Liang Q, Chen C, Li Y G. 3-D Inversion of Gravity Data in Spherical Coordinates with Application to the GRAIL Data[J]. Journal of Geophysical Research: Planets, 2014, 119(6): 1 359-1 373 DOI:10.1002/2014JE004626
(  0) 0) |
| [13] |
Zuber M T, Smith D E, Watkins M M, et al. Gravity Field of the Moon from the Gravity Recovery and Interior Laboratory(GRAIL) Mission[J]. Science, 2013, 339(6 120): 668-671
(  0) 0) |
| [14] |
Neumann G A, Zuber M T, Wieczorek M A, et al. Lunar Impact Basins Revealed by Gravity Recovery and Interior Laboratory Measurements[J]. Science Advances, 2015, 1(9)
(  0) 0) |
| [15] |
Andrews-Hanna J C, Asmar S W, Head J W, et al. Ancient Igneous Intrusions and Early Expansion of the Moon Revealed by GRAIL Gravity Gradiometry[J]. Science, 2013, 339(6 120): 675-678
(  0) 0) |
| [16] |
陆天启, 陈圣波, 朱凯. 基于GRAIL重力数据的月球深部断裂识别和空间分布研究[J]. 地球物理学报, 2019, 62(8): 2 835-2 844 (Lu Tianqi, Chen Shengbo, Zhu Kai. Global Identification and Spatial Distribution of Lunar Subsurface Faults from GRAIL Gravity Data[J]. Chinese Journal of Geophysics, 2019, 62(8): 2 835-2 844)
(  0) 0) |
| [17] |
Saad A H. Understanding Gravity Gradients-A Tutorial[J]. The Leading Edge, 2006, 25(8): 942-949 DOI:10.1190/1.2335167
(  0) 0) |
| [18] |
Zhao G D, Chen B, Uieda L, et al. Efficient 3-D Large-Scale forward Modeling and Inversion of Gravitational Fields in Spherical Coordinates with Application to Lunar Mascons[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(4): 4 157-4 173 DOI:10.1029/2019JB017691
(  0) 0) |
| [19] |
马宗晋, 高祥林, 宋正范. 中国布格重力异常水平梯度图的判读和构造解释[J]. 地球物理学报, 2006, 49(1): 106-114 (Ma Zongjin, Gao Xianglin, Song Zhengfan. Analysis and Tectonic Interpretation to the Horizontal-Gradient Map Calculated from Bouguer Gravity Data in the China Mainland[J]. Chinese Journal of Geophysics, 2006, 49(1): 106-114)
(  0) 0) |
| [20] |
Melosh H J. Global Tectonics of a Despun Planet[J]. Icarus, 1977, 31(2): 221-243 DOI:10.1016/0019-1035(77)90035-5
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China;
3. The First Monitoring and Application Center, CEA, 7 Naihuo Road, Tianjin 300180, China
 2023, Vol. 43
2023, Vol. 43


