2. 西南交通大学土木工程学院,成都市二环路北一段111号,610031;
3. 河北省地震灾害防御与风险评价重点实验室,河北省三河市学院街465号,065201
根据活动时间的差异可以将活动断层分为间接性突然滑动的突发性断层和相对位移速率极其缓慢的蠕动性断层[1]。2种断层的活动都会对断层破碎带及周围岩体的地应力造成扰动[2-3]。正确认识断层活动造成的地应力分布变化规律,可为与之并行或穿越其中的道路、桥梁、隧道等工程的建设提供理论设计依据。
本文主要对蠕动性断层进行研究。断层蠕滑具有规模巨大以及断层结构、蠕滑速度和断层地质条件复杂的特点,且在蠕滑过程中岩体内会孕育大量裂缝节理[4],故采用非连续变形分析(DDA)方法对断层蠕滑的过程进行模拟,原因如下:
1) DDA方法是动态的,其在计算过程中引入了时间因素,可以直观地观察断层蠕滑过程中块体应力的变化;
2) 相比于有限元法中单元不能脱离、错动,DDA方法中的块体不仅允许自身可以发生变形和位移,而且允许块体之间存在错动、滑动、张开等运动方式,这对模拟断层蠕滑过程中产生裂缝导致岩体应力变化更具优势;
3) DDA方法中每个块体都是由线段切割而成,块体可以是任意形状,与具有非连续特征的岩体更加吻合。
最后,本文以嘉黎活动断裂带为例模拟断层蠕滑过程,探究断层蠕滑过程中地应力的变化规律。
1 DDA方法概述在笛卡尔坐标系中,给块体i定义一个给定点(x0, y0),其状态可由以下位移变量矩阵导出:
| $ \boldsymbol{D}_i=\left[\begin{array}{llllll} \boldsymbol{u}_0 & \boldsymbol{v}_0 & r_0 & \boldsymbol{\varepsilon}_x & \boldsymbol{\varepsilon}_y & \gamma_{x y} \end{array}\right] $ | (1) |
式中,u0和v0分别为x向和y向位移,εx和εy分别为x向和y向应变,r0和γxy分别为转角和剪切应变。计算得到当前时间步长的位移矢量[u, v]T:
| $ \left[\begin{array}{l} \boldsymbol{u} \\ \boldsymbol{v} \end{array}\right]=\boldsymbol{T}_i \boldsymbol{D}_i $ | (2) |
式中,Ti为位移变换矩阵。设点(x0, y0)为块体中心,则位移变换矩阵定义为:
| $ \boldsymbol{T}_i=\left[\begin{array}{cccc} 1 & 0 & -\left(y-y_0\right) & \left(x-x_0\right) \\ 0 & 1 & \left(x-x_0\right) & 0 \end{array}\right. \\ \quad\quad \left.\begin{array}{cc} 0 & \left(y-y_0\right) / 2 \\ -\left(y-y_0\right) & \left(x-x_0\right) / 2 \end{array}\right] $ | (3) |
对于包含n个块体的系统,控制平衡方程可以用矩阵形式表示为:
| $ \left[\begin{array}{ccccc} \boldsymbol{K}_{11} & \boldsymbol{K}_{12} & \boldsymbol{K}_{13} & \cdots & \boldsymbol{K}_{1 n} \\ \boldsymbol{K}_{21} & \boldsymbol{K}_{22} & \boldsymbol{K}_{23} & \cdots & \boldsymbol{K}_{2 n} \\ \boldsymbol{K}_{31} & \boldsymbol{K}_{32} & \boldsymbol{K}_{33} & \cdots & \boldsymbol{K}_{3 n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \boldsymbol{K}_{n 1} & \boldsymbol{K}_{n 2} & \boldsymbol{K}_{n 3} & \cdots & \boldsymbol{K}_{m n} \end{array}\right]\left[\begin{array}{c} \boldsymbol{D}_1 \\ \boldsymbol{D}_2 \\ \boldsymbol{D}_3 \\ \vdots \\ \boldsymbol{D}_n \end{array}\right]=\left[\begin{array}{c} \boldsymbol{F}_1 \\ \boldsymbol{F}_2 \\ \boldsymbol{F}_3 \\ \vdots \\ \boldsymbol{F}_n \end{array}\right] $ | (4) |
式中,Kij(i, j=1,2,…,n)表示对与速度、惯量、接触等相关的势能求导得到的刚度子矩阵,Fi为块体i上的广义加载向量。
2 模型建立 2.1 研究背景嘉黎断裂是喀喇昆仑-嘉黎剪切带最东端的一条断裂。针对嘉黎断裂带的活动方式及活动速率,目前仍存在较多争议。Armijo等[5]认为,断裂晚第四纪以来的右旋走滑速率为10~20 mm/a。任金卫等[6]认为,嘉黎断裂晚第四纪早期平均滑动速率约4 mm/a。宋健等[7]认为,嘉黎断裂带西北段为右旋挤压,走滑速率3.2~5.8 mm/a;中段为弱右旋挤压,走滑速率1.3~2.0 mm/a;东南段为左旋挤压,走滑速率3.7~4.0 mm/a。
作为横亘在我国西部开发要道上的活动断裂,嘉黎断裂带蠕滑造成的地应力变化会对工程建设产生一定的影响。因此,本文建立嘉黎活动断裂带断层蠕滑的DDA模型,探究断层蠕滑作用下地应力的变化规律。
2.2 模型假设本文主要研究断层蠕滑作用下断层破碎带及其周边区域地应力分布的变化规律,因此进行以下简化及假设:1)将断层破碎带的不规则形状简化成矩形;2)忽略不同深度下岩体之间相互贯穿的影响,将其简化成二维平面模型;3)将断层蠕滑速度体现在位移量上,忽略模型计算中惯性力被放大的影响。
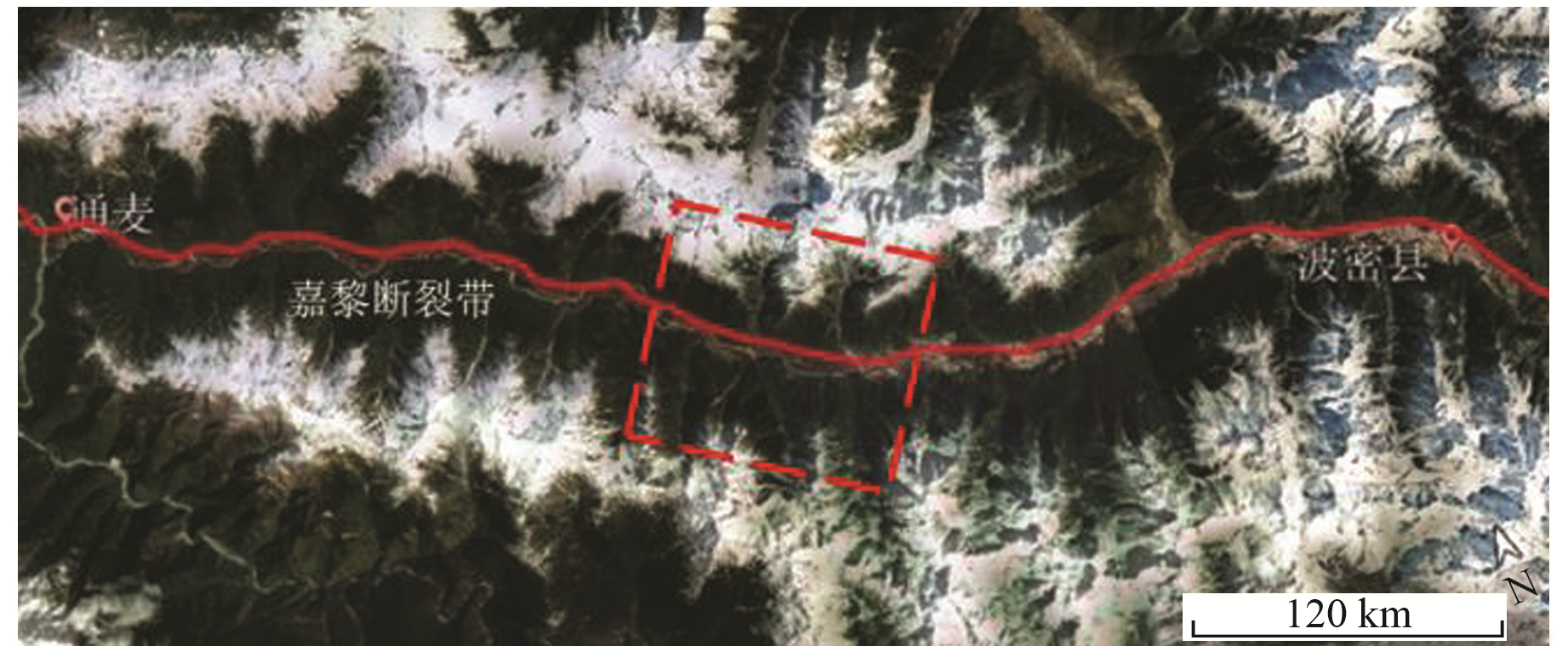
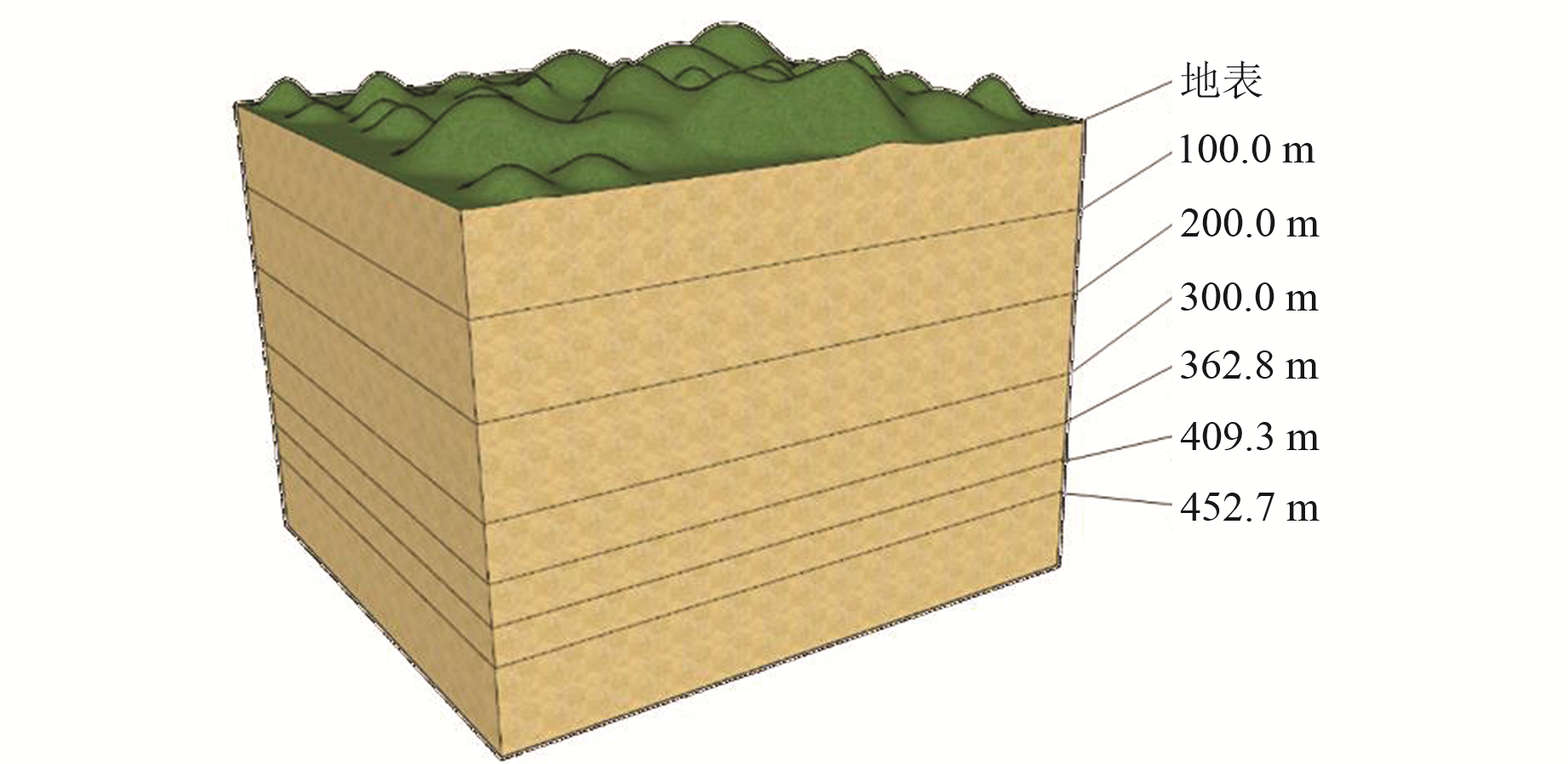
2.3 模型建立与参数选择本文截取嘉黎断裂带部分区域(图 1),选取多个深度的地质界面建立二维平面模型(图 2)。考虑到模型的尺寸有限,建立以断层为中心的矩形模型(图 3)。本文所建模型断层宽度取0.4 km,断层两侧岩体的宽度均取6.5 km,长度取15.0 km。
|
图 1 嘉黎断裂带位置 Fig. 1 Location of Jiali fault |
|
图 2 模型分层示意图 Fig. 2 Schematic diagram of model layering |

|
图 3 DDA模型 Fig. 3 DDA model |
活动断裂带内部岩体破碎程度为极破碎,故断层破碎带部分采用Voronoi分割,块体个数为630个。断裂带两侧为完整岩体,按照距离断层的远近布置相应密度的虚拟节理,得到单侧岩体块体数量为350个,块体总数量为1 330个。模型尺寸及块体划分见图 3。
由嘉黎活动断裂带区域实测地质报告可得模型的物理、节理及控制参数,具体见表 1~3。
|
|
表 1 模型物理参数 Tab. 1 Model material parameters |
|
|
表 2 模型节理参数 Tab. 2 Model joint parameters |
|
|
表 3 模型控制参数 Tab. 3 Model control parameters |
由于建模时所选取的研究对象与周围地质体之间存在相互作用,为确保模拟结果的准确性,需要通过施加边界条件以体现这种相互作用。施加边界条件的步骤为:
1) 已有地质报告显示,在深度为362.8 m、409.3 m、452.7 m处的最大水平主应力呈现为线性增长的趋势。因此,根据已有的深度及最大水平主应力,按线性插值的方式推导出深度为100.0 m、200.0 m、300.0 m处的最大水平主应力,结果见表 4。
|
|
表 4 最大水平主应力 Tab. 4 Maximum horizontal principal stress |
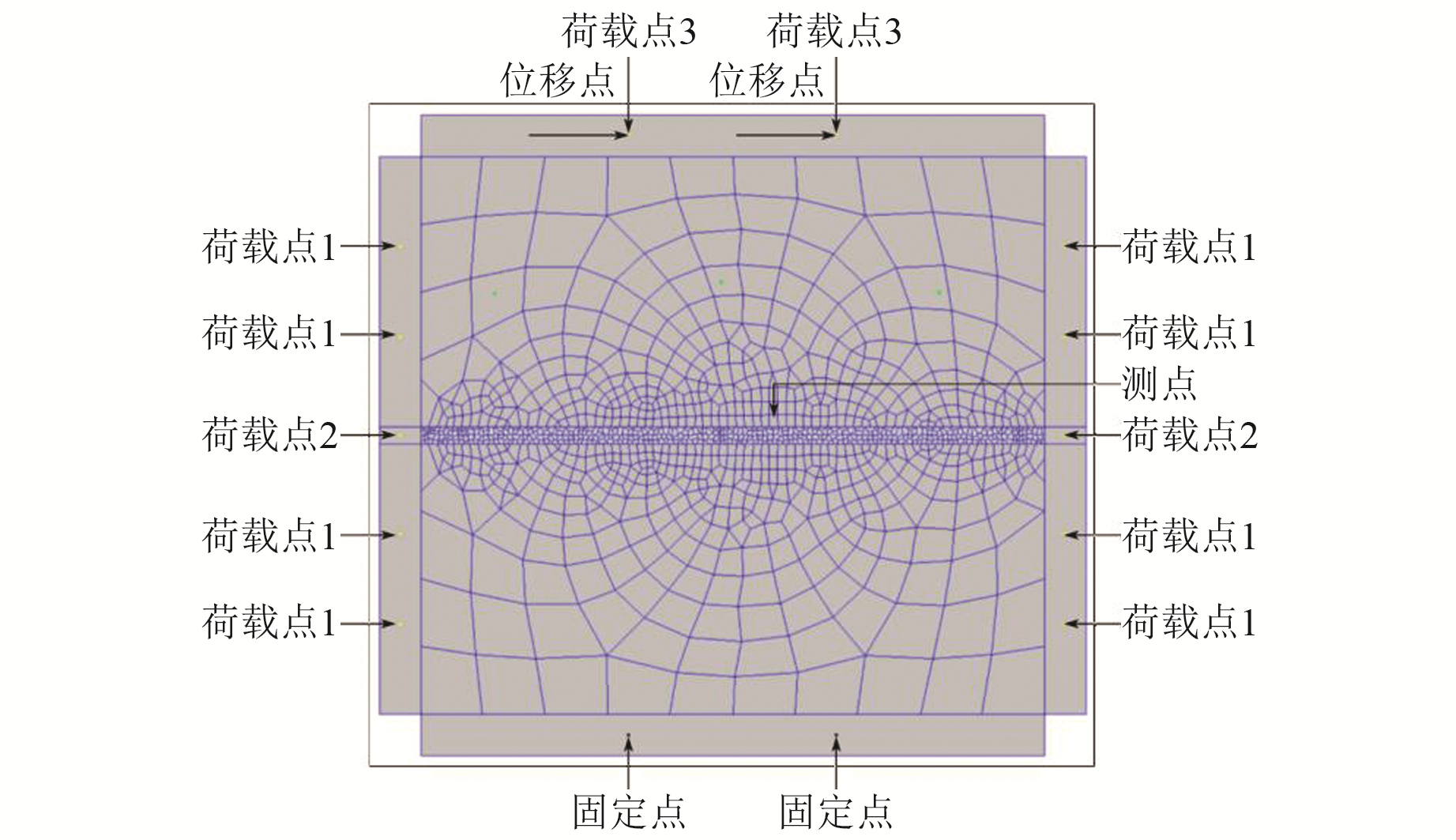
2) 为模拟真实条件下的挤压效果,在模型四周设置加载块。通过在加载块上施加固定的力形成挤压应力。荷载点1及荷载点3布置在加载块三分点处,荷载点2布置在加载块中点处,其方向见图 4。荷载点上施加的荷载大小为:
|
图 4 计算模型 Fig. 4 Computational model |
| $ F=\frac{\sigma \times L}{n} $ | (5) |
式中,F为荷载点上的荷载量值,σ为最大水平主应力,L为加载块与岩体接触的长度,n为加载块上荷载点数量。
3) 上、下加载块都布置2个强制位移点。下部位移点布置在加载块三分点处,x向和y向位移均为0,为固定点。上部位移点与荷载点3重合,仅施加x向的位移,y向位移为0,达到单向位移的效果(图 4)。
4) 为模拟活动断裂带蠕滑,达到断裂带两侧岩体错动的效果,上部加载块将带动所接触的块体一起沿x向移动。因此,将上部加载块的粘聚力设为无限大,带动所接触的块体一起移动。
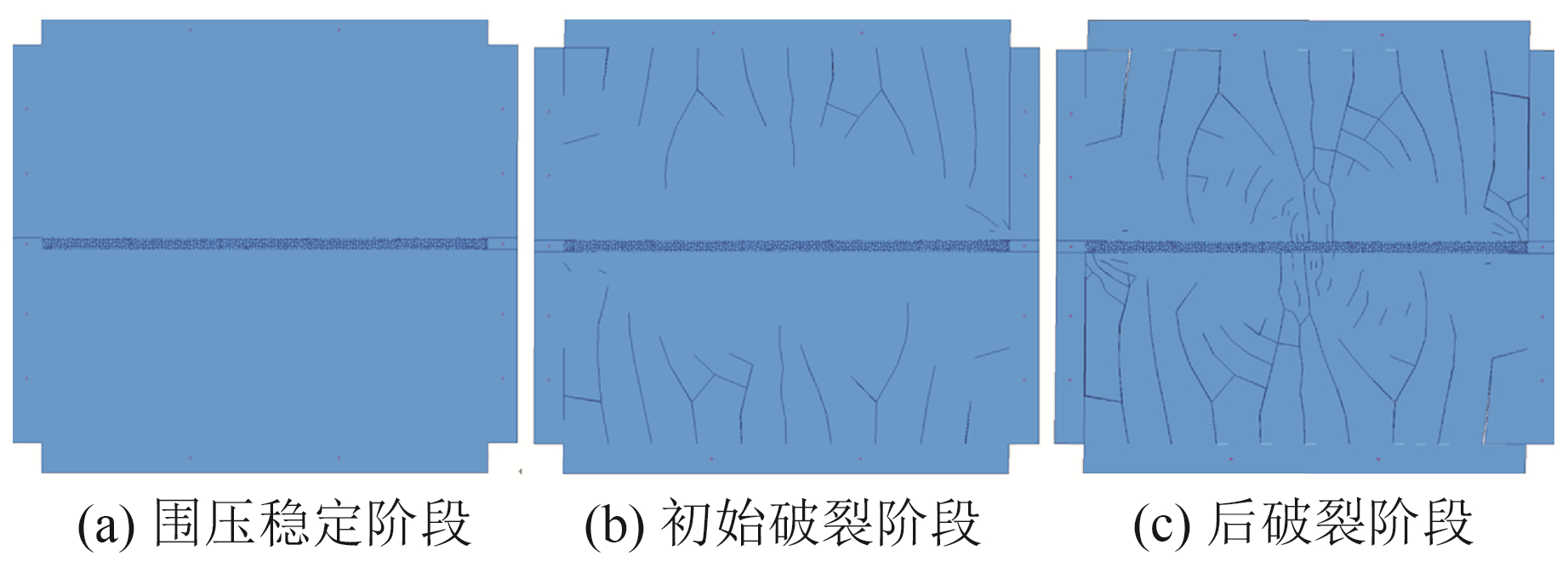
3 结果 3.1 模型裂隙分布情况模型在围压稳定阶段和破裂阶段,断层破碎带及两侧岩体的裂隙发育情况见图 5。由图可知,在围压稳定阶段,断层破碎带内发育大量裂隙。这是由于破碎带节理的粘聚力和抗拉强度被设置为0.0 mPa,在围压的作用下块体之间满足摩尔-库仑定律的滑动条件以及最大拉应力准则,块体之间就会有裂隙产生,符合模型设置要求。断层两侧岩体节理的粘聚力为20.0 mPa,抗拉强度为4.07 mPa,其裂隙发育程度远小于断层破碎带。随着位移加载块的移动,裂隙从围岩与位移加载块接触的部位开始发育,并逐渐向断层方向延伸。围岩中部和顺着位移方向的边界较早出现贯通裂隙,在贯通裂隙周围也发育着较其他地方更为密集的裂隙。
|
图 5 模型裂隙分布 Fig. 5 Model fracture distribution chart |
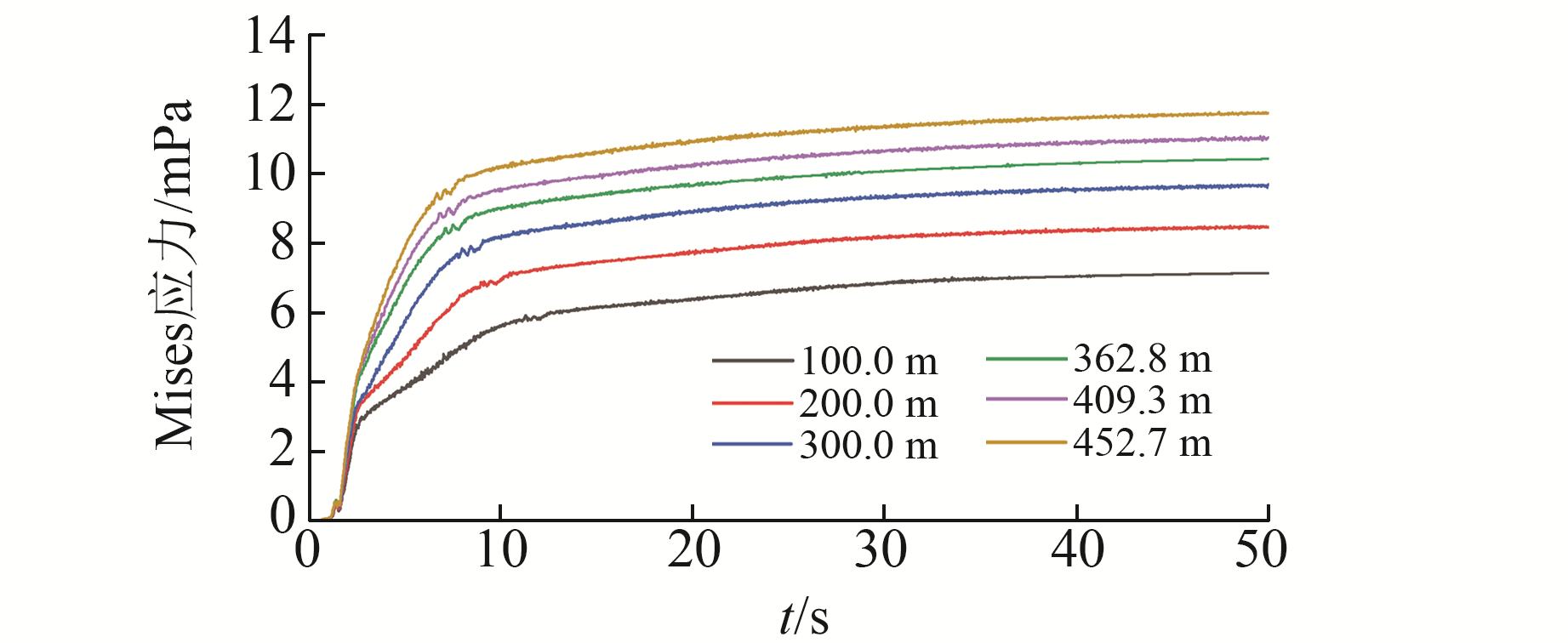
根据模型计算结果,绘制出不同深度下测点应力随时间的变化趋势图(图 6)。
|
图 6 不同深度下测点时间-应力变化 Fig. 6 Time-stress change of measuring point at different depths |
从图 6可知,当位移加载块未开始运动时,在围压的作用下,测点中的应力都会从某一时刻开始趋于平稳地增长。在深度为100.0 m处,测点应力从约12.5 s时开始平稳增长,在12.5~50 s,测点应力从约6.0 mPa增长至7.1 mPa;在深度为300.0 m处,测点应力从约9.2 s时开始平稳增长,在9.2~50 s,测点应力从约8.0 mPa增长至9.6 mPa;在深度为452.7 m处,测点应力从约8.3 s时开始平稳增长,在8.3~50 s,测点应力从约9.9 mPa增长至11.7 mPa。从图 6还可以看出,测点应力量值在位移加载块运动之前随深度的增加而变大,符合地质勘测结果和模型设置要求。
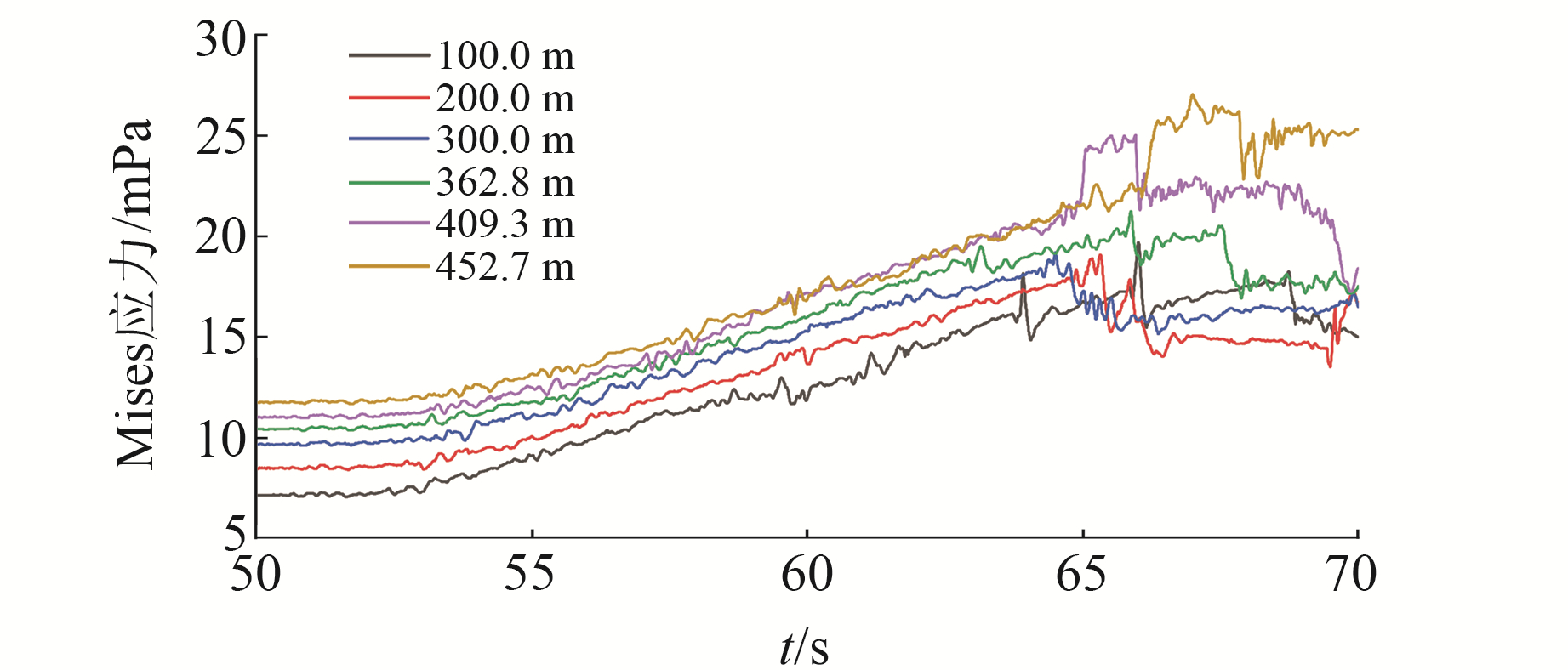
3.3 运动阶段 3.3.1 时间-深度-应力变化位移加载块开始向右运动之后,提取测点随时间变化的应力量值,绘制出不同深度下测点应力随时间变化趋势图(图 7)。
|
图 7 不同深度下测点时间-应力变化 Fig. 7 Time-stress change of measuring point at different depths |
当位移加载块匀速向右运动时,在其带动下,测点中的应力开始快速增长。测点应力变化在此期间可再分为2个阶段:有明显规律性的线性增长阶段和不规则变化阶段。
由图 7可知,在应力变化规律明显的线性增长阶段,深度为100.0 m处,测点应力从约7.1 mPa增长至18.0 mPa;在深度为300.0 m处,测点应力从约9.7 mPa增长至18.5 mPa;在深度为452.7 m处,测点应力从约11.7 mPa增长至22.8 mPa。
在应力变化不规则阶段,测点应力有较大波动,存在突降或猛增的现象,且在不同深度下测点内的应力变化也不相同。这与使用DDA方法的数值模拟有较大关系,因为DDA方法允许块体之间产生裂隙,因此块体内会存在应力集中或应力释放的现象。
由此可以推断,在外力作用下,块体中的应力会快速地线性增长。当应力增长到一定的量值后,块体之间裂隙产生会使块体内的应力出现较大波动,导致岩体中的应力不连续。
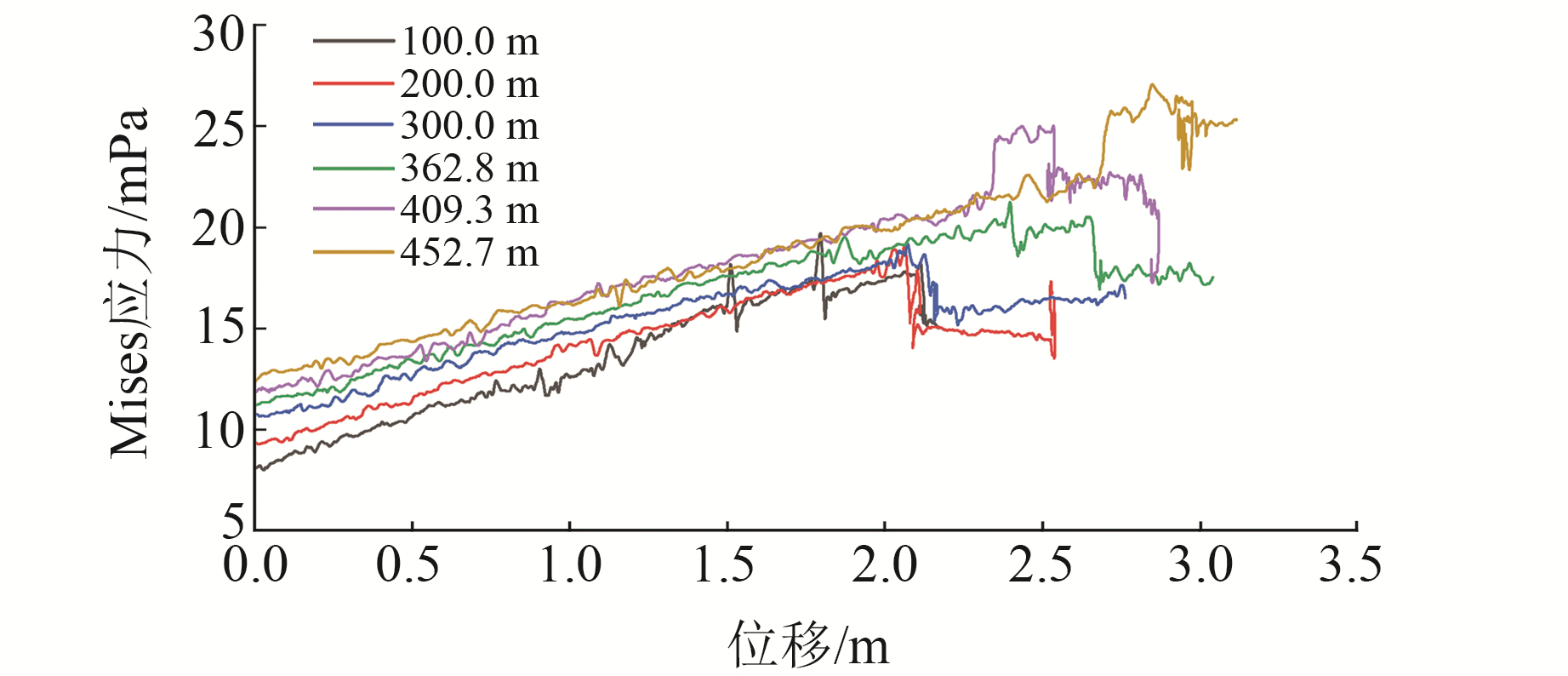
3.3.2 深度-位移-应力变化分析根据模型计算结果,绘制出不同深度下测点应力随位移变化趋势图(图 8)。
|
图 8 不同深度下测点位移-应力变化 Fig. 8 Displacement-stress change of measuring point at different depths |
在位移加载块的带动下,测点发生横向位移,测点内的应力也随之发生变化,并在一定位移量内应力与位移呈线性变化趋势。由图 8可见,100.0 m深度时,位移量在2.1 m之前,应力从约7.1 mPa线性增长至18.0 mPa;300.0 m深度时,位移量在2.1 m之前,应力从约9.6 mPa线性增长至18.5 mPa;409.3 m深度时,位移量在2.3 m之前,应力从约11.8 mPa线性增长至21.8 mPa。在这段线性变化的范围内,应力随位移的变化在不同深度下呈现出近似的变化趋势。
当测点达到一定位移量时,由于块体之间的相互运动,测点与周围块体之间出现裂隙,测点应力发生突降。如图 8,在200.0 m深度、测点位移为2.1 m左右时,应力从18.7 mPa突降至14.8 mPa;在362.8 m深度、测点位移为2.6 m左右时,应力从20.4 mPa突降至17.4 mPa。块体之间裂隙产生造成的能量释放对块体内应力有着明显的扰动。
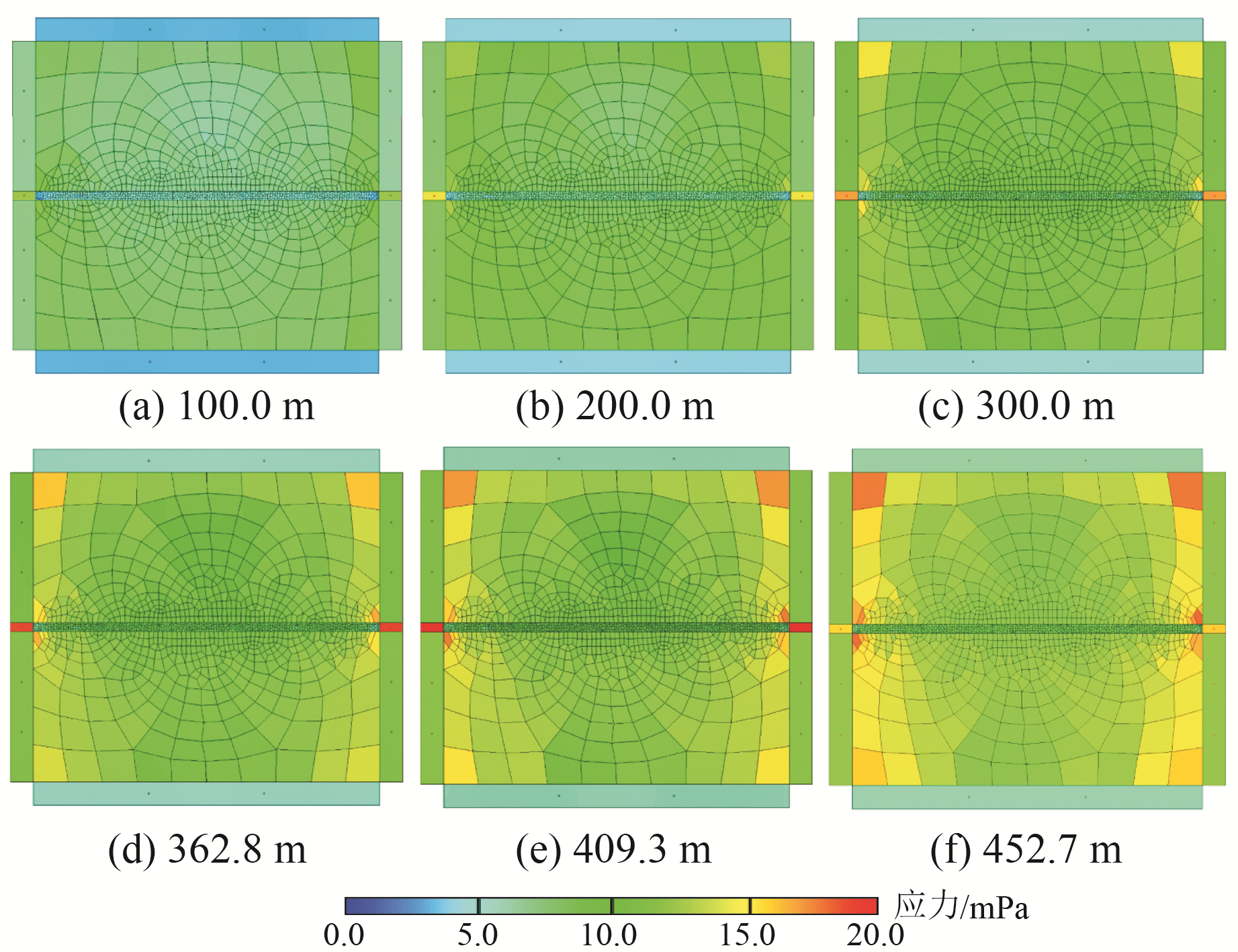
3.3.3 应力云图变化当位移加载块未发生横向位移时,应力云图见图 9。两侧岩体内应力大体相同,100.0 m深度时,应力约为7.1 mPa;300 m深度时,应力约为9.6 mPa;452.7 m深度时,应力约为11.7 mPa;随着深度的增加,岩体中的应力增大,与深度呈线性变化。断层两侧岩体四角都出现应力较大的块体,这是明显的应力集中现象,与选择矩形模型有关。断裂带区域应力与周边区域分布规律类似,但较周边围岩略低。这与陈兴强[8]给出的嘉黎断裂带实测的断层破碎带内应力值低于完整岩体的结果一致。
|
图 9 不同深度处位移0.0 m应力云图 Fig. 9 Stress cloud chart of displacement of 0.0 m at different depths |
当测点发生0.5 m横向位移时,应力云图见图 10。可以看出,整体应力分布呈现增加趋势,断层两侧岩体出现应力超过20.0 mPa的区域,明显高于无横向位移的情况。上侧岩体开始向右移动,而右侧有着向左的荷载加载块的阻挡,因此应力是顺着位移方向靠近边界的位置开始增长,并向内开始扩展,断层破碎带左侧出现应力接近0.0 mPa的区域也与此有关。由于断裂带的存在,上侧岩体应力变化区域明显高于下侧岩体,断裂带的存在对应力的传递起着阻碍作用[9]。由于块体间发育有较多的裂隙,导致断裂带及围岩内的应力并不连续,表现出较强的离散性。
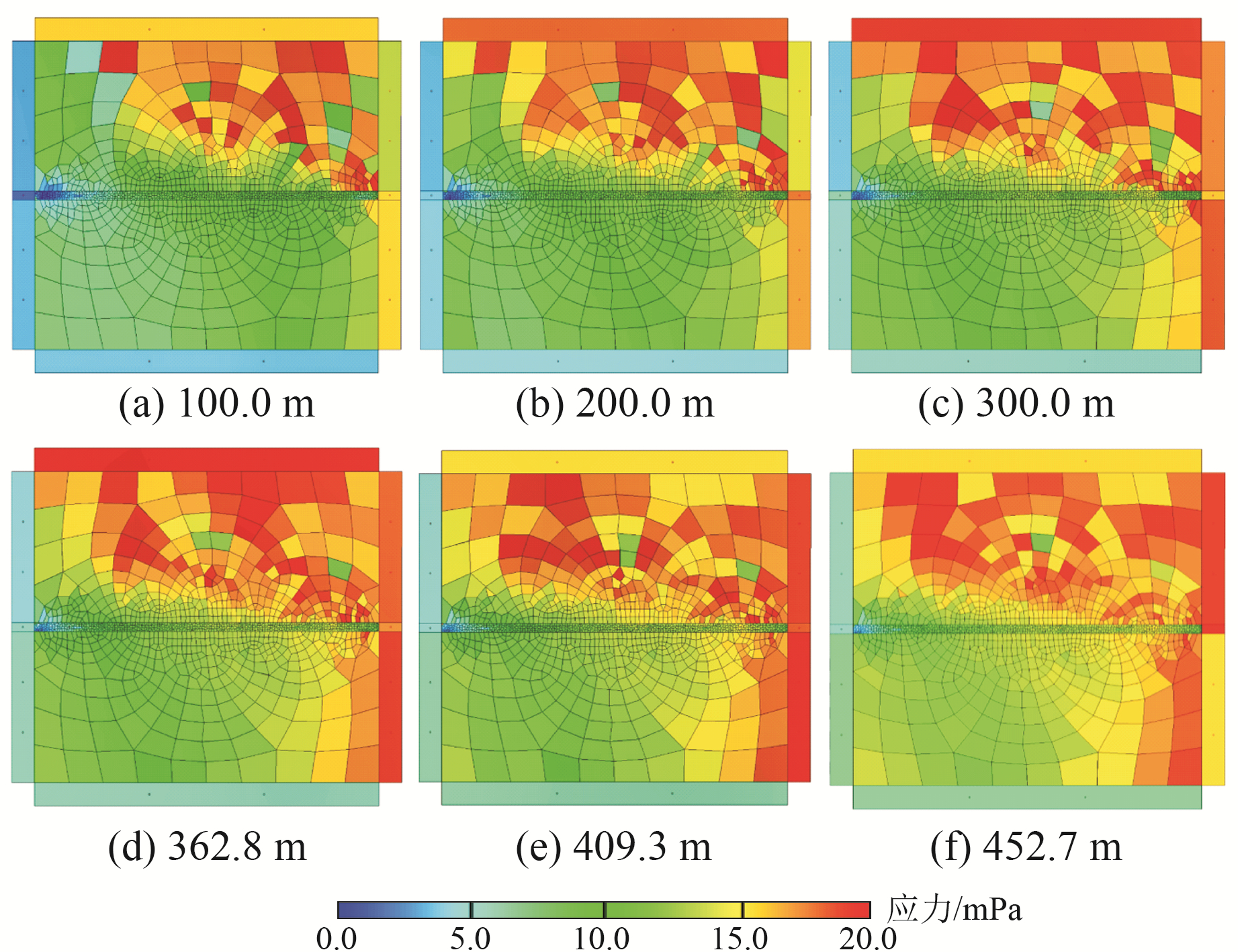
|
图 10 不同深度处位移0.5 m应力云图 Fig. 10 Stress cloud chart of displacement of 0.5 m at different depths |
当测点发生1.0 m横向位移时,应力云图见图 11。相比于发生0.5 m横向位移时,同一深度下断层两侧岩体整体应力发生变化的区域进一步向内扩张,由于块体间的相互错动,围岩中应力分布依然比较离散。断层破碎带内部分区域应力接近15 mPa,出现较为明显的应力集中区域,但整体上仍低于两侧岩体的应力,且破碎带中应力分布具有明显的离散性。

|
图 11 不同深度处位移1.0 m应力云图 Fig. 11 Stress cloud chart of displacement of 1.0 m at different depths |
当测点发生2.0 m横向位移时,应力云图见图 12。断层两侧岩体应力增长区域进一步向内扩张,且块体中应力超过20.0 mPa的区域也随着位移的增大而增加,在断层及其两侧岩体中出现明显的应力集中区域。在不同深度下,应力集中现象均出现在断层中的相同位置。
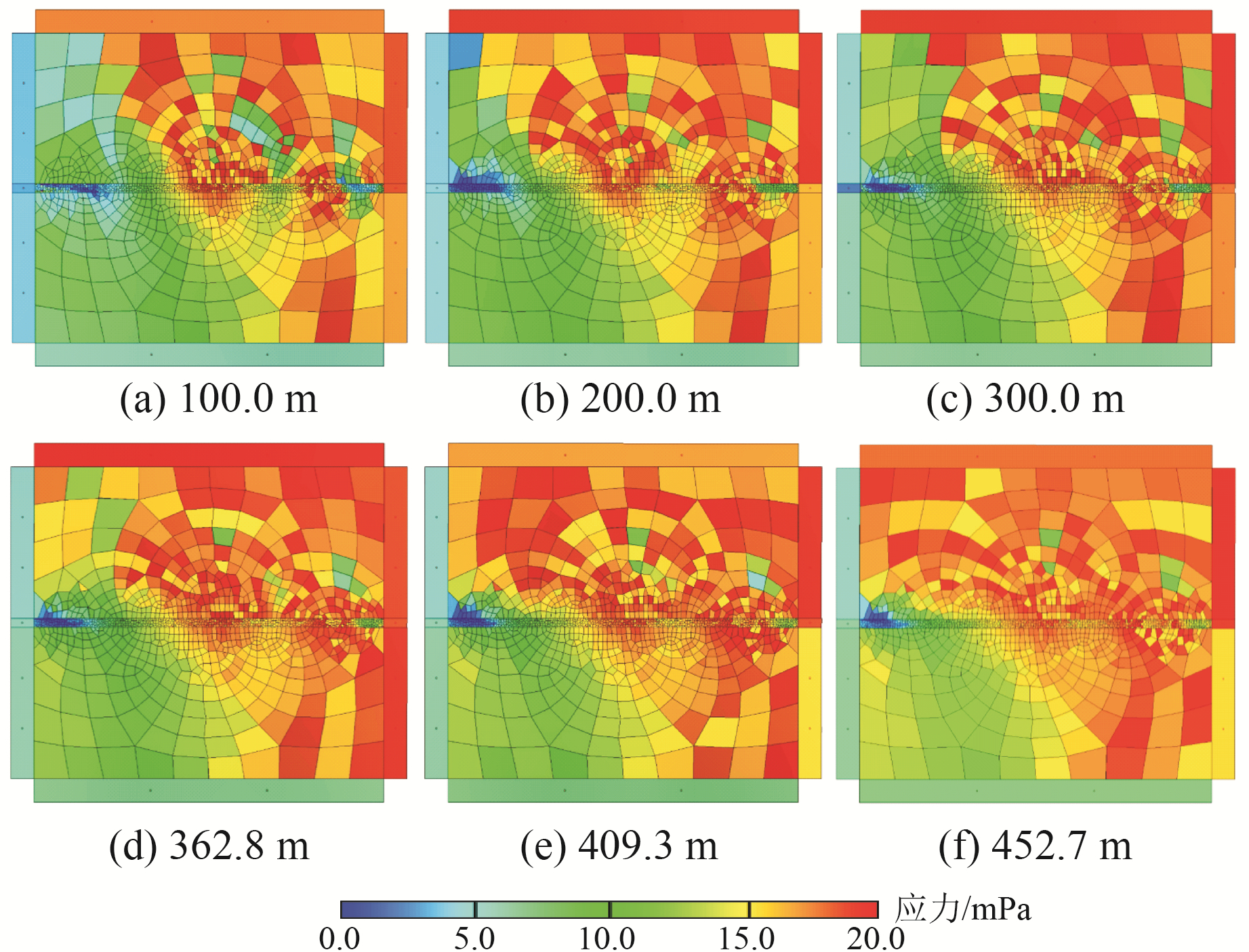
|
图 12 不同深度处位移2.0 m应力云图 Fig. 12 Stress cloud chart of displacement of 2.0 m at different depths |
上侧岩体在加载块的带动下发生横向位移,通过对深度和位移量2个变量的讨论,可以得到以下结论:1)横向位移量增加会使岩体应力发生明显增长;2)断层破碎带应力值普遍低于两侧岩体应力值,且应力分布具有明显的离散性;3)断层的存在会阻隔应力的传递,使下侧岩体应力分布变化速率明显小于上侧岩体;4)随着位移加载块的运动,断层破碎带及两侧岩体开始发育裂隙,导致应力量值分布比较离散;5)不同深度下,断层破碎带中应力集中区域分布具有一定的相似性。
4 结语本文采用非连续变形分析方法建立嘉黎断裂带二维平面模型,研究断层蠕滑作用下地应力分布规律,得到以下结论:
1) 在本文的数值模拟中断层两侧岩体和破碎带应力分布受围压、位移量的影响,其应力数值大小与围压及位移量都呈正相关。
2) 断层错动时,断层两侧岩体的应力增长明显,又由于断层错动过程中块体之间会相互错动、滑动以及张开,导致应力的分布并不连续。国内外的勘察设计规范中对断层的处理原则以避让为主[10],并且不同规范中规定了避让的距离,而断层错动时应力分布的离散性对避让距离的选取造成一定的难度,因此在进行结构设计时要充分考虑选址周围裂隙情况、地应力大小及分布特征、断层的错动速率以及使用年限等因素。
3) 断层破碎带应力大小会随着断层的错动而增大,但会低于周边围岩的应力,并在部分区段内会有应力集中的现象,表现出较大的离散性。当隧道必须穿越断层时,应在穿越处附近实测多个地应力值,避免因应力数值离散性较大造成结构设计过于保守。
| [1] |
董晓光. 试论活动断裂与地震活动关系[J]. 河南地质, 1998, 16(4): 281-285 (Dong Xiaoguang. Attempt to Discuss the Relationship between the Active Fracture and Seismic Activity[J]. Henan Geology, 1998, 16(4): 281-285)
(  0) 0) |
| [2] |
Hudson J A, Harrison J P. Engineering Rock Mechanics: An Introduction to the Principles[M]. Amsterdam: Elsevier Science, 2000
(  0) 0) |
| [3] |
薛霆虓, 傅容珊, 林峰. 几何弯曲断层活动性的模拟[J]. 地球物理学报, 2009, 52(10): 2 509-2 518 (Xue Tingxiao, Fu Rongshan, Lin Feng. The Simulation of Activities of Bend Fault[J]. Chinese Journal of Geophysics, 2009, 52(10): 2 509-2 518)
(  0) 0) |
| [4] |
邵长庆, 杨强, 李浩, 等. 活动断层作用下地裂缝开裂机理研究[J]. 水文地质工程地质, 2019, 46(4): 34-41 (Shao Changqing, Yang Qiang, Li Hao, et al. A Study of the Cracking Mechanism of Ground Fissures under the Action of Active Faults[J]. Hydrogeology and Engineering Geology, 2019, 46(4): 34-41)
(  0) 0) |
| [5] |
Armijo R, Tapponnier P, Han T L. Late Cenozoic Right-Lateral Strike-Slip Faulting in Southern Tibet[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B3): 2 787-2 838 DOI:10.1029/JB094iB03p02787
(  0) 0) |
| [6] |
任金卫, 沈军, 曹忠权, 等. 西藏东南部嘉黎断裂新知[J]. 地震地质, 2002, 22(4): 344-350 (Ren Jinwei, Shen Jun, Cao Zhongquan, et al. Quaternary Faulting of Jiali Fault, Southeast Tibetan Plateau[J]. Seismology and Geology, 2002, 22(4): 344-350)
(  0) 0) |
| [7] |
宋键, 唐方头, 邓志辉, 等. 青藏高原嘉黎断裂晚第四纪运动特征[J]. 北京大学学报: 自然科学版, 2013, 49(6): 973-980 (Song Jian, Tang Fangtou, Deng Zhihui, et al. Late Quaternary Movement Characteristic of Jiali Fault in Tibetan Plateau[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2013, 49(6): 973-980)
(  0) 0) |
| [8] |
陈兴强. 断层破碎带对川藏交通廊道通麦隧道初始地应力场影响[J]. 地球科学, 2022, 47(6): 2 120-2 129 (Chen Xingqiang. Influence of Fault Fracture Zone on Initial In-Situ Stress Field in Tongmai Tunnel of Sichuan-Tibet Traffic Corridor[J]. Earth Science, 2022, 47(6): 2 120-2 129)
(  0) 0) |
| [9] |
苏生瑞. 断裂构造对地应力场的影响及其工程意义[D]. 成都: 成都理工学院, 2001 (Su Shengrui. The Effect of Fractures on Rock Stresses and Its Significance in Geological Engineering[D]. Chengdu: Chengdu University of Technology, 2001)
(  0) 0) |
| [10] |
丁秀丽, 张雨霆, 张传健, 等. 隧洞穿越活动断层应对措施及其适应性研究综述[J]. 隧道与地下工程灾害防治, 2019, 1(1): 20-35 (Ding Xiuli, Zhang Yuting, Zhang Chuanjian, et al. Reviewon Countermeasures and Their Adaptability Evaluation to Tunnels Crossing Active Faults[J]. Hazard Control in Tunnelling and Underground Engineering, 2019, 1(1): 20-35)
(  0) 0) |
2. School of Civil Engineering, Southwest Jiaotong University, 111 North-Section 1 of Erhuan Road, Chengdu 610031, China;
3. Hebei Key Laboratory of Earthquake Disaster Prevention and Risk Assessment, 465 Xueyuan Street, Sanhe 065201, China
 2023, Vol. 43
2023, Vol. 43


