尼泊尔地区GNSS站点是大陆俯冲带站点最为密集的区域之一,国内外学者利用连续GNSS测量研究结果揭示喜马拉雅造山带在不同空间尺度和不同孕震阶段的变形特征,对尼泊尔地震的同震滑移、震间闭锁和区域流变结构进行深入研究[1]。然而,对于尼泊尔地区而言,以往的GNSS数据分析大多局限于孕震周期的某一阶段(震间、同震和震后),缺乏对多孕震阶段时间序列的统一联合分析。事实上,尼泊尔地区的GNSS时间序列包含了丰富的信号特征,既有构造因素引起的变形信号(地震周期变形),也有环境因素引起的变形信号(如降水变化、冰后回弹等机制),这些变形信号相互耦合,难以单独进行观测约束。因此,联合2015-04-25尼泊尔MW7.8地震前后的GNSS观测数据,采用统一的误差分析和噪声分析手段,对于揭示喜马拉雅中段地区地表的长期变形特征尤为必要。
本文收集了尼泊尔近场密集GNSS站点数据,通过研究完整的时间序列数据处理流程,精确获得地表形变位移,并模拟GNSS测站位置的时间变化。数据处理过程考虑测站震间速度、同震位移和地震后指数松弛,研究结果能广泛用于推断尼泊尔MW7.8地震主要的地震源机制和断层几何尺度。
1 数据收集与解算本文数据主要由连续观测站和流动观测站两部分组成,其中连续站包含中国境内的中国大陆构造环境监测网络(陆态网络)基准站(CMONOC)、尼泊尔境内的连续观测站(NEPAL)及中国地震局震后加密的连续观测站(CEA),流动站主要是由中国地质大学(武汉)(CUG)和中国地震局地震研究所科考队野外采集,测站统计情况见表 1。
|
|
表 1 GNSS测站统计 Tab. 1 Statistics of GNSS station |
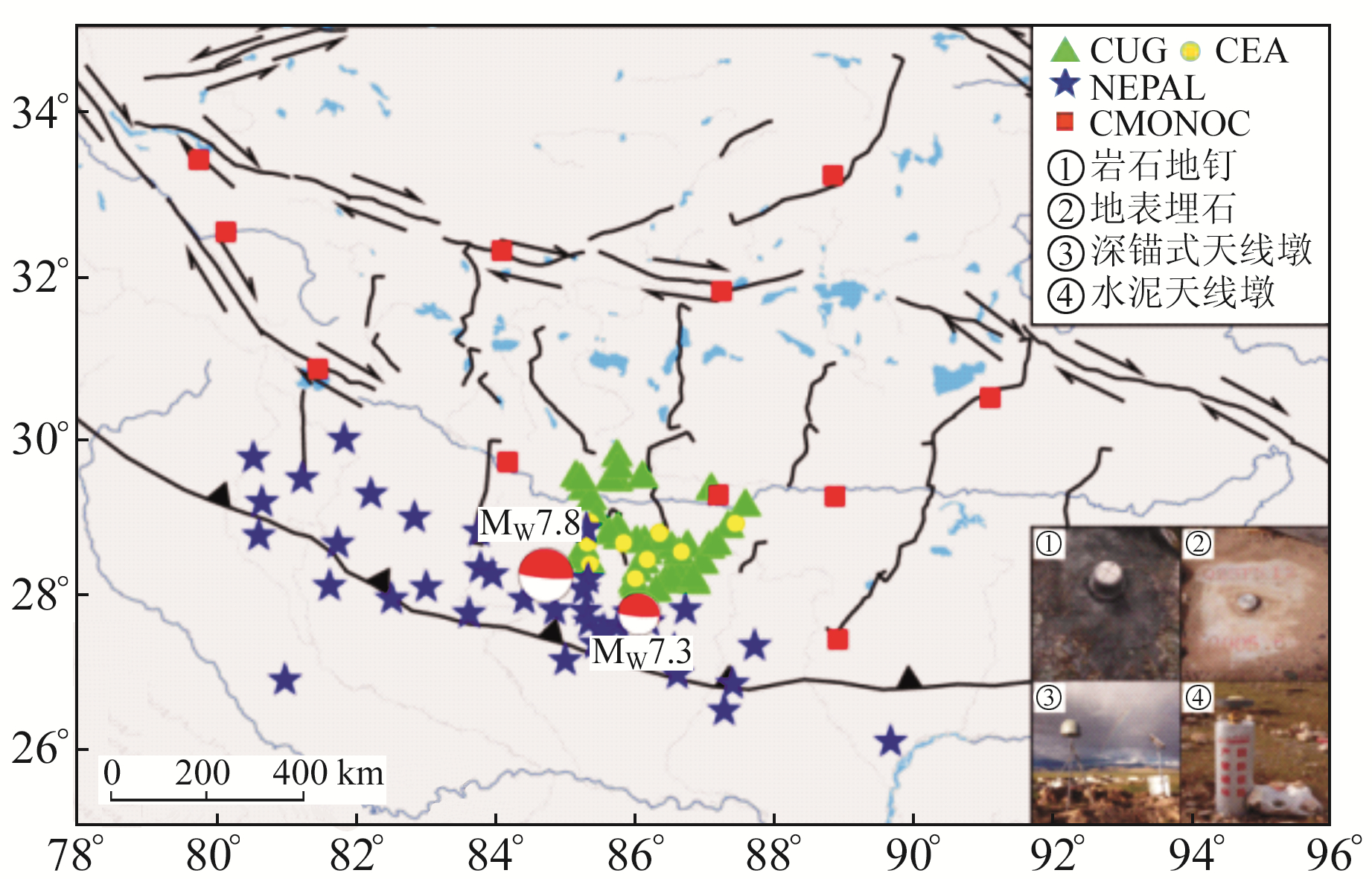
图 1展示了地震震中、GNSS站点分布情况及几种测站建站类型,其中连续观测站以深锚式天线墩和水泥天线墩为主,流动观测站观测方式有强制对中(岩石地钉、水泥天线墩)和架设脚架(地表埋石)两种方式。本文收集震后流动站5期观测数据(2015-05、2015-08、2015-11、2016-04、2016-12),每期观测36 h,保证至少有一个整日观测时段。观测设备包括Trimble 5700、R7、NETR8、NETR9及Topcon NET-G3A等多种型号,外业观测完成后需对数据作预处理、格式整理和数据质量检测。天线高的量取方式有斜高和直高两种,天线外观尺寸不同量取的位置也有差异; 数据解算中天线代码由5个字符组成,前2个字符表示量取方式,后3个字符表示量取位置,如Trimble 5700、R7的天线垂高和斜高量取代码分别为DHARP和SLBGN。
|
图 1 GNSS测站分布 Fig. 1 GNSS station distribution |
本文采用GNSS软件GAMIT/GLOBK处理收集的数据,为减少解算误差,在GAMIT基线处理中加入日/月极潮、固体潮、海潮等改正,同时对卫星轨道、大气压模型、水汽分布、多路径效应及天线相位中心进行改正; GLOBK平差处理中合并IGS全球解文件(igs1、igs2、igs3、igs4、igs5、igs6、igs7),以获得这些站点在ITRF2008框架下的坐标和中误差。
2 原理与方法 2.1 时间序列模型拟合GNSS测站观测的时间序列可用如下线性多项式来表示[2]:
| $ \begin{gathered} y\left(t_i\right)=a+b t_i+c \sin \left(2 \pi t_i\right)+d \cos \left(2 \pi t_i\right)+ \\ e \sin \left(4 \pi t_i\right)+f \cos \left(4 \pi t_i\right)+ \\ \sum\limits_{j=1}^{n_h} g_j H\left(t_i-T_{\mathrm{eq}}\right)+\sum\limits_{j=1}^{n_j} h_j H\left(t_i-T_{\mathrm{post}}\right) t_i+ \\ \sum\limits_{j=1}^{n_g} k_j \exp \left(-\left(t-T_{\mathrm{post}}\right) / \tau_j\right) H\left(t_i-T_{\mathrm{post}}\right)+v_i \end{gathered} $ | (1) |
式中,ti(i=1, …, N)为观测时间,系数a、b、c、d、e、f分别为测站时间序列起始位置、运动速率、年周期运动和半年周期运动,H(*)为阶跃函数,系数gj为地震发生时刻Teq发生的突变值,ng表示有n个地震发生(nh、nk含义相同),hj为地震发生之后测站运动速率的变化,kj为震后Tpost时刻松弛或滑移位移的大小,τj为测站震后松弛时间常数,vi为测量误差(是一个与时间无关的量,即期望E(vi)=0)。
对于尼泊尔地震,发生时刻(2015-04-25 MW7.8,2015-05-12 MW7.3)和震后时间是已知的,也就是式中Teq、Tpost已知,ng=nh=nk=1,τj的最佳估值采用模型不拟合度最小方法确定[2]。
2.2 周期性分析GNSS时间序列可以展现地表在时间变化下的特性,如因板块运动的线性效应及周期性效应等。在周期性效应中,最为常见的为年周期与半年周期,该效应一般被认为由3种原因造成[3]:1)由日、月潮引力造成的影响; 2)由太阳为热源造成的一系列周期变化,如大气压力、非潮汐所引起的海平面变化、地下水效应及热膨胀效应、季节性的降雨等; 3)由GNSS解算模型改正误差引起的周期性变化,如多路径效应、天线相位中心改正等。Dong等[3]分析全球429个GPS连续站周期性效应显示,水平方向的年周期振幅范围在1~3 mm,高程方向则在4~10 mm。
在GNSS数据解算的时候,已经充分考虑第1)和第3)两种原因造成的扰动,因此时间序列中的周期性效应更多来源于第2)种因素的影响。本文采用GARCE时变卫星重力场来计算水文荷载变化引起的地表位移,并用以改正GNSS时间序列中的周期项。
利用GRACE反演地表三分量位移变化(Δe,Δn,Δh)的计算公式为[4-6]:
| $\left\{\begin{aligned} \Delta e= & \frac{R}{\sin \theta} \sum\limits_{n=1}^{\infty} \sum\limits_{m=0}^n \bar{P}_{n m}(\cos \theta) m\left[-\Delta \bar{C}_{n m} \cdot\right. \\ & \left.\sin (m \varphi)+\Delta \bar{S}_{n m} \cos (m \varphi)\right] \frac{l^{\prime}}{1+k^{\prime}}{ }_n \\ \Delta n= & -R \sum\limits_{n=1}^{\infty} \sum\limits_{m=0}^n \frac{\partial}{\partial \theta} \bar{P}_{n m}(\cos \theta)\left[\Delta \bar{C}_{n m} \cdot\right. \\ & \left.\cos (m \varphi)+\Delta \bar{S}_{n m} \sin (m \varphi)\right] \frac{l_n^{\prime}}{1+k_n^{\prime}} \\ \Delta h= & R \sum\limits_{n=1}^{\infty} \sum\limits_{m=0}^n \bar{P}_{n m}(\cos \theta) \cdot\left[\Delta \bar{C}_{n m} \cdot \cos (m \varphi)+\right. \\ & \left.\Delta \bar{S}_{n m} \cdot \sin (m \varphi)\right] \cdot \frac{h^{\prime}{ }_n}{1+k^{\prime}} \end{aligned}\right. $ | (2) |
式中,l′n、h′n和k′n为负荷勒夫数,
本文使用CSR提供的RL05(Level-2 Release-05)月重力场产品GSM,时间跨度为2011~2016年。由于GNSS时间序列数据中没有删除大气及非潮汐海洋负荷影响,所以在GRACE的GSM数据中加回了GAC产品,以保持与GNSS数据一致。具体数据处理步骤为:1)使用SLR计算的C20替换原C20项[4],修正GRACE轨道系统误差; 2)GRACE的所有产品都基于CM框架,不提供一阶项,Swenson等[4]利用重力场球谐系数之间的关系及海底压强模型约束得到一阶项并验证了其有效性,本文采用该一阶项结果; 3)采用高斯平滑滤波方法去除GRACE数据截断误差,选取平滑半径为400 km[5]; 4)GRACE数据同次不同阶之间存在相关性,需要进行去相关性处理[6]。
2.3 共模误差分析GNSS时间序列共模误差采用PCA空域滤波方法[3, 7]。由于存在各种未知原因,GNSS实际数据中不可避免地存在大量缺失数据[8],通常采用插值补齐缺失数据,但这可能造成数据失真,因此本文采用存在缺失数据的GNSS时间序列主成分分析法。
对于区域网GPS站点日解时间序列,每个坐标分量(E、N和U三个方向)的残差坐标序列(去趋势和去均值)都可构造一个m×n维矩阵X,其中n表示测站数,m表示历元数,且满足关系式m≥n。矩阵X的列表示某一测站单分量的所有历元数据,行表示某一历元有观测的所有测站集合。采用存在缺失数据的PCA方法,将基于Dong等[7]的经验正交函数改造如下:
| $ \begin{gathered} a_k\left(t_i\right)=\sum\limits_{j=1}^{j \in S_i} X\left(t_i, j\right) v_k(j)+ \\ \sum\limits_{j=1}^{j \notin S_i} X\left(t_i, j\right) v_k(j), k=1, 2, \cdots, n \end{gathered} $ | (3) |
式中,时间序列在ti历元拥有观测数据的测站构成子集Si,则Si集合包含的最大测站数为n,vk是协方差矩阵B的第k个特征向量,协方差矩阵B的特征值呈降序排列(λ1≥λ2≥…≥λn)。第一主成分对应着最大的特征值λ1,具有整个区域最多的信息,往往反映整个网的共同变化趋势。
2.4 噪声分析对GNSS时间序列进行噪声分析主要有2个目的[9]:1)获得合理的参数估计误差。时间序列不是单纯的高斯白噪声,而是包含与时间相关的噪声,直接采用最小二乘求解会掩盖部分误差; 2)本文收集的GNSS测站有4种不同的布点方式,噪声分析可以探究GNSS建站方式对坐标时间序列噪声模型的影响。
GNSS时间序列的功率谱是经过傅立叶变换的平方除以采样点数N获得的,定义为单位频带内的信号功率,反映信号功率随频率的变化情况,即信号功率在频域的分布状况[9]:
| $ P_x(f)=P_0\left(\frac{f}{f_0}\right)^k $ | (4) |
式中,f为频率; P0和f0为常数; k为待求的谱指数,取值范围-3~1,当-3<k<-1时称为典型的布朗模型(classical Brownian motion),当-1<k<1时称为分式白噪声(fractional white noise)。
3 时间序列分析结果 3.1 周期性变形特征本文利用GRACE改正GNSS时间序列中由水文造成的部分周期影响。经过GRACE改正后,GNSS坐标时间序列3个分量加权均方根分别平均降低26.4%、15.5%、45.0%。
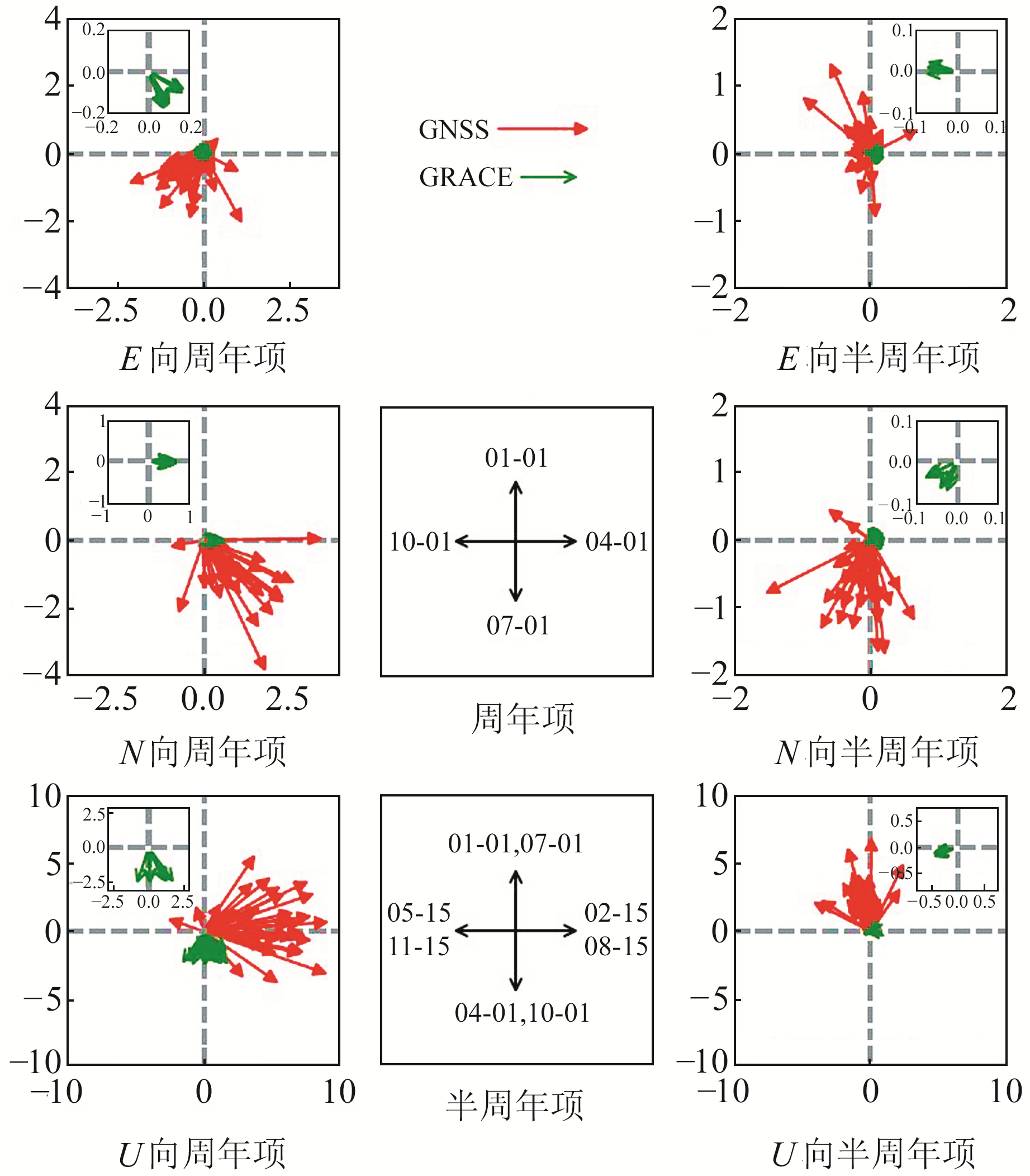
图 2(单位mm)为GNSS测站三分量的周年项、半周年项振幅和相位,图中线段长度代表振幅大小,方向表示相位。相位代表了周期项波峰出现的时间,尼泊尔近场GNSS测站E向周年项波峰和半周年项波峰分别出现在夏季和冬季附近; N向周年项波峰和半周年项波峰出现在春夏之交和秋冬之交; U向周年项波峰和半周年项波峰大多出现在初春和冬、夏季。对比GRACE水文荷载时间序列中的周年项和半周年项的相位和振幅发现,GRACE比GNSS振幅要小且存在相位差,说明除了水文因素影响,GNSS时间序列还存在其他物理因素作用。图 3以KKN4和SNDL测站为例对比了GNSS时间序列中的周期信号和GRACE模型的季节性水文荷载时间序列,亦可以得出相同结论。
|
图 2 GNSS和GRACE周年项和半周年项振幅与相位 Fig. 2 Amplitudes and phases of GNSS and GRACE annual and semi-annual terms |

|
图 3 GNSS和GRACE的周期项时间序列 Fig. 3 Periodic term time series of GNSS and GRACE |
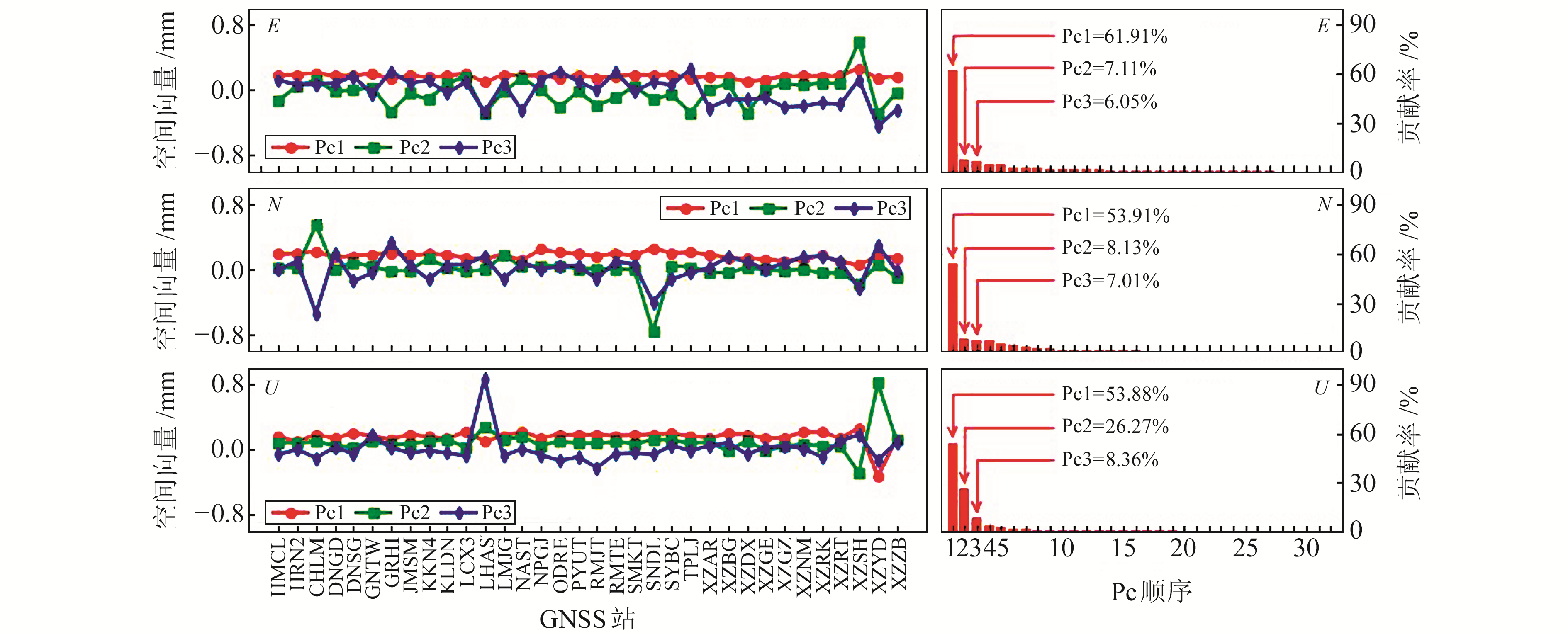
图 4为利用存在缺失数据的PCA方法求得的GNSS站点前三主成分空间向量和各特征值贡献率。结果显示,第一主成分对坐标序列各分量的贡献率分别为61.91%、53.91%和53.88%; 第二和第三主成分空间向量随空间变化波动较大,不能反映整个网的共同特征。第一主成分空间向量很平稳,有非常一致的空间分布模式,具有整个区域最多的信息,反映整个网的空间共同变化趋势,故采用第一主成分计算共模误差:
| $ \varepsilon\left(t_i, j\right)=a_1\left(t_i\right) v_1(j) $ | (5) |
|
图 4 缺失数据的PCA方法前三主成分统计和特征值的贡献率 Fig. 4 Statistics of the first three principal components and contribution rate of eigenvaluesof PCA method with missing data |
式中,a1为第一主成分, v1为协方差矩阵的第一特征向量, ti为历元,j为测站数。
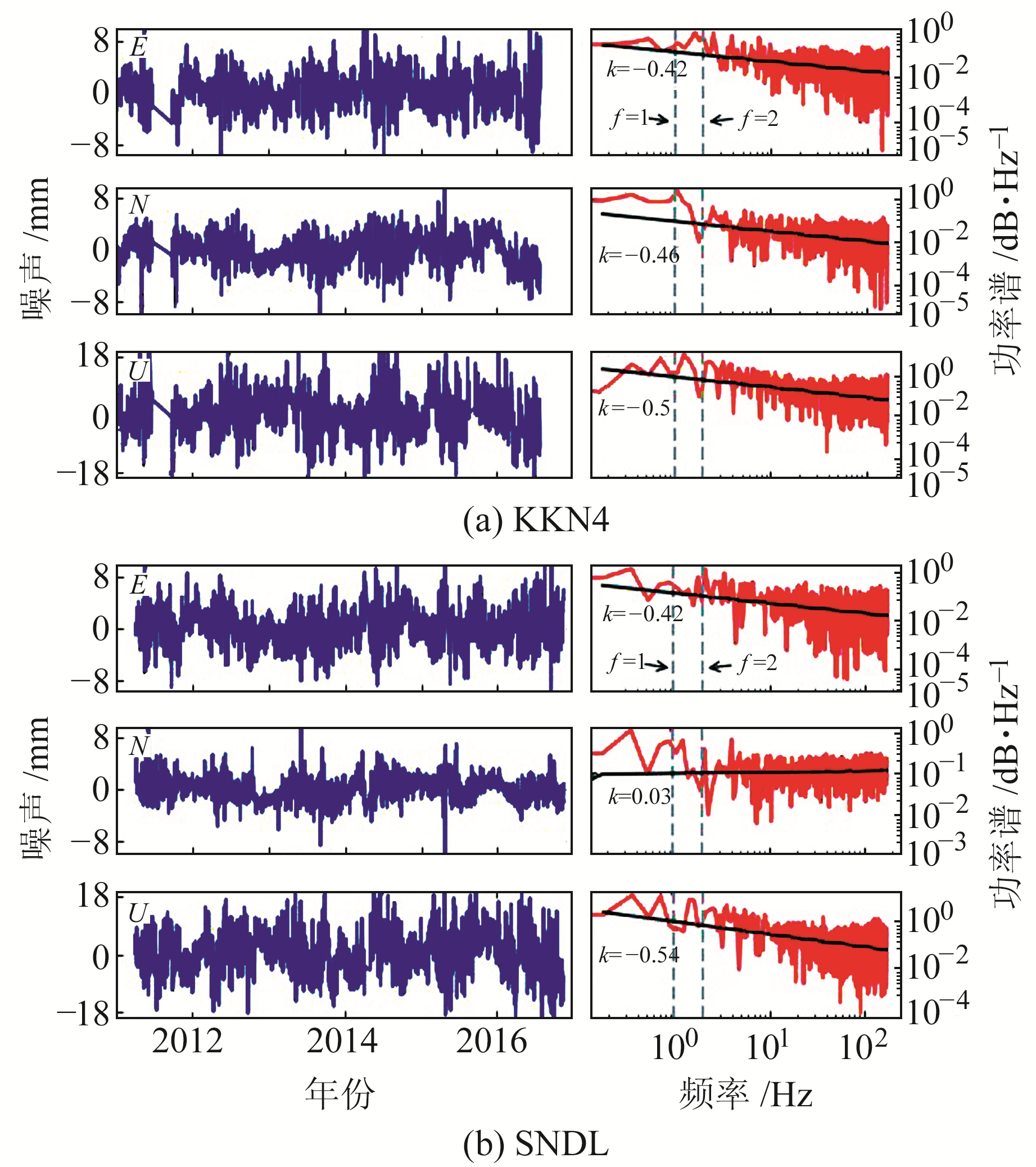
3.3 噪声特性图 5为KKN4和SDNL两个测站的噪声时间序列及其功率谱,可以看出,当频率为1 Hz和2 Hz时功率谱存在明显波动,表示为周年和半周年振幅。
|
图 5 GNSS噪声时间序列和功率谱 Fig. 5 GNSS noise time series and power spectrum |
图 6为研究区GNSS站点的噪声类型统计结果,可以看出,谱指数多数位于-1~0之间,表明多数站点既有闪烁噪声特性也有白噪声特性。选定最佳的噪声类型WN+FN,构建随机模型如下:
| $ \boldsymbol{D}=\boldsymbol{\sigma}_{\mathrm{w}}^2 \boldsymbol Q_{\mathrm{w}}+\boldsymbol{\sigma}_{\mathrm{F}}^2 \boldsymbol Q_{\mathrm{F}} $ | (6) |

|
图 6 GNSS时间序列噪声谱指数概率统计 Fig. 6 GNSS time series noise spectrum exponential probability statistics |
式中,
采用方差分量估计算法定量计算闪烁噪声和白噪声大小,同时估计震间速度、同震和震后位移。
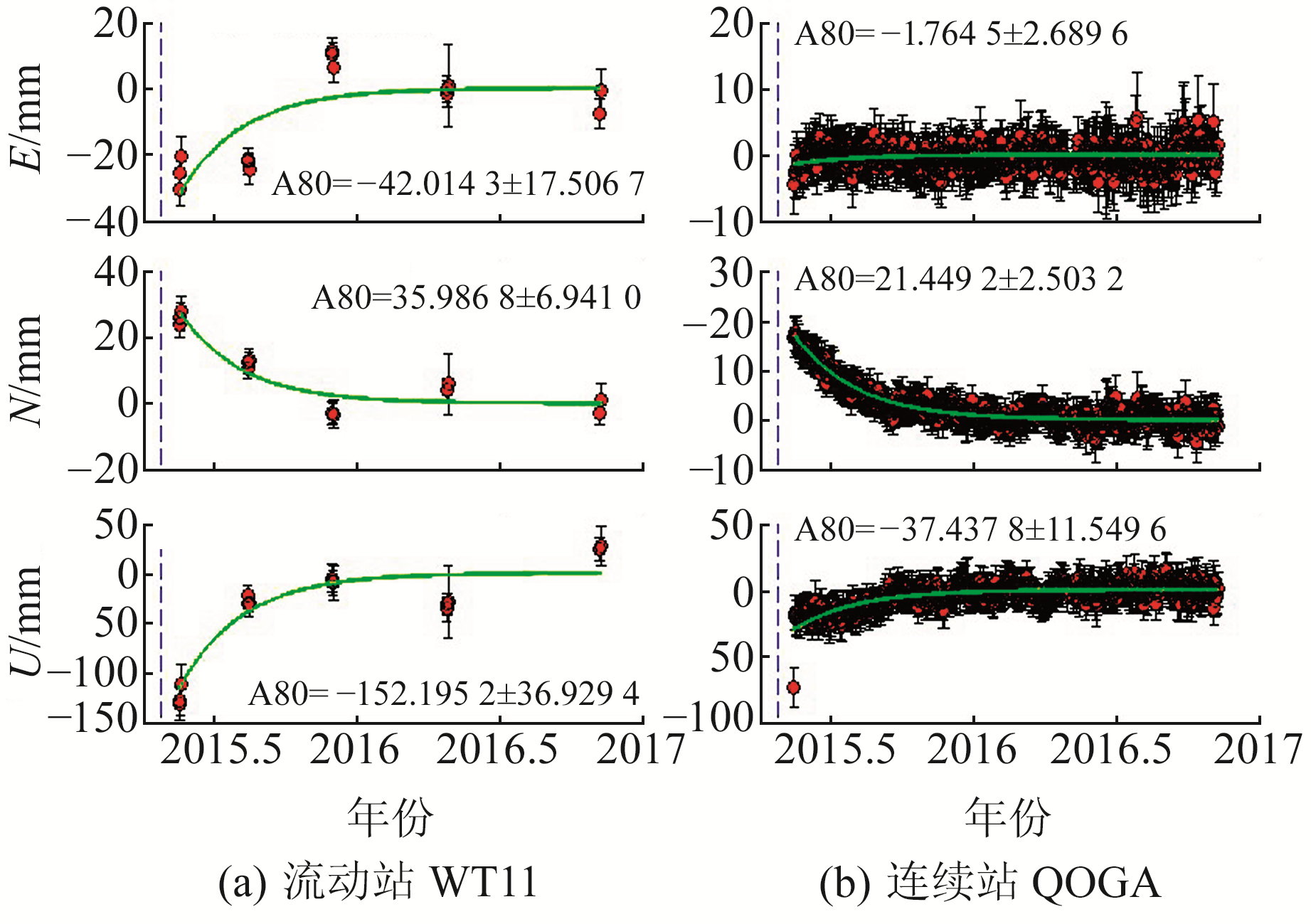
表 2为噪声模型计算测站的N分量与E分量震间速度值、尼泊尔地震同震及震后位移值,上行为经过噪声模型WN+FN处理分析的结果,下行为WN噪声模型分析结果,后面的常数是两者误差的倍数。统计发现,WN+FN模型得出的震间速度、同震和震后位移中误差分别约为WN模型结果的6~9倍、4~7倍和2~4倍,WN模型低估了误差值。图 7为两类观测站震后时间序列。
|
|
表 2 不同噪声模型估计速度、同震和震后结果 Tab. 2 Estimated velocity, coseismic and post-seismic results of different noise models |
|
图 7 震后位移时间序列 Fig. 7 Post-earthquake displacement time series |
利用时间序列分析结果获得同震和震后位移,由图 8可知,地震造成中国藏南地区在水平方向产生永久形变[10],同震垂直位移场尼泊尔境内KKN4站和NAST站处于隆升区,分别抬升125 cm和61 cm,而尼泊尔境内CHLM站和西藏聂拉木县WT11站处于下降区,分别下降57 cm和12.7 cm,此外J041站下降7.8 cm,TNG3站下降7.5 cm。利用指数模型对尼泊尔地震震后20个月的GNSS数据进行分析[11]可知,震后松弛时间常数τj=80,计算每个GNSS测站的震后松弛位移(图 9)发现,尼泊尔地震震后形变主要发生在北部区域,且最大震后位移形变可达约60 mm。

|
图 8 尼泊尔MW7.8地震同震位移场 Fig. 8 Coseismic horizontal displacement field of MW7.8 Nepal earthquake |
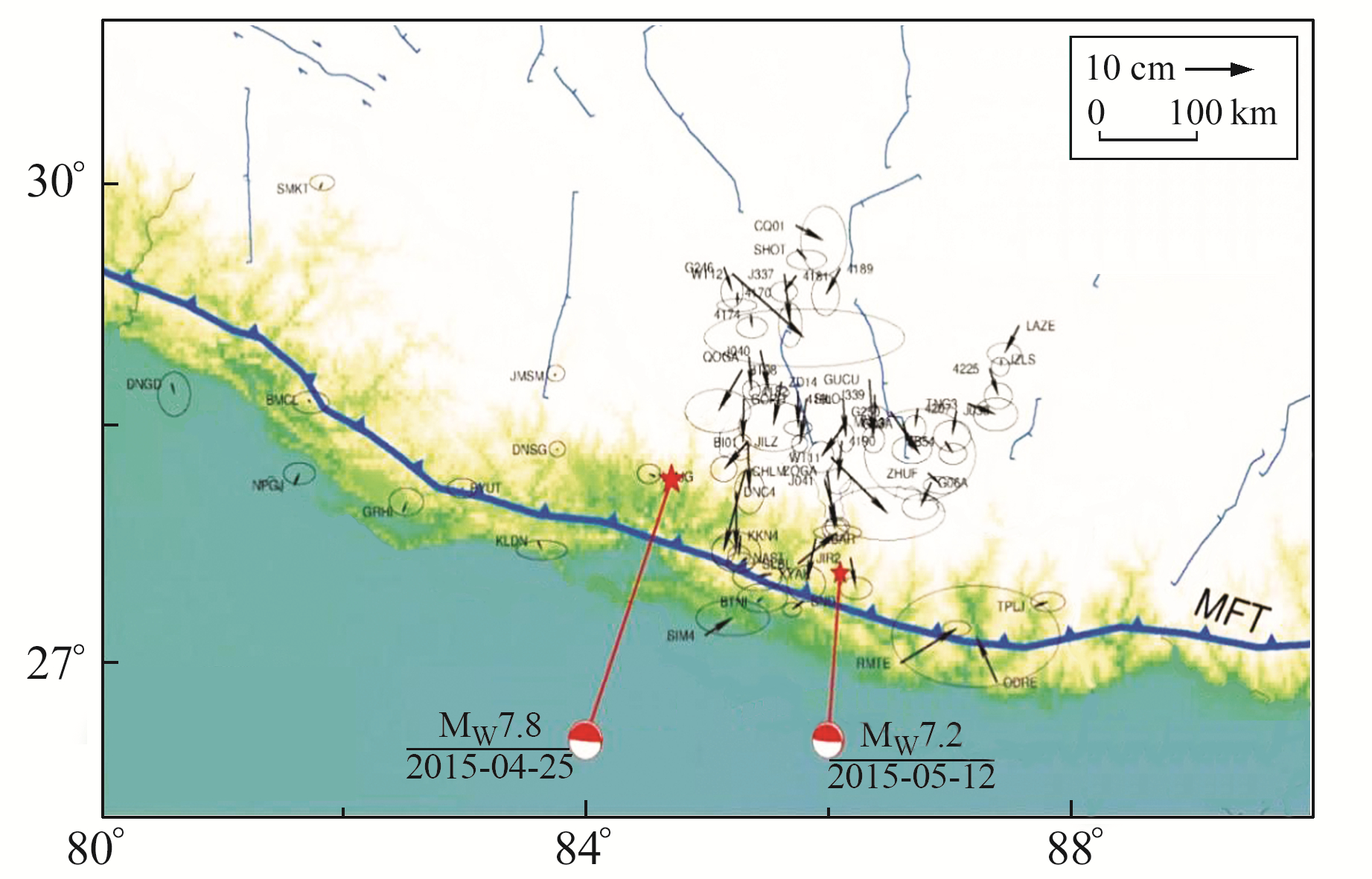
|
图 9 尼泊尔地震GNSS观测震后20个月水平位移场 Fig. 9 Horizontal displacement field 20 months afterthe Nepal earthquake by GNSS observation |
本文系统研究GNSS时间序列后处理分析流程,利用GAMIT/GLOBK软件包解算2011~2017年尼泊尔近场58个GPS连续观测站和41个震后流动观测站,获得ITRF2008高精度坐标序列,并以此为基础,研究GRACE重力数据改正GNSS时间序列的周期项、共模误差和噪声特性。得出以下结论:
1) GRACE改正GNSS数据,使得时间序列3个分量的WRMS平均降低15.52%、26.41%和45.06%;
2) 采用存在缺失数据的PCA方法获得第一主成分并计算共模误差,3个分量有效率达到61.91%、53.91%和53.88%;
3) 频谱分析确定WN+FN为最佳噪声模型,新的噪声模型得出的震间速度、同震和位移中误差是常用的WN模型结果的约6~9倍、4~7倍和2~4倍,即采用WN模型得出的中误差低估了真实值。
4) 通过对尼泊尔地震近场GNSS站点时间序列进行分析可知,结合Mencin等[11]提供的震后余滑模型,尼泊尔地震震后形变主要发生在北部区域,且最大震后位移形变可达约60 mm。
| [1] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报: 信息科学版, 2018, 43(12): 2 112-2 123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 112-2 123)
(  0) 0) |
| [2] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California, 2002
(  0) 0) |
| [3] |
Dong D, Fang P, Bock Y, et al. Anatomy of Apparent Seasonal Variations from GPS-Derived Site Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B4)
(  0) 0) |
| [4] |
Swenson S, Wahr J. Methods for Inferring Regional Surface-Mass Anomalies from Gravity Recovery and Climate Experiment(GRACE) Measurements of Time-Variable Gravity[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B9)
(  0) 0) |
| [5] |
Zou R, Wang Q, Freymueller J, et al. Seasonal Hydrological Loading in Southern Tibet Detected by Joint Analysis of GPS and GRACE[J]. Sensors, 2015, 15(12): 30 525-30 538 DOI:10.3390/s151229815
(  0) 0) |
| [6] |
陈超, 邹蓉, 刘任莉. 联合GPS和GRACE研究青藏高原南部地区垂直形变的季节性波动[J]. 武汉大学学报: 信息科学版, 2018, 43(5): 669-675 (Chen Chao, Zou Rong, Liu Renli. Vertical Deformation of Seasonal Hydrological Loading in Southern Tibet Detected by Joint Analysis of GPS and GRACE[J]. Geomatics and Information Science of Wuhan University, 2018, 43(5): 669-675)
(  0) 0) |
| [7] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3): 1 581-1 600
(  0) 0) |
| [8] |
Shen Y Z, Li W W, Xu G C, et al. Spatiotemporal Filtering of Regional GNSS Network's Position Time Series with Missing Data Using Principle Component Analysis[J]. Journal of Geodesy, 2014, 88(1): 1-12 DOI:10.1007/s00190-013-0663-y
(  0) 0) |
| [9] |
Mao A L, Harrison C G A, Dixon T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B2): 2 797-2 816 DOI:10.1029/1998JB900033
(  0) 0) |
| [10] |
赵斌, 杜瑞林, 张锐, 等. GPS测定的尼泊尔MW7.9和MW7.3级地震同震形变场[J]. 科学通报, 2015, 60(增2): 2 758-2 766 (Zhao Bin, Du Ruilin, Zhang Rui, et al. Co-Seismic Displacements Associated with the 2015 Nepal MW7.9 Earthquake and MW7.3 Aftershock Constrained by Global Positioning System Measurements[J]. Chinese Science Bulletin, 2015, 60(S2): 2 758-2 766)
(  0) 0) |
| [11] |
Mencin D, Bendick R, Upreti B N, et al. Himalayan Strain Reservoir Inferred from Limited Afterslip Following the Gorkha Earthquake[J]. Nature Geoscience, 2016, 9(7): 533-537 DOI:10.1038/ngeo2734
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

