2. 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
我国于2012年正式开通覆盖亚太地区的北斗二号(BDS-2)卫星导航系统。区别于其他GNSS系统,BDS-2使用混合星座设计,由5颗地球静止轨道(GEO)卫星、5颗倾斜地球同步轨道(IGSO)卫星和3颗中圆轨道(MEO)卫星共13颗卫星组网,为亚太地区用户提供定位、导航和授时(PNT)服务[1]。
截至2021-10-31,BDS-2共发射17颗卫星(表 1),其中15颗卫星正常提供服务,2颗卫星被替换。所有卫星均搭载4颗铷原子钟(rubidium atomic frequency standard,RAFS)[2-3]。由表 1可见,除4颗近5 a内发射的备份卫星外,有5颗卫星在轨运行已逾10 a,另有6颗卫星在轨运行超过8 a。由于GNSS本质上是以时间测量为基础的系统[4],要获得各颗卫星到用户的精确距离,其关键是要获得精确的时间测量[5],因此星载原子钟的性能将直接影响导航系统PNT服务的精度。在多颗BDS-2卫星在轨运行时间较长、其星载原子钟可能会出现不可预测的性能下降背景下,及时替换因老化导致的性能下降卫星,可以保证卫星星座提供高精度的服务。但目前仅有的4颗在轨服务备份卫星并不能完全替换所有在轨时间长而老化的卫星。由此可见,通过优化改进钟差预报算法,降低由卫星钟性能下降引起的预报参数精度恶化的需求日趋紧迫。表 1数据资料均来自中国卫星导航系统办公室网站(www.beidou.gov.cn),其中C01、C03卫星已被备份卫星替换。
|
|
表 1 BDS-2卫星在轨状态统计(截至2021-10-31) Tab. 1 BDS-2 satellites in-orbit status(updated to 31st Oct, 2021) |
有关BDS-2卫星钟性能评估的研究成果比较丰富,最常用的方法是评估卫星钟的频率准确度、频率漂移率和频率稳定度这3项指标。研究表明,BDS-2卫星钟频率准确度保持在10-11量级,频率漂移率保持在10-13/d量级,频率稳定度基本保持在10-14量级[6]。同时,在卫星钟差预报方面,国内外学者提出许多钟差预报模型,目前较为成熟和常用的模型包括线性模型、二次多项式模型、灰色模型[7]、谱分析模型[8]、卡尔曼滤波模型[9]、小波神经网络模型[10]、径向基函数神经网络模型、支持向量机预报模型,以及综合多种单一模型的组合预报模型及上述模型中的部分改进模型等。
1 卫星钟末期的性能分析近年来,国内不少学者对BDS-2卫星钟的性能进行评估,尽管评估的时间、跨度以及使用的数据存在不同,但评估结果基本一致,即运行时间长的卫星相比新发射的卫星其性能会有所下降,但总体上依然能满足设计指标要求[5, 11-13]。通过在轨运行的各颗卫星的长期性能分析可以看出,仅个别运行时间超过8 a的卫星星载原子钟会出现性能下降的现象,大多数卫星的星载原子钟仍能提供稳定的时频信号,保证系统高质量的服务。因此,针对个别性能下降的卫星,本节将进一步研究其长期在轨运行后星载原子钟运行的变化情况。
1.1 频率稳定度长期分析BDS-2广播星历是基于TWTT数据产生的钟差参数,因此本节开展BDS-2卫星钟频率稳定度长期分析时,使用跨度为38个月的TWTT钟差产品,起止时间为2018-01-01~2021-02-28。
为方便统计和展示卫星钟的长期性能变化情况,选取单月的钟差数据作为计算和评估单元。在此38个月中,先后发射C16(2018-07-10发射)和C18(2019-05-17发射)两颗备份卫星,并提供服务。因此,仅对这两颗卫星发射后的时间段进行统计,发射前的统计结果均取为零。原C03卫星于2018-09被备份卫星C17(2016-06-12发射)整星替换,原C01卫星于2020-03被备份卫星C18整星替换。在统计时,为不混淆替换前后的卫星,仍采用C01、C03、C17和C18的编号。对于被替换的卫星,其结果均取为零。
在计算频率稳定度时,采用重叠Hadamard方差估计得到天稳定度。由于MEO卫星的TWTT数据缺失严重,不足以计算出天稳定度,仅能计算得到万秒稳定度。因此在分析BDS-2在轨卫星的长期稳定度变化时,使用各颗在轨卫星的万秒稳定度结果进行统计。图 1所示为万秒稳定度结果,图中不同颜色表示不同轨道类型的卫星,其中红色表示GEO卫星,绿色表示IGSO卫星,蓝色表示MEO卫星。

|
图 1 BDS-2卫星钟频率稳定度(万秒稳定度)长期分析结果 Fig. 1 Long-term analysis of frequency stabilityof BDS-2 satellite clocks |
由图 1可知,GEO卫星的万秒稳定度结果最好,其均值为5.46×10-14; IGSO卫星次之,均值为9.34×10-14; MEO卫星的万秒稳均值为13.31×10-14,与前期已有的研究结果接近。可以看出,绝大多数在轨卫星在长达38个月的时间跨度下均能稳定运行,万秒稳定度指标变化平稳,均值基本在2.5×10-13以内。但也存在个别卫星、个别月份的评估结果存在显著波动的现象。如2018-05卫星C09万秒稳定度结果达到3.59×10-13,2021-02卫星C05的万秒稳定度结果达到3.47×10-13。与其他月份的评估结果相比,该月的万秒稳定度结果存在严重恶化。出现此现象的原因比较复杂,可能受空间环境、卫星运行状态、卫星器件老化等因素的影响。相比之下,MEO卫星虽然万秒稳定度结果不如其他两类卫星,但整体运行更为稳定。
1.2 钟差预报情况卫星导航系统要实现高精度的导航与定位,最基础的是精准的卫星轨道参数和卫星钟差参数。而卫星星载原子钟频率稳定度下降,会直接降低卫星钟差参数的预报精度,最终影响导航和定位的精度。
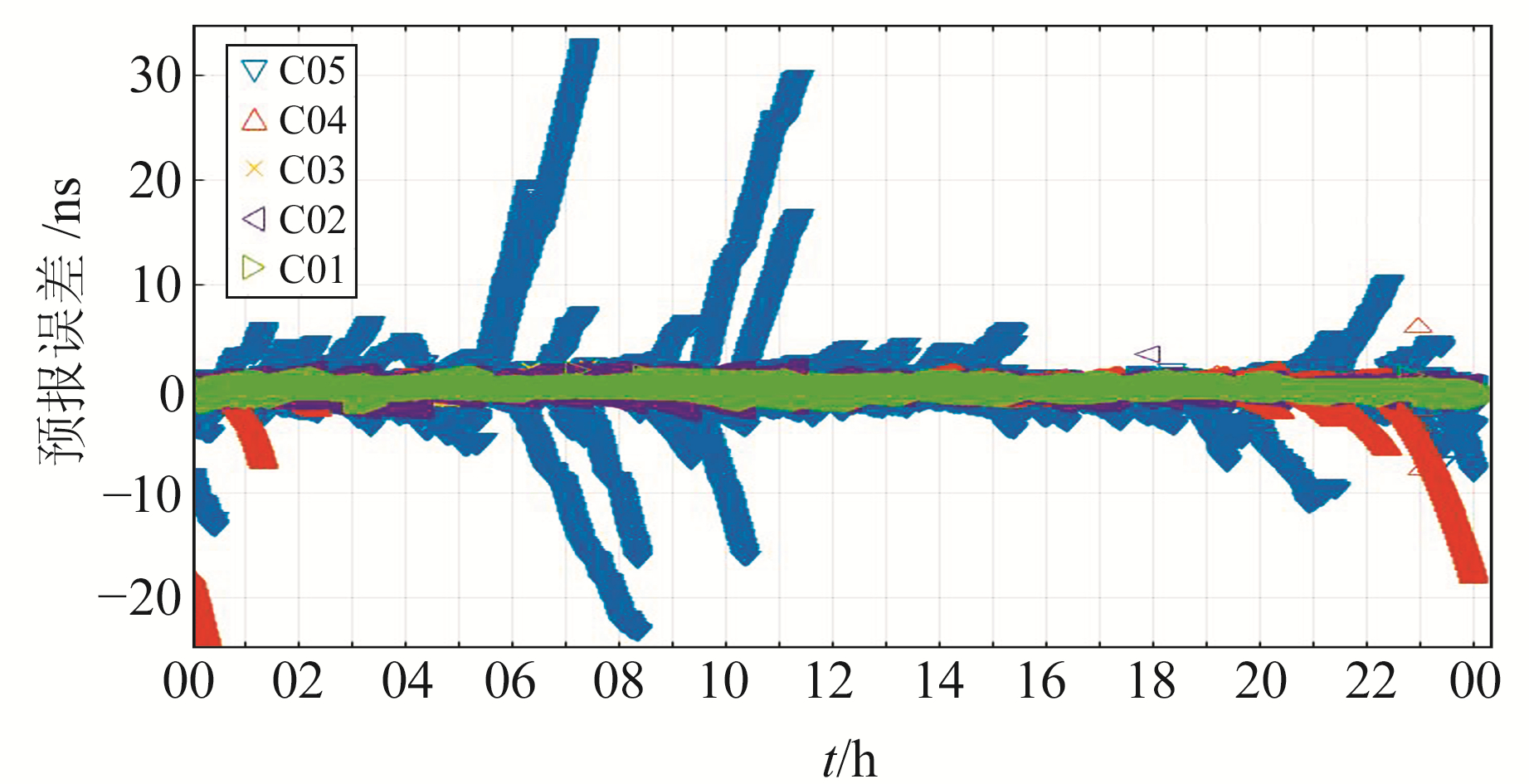
本节针对BDS-2卫星钟开展钟差预报的研究。对2021-02的TWTT数据按h进行线性拟合,将拟合得到的预报参数用于随后1 h卫星钟差预报,并记录预报误差。对于IGSO/MEO卫星存在不可观测的弧段,则利用二次多项式模型对不可视前最后1 h的数据进行计算,得到的预报参数外推至再次可视的弧段。绘图时,将多天的预报误差按h进行展示,如图 2所示。
|
图 2 BDS-2卫星钟末期预报精度 Fig. 2 End-stage prediction accuracy of BDS-2 GEO satellite clocks |
由图可知,GEO卫星中C01(原备份卫星C18)、C02、C03(原备份卫星C17)的预报误差很稳定,均在±2.5 ns以内。两颗备份卫星的预报误差均在±1.5 ns以内,说明备份卫星的卫星钟性能处于良好状态。C02卫星虽然在轨运行时间较长,但预报误差基本上与两颗备份卫星相当,也能继续精稳运行。C04和C05两颗卫星在2月份出现多次预报误差显著恶化的情况,C05的预报误差甚至超过30 ns。出现此类情形,说明卫星钟在1 h内发生了明显的频率变化,线性模型计算得到的a1项参数已不能准确反映卫星钟的真实情况。而卫星钟在短时间内出现显著的频率变化,很可能是由于卫星钟在轨时间长,器件老化所引起的性能波动。
表 2(单位ns)给出5颗GEO卫星的钟差预报结果统计。为充分观察卫星钟出现性能波动对钟差预报的影响,表中选取RMS、95.5%分位点和99.7%分位点的统计值。可以看出,除了C05卫星外其余卫星的RMS统计值均优于2 ns。C05卫星在95.5%分位点的预报值仅为1.35 ns,而99.7%分位点的预报值为15.69 ns。可见,C05卫星受到严重的性能波动影响,钟差预报精度出现显著恶化,但受影响的时间段较短。
|
|
表 2 GEO卫星钟差预报结果 Tab. 2 Statistics results of GEO prediction errors |
由此可见,在轨运行时间长的卫星仍能提供较好服务,但其星载原子钟的性能存在波动的可能性,常见表现为卫星钟的频率在短期内发生剧烈变化,卫星钟差的预报精度迅速恶化,会在很短的一段时间内影响该卫星的正常服务。
2 基于钟差一次差分数据的LSTM神经网络卫星钟差预报模型通过上节使用传统多项式模型进行钟差预报的结果可知,该模型虽然简单高效,且各参数均具有物理含义,但卫星钟在面对复杂多变的空间环境和自身器件逐渐老化的综合影响下,导致钟差数据会出现如C04、C05两颗卫星所表现出的现象。随着卫星在轨时间越来越长,出现上述现象的可能性也会逐渐增大,多项式模型可能越发难以满足此场景下的高精度钟差预报工作。因此,有必要提出一种新型的钟差预报模型,解决该问题。
长短期记忆(long short-term memory,LSTM)网络由Hochreiter于1997年提出以来,因其对时序数据的处理和分析有着较好的适应性,被广泛应用于语义识别、机器翻译等诸多领域。作为一种特殊的时间递归神经网络(recurrent neural network,RNN),LSTM能更有效地避免网络因梯度消失或梯度爆炸而导致的问题[14](图 3)。
|
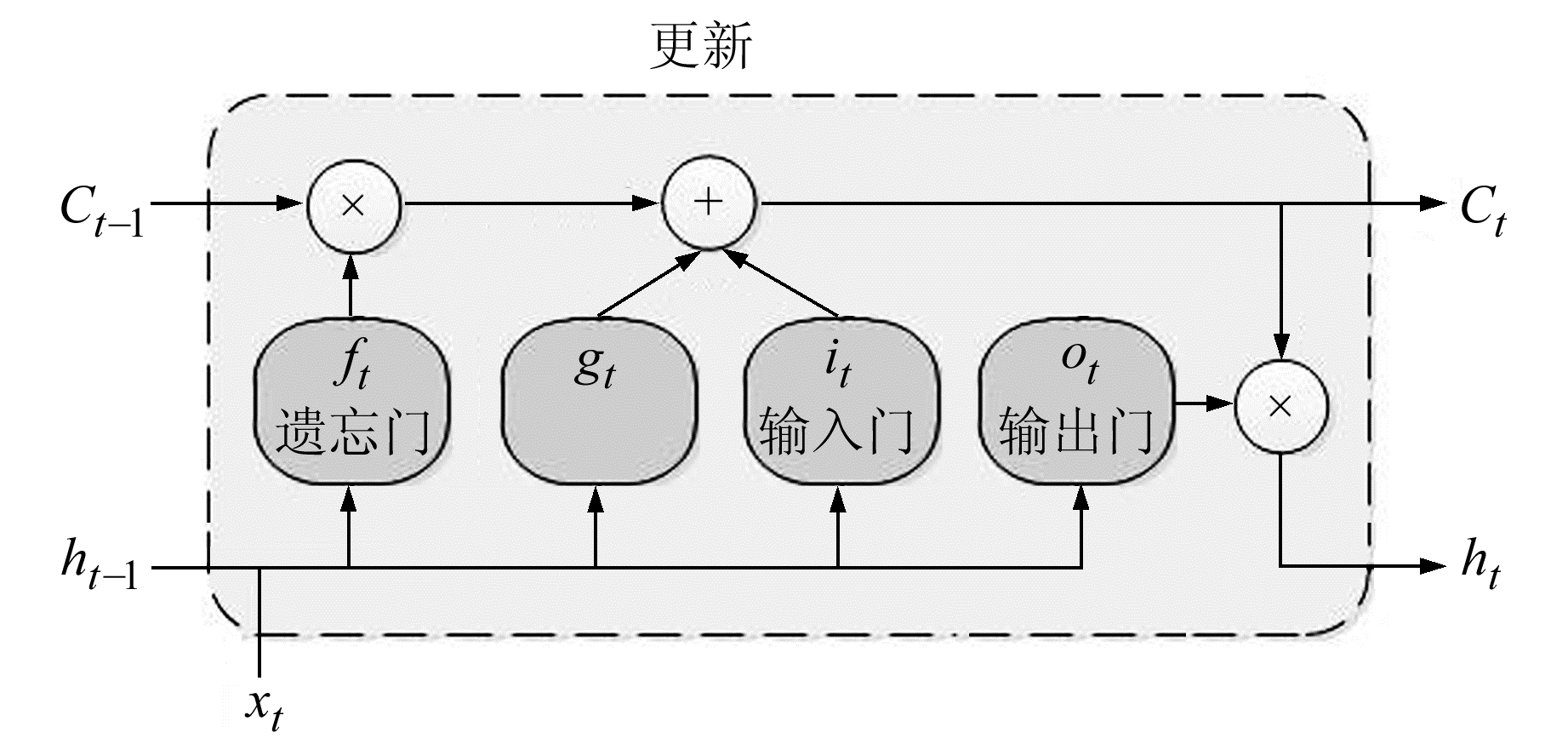
图 3 LSTM模型结构原理 Fig. 3 Schematic diagram of the LSTM model |
图 3中,ft表示遗忘门(forget gate),用于控制当前单元丢弃的信息,并将剩余的信息保存到当前单元内。该门会读取上一个单元的输出ht-1和当前单元的输入xt,经过sigmoid函数计算输出一个在0~1之间的数值,来调整上一个单元的状态Ct-1。1表示“完全保留”,0表示“完全丢弃”。公式表示为:
| $ f_t=\sigma\left(W_f\left[h_{t-1}, x_t\right]+b_f\right) $ | (1) |
gt和it组成了单元内的输入门(input gate),控制着输入到当前单元的信息。其中gt表示用来更新的备选内容,it表示单元中需要更新的信息。将二者联合起来,对单元的状态进行更新。如此一来,Ct-1更新为Ct,并把旧状态与ft相乘,舍弃确定需要丢弃的信息:
| $ \begin{gathered} i_t=\sigma\left(W_i\left[h_{t-1}, x_t\right]+b_i\right) \end{gathered} $ | (2) |
| $g_t=\tanh \left(W_g\left[h_{t-1}, x_t\right]+b_g\right) $ | (3) |
输出ot由ht-1和xt经过sigmoid函数所得; ht则是当前单元状态Ct通过tanh处理,并和ot相乘所得:
| $\begin{gathered} o_t=\tanh \left(W_o\left[h_{t-1}, x_t\right]+b_o\right) \end{gathered} $ | (4) |
| $ h_t=o_t \tanh \left(C_t\right) $ | (5) |
本节所构造的LSTM神经网络模型基于滑动窗口进行数据预报。如表 3所示,在使用采样率为300 s的数据作为网络输入的情况下,假设使用2 h的拟合资料,即24个钟差点输入进神经网络,利用神经网络建立x1、x2、x3、…、x24与x25的映射关系。将LSTM网络对前24个钟差点学习后估计的第25个钟差点作为网络的输出值,即网络输出的钟差预报值[15]。
|
|
表 3 LSTM神经网络多步预报 Tab. 3 LSTM neural network prediction |
为避免梯度爆炸,将网络的梯度门限设为1,初始的学习率为0.005,并设置学习速度的下降率为0.2。为保证LSTM有足够的样本进行学习训练,本文使用14 d的数据作为样本输入至LSTM网络。
2.2 应用于末期卫星钟差数据的预报效果本节利用2021-02的TWTT卫星钟差数据进行LSTM神经网络的预报研究,与QP模型预报2 h的预报误差进行对比分析。根据前文构建的LSTM神经网络模型,对两种模型均使用滑动窗口的方式进行预报,窗口跨度设置为8 h,预报随后2 h的钟差值,重复进行10次,并对每个历元的预报误差取平均值。选取5颗GEO卫星用于预报实验,并在表 4(单位ns)中统计两种模型预报误差的RMSE值。图 4和图 5展示了C01和C05卫星的钟差预报情况,其中LSTM模型的预报曲线为从10次重复实验中随机选取的。
|
|
表 4 两种模型的卫星钟差预报结果 Tab. 4 Statistics results of prediction errors of two models |
|
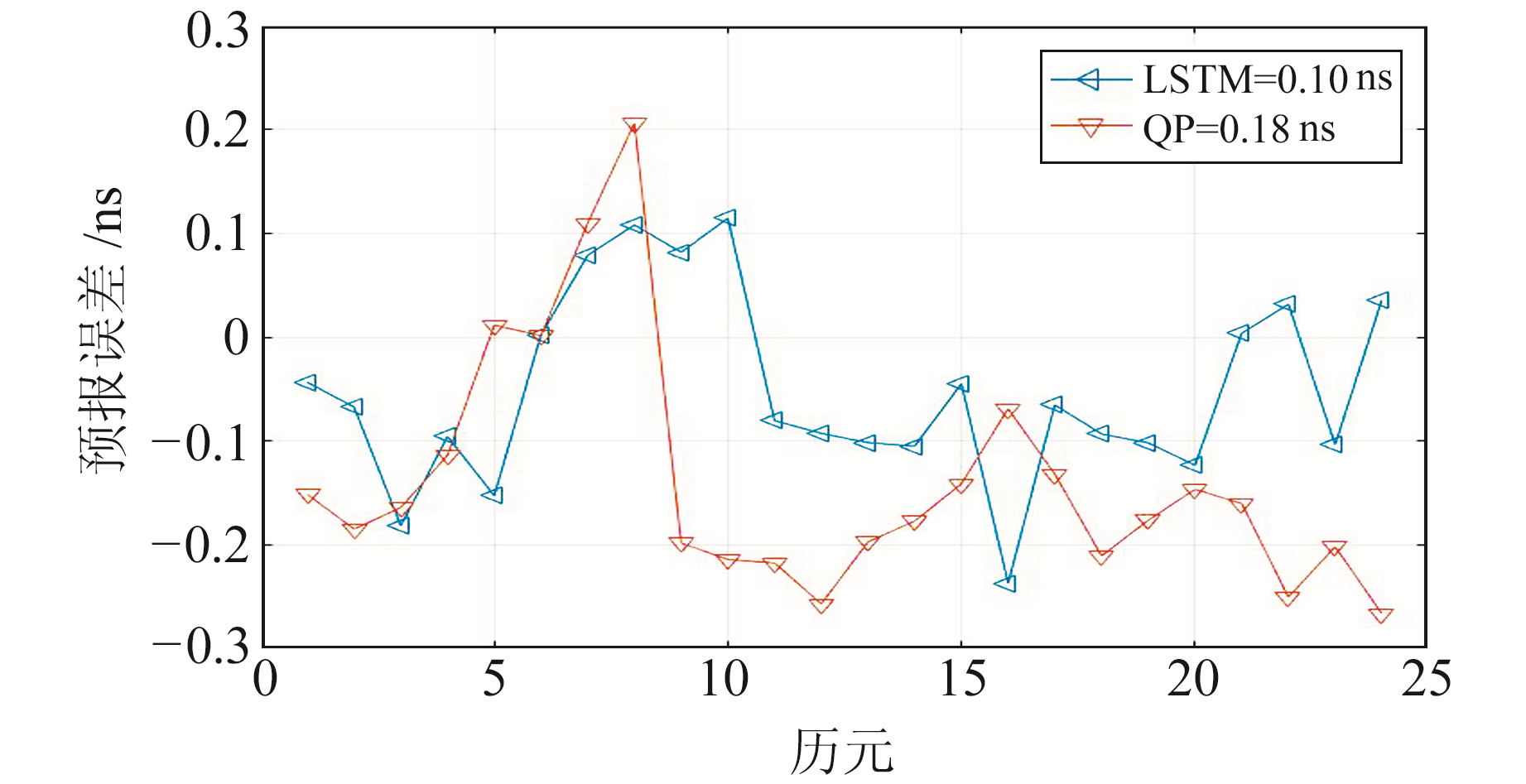
图 4 C01卫星使用LSTM模型与QP模型的预报精度对比 Fig. 4 Comparison of prediction accuracy between LSTM model and QP model of C01 |

|
图 5 C05卫星使用LSTM模型与QP模型的预报精度对比 Fig. 5 Comparison of prediction accuracy between LSTM model and QP model of C05 |
从图中结果可知,对于C01卫星而言,在卫星钟运行状态良好的情况下,使用滑动窗口的LSTM模型可以得到较好的预报精度,2 h预报精度可以达到0.1 ns,而且预报的钟差值也较为平稳。QP模型精度与之十分接近,两种模型均有较好的预报精度。对于C05卫星而言,该段数据包含卫星钟出现异常频率变化现象,QP模型的预报精度迅速下降,预报精度的RMSE达9.9 ns。然而在此条件下,LSTM神经网络的预报精度依然稳定,预报精度优于0.2 ns,明显优于QP模型。可见LSTM神经网络通过必要的训练,能较好地适应卫星钟频率变化,在卫星钟出现频率变化期间仍能提供高精度的预测值。
3 结语通过对BDS-2在轨卫星钟进行性能分析看出,大部分在轨运行达到8 a或10 a的卫星仍能继续稳定运行,但存在偶发性能波动的风险,备份卫星在轨运行状态则更为稳定。在出现性能波动现象时,由于传统的二次多项式模型不能很好地描述钟差数据的快速变化情况,其拟合所得的预报参数精度会快速恶化,严重影响卫星导航服务的精度。因此,为了适应在轨运行时间长、器件老化的卫星钟的运行特点和规律,我们提出基于LSTM神经网络的预报模型。该模型在卫星钟运行平稳时,预报精度与传统二次多项式模型相当; 在卫星钟出现性能恶化、频率变化时,预报精度仍能优于0.2 ns,显著优于传统的二次多项式模型。可见,使用本文提出的方法,能较好地应对卫星钟频率快速变化期间钟差预报精度下降的问题。
| [1] |
Wang B, Lou Y D, Liu J N, et al. Analysis of BDS Satellite Clocks in Orbit[J]. GPS Solutions, 2016, 20(4): 783-794 DOI:10.1007/s10291-015-0488-7
(  0) 0) |
| [2] |
Rochat P. Onboard Atomic Clocks in Global Navigation Satellite System[C]. SATW Congress 2010, Zurich, 2010
(  0) 0) |
| [3] |
贾小林, 冯来平, 毛悦, 等. GPS星载原子钟性能评估[J]. 时间频率学报, 2010, 33(2): 115-120 (Jia Xiaolin, Feng Laiping, Mao Yue, et al. Performance Evaluation of GPS On-Board Clock[J]. Journal of Time and Frequency, 2010, 33(2): 115-120)
(  0) 0) |
| [4] |
郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州: 信息工程大学, 2006 (Guo Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou: Information Engineering University, 2006)
(  0) 0) |
| [5] |
王威, 王宇谱, 王彬, 等. BDS卫星精密钟差性能综合评定[J]. 导航定位学报, 2020, 8(1): 20-25 (Wang Wei, Wang Yupu, Wang Bin, et al. Accuracy Evaluation of BDS Satellite Precise Clock Bias[J]. Journal of Navigation and Positioning, 2020, 8(1): 20-25)
(  0) 0) |
| [6] |
Chao X, Zhao Q L, Hu Z G. Performance Evaluation of COMPASS Clock[C]. CSNC 2012, Guangzhou, 2012
(  0) 0) |
| [7] |
路晓峰, 杨志强, 贾小林, 等. 灰色系统理论的优化方法及其在卫星钟差预报中的应用[J]. 武汉大学学报: 信息科学版, 2008, 33(5): 492-495 (Lu Xiaofeng, Yang Zhiqiang, Jia Xiaolin, et al. Parameter Optimization Method of Gray System Theory for the Satellite Clock Error Predicating[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 492-495)
(  0) 0) |
| [8] |
周佩元, 杜兰, 方善传. 北斗系统精密卫星钟差精度评价[J]. 测绘科学, 2015, 40(12): 86-90 (Zhou Peiyuan, Du Lan, Fang Shanchuan. Precision Evaluation of BDS Precise Clock Products[J]. Science of Surveying and Mapping, 2015, 40(12): 86-90)
(  0) 0) |
| [9] |
Epstein M, Freed G, Rajan J. GPS ⅡR Rubidium Clocks: In-Orbit Performance Aspects[C]. 35th Annual Precise Time and Time Interval(PTTI) Systems and Applications Meeting, San Diego CA, 2003
(  0) 0) |
| [10] |
王宇谱, 吕志平, 陈正生, 等. 一种新的钟差预处理方法及在WNN钟差中长期预报中的应用[J]. 武汉大学学报: 信息科学版, 2016, 41(3): 373-379 (Wang Yupu, Lü Zhiping, Chen Zhengsheng, et al. A New Data Preprocessing Method for Satellite Clock Bias and Its Application in WNN to Predict Medium-Term and Long-Term Clock Bias[J]. Geomatics and Information Science of Wuhan University, 2016, 41(3): 373-379)
(  0) 0) |
| [11] |
王阳, 胡彩波, 徐金锋, 等. BD-2在轨卫星钟性能分析[J]. 大地测量与地球动力学, 2019, 39(3): 252-255 (Wang Yang, Hu Caibo, Xu Jinfeng, et al. Performance Analysis of In-Orbit BD-2 Satellite Clock[J]. Journal of Geodesy and Geodynamics, 2019, 39(3): 252-255)
(  0) 0) |
| [12] |
程梦飞, 王宇谱, 薛申辉, 等. 北斗二号卫星导航系统运行末期卫星钟性能评估[J]. 中国惯性技术学报, 2020, 28(3): 372-379 (Cheng Mengfei, Wang Yupu, Xue Shenhui, et al. The Performance Evaluation of Satellite Clocks for BD-2 Navigation Satellite System in the Final Phase[J]. Journal of Chinese Inertial Technology, 2020, 28(3): 372-379)
(  0) 0) |
| [13] |
孙大双, 王宇谱, 万琪, 等. 北斗在轨卫星钟产品质量分析[J]. 测绘科学技术学报, 2017, 34(3): 251-257 (Sun Dashuang, Wang Yupu, Wan Qi, et al. On-Orbit Beidou Satellite Clock Products Quality Analysis[J]. Journal of Geomatics Science and Technology, 2017, 34(3): 251-257)
(  0) 0) |
| [14] |
Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1 735-1 780
(  0) 0) |
| [15] |
吕栋, 欧吉坤, 于胜文. 基于MEA-BP神经网络的卫星钟差预报[J]. 测绘学报, 2020, 49(8): 993-1 003 (Lü Dong, Ou Jikun, Yu Shengwen. Prediction of the Satellite Clock Bias Based on MEA-BP Neural Network[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(8): 993-1 003)
(  0) 0) |
2. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2023, Vol. 43
2023, Vol. 43

