2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054
随着北斗卫星导航系统(BDS)全面建成,BDS开始向全球提供全天候、高精度的导航、定位与授时服务[1]。截至目前,BDS由44颗在轨运行卫星组成,其中北斗二号系统(BDS-2)包括5颗地球静止轨道(GEO)卫星、3颗中圆地球轨道(MEO)卫星和7颗倾斜地球同步轨道(IGSO)卫星,北斗三号系统(BDS-3)包括2颗GEO卫星、24颗MEO卫星和3颗IGSO卫星[2]。与BDS-2不同的是,BDS-3在轨运行的24颗MEO卫星和3颗IGSO卫星播发新体制信号B1C和B2a。由于卫星信号质量直接影响其定位性能,因此BDS-3新信号质量受到业界普遍关注。观测噪声作为信号质量的一个重要指标,泛指导航信号产生端、传播路径、信号接收端产生或引入的各种随机误差对伪距或载波相位测量的综合影响值[3],精确评估观测噪声对衡量测距信号质量以及建立准确的观测值随机模型具有重要意义。
评估接收机观测噪声的主要方法有超短基线比对检验法[4]和零基线测试法[5],超短基线方法无法完全消除接收机的有色噪声[6],而零基线测试法可以消除噪声以外的所有误差源,因此被广泛应用于接收机观测噪声评估。Freymueller[7]利用零基线测试法分析不同类型接收机间的内在偏差,结果表明,零基线测试可去除天线因素的影响,很好地反映接收机间的内部偏差。Bakker等[8]利用零基线实验评估GPS和Galileo信号的热噪声,结果显示,其热噪声约为6 cm,但在较长时段内,伪距测量结果变化很大。Cai等[9]进一步利用零基线法对比分析四大全球卫星导航系统(GNSS)在所有可用频率上的接收机观测噪声。现有研究大多是针对静态数据进行观测噪声评估,为分析GNSS信号在动态条件下的观测噪声,本文在动态环境下采用零基线法分析BDS-3新频点B1C和B2a的伪距和载波相位观测值噪声,并与BDS其他频点及其他GNSS信号频率上的观测噪声进行对比。
1 噪声测量方法零基线是指利用功分器将两个接收机连接到同一天线上,即基线长度为零[6]。在零基线测试中,使用卫星间与测站间观测值双差操作可消除观测噪声以外的其他误差项,双差载波相位和伪距观测值计算公式为:
| $ \begin{gathered} \mathrm{DD}_{\varphi}=\left(L^p-L^q\right)_m-\left(L^p-L^q\right)_n= \\ N_{m n}^{p q}+\left(\varepsilon_{\varphi}\right)_{m n}^{p q} \end{gathered} $ | (1) |
| $ \mathrm{DD}_P=\left(P^p-P^q\right)_m-\left(P^p-P^q\right)_n=\left(\varepsilon_P\right)_{m m}^{p q} $ | (2) |
式中,DDφ和DDP分别为双差载波相位观测值和伪距观测值,m、n为接收机标识,p、q为卫星标识,L为测量的载波相位观测值,P为测量的伪距观测值,Nmnpq为载波相位双差模糊度,(εφ)mnpq和(εP)mnpq分别为双差载波相位和伪距观测噪声。
零基线双差伪距观测值已消除卫星钟差、轨道误差、接收机钟差和大气延迟等误差,故双差观测值仅包含伪距观测噪声。与伪距观测值类似,双差载波相位观测值仅包含载波相位观测噪声和整周模糊度。因此,通过去除双差载波相位观测值中的模糊度,可以得到载波相位观测噪声。对于GPS、Galileo和BDS,双差模糊度序列的均值非常接近整数,而其理论上为整数,因此可以直接四舍五入为最接近的整数。但GLONASS并非如此,由于不同GLONASS卫星的信号频率不同[10],其双差载波相位观测值无法表示为固定波长与双差模糊度的乘积,这会导致固定GLONASS双差模糊度变得较为复杂,考虑到模糊度为常数且观测噪声具有零均值统计特征,因此可将GLONASS双差载波相位观测序列的均值作为模糊度[9]。
2 零基线接收机观测噪声分析为分析BDS-3在新频点B1C和B2a上的观测噪声水平,开展静态和动态环境下的零基线实验,并将BDS-3新频点B1C和B2a上的观测噪声与BDS其他频点以及其他GNSS信号观测噪声进行对比。
2.1 静态零基线实验在中南大学新校区地科楼楼顶进行GNSS零基线数据采集,采样时间为2021-10-17。该实验使用一对Trimble Alloy接收机,通过功分器与Trimble GNSS-Ti第二代扼流圈天线连接组成零基线,该型号接收机可以接收BDS、GPS、GLONASS、Galileo四星座多频信号,采样间隔设置为1 s。
利用式(1)和(2)对各频率载波相位观测值和伪距观测值分别进行双差处理,获得双差观测值序列。图 1和图 2分别为四星座GNSS各频点双差伪距和载波相位观测值的噪声分布,不同颜色代表不同的卫星类型。对于BDS系统,分别给出BDS-2和BDS-3不同卫星类型的噪声分布情况。从图 1可以看出,BDS-3在新频点B1C和B2a上的双差伪距观测噪声分布相当稳定,其中B2a频点上的双差伪距噪声分布与B3I类似,比B1C、B1I和B2I频点更为集中。从卫星类型来看,BDS-3在新频点B1C和B2a上IGSO卫星的噪声分布相对于MEO卫星更集中。从图 1还可以看出,Galileo E1频点的双差伪距观测噪声分布与BDS-3 B1C频点类似,且Galileo其他频点上的伪距观测噪声比E1频点稍小; GPS在L5频点上的双差伪距观测噪声分布与BDS-3 B2a频点相似,且比L1和L2频点更稳定集中; GLONASS在G1和G2信号频率上的噪声变化范围明显更大,可能是由其采用频分多址造成。从图 2可以看出,四星座GNSS大部分相位观测值噪声在-1~1 cm范围内变化,且分布均十分相似。由图 2和表 1(单位cm)可知,GPS BLOCK Ⅲ卫星的相位噪声分布比BLOCK Ⅱ F卫星更集中,但BDS-3 MEO卫星的相位噪声分布比IGSO卫星更分散,噪声RMS值更小。进一步分析得知,个别IGSO卫星在前部分历元即将远离视线,高度角较低,导致观测噪声较大,从而提高了总体的RMS统计值。

|
图 1 四星座GNSS在不同频点上的静态双差伪距观测值噪声分布 Fig. 1 Distribution of double-differenced pseudorange measurement noise for quad-constellation GNSS ondifferent frequencies in static mode |

|
图 2 四星座GNSS在不同频点上的静态双差相位观测值噪声分布 Fig. 2 Distribution of double-differenced phasemeasurement noise for quad-constellation GNSS on different frequencies in static mode |
|
|
表 1 四星座静态GNSS在不同频点上非差载波相位值观测噪声RMS统计 Tab. 1 RMS statistics of undifferenced carrierphase measurement noise for quad-constellationGNSS on different frequencies in static mode |
假设同一类型卫星与接收机的测量噪声水平相同,根据误差传播规律,双差观测噪声将非差观测噪声放大两倍,故非差伪距和载波相位观测噪声的均方根(RMS)统计值可由双差观测噪声RMS除以2得到。表 1(单位cm)和表 2(单位cm)分别为非差载波相位和伪距观测噪声水平。由表 1可知,在相位观测噪声方面,BDS-3在B1C和B2a频点上MEO卫星的观测噪声分别为0.032 cm和0.041 cm,而IGSO卫星的观测噪声分别为0.081 cm和0.096 cm,可见后者观测噪声显著高于前者。与BDS其他频点和其他卫星系统各频点相比,BDS-3 IGSO卫星在B2a频点上的相位观测噪声水平最高,相比之下,Galileo在E1频点上的相位观测噪声水平最低,其值为0.025 cm。总体来说,四星座GNSS的相位观测噪声处于较为类似的水平,RMS变化范围为0.025~0.096 cm,除BDS-3 IGSO卫星,所有GNSS同一类型卫星的频间差异均较小。从表 2可以看出,在伪距观测噪声方面,BDS-3在B1C和B2a频点上MEO卫星的观测噪声RMS值分别为8 cm和5 cm,IGSO卫星的观测噪声分别为8 cm和4 cm,可见B2a频点的伪距观测噪声明显小于B1C频点,通过查阅B1C和B2a信号接口控制文件可知,B2a频点的测距码速率为B1C频点的10倍,因此推断,二者噪声的差异可能是由其测距码速率(或码元宽度)不同所致。BDS-3 GEO和IGSO卫星在B2b频点上的伪距观测噪声均为2 cm,明显低于其他频点及其他类型卫星的噪声水平。相比之下,GLONASS卫星噪声水平最差,其在G1和G2频点上的伪距观测噪声分别为20 cm和24 cm。总的来说,四星座GNSS各频点的伪距观测噪声范围为2~24 cm。
|
|
表 2 四星座静态GNSS在不同频点上非差伪距观测值噪声RMS统计 Tab. 2 RMS statistics of undifferenced pseudorange measurement noise for quad-constellation GNSS on different frequencies in static mode |
在湖南省内进行零基线车载动态数据采集,采样时间为2021-11-18,时长约3 h,采用和静态实验同型号的接收机和天线,采样间隔设置为1 s。运动轨迹和采集设备如图 3所示,动态实验从长沙市中南大学新校区出发,沿西二环路、岳麓大道、长益高速公路和许广高速公路行驶至岳阳市后往南折转,沿京港澳高速公路行驶约55 km后结束。除起始路段存在建筑物和树木遮挡外,其他路段多为公路和高速公路等相对开阔环境。

|
图 3 动态零基线数据采集轨迹及设备 Fig. 3 Trace and equipment of zero-baselinedata acquisition in kinematic mode |
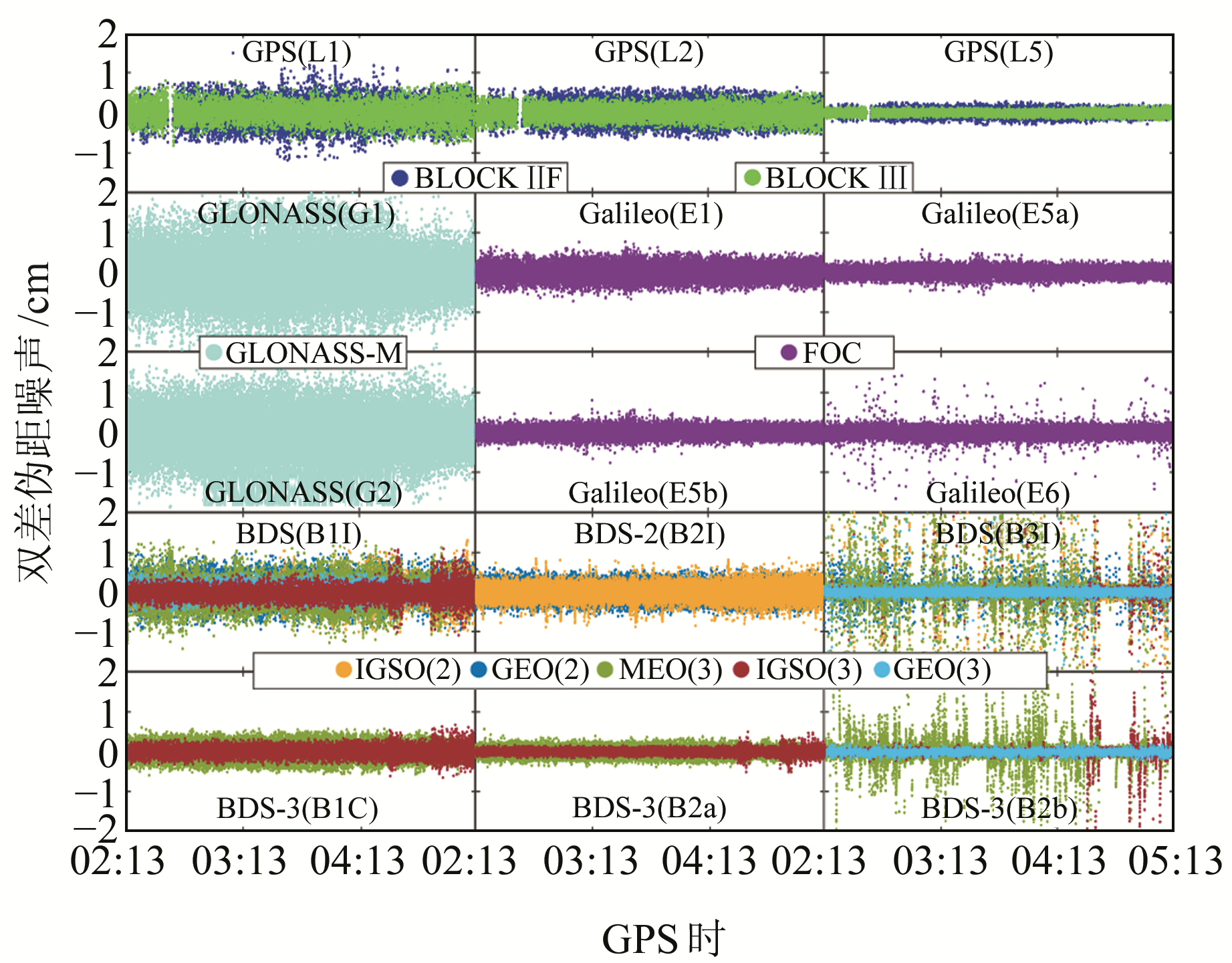
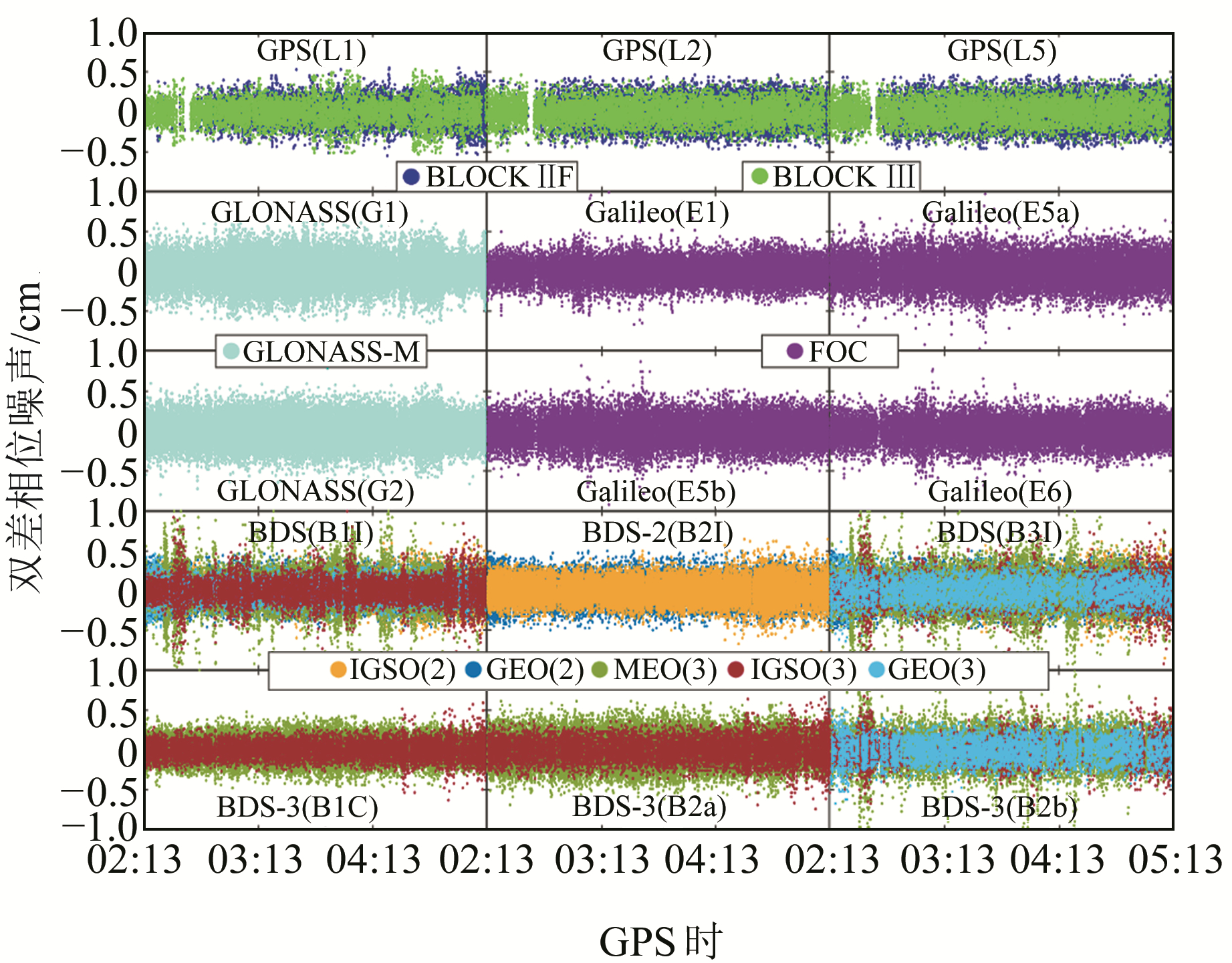
图 4和图 5分别为车载动态环境下使用零基线双差法测量的双差伪距和载波相位观测噪声的分布情况。由图 4可见,BDS-3在新频点B1C和B2a上的双差伪距观测噪声分布较为稳定,B2a频点上的双差伪距噪声分布比B1C频点更集中,表现出与静态实验类似的特性。与静态实验结果不同的是,BDS在B2b和B3I频点上部分卫星的双差伪距噪声分布极为分散,Galileo在E6频点也存在类似情况,且BDS-3 MEO卫星在B1I频点上的双差伪距观测噪声分布比静态环境更为分散,说明部分BDS卫星观测噪声对环境较为敏感。此外,GPS三个频点的双差伪距噪声均分布良好,且L5频点的双差伪距观测噪声分布比BDS B2a频点更稳定集中,表明GPS伪距观测噪声受动态环境影响较小。由图 5可见,与静态实验结果相同,四星座GNSS的相位观测噪声基本在-1~1 cm范围内变化,且分布相似; 与静态实验结果不同的是,BDS部分卫星在B1I、B2b和B3I频点上的双差相位噪声分布较为分散,且多为BDS-3 MEO和IGSO卫星。值得注意的是,尽管动态实验采用跟静态实验同型号的接收机,但并非同一接收机,可能存在不同接收机引起的细微差异。
|
图 4 四星座GNSS在不同频点上的动态双差伪距观测噪声分布 Fig. 4 Distribution of double-differenced pseudorange measurement noise forquad-constellation GNSS on different frequencies in kinematic mode |
|
图 5 四星座GNSS在不同频点上的动态双差载波相位观测噪声分布 Fig. 5 Distribution of double-differenced carrier phase measurement noise for quad-constellation GNSS on different frequencies in kinematic mode |
表 3(单位cm)和表 4(单位cm)分别为车载动态环境下非差载波相位和伪距观测噪声水平。由表 3可知,在载波相位观测噪声方面,BDS-3在B1C和B2a频点上MEO卫星的观测噪声分别为0.061 cm和0.082 cm,而IGSO卫星的观测噪声分别为0.070 cm和0.091 cm,可见B2a频点的相位观测噪声水平高于B1C频点,这可能是由B2a频点的载波波长较长所致。从整体上看,与静态实验相似,四星座GNSS的相位观测噪声处于较为接近的水平,精度范围为0.056~0.097 cm,且4个卫星系统同一类型卫星在不同频率上的频间差异均较小,最大频间差异为0.030 cm,即BDS-3 MEO卫星在B1C和B3I频点上的差值。表 4结果表明,在伪距观测噪声方面,BDS-3在B1C和B2a频点上MEO卫星的观测噪声RMS值分别为8 cm和4 cm,而IGSO卫星的观测噪声分别为8 cm和5 cm,可见B2a频点的伪距观测噪声明显小于B1C频点,该结论与静态实验结果类似。在动态环境下,BDS各类型卫星各频点的伪距观测噪声水平多数高于静态。与其他频点相比,BDS-3 GEO卫星在B2b频点和GPS BLOCK Ⅲ卫星在L5频点上的伪距观测噪声均为3 cm,与B2a频点近似,而GLONASS在G1和G2频点上的伪距观测噪声水平依然最高。
|
|
表 3 四星座动态GNSS在不同频点上非差载波相位观测噪声RMS统计 Tab. 3 RMS statistics of undifferenced carrier phase measurement noise for quad-constellation GNSS on different frequencies in kinematic mode |
|
|
表 4 四星座动态GNSS在不同频点上非差伪距观测噪声RMS统计 Tab. 4 RMS statistics of undifferenced pseudorange measurement noise for quad-constellation GNSS on different frequencies in kinematic mode |
总体来说,从双差噪声的分布情况和非差噪声的RMS统计值来看,BDS-3新频点B1C和B2a的伪距观测噪声在静态和动态环境下差异不大,但载波相位观测噪声的差异较为显著,MEO卫星在静态环境下的相位观测噪声RMS值明显低于动态,其在B1C和B2a频点上的差值分别为0.029 cm和0.041 cm。从四星座整体上看,静态环境下的伪距观测噪声水平和噪声分布比动态更集中,而对于载波相位观测值来说,观测噪声分布差异并不显著,但静态环境下的噪声水平则比动态环境下小。
3 结语本文基于静态和动态零基线实验,对比分析BDS-3 B1C和B2a新信号在静态和动态两种环境下的伪距和载波相位观测值噪声,并与BDS其他频点及其他GNSS频点的观测噪声进行比较。
通过动态零基线实验可知,BDS-3在B1C和B2a频点上MEO卫星的非差伪距观测噪声RMS值分别为8 cm和4 cm,相位噪声分别为0.061 cm和0.082 cm,而IGSO卫星的伪距噪声分别为8 cm和5 cm,相位噪声分别为0.070 cm和0.091 cm。结果表明,BDS-3在B1C频点上的载波相位观测噪声优于B2a频点,而在伪距噪声上却差于B2a频点。与其他频点相比,BDS-3 GEO卫星在B2b频点和GPS BLOCK Ⅲ卫星在L5频点上的伪距观测噪声均为3 cm,与B2a频点近似。相比之下,GLONASS卫星噪声水平最差,其在G1频点上的伪距观测噪声为26 cm。而四星座GNSS的载波相位观测噪声处于较为接近的水平,RMS变化范围为0.056~0.097 cm。
尽管动态数据质量变差,但从零基线分析结果来看,动态环境下B1C和B2a频点的伪距观测噪声与静态相比差异不大,载波相位观测噪声的差异却较为显著,BDS-3 MEO卫星在静态环境下的相位观测噪声RMS值明显低于动态,其在B1C和B2a频点上的差值分别为0.029 cm和0.041 cm。对四星座整体而言,静态环境下的伪距观测噪声水平和分布比动态更集中,而载波相位观测噪声分布的差异并不显著,相比之下,静态环境下的噪声水平比动态环境下更小。
| [1] |
许扬胤, 杨元喜, 曾安敏, 等. 北斗三号全球系统空间信号精度评估分析[J]. 大地测量与地球动力学, 2020, 40(10): 1 000-1 006 (Xu Yangyin, Yang Yuanxi, Zeng Anmin, et al. Accuracy Assessment of Signal in Space of BDS-3 Global System[J]. Journal of Geodesy and Geodynamics, 2020, 40(10): 1 000-1 006)
(  0) 0) |
| [2] |
Test and Assessment Research Center of China Satellite Navigation Office. BDS Constellation Status[EB/OL]. http://www.csno-tarc.cn/en/system/constellation
(  0) 0) |
| [3] |
China Satellite Navigation Office. Observation Data Quality Assessment Methods for BDS/GNSS Geodetic Receiver[Z]. 2019
(  0) 0) |
| [4] |
Amiri-Simkooei A R, Tiberius C C J M. Assessing Receiver Noise Using GPS Short Baseline Time Series[J]. GPS Solutions, 2007, 11(1): 21-35
(  0) 0) |
| [5] |
Zhang H Y, Ji S Y, Wang Z J, et al. Detailed Assessment of GNSS Observation Noise Based Using Zero Baseline Data[J]. Advances in Space Research, 2018, 62(9): 2 454-2 466 DOI:10.1016/j.asr.2018.07.023
(  0) 0) |
| [6] |
张文峰, 胡玉坤. BDS/GPS兼容接收机噪声检测方法研究[J]. 测绘地理信息, 2019, 44(3): 77-80 (Zhang Wenfeng, Hu Yukun. Research on Noise Detection Method of BDS/GPS Compatible Receiver[J]. Journal of Geomatics, 2019, 44(3): 77-80)
(  0) 0) |
| [7] |
Freymueller J T. Comparison of Baseline Results for the TI-4100 and Trimble 4000SDT Geodetic GPS Receivers[J]. Bulletin Géodésique, 1992, 66(3): 272-280 DOI:10.1007/BF02033187
(  0) 0) |
| [8] |
Bakker P F, Tiberius C C J M, Marel H, et al. Short and Zero Baseline Analysis of GPS L1 C/A, L5Q, GIOVE E1B, and E5aQ Signals[J]. GPS Solutions, 2012, 16(1): 53-64 DOI:10.1007/s10291-011-0202-3
(  0) 0) |
| [9] |
Cai C S, He C, Santerre R, et al. A Comparative Analysis of Measurement Noise and Multipath for Four Constellations: GPS, BeiDou, GLONASS and Galileo[J]. Survey Review, 2016, 48(349): 287-295 DOI:10.1179/1752270615Y.0000000032
(  0) 0) |
| [10] |
刘志强, 王解先, 段兵兵. 单站多参数GLONASS码频间偏差估计及其对组合精密单点定位的影响[J]. 测绘学报, 2015, 44(2): 150-159 (Liu Zhiqiang, Wang Jiexian, Duan Bingbing. Estimation of GLONASS Code Inter-Frequency Biases with Multiple Parameters Based on a Single Station and Its Impact on Combined Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 150-159)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China
 2023, Vol. 43
2023, Vol. 43


