北斗卫星导航系统BDS由我国自主研发,已经完成了从区域定位系统BDS-2到全球定位系统BDS-3的建设[1]。2020-07-31,BDS-3正式开通,为全球用户提供高精度的定位、导航与授时(positioning navigation and timing, PNT)服务,这标志着我国北斗“三步走”的发展战略圆满完成。BDS-2目前的在轨运行卫星包括5颗地球静止轨道GEO卫星、7颗倾斜地球同步轨道IGSO卫星和3颗中圆地球轨道MEO卫星,分别在B1I、B2I和B3I三个频率上播发信号。BDS-3由3颗GEO卫星、3颗IGSO卫星和24颗MEO卫星组成,除了支持传统的B1I和B3I信号外,还播发B1C、B2a和B2b新信号。BDS-3包含更多的MEO卫星,其轨道精度高、几何结构变化快,可以进一步加快收敛速度、提升定位精度[2-3]。
精密单点定位(PPP)技术利用精密轨道和钟差产品,对各项误差模型进行精确改正,实现单台接收机的cm级绝对定位[4-5]。随着BDS-3的不断完善和各机构提供的精密产品精度不断提升,国内外许多学者对BDS-2/BDS-3精密单点定位的性能进行分析:王利军等[6]分析BDS-3实时精密单点定位精度;马会林等[7]分析BDS-3对BDS-2 PPP的增强效果,但并未考虑BDS-2/BDS-3存在系统间偏差ISB的问题;由于信号调制方式和特性不一致,Qin等[8]证实接收机在处理BDS-2和BDS-3信号时会产生一定的系统性偏差,可以将两者建模为2个系统进行数据处理;Zhao等[9]评估BDS-2和BDS-3系统间偏差的特性及其对PPP性能的影响。
上述研究在进行BDS-2/BDS-3 PPP性能分析时,均采用共有的B1I/B3I信号,在估计ISB参数时,也是针对这2种信号,鲜有文献对BDS-2 B1I/B3I和BDS-3 B1C/B2a组合的PPP定位性能进行研究。本文首先介绍顾及ISB参数的BDS-2/BDS-3 PPP函数模型,然后分别进行BDS-2 B1I/B3I信号与BDS-3 B1I/B3I、B1C/B2a信号的ISB参数特性分析,最后分别使用B1I/B3I和B1C/B2a信号对BDS-2/BDS-3静态和动态PPP的定位性能进行评估。
1 BDS-2/BDS-3 PPP函数模型无电离层组合(ionosphere-free, IF)观测值可以消除一阶电离层延迟的影响,常用于BDS精密单点定位。BDS伪距和载波相位观测值的IF组合模型可以表示为:
| $ \left\{\begin{array}{l} p_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{Q}}=\rho_{\mathrm{r}}^{\mathrm{s}, \mathrm{Q}}+c\left(\mathrm{~d} t_{\mathrm{r}}-\mathrm{d} t^{\mathrm{s}, \mathrm{Q}}\right)+T_{\mathrm{r}}^{\mathrm{s}, \mathrm{Q}}+ \\ \quad d_{{\rm{r}}, {\rm{IF}}}^Q - d_{{\rm{IF}}}^{{\rm{s}}, {\rm{Q}}} + {\varepsilon _{p_{{\rm{r}}, {\rm{IF}}}^{{\rm{s}}, {\rm{Q}}}}} \\ L_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{Q}}=\rho_{\mathrm{r}}^{\mathrm{s}, \mathrm{Q}}+c\left(\mathrm{~d} t_{\mathrm{r}}-\mathrm{d} t^{\mathrm{s}, \mathrm{Q}}\right)+T_{\mathrm{r}}^{\mathrm{s}, \mathrm{Q}}+ \\ \quad \lambda_{\mathrm{IF}}\left(N_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{Q}}+b_{\mathrm{r}, \mathrm{IF}}^Q-b_{\mathrm{IF}}^{\mathrm{s}, \mathrm{Q}}\right)+\varepsilon_{l_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{Q}}} \end{array}\right. $ | (1) |
式中,上标s和下标r分别为卫星和接收机,上标Q为卫星系统,ρrs, Q为卫星和接收机之间的几何距离,c为光速,dtr和dts, Q分别为接收机和卫星钟差,Trs, Q为倾斜路径对流层延迟,dr, IFQ和dIFs, Q分别为接收机和卫星端伪距IF组合硬件延迟,br, IFQ和bIFs, Q分别为接收机和卫星端的载波相位IF组合硬件延迟,λIF为IF组合的波长,Nr, IFs, Q为IF组合的模糊度,εpr, IFs, Q和εLr, IFs, Q分别为伪距和载波IF组合未模型化的误差和观测噪声。
在PPP参数解算过程中,硬件延迟和钟差参数难以分离,卫星的伪距硬件延迟被卫星钟差吸收,接收机伪距硬件延迟被接收机钟差吸收。由于信号频率和结构存在差异,因此不同系统间的接收机伪距硬件延迟也不同,导致BDS-2和BDS-3之间存在系统间偏差。为研究BDS-2和BDS-3之间的ISB特性,本文选取BDS-3的接收机钟差作为参考,在BDS-2的观测方程中引入ISB参数。BDS-2/BDS-3的PPP数学模型可表示为:
| $ \left\{ \begin{array}{l} p_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 2}=\rho_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 2}+c\left(\mathrm{~d} t_{\mathrm{r}}^{\prime {C} 3}-\mathrm{d} t^{\prime \mathrm{s}, \mathrm{C} 2}\right)+ \\\;\;\;\; T_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 2}+\mathrm{ISB}_{\mathrm{r}}+\varepsilon_{p_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C2}}} \\ p_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3}=\rho_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 3}+c\left(\mathrm{~d} t_{\mathrm{r}}^{\prime {C} 3}-\mathrm{d} t^{\prime \mathrm{s}, \mathrm{C} 3}\right)+ \\\;\;\;\; T_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 3}+\varepsilon_{p_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3}} \\ L_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 2}=\rho_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 2}+c\left(\mathrm{~d} t_{\mathrm{r}}^{\prime {C} 3}-\mathrm{d} t^{\prime \mathrm{s}, \mathrm{C} 2}\right)+ \\\;\;\;\; T_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 2}+\lambda_{\mathrm{IF}} B_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 2}+\mathrm{ISB}_{\mathrm{r}}+\varepsilon_{l_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 2}} \\ L_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3}=\rho_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 3}+c\left(\mathrm{~d} t_{\mathrm{r}}^{\prime {C} 3}-\mathrm{d} t^{\prime \mathrm{s}, \mathrm{C} 3}\right)+ \\ \;\;\;\; T_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 3}+\lambda_{\mathrm{IF}} B_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3}+\varepsilon_{l_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C3}}} \end{array} \right. $ | (2) |
其中,
| $ \left\{\begin{array}{l} c \mathrm{~d} t_{\mathrm{r}}^{\prime \mathrm{C} 3}=c \mathrm{~d} t_{\mathrm{r}}+\mathrm{d}_{\mathrm{r}, \mathrm{IF}}^{\mathrm{C} 3} \\ c \mathrm{~d} t^{\prime \mathrm{s}, \mathrm{C} 2}=c \mathrm{~d} t^{\mathrm{s}, \mathrm{C} 2}+\mathrm{d}_{\mathrm{IF}}^{\mathrm{s}, \mathrm{C} 2} \\ c \mathrm{~d} t^{\prime \mathrm{s}, \mathrm{C} 3}=c \mathrm{~d} t_{\mathrm{r}}^{\mathrm{s}, \mathrm{C} 3}+\mathrm{d}_{\mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3} \end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l} \mathrm{ISB}_{\mathrm{r}}=d_{\mathrm{IF}}^{\mathrm{s} , \mathrm{C} 2}-d_{\mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3} \\ B_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{CF}}=N_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 2}+\left(b_{\mathrm{r}, \mathrm{FF}}^{{C} 2}-b_{\mathrm{IF}}^{\mathrm{s}, \mathrm{C} 2}\right)- \\ \quad\left(d_{\mathrm{r}, \mathrm{IF}}^{{C} 2}-d_{\mathrm{IF}}^{\mathrm{s}, \mathrm{C} 2}\right) / \lambda_{\mathrm{IF}} \\ B_{\mathrm{r}, \mathrm{CF}}^{\mathrm{s}, \mathrm{C} 3}=N_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3}+\left(b_{\mathrm{r}, \mathrm{IF}}^{{C} 3}-b_{\mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3}\right)- \\ \quad\left(d_{\mathrm{r}}^{{C} 3}-d_{\mathrm{IF}}^{\mathrm{s}, \mathrm{C} 3}\right) / \lambda_{\mathrm{IF}} \end{array}\right. $ | (4) |
式中,C2为BDS-2,C3为BDS-3。
2 数据来源与解算策略为验证BDS-2/BDS-3静态和动态PPP的性能,选取亚太区域的10个MGEX测站(图 1)2022年年积日(doy)001~030的观测数据。测站共包含4种类型的接收机,均可接收BDS-2 B1I/B3I和BDS-3 B1I/B3I、B1C/B2a信号,观测数据的采样间隔为30 s,测站接收机类型如表 1所示。
|
图 1 亚太区域10个MGEX测站分布 Fig. 1 Distribution of 10 MGEX stations in Asia Pacific area |
|
|
表 1 测站接收机类型 Tab. 1 Types of receivers at different stations |
本文使用武汉大学发布的精密轨道和钟差产品WUM以及中国科学院发布的多系统DCB产品,进行BDS-2/BDS-3卫星的伪距偏差改正。测站接收机钟差作为白噪声估计,BDS-2与BDS-3之间的ISB作为常量进行参数估计;对流层干延迟采用Saastamoinen模型进行改正[10],湿延迟采用随机游走模型进行估计;天线相位中心偏差(phase center offset, PCO)和天线相位中心变化(phase center variation, PCV)通过IGS提供的文件igs14_2190.atx进行改正。此外,相位缠绕、地球固体潮汐、海洋潮汐、地球自转、相对论效应等采用相应的模型进行改正。具体的解算策略如表 2所示。
|
|
表 2 BDS-2/BDS-3 PPP解算策略 Tab. 2 BDS-2/BDS-3 PPP solution strategy |
按照表 2的解算策略,首先计算图 1中10个MGEX测站BDS-2和BDS-3之间的ISB参数,并对其量级和稳定性进行分析;然后分别计算静态和动态模式下BDS-2、BDS-3和BDS-2/BDS-3 PPP的性能。其中,BDS-3分别使用B1I/B3I和B1C/B2a两种信号;BDS-2和BDS-3组合时,对比分析改正ISB参数对PPP性能的影响。
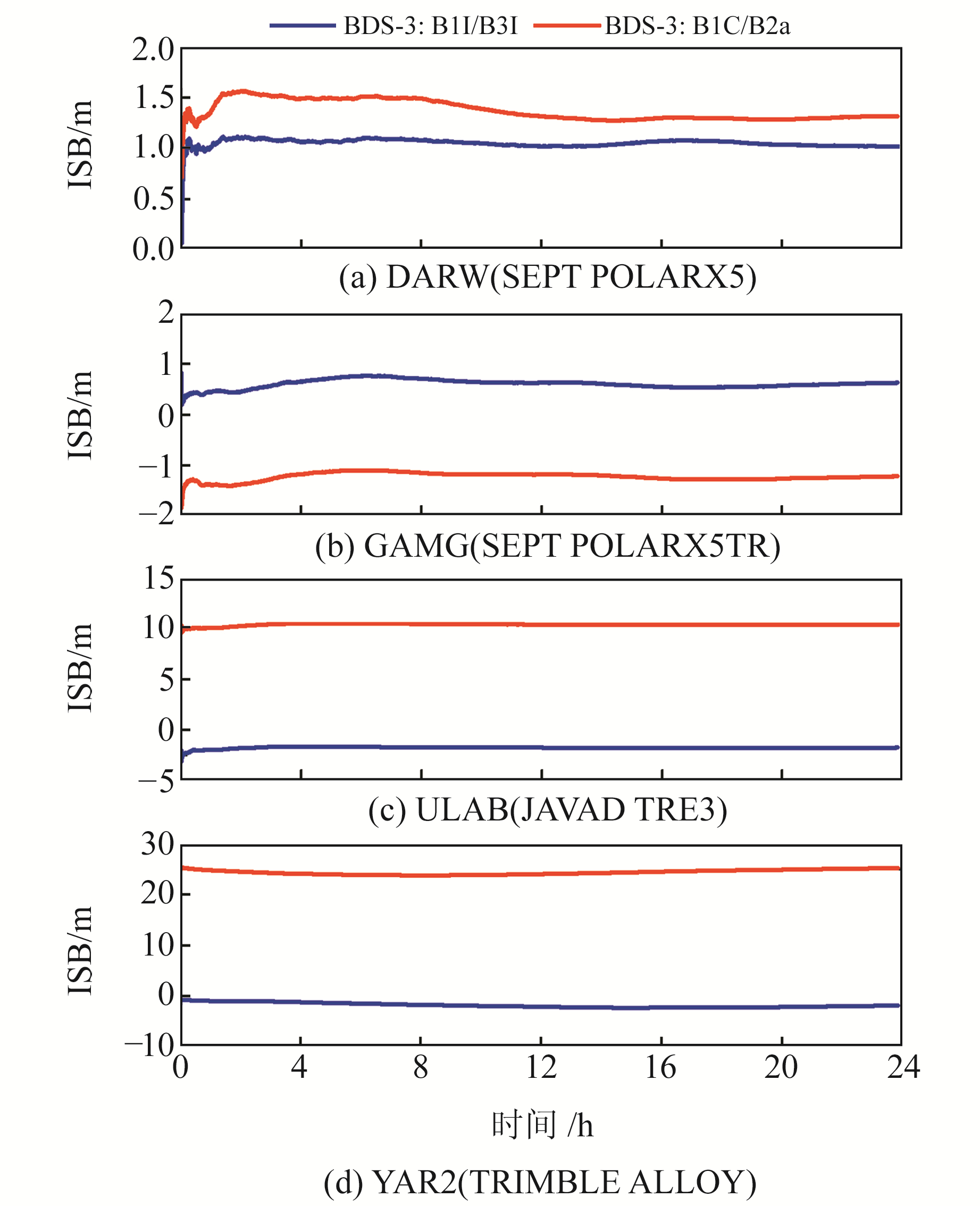
3.1 BDS-2和BDS-3之间的ISB特性分析由表 1的测站接收机类型可知,本文选取的10个MGEX站共包含4种类型的接收机,以这4种类型接收机为代表的测站DARW、GAMG、ULAB及YAR2的BDS-2/BDS-3 ISB的时间序列如图 2所示。由图可见,BDS-2与BDS-3 B1I/B3I信号之间的ISB参数均在2 m以内,且在1 d内具有较好的稳定性,其天内STD均在0.1 m以内;BDS-2 B1I/B3I与BDS-3 B1C/B2a信号之间ISB参数的量级明显较大,甚至超过20 m。这是由于BDS-3新信号采用了不同的信号频率和调制方式。BDS新、老信号间的ISB参数同样具有较好的稳定性,其天内STD也均在0.1 m以内。
|
图 2 部分测站在doy 002的BDS-2/BDS-3 ISB时间序列 Fig. 2 The time series of BDS-2/BDS-3 ISB of partial station at doy 002 |
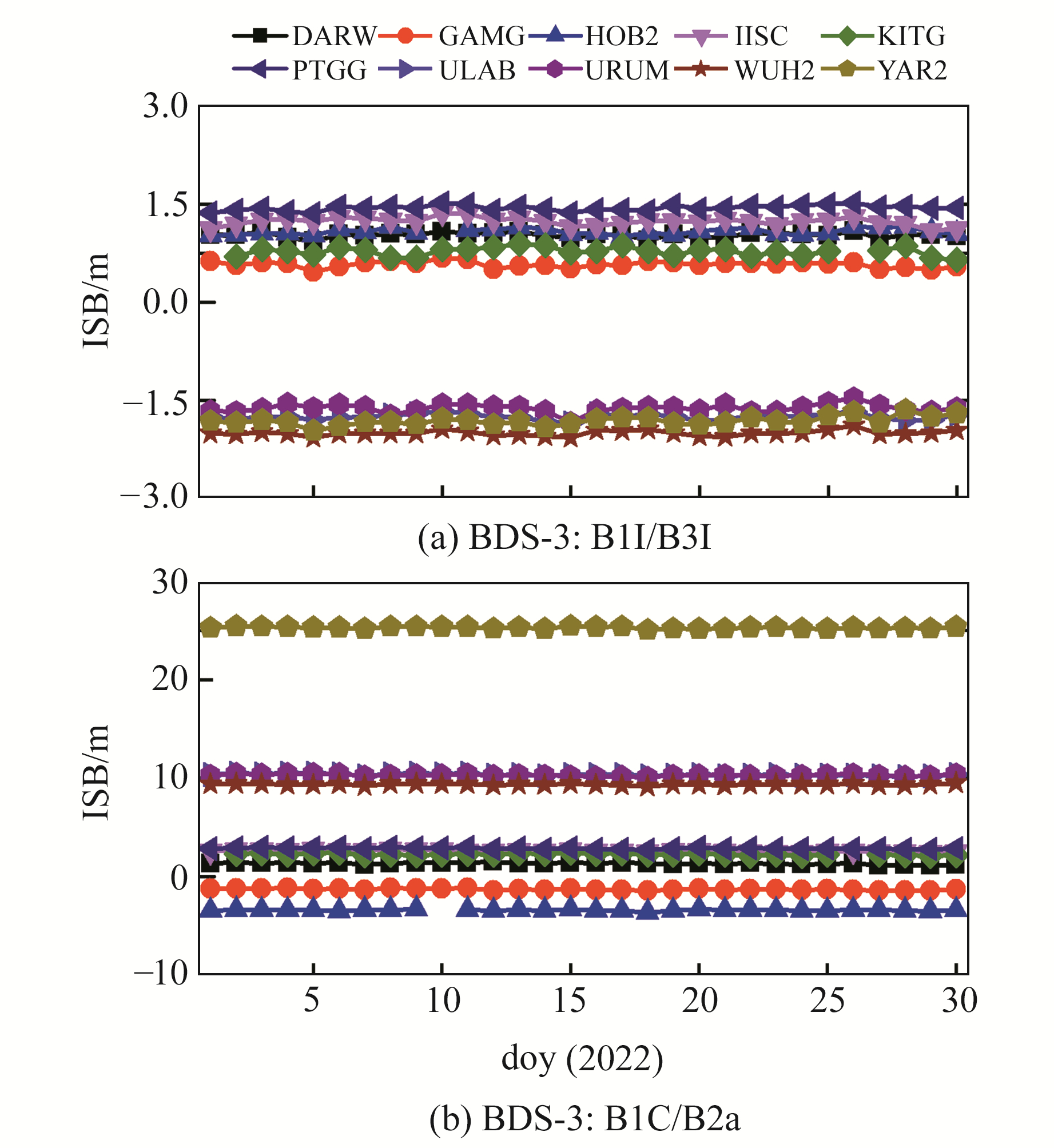
图 3为10个MGEX测站连续30 d的BDS-2/BDS-3 ISB天均值。由图可见,BDS-2与BDS-3 B1I/B3I信号之间的ISB均具有较好的天间稳定性,所有站的平均天间STD为0.053 m;BDS-2 B1I/B3I与BDS-3 B1C/B2a信号之间ISB的天间稳定性稍差,这也和不同频率信号混用有关,所有站的平均天间STD为0.086 m。
|
图 3 10个MGEX测站30 d的BDS-2/BDS-3 ISB天均值 Fig. 3 30 days average of BDS-2/BDS-3 ISB for 10 MGEX stations |
由此可知,无论BDS-3使用B1I/B3I还是B1C/B2a信号,在进行BDS-2/BDS-3 PPP研究时,均应考虑系统间偏差,并在PPP解算过程中对其进行估计。
3.2 静态PPP性能分析在静态PPP实验中,将IGS发布的周解算坐标(snx文件)作为参考值,收敛条件设置为E、N、U三个方向上连续10 min的位置误差分别小于5 cm、5 cm和10 cm。图 4为WUH2测站在doy 002的BDS静态PPP误差序列,其中BDS-3使用B1C/B2a信号。由图可见,BDS-3的静态PPP性能明显优于BDS-2,加入BDS-2卫星后,可以进一步加快BDS-2/BDS-3静态PPP的收敛速度。
|
图 4 WUH2测站在doy 002的BDS静态PPP误差序列 Fig. 4 BDS static PPP error sequence of WUH2 station at doy 002 |
图 5为10个MGEX测站10 d的BDS静态PPP平均收敛时间和定位精度(有ISB表示估计ISB参数,无ISB表示不估计ISB参数),表 3为收敛时间与定位误差统计信息(C3表示BDS-3,C23表示BDS-2+BDS-3,下表相同)。由图 5和表 3可以看出,BDS-3静态PPP的定位性能显著优于BDS-2,BDS-2和BDS-3联合解算均可显著提升单系统的定位性能。与单BDS-2相比,BDS-2与BDS-3组合静态PPP定位收敛时间由75.6 min缩短至36.4 min,提高51.9%,E、N、U三个方向上的定位精度也分别提升43.0%、32.7%和62.6%。BDS-3 B1C/B2a信号参与解算后,静态PPP的收敛时间比B1I/B3I信号缩短约6.4%,收敛后的定位精度基本相当。
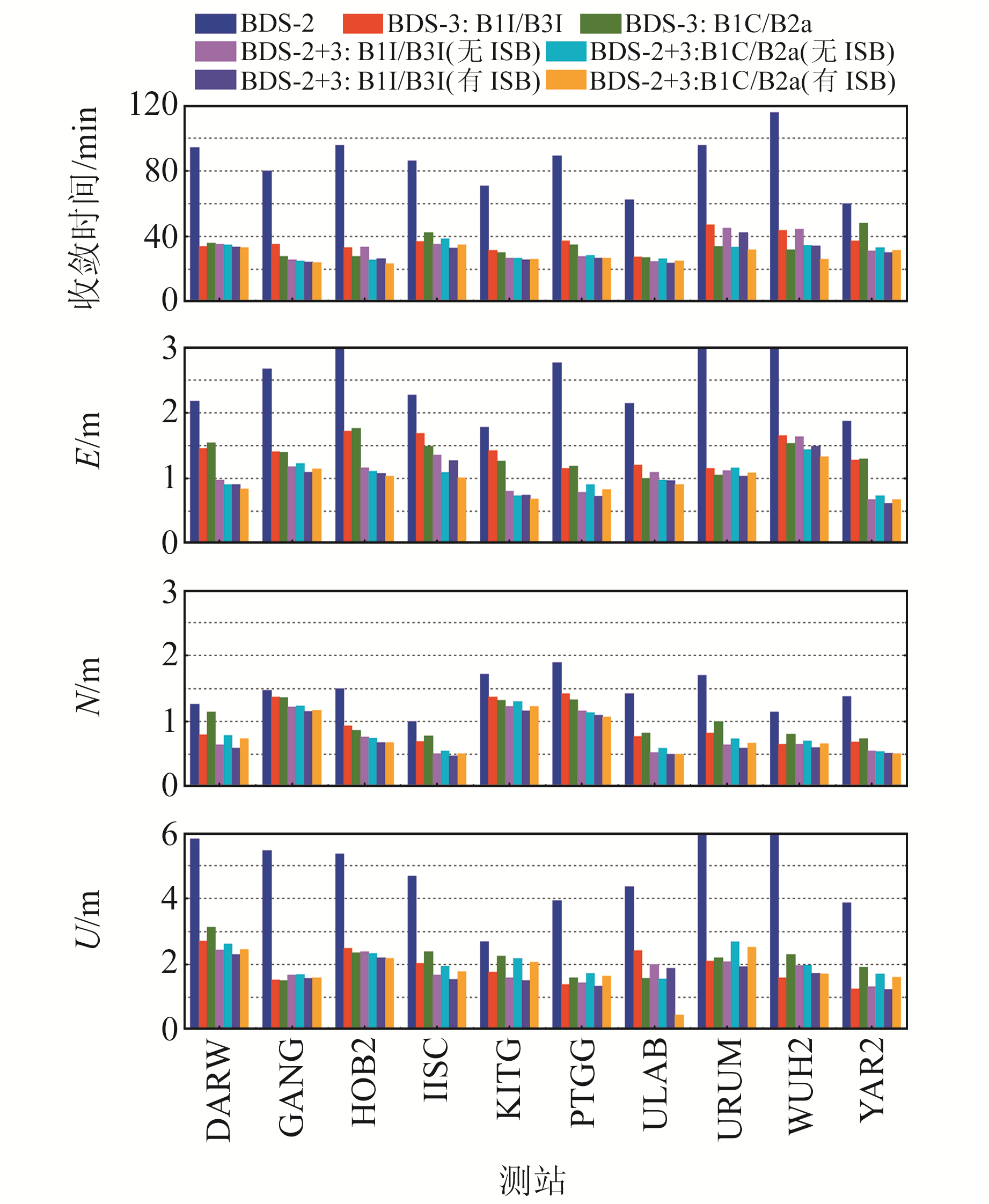
|
图 5 10个MGEX测站10 d的BDS静态PPP平均收敛时间和定位精度 Fig. 5 10 days BDS static PPP average convergence time and positioning accuracy for 10 MGEX stations |
|
|
表 3 BDS静态PPP收敛时间与定位误差统计 Tab. 3 BDS static PPP convergence time and positioning error statistics |
BDS-3 B1I/B3I信号参与解算估计ISB参数后,静态PPP的收敛时间由33.0 min缩短至30.1 min,收敛后的定位精度提升7.1%;BDS-3 B1C/B2a信号参与解算估计ISB参数后,静态PPP的收敛时间由30.8 min缩短至28.4 min,收敛后的定位精度提升6.7%,上述差异可能与伪距偏差的改正有关。若不估计ISB参数,BDS-2和BDS-3的伪距观测值之间存在伪距偏差;估计ISB参数后,BDS-2和BDS-3的伪距观测值精度得到提升,进而提升定位性能。
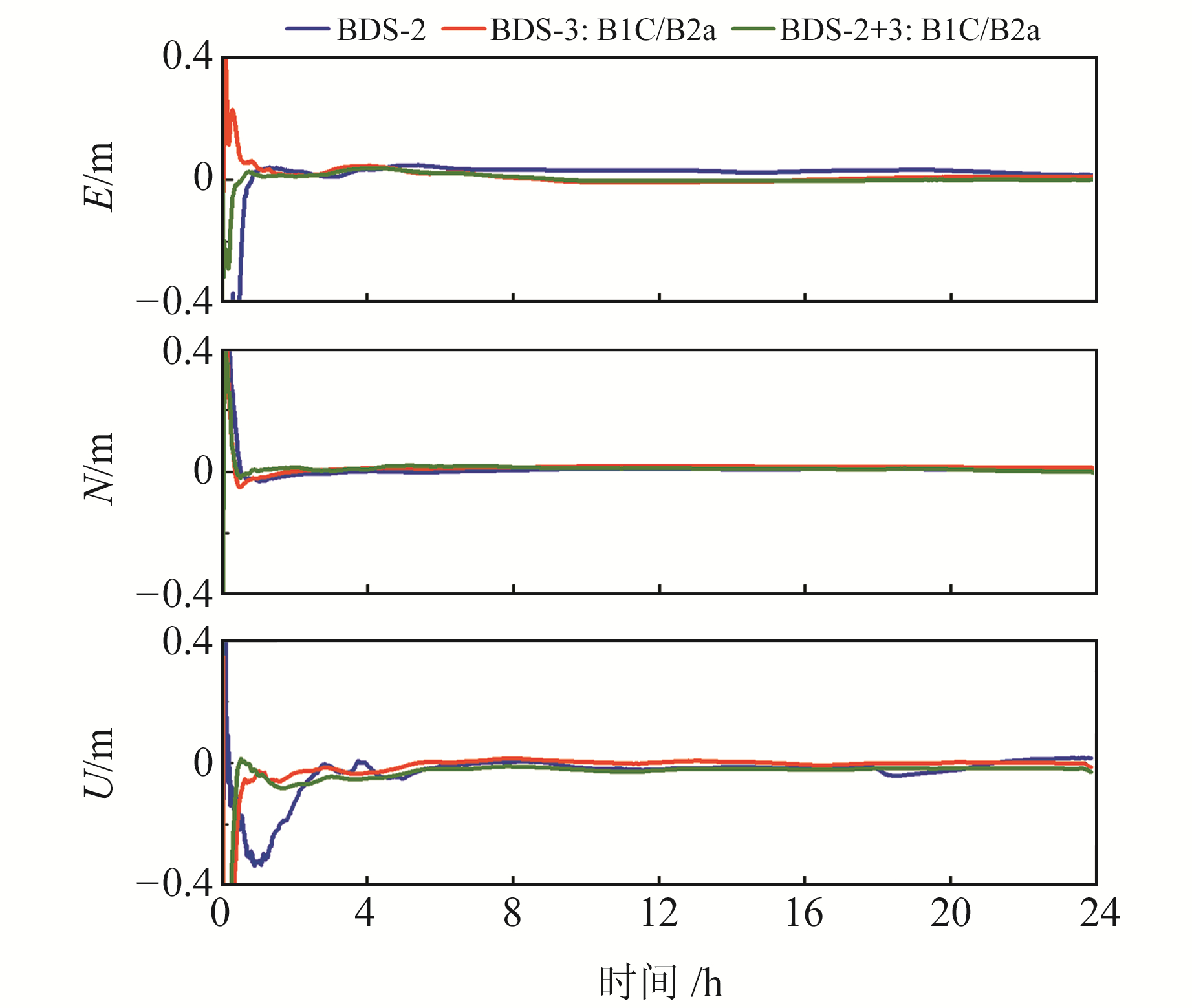
3.3 动态PPP性能分析在动态PPP实验中,收敛条件设置为E、N、U三个方向上连续10 min的位置误差分别小于10 cm、10 cm和15 cm。图 6为WUH2测站在doy 002的BDS动态PPP误差序列,其中BDS-3使用B1C/B2a信号。由图可见,单BDS-2的动态PPP性能较差,BDS-3的动态PPP性能也明显优于BDS-2,可以改善定位发散的情况。
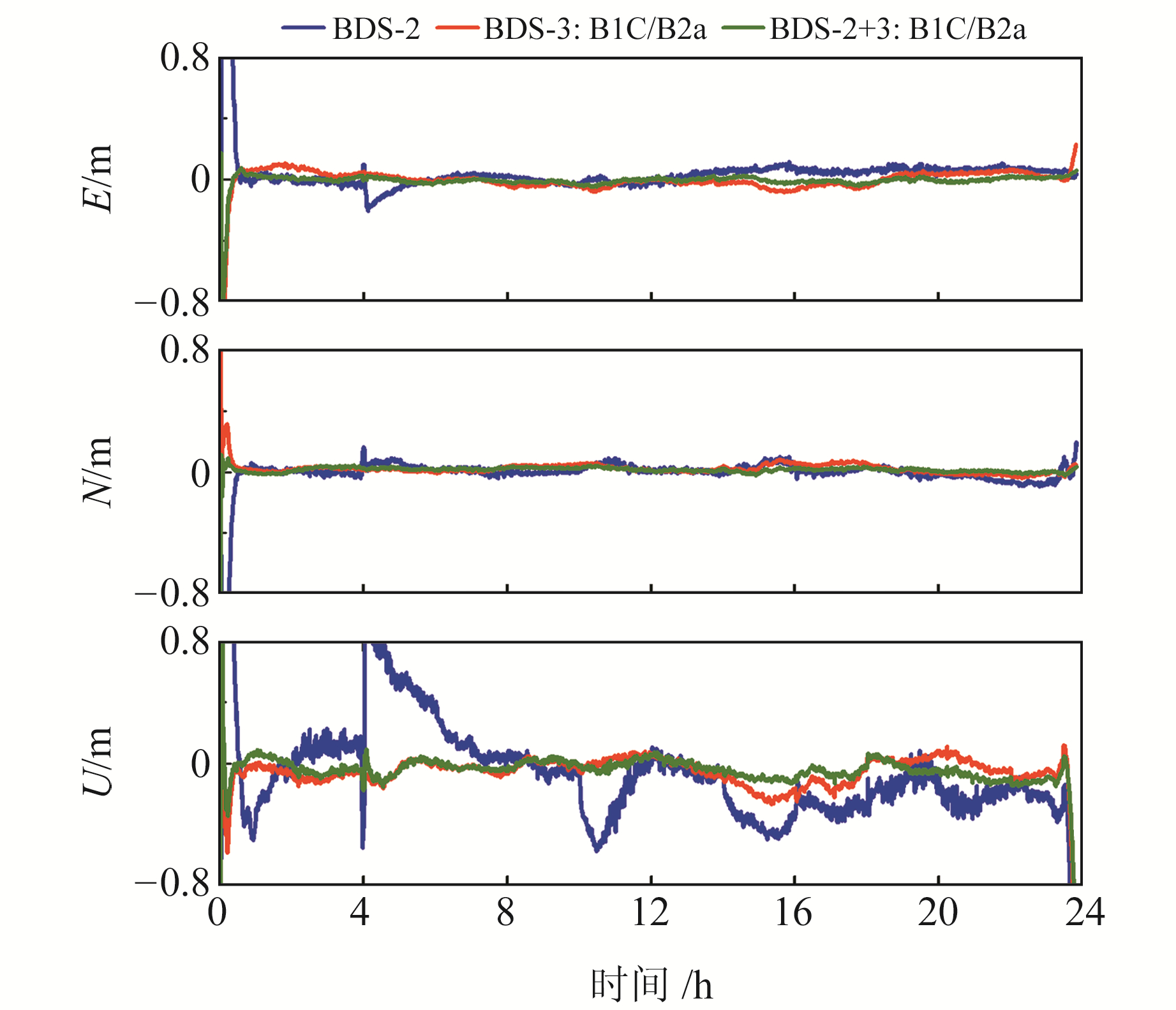
|
图 6 WUH2站在doy 002的BDS动态PPP误差序列 Fig. 6 BDS kinematic PPP error sequence of WUH2 station at doy 002 |
图 7为10个MGEX测站10 d的BDS动态PPP平均收敛时间和定位精度结果,表 4为收敛时间与定位误差统计信息。由图 7和表 4可以看出,BDS-2和BDS-3联合解算均可显著提升单系统的动态定位性能。与单BDS-2相比,BDS-2与BDS-3组合动态PPP收敛时间由79.0 min缩短至36.8 min,提高53.4%,E、N、U三个方向上的定位精度也分别提升50.1%、54.0%和53.8%。与静态PPP类似,BDS-3 B1C/B2a信号参与解算后,动态PPP的收敛时间也比B1I/B3I信号缩短约6.7%,收敛后的定位精度基本相当。

|
图 7 10个MGEX测站10 d的BDS动态PPP平均收敛时间和定位精度 Fig. 7 10 days BDS kinematic PPP average convergence time and positioning accuracy of 10 MGEX stations |
|
|
表 4 BDS动态PPP收敛时间与定位误差统计 Tab. 4 BDS kinematic PPP convergence time and positioning error statistics |
当BDS-3 B1I/B3I信号参与解算估计ISB参数后,可使动态PPP的收敛时间由32.7 min缩短至28.6 min,收敛后的定位精度提升7.1%;当BDS-3 B1C/B2a信号参与解算估计ISB参数后,可使动态PPP的收敛时间由30.5 min缩短至26.4 min,收敛后的定位精度提升6.0%。
4 结语1) BDS-2与BDS-3 B1I/B3I信号之间的ISB参数均在2 m以内,与B1C/B2a信号之间的ISB参数较大,部分接收机超过20 m,但均具有较好的天内和天间稳定性;
2) 与BDS-3 B1I/B3I数据相比,BDS-3 B1C/B2a数据参与PPP解算后,静态和动态PPP的收敛时间均缩短约6%;
3) 估计ISB参数后,BDS-2/BDS-3静态和动态PPP的收敛时间分别缩短8.8%和12.6%,定位精度均提升7.1%。
随着BDS-3系统和精密产品的不断完善,基于多种信号的BDS PPP定位性能将得到进一步提升,能够满足各类高精度应用的需求。
| [1] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测: 试验验证数据分析[J]. 中国科学: 地球科学, 2018, 48(5): 584-594 (Yang Yuanxi, Xu Yangyin, Li Jinlong, et al. Progress and Performance Evaluation of Beidou Global Navigation Satellite System: Data Analysis Based on BDS-3 Demonstration System[J]. Scientia Sinica(Terrae), 2018, 48(5): 584-594)
(  0) 0) |
| [2] |
Shi J B, Ouyang C H, Huang Y S, et al. Assessment of BDS-3 Global Positioning Service: Ephemeris, SPP, PPP, RTK, and New Signal[J]. GPS Solutions, 2020, 24(3): 1-14
(  0) 0) |
| [3] |
许扬胤, 杨元喜, 曾安敏, 等. 北斗三号全球系统空间信号精度评估分析[J]. 大地测量与地球动力学, 2020, 40(10): 1000-1006 (Xu Yangyin, Yang Yuanxi, Zeng Anmin, et al. Progress and Performance Evaluation of Beidou Global Navigation Satellite System: Data Analysis Based on BDS-3[J]. Journal of Geodesy and Geodynamics, 2020, 40(10): 1000-1006)
(  0) 0) |
| [4] |
Zumberge J F, Heflin M B, Jefferson D C, et al. PrecisePoint Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017 DOI:10.1029/96JB03860
(  0) 0) |
| [5] |
叶世榕. GPS非差相位精密单点定位理论与实现[D]. 武汉: 武汉大学, 2002 (Ye Shirong. Theory and Its Realization of GPS Precision Point Positioning Using Un-Differenced Phase Observation[D]. Wuhan: Wuhan University, 2002)
(  0) 0) |
| [6] |
王利军, 焦文海, 贾小林, 等. BDS-3精密单点定位性能比较分析[J]. 大地测量与地球动力学, 2021, 41(4): 357-361 (Wang Lijun, Jiao Wenhai, Jia Xiaolin, et al. Comparative Analysis of BDS-3 Precise Point Positioning Performance[J]. Journal of Geodesy and Geodynamics, 2021, 41(4): 357-361)
(  0) 0) |
| [7] |
马会林, 吴文坛, 吴秀丽. 亚太区域北斗三号对北斗二号精密单点定位的增强效果分析[J]. 测绘通报, 2022(1): 56-60 (Ma Huilin, Wu Wentan, Wu Xiuli. Performance Analysis of BDS-2 Precise Point Positioning Augmented by BDS-3 within the Asia-Pacific Region[J]. Bulletin of Surveying and Mapping, 2022(1): 56-60)
(  0) 0) |
| [8] |
Qin W J, Ge Y L, Zhang Z, et al. Accounting BDS3-BDS2 Inter-System Biases for Precise Time Transfer[J]. Measurement, 2020, 156
(  0) 0) |
| [9] |
Zhao W, Chen H, Gao Y, et al. Evaluation ofInter-System Bias between BDS-2 and BDS-3 Satellites and Its Impact on Precise Point Positioning[J]. Remote Sensing, 2020, 12(14): 2185
(  0) 0) |
| [10] |
Saastamoinen J. AtmosphericCorrection for the Troposphere and Stratosphere in Radio Ranging Satellites[J]. The Use of Artificial Satellites for Geodesy, 1972, 15: 247-251
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

