全球导航卫星系统的发展与完善为多系统GNSS融合定位、导航和授时奠定了良好基础[1]。2020-07-31我国北斗三号导航卫星系统BDS-3建设成功,开始为全球用户提供服务[2]。由于卫星所处的空间环境极其复杂,卫星在轨运动会受到多种摄动力的影响,导致卫星的轨道参数发生复杂的非线性变化,因此提高卫星的轨道预报精度对卫星的应用研究具有重要意义[3]。目前卫星轨道预报方法均以动力学模型为基础,主要分为两类:一类是直接利用动力学模型进行预报[4],另一类是利用动力学模型与补偿模型构建的混合模型来完成轨道预报。
由于动力学模型的轨道预报误差会随预报弧长的增加而显著增大,因此利用轨道预报误差的拟合建立补偿模型能够有效提高动力学模型的轨道预报精度[5]。朱俊鹏等[6]利用长短时记忆神经网络进行GPS卫星轨道预报,对卫星的轨道数据进行分析;周建华等[7]在原动力学模型的基础上引入神经网络模型作为补偿,构建混合预报模型;李晓杰等[8]采用Robust-Loess数值滤波方法进行轨道预报误差平滑,有效提高了北斗导航系统的轨道预报精度。
神经网络作为一种新型建模工具,具有优秀的学习能力和善于处理非线性高维数据的优势,被广泛用于时变问题的研究。由于前馈式神经网络预测模型很难显示出时间序列的动态变化过程,对轨道误差的预报精度有一定的影响,因此本文采用辅助噪声经验模态分解模型(ensemble empirical mode decomposition,EEMD)与神经网络模型(long-short term memory,LSTM)相结合的EEMD-LSTM模型对北斗导航卫星轨道进行预报,利用均方根误差RSME和平均日改进率(imp)来评定模型的预报精度。本文对于不同弧段卫星轨道的预报具有重要参考意义。
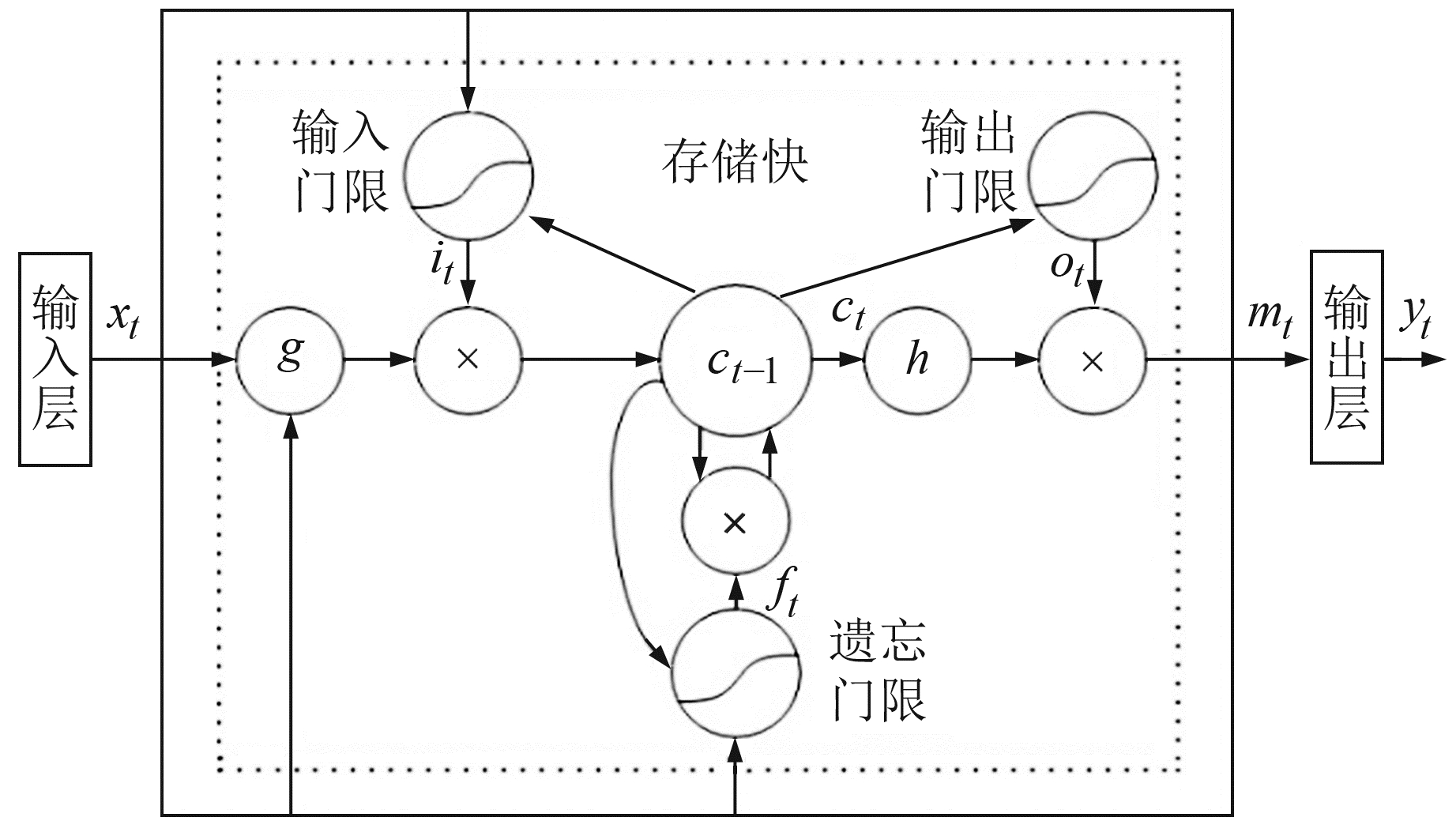
1 算法原理 1.1 递归神经网络在进行时间序列数据的非线性建模时,递归神经网络(recurrent neural network,RNN)能够有效表达时间序列的变化情况[9]。将RNN的神经元替换成LSTM模型神经元,添加门限结构,从而抑制RNN的梯度问题。此门限结构有输入处理功能、记忆权重功能和输出处理功能,这一系列功能的实现是通过设定输入门、遗忘门、输出门且设定各个门的阈值来完成的,其结构如图 1所示。
|
图 1 LSTM模型神经元结构 Fig. 1 Neuron structure of LSTM model |
一旦出现梯度问题,便会直接调节参数。LSTM模型调节参数的输出与状态如下:
| $ i_t=\sigma\left(W_{x i} x_t+W_{i m} m_{t-1}+W_{i c} c_{t-1}+b_i\right) $ | (1) |
| $ f_t=\sigma\left(W_{x f} x_t+W_{f m} m_{t-1}+W_{fc } c_{t-1}+b_f\right) $ | (2) |
| $ c_t=f_t \odot c_{t-1}+i_t \odot \tan h\left(\boldsymbol{W}_{c x} x_t+\boldsymbol{W}_{c m} m_{t-1}+b_c\right) $ | (3) |
| $ o_t=\sigma\left(\boldsymbol{W}_{x o} x_t+\boldsymbol{W}_{o m} m_{t-1}+\boldsymbol{W}_{o c} c_{t-1}+b_o\right) $ | (4) |
| $ m_t=o_t \odot \tan h (c) $ | (5) |
| $ y_t=\boldsymbol{W}_{y m} m_t+b_y $ | (6) |
式中,it、ot和ft为某时刻t的输入门、遗忘门和输出门,mt为某时刻t记忆元的激活状态,ct为时刻t的神经元,W为LSTM模型的权系数矩阵,b为偏置,tanh为双曲正切激活函数,σ为激活函数。
1.2 辅助噪声经验模态分解法EMD分解是指信号局部时间特征将信号从小到大分解为有限个内涵模态分量(intrinsic mode functions,IMF),其中阶数较小的IMF对应信号的高频部分,阶数较大的IMF对应低频部分,低频部分中噪声影响很小[10]。EMD分解的公式为:
| $ x(t)=\sum\limits_{j=1}^n c_j(t)+r_n(t) $ | (7) |
式中,x(t)为待分解时间序列,n为IMF分量个数,cj(t)为第j个IMF分量,rn(t)为趋势项。
为解决模态混叠问题,在EMD分解的基础上将EEMD算法原理引入轨道残差数据信号分解中。EEMD模型去噪的原理就是查找临界值k,IMF分量从高到低排列,噪声量递减,当显示信号主导模态时,此时该极值点为信号和噪声主导模态的分界点[11]。向原始时间序列中均匀加入白噪声序列,大量的白噪声会相互抵消,不会影响原始序列的分解,因此分解后仍然为真值,解决了EMD中模态混叠的问题。
能量谱密度由原始时序通过EEMD分解成为模态分量,能量谱密度计算公式为:
| $ E_i=\int_{-\infty}^{+\infty}\left|\mathrm{IMF}_i\right|^2 \mathrm{~d} t $ | (8) |
式中,Ei为第i阶能量谱密度,IMFi为IMF的不同阶数(i=1, 2, …, 13)。
1.3 LSTM补偿的轨道预报模型考虑到动力学模型轨道预报误差时间序列特性,以及LSTM补偿模型预测误差特征,建立LSTM补偿模型,包括5类模块:输入层包含划分训练集、数据分割和轨道误差时间序列;隐藏层包含LSTM模型神经元;输出层包含模型补偿结果、迭代预测和网络输出;网络训练包含模型输出、损失计算的Adam优化和理论输出;参数优化包含网络搜索算法、K折交叉和最优参数。
1) 数据标准化。将LSTM补偿模型中训练所需的轨道误差时间序列T0=(t0, t1, …, tn)划分为训练集Ttr=(t1, t2, …, tm)和测试集Tte=(ti, ti+1, …, tn),将训练集中元素Z-score标准化,即标准差为1、均值为0,得到标准化的训练集为TNtr=(tN1, tN2, …, tNm),标准化的训练集公式为:
| $ t_{N i}=\frac{t_i-\mu}{\lambda} $ | (9) |
式中,μ为训练集的均值;λ为训练集的标准差;Tt为训练集中元素,t满足1≤t≤m,m为训练集中元素对应某点的轨道误差时间序列。
2) 数据分割与训练。对标准化后的数据进行分割处理。
3) 模型训练。输入模型由隐藏层计算得到:
| $ P=\left\{P_1, P_2, \cdots, P_L\right\} $ | (10) |
| $ P_P=\mathrm{LSTM}_{\text {forward }}\left(X_P, C_{P-1}, H_{P-1}\right) $ | (11) |
式中,CP-1和HP-1为前一历元LSTM神经元的状态和输出,XP为此时的历元输入,LSTMforward为更新公式,L为窗口分割长度。
1.4 EEMD-LSTM组合模型利用LSTM模型对轨道误差时间序列采用逐元素的迭代方法,将神经元中上一步输出作为下一步输入导入到输入层中。输入的神经元会使上一步神经元输入受到影响,此模型对时间序列噪声造成的误差在预测过程中不断积累,最终影响预测精度。将重构后的数据输入LSTM模型中进行训练,最后对以信号为主导的IMF分量重构信号进行预测。
利用imp和RMSE指标对卫星轨道误差补偿进行比较,这两个指标越小,则预报值与真实值的误差越小,得到的拟合精度越高:
| $ \operatorname{imp}=\frac{1}{n} \sum\limits_{i=1}^n\left|\frac{D_i-P_i}{D_i}\right| \times 100 \% $ | (12) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(D_i-P_i\right)^2} $ | (13) |
式中,Pi为i时刻的预报值,Di为i时刻的真值,n为对应轨道所选用的弧长。
2 动力学模型的轨道预报误差分析神经网络补偿模型是通过拟合动力学模型的轨道预报误差来实现对动力学模型的补偿,在引入神经网络补偿模型之前,需要对不同初始历元影响动力学模型预报的误差进行分析。
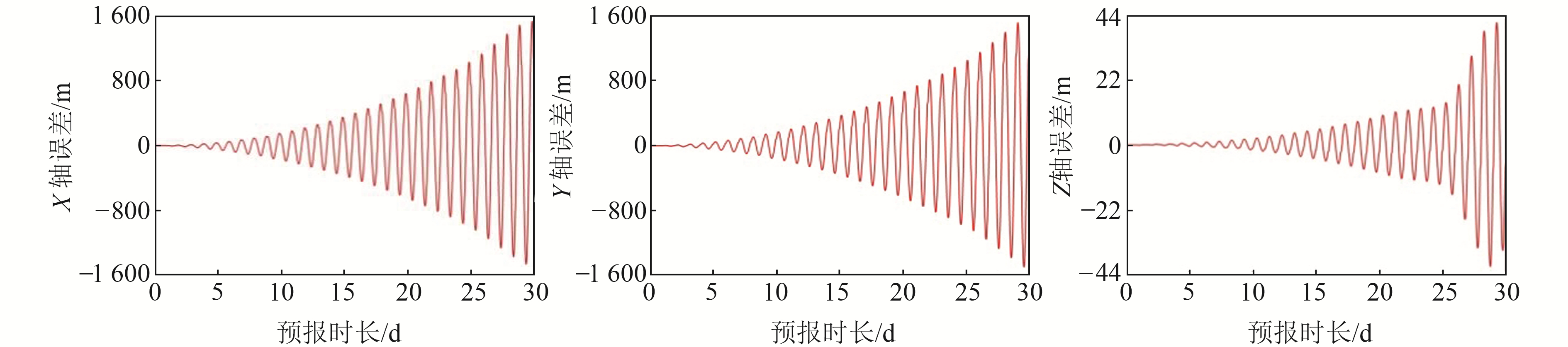
2.1 动力学模型预报误差分析选用BDS中的GEO卫星(C04)进行分析。将2020-02-01 12:00:00作为卫星轨道预报的初始历元开展30 d的动力学模型轨道外推实验。实验对象为BDS导航卫星,动力学模型的摄动力包括地球非球形引力、日月星历、太阳光压和潮汐力。动力学模型预报误差的计算策略如下:地球非球形引力采用EGM2008模型,日月星历选用美国航空航天局JPL中心发布的DE405星历表,光压模型为BERNE模型,潮汐力模型为IERS 2003中的固体潮模型。GEO卫星外推30 d的预报误差在X、Y、Z轴方向上的曲线如图 2所示。
|
图 2 GEO卫星预报30 d的预报误差 Fig. 2 Prediction error of GEO satellite forecast for 30 days |
由图 2可见,采用动力学模型外推GEO卫星轨道得到的轨道误差具有明显的周期性和发散性,GEO卫星的轨道回归周期约为1 d。在地心惯性坐标系下,X轴和Y轴30 d长期预报误差的最大值约为1 600 m和1 500 m,Z轴的30 d长期预报误差的最大值约为50 m。
2.2 不同初始历元对动力学模型预报误差的影响由于动力学轨道预报是通过计算动力学轨道微分方程组对初始轨道的精度与准确性进行的改进[12],因此不同的初始历元对动力学模型的轨道预报误差会有影响。以2020-02-01~04-30每日12:00:00作为初始积分时刻进行实验分析,图 3以GEO(C04)卫星X轴和Y轴为例,给出90个连续初始历元为期15 d的轨道预报最大值。

|
图 3 GEO(C04)卫星误差曲线 Fig. 3 GEO(C04) satellite error curve |
由图 3可见,X轴向最大误差的周期为14 d,波动区间为0~700 m,以(5+14n) d为初始积分时出现误差最大值,以(7+14n) d为初始积分时出现误差最小值;Y轴向的规律与X轴向相同,最大误差的周期为14 d,波动区间为0~800 m,以(5+14n) d为初始积分时出现误差最大值,以(7+14n) d为初始积分时出现误差最小值,但2个轴向的最大值和最小值并不相同。因此,不同轨道的卫星预报误差会随不同初始历元变化轨道呈现周期性,在14 d附近的预报结果相近,随预报弧长的增加发散变快。
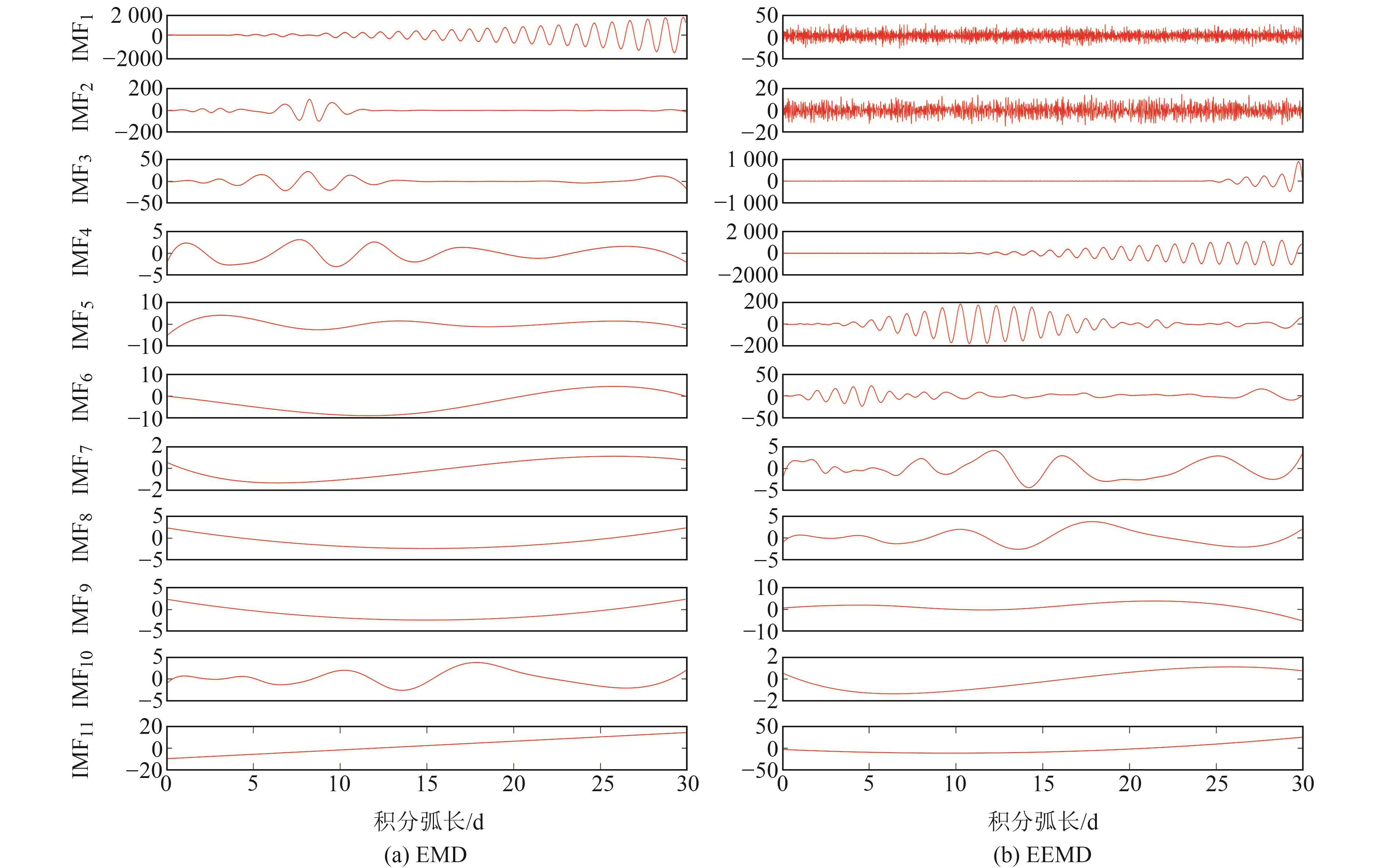
3 EEMD-LSTM组合模型的轨道预报误差分析 3.1 EEMD在序列噪声中的分解与应用以GEO卫星(C04)为例,以UTC 2020-01-18 12:00:00作为轨道预报的初始时间,使用动力学模型外推30 d,与标准轨道的重叠弧段进行对比得到轨道预报误差。图 4为采用EMD和EEMD方法分解轨道预报误差得到的各IMF分量和趋势向量。由图 4(a)可见,经过EMD分解得到的各IMF分量频率并没有明显突变,因此连续均方误差准则并不适用;由图 4(b)可见,IMF2分量和IMF3分量有明显的能量突变。
|
图 4 分解结果 Fig. 4 Decomposition results |
图 5为利用基于连续均方差准则得到的该信号经EMD和EEMD分解后的各IMF能量曲线。由图 5(a)可见,在第10阶IMF分量处出现第一个局部极小值点,重构信号为趋势向量,这显然是错误的。因此对于GEO卫星的轨道预报误差序列而言,EMD分解的去噪方法并不适用。由图 5(b)可见,对于EEMD分解后的各IMF能量曲线,第一个局部最小点对应的阶数为2,因此按照该阶数k=3,重构第3个和之后的所有IMF向量以获得滤波结果。

|
图 5 基于连续均方差准则的能量变化曲线 Fig. 5 Energy change curve based on continuous mean square deviation criterion |
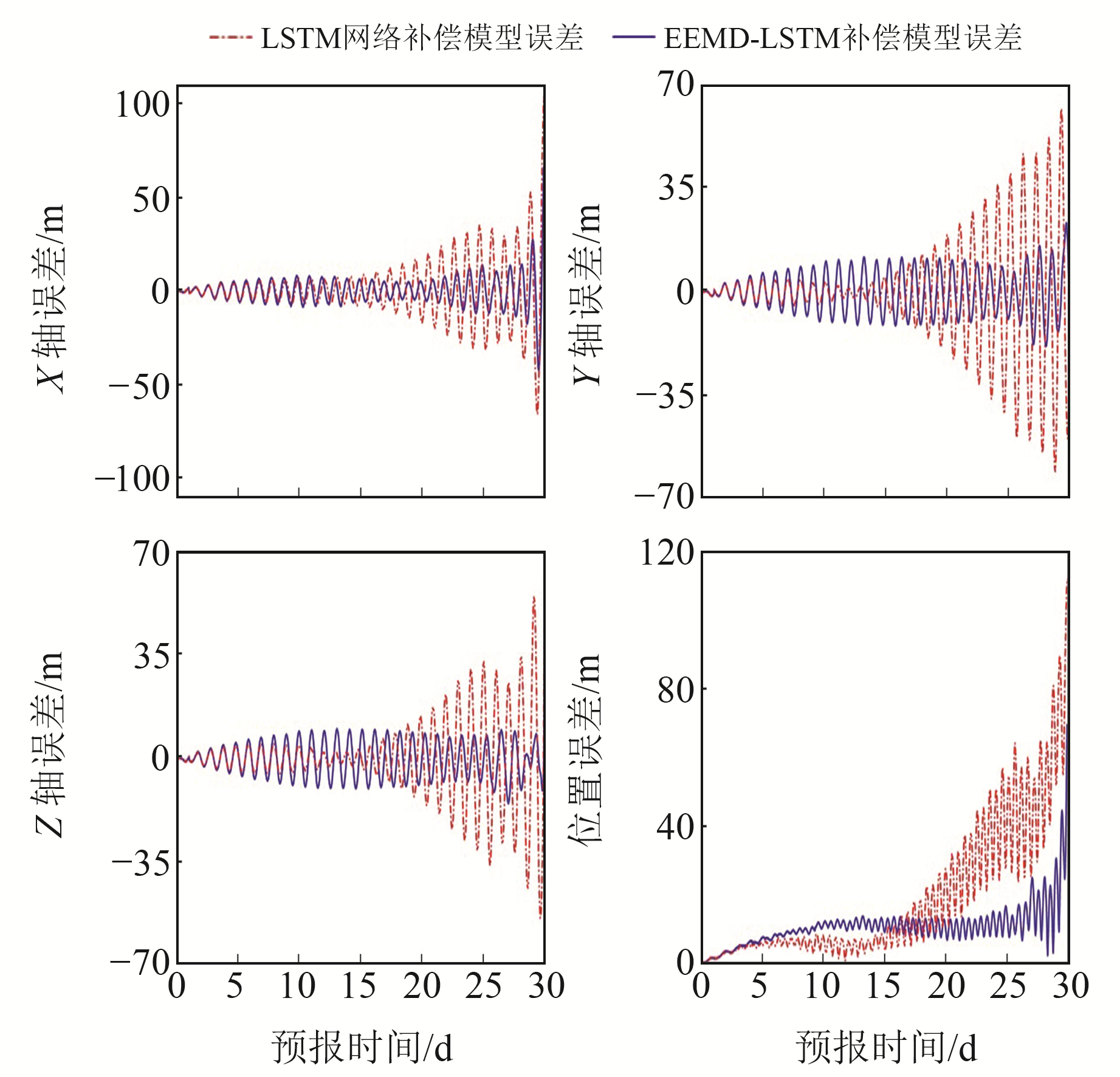
实验数据以UTC 2020-02-01 12:00:00为轨道预报误差的开始历元,训练数据用预报前28 d,训练间隔为15 min,分别采用两种模型外推30 d作为长期预报的补偿波形。图 6~8为GEO卫星(C04)、IGSO卫星(C07)和MEO卫星(C12)分别采用LSTM神经网络补偿模型和EEMD-LSTM组合模型的长期预报结果在X、Y和Z轴方向的30 d预报误差曲线和位置误差。

|
图 6 GEO卫星(C04)30 d轨道预报 Fig. 6 GEO satellite (C04) 30 days orbit prediction |
|
图 7 IGSO卫星(C07)30 d轨道预报 Fig. 7 IGSO satellite (C07) 30 days orbit prediction |
|
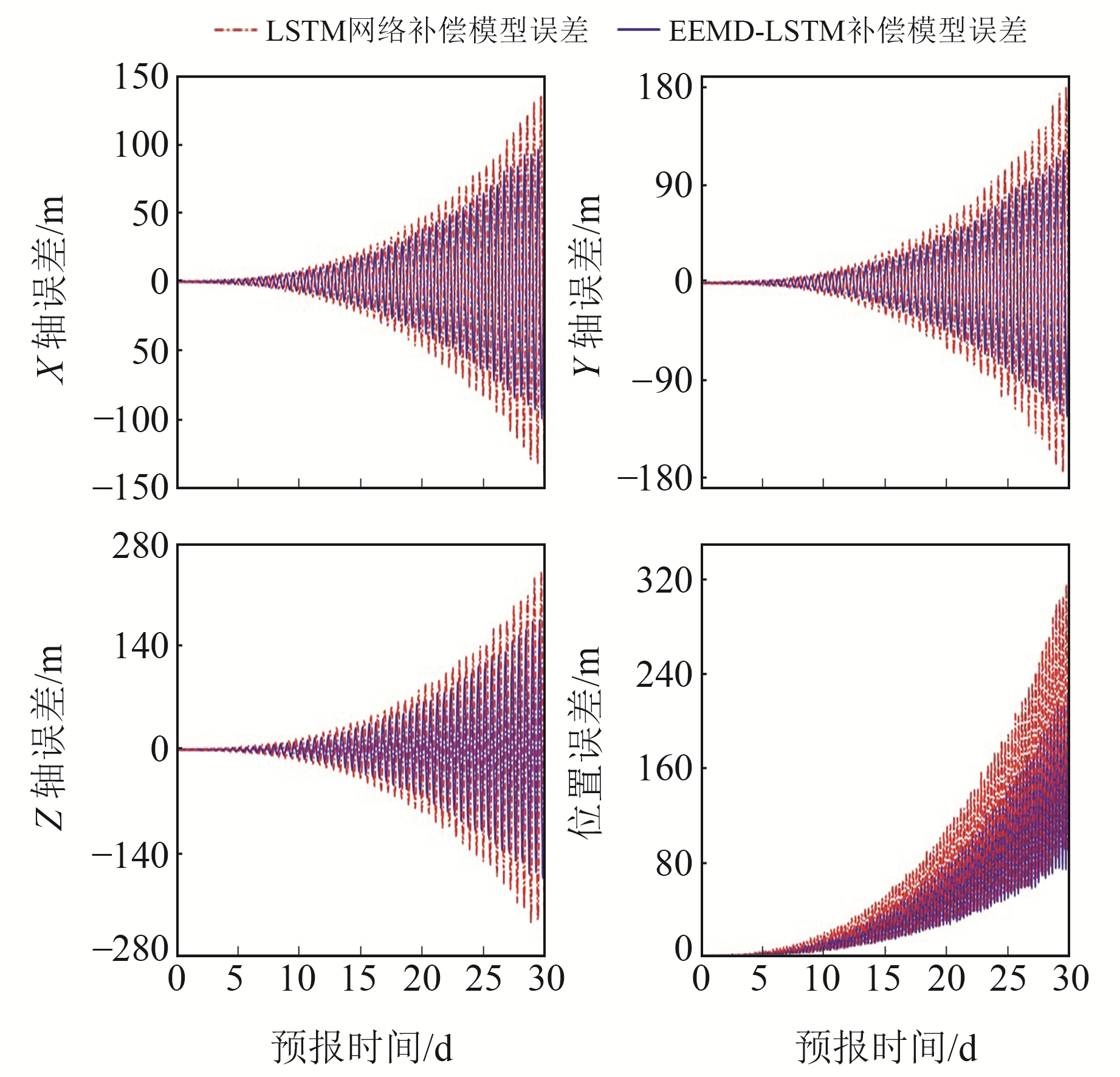
图 8 MEO卫星(C12)30 d轨道预报 Fig. 8 MEO satellite (C12) 30 days orbit prediction |
由图 6可见,预测位置误差将降到70 m以下,EEMD-LSTM模型精度明显低于单一的LSTM模型,说明EEMD-LSTM模型的补偿效果更好。由图 7~8可见,EEMD-LSTM模型中的IGSO和MEO卫星预报结果将保持约70 m和150 m的位置误差,同样表现出明显的优势。对于GEO、IGSO、MEO三类卫星而言,LSTM模型和EEMD-LSTM组合模型的预报结果在预测的初始阶段精度相近,随着弧长的增加,预测精度逐渐提高,EEMD-LSTM模型的补偿效果更好,在不同的弧段预报轨道中,EEMD-LSTM模型对单个LSTM模型的精度改进效果最好。
4 模型预报精度分析为了更好地反映LSTM模型和EEMD-LSTM组合模型对动力学模型轨道的误差补偿结果,根据式(12)~(13),通过真值和预测值对应某点时刻及轨道所选用的弧长长度进行轨道积分计算,统计GEO、IGSO、MEO三类卫星在两种方法下的imp和RMSE。15~30 d弧段对应的GEO、IGSO、MEO三类卫星EEMD-LSTM组合模型和LSTM模型的imp结果如表 1(单位%)所示,15~30 d弧段对应的GEO、IGSO、MEO三类卫星EEMD-LSTM组合模型和LSTM模型的RMSE结果如表 2所示(单位m)。
|
|
表 1 不同弧段GEO、IGSO和MEO平均日改进率 Tab. 1 Average daily improvement rates of GEO, IGSO and MEO in different arcs |
|
|
表 2 不同弧段GEO、IGSO及MEO卫星均方根误差 Tab. 2 RMSE of GEO, IGSO and MEO satellites in different arcs |
由表 1可知,EEMD-LSTM组合模型的改进率比单一模型的改进率更能反映对误差积累的抑制作用。在不同弧段的卫星轨道预报中,EEMD-LSTM组合模型对GEO、IGSO和MEO三类卫星的平均改正率分别为97.54%、96.89%和73.90%;与LSTM模型对比,平均改正率分别提高2.70百分点、2.46百分点和8.33百分点。
当用EEMD-LSTM混合模型和LSTM神经网络模型的方法进行误差补偿时,平均均方根误差统计结果表明,RMSE越小,其对应模型的误差补偿效果越好。由表 2可知,2个模型的改进效果随预报弧长的递增而减弱,EEMD-LSTM组合模型的RMSE小于LSTM模型,且随着预报弧长的增加,两种预测模型改进效果更加明显。在短期预报中,相比于LSTM模型,EEMD-LSTM组合模型在短期预测中的抑制作用并不稳定。
5 结语1) 针对动力学模型的预报误差随预报弧长的增加而周期性发散的问题,提出将LSTM的补偿模型应用于轨道预报误差中,选择EEMD进行轨道数据分解(EMD在轨道预报误差分析中存在模态混叠现象),在信噪主导模态中引入夹角余弦法,从而稳定地判别信噪主导模态分界现象。
2) 组合模型能够很好地抑制单一模型在长期外推中的误差积累。由不同弧段预报中的RMSE可知,相比于LSTM预测模型,EEMD-LSTM预测模型的拟合精度更高;由不同弧段预报中的imp可知,EEMD-LSTM组合模型对GEO、IGSO和MEO三类卫星的imp值分别提高2.70百分点、2.46百分点和8.33百分点。
本文EEMD-LSTM组合预测模型所选的轨道预报弧长最多为30 d,下一步的研究中应考虑建立更长期的弧长预报模型和算法,进行更深入的研究。
| [1] |
赵昂, 杨元喜, 许扬胤, 等. GNSS单系统及多系统组合完好性分析[J]. 武汉大学学报: 信息科学版, 2020, 45(1): 72-80 (Zhao Ang, Yang Yuanxi, Xu Yangyin, et al. Integrity Analysis of GNSS Single System and Multi-System Combination[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1): 72-80)
(  0) 0) |
| [2] |
顾晨钟, 李建文, 李林阳, 等. 两种预报轨道的BDS实时钟差估计与分析[J]. 测绘科学技术学报, 2021, 38(3): 228-234 (Gu Chenzhong, Li Jianwen, Li Linyang, et al. BDS Real-Time Clock Estimation and Analysis Based on Two Kinds of Predicted Orbit[J]. Journal of Geomatics Science and Technology, 2021, 38(3): 228-234)
(  0) 0) |
| [3] |
王琰. 北斗导航卫星轨道精度提升关键技术研究[D]. 郑州: 信息工程大学, 2017 (Wang Yan. Study on the Accuracy Improvement of Bds Orbit Determination[D]. Zhengzhou: Information Engineering University, 2017)
(  0) 0) |
| [4] |
姚宜斌. GPS轨道合成原理及其实现[J]. 武汉大学学报: 信息科学版, 2007, 32(6): 510-514 (Yao Yibin. Theory and Realization of GPS Orbit Integration[J]. Geomatics and Information Science of Wuhan University, 2007, 32(6): 510-514)
(  0) 0) |
| [5] |
张如伟, 刘根友. 低轨卫星轨道拟合及预报方法研究[J]. 大地测量与地球动力学, 2008, 28(4): 115-120 (Zhang Ruwei, Liu Genyou. Discussion on Orbit Fitting and Orbit Forecasting of Low Earth Orbit Satellites[J]. Journal of Geodesy and Geodynamics, 2008, 28(4): 115-120)
(  0) 0) |
| [6] |
朱俊鹏, 赵洪利, 杜鑫, 等. 长短时记忆神经网络在卫星轨道预报中的研究[J]. 兵器装备工程学报, 2017, 38(10): 127-132 (Zhu Junpeng, Zhao Hongli, Du Xin, et al. Application of Long Short-Term Memory Neural Network to Orbit Prediction of Satellite[J]. Chinese Journal of Ordnance Equipment Engineering, 2017, 38(10): 127-132)
(  0) 0) |
| [7] |
周建华, 杨龙, 徐波, 等. 一种导航卫星中长期轨道预报方法[J]. 测绘学报, 2011, 40(增1): 39-45 (Zhou Jianhua, Yang Long, Xu Bo, et al. A Long Duration Orbit Prediction Method for Navigation Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 39-45)
(  0) 0) |
| [8] |
李晓杰, 郭睿, 黄金, 等. 神经网络在北斗导航卫星轨道预报中的应用[J]. 武汉大学学报: 信息科学版, 2015, 40(9): 1253-1258 (Li Xiaojie, Guo Rui, Huang Jin, et al. Application of Artificial Neural Network to Orbit Prediction of BeiDou Navigation Satellites[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1253-1258)
(  0) 0) |
| [9] |
Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780
(  0) 0) |
| [10] |
Liu J C, Gu Y, Chou Y X, et al. Seismic Data Random Noise Reduction Using a Method Based on Improved Complementary Ensemble EMD and Adaptive Interval Threshold[J]. Exploration Geophysics, 2021, 52(2): 137-149
(  0) 0) |
| [11] |
吉长东, 吕广涵, 张恒璟, 等. 一种CORS站高程序列噪声识别算法[J]. 测绘科学, 2021, 46(3): 8-16 (Ji Changdong, Lü Guanghan, Zhang Hengjing, et al. A Noise Recognition Algorithm of CORS Station Elevation Series[J]. Science of Surveying and Mapping, 2021, 46(3): 8-16)
(  0) 0) |
| [12] |
祝转民, 徐宗本. 卫星初始轨道确定方法研究[J]. 中国空间科学技术, 2007, 27(3): 1-6 (Zhu Zhuanmin, Xu Zongben. Study of Satellite Initial Orbit Determination Method[J]. Chinese Space Science and Technology, 2007, 27(3): 1-6)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


