2. 中国地质大学(武汉)地理与信息工程学院,武汉市鲁磨路388号,430079;
3. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079
日长(length of day,LOD)变化是地球定向参数(earth orientation parameter,EOP)中描述地球自转速率的参数,EOP是地心天球参考系和国际地球参考系之间进行转换所必需的参数,其在空间大地测量、全球卫星定位定轨以及地球物理等方面有着重要作用。
目前最小二乘(least squares, LS)外推模型和自回归(autoregressive,AR)模型是常用的LOD预报方法。进行最小二乘外推时需要通过频谱分析确定LOD序列中的周期项[1],而LOD序列中的测量噪声会导致频谱分析结果存在误差[2]。因此在构建预报模型前,要先对原始LOD序列进行拟合,目前主要采用含有常数项、一次项以及周期项的LS外推模型[3],但阶次不足时会导致其整体的拟合精度较差[4]。因此,开展地球自转参数拟合模型的相关研究对于地球自转参数预报至关重要。
本文首先对IERS发布的EOP 14 C04数据中1984~2022年的LOD序列进行频谱分析;然后采用LS外推模型与PCF模型等方法对LOD序列进行拟合,并尝试将LS外推模型拟合与PCF模型结合起来,以达到优于两者的拟合效果。在拟合过程中,分别利用单位阵和利用LOD观测精度序列构建权矩阵,对比其优劣;最后分别利用前述的几种拟合方法构建的LOD序列预报模型对近1 a的LOD序列进行拟合,并与实测值进行对比。
1 日长变化统计分析基础 1.1 地球自转速率变化地球自转参数是利用一系列位于地球表面的天文站来对地球外的自然天体或人造天体进行观测所获得的。当前国际上采用的地球定向参数测量技术主要包括卫星激光测距[5]、月球激光测距、多普勒无线电定轨定位系统、全球导航卫星系统、甚长基线干涉测量等[6]。
地球自转速率时间尺度变化主要表现为长期缓慢变化、10 a尺度变化、年际尺度变化、季节性变化以及高频变化[7]。
1.2 地球自转速率数据预处理本文利用的LOD实测参数来自IERS发布的EOP 14 C04产品,自1984年以来,地球自转参数的测定精度较之前有极大提高[8]。鉴于此,本文使用1984年至今的LOD序列作为研究数据。
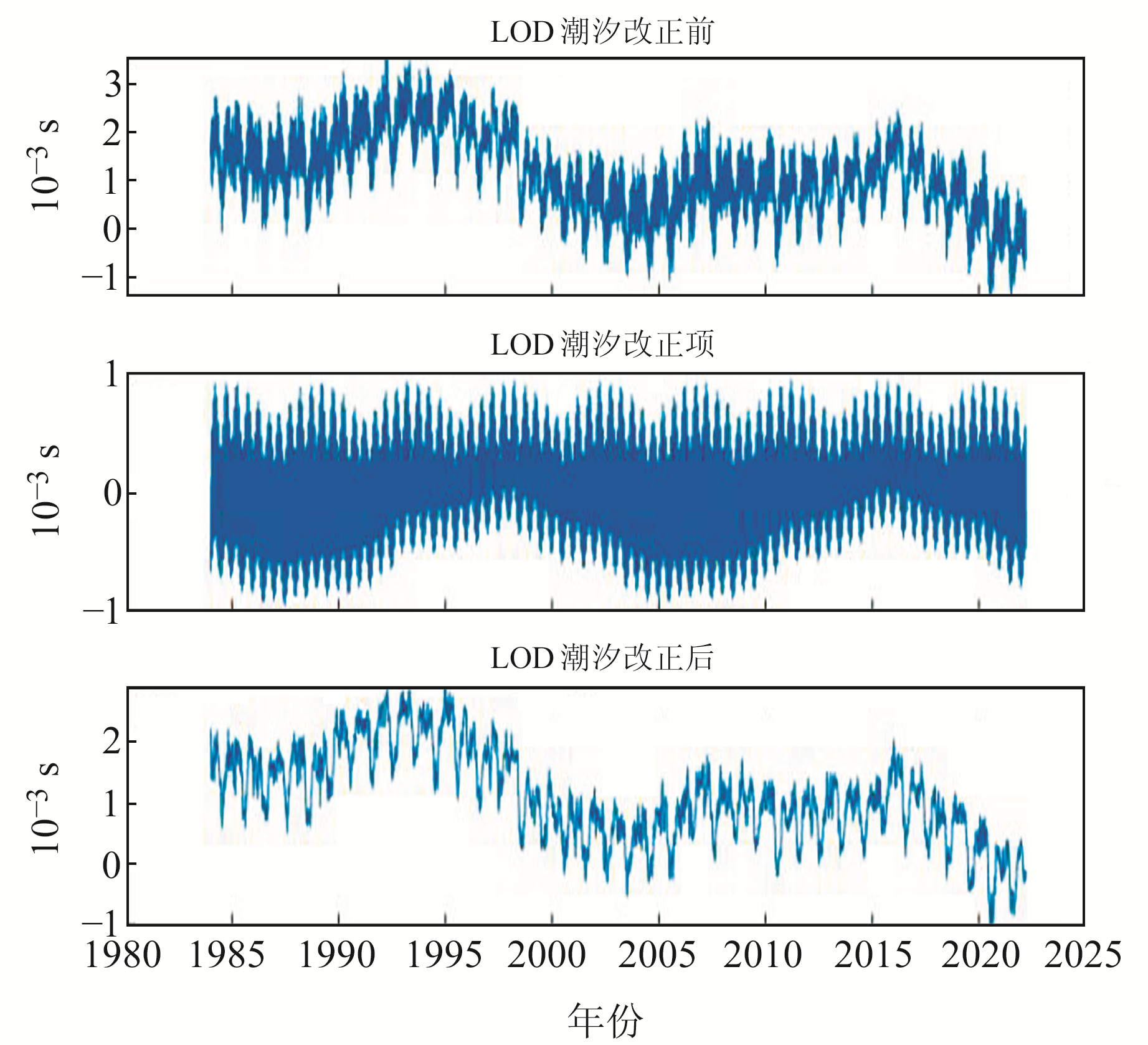
国内外大量研究表明,LOD序列中的短周期信号来源于潮汐激发。LOD序列中的潮汐项包括固体地球潮汐项和海洋潮汐项,其中前者是5 d~18.6 a周期的固体地球带谐潮汐项,可以通过IERS网站公布的IERS Conventions(2010)中给出的固体地球潮汐经验模型进行改正[6]。图 1绘制了1984~2022年LOD扣除固体地球潮汐项前后的对比。
|
图 1 LOD中的固体地球带谐潮汐改正 Fig. 1 Harmonic tidal correction of solid earth in LOD |
频谱分析就是把较为复杂且离散的信号经过傅里叶变换,分解成为若干单一的谐波分量。对于LOD观测序列中所包含的周期信号,其在信号振幅频谱图中会呈现出局部最大的谱峰,即谱峰对应的频率就是该观测序列的一个频率。振幅频谱的计算式为:
| $ s_i=\sqrt{\left(\frac{2}{n} \sum\limits_{t=1}^{n-1} x_t \cos \frac{2 \pi i t}{n}\right)^2+\left(\frac{2}{n} \sum\limits_{t=1}^{n-1} x_t \sin \frac{2 \pi i t}{n}\right)^2} $ | (1) |
式中,xt表示LOD序列,t=1, 2, …, n;si为信号中i次谐波分量的频谱振幅,i=1, 2, …, int(n/2),int表示向下取整。
周期项提取步骤如下:
1) 对LOD序列进行傅里叶频谱分析,选出振幅最大的周期项;
2) 判断频谱分析结果中的最大振幅是否小于设定的阈值,若是则结束周期项提取,若否则进入步骤3);
3) 用原始序列减去该振幅最大的周期项在原始序列中所占的部分,形成新的序列,再返回步骤1)对新序列进行傅里叶频谱分析。
对于步骤3),详细解释如下:将第nc次提取的周期Tnc代入式(2),计算出新的LOD序列:
| $ \left\{\begin{array}{l} X_{t_{\mathrm{nc}}}=X_{t_{\mathrm{nc}-1}}-\left(c_{\mathrm{nc}} \cos \left(\frac{2 \pi t}{T_{\mathrm{nc}}}\right)+\right. \\\;\;\;\; \left.d_{\mathrm{nc}} \sin \left(\frac{2 \pi t}{T_{\mathrm{nc}}}\right)\right) \\ c_{\mathrm{nc}}=A_{\mathrm{nc}} \sin \left(\varphi_{\mathrm{nc}}\right) \\ d_{\mathrm{nc}}=A_{\mathrm{nc}} \cos \left(\varphi_{\mathrm{nc}}\right) \end{array}\right. $ | (2) |
式中,nc代表提取周期的次数,nc=1, 2, …, tc,tc是提取的周期项总数,tc的值取决于设定的阈值大小;Xtnc-1为第nc次提取前第t个LOD值;Xtnc为减去第nc次提取的周期项后的第t个地球自转参数值;Anc是信号在周期Tnc时的振幅;φnc是信号在周期Tnc时的相位。
2.2 拟合模型建立 2.2.1 最小二乘外推模型最小二乘(least squares, LS)外推模型包含常数项、趋势项以及周期项,其数学表达式为:
| $ \left\{\begin{array}{l} X_t=a+b t+\sum\limits_{i=1}^k\left(c_i \cos \left(\frac{2 \pi t}{T_i}\right)+\right. \\ \left.\quad d_i \sin \left(\frac{2 \pi t}{T_i}\right)\right)+\varepsilon_{\mathrm{LS}}(t) \\ c_i=A_i \sin \left(\varphi_i\right) \\ d_i=A_i \cos \left(\varphi_i\right) \end{array}\right. $ | (3) |
式中,t为时间,Xt为t时刻的地球自转参数,a为常数项,b为线性项的系数,Ai、Ti、φi分别为地球自转参数序列中所包含的周期项的振幅、周期和相位,k是周期项的个数,εLS(t)为观测噪声。假设存在n组观测数据(n>2k+2),则LS外推模型参数为:
| $ \left\{ \begin{array}{l} \begin{aligned} & \left(\boldsymbol{\alpha}=\left[\begin{array}{lllllll} a & b & c_1 & d_1 & \cdots & c_k & d_k \end{array}\right]^{\mathrm{T}}\right. \\ & \boldsymbol{L}=\left[\begin{array}{llll} x_{t_1} & x_{t_2} & \cdots & x_{t_n} \end{array}\right]^{\mathrm{T}} \\ & \boldsymbol{A}=\left[\begin{array}{ccccccc} 1 & t_1 & \cos \left(\frac{2 \pi t_1}{T_1}\right) & \sin \left(\frac{2 \pi t_1}{T_1}\right) & \cdots & \cos \left(\frac{2 \pi t_1}{T_k}\right) & \sin \left(\frac{2 \pi t_1}{T_k}\right) \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & t_n & \cos \left(\frac{2 \pi t_n}{T_1}\right) & \sin \left(\frac{2 \pi t_n}{T_1}\right) & \cdots & \cos \left(\frac{2 \pi t_n}{T_k}\right) & \sin \left(\frac{2 \pi t_n}{T_k}\right) \end{array}\right] \\ & \boldsymbol{\alpha}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{E} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{E} \boldsymbol{L} \\ & \end{aligned} \end{array} \right. $ | (4) |
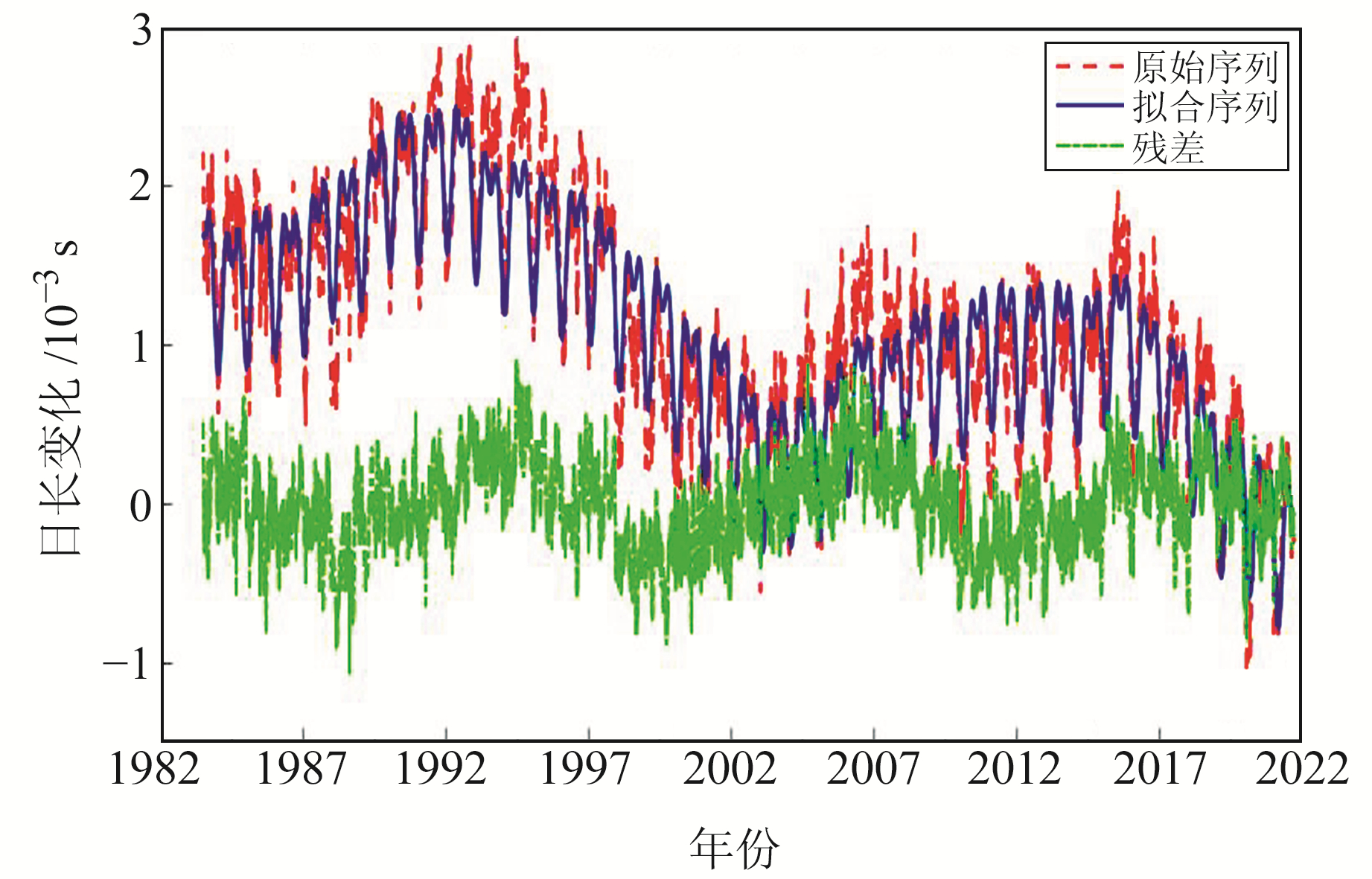
式中,α为待求参数,A为系数矩阵,L为观测向量,E为观测向量权矩阵且通常为单位矩阵。图 2是利用表 1中的周期进行LS外推模型的拟合结果。
|
图 2 LS外推模型拟合结果 Fig. 2 LS results based on fractional step periodic extraction |
|
|
表 1 周期提取结果(振幅大于等于0.03 ms) Tab. 1 Period extraction results(amplitude≥0.03 ms) |
多项式曲线拟合(polynomial curve fitting,PCF)模型包含常数项以及各阶次项[9],其数学表达式为:
| $ X_t=a+\sum\limits_{i=1}^m b_i t^i+\varepsilon_{\mathrm{PCF}}(t) $ | (5) |
式中,bi是各阶次项的系数,m是阶次项的个数,εPCF(t)是观测噪声。假设存在n组观测数据(n>m+1),则PCF模型的参数计算公式为:
| $ \left\{\begin{array}{l} \boldsymbol{\alpha}=\left[\begin{array}{llll} a & b_1 & \cdots & b_m \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{L}=\left[\begin{array}{llll} x_{t_1} & x_{t_2} & \cdots & x_{t_n} \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{A}=\left[\begin{array}{cccc} 1 & t_1 & \cdots & t_1^m \\ \vdots & \vdots & \vdots & \vdots \\ 1 & t_n & \cdots & t_n^m \end{array}\right] \\ \boldsymbol{\alpha}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{E} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{E} \boldsymbol{L} \end{array}\right. $ | (6) |
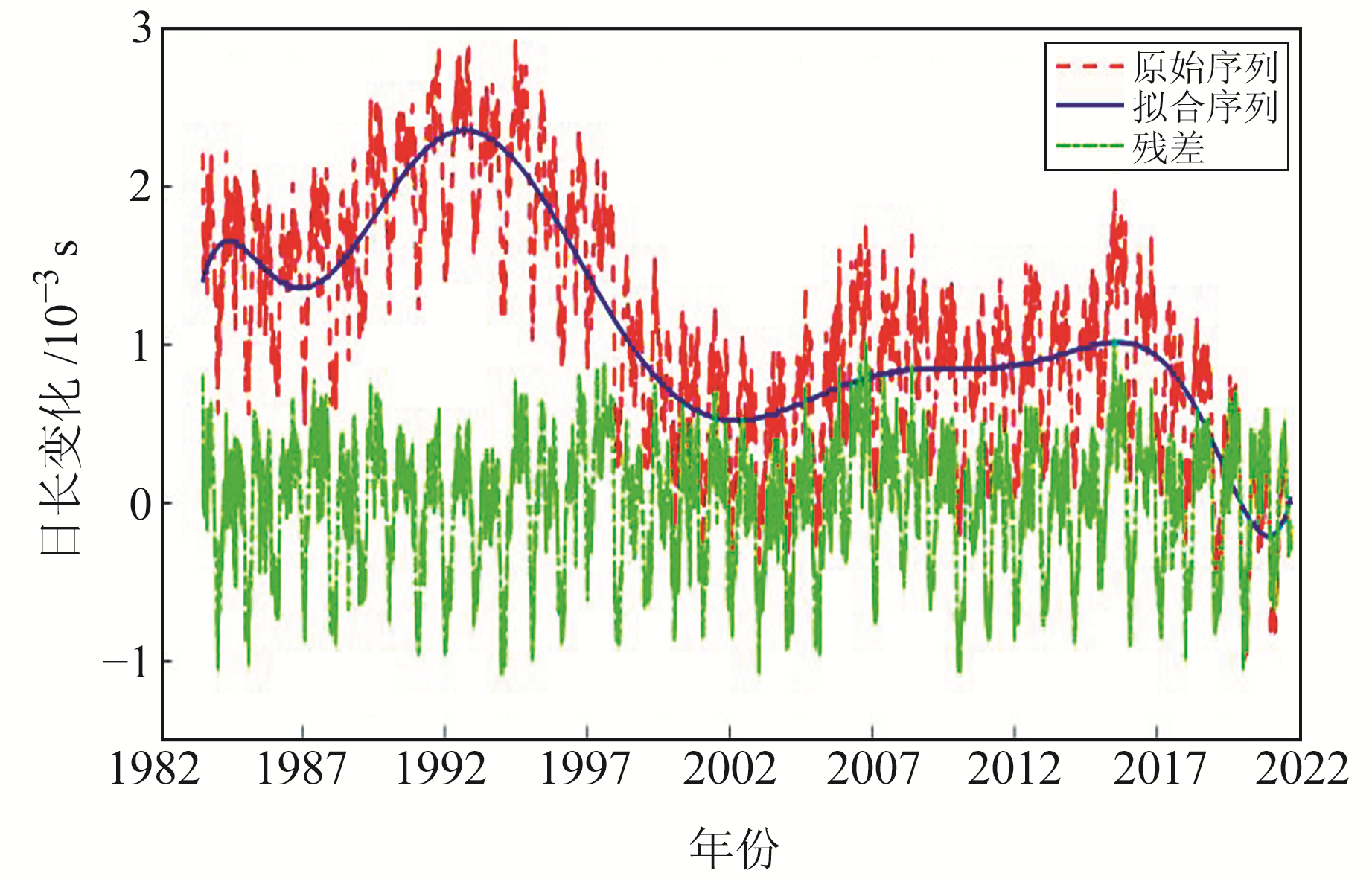
式中,α为待求参数,A为系数矩阵,L为观测向量,E为观测向量权矩阵且通常为单位矩阵。经过1~30阶的PCF模型拟合计算,综合考虑计算效率与拟合精度,其中10阶的综合效果最优,图 3为10阶PCF模型拟合结果。
|
图 3 10阶PCF模型拟合结果 Fig. 3 10 order PCF results |
由图 3可见,PCF模型拟合曲线在整个时间段的拟合效果都很稳定,并没有出现在某时间段误差过大的情况,其残差的绝对值没有超过0.001 s。
2.3 拟合模型结果计算§2.2中两种模型的和方差(sum of squares for error,SSE)、均方根误差(root mean squared error,RMSE)、拟合数据与原始数据均值之差的平方和(sum of squares for regression,SSR)以及确定系数(coefficient of determination,R-Square),并通过绘图进行分析[9]。
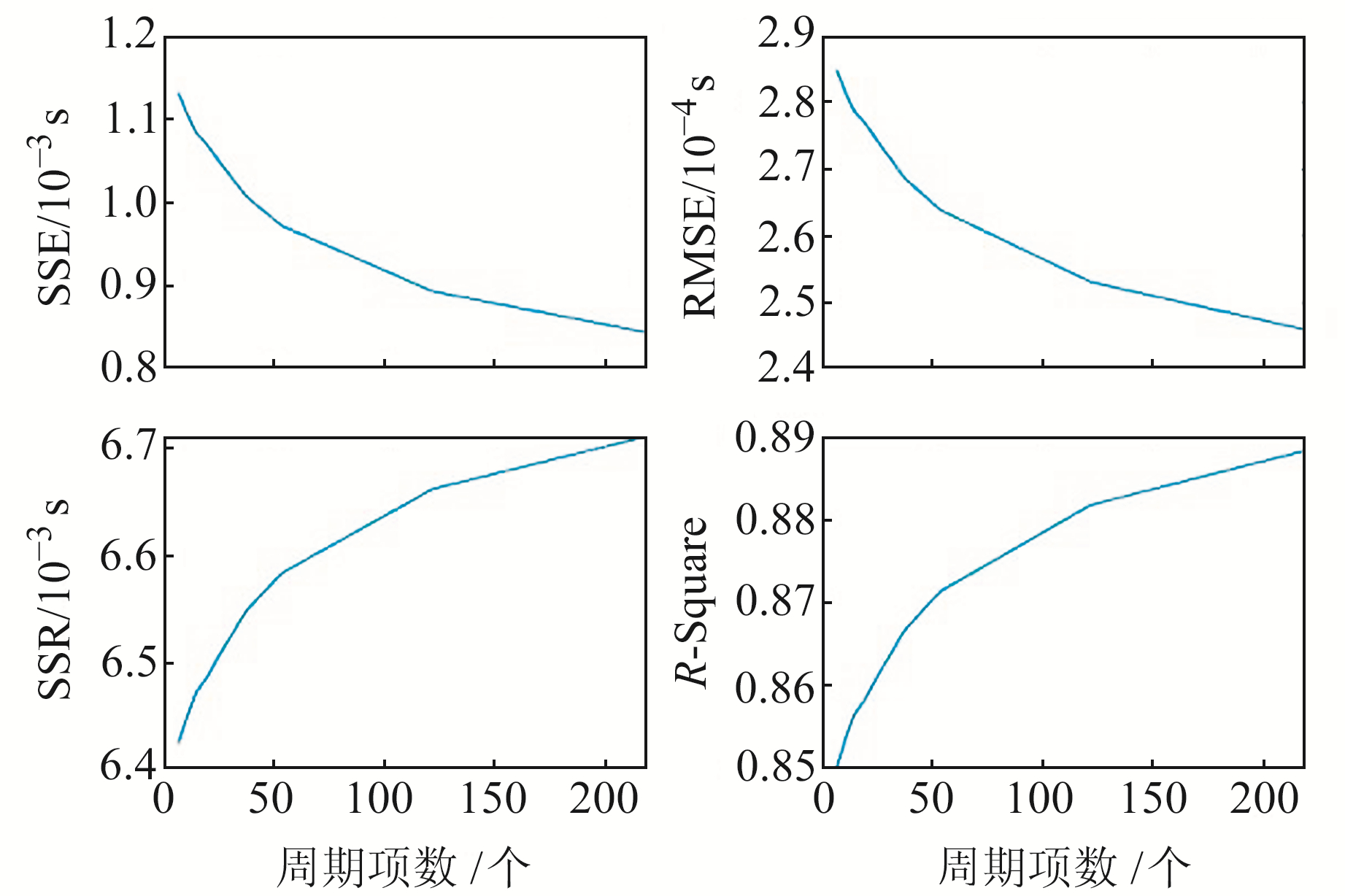
2.3.1 LS模型拟合效果分析在提取周期项时改变振幅的阈值,从而提取出不同数量的周期项,进而利用不同数量的周期项进行LS外推模型拟合,达到对比不同的周期项拟合效果的目的。图 4为不同周期项的LS外推模型拟合的各项指标。
|
图 4 不同周期项的LS外推模型拟合的各项指标 Fig. 4 Indexes of LS with different period terms |
由图 4可见,随着周期数量的增大,RMSE在下降;而确定系数R-Square的图像也显示,拟合的结果越来越好。
2.3.2 PCF模型拟合效果分析在PCF模型拟合中,在拟合函数中增加更高的阶次来进行不同程度的拟合,并计算SSE、RMSE、SSR、SST、R-Square,从而对比不同阶次下的拟合效果。
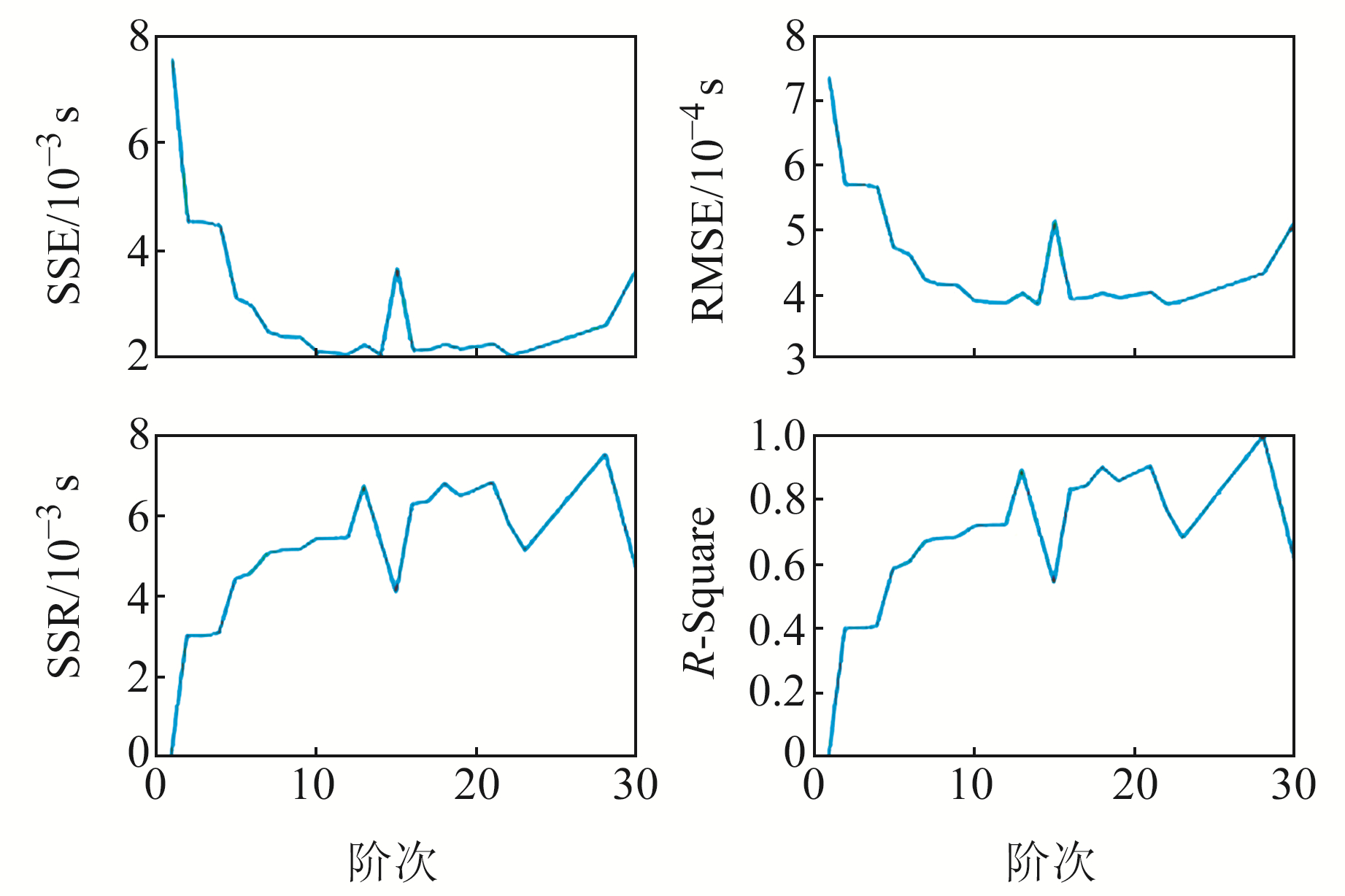
实验中发现,在一些阶次的拟合中RMSE和R-Square指标出现异常,本应该在[0, 1]之间的R-Square值却超出该范围。我们判断,应该是在拟合间接平差过程中出现的矩阵求逆异常所导致,所以在绘制图像时去除这类异常的阶次。图 5为不同阶次下PCF模型拟合的各项指标。
|
图 5 不同阶次下PCF模型拟合的指标 Fig. 5 Index of PCF at different orders |
由于SSE与RMSE、SSR与R-Square的走势相一致,所以在精度分析中,我们只需要关注RMSE与R-Square即可。由图 5可见,R-Square值在14阶之前是逐步上升的,14阶之后出现不正常的跳变并且一直持续到30阶。对此我们判断,在14阶后PCF模型发生了过拟合问题,所以只关注14阶之前的指标即可。从RMSE图像可以看出,在14阶之前,随着参与拟合的阶次的增大,RMSE值在逐渐下降。
3 日长变化序列拟合方法改进及预报前文实验结果表明,LS外推模型拟合时加入了周期项,在某些时段可以达到非常好的拟合效果,不足之处在于不能在整个时段上完美拟合;而PCF模型拟合则相反,虽然不能达到很高的拟合精度,但是在整个时间序列上的拟合更为稳定。
鉴于此,本文尝试将LS外推模型与PCF模型相结合,以期可以利用PCF模型的整体稳定性,又能够利用LS外推模型在部分时间段拟合精度高的优势,从而达到相较二者更好的拟合效果。
3.1 LOD序列拟合模型改进 3.1.1 LS+PCF模型拟合LS+PCF模型是结合了LS外推模型中的常数项、趋势项、周期项以及PCF模型中的阶次项的一种拟合模型,其数学表达式为:
| $ \left\{\begin{array}{l} X_t=a+\sum\limits_{i=1}^m\left(b_i t^i\right)+\sum\limits_{i=1}^k\left(c_i \cos \left(\frac{2 \pi t}{T_i}\right)+\right. \\ \left.\quad d_i \sin \left(\frac{2 \pi t}{T_i}\right)\right)+\varepsilon_{\mathrm{LS}+\mathrm{PCF}}(t) \\ c_i=A_i \sin \left(\varphi_i\right) \\ d_i=A_i \cos \left(\varphi_i\right) \end{array}\right. $ | (7) |
式中,εLS+PCF(t)是观测噪声。假设存在n组观测数据(n>2k+m+1),则LS+PCF模型参数为:
| $ \left\{ \begin{array}{l} \boldsymbol{\alpha}=\left[\begin{array}{lllllllll} a & b_1 & \cdots & b_m & c_1 & d_1 & \cdots & c_k & d_k \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{L}=\left[\begin{array}{llll} x_{t_1} & x_{t_2} & \cdots & x_{t_n} \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{A}=\left[\begin{array}{ccccccccc} 1 & t_1 & \cdots & t_1^m & \cos \left(\frac{2 \pi t_1}{T_1}\right) & \sin \left(\frac{2 \pi t_1}{T_1}\right) & \cdots & \cos \left(\frac{2 \pi t_1}{T_k}\right) & \sin \left(\frac{2 \pi t_1}{T_k}\right) \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & t_n & \cdots & t_n^m & \cos \left(\frac{2 \pi t_n}{T_1}\right) & \sin \left(\frac{2 \pi t_n}{T_1}\right) & \cdots & \cos \left(\frac{2 \pi t_n}{T_k}\right) & \sin \left(\frac{2 \pi t_n}{T_k}\right) \end{array}\right] \\ \boldsymbol{\alpha}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{E} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{E} \boldsymbol{L} \end{array} \right. $ | (8) |
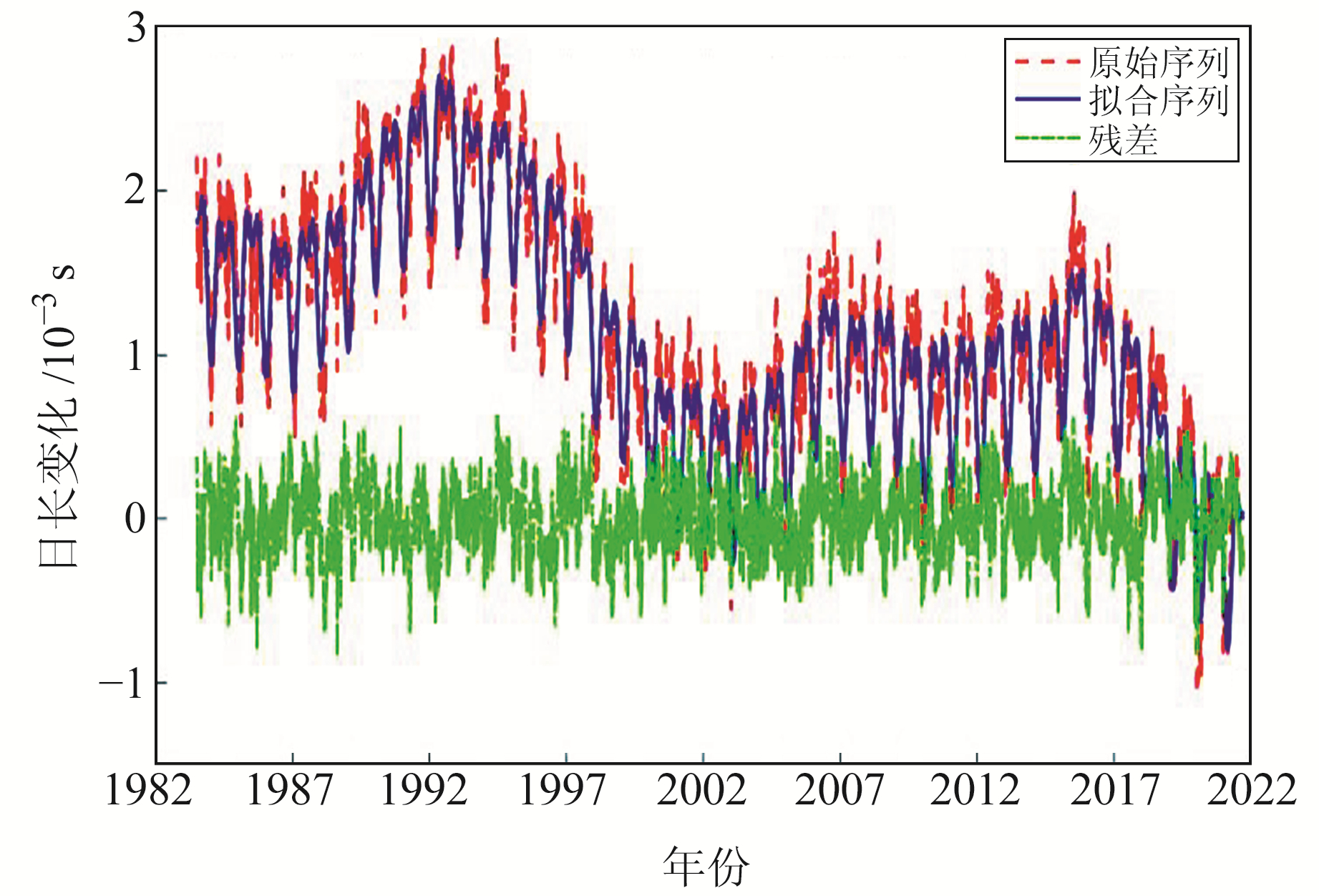
式中,α为待求参数,A为系数矩阵,L为观测向量,E为观测向量权矩阵且通常为单位矩阵。图 6为LS+PCF模型拟合结果。
|
图 6 LS+PCF模型拟合结果 Fig. 6 Fitting results of LS+PCF model |
由图 6可见,拟合效果非常好,不仅拥有LS外推模型在部分时间段拟合精度高的优点,而且继承了PCF模型拟合的整体稳定性,拟合序列与原始序列的结合比单一的LS外推模型拟合要更加紧密,而残差序列也更加平稳,甚至残差序列的绝对值维持在0.000 5 s以内,这也证明了将两种方法进行结合的确能极大提升LOD序列的拟合效果。
3.1.2 加权LS+PCF模型拟合本节利用LOD序列的观测精度构建拟合模型计算过程中的权矩阵,期望能够达到更好的拟合效果。式(9)是权矩阵P,用来代替式(8)中的E:
| $ \boldsymbol{P}=\left[\begin{array}{cccc} \frac{\sigma_0^2}{\sigma_1^2} & 0 & 0 & 0 \\ 0 & \frac{\sigma_0^2}{\sigma_2^2} & 0 & 0 \\ 0 & 0 & \ddots & \vdots \\ 0 & 0 & \cdots & \frac{\sigma_0^2}{\sigma_n^2} \end{array}\right] $ | (9) |
式中,σ12~σn2是LOD序列中各个元素的观测精度,其值在EOP 14 C04中对应列,取σ12~σn2的算术平均值作为单位权中误差σ02。图 7为LS+PCF模型拟合结果。

|
图 7 加权LS+PCF模型拟合结果 Fig. 7 Fitting results of weighted LS+PCF model |
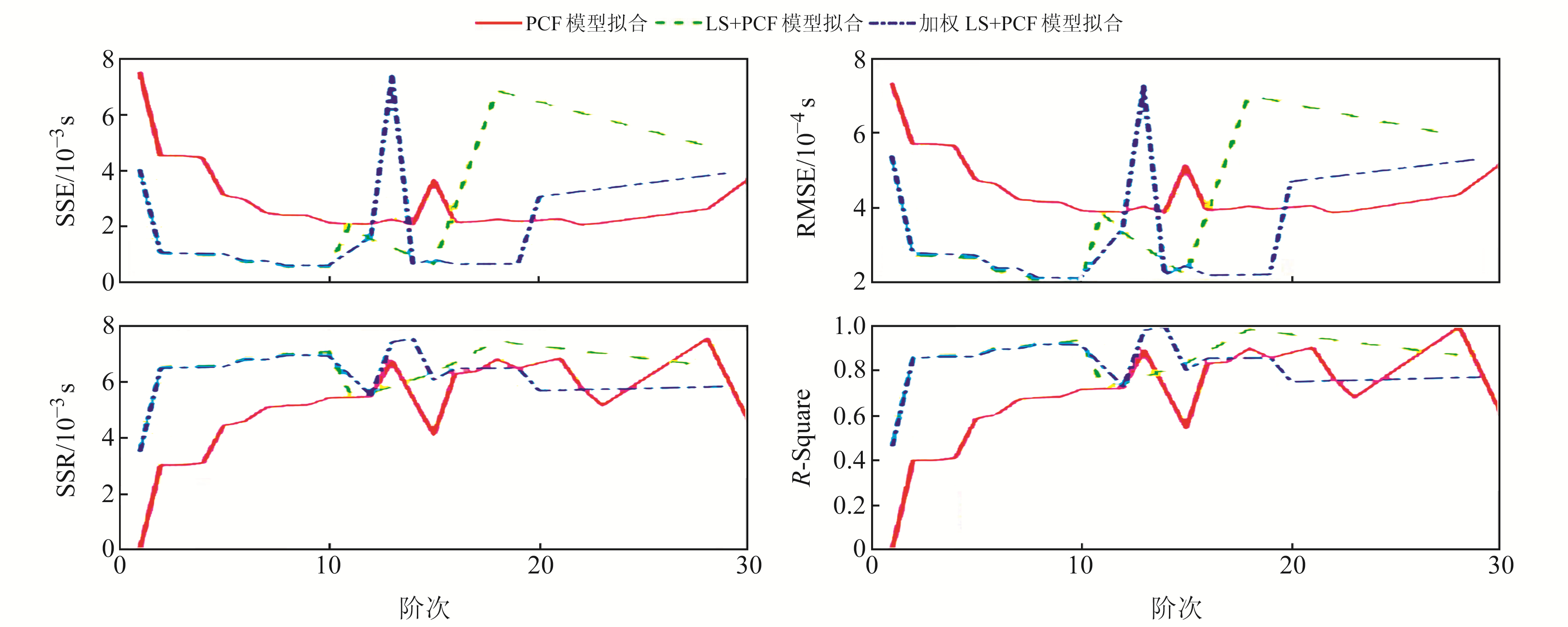
计算§3.1.1和§3.1.2中两种模型的SSE、RMSE、SSR以及R-Square,图 8为不同阶次下PCF、LS+PCF与加权LS+PCF模型拟合的各项指标。
|
图 8 不同阶次PCF模型拟合、LS+PCF模型拟合与加权LS+PCF模型拟合的各项指标 Fig. 8 Comparison of indexes of PCF, LS+PCF and weighted LS+PCF under different orders |
由图 8可见,RMSE从LS外推模型拟合的0.000 3 s降低到0.000 1 s。随着参与拟合函数阶次的增大,拟合数据和原始数据对应点误差平方和均值的平方根并不是一直在下降。同时可以看出,阶数在16之前,LS+PCF模型拟合误差要小于PCF模型拟合所产生的误差;但随着阶数的增大,两者互有优劣。
而确定系数R-Square的图像也证明了这一点。加权LS+PCF模型拟合方法将确定系数从0.80提高到了0.97左右,这说明LS外推模型与PCF模型的结合确实可以提高拟合精度。
同时,在整个时段中,加权LS+PCF模型拟合的RMSE更小,但与不加权的结果差异较小,推测可能是由于1984年以来LOD的观测精度没有数量级的提升,所以分别使用单位权矩阵和利用观测精度序列构造的权矩阵来计算所得到的提升效果不明显。
总的来说,加权LS+PCF模型拟合确实能够提升拟合的精度。
3.2 LOD序列预报为了验证不同拟合函数在LOD序列短期预报的效果,采用1984-01-01~2021-03-15的实测LOD序列作为原始数据进行函数拟合,利用拟合得到的曲线预报2021-03-15~2022-03-15之间365 d的LOD参数,最后利用2021-03-15~2022-03-15的实测数据作为标准进行对比分析。图 9为4种模型的LOD预报绝对误差。

|
图 9 4种模型的LOD预报绝对误差 Fig. 9 Absolute error of LOD prediction for 4 models |
由图 9可见,在拟合方法一定的情况下,随着预报跨度的增大,其绝对精度也在下降。从整体的预报情况来看,加权LS+PCF模型表现最好,其次是LS+PCF模型,传统的LS外推模型表现不理想。
4 结语本文首先采用分步方式对LOD参数时间序列频谱分析结果进行周期提取,然后利用周期提取结果进行LOD的加权LS+PCF模型拟合。实验结果显示,该拟合方法将RMSE从LS外推模型拟合的0.000 3 s降至0.000 1 s,将确定系数从0.80提高到了0.97左右,这说明LS+PCF模型拟合可以提升LOD序列拟合效果。上述研究成果可为LOD序列的预报研究提供参考。
| [1] |
Zhu S Y. Prediction of Polar Motion[J]. Bulletin Géodésique, 1982, 56(3): 258-273 DOI:10.1007/BF02525586
(  0) 0) |
| [2] |
Kosek W, Kalarus M, Niedzielski T. Forecasting of the Earth Orientation Parameters - Comparison of Different Algorithms[J]. Nagoya Journal of Medical Science, 2007(1): 155-158
(  0) 0) |
| [3] |
Egger D. Neuronales Netz Pradiktion Von Erdrotation[J]. Allgemeine Vermessungs Nachrichten, 1992, 12(11): 247-258
(  0) 0) |
| [4] |
Kalarus M. The Application of Artificial Neural Networks and Autoregressive Techniques for Earth Orientation Parameters Prediction[C]. European Geosciences Union General Assembly 2005, Vienna, Austria, 2005
(  0) 0) |
| [5] |
Freedman A P, Steppe J A, Dickey J O, et al. The Short-Term Prediction of Universal Time and Length of Day using Atmospheric Angular Momentum[J]. Journal of Geophysical Research Solid Earth, 1994, 99(B4)
(  0) 0) |
| [6] |
雷雨. 地球自转参数高精度预报方法研究[D]. 北京: 中国科学院大学, 2016 (Lei Yu. Study on Methods for High Accuracy Prediction of Earth Rotation Parameters[D]. Beijing: University of Chinese Academy of Sciences, 2016)
(  0) 0) |
| [7] |
魏二虎, 刘学习, 孙浪浪, 等. 测站数目和观测弧段对GPS解算地球自转参数的影响分析[J]. 大地测量与地球动力学, 2017, 37(2): 187-191 (Wei Erhu, Liu Xuexi, Sun Langlang, et al. Analysis of the Influence of Number of Station and Observation Arcs to Earth Rotation Parameters by GPS[J]. Journal of Geodesy and Geodynamics, 2017, 37(2): 187-191)
(  0) 0) |
| [8] |
孙张振. 高精度地球自转参数预报模型与算法研究[D]. 济南: 山东大学, 2020 (Sun Zhangzhen. Research on the Models and Algorithms for High Accuracy Prediction of Faith Rotation Rotamters[D]. Jinan: Shandong University, 2020)
(  0) 0) |
| [9] |
魏二虎, 李岩林, 韩玉琴, 等. 地球自转速度变化与全球气温变化的相关性研究[J]. 测绘地理信息, 2021, 46(6): 1-7 (Wei Erhu, Li Yanlin, Han Yuqin, et al. Study on the Correlation between the Change of Earth Rotation Speed and the Change of Global Temperature[J]. Journal of Geomatics, 2021, 46(6): 1-7)
(  0) 0) |
2. School of Geography and Information Engineering, China University of Geosciences, 388 Lumo Road, Wuhan 430079, China;
3. GNSS Research Centre, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2023, Vol. 43
2023, Vol. 43

