线性度是地震数据采集器的关键性能指标之一,可反映地震数据采集器输出信号是否失真。评价线性度的常用方法有最小二乘法[1-3]和端基直线法[4],地震数据采集器线性度计算多采用最小二乘法。
为评估最小二乘法和端基直线法对地震数据采集器线性度测量不确定度的影响,本文从理论上给出2种方法评价线性度的区别,通过实例展示不确定度的计算过程。最后通过对比多种型号的地震数采测量结果,分析2种方法的差别及不同输入点个数和位置对线性度不确定度的影响。
1 最小二乘法和端基直线法的线性度理论对于线性系统,输入量x和输出量y之间的关系为:
| $ f(x)=k x+b $ | (1) |
式中,k为直线斜率,b为直线截距。
用xi、yi(i=1, 2, …, n)分别表示输入值和测量值,则在信号点xi上测量值yi与线性回归值f(xi)的残差可表示为:
| $ \Delta y_i=y_i-\left(k x_i+b\right) $ | (2) |
根据线性度定义,最大残差可反映线性度大小。线性度公式为:
| $ L=\max \left(L_i\right)=\frac{\max \left|\Delta \bar{y}_i\right|}{\hat{k} E_r}, i=1, \cdots, n $ | (3) |
式中,Er为量程,
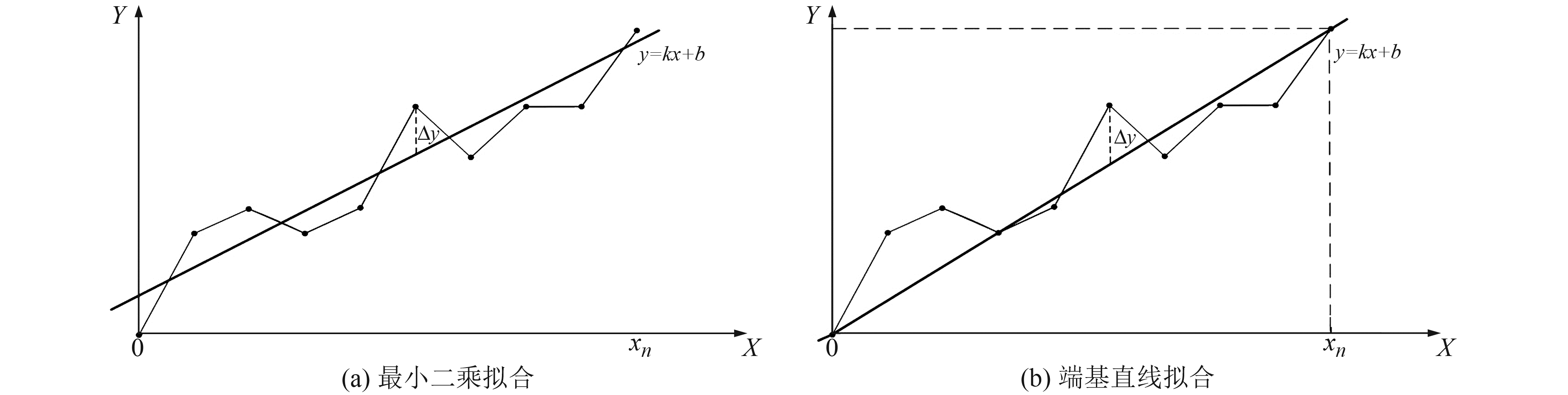
图 1为最小二乘法和端基直线法拟合示意图。可以看出,二者计算线性度的区别在于k和b的估计值不同导致残差Δy不同,残差的正负和大小可表征测量值在拟合直线两侧的分散程度。按照最小二乘法原理,当残差平方和最小时,k和b估计值最佳;端基直线法中,k和b只与首尾点有关。
|
图 1 线性拟合示意图 Fig. 1 Schematic diagram of linear fitting |
在地震数据采集器测量范围(EL, EH)内选择n个校准点Ei(i=1, 2,…,n)进行测试,在每个信号点Ei上测量m个数据yij,取其平均值yi作为测量结果,其方差为:
| $ s^2\left(\bar{y}_i\right)=\frac{1}{m(m-1)} \sum\limits_{j=1}^m\left(y_{i j}-\bar{y}_i\right)^2 $ | (4) |
2种方法的估计值
| $\;\;\;\;\;\;最小二乘法\\ \left\{\begin{array}{l} \hat{k}=\frac{n \sum\limits_{i=1}^n \bar{y}_i E_i-\left(\sum\limits_{i=1}^n \bar{y}_i\right)\left(\sum\limits_{i=1}^n E_i\right)}{n \sum\limits_{i=1}^n E_i^2-\left(\sum\limits_{i=1}^n E_i\right)^2} \\ \hat{b}=\frac{\left(\sum\limits_{i=1}^n \bar{y}_i\right)\left(\sum\limits_{i=1}^n E_i^2\right)-\left(\sum\limits_{i=1}^n \bar{y}_i E_i\right)\left(\sum\limits_{i=1}^n E_i\right)}{n \sum\limits_{i=1}^n E_i^2-\left(\sum\limits_{i=1}^n E_i\right)^2} \end{array}\right. $ | (5) |
| $ \text { 端基直线法 }\left\{\begin{array}{l} \hat{k}=\frac{\bar{y}_n-\bar{y}_1}{E_n-E_1} \\ \hat{b}=\frac{E_n \bar{y}_1-E_1 \bar{y}_n}{E_n-E_1} \end{array}\right. $ | (6) |
线性度L的测量不确定度u(L)的来源主要有:1)由标准仪器引入的标准不确定度u(Ei);2)Ei测量重复性引入的不确定度u1(yi);3)被校数据采集器分辨力(A/D位数)引入的不确定度u2(yi)。
考虑到被测数据采集器的重复性和分辨力存在重复,合成不确定度时将二者中的最小值舍去。
根据不确定度理论公式[5]与文献[1, 4]可得,线性度L的合成标准不确定度为:
| $ \begin{gathered} u_c(L)=\sqrt{\sum\limits_{i=1}^n c_L^2\left(E_i\right) u^2\left(E_i\right)+\sum\limits_{i=1}^n c_L^2\left(\bar{y}_i\right) u^2\left(\bar{y}_i\right)+2 \sum\limits_{i=1}^n c_L\left(E_i\right) c_L\left(\bar{y}_i\right) u\left(E_i\right) u\left(\bar{y}_i\right)}= \\ \sqrt{\sum\limits_{i=1}^n\left(c_L\left(E_i\right) u\left(E_i\right)+c_L\left(\bar{y}_i\right) u\left(\bar{y}_i\right)\right)^2} \end{gathered} $ | (7) |
其有效自由度veff=m-3。
由式(7)可知,要得到线性度的标准不确定度,首先需计算灵敏系数cL(Ei)和cL(yi)以及不确定度分量u(Ei)和u(yi)。最小二乘法和端基直线法的灵敏系数cL(Ei)和cL(yi)不同,具体计算可参见文献[1, 4]。
3 测量数据处理及分析 3.1 测量数据获取及处理采用标准源法,利用5730A输出标准直流电压信号作为地震数据采集器的输入。选用EDAS-27HR型号地震数据采集器,测量范围设为(-10 V, 10 V),采样率设为100 Hz,其A/D位数为28 bits,分辨率为0.149 μV/count。根据地震监测专业设备入网测试规程[6]选择测试点,从-10~10 V每隔1 V选取1个点,首尾选取-9.5 V和9.5 V,共21个测试点。每个测试点测量2 min,截取20 s的数据计算其平均值,并将平均值折合到对应的输入端作为最终的测量结果,由5730A标准仪器引入的不确定度分量u(Ei)采用B类评定,Ei的允许误差极限由仪器说明书获得。如参照5730A技术指标,测量2 V直流电压时的扩展不确定度为5 ppm×Vout+0.7 μV,k=2,则其区间半宽为:
| $ \begin{gathered} u\left(E_i\right)=\frac{5 \times 10^{-6} \times 2 \mathrm{~V}+0.7 \mu \mathrm{V}}{2}= \\ 5.35 \times 10^{-6} \mathrm{~V} \end{gathered} $ |
由被测仪器分辨力引入的不确定度u2(yi)的分辨力为0.149 μV,在±0.074 5 μV区间内为均匀分布,包含因子
| $ u_2\left(\bar{y}_i\right)=\frac{0.000\;000\;074\;5 \mathrm{~V}}{\sqrt{3}}=4.3 \times 10^{-8} \mathrm{~V} $ |
在日常测量中,一般取2 000(20 s)个点的平均值作为测量结果,测量结果的实验方差由式(4)获得。最终的不确定度分量以及灵敏系数见表 1。
|
|
表 1 不确定度分量及灵敏系数 Tab. 1 Uncertainty components and sensitivity coefficients |
对于最小二乘法,由式(2)和式(3)可得线性度估计值L=4.74×10-6,j=1。将表 1中灵敏系数代入式(7),计算得到最小二乘法线性度的合成标准不确定度为7.8×10-7 V。
对于端基直线法,由式(2)和式(3)可得线性度估计值L=9.1×10-7,j=12。将表 1中灵敏系数代入式(7),计算得到端基直线法线性度的合成标准不确定度为6.5×10-7 V,有效自由度均为veff=21-3=18。
3.2 测量数据分析 3.2.1 不同方法对计算结果的影响分别采用最小二乘法和端基直线法对不同分辨力(数据位数)、不同型号的地震数据采集器的线性度结果进行不确定度评定,结果见表 2。
|
|
表 2 最小二乘法与端基直线法线性度的标准不确定度 Tab. 2 Standard uncertainty of linearity of the least squares method and the terminal-based straight line method |
从表 2可以看出,最小二乘法与端基直线法线性度不确定度评定结果在同一数量级,与分辨力无关。因此,对于目前常用的地震数据采集器而言,无论采用最小二乘法还是端基直线法计算的线性度,其结果的离散度均很小。端基直线法线性度不确定度的评定结果较最小二乘法稳定,这主要与不确定度计算公式有关。
3.2.2 数据点数和位置对计算结果的影响为研究数据点数和位置对不确定度评定结果的影响,分别对19点、17点、15点、13点、11点、9点和7点数据在不同位置组合下线性度的不确定度进行评定。为不失一般性,仍然采用对称的选点原则。如图 2所示,以19点数据为例,即在原21点数据的基础上从大到小依次去掉对称的一组数据,因此有9个位置组合。同理,17点、15点、13点、11点、9点和7点分别有8个、7个、6个、5个、4个和3个位置组合。2种方法在不同数据点及不同位置组合下的不确定度评定结果见图 3。

|
图 2 不同数据点数的位置组合示意图 Fig. 2 Schematic diagram of the location combination of different data points |

|
图 3 不同数据点数和位置对不确定度的影响 Fig. 3 The influence of different data points and locations on uncertainty |
从图 3可以看出,最小二乘法线性度不确定度随数据点数的增加而增加,其主要原因是不确定度计算公式为求和过程,数据点数越多其不确定度值越大。相对于最小二乘法,端基直线法线性度不确定度评定结果受数据点数影响较小,虽然不确定度的理论公式相同,但从灵敏系数可以看出,实际有效点数为3个值累加,因此其受数据点数的影响较小。
对于最小二乘法线性度不确定度而言,数据点数越多,对数据位置越不敏感;选取的数据越靠两侧,不确定度越小,说明靠边的数据对不确定度的影响较大。端基直线法线性度不确定度均在末位位置组合处发生突变,这是因为除末位位置组合外,其他位置组合的最大残差均在1 V点处出现,因此不确定度未发生任何变化,而末位位置组合已剔除1 V点,最大残差点发生变化,因此出现不确定度不同程度的突变。
4 结语本文对地震数据采集器线性度不确定度进行评定,分析目前常用的最小二乘法和端基直线法线性度不确定度的差别。多种型号的地震数据采集器线性度不确定度评定结果表明,2种方法线性度不确定度评定结果在同一数量级,可以满足地震数据采集器线性度不确定度评定的要求,但最小二乘法线性度不确定度受测试点数的影响较大,端基直线法线性度受测试点数的影响较小。
| [1] |
梁志国, 孙璟宇, 李滨. 最小二乘独立线性度的测量不确定度[J]. 航空计测技术, 2002, 22(4): 28-33 (Liang Zhiguo, Sun Jingyu, Li Bin. Evaluation of Uncertainty of Linearity Using LMS Method[J]. Aviation Metrology and Measurement Technology, 2002, 22(4): 28-33)
(  0) 0) |
| [2] |
杨颖. 测汞仪线性误差测量值的不确定度评定[J]. 计量与测试技术, 2016, 43(7): 86-87 (Yang Ying. Uncertainty Evaluation of Linear Error Measurement Results of Mercury Analyzers[J]. Metrology and Measurement Technique, 2016, 43(7): 86-87)
(  0) 0) |
| [3] |
许金鑫, 由强. 任意阶次多项式最小二乘拟合不确定度计算方法与最佳拟合阶次分析[J]. 计量学报, 2020, 41(3): 388-392 (Xu Jinxin, You Qiang. Uncertainty Calculation for Arbitrary Order Polynomial Least-Square Fitting and Analysis of the Best Fitting Order[J]. Acta Metrologica Sinica, 2020, 41(3): 388-392)
(  0) 0) |
| [4] |
梁志国. 端基线性度的测量不确定度[J]. 测试技术学报, 2003, 17(1): 37-41 (Liang Zhiguo. The Uncertainty of Evaluation of Terminal Base Linearity[J]. Journal of Test and Measurement Technology, 2003, 17(1): 37-41)
(  0) 0) |
| [5] |
倪育才. 实用测量不确定度评定[M]. 北京: 中国标准出版社, 2016 (Ni Yucai. Evaluation of Practical Measurement Uncertainty[M]. Beijing: China Standards Press, 2016)
(  0) 0) |
| [6] |
中国地震局. DB/T 22-2020地震观测仪器进网技术要求: 地震仪[S]. 北京: 中国标准出版社, 2020 (China Earthquake Administration. DB/T 22-2020 Technical Requirements of Instruments in Network for Earthquake Monitoring—Seismograph[S]. Beijing: China Standards Press, 2020)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

