2. 武汉引力与固体潮国家野外科学观测研究站,武汉市洪山侧路40号,430071;
3. 河北省地震动力学重点实验室,河北省三河市学院街465号,065201;
4. 河北省地震局易县地震台,河北省保定市易县,074211
倾斜仪故障会影响地震监测数据的质量。目前地震台站部署的倾斜仪主要有VS型、DSQ型以及SSQ型等[1]。这些传统倾斜仪的运维已有较成熟的配套方案,可依赖具有丰富仪器故障处理经验的专业技术人员和仪器生产厂家进行故障诊断与排除工作。VP型倾斜仪是中国地震局地震研究所自主研发的一种新型宽频带垂直摆式地形变观测设备,其故障分析诊断主要依赖人工判断并依照既定检修流程的传统方式,存在一定主观性,会影响仪器故障判断检修效率。
随着人工智能技术在故障诊断领域的快速应用,诸多模式识别模型已成功应用于部分较复杂设备的电机轴承故障诊断、工业过程故障分析或天气干扰异常识别等领域[2-3],诊断精度与结果可信度均较高。本文在综合研究神经网络模型和群体智能优化算法的基础上,提出一种VP型倾斜仪故障智能诊断方法。首先引入经验模态分解(EMD)和近似熵进行故障信号的多尺度特征提取;然后基于蝗虫优化算法改进自组织映射神经网络的关键参数,利用改进后的新模型进行故障智能诊断。
1 数据来源以河北易县地震台VP型倾斜仪为研究对象。该仪器安装于华北平原与太行山交界处断裂带附近的观测山洞中,场地岩性以闪长岩、石灰岩及页岩为主。仪器采集到大量故障数据,主要类型为数据采集设备故障、电源设备故障以及天气干扰。实验利用上述3种倾斜仪故障类型数据,时间跨度为2016-04-15~2021-11-20,采集到有效故障记录数目依次为96、149、206条,包含NS与EW两个方向的数据,原始记录长度为86 400。将空缺值或null点设置为0,并以最大异常绝对值为中心将数据长度截取成4 000。最后,对数据进行归一化处理,将幅值限定在[-1, 1]范围内,以消除量纲带来的影响。
2 方法与原理 2.1 蝗虫优化算法蝗虫优化算法[4](grasshopper optimization algorithm, GOA)是一种模仿蝗虫群体幼虫与成虫同时杂居与迁移的新型群体仿生优化算法,其利用蝗虫幼虫行动迟缓和成虫移动较快的特性同时开展局部搜索与全局寻优。GOA更新蝗虫位置的核心公式为:
| $ \begin{gathered} x_{i+1, d}=c\left(\sum\limits_{j=l, j \neq i}^N c \frac{u b_d-l b_d}{2}\right. \\ \left.s\left(\left|x_{j, d}-x_{i, d}\right|\right) \frac{x_j-x_i}{d_{i j}}\right)+T_d^{\prime} \end{gathered} $ | (1) |
式中,xi+1, d为第i只蝗虫个体在位置向量第d维上的坐标值;c为与最大迭代次数有关,可影响蝗虫全局寻优或局部搜索能力的动态衰减系数;ubd与lbd分别为蝗虫个体位置第d维上的阈值上下限;s(·)为蝗虫i受到蝗虫j影响的相互作用力函数;dij为蝗虫i与蝗虫j之间的绝对距离;T′d为蝗虫群体此前得到的最优位置。
2.2 SOM神经网络自组织特征映射(self-organizing feature map, SOM)神经网络[5]是一种无教师、自主学习型网络算法,既可以学习输入矩阵向量的分布特征,又可以学习其拓扑结构,通过更新神经元及其近邻神经元的权值向量来进行分类与排序,最后只需要比对测试数据的类标与训练数据的类标是否匹配即可得到预测结果。
SOM网络一般只由输入层和二维平面型竞争层组成,二者的神经元之间以全连接的方式产生联系,而竞争层维数、网络学习速率、步长、领域距离等参数对神经网络学习效果具有一定影响,不恰当的网络参数值将直接影响网络训练效率并降低网络预测的精度。
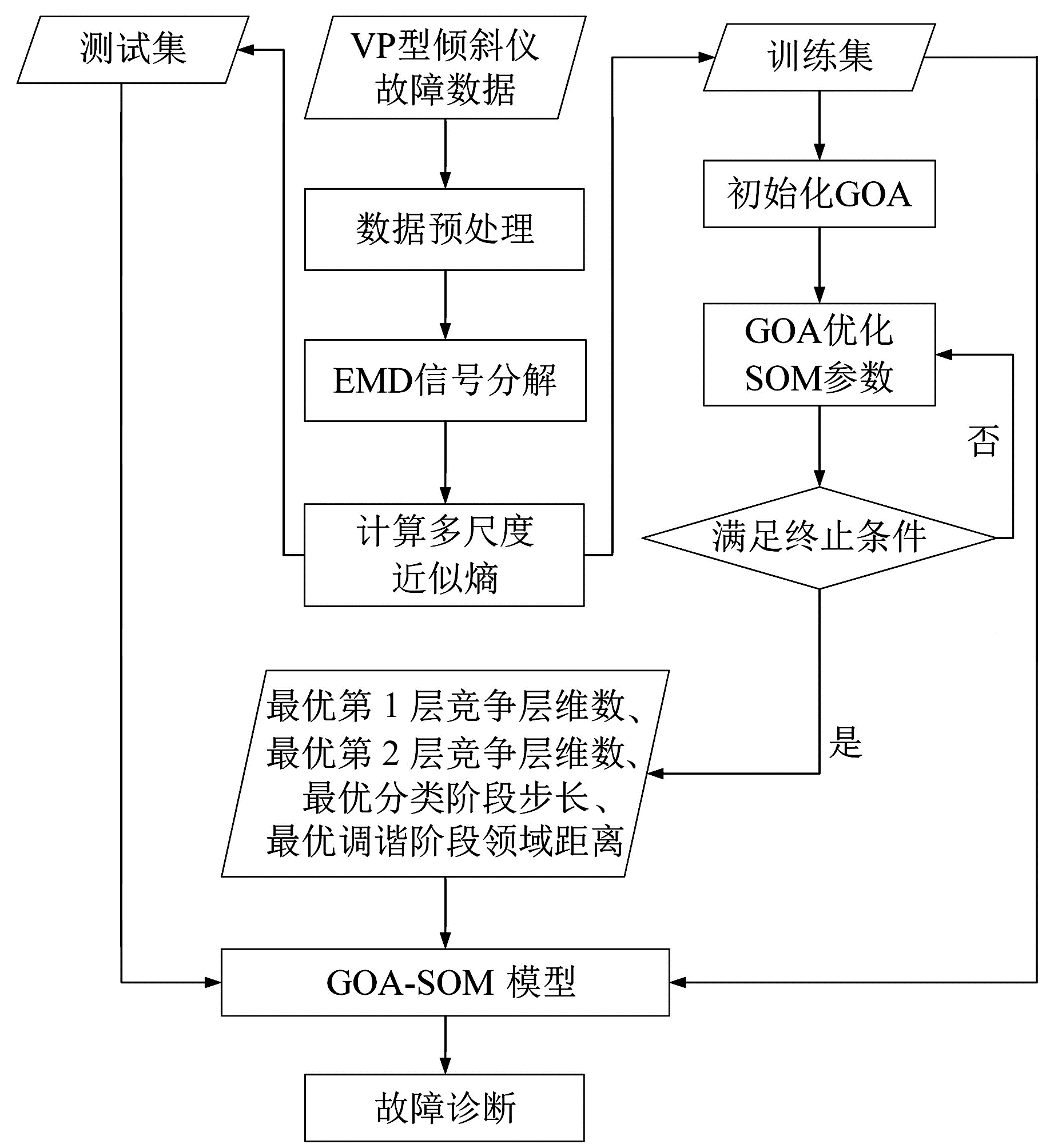
2.3 故障智能诊断原理基于EMD多尺度近似熵和GOA-SOM神经网络模型(简称GOA-SOM模型)的VP型垂直摆倾斜仪故障诊断流程如图 1所示,具体过程为:
|
图 1 VP型倾斜仪故障智能辨识流程 Fig. 1 Flow chart of intelligent fault identification method for VP tiltmeter |
1) 对N个倾斜仪原始故障数据进行畸变点定位、统一长度截取、数据归一化等预处理,得到故障特征分析输入向量Xi(i=1, 2, …, N)。
2) 使用EMD将故障信号Xi分解为6个本征模态函数IMFi, j(j=1, 2, …, 6)和1个剩余信号Ri,并线性重构为:
| $ \boldsymbol{X}_i=\sum\limits_{j=1}^6 \mathrm{IMF}_{i, j}+\boldsymbol{R}_i $ | (2) |
3) 计算各个IMF分量的近似熵,得到该信号的EMD多尺度近似熵向量,并重复步骤1)~2),依次计算各个故障信号Xi的EMD多尺度近似熵值,从而组建SOM神经网络输入矩阵S0。
近似熵是表征信号混乱程度的特征参量,其运算速度和特征区分效果与嵌入维数、容忍系数以及延迟时间有关,在实验中3者可分别取值为2、0.15或0.2、8[5]。
4) 将S0以随机抽样的方式划分成训练集S1和测试集S2, 并固定比例8 ∶2。以训练集为对象,应用GOA算法优化SOM模型的第1层竞争层维数、第2层竞争层维数、分类阶段步长以及调谐阶段领域距离等网络参数,以诊断错误率表达式(式(3))为适应度函数,将得到的最优值替换SOM模型中的原参数值,得到GOA-SOM模型:
| $ y=\mid 100-\text { Acc } \mid / 100 $ | (3) |
5) 将GOA-SOM模型应用于上述故障数据的训练集和测试集,以训练集S1为基础得到P个故障信号的SOM聚类标签值lp(p=1, 2, …, P),以测试集S2为基础得到Q个故障信号的SOM聚类标签值Lq(q=1, 2, …, Q)。将Lq与lp进行匹配,若标签值相同,则二者被GOA-SOM模型视作同类故障;如果Lq与lp所代表的故障信号真实属性标签值Tq与Tp也完全相同,则判定该次诊断正确,否则判定诊断错误。测试集中Q个故障待测信号全部执行完上述诊断步骤后,诊断结束,得到最终诊断结果。
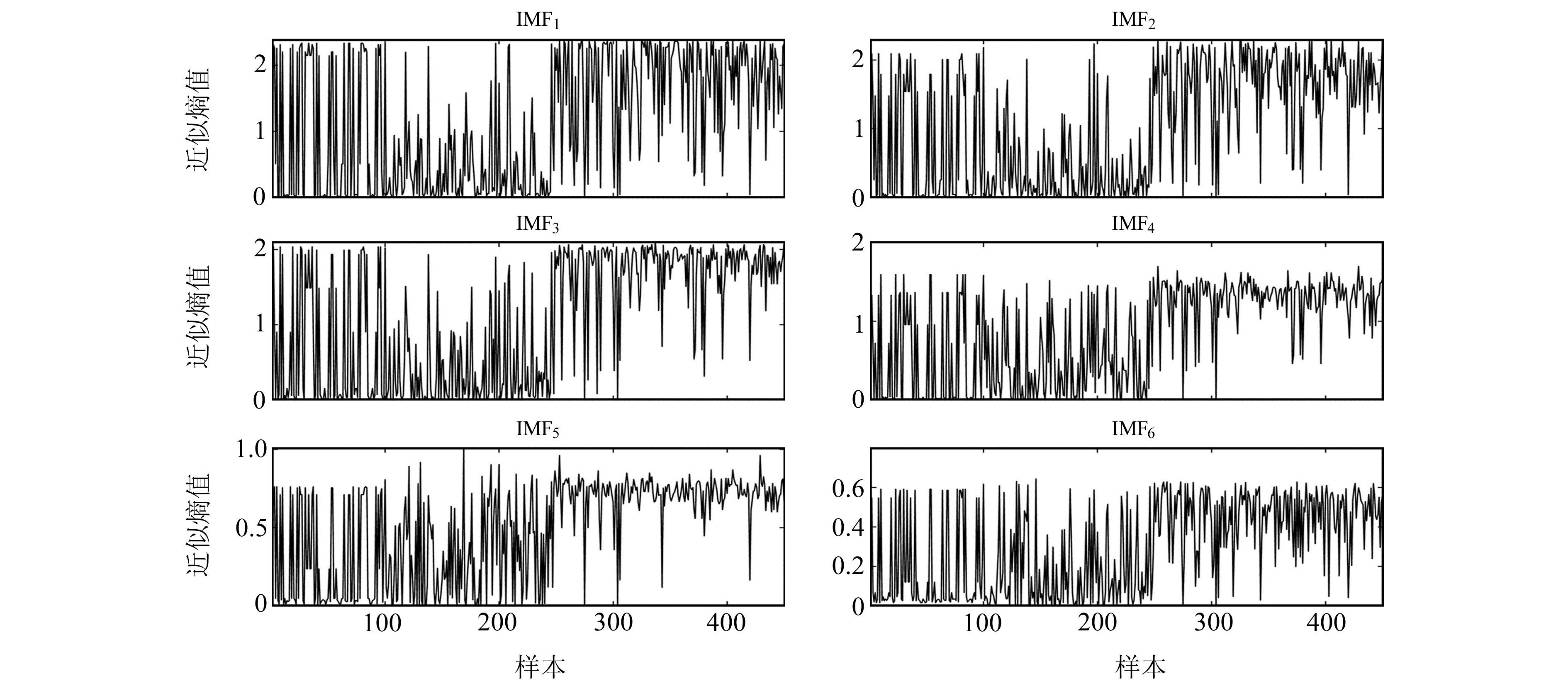
3 实验与分析 3.1 EMD多尺度近似熵计算结果图 2和表 1为经过EMD分解和多尺度近似熵计算的VP倾斜仪故障特征。可以看出,3种故障类型的IMF1、IMF2、IMF3的近似熵均值都表现出显著差异性,其比例接近2 ∶1 ∶4;从IMF4开始,电源故障和数采故障的近似熵均值相似性较高,二者的故障信号中存在大量零值数据,区分难度较大,这对诊断模型在线性判据上的抗干扰能力具有一定检验作用。
|
图 2 EMD多尺度近似熵计算结果 Fig. 2 Results of EMD multiscale approximate entropy |
|
|
表 1 EMD各IMF分量的近似熵均值和标准差 Tab. 1 The mean values and STD of approximate entropy of each IMF component of EMD |
为测试GOA-SOM模型在VP型倾斜仪故障诊断中的有效性,采用100轮随机抽取样本的实验方式,对电源故障、数采故障和环境异常3种故障类型数据进行智能诊断,训练集与测试集样本量比例约为8 ∶2,测试结果如图 3~5所示。

|
图 3 SOM和GOA-SOM模型诊断结果 Fig. 3 Identification results of SOM and GOA-SOM model |
|
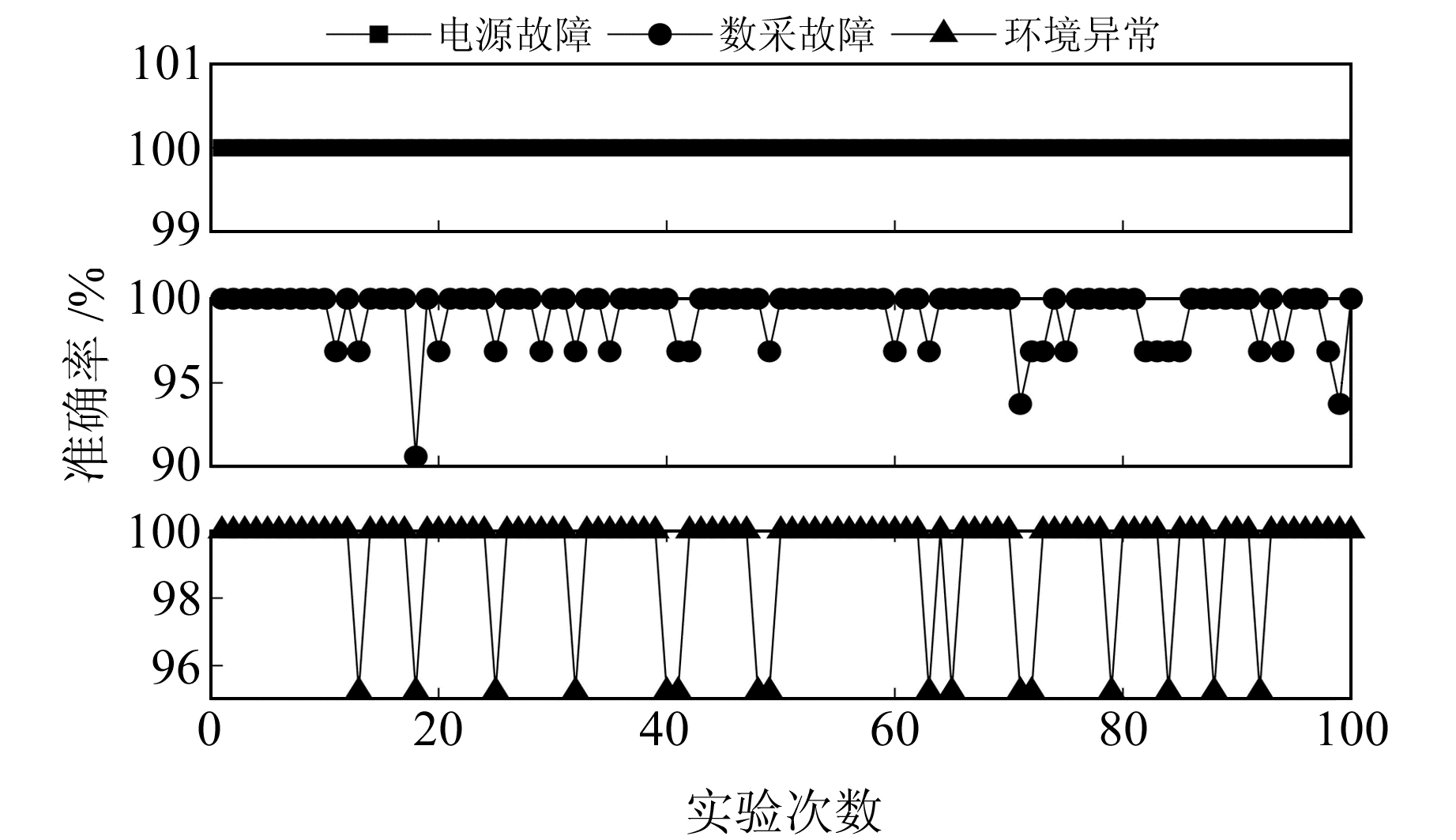
图 4 GOA-SOM模型各故障类型诊断结果 Fig. 4 Identification results of each fault type of GOA-SOM model |
|
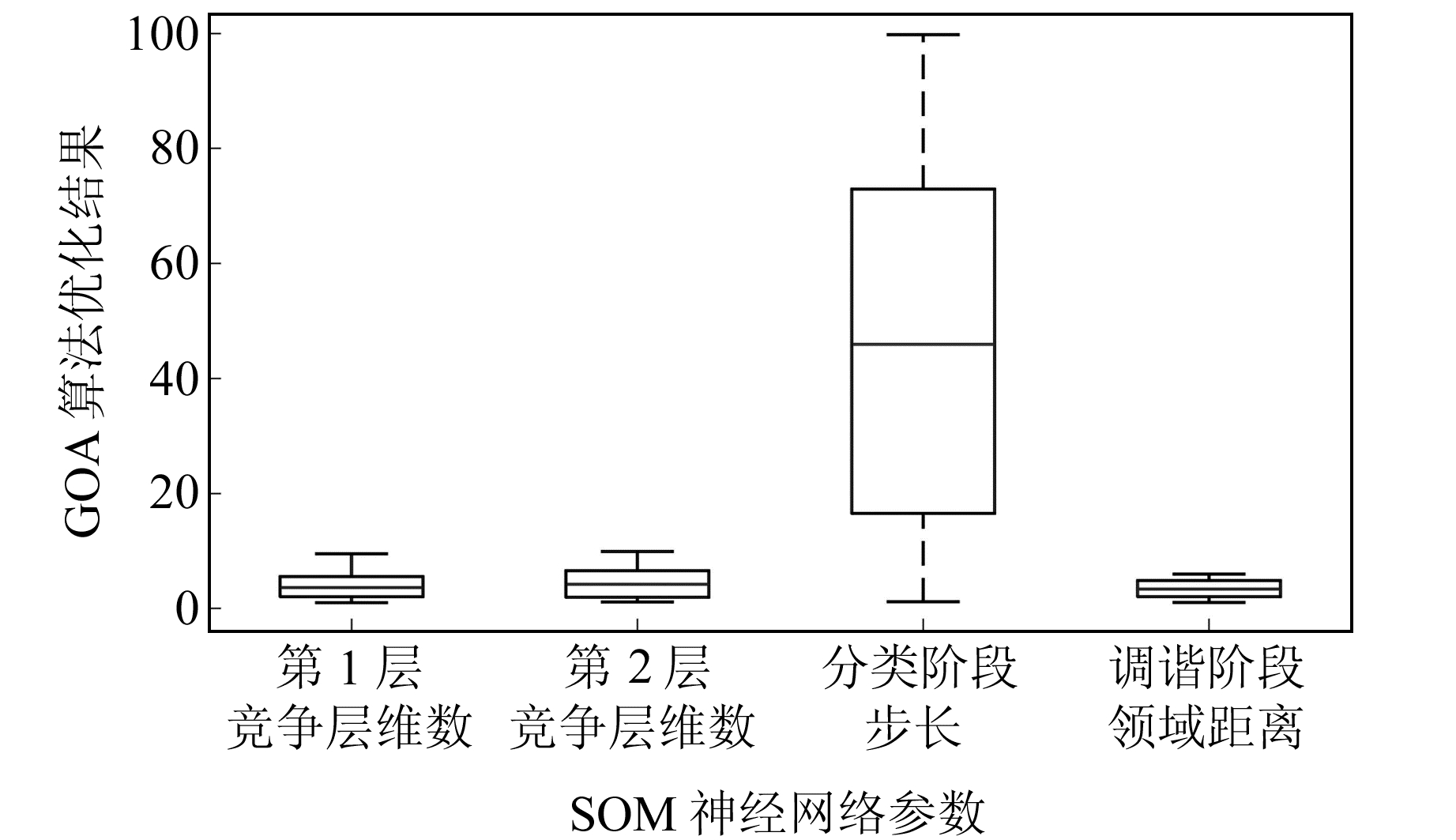
图 5 GOA算法优化SOM神经网络参数结果箱线图 Fig. 5 Boxplot of the results of optimizing SOM neural network parameters by GOA algorithm |
由图 3~4可知,GOA-SOM模型的整体诊断效果优于SOM模型,其电源故障类型的诊断率达到100%,在数采故障类型存在少许跳跃较大的峰值点,但准确率也在90%以上。
图 5为100次随机诊断实验下GOA算法优化SOM神经网络参数结果箱线图。可以看出,第1层竞争层维数、第2层竞争层维数、分类阶段步长及调谐阶段领域距离等SOM神经网络参数优化后的中位数分别为3.635 0、4.204 7、45.930 6和3.373 0,各参数优化后未出现显著的偏移和离群值。
3.3 机器学习模型故障辨识效果对比为检验GOA-SOM模型的性能,选取标准SOM神经网络、朴素贝叶斯、K最近邻(KNN)、支持向量机以及决策树等5种模型[6-8]作为参照,利用100次诊断实验下的正确率均值作为评价指标,具体对比结果如表 2~3和图 6所示。
|
|
表 2 GOA模型和GOA-SOM模型对比 Tab. 2 Comparison between GOA-SOM model and SOM model |
|
|
表 3 常见模型的诊断率均值结果对比 Tab. 3 Comparison of average values of identification for some common methods |
|
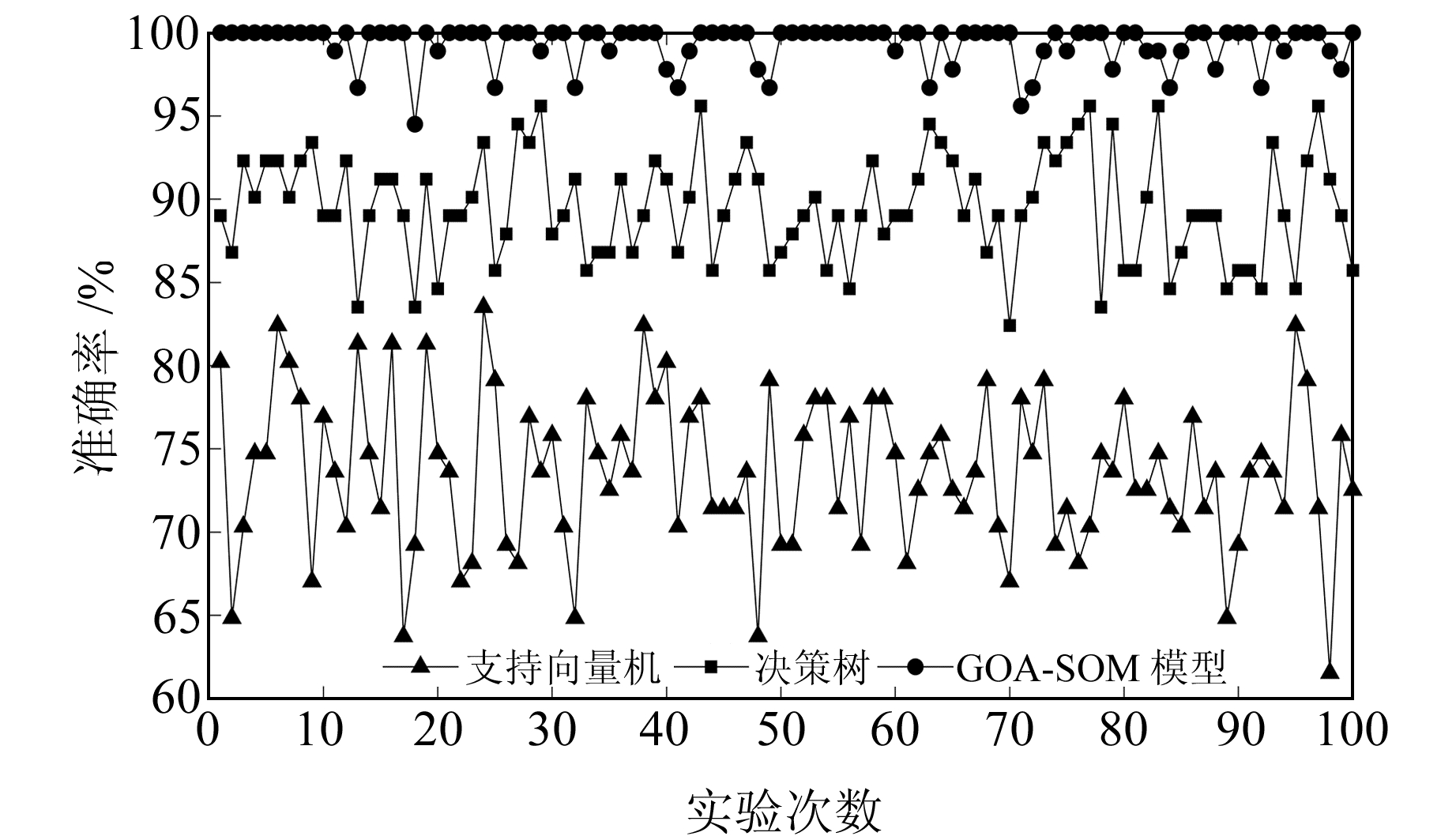
图 6 3种模型准确率对比 Fig. 6 Comparison of identification accuracy of 3 methods |
表 2为SOM模型和GOA-SOM模型在100次倾斜仪故障诊断随机子实验下的对比结果。可以看出,二者的诊断精确度均较高,尤其是对电源故障类型数据的识别都极为准确;二者差异主要在数采故障类型上,SOM模型的诊断正确率只有92.676 3%,低于GOA-SOM模型的99.093 8%;SOM模型诊断结果的稳定性也存在不足,其数采故障类型诊断精度的标准差是GOA-SOM模型的3倍。总体而言,GOA-SOM模型相对于SOM模型,在诊断率和稳定性上均有较显著的进步。
表 3为4种经典机器学习模型和GOA-SOM模型对比结果,图 6为3种诊断模型的对比细节。可以看出,GOA-SOM模型具有较优越的诊断性能,对线性相关判据的抗干扰效果较为显著,未受到相似判据属性值的影响。
4 结语本文以VP型倾斜仪各类故障数据为研究对象,利用GOA算法改进SOM神经网络,设计了一种VP倾斜仪故障智能诊断模型GOA-SOM。实验结果表明,该诊断模型具有精度高、较稳健等特点,对台站VP型倾斜仪故障分析准确判断、运维巡修、提高仪器运行率具有重要意义。
本研究有以下几个方面需要注意:
1) 本文模型忽视了GOA算法优化SOM神经网络参数带来的诊断效率问题,受最大迭代次数、适应度值计算速度等因素影响,故障诊断平均耗时较长,达到72.737 9 s。
2) 受制于部分故障类型(爆破或塌陷、雷电干扰、人工检修等)样本数目极少,本文故障诊断实验数据的种类和代表性存在一定不足;同时,本文缺少其他台站的样本,这在一定程度上会影响本文诊断模型的可靠性验证和应用推广。
3) 本文诊断模型可推广应用于VS倾斜仪、水管仪、伸缩仪等仪器的故障判准。但传感原理和技术参数存在显著不同的仪器,其分量受环境影响变化趋势差异较大,进而会影响故障特征提取的质量,这对模型的有效推广是一个挑战。
| [1] |
唐春呈, 岳冲, 张羽, 等. 双阳台DSQ型水管倾斜仪异常分析[J]. 防灾减灾学报, 2021, 37(3): 36-41 (Tang Chuncheng, Yue Chong, Zhang Yu, et al. Anomaly Analysis of DSQ Water-Tube Tiltmeter at Shuangyang Seismic Station[J]. Journal of Disaster Prevention and Reduction, 2021, 37(3): 36-41)
(  0) 0) |
| [2] |
李辉, 郝如江. 基于信息融合和广义循环互相关熵的电机轴承故障诊断[J]. 振动与冲击, 2022, 41(2): 200-207 (Li Hui, Hao Rujiang. Rolling Bearing Fault Diagnosis Based on Sensor Information Fusion and Generalized Cyclic Cross Correntropy Spectrum Density[J]. Journal of Vibration and Shock, 2022, 41(2): 200-207)
(  0) 0) |
| [3] |
陈维兴, 崔朝臣, 李小菁, 等. 基于多种小波变换的一维卷积循环神经网络的风电机组轴承故障诊断[J]. 计量学报, 2021, 42(5): 615-622 (Chen Weixing, Cui Chaochen, Li Xiaojing, et al. Bearing Fault Diagnosis of Wind Turbine Based on Multi-Wavelet-1D Convolutional LSTM[J]. Acta Metrologica Sinica, 2021, 42(5): 615-622)
(  0) 0) |
| [4] |
徐新, 蒋波涛, 曹雯. 蝗虫优化神经网络在变压器故障诊断中的应用[J]. 电网与清洁能源, 2021, 37(5): 17-23 (Xu Xin, Jiang Botao, Cao Wen. Application of Grasshopper Optimization Neural Network in Power Transformer Fault Diagnosis[J]. Power System and Clean Energy, 2021, 37(5): 17-23)
(  0) 0) |
| [5] |
蔡润, 武震, 云欢, 等. 基于BP和SOM神经网络相结合的地震预测研究[J]. 四川大学学报: 自然科学版, 2018, 55(2): 307-315 (Cai Run, Wu Zhen, Yun Huan, et al. Research on Earthquake Prediction Based on BP and SOM Neural Network[J]. Journal of Sichuan University: Natural Science Edition, 2018, 55(2): 307-315)
(  0) 0) |
| [6] |
庞聪, 江勇, 廖成旺, 等. 基于机器学习的强震动监测环境抗干扰方法对比研究[J]. 内陆地震, 2020, 34(2): 119-124 (Pang Cong, Jiang Yong, Liao Chengwang, et al. Research on Anti-Jamming Technology of Strong Motion Based on Machine Learning[J]. Inland Earthquake, 2020, 34(2): 119-124)
(  0) 0) |
| [7] |
庞聪, 江勇, 廖成旺, 等. 基于AdaBoost集成学习的强震动观测抗干扰技术研究[J]. 四川地震, 2020(4): 14-18 (Pang Cong, Jiang Yong, Liao Chengwang, et al. Research on Anti-Jamming Technology of Strong Seismograph Based on Machine Learning[J]. Earthquake Research in Sichuan, 2020(4): 14-18)
(  0) 0) |
| [8] |
庞聪, 廖成旺, 江勇, 等. 基于最小二乘支持向量机与熵特征的地震事件性质辨识研究[J]. 大地测量与地球动力学, 2022, 42(6): 655-660 (Pang Cong, Liao Chengwang, Jiang Yong, et al. Research on Identification of Seismic Event Properties Based on Least Squares Support Vector Machine and Entropy Feature[J]. Journal of Geodesy and Geodynamics, 2022, 42(6): 655-660)
(  0) 0) |
2. Wuhan Gravitation and Solid Earth Tides, National Observation and Research Station, 40 Hongshance Road, Wuhan 430071, China;
3. Hebei Key Laboratory of Earthquake Dynamics, 465 Xueyuan Street, Sanhe 065201, China;
4. Yixian Seismic Station of Hebei Earthquake Agency, Yixian, Baoding 074200, China
 2023, Vol. 43
2023, Vol. 43


