2. 海洋环境专项办公室,北京市,100081;
3. 91208部队,青岛市,266000
地磁变化场是地磁学和空间物理学的研究重点[1]。叠加在地球稳定磁场上的变化磁场可以分为2类:1)随时间缓慢变化的长期变化地磁场,其变化周期一般为几十年甚至更长;2)受到固体地球外部各种空间电流体系影响产生的短期变化地磁场[2]。短期变化地磁场又可分为平静变化和扰动变化2类:地磁平静变化比较平缓,有一定的周期性,分为太阳静日变化和太阴日变化;扰动变化的发生较为偶然,持续一段时间后消失,变化短暂且不规律[2]。
变化磁场在地球总磁场中占比仅1%左右,但却对地磁导航影响巨大[3]。通常情况下,地磁平均日变幅可达几十nT,因此对于地磁导航而言,地磁图除了需要高精度的稳定磁场外,还需要高时空分辨率的变化磁场,而现有的地磁变化场模型的时间分辨率不足以满足地磁导航的需求。针对变化磁场,传统的建模方法是根据其物理机制、观测数据、形成猜想以及物理方程建立空间电流体系模型,但其物理过程极为复杂、理论化难度较大,无法达到相应的导航精度[4]。随着计算机技术和人工智能的发展,在变化磁场建模的过程中可以依靠神经网络等方法避开复杂的物理机制,仅在数据驱动下开展研究。Sutcliffe[5]首次提出将人工智能应用于地磁日变化模型的开发;Yi等[6]建立地磁变化场多时间尺度组合模型,该方法结合可变地磁场的物理特征,融合多个模型,预测时间跨度较长;Moghadam等[7]提出一种ENN神经网络算法,并对Kp和Dst等地磁活动指数进行预测;程文凯等[8]提出基于XGBoost的机器学习方法重构地磁日变数据,相较于反向传播神经网络,其精度更高。
本文提出融合混沌理论和RBF神经网络的预测模型,在变化磁场的重构相空间中,利用RBF神经网络逼近相点的演化规律,对变化磁场进行预测。
1 理论与方法 1.1 混沌理论混沌是非线性动力系统的固有特性,广泛存在于自然系统和社会系统中[9]。混沌系统是指在一个确定的系统里,存在看似随机发展的不规则运动,这种运动无周期性、不收敛,具有不确定性和不可重复性,并且对于初始值极为敏感。混沌理论是非线性系统在一定的参数条件下,发生分叉、周期与非周期运动相互纠缠而产生的某种非周期有序运动的理论。
相空间重构是混沌时间序列预测的重要基础理论,可以从单一时间序列中提取和恢复出原系统的规律[10]。假设变化磁场时间序列为{z}j, j=1, 2, …, n,用时间延迟的方法构造M=N-(m-1)τ个m维相空间矢量:
| $ \boldsymbol{Z}\left(t_i\right)=\left(z_i, z_{i+\tau}, \cdots, z_{i+(m-1) \tau}\right) \in R^n $ | (1) |
重构轨道为:
| $ \boldsymbol{Z}=\left[Z_1, Z_2, \cdots, Z_m\right]^{\mathrm{T}} $ | (2) |
式中,m和τ分别为嵌入维数和延迟时间,Z为M×m维矩阵,Zj由m个分量组成,n个相点在m维相空间中构成一个相型,各相点连线即为描述动力系统在m维相空间里的演化轨迹[10]。在相空间重构过程中,合适的m和τ对于地磁变化时间序列中的信息挖掘具有重要意义。
地磁变化场起源于磁层和电流层体系,是一个极为复杂的系统,难以用理论模型进行精准建模。但变化磁场数据是一个非线性、非平稳的时间序列,具有混沌特性[11],因此本文引入混沌理论来挖掘数据深层特征,利用数据驱动寻找隐藏规律,从而完成预测。
1.2 RBF神经网络RBF神经网络是一种使用径向基函数作为激活函数的人工神经网络,其输出是输入的径向基函数和神经元参数的线性组合。RBF神经网络由3层结构组成,网络拓扑结构见图 1。第1层是输入层,其节点个数等于输入向量维数;第2层是隐含层,该层是网络的核心部分,决定网络性能,其变换函数是局部分布的非负非线性函数,对中心点径向对称且逐渐减弱;第3层是输出层,该层是隐含层输出的线性加权求和[10]。RBF神经网络有较强的线性拟合能力,收敛速度较快,有较好的泛化能力,可用于构建变化磁场预测模型。

|
图 1 RBF神经网络拓扑结构 Fig. 1 RBF neural network topology |
首先使用李雅普诺夫特性指数(Lyapunov characteristic exponents,LCE)判断地磁变化时间序列是否具有混沌特性。
假设某一段时间内采集的地磁变化场时间序列为{zj}, j=1, 2, …, n,具体判断步骤如下:
1) 通过FFT变换计算地磁变化时间序列的延迟时间τ和平均周期p。
2) 根据m≥2D+1的原则确定嵌入维数m,根据τ和m重构相空间:
| $ \boldsymbol{Z}\left(t_i\right)=\left(z_i, z_{i+\tau}, \cdots, z_{i+(m-1) \tau}\right) \in R^n $ | (3) |
式中,i=1, 2, …, M,N=M+(m+1)τ。将新产生的序列定义为{Zj}, j=1, 2, …, M。
3) 根据最小值原理找出离中心点最近的邻点
| $ d_t(0)=\min\limits_{z(\hat{t})}\|\boldsymbol{Z}(t)-\boldsymbol{Z}(\hat{t})\| $ | (4) |
式中,
4) 计算中心点Z(t)的dt(i):
| $ \begin{gathered} d_t(i)=\|\boldsymbol{Z}(t+i)-\boldsymbol{Z}(\hat{t}+i)\|, \\ i=1, 2, \cdots, \min (M-t, M-\hat{t}) \end{gathered} $ | (5) |
5) 计算平均z(i):
| $ z(i)=\frac{1}{q \Delta t} \sum\limits_{j=1}^q \ln d_j(i) $ | (6) |
式中,q为dt(i)的数量。由最小二乘法计算式(5)中dt(i)的偏微分,从而求得上式斜率,即最大李雅普诺夫指数λ[12]。当λ < 0时,系统有稳定的不动点;当λ=0时,对应分叉点或系统的周期解,即系统出现周期现象;当λ>0时,系统具有混沌特性。
2.2 伪最近邻域法确定嵌入维数混沌时间序列是高维相空间混沌运动的轨迹在低维空间上的投影,在投影过程中,混沌轨迹会发生一定程度的扭曲,可能导致高维空间中不相邻的2个相点投影到低维空间后成为相邻相点,即伪最近邻点,导致混沌时间序列无规律[13]。伪最近邻域法确定嵌入维数的方法如下:
在地磁变化时间序列重构后的m维相空间中,每个相点Z(t)={z(t), z(t+τ), …, z[t+(m-1)τ]}都存在某个距离内的最近邻点ZF,采用欧氏度量计算2点间距Rm(t)=||Z(t)-ZF(t)||。将m维相空间扩展到(m+1)维上,2相点间距会随之发生变化,变为Rm+12(t)=Rm2(t)+||Z(t+mτ)-ZF(t+mτ)||2。
若Rm+1(t)与Rm(t)差别较大,则可以认为是高维混沌吸引子2个点在投影到低维空间上时变为伪最近邻点。令
| $ S_m=\frac{\left\|\boldsymbol{Z}(t+m \tau)-\boldsymbol{Z}_F(t+m \tau)\right\|}{R_m(t)} $ | (7) |
若Sm>ST,则判定ZF(t)是Z(t)的虚假最近邻点。ST为阈值,可在[10, 50]之间选择。
从最小嵌入维数m0开始计算伪最近邻点比值,逐渐增大嵌入维数m,当m增大到伪最近邻点比值小于5%或伪最近邻点不随嵌入维数的增加而减少时,可以认为奇异吸引子已经完全展开,此时的m即为最佳嵌入维数[13]。
2.3 自相关函数法确定延迟时间对于地磁变化序列{zj}, j=1, 2, …, n,其时间跨度为jτ的自相关函数定义为:
| $ R_{x x}(j \tau)=\frac{1}{N} \sum\limits_{t=0}^{N-1} x(t) x(t+j \tau) $ | (8) |
固定j,绘制自相关函数关于时间τ的函数图像,当自相关函数下降到初始值的1-1/e倍时,所得时间τ即为延迟时间[13]。
2.4 混沌RBF神经网络组合预测在RBF神经网络的基础上,融合混沌理论对样本集进行优化,得到更适用于预测地磁变化的混沌RBF神经网络模型,具体步骤如下。
1) 将已知的地磁变化垂向分量数据作为预测的初始时间序列,根据混沌理论中的伪最近邻域法和自相关函数法计算最优嵌入维数m和延迟时间τ,重构相空间,得到经混沌参数优化的数据集:
| $ \boldsymbol{Z}=\left[Z_1, Z_2, \cdots, Z_m\right]^{\mathrm{T}} $ | (9) |
| $ \boldsymbol{Z}\left(t_i\right)=\left(z_i, z_{i+\tau}, \cdots, z_{i+(m-1) \tau}\right) \in R^n $ | (10) |
2) 将经相空间重构后的地磁变化垂向分量数据作为RBF神经网络输入数据,一部分数据作为训练样本集,另一部分数据作为测试样本集。
3) 利用优化后的训练样本对神经网络进行训练,并通过调试参数构建合理网络,最终通过测试样本得到地磁变化垂向分量的预测数据。
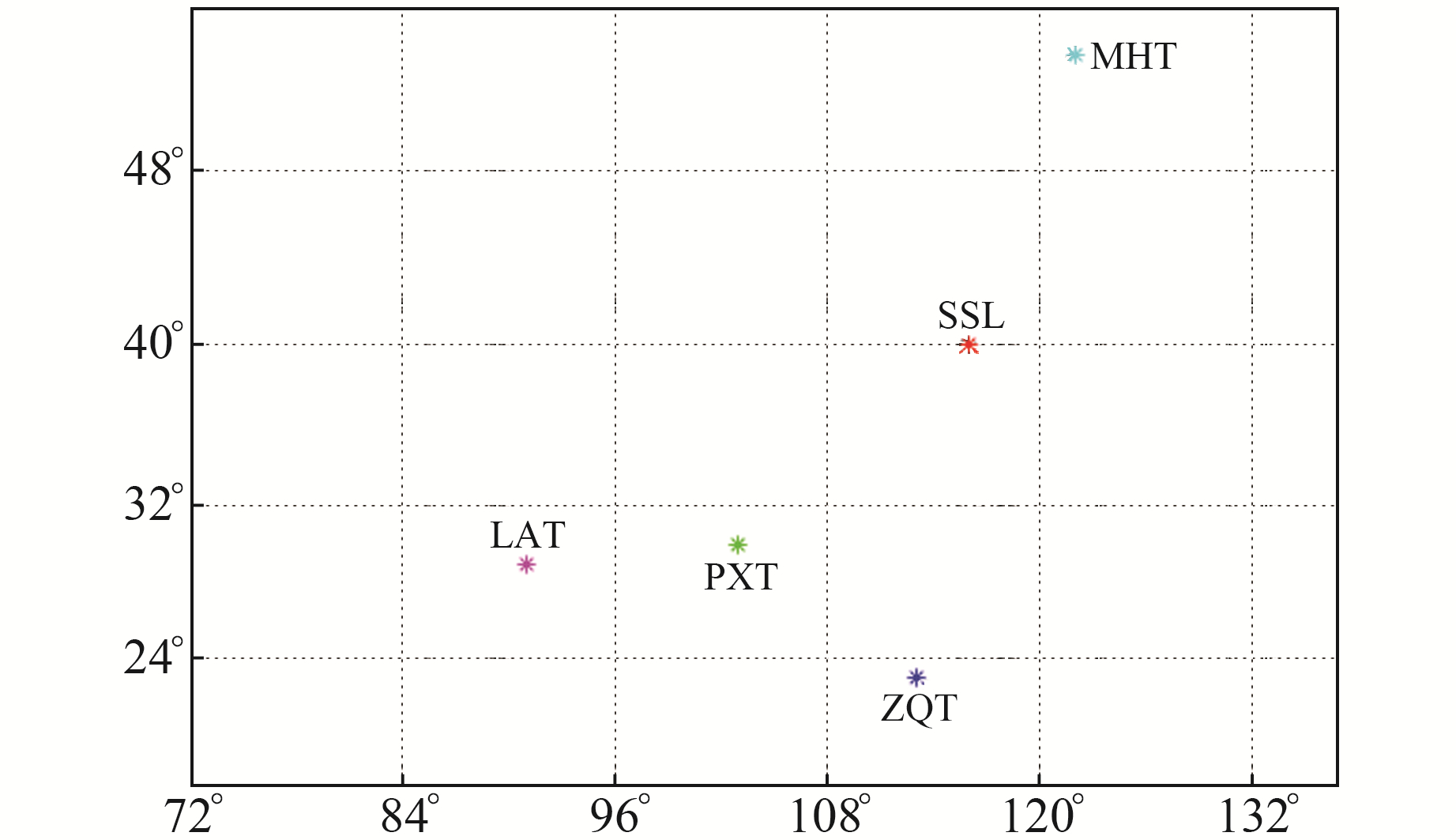
3 实验验证使用5个台站的数据进行实验验证,分别是北京十三陵(SSL)站、四川郫县(PXT)站、黑龙江漠河(MHT)站、西藏拉萨(LAT)站、广州肇庆(ZQT)站,所选台站分布较分散,可以代表我国大部分区域的地磁变化特征(图 2)。使用磁通门磁力仪测得秒采样数据,时间跨度为2020-02-12~03-09。在实际应用中,匹配分量的时间分辨率越高越好,但是过高的分辨率会导致计算量剧增、预测时间缩短。目前常用的地磁匹配分量为地磁垂向分量Z和磁场总强度F[14]。综合考虑后,采用Z的30 min均值作为实验数据,并以样本集前20 d的数据训练预测模型,选取1周的测试数据作为预测检验样本集。
|
图 2 台站分布 Fig. 2 Distribution of the stations |
由于混沌动力系统中噪声信号的不可预测性和高破坏性会掩盖系统的内在动力学特性,影响后续的预测精度以及对系统的准确描述,因此首先要对地磁数据进行去噪和平滑处理[13]。采用较为简单的拉依达准则剔除粗大误差,以SSL站为例进行建模及预测。
首先使用MATLAB计算得到地磁变化Z分量数据的最大李雅普诺夫指数λ=0.35,可知地磁变化Z分量具有混沌特性。
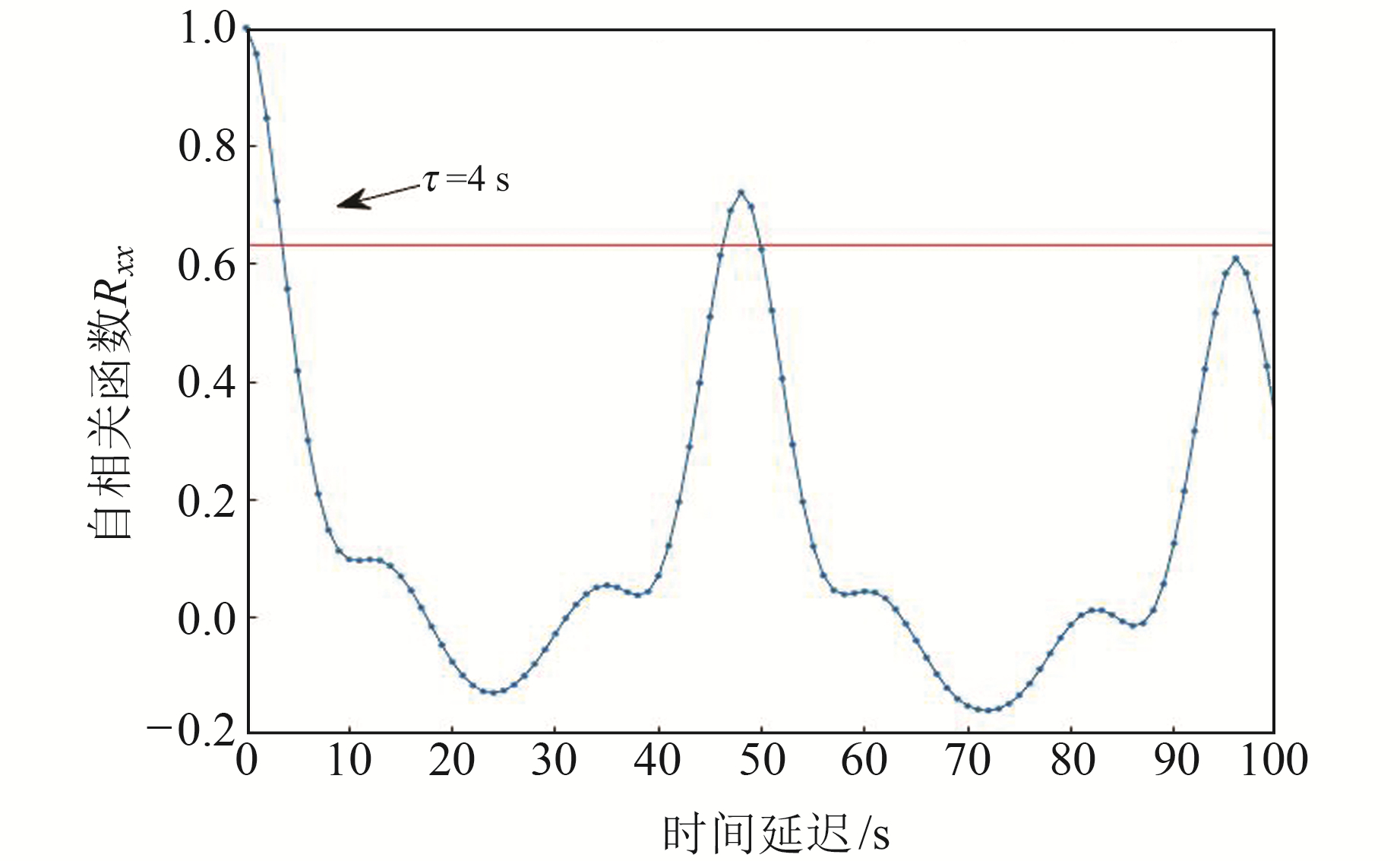
然后采用自相关函数法和伪最近邻域法确定延迟时间τ和嵌入维数m,结果见图 3、4。
|
图 3 自相关函数法计算时间延迟τ Fig. 3 Calculation of time delay τ by autocorrelation function method |
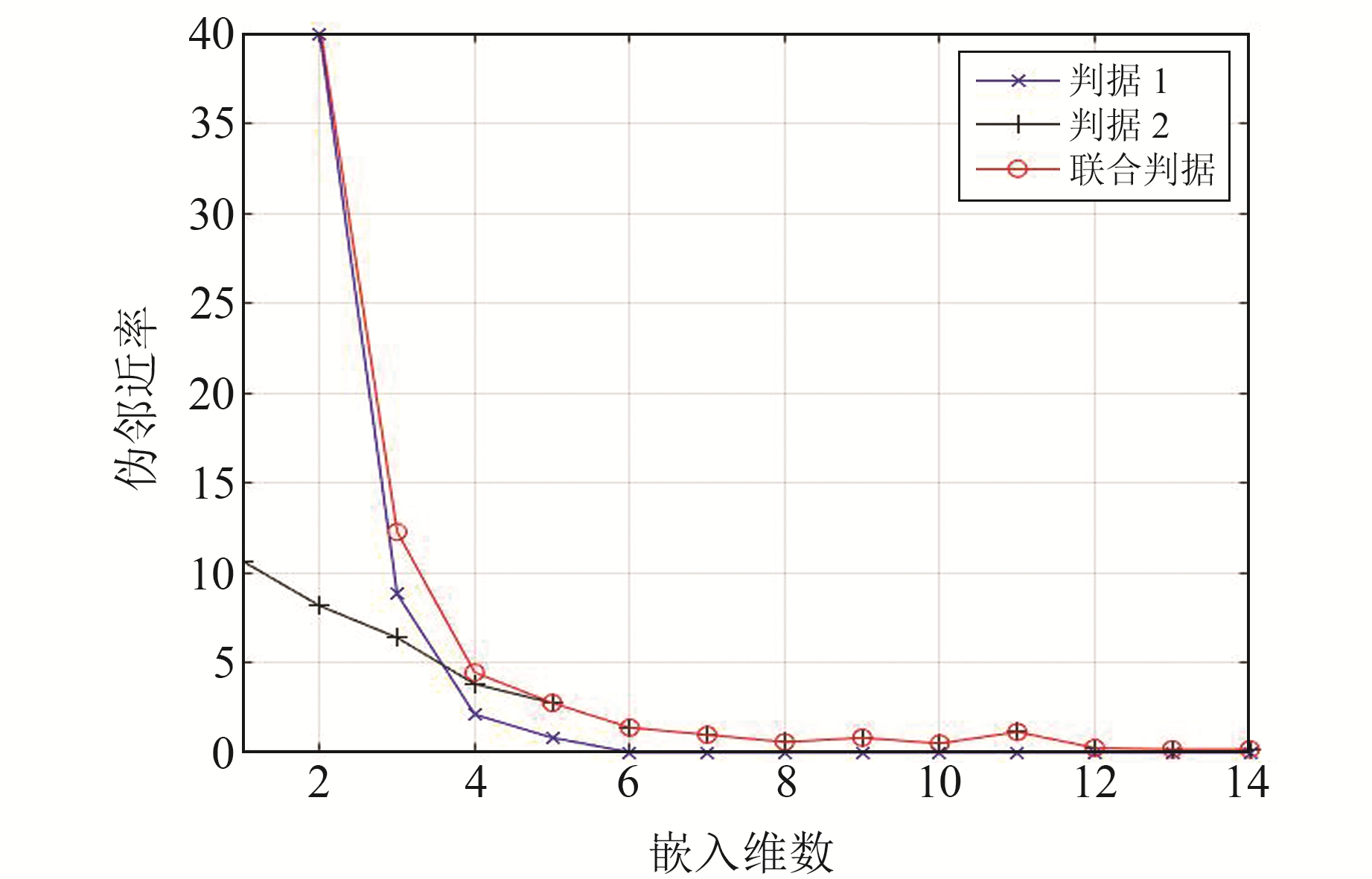
|
图 4 伪最近邻域法计算嵌入维数m Fig. 4 Calculation of embedding dimension m by false nearest neighbor method |
图 3中红色直线为Rxx=1-1/e,由图可知,当自相关函数Rxx下降到初始值的1-1/e倍时,Z分量的延迟时间τ=4 s。由图 4可见,伪邻近率随m的增大逐渐减小,并在m=14时成为常数值,不再随m发生变化,说明此时m已经能够还原混沌吸引子的结构,m=14即为模型的最佳嵌入维数。当RBF神经网络每层神经元数目与混沌时间序列重构相空间的嵌入维数m相等时,预测效果最佳[15]。因此,本文选取的神经元数目为14。
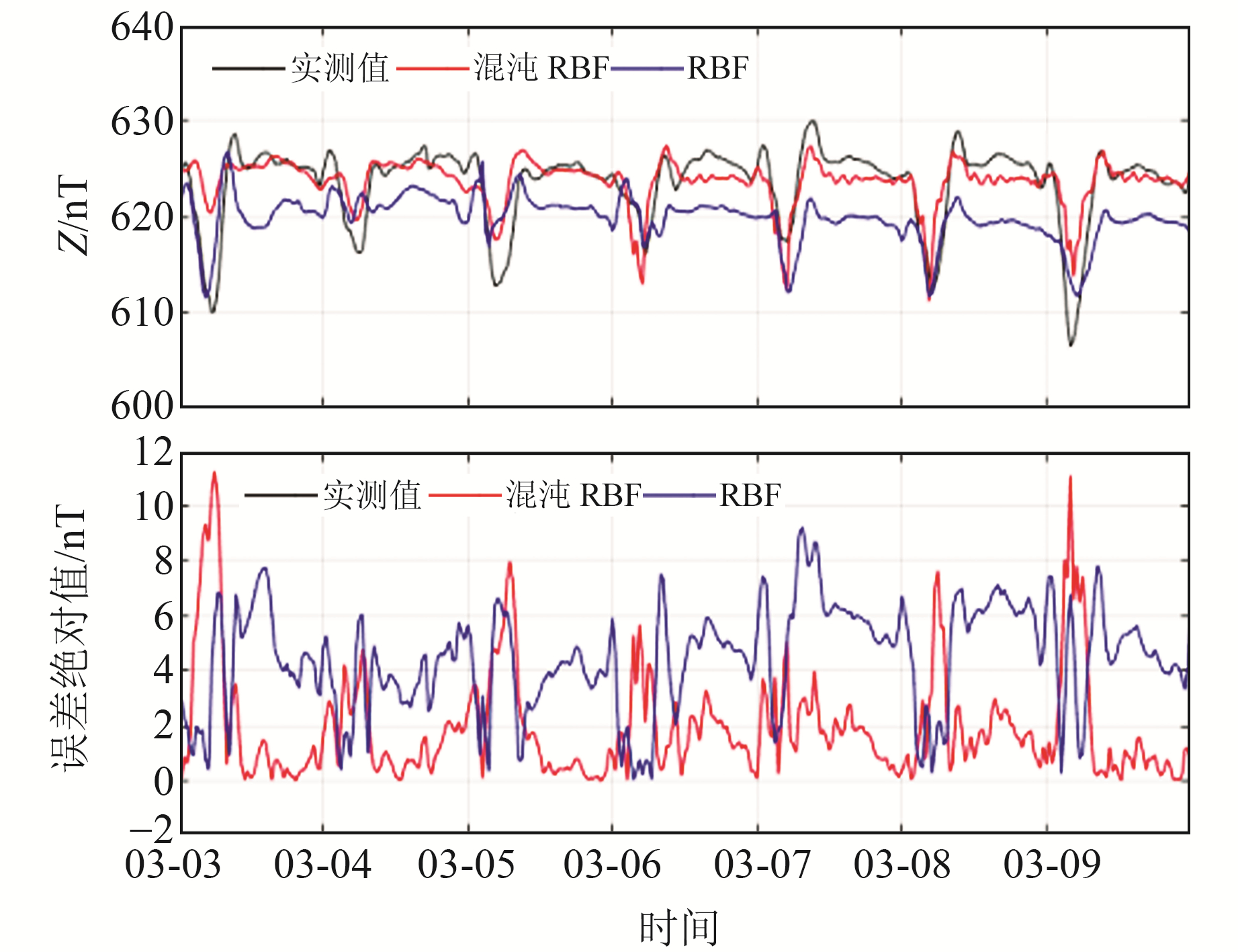
将经过平滑和归一化处理后的研究时段前20 d共1 296个Z分量数据的前960个作为训练样本集,经相空间重构后分为训练输入样本集和训练期望输出样本集;将后336个样本作为需要预测的未知样本,经相空间重构后分为测试输入样本集和测试期望输出样本集[10]。选取训练输入样本集中最后(m-1)τ+1个数据作为预测输入样本集进行递推预测,将预测结果与传统RBF神经网络算法的预测结果进行比较(图 5)。其中,测试输入样本集不参与预测,期望输出样本集作为模型预测结果的参照值[10]。
|
图 5 算法改进前后预测结果及误差绝对值 Fig. 5 Prediction results and absolute values of errors before and after algorithm improvement |
由图 5可见,2种模型均可以跟踪预测Z分量的趋势变化,但与传统RBF神经网络算法相比,混沌RBF神经网络模型的预测结果明显更接近于实际观测值,这种优势在地磁平缓变化时更加显著。在地磁场发生较大变化时,预测拟合程度是评价模型性能的重要指标。可以发现,相比于RBF神经网络算法,混沌RBF神经网络模型对曲线突变的反映效果更好,但是误差仍偏大,这可能是因为受到太阳活动等因素的影响发生地磁扰动时,地磁变化场复杂性增大、可预测性降低。从图 5还可以看出,RBF神经网络模型误差的绝对值大约在8 nT以内,且离散程度较大;本文改进模型误差的绝对值大约在4 nT以内,且分布较为集中,精度提高约50%。
3.2 模型泛用性评估为了评估改进模型在我国其他区域的适用性,对5个台站进行建模预测,并计算模型结果的最大误差、平均绝对误差MAD和均方根误差RMSE,结果见表 1。
|
|
表 1 各台站误差结果 Tab. 1 Error results of each station |
由表 1可见,预测结果的MAD均小于4 nT,RMSE均小于5 nT,误差较小,说明基于混沌RBF神经网络的地磁变化预测模型能较好地描述变化磁场的特性。模型对MHT和SSL站的预测效果较好,MAD小于2 nT,RMSE小于3 nT,但对ZQT和LAT站的预测结果误差偏大。
为了更准确地研究模型的预测精度,计算各台站误差范围所占比例,结果见表 2(单位%)。
|
|
表 2 绝对误差统计 Tab. 2 Absolute error statistics |
由表 2可见,所有台站的预测结果绝对误差小于6 nT的占比均超过80%,小于4 nT的占比均超过70%,除LAT站以外,其他台站小于2 nT的占比均超过55%;MHT站的预测效果最好,绝对误差小于4 nT的占比超过90%。综合分析可知,本文模型对中高纬度地区的预测精度略高于低纬度地区。
4 结语1) 混沌RBF神经网络地磁变化单站预测模型能够有效预测地磁变化垂向分量Z的变化趋势,相较于传统的预测模型,该模型的预测效果更好,精度提高约50%。
2) 模型预测精度对纬度变化较为敏感,中高纬度地区精度较高,MAD不超过2 nT;低纬度地区精度相对较低,MAD约为3 nT。
| [1] |
牛超, 李夕海, 魏一苇. 区域地磁变化场分析与建模关键技术研究[M]. 西安: 西安电子科技大学出版社, 2021 (Niu Chao, Li Xihai, Wei Yiwei. Research on Key Technology of Regional Geomagnetic Variation Field Analysis and Modeling[M]. Xi'an: Xidian University Press, 2021)
(  0) 0) |
| [2] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005 (Guan Zhining. Geomagnetic Field and Magnetic Exploration[M]. Beijing: Geological Publishing House, 2005)
(  0) 0) |
| [3] |
王仕成. 地磁变化场对地磁匹配制导影响分析[M]. 西安: 西安地图出版社, 2008 (Wang Shicheng. Analysis of the Influence of Earth's Magnetic Field on Geomagnetic Matching Guidance[M]. Xi'an: Xi'an Map Publishing House, 2008)
(  0) 0) |
| [4] |
牛超, 齐玮, 李夕海, 等. 地磁场静日变化Sq研究概述[C]. 第9届国家安全地球物理专题研讨会, 北京, 2013 (Niu Chao, Qi Wei, Li Xihai, et al. Overview of Research on the Geomagnetic Diurnal Variation Sq[C]. 9th National Security Geophysics Symposium, Beijing, 2013)
(  0) 0) |
| [5] |
Sutcliffe P R. The Development of a Regional Geomagnetic Daily Variation Model Using Neural Networks[J]. Annales Geophysicae, 1999, 18(1): 120-128
(  0) 0) |
| [6] |
Yi S H, Huang S Q, Li X H, et al. Modeling and Forecasting of the Variable Geomagnetic Field at Multiple Time Scales[C]. IEEE 10th International Conference on Signal Processing Proceedings, Beijing, 2010
(  0) 0) |
| [7] |
Moghadam R A, Yaghoubi M. Interval Emotional Neural Network for Prediction of Kp, AE and Dst Geomagnetic Activity Indices[C]. International Congress on Technology, Communication and Knowledge(ICTCK), Mashhad, 2015
(  0) 0) |
| [8] |
程文凯, 杜劲松, 陈超, 等. 基于XGBoost机器学习的地磁日变重构方法研究[J]. 地震学报, 2021, 43(1): 100-112 (Cheng Wenkai, Du Jinsong, Chen Chao, et al. Reconstruction Method for Diurnal Variations of the Geomagnetic Field by XGBoost Machine Learning[J]. Acta Seismologica Sinica, 2021, 43(1): 100-112)
(  0) 0) |
| [9] |
韩敏, 任伟杰, 李柏松, 等. 混沌时间序列分析与预测研究综述[J]. 信息与控制, 2020, 49(1): 24-35 (Han Min, Ren Weijie, Li Baisong, et al. Survey of Chaotic Time Series Analysis and Prediction[J]. Information and Control, 2020, 49(1): 24-35)
(  0) 0) |
| [10] |
李松, 刘力军. 混沌时间序列智能预测方法及其应用[M]. 北京: 科学出版社, 2019 (Li Song, Liu Lijun. Intelligent Forecasting of Chaotic Time Series and Its Application[M]. Beijing: Science Press, 2019)
(  0) 0) |
| [11] |
王赤, 陈金波, 王水. 地球变化磁场的分形和混沌特征[J]. 地球物理学报, 1995, 38(1): 16-24 (Wang Chi, Chen Jinbo, Wang Shui. Fractal and Chaotic Features for Varying Component of the Earth's Magnetic Field[J]. Chinese Journal of Geophysics, 1995, 38(1): 16-24)
(  0) 0) |
| [12] |
Qin H, Tang W B. Safety Evaluation of Microgrid Using Chaotic Time Series and RBF Neural Network[J]. IOP Conference Series: Materials Science and Engineering, 2020, 853(1)
(  0) 0) |
| [13] |
韩敏. 混沌时间序列预测理论与方法[M]. 北京: 中国水利水电出版社, 2007 (Han Min. Prediction Theory and Method of Chaotic Time Series[M]. Beijing: China Water Resources and Hydropower Press, 2007)
(  0) 0) |
| [14] |
齐玮, 王秀芳, 李夕海, 等. 基于统计建模的地磁匹配特征量选择[J]. 地球物理学进展, 2010, 25(1): 324-330 (Qi Wei, Wang Xiufang, Li Xihai, et al. Selection of Characteristic Components for Geomagnetic Matching Based on Statistical Modeling[J]. Progress in Geophysics, 2010, 25(1): 324-330)
(  0) 0) |
| [15] |
阎平凡, 张长水. 人工神经网络与模拟进化计算[M]. 北京: 清华大学出版社, 2005 (Yan Pingfan, Zhang Changshui. Artificial Neural Network and Evolutionary Computation[M]. Beijing: Tsinghua University Press, 2005)
(  0) 0) |
2. Military Marine Environment Construction Office, Beijing 100081, China;
3. 91208 Troops of PLA, Qingdao 266000, China
 2023, Vol. 43
2023, Vol. 43


