2. 湖北科技学院资源环境科学与工程学院,湖北省咸宁市咸宁大道88号,437100
大气颗粒物PM2.5能够深入人体肺部,损害肺功能[1]。杨忠等[2]使用粒子群优化算法(particle swarm optimization,PSO)对支持向量回归模型进行优化,并结合加权因子进行PM2.5预测;李建更等[3]通过建立互补集合经验模态分解(complementary ensemble empirical mode decomposition, CEEMD)和支持向量回归的组合模型(CEEMD-SVR)预测PM2.5浓度;谢劭峰等[4]使用WPA(wolf pack algorithm)和WOA(whale optimization algorithm)2种算法对BP神经网络模型进行优化;Chen等[5]使用SVR与Elman结合的方法对武汉的PM2.5浓度进行预测,并与多元线性回归、BP神经网络、SVR模型预测结果进行对比;王勇等[6]根据PWV与ZTD之间的联系探究ZTD与PM2.5的相关性;查艳芳[7]使用优化后的灰狼算法(grey wolf optimize,GWO)对支持向量回归模型进行优化,使用武汉市的日均大气污染物及气象数据等建立模型,对PM2.5浓度进行预测。
上述研究均采用模型优化或结合大气污染资料、气象资料、PWV、ZTD等多方面因素对PM2.5浓度进行建模预测,结果表现良好,但多数研究仅针对单一城市的空气质量进行预测,未考虑到模型在不同城市的适用性。相较于BP及其优化模型,SVR及其优化模型的性能更佳,对于高维数据问题具有更强的处理能力[8]。
考虑到不同海拔城市PM2.5浓度存在差异,且相较于春、夏、秋3个季节,冬季的PM2.5浓度波动幅度较大、受影响因素较多、预测难度较大,因此本文结合冬季的大气污染物、气象因素、ZTD的小时数据资料,选取SVR及其优化模型预测5个不同海拔城市的PM2.5浓度变化情况。
1 数学模型 1.1 SVR模型SVR模型的基本思路是:将与预测变量非线性相关的原始输入空间通过非线性映射函数(核函数)映射到高维特征空间上,得到一个尽可能适合拟合训练集样本的模型。常用的方法是在样本标签和模型预测值之间构造一个损失函数,通过最小化损失函数确定函数模型。建立一个考虑输出向量的数据集,SVR的目标是基于给定的数据集S找到多元回归函数来预测未知物体的期望输出性质。SVR模型如下[9]:
| $ f(x) = \sum\limits_{i, j = 1}^N {\left( {{\alpha _i} - \alpha _i^*} \right)} \left\langle {\varphi \left( {{x_i}} \right)\varphi \left( {{x_j}} \right)} \right\rangle + b $ | (1) |
式中,αi和αi*为满足约束条件的拉格朗日乘数,φ(xi)和φ(xj)为非线性映射函数,b为回归函数f(x)的偏移量。
1.2 GWO-SVR模型灰狼优化算法GWO通过模拟灰狼的狩猎过程搜索代理获取最优值,寻找到灰狼捕猎时的最优位置,从而计算得到最佳参数[10]。将参数代入SVR模型中建立GWO-SVR模型,获取最优值的具体过程如下。
1) 灰狼首先对猎物进行追踪、包围:
| $ \left\{\begin{array}{l} \vec{D}=\left|\vec{C} \cdot \vec{X}_P(t)\right| \\ \vec{X}(t+1)=\vec{X}_P(t)-\vec{A} \cdot \vec{D} \end{array}\right. $ | (2) |
2) 通过骚扰让猎物停止移动,对猎物发动攻击:
| $ \begin{gathered} \vec{D}_\alpha=\left|\vec{C}_1 \cdot \vec{X}_\alpha-\vec{X}\right|, \vec{D}_\beta=\left|\vec{C}_2 \cdot \vec{X}_\beta-\vec{X}\right|, \\ \vec{D}_\delta=\left|\vec{C}_3 \cdot \vec{X}_\delta-\vec{X}\right| \\ \vec{X}_1=\vec{X}_\alpha-\vec{A}_1 \cdot \vec{D}_\alpha, \vec{X}_2=\vec{X}_\beta-\vec{A}_2 \cdot \vec{D}_\beta, \\ \vec{X}_3=\vec{X}_\delta-\vec{A}_3 \cdot \vec{D}_\delta \\ \vec{X}(t+1)=\frac{\vec{X}_1+\vec{X}_2+\vec{X}_3}{3} \end{gathered} $ | (3) |
式中,
鲸鱼优化算法WOA通过模拟鲸鱼搜索、合围及狩猎等一系列行为在全局中寻找到最优值,进而输出全局最优个体[11]。将最优参数代入SVR模型建立WOA-SVR模型,具体过程如下。
1) 识别猎物的位置,对猎物进行合围:
| $ \left\{\begin{array}{l} \vec{D}=\left|\vec{C} \cdot \vec{X}^*(t)-\vec{X}(t)\right| \\ \vec{X}(t+1)=\vec{X}^*(t)-\vec{A} \cdot \vec{D} \end{array}\right. $ | (4) |
2) 通过螺旋搜索,采用环形游动喷出气泡来驱赶猎物,最后游向水面捕食猎物:
| $ \vec{X}(t+1)=\vec{D}^{\prime} \cdot \mathrm{e}^{b l} \cos (2 \pi l)+\vec{X}^*(t) $ | (5) |
式中,
天鹰算法AO是根据天鹰在捕食猎物过程中的自然行为提出的一种基于种群的优化方法[12],可以用来搜索模型的最优参数。天鹰狩猎可分为4种方式,具体过程如下。
1) 识别猎物区域,采用垂直弯腰高飞的方式选取最佳狩猎区域,进行攻击:
| $ \begin{gathered} X_1(t+1)=X_{\text {best }}(t) \times\left(1-\frac{t}{T}\right)+ \\ \left(X_M(t)-X_{\text {best }}(t) \times \text { rand }\right) \end{gathered} $ | (6) |
2) 从高空发现猎物区域,在猎物区域的上方盘旋,使用短滑翔攻击的轮廓飞行:
| $ \begin{gathered} X_2(t+1)=X_{\text {best }}(t) \times \operatorname{Levy}(D)+ \\ X_R(t)+(y-x) \times \text { rand } \end{gathered} $ | (7) |
3) 确定猎物区域,准备好着陆和攻击后采用低飞慢降攻击:
| $ \begin{aligned} & X_3(t+1)=\left(X_{\text {best }}(t)-X_M(t)\right) \times \alpha- \\ & \text { rand }+((\mathrm{UB}-\mathrm{LB}) \times \text { rand }+\text { LB }) \times \delta \end{aligned} $ | (8) |
4) 当天鹰接近猎物时,会根据猎物的随机移动规律在陆地行走并抓住猎物:
| $ \begin{array}{c} {X_4}(t + 1) = {\rm{QF}} \times {X_{{\rm{best }}}}(t) - \left( {{G_1} \times X(t)} \right. \times \\ {\rm{ rand }}) - {G_2} \times {\mathop{\rm Levy}\nolimits} (D) + {\mathop{\rm rand}\nolimits} \times {G_1} \end{array} $ | (9) |
式中,X1, 2, 3, 4(t+1)为下一次迭代t的解,Xbest(t)为最佳解,XM(t)为位置均值,rand为[0, 1]的随机值,Levy(D)为飞行分布函数,XR(t)为[1, N]的随机解,UB为上界,LB为下界,QF为质量函数,G1、G2为跟踪猎物时的各种运动,X(t)为第t次迭代时的当前解。
根据目标需要选择算法捕获最优参数,将最优参数代入SVR模型中建立AO-SVR模型。AO算法优化SVR模型的基本步骤如下:
1) 导入并读取数据,进行数据预处理,初步建立SVR模型。
2) 初始化天鹰算法的种群数量及其迭代次数,确认惩罚参数C和核惩罚参数g的取值范围。
3) 依据天鹰捕猎的4种方法选取最优的适应度函数,并作为天鹰捕猎时与猎物的最佳距离,通过搜索确定天鹰捕猎的最佳位置。
4) 根据天鹰捕猎所在的最优位置,获取最优的惩罚参数和核惩罚参数。
5) 将获取到的最优参数值加入到SVR中,通过多次训练,确定最终优化的SVR预测模型。
6) 将测试数据分为训练集和预测集导入到优化后的AO-SVR模型中,将结果与预测集进行对比,分析模型具体误差。
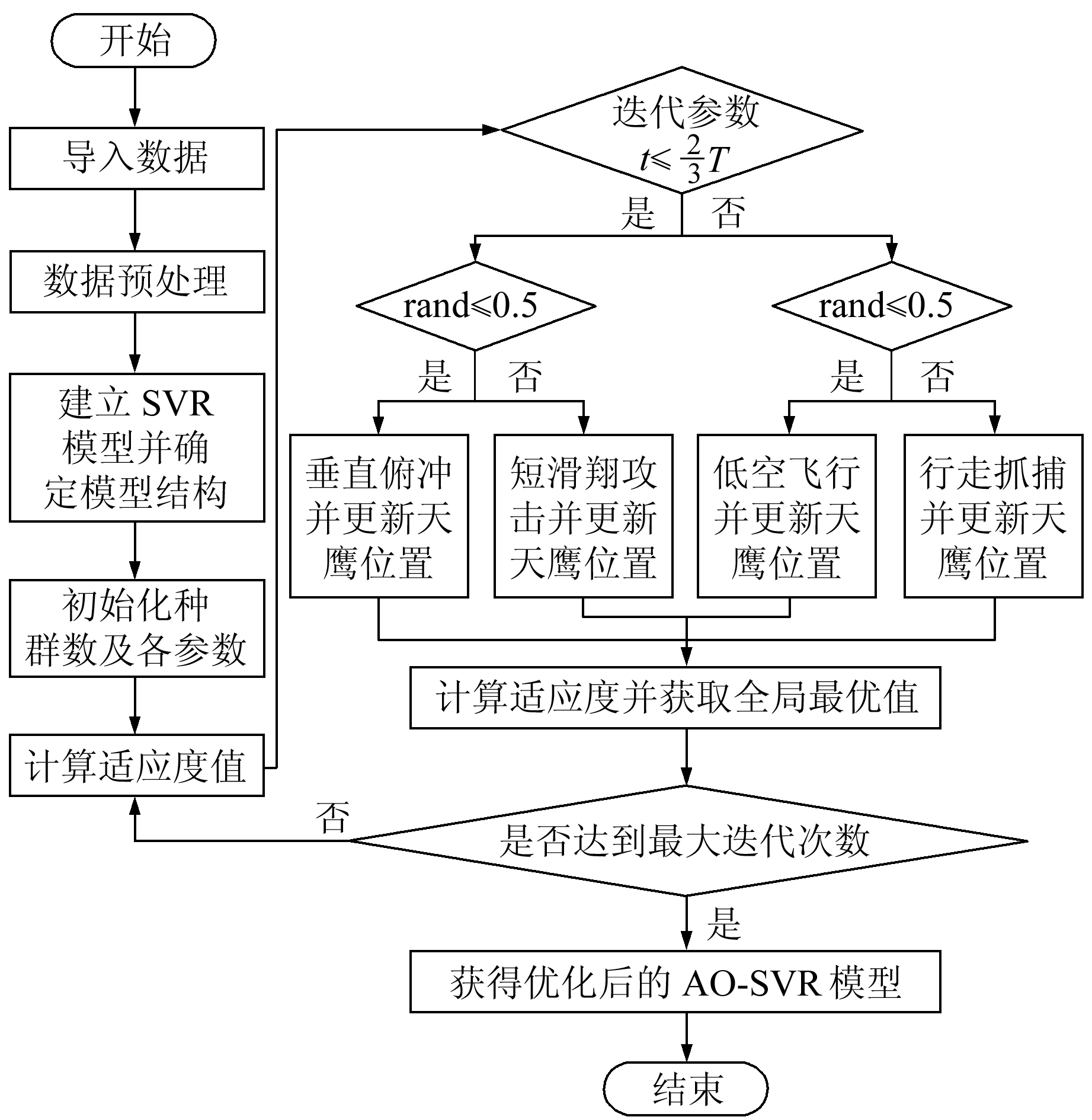
AO-SVR算法流程见图 1。
|
图 1 AO-SVR算法流程 Fig. 1 AO-SVR algorithm flow chart |
各个城市间的PM2.5浓度具有时空差异性,通常会随海拔的升高而降低,且东部、北部城市的PM2.5浓度通常高于西部、南部城市[13]。本文选取海拔呈递减趋势的拉萨(3 656 m)、乌鲁木齐(918 m)、长春(237 m)、武汉(35 m)、上海(5 m)等5个城市作为实验对象。由于PM2.5浓度在冬季波动最大,因此选取2020-01的数据进行建模。使用的数据主要包括:SO2、NO2、CO、O3、PM10及PM2.5的逐小时大气污染物浓度数据;气温、气压、相对湿度、风级的逐小时气象数据;IGS提供的逐小时ZTD数据。为确定各要素与PM2.5之间的相关性,通过SPSS软件对大气污染物、气象因素及ZTD数据进行相关性分析,使用Spearman相关系数进行计算,结果见表 1和表 2。
|
|
表 1 PM2.5与大气污染物相关性 Tab. 1 Correlation of PM2.5 and atmospheric pollutants |
|
|
表 2 PM2.5与气象因素及ZTD相关性 Tab. 2 Correlation of PM2.5 and meteorological factors and ZTD |
由表 1和表 2可知,5个城市的PM2.5与PM10、SO2、NO2、CO、相对湿度、气压基本呈正相关,与O3、温度、风级基本呈负相关;PM2.5与拉萨、武汉的ZTD呈正相关,与乌鲁木齐、长春、上海的ZTD呈负相关。PM2.5与空气污染物、气象因素及ZTD的相关性显著,在对PM2.5浓度进行建模预测时,可将上述因子作为预测输入。
2.2 PM2.5变化规律为探究不同海拔的5个城市在2020-01的PM2.5浓度变化趋势,将5个城市PM2.5浓度小时数据组成一个连续时间序列进行整体变化趋势对比(图 2)。

|
图 2 PM2.5变化趋势 Fig. 2 Variation trend of PM2.5 |
由图 2可知,在1月份供暖期间,拉萨的PM2.5浓度为0~75 μg/m3,空气质量良好;乌鲁木齐、长春的PM2.5浓度波动较大,整体浓度偏高,可能是因为2020-01疫情严重,人流量及车流量均有所降低,但供暖及用电量高于往常年份,导致PM2.5浓度整体偏高;该时段内武汉疫情封城,PM2.5浓度降低,短时期内空气质量得到改善;上海在疫情影响下人流量及车流量有所减少,且1月中有19 d降雨,极大改善了空气质量。乌鲁木齐、长春的海拔高于武汉、上海,但在疫情、供暖、天气等因素的影响下,乌鲁木齐、长春的PM2.5浓度均高于武汉和上海,且波动变化更为剧烈,说明在冬季仅依靠海拔高低无法准确判断PM2.5的变化趋势。通过模型预测不同海拔的城市在冬季的PM2.5浓度变化,能为PM2.5浓度预测及其变化趋势研究提供借鉴,对未来空气环境治理也具有指导意义。
3 实验结果 3.1 变量选择分别采用SVR、GWO-SVR、WOA-SVR和AO-SVR四种回归模型对5个城市2020-01的PM2.5浓度进行预测,选取表 1、2中各城市在0.01级别相关性显著的因素作为因子集,预测模型中每种因子采用的时间长度完全一致,数据采样率为1 h。各城市1月份的样本数据集长度均为744 h,选取前720 h的数据作为训练样本集,后24 h作为校验样本集,使用训练样本集进行建模,将模型预测的24 h PM2.5数据与校验样本集PM2.5数据进行分析对比。
3.2 预测结果评价与分析5个城市4种模型的预测结果与预测相对误差绝对值见图 3、4。

|
图 3 2020-01-31预测结果 Fig. 3 Prediction results of January 31, 2020 |

|
图 4 2020-01-31相对误差 Fig. 4 The relative error of January 31, 2020 |
由图 3可见,4种模型的预测结果与观测值之间具有相似的变化趋势,但相较于基础SVR模型,优化后的SVR模型预测结果的整体趋势更优,其中AO-SVR模型最贴近实际观测值。从2020-01-31的数据可以看出,拉萨全天PM2.5浓度均为优;乌鲁木齐、长春PM2.5浓度在10:00开始降低并在15:00左右开始回升,其中,长春的回升幅度更明显,PM2.5浓度在晚间突破240 μg/m3。查询资料可知,长春常住人口远多于乌鲁木齐,且疫情阶段居家人数增多,供暖需求加大,导致污染加重;武汉、上海在疫情的影响下,人流量和车流量有所减少,但人均用电量增加,使得PM2.5浓度值并未出现大幅度降低,均呈现升-降-升的变化趋势。由图 4可见,模型预测的相对误差随时间的增长不断增加,SVR模型相对误差的增大趋势最显著,在拉萨和上海2市共有7 h的误差比例超过40%。WOA-SVR模型的误差比例基本低于GWO-SVR模型,AO-SVR模型相对误差变化趋势表现最好,整体趋势随时间的增长而降低,在乌鲁木齐的24:00,相对误差比例仅为0.04%。
为更好地展示模型的预测结果,采用RMSE、MAE和MAPE来判断模型的适用性、对比模型的预测精度,各模型预测精度结果见表 3:
| $ \begin{aligned} \text { RMSE } & =\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(x_i-\hat{x}_i\right)^2} \\ \text { MAE } & =\frac{1}{n} \sum\limits_{i=1}^n\left|x_i-\hat{x}_i\right| \\ \text { MAPE } & =\frac{1}{n} \sum\limits_{i=1}^n\left|\frac{x_i-\hat{x}_i}{x_i}\right| \end{aligned} $ | (10) |
|
|
表 3 各模型预测精度对比 Tab. 3 Comparison of prediction accuracy of each model |
式中,xi为实际观测值,
由表 3可知,对于海拔不同的5个城市,4种模型的适用性均表现良好,但GWO-SVR、WOA-SVR、AO-SVR模型的RMSE要显著低于SVR模型,说明3种算法对于SVR模型都有一定程度的优化,使得误差的离散性减小。由RMSE可以看出,AO-SVR模型的效果最好,相比于SVR模型,拉萨、乌鲁木齐、长春、武汉和上海的RMSE分别提高33.9%、56.3%、56.2%、63.8%和68.1%,其中上海市的优化程度最高。从5个城市的MAE和MAPE指标来看,GWO-SVR、WOA-SVR、AO-SVR模型对于SVR模型均有一定程度的提升,WOA-SVR模型的优化效果要稍优于GWO-SVR,其中上海的优化程度最明显。相比于SVR模型,GWO-SVR与WOA-SVR模型的MAE指标分别提高54.0%和61.0%,MAPE指标分别提高61.6%和68.7%。由整体数据可知,AO-SVR模型在5个城市的PM2.5预测中表现最为出色,相比于SVR模型,AO-SVR模型的MAE和MAPE在拉萨提高32.4%和38.4%,在乌鲁木齐提高58.5%和58.8%,在长春提高57.1%和46.1%,在武汉提高60.6%和58.3%,在上海提高75.3%和77.0%。由此可见,相较于SVR模型,AO-SVR模型在5个城市的PM2.5预测精度均有所提升,武汉、上海的MAE和MAPE提高最多,可能是由于乌鲁木齐、长春的数据波动幅度相对较大,数据的稳定性以及整体水平对模型预测精度存在一定程度的影响。通过图 2、3和表 3可知,相比于SVR模型,GWO-SVR、WOA-SVR、AO-SVR模型预测精度均有明显改善;AO-SVR模型在4个模型中的预测值最贴合实际观测值,在多种因素的影响下,表现出较为优秀的适用性,能展现不同海拔城市冬季PM2.5的趋势变化规律。
4 结语本文基于5个不同海拔城市的2020-01大气污染物、气象因素以及ZTD的小时数据,利用SVR、GWO-SVR、WOA-SVR、AO-SVR四种模型对PM2.5浓度进行预测和对比。实验结果表明,AO-SVR模型的预测结果整体精度最高,且对于不同海拔城市PM2.5浓度变化的预测均有很好的适用性。
本文仅预测了不同海拔城市24 h的PM2.5浓度变化,后续可考虑增加数据量并增加预测时长,对不同海拔城市的PM2.5浓度变化趋势作更深入的探究。
| [1] |
Wu X M, Zhu B, Zhou J, et al. The Epidemiological Trends in the Burden of Lung Cancer Attributable to PM2.5Exposure in China[J]. BMC Public Health, 2021, 21(1): 737 DOI:10.1186/s12889-021-10765-1
(  0) 0) |
| [2] |
杨忠, 童楚东, 俞杰, 等. 加权因子的PSO-SVR区域空气PM2.5浓度预报方法[J]. 计算机应用研究, 2017, 34(2): 405-408 (Yang Zhong, Tong Chudong, Yu Jie, et al. Regional PM2.5 Concentration Prediction Method of PSO-SVR Model with Weighting Factors[J]. Application Research of Computers, 2017, 34(2): 405-408 DOI:10.3969/j.issn.1001-3695.2017.02.019)
(  0) 0) |
| [3] |
李建更, 罗奥荣, 李晓理. 基于互补集合经验模态分解与支持向量回归的PM2.5质量浓度预测[J]. 北京工业大学学报, 2018, 44(12): 1 494-1 502 (Li Jiangeng, Luo Aorong, Li Xiaoli. Prediction of PM2.5 Mass Concentration Based on Complementary Ensemble Empirical Mode Decomposition and Support Vector Regression[J]. Journal of Beijing University of Technology, 2018, 44(12): 1 494-1 502)
(  0) 0) |
| [4] |
谢劭峰, 赵云, 李国弘, 等. 基于WPA-WOA-BP神经网络的PM2.5浓度预测[J]. 大地测量与地球动力学, 2021, 41(1): 12-16 (Xie Shaofeng, Zhao Yun, Li Guohong, et al. Prediction of PM2.5 Concentration Based on WPA-WOA-BP Neural Network[J]. Journal of Geodesy and Geodynamics, 2021, 41(1): 12-16)
(  0) 0) |
| [5] |
Chen Y L, Li F Y, Deng Z, et al. PM2.5 Forecasting with Hybrid LSE Model-Based Approach[J]. Software: Practice and Experience, 2017, 47(3): 379-390 DOI:10.1002/spe.2413
(  0) 0) |
| [6] |
王勇, 任栋, 郝振航, 等. 一种对流层延迟的ZTD与PM2.5浓度相关性研究[J]. 测绘科学, 2018, 43(5): 40-44 (Wang Yong, Ren Dong, Hao Zhenhang, et al. Study on the Correlation between ZTD of CMONOC and PM2.5 Concentration[J]. Science of Surveying and Mapping, 2018, 43(5): 40-44)
(  0) 0) |
| [7] |
查艳芳. 基于改进灰狼算法和SVR的武汉PM2.5浓度预测研究[D]. 武汉: 中南财经政法大学, 2019 (Zha Yanfang. On Prediction of PM2.5 Concentration in Wuhan Based on Improved Grey Wolf Algorithm and SVR[D]. Wuhan: Zhongnan University of Economics and Law, 2019)
(  0) 0) |
| [8] |
陈传亮, 田英杰, 别荣芳. 基于粒子群优化的SVR算法与BP网络的比较研究[J]. 北京师范大学学报: 自然科学版, 2008, 44(5): 449-453 (Chen Chuanliang, Tian Yingjie, Bie Rongfang. Research of SVR Optimized by PSO Compared with BP Network Trained by PSO[J]. Journal of Beijing Normal University: Natural Science, 2008, 44(5): 449-453 DOI:10.3321/j.issn:0476-0301.2008.05.001)
(  0) 0) |
| [9] |
Ustünu B, Melssen W J, Buydens L M C. Visualisation and Interpretation of Support Vector Regression Models[J]. Analytica Chimica Acta, 2007, 595(1-2): 299-309 DOI:10.1016/j.aca.2007.03.023
(  0) 0) |
| [10] |
Mirjalili S, Mirjalili S M, Lewis A. Grey Wolf Optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61
(  0) 0) |
| [11] |
Mirjalili S, Lewis A. The Whale Optimization Algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67 DOI:10.1016/j.advengsoft.2016.01.008
(  0) 0) |
| [12] |
Abualigah L, Yousri D, Abd Elaziz M, et al. Aquila Optimizer: A Novel Meta-Heuristic Optimization Algorithm[J]. Computers and Industrial Engineering, 2021, 157
(  0) 0) |
| [13] |
Wang J Y, Wang S J, Li S J. Examining the Spatially Varying Effects of Factors on PM2.5 Concentrations in Chinese Cities Using Geographically Weighted Regression Modeling[J]. Environmental Pollution, 2019, 248: 792-803 DOI:10.1016/j.envpol.2019.02.081
(  0) 0) |
2. School of Resources and Environmental Science and Engineering, Hubei University of Science and Technology, 88 Xianning Road, Xianning 437100, China
 2023, Vol. 43
2023, Vol. 43


