2. 武汉梦芯科技有限公司,武汉市高新大道980号,430079
低成本的MEMS IMU由于随机误差较大,应用于惯性导航系统时误差增长较快。利用多个传感器构建IMU阵列,通过不同的融合方式融合冗余的观测数据能有效降低随机误差[1]。但由于集成电路制造工艺的缺陷,每个IMU的输出都会存在因零偏、比例因子和非正交[2]偏离理想值引起的差异。此外,多个传感器放置在一起时,安装误差也会导致IMU的输出存在差异。因此,为了更好地运用IMU,在使用前需要对传感器进行校准。
传统的IMU阵列的校准需要通过昂贵的精密转台提供所需的已知激励[3-5]。但转台的使用增加了IMU阵列的使用成本,因此,不使用转台的IMU阵列在线校准方法成为研究热点。在静态条件下,可利用地球重力加速度作为激励校准加速度计[6]误差参数,但由于地球自转角速度数值较小,无法从MEMS IMU的噪声中分离,缺少参考激励使得陀螺仪误差校准方法较少使用。Rohac等[7]使用激光陀螺获得参考激励的精确数值,但增加了额外成本。Carlsson等[8]提出一种块坐标下降法(block coordinate descent, BCD)联合估计误差参数(包含IMU之间的距离)和载体的运动参数,但该方法需要提供较大激励,难以控制输入。
本文提出一种IMU阵列在线校准方法,通过对IMU阵列的误差参数构建相应的损失函数,利用LM优化算法估计加速度计和陀螺仪的误差参数。该方法无需任何外部参考设备,只需在手机支架上获得一系列静置和运动数据。
1 在线校准模型及算法 1.1 IMU误差建模加速度计与陀螺仪存在零偏、比例因子和非正交的确定性误差,在构建IMU阵列时,会引入灵敏轴不对齐的安装误差。只考虑最重要的误差源,IMU量测输出建模如式(1)。为减少误差参数数目,将比例因子误差、非正交误差和安装误差3种误差耦合构成尺度变换矩阵Tki,如式(2):
| $ \boldsymbol{y}_{k, n}^i=\boldsymbol{T}_k^i \boldsymbol{u}_{k, n}^i+\boldsymbol{b}_k^i+\boldsymbol{\varepsilon}_{k, n}^i, \;\;i \in\{a, c\} $ | (1) |
| $ \boldsymbol{T}_k^i=\left[\begin{array}{lll} K_{x x} & K_{y x} & K_{z x} \\ K_{x y} & K_{y y} & K_{z y} \\ K_{x z} & K_{y z} & K_{z z} \end{array}\right] $ | (2) |
式中,a和c分别为加速度计参数和陀螺仪参数,k和n分别表示第k个IMU、第n次测量,yk, ni和uk, ni分别为在正交的参考框架中时间独立的IMU的量测输出和量测输入,bki为常值零偏,εk, ni为量测值的随机误差。假设各传感器之间的噪声没有相关性,可建模为均值为03×1、方差为diag(σ(a)2/σ(c)2) 的高斯白噪声。
将IMU1的加速度计体坐标系定义为参考坐标系,即2个坐标系的z轴对齐,参考坐标系y轴位于IMU1加速度计的z轴与y轴构成的平面,并垂直于z轴,x轴通过右手定理获得。此时,可简化IMU1的尺度变换矩阵T1a为:
| $ \boldsymbol{T}_1^a=\left[\begin{array}{ccc} K_{x x} & K_{y x} & K_{z x} \\ 0 & K_{y y} & K_{z y} \\ 0 & 0 & K_{z z} \end{array}\right] $ | (3) |
针对加速度计和陀螺仪构造2个损失函数:1)利用当地重力加速度和加速度计输出构造加速度计的损失函数;2)利用校准后的加速度计和陀螺仪输出构造陀螺仪的损失函数。
1.2.1 加速度计损失函数将第k个加速度计需要校准的参数定义为:
| $ \boldsymbol{\theta}_k^a=\left\{\boldsymbol{b}_k^a, \boldsymbol{T}_k^a\right\} $ | (4) |
静止状态下,加速度计的比力输出只与当地重力加速度有关,则加速度计输出估计函数为:
| $ \hat{\boldsymbol{y}}_{k, n}^a=f\left(\boldsymbol{\theta}_k^a, \boldsymbol{u}_{k, n}^a\right)=\boldsymbol{T}_k^a \boldsymbol{u}_{k, n}^a+\boldsymbol{b}_k^a $ | (5) |
将导航坐标系定义为北东地,载体坐标系定义为前右下,此时:
| $ \boldsymbol{u}_{k, n}^a=g\left[\begin{array}{lll} -\sin \gamma & \sin \varphi \cos \gamma & \cos \varphi \cos \gamma \end{array}\right]^{\mathrm{T}} $ | (6) |
式中,φ、γ分别为横滚角、俯仰角,g为当地的重力加速度。
由式(6)可以看出,每个静态位置存在横滚角和俯仰角2个未知数,因此加速度计在每个位置多输出了1个冗余量。若要校准加速度计的所有参数,至少需要放置12个或者9个非共面的位置。本文采用一种多个位置的静态校准方式校准加速度计,将加速度计校准参数的损失函数建模为:
| $ \left\{ {\mathit{\boldsymbol{\widehat \theta }}_k^a} \right\}_1^M = {\mathop{\rm argmin}\nolimits} \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left\| {\mathit{\boldsymbol{y}}_{k, n}^a - \mathit{\boldsymbol{\widehat y}}_{k, n}^a} \right\|_{\mathit{\boldsymbol{Q}}_{k, n}^a}^2} } $ | (7) |
式中,Qk, na为第k个加速度计在第n个静态位置的协方差矩阵,M为IMU的数量。
1.2.2 陀螺仪损失函数将第k个陀螺仪需要校准的参数定义为:
| $ \boldsymbol{\theta}_k^c=\left\{\boldsymbol{b}_k^c, \boldsymbol{T}_k^c\right\} $ | (8) |
由于MEMS工艺制造的IMU噪声太大,地球自转角速度无法分离而不能成为参考源。静置的加速度输出通过校准后具有很好的稳定性,且能得到各个静态位置重力的投影值,本文将其作为陀螺仪校准的参考值。在假定陀螺仪是无偏的前提下,即陀螺仪的数据通过一定时间内的平均可以得到零偏,利用2个静态位置之间转动过程中陀螺仪的数据,通过数值积分方法得到2个静态位置之间的旋转矩阵。利用静态位置和旋转矩阵估计下一个静态位置的重力投影估计值(式(9)),进而构建陀螺仪损失函数(式(10)):
| $ \hat{\boldsymbol{u}}_{k, n}^c=\boldsymbol{R}_{n-1}^n \boldsymbol{u}_{k, n-1}^a $ | (9) |
| $ \left\{\hat{\boldsymbol{\theta}}_k^c\right\}_1^M=\operatorname{argmin} \sum\limits_{m=1}^M \sum\limits_{n=2}^N\left\|\boldsymbol{u}_{k, n}^a-\hat{\boldsymbol{u}}_{k, n}^c\right\|^2 $ | (10) |
式中,Rn-1n为2个静态位置之间的旋转矩阵。
1.3 算法设计式(7)和式(10)是非线性函数,本文利用LM优化算法迭代求解出待定误差参数最优解。LM优化算法对于初值的设定比较严格,初值误差较大会使迭代进入局部最优。因此,除了陀螺仪的零偏,将加速度计和陀螺仪的确定性误差初值都设定为理想值,N个静态位置的横滚角和俯仰角的初值使用加速度计的原始输出计算:
| $ \varphi_n=a\operatorname{tan} 2\left(\left[\boldsymbol{y}_n^a\right]_y, \left[\boldsymbol{y}_n^a\right]_z\right) $ | (11) |
| $ \gamma_n=a\operatorname{tan} 2\left(-\left[\boldsymbol{y}_n^a\right]_x, \sqrt{\left[\boldsymbol{y}_n^a\right]_y^2+\left[\boldsymbol{y}_n^a\right]_z^2}\right) $ | (12) |
其中,[p]i为向量p中的第i维数值。
数值积分使用经典的4阶Runge-Kutta积分,通过对2个历元之间的角速度积分得到当前历元的姿态四元素,并通过递推得到2个静态位置之间的旋转矩阵[9]。
图 1为在线校准算法流程,首先利用加速度计的方差构建一个静态检测器,将静态和动态数据分离;然后使用LM算法和静态数据对式(7)进行迭代求解,当整体误差和小于阈值时,加速度计校准完成;最后利用加速度计校准后的静态数据和动态数据对式(10)进行迭代求解,得到陀螺仪的误差参数。

|
图 1 在线校准算法流程 Fig. 1 Flow chart of online calibration algorithm |
为验证本文算法的有效性,分别进行仿真实验、实测校准实验和车载导航实验。
2.1 仿真实验IMU误差参数根据ICM42688P数据手册中的标称值设定,如表 1所示。尺度变换矩阵T由3种误差耦合而成,比例因子和非正交误差均设定在标称参数临界值附近,安装误差使用小角度,设置为2 000″(小于1°)。零偏设置:加速度计[20 16 18]T mg,陀螺仪[0.5 0.38 0.44]T dps。随机误差设置:σ(a)2=70 ug/
|
|
表 1 ICM42688P误差标称参数 Tab. 1 Error nominal parameters of ICM42688P |
利用文献[10]的开源MATLAB惯导工具箱中的轨迹生成器进行如式(13)和(14)的拓展,得到IMU阵列的仿真数据,其频率为100 Hz:
| $ \begin{gathered} \boldsymbol{u}_k^a=\boldsymbol{R}_{b_1^n}^{b}\left(\boldsymbol{u}_1^a+\dot{\boldsymbol{u}}_1^c \times \right. \\ \left.\boldsymbol{r}_{b_n}^{b_1}+\boldsymbol{u}_1^c \times\left(\boldsymbol{u}_1^c \times \boldsymbol{r}_{b_n}^{b_1}\right)\right) \end{gathered} $ | (13) |
| $ \boldsymbol{u}_k^c=\boldsymbol{R}_{b_1^n}^b \boldsymbol{u}_1^c $ | (14) |
式中,Rb1bn为第1个IMU与第n个IMU之间的旋转矩阵,rbnb1为在参考坐标系下的坐标位置。
将Rb1bn设置为3×3的单位矩阵,rbnb1设置为各加速度计在参考坐标系中的位置,IMU阵列的数量及位置如图 2所示。
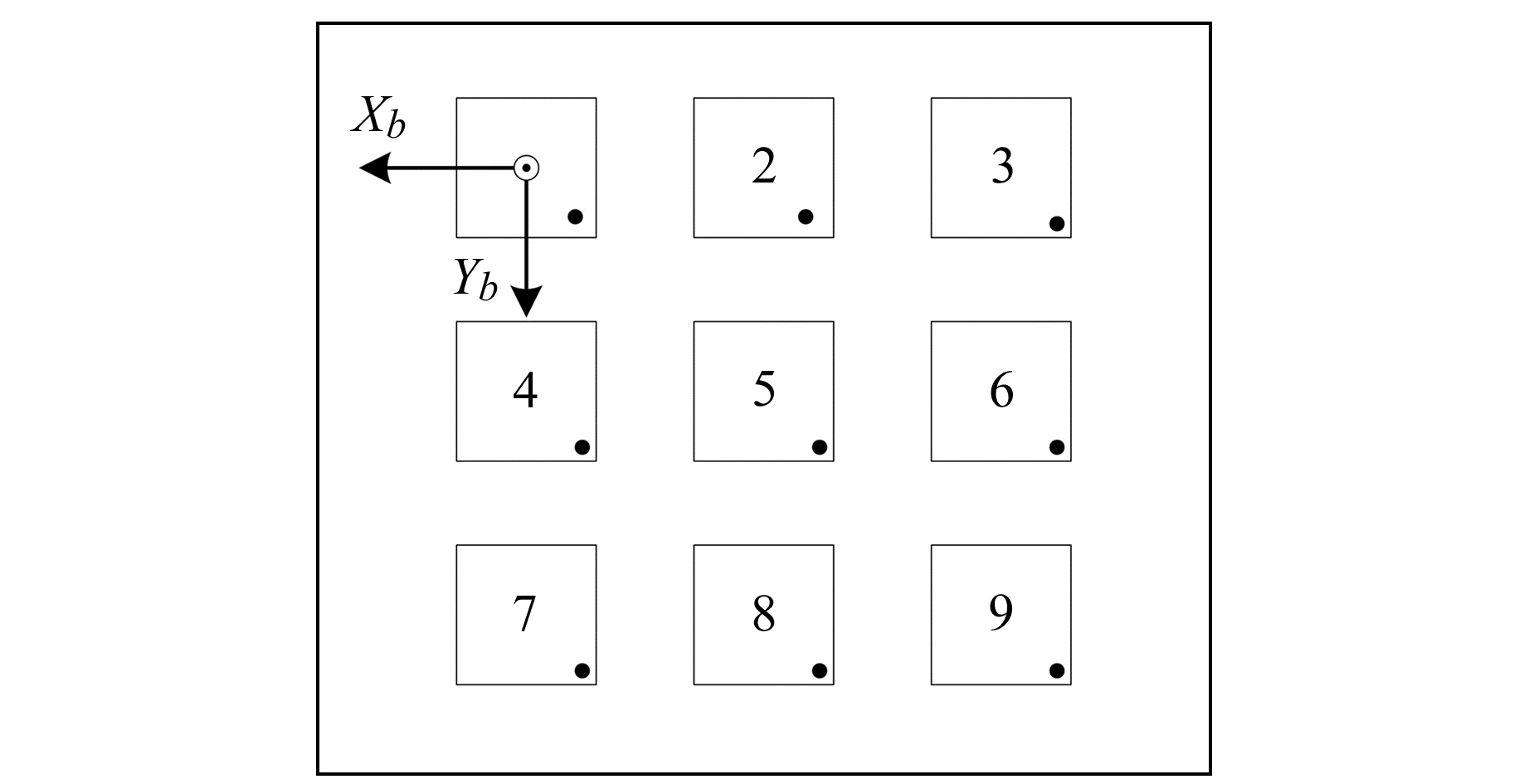
|
图 2 IMU阵列分布 Fig. 2 Distribution of IMU array |
将校准结果与设定的误差参数作差得到参数的残差值,结果如图 3所示。从图 3(a)看出,加速度计和陀螺仪的零偏精度分别达到1.3×10-4 m/s2和1.3×10-3 dps;从图 3(b)看出,加速度计和陀螺仪的尺度变换矩阵精度分别达到3.3×10-5和7.9×10-5,校准结果与设定的误差参数值一致性较好。
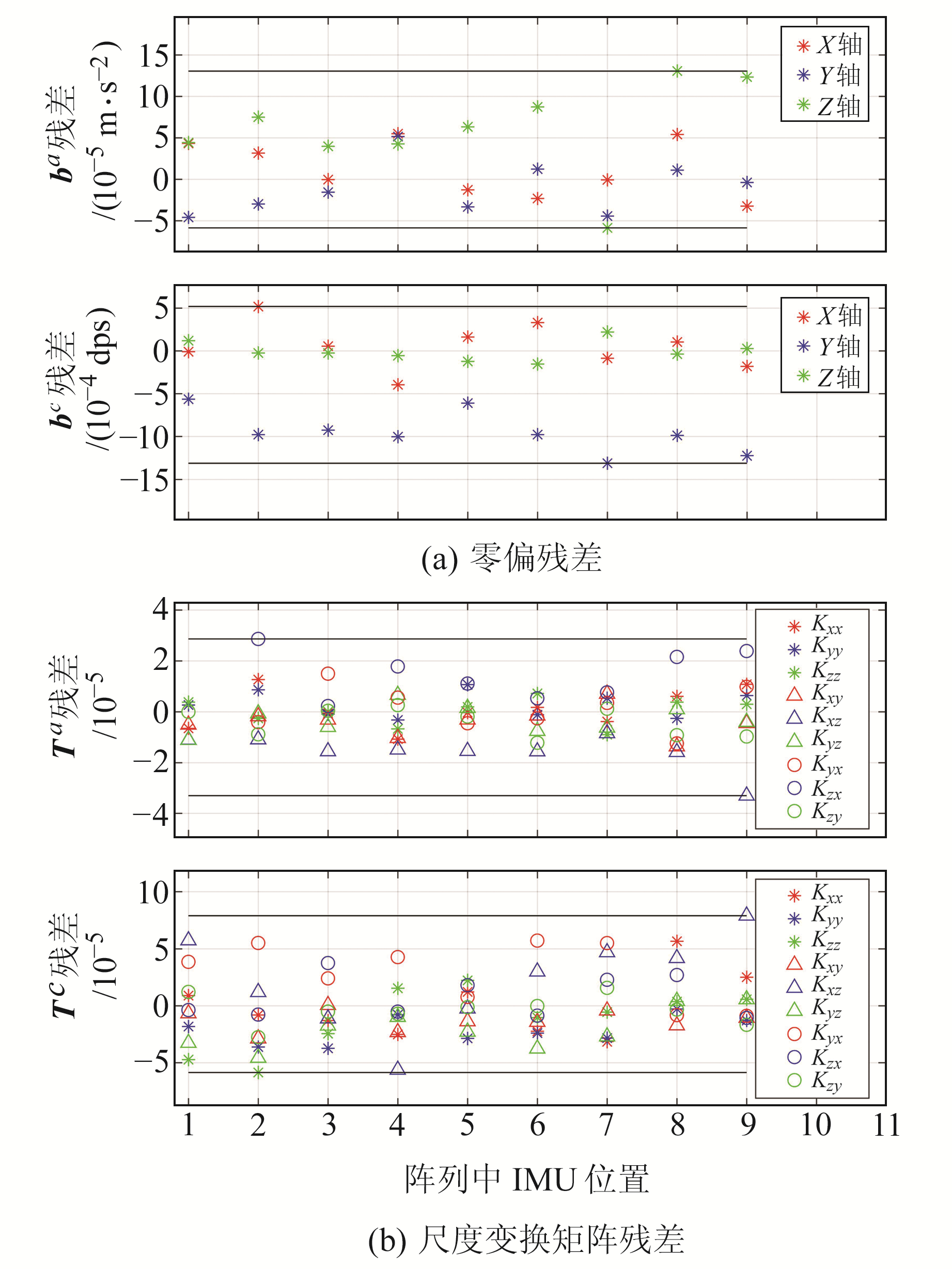
|
图 3 残差统计 Fig. 3 Residuals statistics |
实测校准实验使用实验室内部设计的一款IMU阵列,其中IMU使用InvenSense公司的ICM系列产品。为兼顾IMU阵列的性能和MCU管脚的使用情况,所设计的阵列由9个IMU构成3×3的矩阵,如图 4(a)所示。在IMU阵列的驱动设计过程中,使用串行外设接口(serial peripheral interface, SPI)通信协议,并利用ICM42688P内部的FIFO获取原始数据,减少SPI片选信号的开关次数,提高系统的时间同步可靠性。加速度计量程设置为±2 g,陀螺仪量程设置为±250 dps,量程范围与常用的车载量程设置相同,便于将校准参数应用于车载导航解算中。

|
图 4 IMU阵列及校准平台 Fig. 4 IMU array and calibration platform |
阵列校准平台如图 4(b),该校准平台上是一个手机支架,可以进行360°手动旋转,并且在数据采集过程中,能使阵列数据在运动后短时间内稳定为静态数据,同时保证转动角速度控制在量程范围内。为降低加速度的噪声以及减少Runge-Kutta积分过程造成的误差,将IMU阵列在校准平台上的静置时间设定为8~10 s,动态间隔时间设定为1~4 s,每组校准实验采集35~50个静态和动态数据。表 2、3分别是8组校准实验的均值和误差参数范围统计。可以看出,加速度计零偏及尺度变换波动范围分别为-83~59 mg和-0.005~0.008,陀螺仪零偏及尺度变换波动范围分别为-1.1~0.54 dps和0.013~0.016。ICM42688P的各项误差数值都偏小,因此对传感器补偿后性能提升有限制。
|
|
表 2 校准实验均值统计 Tab. 2 Statistics of mean value of calibration experiments |
|
|
表 3 IMU阵列误差参数范围统计 Tab. 3 Error parameter range statistics of IMU array |
使用图 4(a)中的IMU阵列进行车载动态组合导航实验。将IMU阵列数据通过直接平均的方式拟合成一个虚拟IMU,并利用虚拟IMU与GNSS进行松组合导航;通过后处理设置GNSS中断,中断时间为20 s,中断间隔为60 s,比较GNSS中断后校准前后的导航误差。参考设备为高精度、具有双频RTK的NovAtel CPT6,定位精度可达cm级。由于ICM42688P的加速度计高程方向存在低频噪声、误差较大,因此本文只评价导航结果的平面误差。
图 5展示了一组GNSS中断后动态导航的平面、北向和东向误差。可以看出,校准后的导航误差精度整体有所提升,尤其是误差较大的路段。GNSS中断后的不同时间段误差发散程度不一致是由IMU的随机误差引起的,随机误差越大,误差发散越快。校准后,能补偿IMU阵列的确定性误差,进行数据融合时能有效降低随机误差,在随机误差较大的路段,校准后的IMU阵列能大幅度降低随机误差,改善效果较为明显。
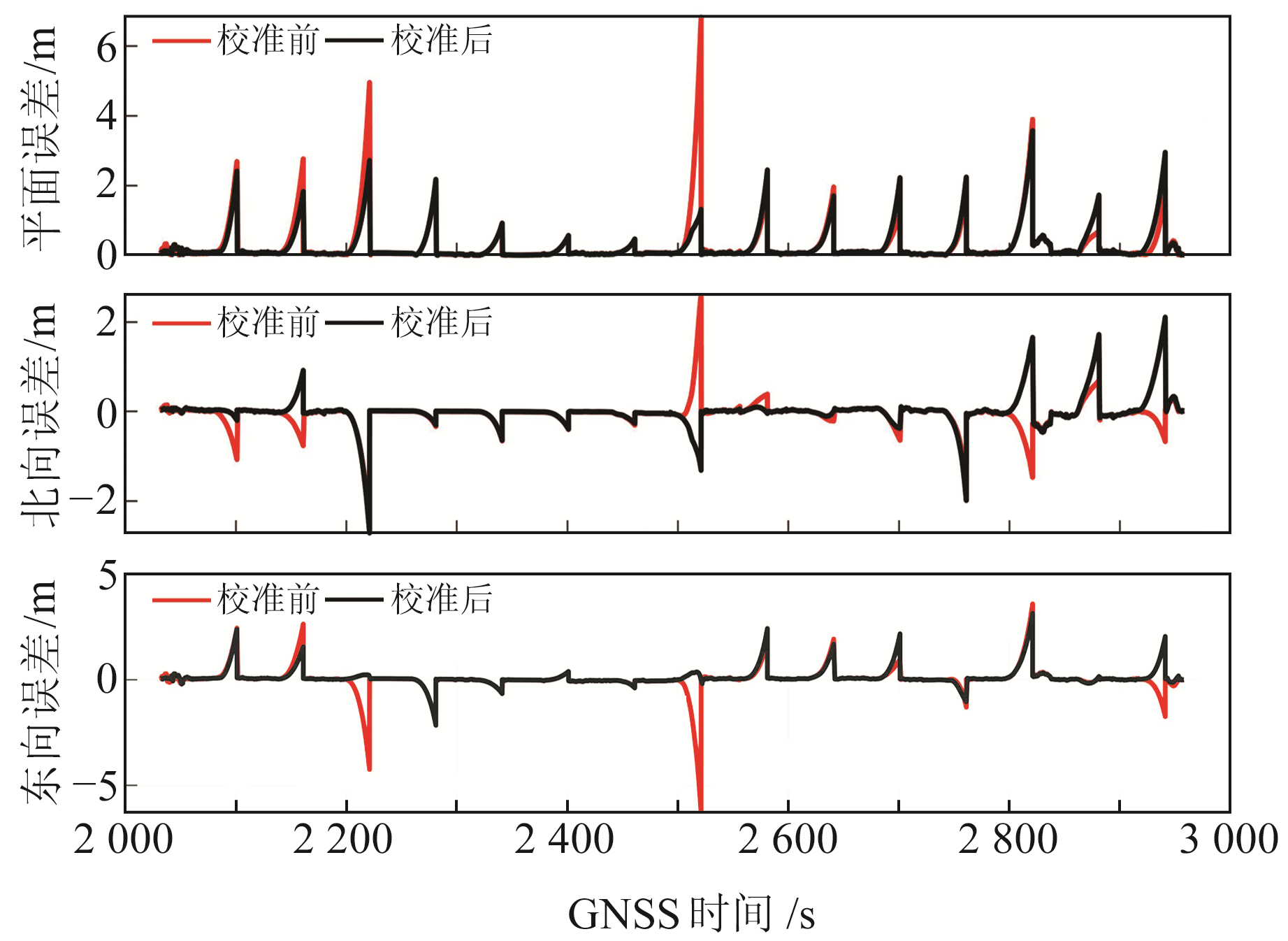
|
图 5 动态导航误差 Fig. 5 Dynamic navigation errors |
3组不同GNSS中断实验的平面误差RMS统计结果如表 4所示(t_sta为起始导航时刻,t_sta+50 s为起始中断时刻)。可以看出,IMU阵列校准后,3组中断实验精度均有提升,平均提升19.1%。精度提升数值较小可能是因为所使用的IMU阵列的误差数值较小,同时直接平均的数据融合方式对随机误差的降低有限;另外,大量的数值积分会存在计算误差,使得校准的数值精度下降,进而影响动态导航的精度。
|
|
表 4 动态导航平面RMS值 Tab. 4 Plane RMS of dynamic navigation |
本文提出一种在线IMU阵列校准方式,分别对加速度计和陀螺仪构建损失函数,利用求解非线性函数的LM优化算法,迭代得出IMU阵列的各个误差项。仿真实验结果显示,加速度计校准的零偏和尺度变换误差残差精度达到1.3×10-4 m/s2和3.3×10-5,陀螺仪校准的零偏和尺度变换误差残差精度达到1.3×10-3 dps和7.9×10-5,误差参数设定值与校准值一致性较好。3组实物测试结果显示,校准后IMU阵列的动态导航精度平均提升19.1%,表明该方法能有效校准IMU阵列的误差参数,提高动态导航性能。
| [1] |
龚大伟. 微惯性姿态测量系统的MEMS传感器校准与补偿算法研究[D]. 重庆: 重庆邮电大学, 2016 (Gong Dawei. Research MEMS Sensor Calibration and Compensation Algorithms in IMU[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2016)
(  0) 0) |
| [2] |
严恭敏. 惯性仪器测试与数据分析[M]. 北京: 国防工业出版社, 2012 (Yan Gongmin. Inertial Instrument Testing and Data Analysis[M]. Beijing: National Defense Industry Press, 2012)
(  0) 0) |
| [3] |
Jafari M, Sahebjameyan M, Moshiri B, et al. Skew Redundant MEMS IMU Calibration Using a Kalman Filter[J]. Measurement Science and Technology, 2015, 26(10)
(  0) 0) |
| [4] |
He K P, Han J T, Shao Y P. A Novel Redundant Inertial Measurement Unit and Calibration Algorithm[C]. International Conference on Optoelectronics and Microelectronics(ICOM), Harbin, 2013
(  0) 0) |
| [5] |
Wang L Q, Tang H L, Zhang T S, et al. Improving the Navigation Performance of the MEMS IMU Array by Precise Calibration[J]. IEEE Sensors Journal, 2021, 21(22): 26 050-26 058 DOI:10.1109/JSEN.2021.3118455
(  0) 0) |
| [6] |
Schopp P, Graf H, Burgard W, et al. Self-Calibration of Accelerometer Arrays[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(8): 1 913-1 925 DOI:10.1109/TIM.2016.2549758
(  0) 0) |
| [7] |
Rohac J, Sipos M, Simanek J. Calibration of Low-Cost Triaxial Inertial Sensors[J]. IEEE Instrumentation and Measurement Magazine, 2015, 18(6): 32-38 DOI:10.1109/MIM.2015.7335836
(  0) 0) |
| [8] |
Carlsson H, Skog I, Jaldén J. Self-Calibration of Inertial Sensor Arrays[J]. IEEE Sensors Journal, 2021, 21(6): 8 451-8 463 DOI:10.1109/JSEN.2021.3050010
(  0) 0) |
| [9] |
Tedaldi D, Pretto A, Menegatti E. A Robust and Easy to Implement Method for IMU Calibration without External Equipments[C]. IEEE International Conference on Robotics and Automation, Hong Kong, 2014
(  0) 0) |
| [10] |
Bancroft J B, Lachapelle G. Data Fusion Algorithms for Multiple Inertial Measurement Units[J]. Sensors(Basel, Switzerland), 2011, 11(7): 6 771-6 798
(  0) 0) |
2. Wuhan Mengxin Technology Ltd Co, 980 Gaoxin Road, Wuhan 430079, China
 2023, Vol. 43
2023, Vol. 43

