为解决卫星机动期间名义姿态失效的问题,不同IGS分析中心采用不同的姿态模型在卫星机动时期代替名义姿态[1]。在PPP解算时,选用的卫星轨道和钟差等产品中隐含了该分析中心对卫星姿态的定义,用户在使用这些产品时应注意保持卫星姿态的定义与各分析中心的定义一致,否则将引入由于姿态模型不一致带来的偏差,最终影响定位结果的质量[2]。Loyer等[3]提出ORBEX格式,分析中心可以利用这种格式以四元数的形式发布其采用的卫星姿态产品(以下简称四元数姿态产品),帮助实现用户端与分析中心误差改正的一致性。学者们利用卫星姿态产品对GPS、GLONASS和Galileo系统的PPP开展研究,结果表明,卫星机动期间采用姿态产品有利于提高3个系统的定位精度[2, 4]。目前已有多家分析中心公开发布BDS姿态信息,但BDS卫星种类多,机动方式各有不同,不同分析中心对BDS实际姿态建模差异缺少分析。相比于采用名义姿态的传统解算,四元数姿态产品应用于BDS PPP的实际效果分析较少。
基于以上研究,本文首先对比不同分析中心对BDS卫星姿态建模的差异,其次分析不同姿态模型对载波相位缠绕改正的差异,并进一步利用仿动态PPP实验实际分析不同卫星姿态计算策略对PPP结果的影响。
1 基于四元数的卫星姿态表示方法ORBEX格式中以单位Hamilton四元数的形式给出地心地固系与星固系间的转换关系,Hamilton四元数的表达方式为:
| $ \begin{gathered} \boldsymbol{q}=(s \boldsymbol{V})=\left(\begin{array}{llll} \boldsymbol{q}_0 & \boldsymbol{q}_1 & \boldsymbol{q}_2 & \boldsymbol{q}_3 \end{array}\right)= \\ \boldsymbol{q}_0+\boldsymbol{q}_1 \cdot i+\boldsymbol{q}_2 \cdot j+\boldsymbol{q}_3 \cdot k \end{gathered} $ | (1) |
式中,s为标量部分,V为向量部分。任意三维空间向量X可以表示为一组纯虚四元数q0, x=(0, X),使用四元数实现三维空间向量X的旋转可按式(2)完成:
| $ \boldsymbol{q}_{0, x^{\prime}}=\boldsymbol{q}_{\theta, V} \cdot \boldsymbol{q}_{0, x} \cdot \overline{\boldsymbol{q}}_{\theta, V} $ | (2) |
式中,
| $ \boldsymbol{q}_{0, x}=\overline{\boldsymbol{q}}_{\theta, {V}} \cdot \boldsymbol{q}_{0, x^{\prime}} \cdot \boldsymbol{q}_{\theta, V} $ | (3) |
四元数的乘积依然是四元数,且不满足交换律:
| $ \begin{gathered} \boldsymbol{q}_{v_1} \boldsymbol{q}_{v_2}= \\ \left(s_1 s_2-\boldsymbol{V}_1 \cdot \boldsymbol{V}_2, s_1 \boldsymbol{V}_2+s_2 \boldsymbol{V}_1+\boldsymbol{V}_1 \times \boldsymbol{V}_2\right) \end{gathered} $ | (4) |
星固系与地固系转换的旋转矩阵即为星固系轴向在地固系下的单位向量,星固系下三轴(e′x=[1, 0, 0]T, e′y=[0, 1, 0]T, e′z=[0, 0, 1]T)经式(3)旋转可得:
| $ \begin{aligned} & \left(0, \boldsymbol{e}_x^{\mathrm{T}}\right)=\overline{\boldsymbol{q}}_{\theta, V} \cdot\left(0, \boldsymbol{e}_{x^{\prime}}^{\mathrm{T}}\right) \cdot \boldsymbol{q}_{\theta, V} \\ & \left(0, \boldsymbol{e}_y^{\mathrm{T}}\right)=\overline{\boldsymbol{q}}_{\theta, V} \cdot\left(0, \boldsymbol{e}_{y^{\prime}}^{\mathrm{T}}\right) \cdot \boldsymbol{q}_{\theta, V} \\ & \left(0, \boldsymbol{e}_z^{\mathrm{T}}\right)=\overline{\boldsymbol{q}}_{\theta, V} \cdot\left(0, \boldsymbol{e}_{z^{\prime}}^{\mathrm{T}}\right) \cdot \boldsymbol{q}_{\theta, V} \end{aligned} $ | (5) |
计算展开得:
| $ \begin{aligned} & \boldsymbol{e}_x=\left[\begin{array}{llll} \boldsymbol{q}_0^2+\boldsymbol{q}_1^2-\boldsymbol{q}_2^2-\boldsymbol{q}_3^2 & 2\left(\boldsymbol{q}_1 \boldsymbol{q}_2-\boldsymbol{q}_0 \boldsymbol{q}_3\right) & 2\left(\boldsymbol{q}_1 \boldsymbol{q}_2+\boldsymbol{q}_0 \boldsymbol{q}_2\right) \end{array}\right]^{\mathrm{T}} \\ & \boldsymbol{e}_y=\left[\begin{array}{lll} 2\left(\boldsymbol{q}_1 \boldsymbol{q}_2+\boldsymbol{q}_0 \boldsymbol{q}_3\right) & \boldsymbol{q}_0^2-\boldsymbol{q}_1^2+\boldsymbol{q}_2^2-\boldsymbol{q}_3^2 & 2\left(\boldsymbol{q}_2 \boldsymbol{q}_3-\boldsymbol{q}_0 \boldsymbol{q}_1\right) \end{array}\right]^{\mathrm{T}} \\ & \boldsymbol{e}_z=\left[\begin{array}{lll} 2\left(\boldsymbol{q}_1 \boldsymbol{q}_3-\boldsymbol{q}_0 \boldsymbol{q}_2\right) & 2\left(\boldsymbol{q}_2 \boldsymbol{q}_3+\boldsymbol{q}_0 \boldsymbol{q}_1\right)\;\; \boldsymbol{q}_0^2-\boldsymbol{q}_1^2-\boldsymbol{q}_2^2+\boldsymbol{q}_3^2 \end{array}\right]^{\mathrm{T}} \end{aligned} $ | (6) |
根据式(6)可以直接采用四元数计算星固系在地固系的轴向,确定2个坐标系的关系。
由于不同姿态产品星固系Z轴指向地心且保持一致,在比较2个分析中心同时刻姿态产品差异时,可先使用式(6)计算分析中心A和分析中心B产品的X轴星固系指向exA和exB,再通过式(7)计算偏航角差异:
| $ \Delta \varphi=\operatorname{acos}\left(\boldsymbol{e}_{x_A} \cdot \boldsymbol{e}_{x_B}\right) $ | (7) |
式中,Δφ为2个产品偏航角差异的绝对值。
2 不同分析中心四元数姿态产品对比分析目前有WHU、CODE和GFZ三家分析中心发布BDS姿态信息,其中,WHU和GFZ发布的产品间隔为900 s。BDS-2和BDS-3都包含MEO、IGSO、GEO三类轨道卫星,针对BDS卫星的复杂性,本文分类对比不同分析中心对不同型号BDS卫星机动时期姿态建模的差异。实验选用上述3家分析中心发布的2021年doy260~267四元数姿态产品,实验时段内多颗卫星太阳高度角小于3°,存在机动。
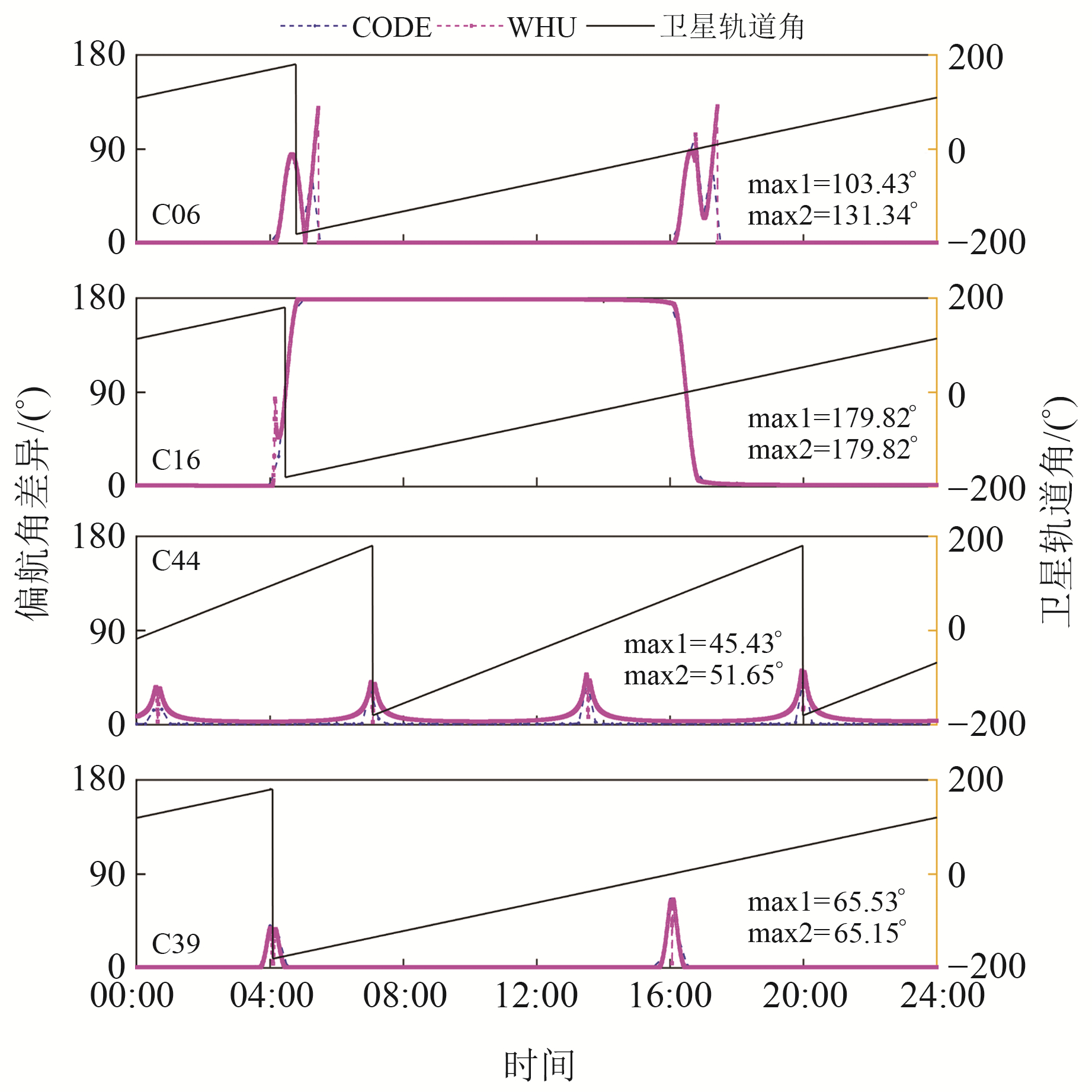
采用式(7)计算实验时段内CODE和WHU产品相对于GFZ产品的偏航角差异。结果表明,3家分析中心对BDS-2 GEO卫星、BDS-2 MEO卫星和BDS-3 GEO卫星机动时期偏航角差异均在0.01°以内,可认为3家分析中心对这3类卫星姿态建模一致。对于BDS-2 IGSO卫星、BDS-3 MEO卫星、BDS-3 IGSO卫星,分别以C06和C16(BDS-2 IGSO)、C44(BDS-3 MEO)、C39(BDS-3 IGSO)卫星为例进行分析。图 1为3家分析中心产品4颗卫星doy264姿态比较结果,图中蓝色和粉色虚线分别表示CODE和WHU产品相对于GFZ产品的卫星偏航角差异,黑色直线表示该日卫星轨道角变化,轨道角为180°和0°分别表示正午和子夜时刻,max1和max2分别表示CODE和WHU产品相对于GFZ产品偏航角差异最大值。
|
图 1 2021年doy264部分BDS卫星IGS姿态产品差异 Fig. 1 Differences of IGS attitude products of some BDS satellites on doy 264 in 2021 |
由图 1可见,对于BDS-2 IGSO卫星,CODE和WHU产品C06和C16卫星姿态差异相对较小,但3家分析中心产品对C06和C16卫星建模姿态差异有明显区别。对于C06卫星,3家产品姿态差异主要在正午和子夜附近;对于C16卫星,CODE和WHU产品相较于GFZ产品非正午和子夜时刻的姿态差异也可以持续保持在170°以上。可以发现,尽管都是BDS-2 IGSO卫星,3家分析中心对不同卫星机动模式建模不同。对于BDS-3 MEO卫星,3家分析中心产品对C44卫星姿态差异主要在正午和子夜机动期间,但在非正午和子夜时刻,WHU产品相对于GFZ和CODE产品始终存在2°左右偏航角差异。对于BDS-3 IGSO卫星,CODE和WHU产品对C39卫星姿态建模较为一致,相比于GFZ产品,差异仅出现在正午和子夜机动时期。
综上,对于BDS-2 IGSO、BDS-3 MEO、BDS-3 IGSO卫星,3家分析中心卫星姿态建模存在差异,而这种差异会体现在卫星轨道和钟差等精密产品中,有必要在使用分析中心轨道和钟差产品时配套采用四元数姿态产品计算卫星姿态。
3 卫星姿态产品对PPP影响分析 3.1 实验方案设计为分析BDS四元数姿态产品对卫星机动期间仿动态PPP解算的影响,采用3种不同的姿态策略对卫星姿态建模,比较3种姿态策略下相位缠绕改正的差异,进一步通过分析载波相位残差和定位结果比较3种卫星姿态计算策略对PPP的影响。3种姿态计算策略分别是:策略1,GFZ姿态产品,称之为四元数姿态(OBX attitude);策略2,卫星采用名义姿态,称之为名义姿态(nominal attitude);策略3,采用文献[5]介绍的根据不同卫星机动方式的建模方法,具体模型设置如表 1所示,称之为模型姿态(model attitude)。
|
|
表 1 BDS不同类型卫星机动模型设置 Tab. 1 Different types of maneuvering model setting for BDS satellites |
策略3中BDS-2 IGSO和BDS-2 MEO卫星切换条件的设置目的是在低太阳高度角时避免因最大偏航率引起与动偏模式的姿态差异,同时保持2种机动方式切换时的连续性,连续偏航角具体计算方法见文献[6],该模型是四元数姿态产品推出之前常用的一种方式[6-7]。PPP实验采用B1B3消电离层组合仿动态模式解算,参数设置见文献[8]。
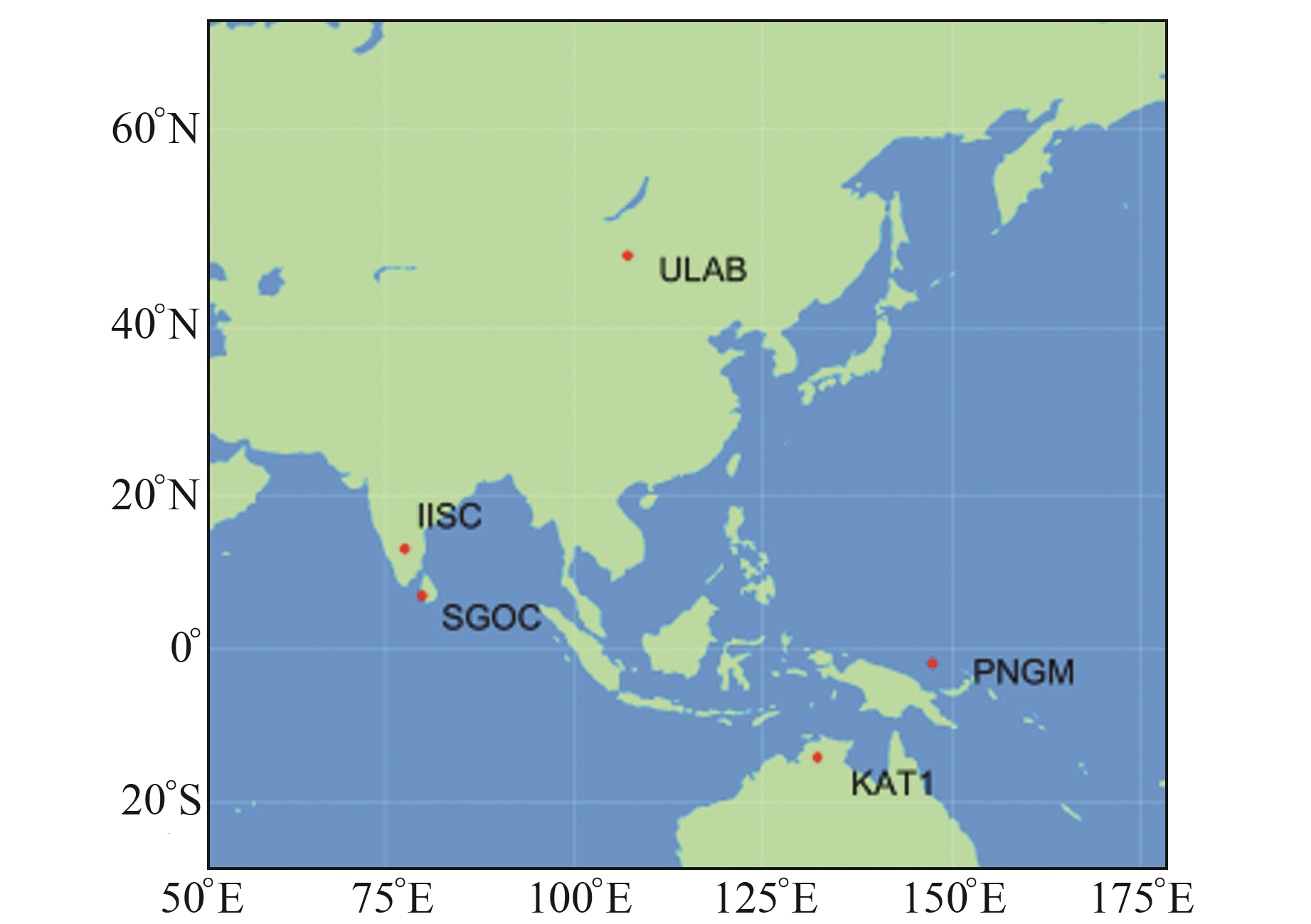
实验数据方面,为满足卫星机动时期地面测站可见,选取图 2中MGEX测站2021年doy263~267(存在BDS卫星机动)的观测数据进行计算,产品为从武汉大学IGS数据中心下载的实验时段内GFZ精密轨道钟差和四元数姿态产品。
|
图 2 测站分布 Fig. 2 Distribution of the stations |
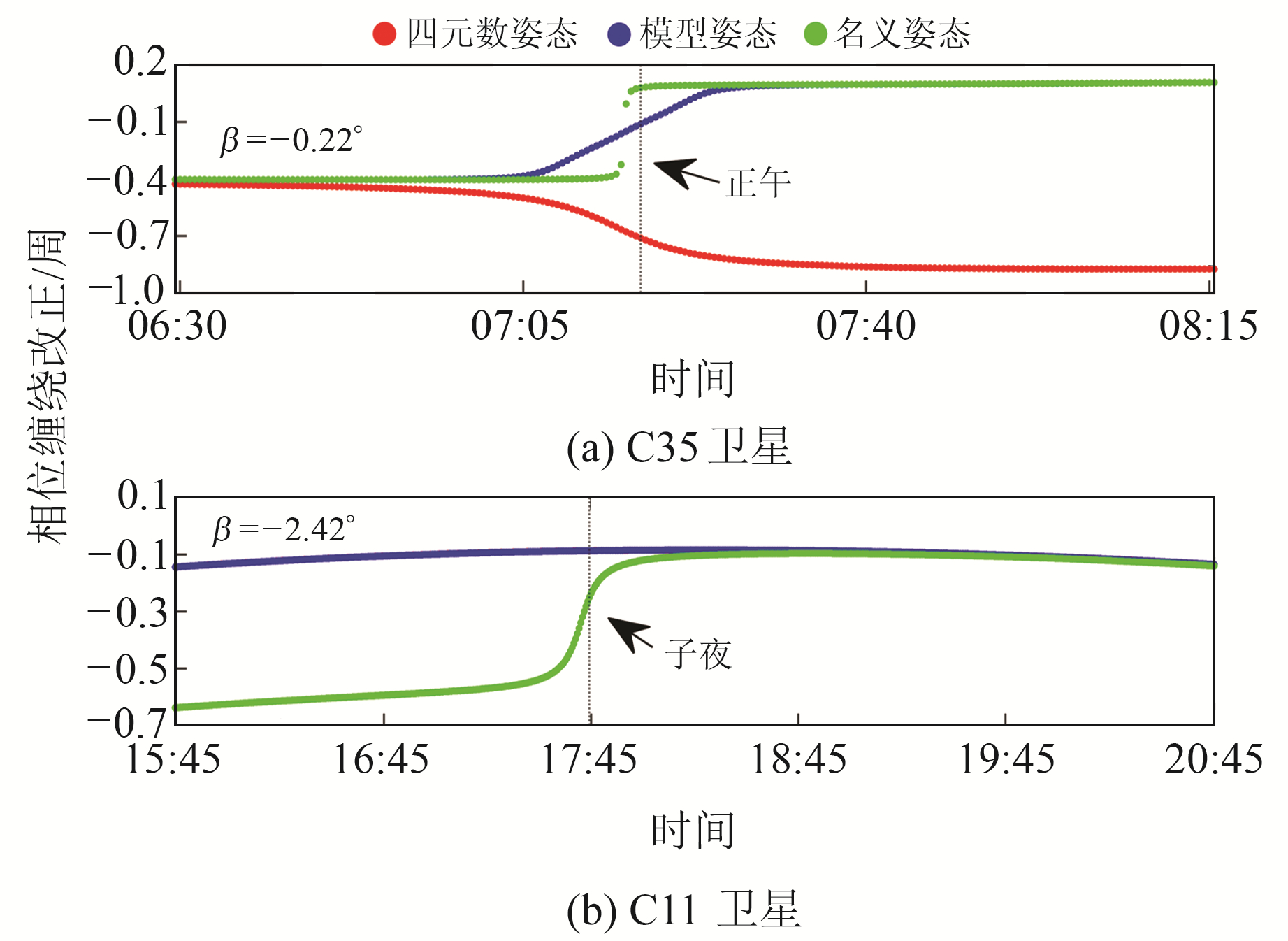
为分析不同策略下相位缠绕改正的差异,以C35和C11卫星为例,比较二者在IISC站doy265三种不同策略在卫星正午和子夜时刻前后的相位缠绕改正值,结果如图 3所示。图中,β表示该日C35和C11卫星的平均太阳高度角。需要注意的是,由于C11卫星四元数姿态和模型姿态结果一致,所以红色和蓝色散点重合。
|
图 3 C35卫星和C11卫星IISC站doy265部分观测时段相位缠绕改正 Fig. 3 Wind-up of C35 and C11 satellite at IISC station during part observation period on doy 265 |
对于C35卫星,正午前后3种策略计算的相位缠绕改正数存在明显区别,时长大约持续100个历元(30 s采样间隔)。在此期间,模型姿态与四元数姿态计算得到的相位缠绕改正值呈现出大小相同、符号相反的变化趋势;机动结束后,四元数姿态与另外2种姿态产生的相位缠绕改正相差1周。这种现象反映出不同姿态计算方法之间存在航向角偏差[9]。相比于四元数姿态和模型姿态,名义姿态计算的相位缠绕改正变化率更大,这与名义姿态下随太阳高度角越小机动时姿态变化越大的特点有关。对于C11卫星,红色散点和蓝色散点重合,说明模型姿态与四元素姿态相位缠绕改正值一致,而名义姿态下C11卫星子夜机动前后与四元数姿态相差近0.7周。可以看出,不同卫星采用不同姿态策略得到的相位缠绕改正各有不同,差异可达1周。
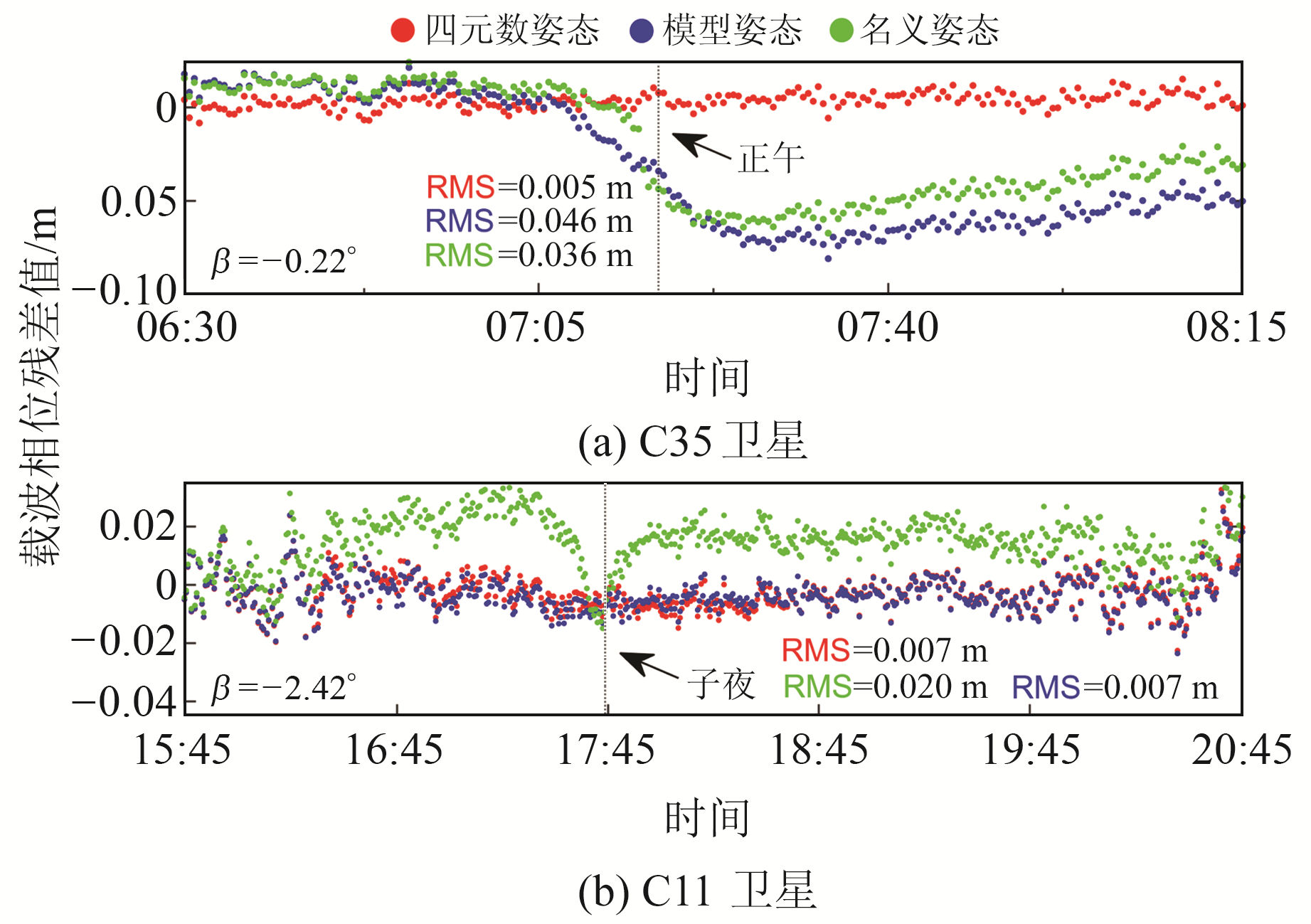
通过载波相位残差(图 4)和定位结果(图 5)检验不同姿态策略的正确性。
|
图 4 C35和C11卫星3种姿态策略的载波相位残差 Fig. 4 Carrier phase residuals of C35 and C11 satellites of three attitude strategies |
|
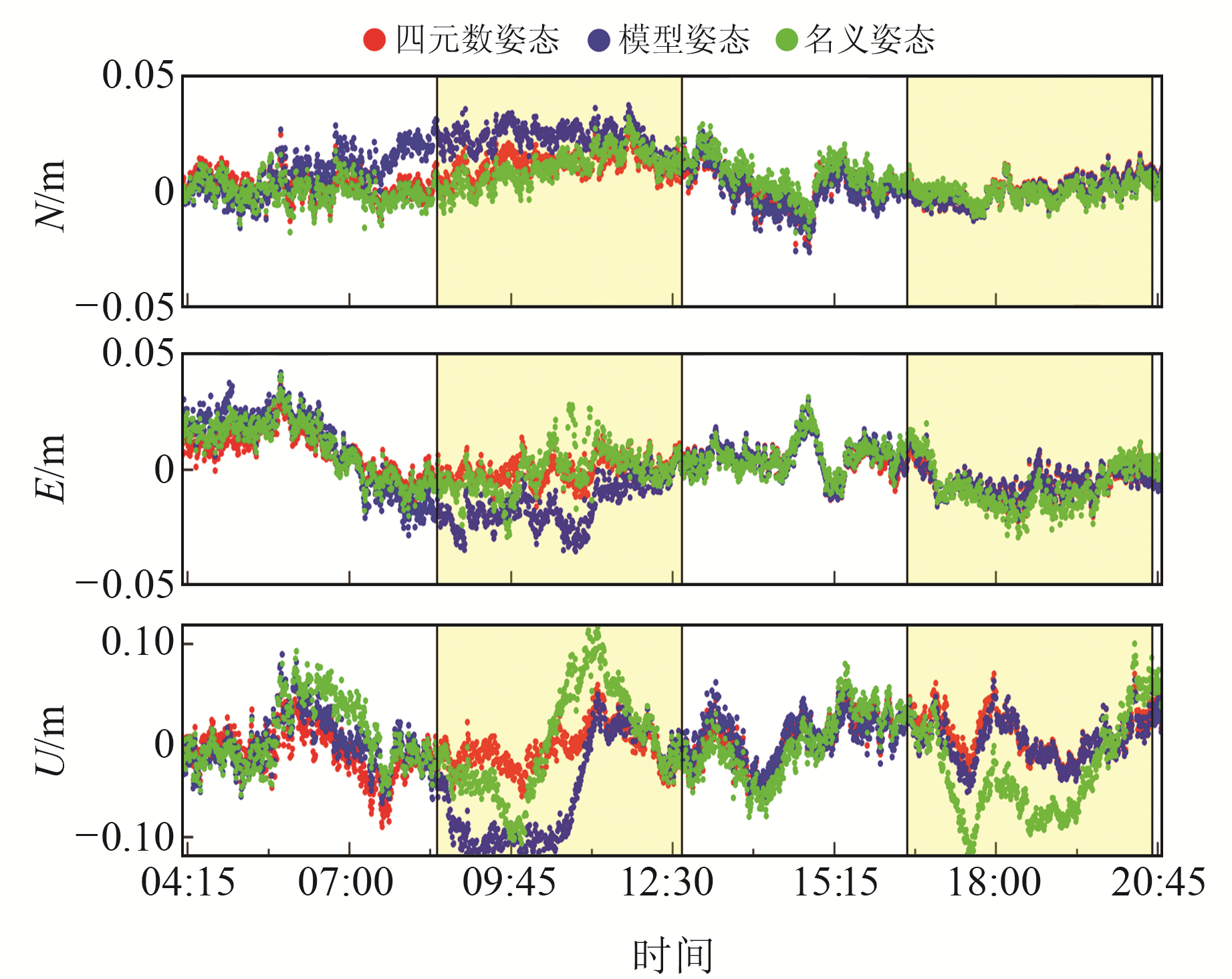
图 5 IISC站doy265仿动态PPP结果残差 Fig. 5 Residuals of imitation dynamic PPP results at IISC station on doy 265 |
由图 4可见,C35卫星正午时刻附近模型姿态和名义姿态载波相位残差绝对值明显增大,机动结束后,载波相位残差保持近0.05 m的水平,这是由于模糊度参数连续弧段内按常数估计,姿态引起的偏差无法快速被模糊度参数吸收,导致偏差反映在载波相位残差中,使模型姿态和名义姿态相对于四元数姿态相位残差RMS提高7~8倍。对于C11卫星,该时段内四元数姿态与模型姿态载波相位后验残差RMS一致,相较名义姿态减小近2/3。在所示5 h内,名义姿态下计算的C11卫星载波相位残差保持近0.02 m水平,说明该卫星机动带来的影响不仅体现在正午和子夜时刻附近。因此,采用名义姿态时,剔除正午和子夜机动期间观测数据的方法不能解决姿态异常的影响。综上,相比于模型姿态和名义姿态,四元数姿态具有更小的相位残差,模型更精确。
图 5为IISC站仿动态PPP结果与IGS周解的对比,图中2块黄色阴影所示期间均有4颗以上卫星机动。可以看出,3种姿态策略表现出的定位精度明显不同,尤其是在U方向;非阴影时段内也存在卫星机动,但数目较少,对定位精度影响不大。使用四元数姿态的定位结果偏差在E、N、U方向的RMS分别为1.0 cm、0.8 cm、4.2 cm,模型姿态为2.1 cm、1.3 cm、4.8 cm,名义姿态为1.4 cm、0.9 cm、4.7 cm。相对于模型姿态和名义姿态,四元数姿态下定位结果最好,模型姿态RMS大于名义姿态,可能是该时段内卫星名义姿态更接近四元数姿态。
为进一步说明四元数姿态产品对定位结果的影响,基于上述5个MGEX站2021年doy263~267的观测数据,分别使用3种卫星姿态策略进行仿动态PPP实验,并统计最终定位结果指标。将定位结果与IGS周解对比,得到5个测站每天的平均RMS(表 2)。可以看出,使用GFZ产品时,四元数姿态相比于名义姿态在E、N、U方向的定位精度平均提高17%、25%、34%,相比于模型姿态分别提高11%、7%、7%。本文采用的模型姿态与GFZ四元数姿态产品建模较为接近,一定程度上可以采用模型姿态代替四元数姿态。综上,相比于使用名义姿态,配套使用四元数姿态可以提高仿动态PPP定位精度;本文采用的模型姿态可以在一定程度上替代GFZ四元数姿态产品,但由于不同分析中心对BDS姿态建模存在差异,所以模型姿态不适用于所有分析中心产品,配套使用各分析中心轨道钟差姿态产品才能达到较好的定位效果。
|
|
表 2 3种姿态计算的仿动态PPP精度 Tab. 2 Imitation dynamic PPP accuracy of three attitudes |
本文基于GFZ、WHU和CODE分析中心公开发布的四元数姿态产品,对比3家分析中心BDS卫星姿态差异,进一步研究使用四元数姿态产品对BDS仿动态PPP的影响,得到以下结论:
1) 不同分析中心姿态产品间存在姿态差异,相较于其他类型卫星,BDS-2 IGSO卫星姿态差异表现复杂,部分卫星姿态差异不仅仅出现在正午和子夜附近,最大可达180°,因此必须使用同一家分析中心产品进行计算。
2) 卫星姿态影响天线相位缠绕改正的大小,分析中心四元数产品相比于名义姿态产生近1周的相位缠绕改正差异,这使得采用名义姿态定位解算时载波相位验后残差过大。对BDS-2 MEO卫星来说,名义姿态下采用删除正午和子夜机动期观测数据的方式无法消除姿态差异的影响,在没有四元数姿态产品的情况下使用模型姿态能减小载波相位验后残差。
3) 用户端采用的卫星姿态模型不一定适用于所选择的轨道钟差产品,配套使用四元数姿态产品能够保持用户端与服务端产品的一致性,从而避免引入误差改正偏差。配套使用GFZ轨道钟差和四元数姿态产品能使仿动态PPP精度较名义姿态在E、N、U方向分别提高17%、25%、34%,较本文模型姿态分别提高11%、7%、7%。
| [1] |
Mayer-Gürr T, Behzadpour S, Eicker A, et al. GROOPS: A Software Toolkit for Gravity Field Recovery and GNSS Processing[J]. Computers and Geosciences, 2021, 155
(  0) 0) |
| [2] |
Loyer S, Banville S, Geng J H, et al. Exchanging Satellite Attitude Quaternions for Improved GNSS Data Processing Consistency[J]. Advances in Space Research, 2021, 68(6): 2 441-2 452 DOI:10.1016/j.asr.2021.04.049
(  0) 0) |
| [3] |
Loyer S, Montenbruck O, Hilla S. ORBEX: The Orbit Exchange Format, Draft Version 0.09[EB/OL]. http://acc.igs.org/misc/ORBEX009.pdf, 2019
(  0) 0) |
| [4] |
Liu T J, Chen H, Jiang W P, et al. Assessing the Exchanging Satellite Attitude Quaternions from CNES/CLS and Their Application in the Deep Eclipse Season[J]. GPS Solutions, 2021, 26(1): 1-14
(  0) 0) |
| [5] |
中国卫星导航系统管理办公室. BD 420025-2019北斗/全球卫星导航系统(GNSS)卫星高精度应用参数定义及描述[S]. 北京: 中国卫星导航系统管理办公室, 2019 (China Satellite Navigation System Administration Office. BD 420025-2019 Definitions and Descriptions of BDS/GNSS Satellite Parameters for High Precision Application[S]. Beijing: China Satellite Navigation System Administration Office, 2019)
(  0) 0) |
| [6] |
Wang C, Guo J, Zhao Q L, et al. Yaw Attitude Modeling for Beidou I06 and Beidou-3 Satellites[J]. GPS Solutions, 2018, 22(4): 1-10
(  0) 0) |
| [7] |
Li X J, Hu X G, Guo R, et al. Orbit and Positioning Accuracy for New Generation Beidou Satellites during the Earth Eclipsing Period[J]. Journal of Navigation, 2018, 71(5): 1 069-1 087 DOI:10.1017/S0373463318000103
(  0) 0) |
| [8] |
王何鹏, 郭杭, 黄聪. 三种多系统开源PPP软件性能比较与分析[J]. 大地测量与地球动力学, 2021, 41(5): 520-524 (Wang Hepeng, Guo Hang, Huang Cong. Performance Comparison and Analysis of Three Kinds of Multi-System Open Source PPP Software[J]. Journal of Geodesy and Geodynamics, 2021, 41(5): 520-524)
(  0) 0) |
| [9] |
Kuang D, Desai S, Sibois A. Observed Features of GPS Block ⅡF Satellite Yaw Maneuvers and Corresponding Modeling[J]. GPS Solutions, 2017, 21(2): 739-745 DOI:10.1007/s10291-016-0562-9
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


