2. 海军航空大学,山东省烟台市,264001;
3. 山东东海热电有限公司,山东省龙口市东海工业园,265713
无迹卡尔曼滤波UKF在GNSS/SINS组合导航系统中具有高精度特性[1]。但UKF是在量测噪声方差恒定的基础上建立的,当量测噪声方差发生变化时,其滤波精度会降低。目前主要采用基于新息的自适应滤波方法解决该问题。田甜[2]将自适应因子引入UKF算法中以消除粗差对系统的影响;陈光武等[3]利用UKF对组合导航进行处理,当GPS信号丢失时利用训练好的神经网络来增强UKF的滤波效果,但该算法严重依赖训练样本的质量与数量;吴涛等[4]引入时变噪声估计器来估计时变噪声以提高UKF滤波的自适应能力,但其状态方程依然采取线性化处理方式,限制了滤波精度的提高;马晓杰等[5]引入自适应因子以减小滤波器初值偏差和系统模型异常扰动对UKF的影响,但该算法在量测噪声异常扰动的情况下性能不佳。
基于Sage-Husa的自适应滤波在组合导航系统中应用广泛,但该方法存在对滤波初值敏感、直接使用时滤波易发散以及噪声统计特性估计有偏差等缺陷[6]。而基于变分贝叶斯原理的自适应滤波方法可以克服上述缺点,并能实现系统状态与量测噪声方差的同步估计[7]。基于上述讨论,本文重点针对量测噪声异常扰动情况,引入变分贝叶斯原理,提出一种自适应UKF算法以适应量测噪声方差的变化。
1 组合导航非线性滤波模型以ENU地理坐标系为导航坐标系,基于UKF的GNSS/SINS组合导航系统状态方程为[7]:
| $ \left\{ \begin{array}{l} \dot{\boldsymbol{X}}(t)=f\left(\boldsymbol{X}(t), \boldsymbol{\omega}_{i b}^b, \boldsymbol{f}^b, t\right)\\ \boldsymbol{X}(t)=\left[\begin{array}{llllllllll} \gamma & \theta & \varphi & v_E & v_N & v_U & \lambda & L & H \end{array}\right]^{\mathrm{T}} \end{array} \right. $ | (1) |
式中,X(t)为系统状态向量;γ、θ、φ分别为横滚角、俯仰角和航向角;vE、vN、vU分别为E、N和U向速度;λ、L、H分别为经度、纬度和高度;ωibb为陀螺仪输出;fb为加速度计输出;t为时间。
假设导航系统的先验状态、过程噪声与未知量测噪声间相互独立。选取GNSS输出速度和位置作为观测量,即
| $ \left\{ \begin{array}{l} {\boldsymbol{Z}}(t) = {\boldsymbol{H}}(t){\boldsymbol{X}}(t) + {\boldsymbol{V}}(t)\\ {\boldsymbol{Z}}(t) = {\left[ {\begin{array}{*{20}{l}} {{v_E}}&{{v_N}}&{{v_U}}&\lambda &L&H \end{array}} \right]^{\rm{T}}}\\ {\boldsymbol{H}}(t) = \left[ {\begin{array}{*{20}{l}} {{{\bf{0}}_{6 \times 3}}}&{{{\boldsymbol{I}}_{6 \times 6}}} \end{array}} \right] \end{array} \right. $ | (2) |
式中,Z(t)和V(t)分别为量测向量和量测噪声向量,且满足V(t)∈N(0, R(t))。
2 组合导航自适应UKF算法 2.1 变分贝叶斯原理变分贝叶斯算法近似使用一种分解的自由形式递归逼近误差状态和量测噪声方差的联合后验分布,然后通过递归算法中的定点迭代估计状态和量测噪声的方差[8]。在系统噪声方差已知、量测噪声方差未知的情况下,变分贝叶斯算法可分为预测阶段和更新阶段[9]。预测阶段可利用C-K(Chapman-Kolmogorov)方程拟合出误差状态和量测噪声方差的条件分布。
预测阶段:
| $ \begin{gathered} p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k-1}\right)=\int p\left(\boldsymbol{X}_k \mid \boldsymbol{X}_{k-1}\right) p\left(\boldsymbol{R}_k \mid \boldsymbol{R}_{k-1}\right) \cdot \\ p\left(\boldsymbol{X}_{k-1}, \boldsymbol{R}_{k-1} \mid \boldsymbol{Z}_{1: k-1}\right) \cdot \mathrm{d} \boldsymbol{X}_{k-1} \cdot \mathrm{d} \boldsymbol{R}_{k-1} \end{gathered} $ | (3) |
更新阶段:
| $ \begin{gathered} p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k}\right) \propto \\ p\left(\boldsymbol{Z}_k \mid \boldsymbol{X}_k, \boldsymbol{R}_k\right) p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k-1}\right) \end{gathered} $ | (4) |
虽然式(3)和式(4)在理论上最优,但由于引入了噪声方差矩阵及多维数值积分,因此在实际情况中很难求解。而变分贝叶斯原理可以采用近似的方法,利用多个已知分布近似求解后验分布。根据变分贝叶斯原理,式(3)、(4)中的量测方差与联合预测和后验分布可转换为如下的逆Gamma分布和高斯分布:
| $ \begin{gathered} p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k-1}\right)=N\left(\boldsymbol{X}_k \mid \hat{\boldsymbol{X}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \cdot \\ \prod\limits_{i=1}^m \operatorname{IG}\left(\sigma_{k, i}^2 \mid \alpha_{k \mid k-1, i}, \beta_{k \mid k-1, i}\right) \end{gathered} $ | (5) |
| $ \begin{gathered} p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k}\right)=N\left(\boldsymbol{X}_k \mid \hat{\boldsymbol{X}}_{k \mid k}, \boldsymbol{P}_{k \mid k}\right) \cdot \\ \prod\limits_{i=1}^m \operatorname{IG}\left(\sigma_{k, i}^2 \mid \alpha_{k \mid k, i}, \beta_{k \mid k, i}\right) \end{gathered} $ | (6) |
式中,σk, i2为高斯分布的未知噪声方差。
引入预测加权系数ρi∈(0, 1],对式(3)中的量测噪声方差的预测分布作一阶近似:
| $ \left\{\begin{array}{l} \alpha_{k \mid k-1, i}=\rho_i \alpha_{k-1 \mid k-1, i} \\ \beta_{k \mid k-1, i}=\rho_i \beta_{k-1 \mid k-1, i} \end{array}\right. $ | (7) |
式中,αk-1|k-1, i和βk-1|k-1, i为逆Gamma分布的2个参数,详细推导过程见文献[10]。
2.2 自适应UKF算法将变分贝叶斯原理与UKF算法结合,得到适用于GNSS/SINS组合导航系统的自适应UKF算法。系统增广状态向量如下:
| $ \left\{ \begin{array}{l} {{\boldsymbol{X}}^a} = {\left[ {\begin{array}{*{20}{l}} {\boldsymbol{X}}&{\boldsymbol{W}} \end{array}} \right]^{\rm{T}}}\\ {{\boldsymbol{\chi }}^a} = {\left[ {\begin{array}{*{20}{l}} {{{\left( {{{\boldsymbol{\chi }}^X}} \right)}^{\rm{T}}}}&{{{\left( {{{\boldsymbol{\chi }}^W}} \right)}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (8) |
式中,χa的维数定义为n。具体步骤如下:
1) 初始化。
| $ \left\{\begin{array}{l} \hat{\boldsymbol{X}}_0=E\left[\boldsymbol{X}_0\right] \\ \boldsymbol{P}_0=E\left[\left(\boldsymbol{X}_0-\hat{\boldsymbol{X}}_0\right)\left(\boldsymbol{X}_0-\hat{\boldsymbol{X}}_0\right)^{\mathrm{T}}\right] \\ \hat{\boldsymbol{X}}_0^a=E\left[\boldsymbol{X}^a\right]=\left[\begin{array}{ll} \hat{\boldsymbol{X}}_0^{\mathrm{T}} \quad \bf{0} \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{P}_0^a=E\left[\left(\boldsymbol{X}_0^a-\hat{\boldsymbol{X}}_0^a\right)\left(\boldsymbol{X}_0^a-\hat{\boldsymbol{X}}_0^a\right)^{\mathrm{T}}\right]= \\ \;\; \;\;{\left[\begin{array}{ll} \boldsymbol{P} & \bf{0} \\ \bf{0} & \boldsymbol{Q} \end{array}\right]} \end{array}\right. $ | (9) |
2) 样点计算。
| $ \left\{\begin{array}{l} \boldsymbol{\chi}_{0, k-1}^a=\hat{\boldsymbol{X}}_{k-1}^a \\ \boldsymbol{\chi}_{i, k-1}^a=\hat{\boldsymbol{X}}_{k-1}^a+\left(\sqrt{(n+\lambda) \boldsymbol{P}_{k-1}^a}\right)_i, \\ \;\; \;\;i=1, \cdots, n \\ \boldsymbol{\chi}_{i, k-1}^a=\hat{\boldsymbol{X}}_{k-1}^a-\left(\sqrt{(n+\lambda) \boldsymbol{P}_{k-1}^a}\right)_i, \\ \;\; \;\;i=n+1, \cdots, 2 n \end{array}\right. $ | (10) |
式中,
| $ \left\{\begin{array}{l} W_0^m=\frac{\lambda}{n+\lambda} \\ W_0^c=\frac{\lambda}{n+\lambda}+\left(1-\alpha^2+\beta\right) \\ W_i^m=W_i^c=\frac{1}{2(n+\lambda)}, i=1, \cdots, 2 n \end{array}\right. $ | (11) |
式中,λ=α2(n+κ)-n;α、β和κ为比例因子。
3) 时间更新。
| $ \left\{\begin{array}{l} \boldsymbol{\alpha}_{k \mid k-1}=\boldsymbol{\rho} \cdot \boldsymbol{\alpha}_{k-1 \mid k-1} \\ \boldsymbol{\beta}_{k \mid k-1}=\boldsymbol{\rho} \cdot \boldsymbol{\beta}_{k-1 \mid k-1} \end{array}\right. $ | (12) |
| $ \left\{\begin{array}{l} \boldsymbol{\chi}_{i, k \mid k-1}^X=f\left(\boldsymbol{\chi}_{i, k-1}^X, \boldsymbol{\chi}_{i, k-1}^W\right) \\ \hat{\boldsymbol{X}}_{k \mid k-1}=\sum\limits_{i=0}^{2 L_a} W_i^m \boldsymbol{\chi}_{i, k \mid k-1}^X \end{array}\right. $ | (13) |
| $ \begin{gathered} \boldsymbol{P}_{k \mid k-1}=\sum\limits_{i=0}^{2 n} W_i^c\left[\boldsymbol{X}_{i, k \mid k-1}^X-\hat{\boldsymbol{X}}_{k \mid k-1}\right] \\ {\left[\boldsymbol{X}_{i, k \mid k-1}^X-\hat{\boldsymbol{X}}_{k \mid k-1}\right]^{\mathrm{T}}} \end{gathered} $ | (14) |
4) 量测更新。
| $ \hat{\boldsymbol{Z}}_{k \mid k-1}=\boldsymbol{H} \hat{\boldsymbol{X}}_{k \mid k-1} $ | (15) |
| $ \left\{\begin{array}{l} \boldsymbol{P}_{Z Z}=\boldsymbol{H P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}}+\hat{\boldsymbol{R}} \\ \boldsymbol{P}_{X Z}=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} \end{array}\right. $ | (16) |
| $ \left\{ \begin{array}{l} \boldsymbol{\alpha}_{k \mid k}= \frac{1}{2}+\boldsymbol{\alpha}_{k-1 \mid k-1} \\ \boldsymbol{\beta}_{k \mid k}^{-}= \boldsymbol{\beta}_{k \mid k-1} \\ \hat{\boldsymbol{R}}_{k+1}= \operatorname{diag}\left(\boldsymbol{\beta}_{k \mid k}^{-} \cdot / \boldsymbol{\alpha}_{k \mid k}\right) \\ \boldsymbol{\beta}_{k \mid k}= \left(\boldsymbol{Z}_k-\boldsymbol{H}\hat{\boldsymbol{X}}_{k \mid k-1}\right) \cdot\left(\boldsymbol{Z}_k-\boldsymbol{H}\hat{\boldsymbol{X}}_{k \mid k-1}\right) / 2+ \\ \;\;\;\;\;\;\;\;\;\;\operatorname{diag}\left[\boldsymbol{H}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}}\right] / 2+\boldsymbol{\beta}_{k \mid k}^{-} \end{array} \right. $ | (17) |
式中,
5) 滤波更新。
| $ \left\{\begin{array}{l} \boldsymbol{K}_k=\boldsymbol{P}_{X Z} \boldsymbol{P}_{Z Z}^{-1} \\ \hat{\boldsymbol{X}}_k=\hat{\boldsymbol{X}}_{k \mid k-1}+\boldsymbol{K}_k\left(\boldsymbol{Z}_k-\hat{\boldsymbol{Z}}_{k \mid k-1}\right) \\ \boldsymbol{P}_k=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{K}_k \boldsymbol{P}_{Z Z} \boldsymbol{K}_k^{\mathrm{T}}=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{K}_k \boldsymbol{P}_{{XZ}}^{\mathrm{T}} \end{array}\right. $ | (18) |
以小型飞行器作为载体构建仿真系统,载体飞行航迹包含加速、爬升、转弯等各种运动。载体起飞初始经度、纬度、高度分别为29°E、118°N、50 m,初始航向角为90°,飞行时间为3 600 s,捷联解算周期为0.02 s,滤波周期为1 s。滤波初始参数设置如下:三维姿态角误差均为0.5°,三维速度误差均为0.1 m/s,三维位置误差均为5 m。设定陀螺随机游走驱动噪声及陀螺白噪声均为0.2°/h,加速度计随机游走驱动噪声及陀螺白噪声均为0.5×10-5g。GNSS位置误差和测速误差分别为8 m和0.2 m/s,采样周期为1 s。在仿真实验中,式(12)、式(17)中 ρ、α、β的初始值分别取为:
| $ \left\{\begin{array}{l} \boldsymbol{\rho}=\left[\begin{array}{llllll} 0.99 & 0.99 & 0.99 & 0.99 & 0.99 & 0.99 \end{array}\right] \\ \boldsymbol{\alpha}=\left[\begin{array}{llllll} 1 & 1 & 1 & 1 & 1 & 1 \end{array}\right] \\ \boldsymbol{\beta}=\left[\begin{array}{llllll} 0.1 & 0.1 & 0.1 & 2 & 2 & 2 \end{array}\right] \end{array}\right. $ | (19) |
根据GNSS测量精度设定及式(2),正常情况下,GNSS量测噪声的均方差可以表示为:
| $ \begin{gathered} \boldsymbol{R}_{\text {root }}=\operatorname{sqrtm}(\boldsymbol{R})= \\ \operatorname{diag}\left(\left[\begin{array}{llllll} 0.2 & 0.2 & 0.2 & 8 & 8 & 8 \end{array}\right]\right) \end{gathered} $ | (20) |
式中,sqrtm(·)为对矩阵中每个元素取开平方的函数;diag(·)为用于构造对角矩阵的函数。
在仿真过程的不同时段内设定GNSS量测噪声的突变与缓变2种情况的均方差:
| $ \boldsymbol{r}_{\text {real }}=\left\{\begin{array}{l} 6 \boldsymbol{r}_{\text {root }}, 600<t \leqslant 1\;200 \\ \boldsymbol{r}_{\text {root }}\left[1+9 \sin \left(2 {\rm{ \mathsf{ π} }} \cdot \frac{t-2\;400}{1\;200}\right)\right], \\ \;\;\;\;\;2\;400<t \leqslant 3\;000 \\ \boldsymbol{r}_{\text {root }}, \text { others } \end{array}\right. $ | (21) |
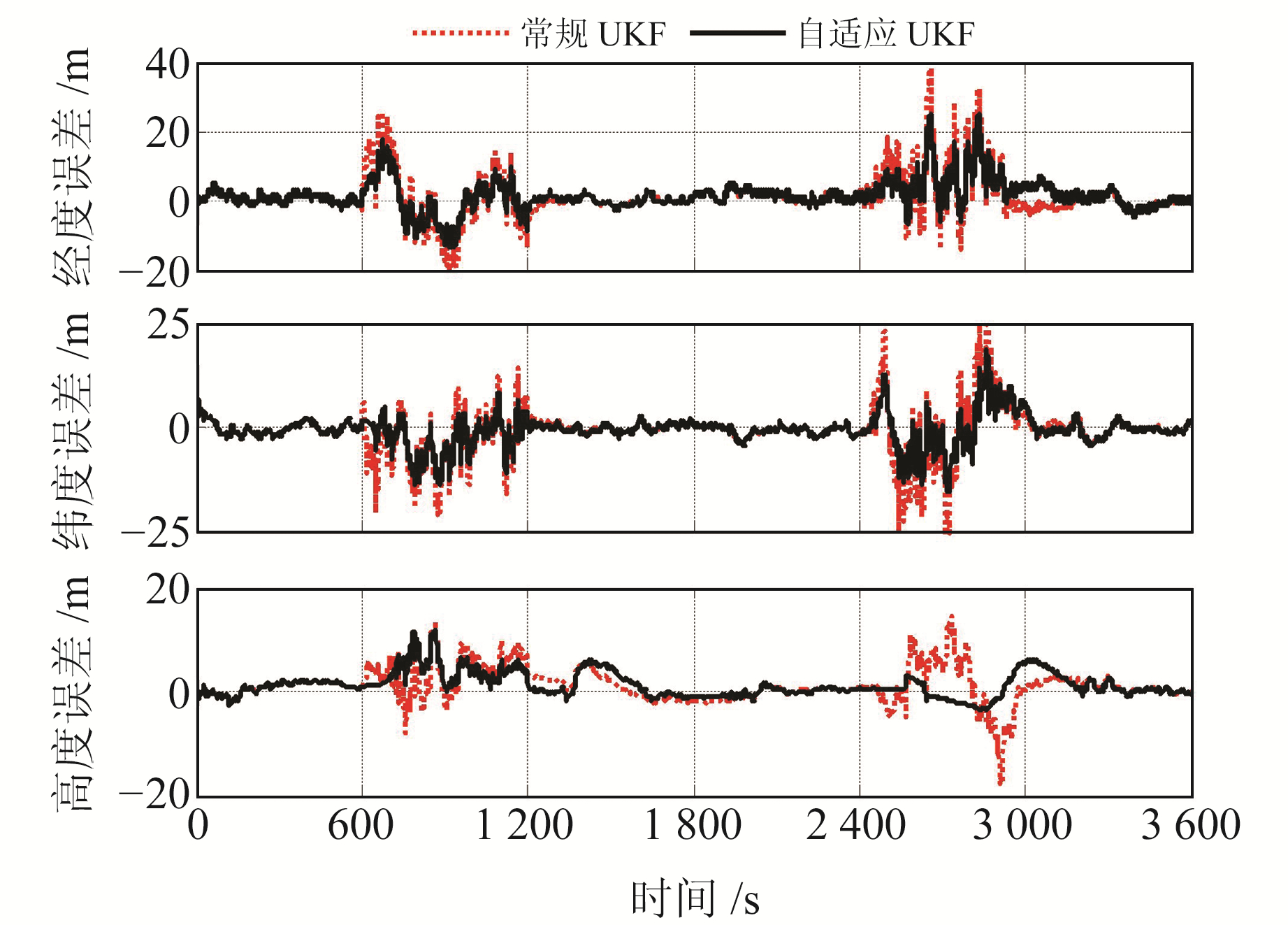
根据上述设定,分别进行基于常规UKF算法及自适应UKF算法的GNSS/SINS组合导航系统性能仿真验证。图 1~3分别为位置误差、速度误差及姿态误差对比曲线。
|
图 1 位置误差 Fig. 1 Position error |
|
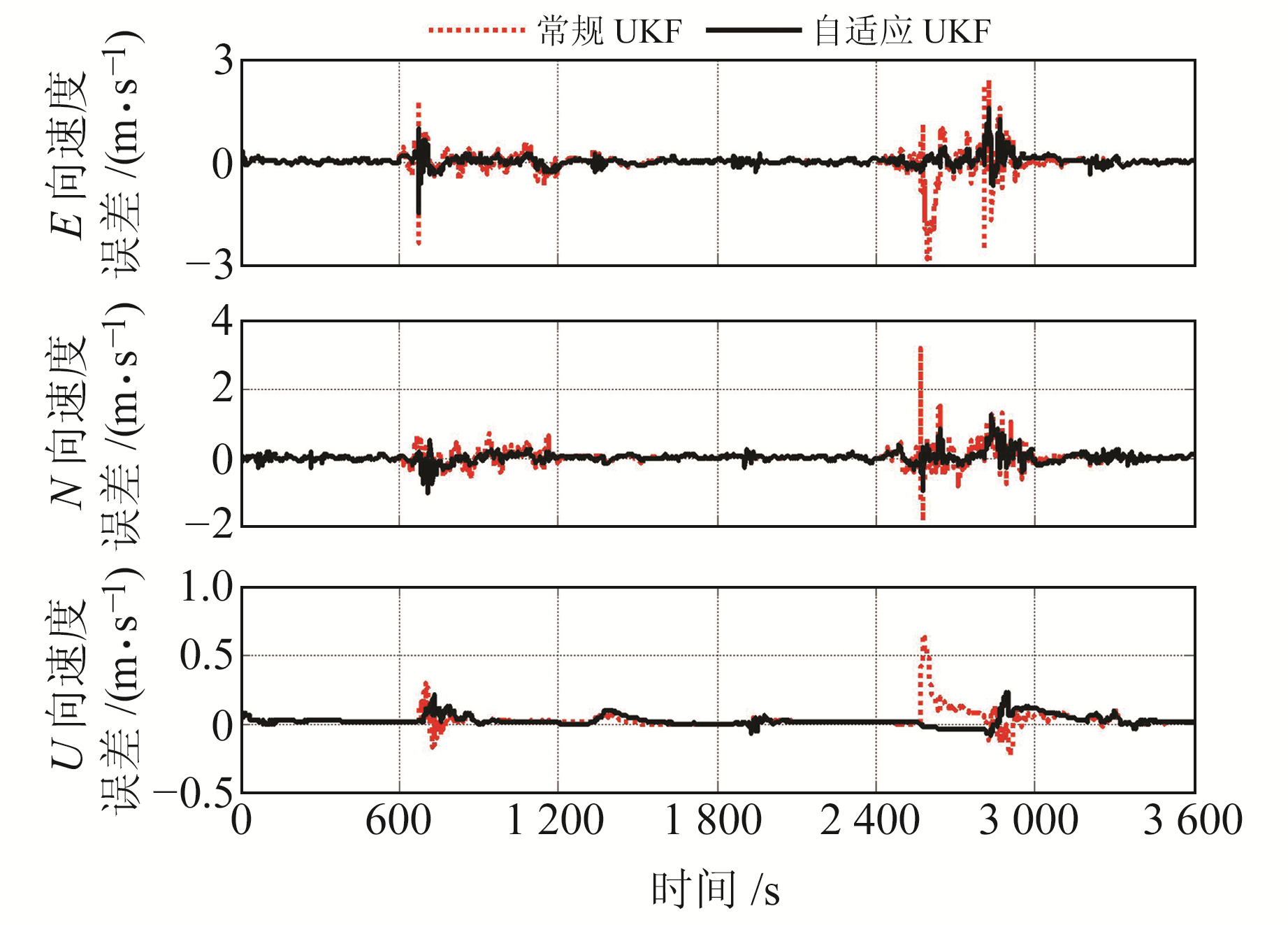
图 2 速度误差 Fig. 2 Velocity error |

|
图 3 姿态误差 Fig. 3 Attitude error |
由图 1~3可见,在0~600 s内,GNSS量测噪声的实际均方差与正常情况完全一致,此时常规UKF算法与本文算法得到的各导航参数误差完全相同;而在GNSS量测噪声的均方差发生突变与缓变的2个阶段内,本文算法得到的各导航参数误差明显小于常规UKF算法。
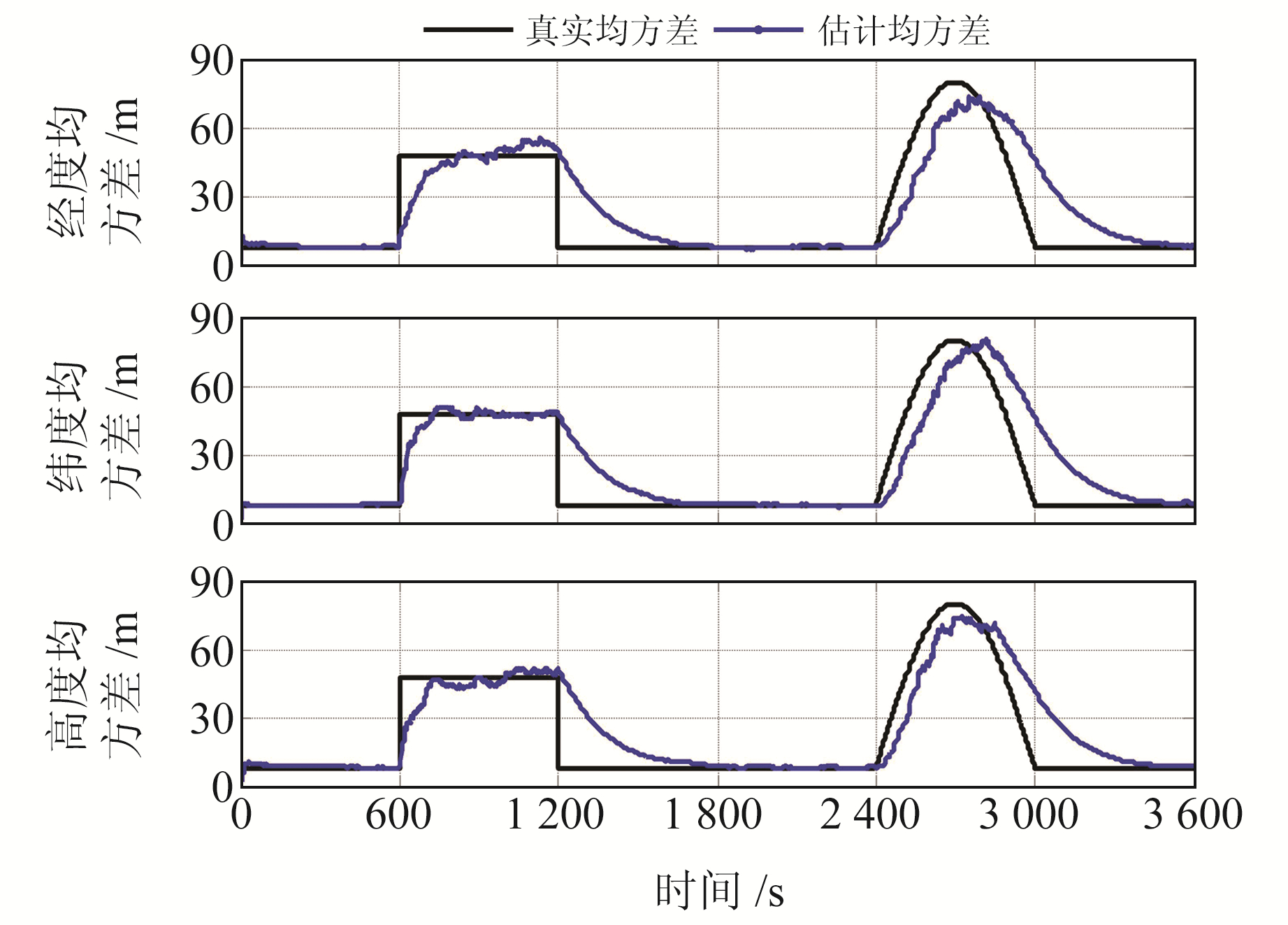
为了评估本文算法对GNSS量测噪声均方差变化的跟踪能力,绘制本文算法对GNSS位置量测噪声均方差的跟踪图(图 4)。由图可见,本文算法能实时跟踪并反映出GNSS位置量测噪声均方差的变化情况,但有一定的滞后性。对于速度量测噪声均方差,本文算法得到的跟踪图与图 4相似。
|
图 4 GNSS位置均方差跟踪图 Fig. 4 Tracking figures of MSE of GNSS position |
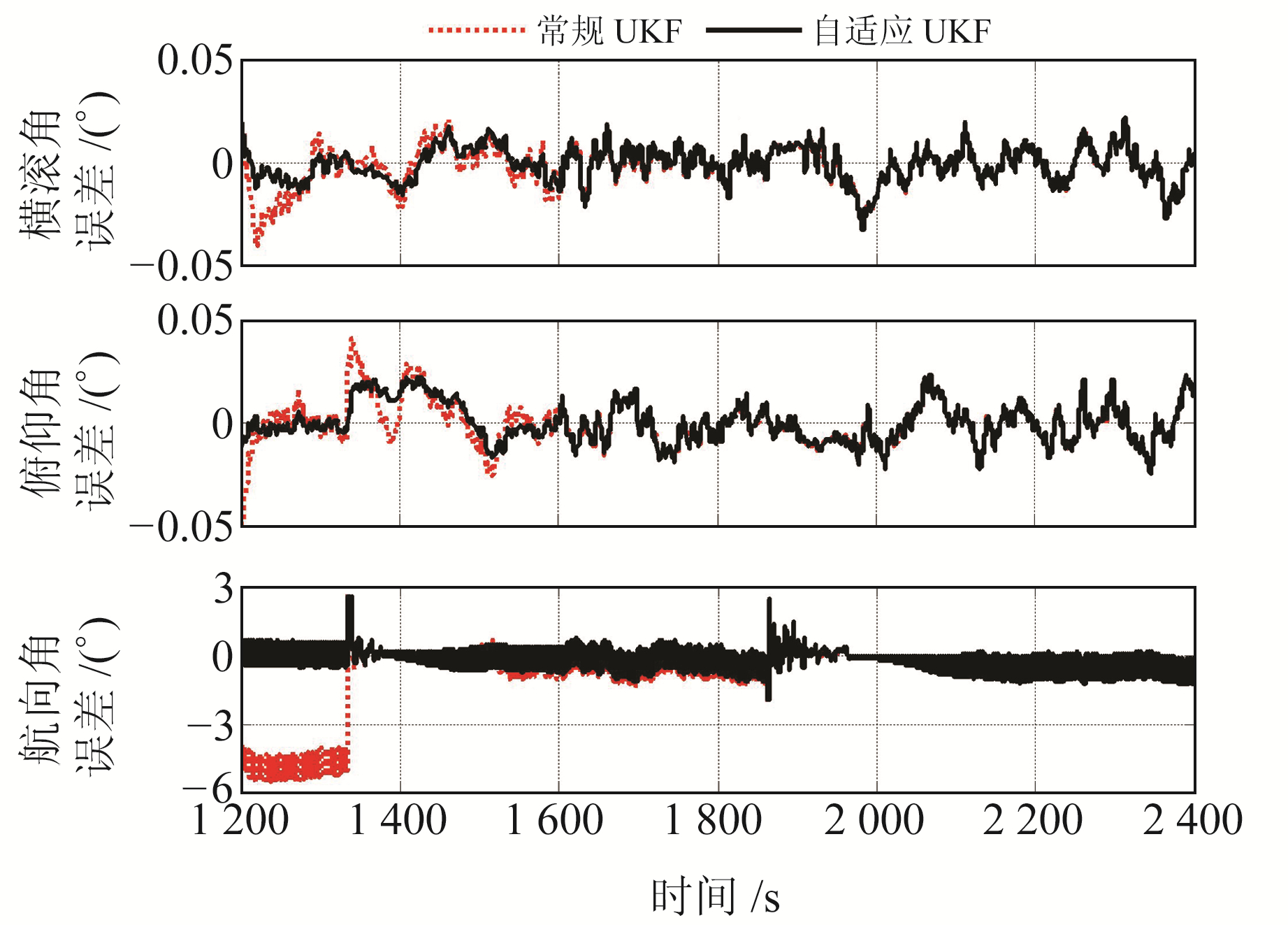
为了详细说明GNSS量测噪声均方差变化终止后各导航参数的误差变化情况,列出不同时段内部分导航参数的误差曲线(图 5、6)。
|
图 5 1 200~2 400 s期间姿态误差曲线 Fig. 5 Attitude error curve from 1 200 s to 2 400 s |
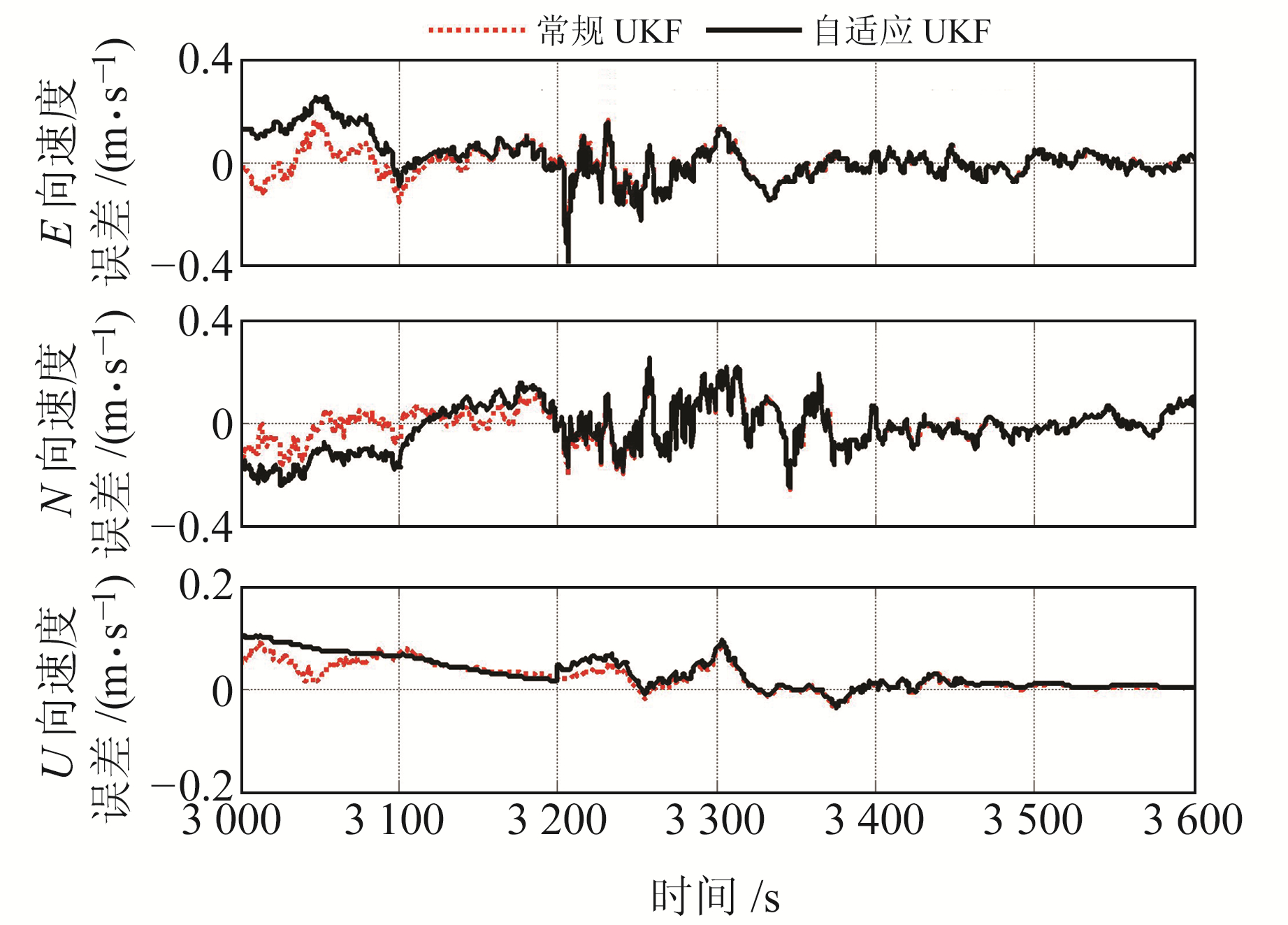
|
图 6 3 000~3 600 s期间速度误差曲线 Fig. 6 Velocity error curve from 3 000 s to 3 600 s |
由图 5、6可见,本文算法能够实时跟踪GNSS量测噪声均方差的变化,当GNSS量测噪声均方差变化终止并回归正常状态后,本文算法得到的各导航参数也能够快速收敛至正常状态,并最终达到与常规UKF算法相同的滤波精度。由图 5的姿态误差曲线可见,当GNSS量测噪声均方差突变终止后,本文算法收敛速度较快。由图 6的速度误差曲线可见,当GNSS量测噪声均方差缓变终止后,常规UKF算法收敛速度较快。综上所述,整体而言,本文算法的自适应性较强且性能高于常规UKF算法。
4 结语在GNSS/SINS组合导航系统常规UKF算法的时间更新及量测更新过程中引入变分贝叶斯估计理论,提出GNSS/SINS组合导航系统的自适应UKF算法以提高系统在量测噪声统计特性发生变化时的滤波精度。仿真结果表明,该算法能有效跟踪量测噪声均方差的变化,提高组合导航系统的滤波精度。当量测噪声均方差变化终止时,该算法也能快速收敛至正常状态。相比于常规UKF算法,本文算法优势明显。
由于本文自适应滤波算法涉及到3个参数,因此3个参数对量测噪声均方差估计精度的影响规律是下一步的研究重点。
| [1] |
洪志强. 无迹卡尔曼滤波的改进算法及其在GPS/INS组合导航中的应用研究[D]. 抚州: 东华理工大学, 2019 (Hong Zhiqiang. Improved Algorithm of Unscented Kalman Filter and Its Application in GPS/INS Integrated Navigation[D]. Fuzhou: East China University of Science and Technology, 2019)
(  0) 0) |
| [2] |
田甜. 基于自适应UKF的SINS/GPS紧组合导航系统的应用研究[D]. 青岛: 青岛科技大学, 2019 (Tian Tian. Study on the Application of Based on Unscented Kalman Filter of SINS/GPS Tight Coupling Integrated Navigation System[D]. Qingdao: Qingdao University of Science and Technology, 2019)
(  0) 0) |
| [3] |
陈光武, 程鉴皓, 杨菊花, 等. 基于改进神经网络增强自适应UKF的组合导航系统[J]. 电子与信息学报, 2019, 41(7): 1 766-1 773 (Chen Guangwu, Cheng Jianhao, Yang Juhua, et al. Improved Neural Network Enhanced Navigation System of Adaptive Unsented Kalman Filter[J]. Journal of Electronics and Information Technology, 2019, 41(7): 1 766-1 773)
(  0) 0) |
| [4] |
吴涛, 戴卿, 匡秀梅, 等. 组合导航数据融合自适应UKF算法研究[J]. 西安航空学院学报, 2020, 38(3): 71-77 (Wu Tao, Dai Qing, Kuang Xiumei, et al. A Novel Efficient Adaptive UKF Algorithm for Integrate Navigation Data Fusion Processes[J]. Journal of Xi'an Aeronautical University, 2020, 38(3): 71-77)
(  0) 0) |
| [5] |
马晓杰, 林雪原, 孙巧妍, 等. 一种改进的UKF滤波算法在BDS/SINS组合导航系统中的应用研究[J]. 大地测量与地球动力学, 2021, 41(4): 351-356 (Ma Xiaojie, Lin Xueyuan, Sun Qiaoyan, et al. Improved UKF Algorithm for BDS/SINS Integrated Navigation System[J]. Journal of Geodesy and Geodynamics, 2021, 41(4): 351-356)
(  0) 0) |
| [6] |
付梦印, 邓志红, 张继伟. Kalman滤波理论及其在组合导航系统中的应用[M]. 北京: 科学出版社, 2003 (Fu Mengyin, Deng Zhihong, Zhang Jiwei. Kalman Filtering Theory and Its Application in Integrated Navigation System[M]. Beijing: Science Press, 2003)
(  0) 0) |
| [7] |
Vrettas M D, Cornford D, Opper M. Estimating Parameters in Stochastic Systems: A Variational Bayesian Approach[J]. Physica D: Nonlinear Phenomena, 2011, 240(23): 1 877-1 900 DOI:10.1016/j.physd.2011.08.013
(  0) 0) |
| [8] |
Lim K L, Wang H. MAP Approximation to the Variational Bayes Gaussian Mixture Model and Application[J]. Soft Computing, 2018, 22(10): 3 287-3 299 DOI:10.1007/s00500-017-2565-z
(  0) 0) |
| [9] |
Davari N, Gholami A. Variational Bayesian Adaptive Kalman Filter for Asynchronous Multirate Multi-Sensor Integrated Navigation System[J]. Ocean Engineering, 2019, 174: 108-116 DOI:10.1016/j.oceaneng.2019.01.012
(  0) 0) |
| [10] |
Sarkka S, Nummenmaa A. Recursive Noise Adaptive Kalman Filtering by Variational Bayesian Approximations[J]. IEEE Transactions on Automatic Control, 2009, 54(3): 596-600
(  0) 0) |
2. Naval Aeronautical University, Yantai 264001, China;
3. Shandong Donghai Thermal Power Co Ltd, Donghai Industrial Park, Longkou 265713, China
 2023, Vol. 43
2023, Vol. 43


