2. 东华理工大学测绘工程学院,南昌市广兰大道418号,33001;
3. 自然资源部环鄱阳湖区域矿山环境监测与治理重点实验室,南昌市广兰大道418号,330013
传统SBAS-InSAR技术通过同时处理覆盖研究区一定时间段内的所有SAR影像来获取该时段内的地表形变结果[1]。若新增SAR影像,则需将所有影像重新处理以获取新增SAR影像时刻的地表形变信息,难以满足高效、持续、动态的监测要求。为解决这一难题,许多学者提出各种解决办法[2-5],取得了较好效果。本文提出渐进式SBAS-InSAR技术,即在传统SBAS-InSAR技术获取的解算结果基础上,将较新的少部分已有SAR影像结合新增SAR影像进行增量解算,以得到所有影像获取时刻的地表形变结果,并在绝大部分已有数据形变参数和已有数据参数矩阵不变的情况下,实现高效、持续、精确的地表形变监测。以2019-06~2020-04覆盖北京平原地区的26景Sentinel-1A SAR影像为例,利用渐进式SBAS-InSAR进行实验,并从精度和计算效率2个方面与SBAS-InSAR地表形变监测结果进行对比。
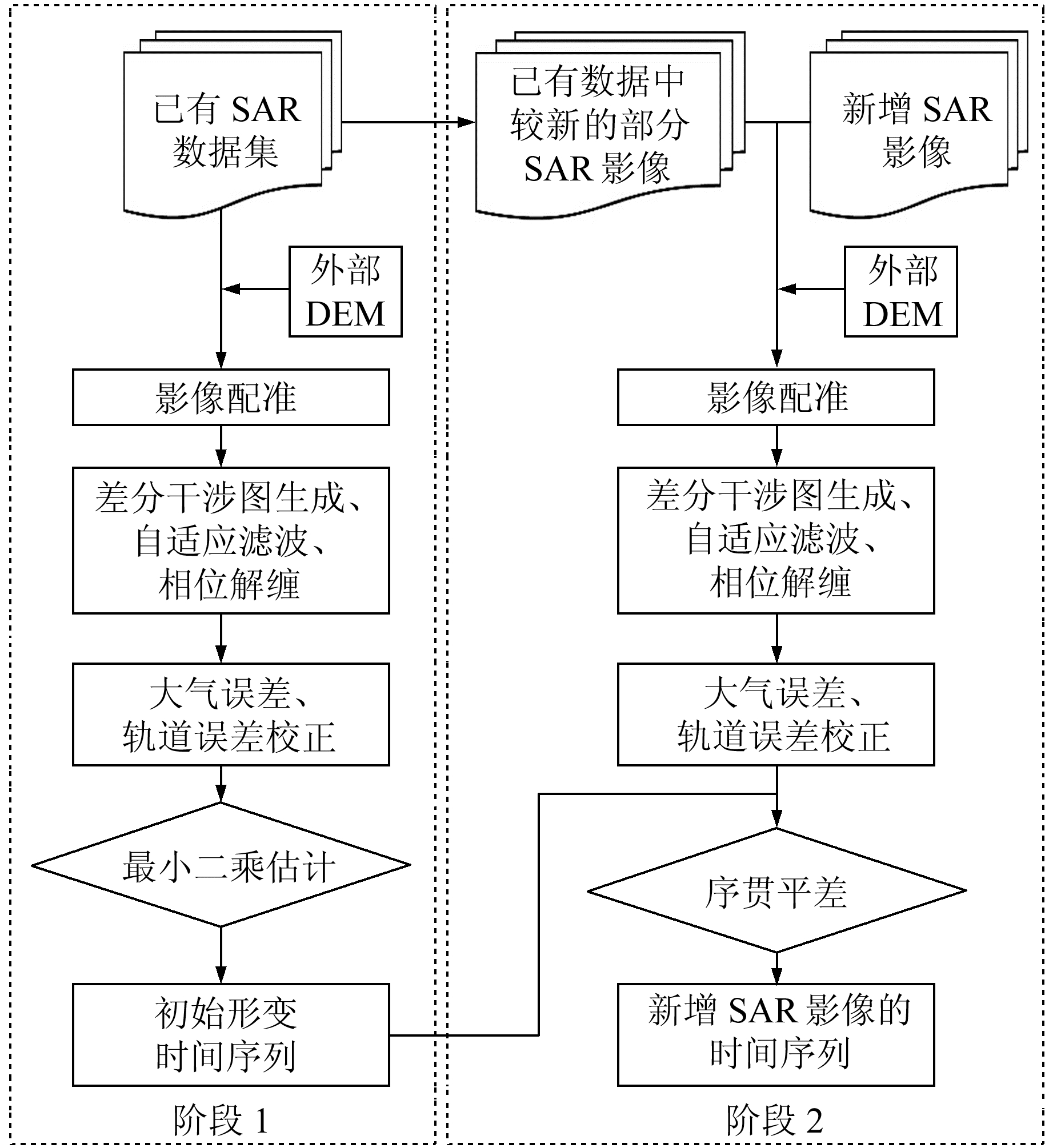
1 渐进式SBAS-InSAR原理如图 1所示,渐进式SBAS-InSAR分为2个阶段:1)利用SBAS-InSAR求解已有SAR影像数据集的地表形变时间序列(阶段1);2)以阶段1获取的已有SAR影像数据集的形变参数为基础,结合已有SAR影像数据集中较新部分SAR影像与新增SAR影像进行高相干点选取、相位解缠、大气延迟、轨道误差和高程误差纠正,获取新增干涉对的解缠相位,并以此作为观测值进行序贯平差解算,得到更新后全部影像时刻的地表形变时间序列(阶段2)。
|
图 1 渐进式SBAS-InSAR流程 Fig. 1 Flow chart of progressive SBAS-InSAR |
首先,采用SBAS-InSAR对已有SAR影像数据集进行处理,获取对应地表形变时间序列结果;在此基础上,将已有SAR影像数据集中较新的部分(tn1时刻以后,共包含n景)SAR影像与新增SAR影像数据组合进行差分干涉处理,若研究区内新增N1景SAR影像(对应时间段为tN+1-tN+N1),在相同时空基线阈值下形成M1个差分干涉对,以去除大气延迟、轨道误差后的解缠相位作为观测值,则可构建如下观测方程:
| $ \underbrace{\left[\begin{array}{cccc} t_1-t_0 & 0 & \cdots & 0 \\ t_1-t_0 & t_2-t_1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & t_{n_1-1}-t_{n_1-2} \end{array}\right]}_\boldsymbol{A} \underbrace{\left[\begin{array}{c} v_1 \\ v_2 \\ \vdots \\ v_{t_{n_1-1}} \end{array}\right]}_{\boldsymbol{X}_1}+\underbrace{\left[\begin{array}{cccc} t_{n_1}-t_{n_1-1} & 0 & \cdots & 0 \\ t_{n_1}-t_{n_1-1} & t_{n_1+1}-t_{n_1} & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & t_N-t_{N-1} \end{array}\right]}_{\boldsymbol{B}_1} \underbrace{\left[\begin{array}{c} v_{t_{n_1}} \\ v_{t_{n_1+1}} \\ \vdots \\ v_{t_N} \end{array}\right]}_{\boldsymbol{X}_2}=\underbrace{\left[\begin{array}{c} \delta \varphi_1 \\ \delta \varphi_2 \\ \vdots \\ \delta \varphi_M \end{array}\right]}_{\boldsymbol{L}_1} $ | (1) |
| $ \begin{array}{c} \underbrace {\left[ {\begin{array}{*{20}{c}} 0&0& \cdots &0\\ 0&{{t_{{n_1} + 1}} - {t_{{n_1}}}}& \cdots &0\\ \vdots & \vdots & \vdots & \vdots \\ 0&0& \cdots &{{t_N} - {t_{N - 1}}} \end{array}} \right]}_{{\mathit{\boldsymbol{B}}_2}}\underbrace {\left[ {\begin{array}{*{20}{c}} {{v_{{t_{{n_1}}}}}}\\ {{v_{{t_{{n_1} + 1}}}}}\\ \vdots \\ {{v_{{t_N}}}} \end{array}} \right]}_{{\mathit{\boldsymbol{X}}_2}} + \\ \underbrace {\left[ {\begin{array}{*{20}{c}} {{t_{N + 1}} - {t_N}}&0& \cdots &0\\ {{t_{N + 1}} - {t_N}}&{{t_{N + 2}} - {t_{N + 1}}}& \cdots &0\\ \vdots & \vdots & \vdots & \vdots \\ 0&0& \cdots &{{t_{N + {N_1}}} - {t_{N + {N_1} - 1}}} \end{array}} \right]}_\mathit{\boldsymbol{C}} \times \\ \underbrace {\left[ {\begin{array}{*{20}{c}} {{v_{{t_{N + 1}}}}}\\ {{v_{{t_{N + 2}}}}}\\ \vdots \\ {{v_{{t_{N + {N_1}}}}}} \end{array}} \right]}_{{\mathit{\boldsymbol{X}}_3}} = \underbrace {\left[ {\begin{array}{*{20}{c}} {\delta {\varphi _{M + 1}}}\\ {\delta {\varphi _{M + 2}}}\\ \vdots \\ {\delta {\varphi _{M + {M_1}}}} \end{array}} \right]}_{{\mathit{\boldsymbol{L}}_2}} \end{array} $ | (2) |
式中,A、B1、B2、C分别为系数矩阵,由0或相邻两景SAR影像的时间间隔构成(如12、24等);X1、X2、X3为未知参数,由相邻两景SAR数据间的形变相位速率构成。
若将已有SAR数据和新增SAR数据的解算认为是2次平差过程,则从形式上看,式(1)和式(2)与测量平差中的序贯平差方法一致,故可将SBAS-InSAR求解已有SAR影像集的形变相位速率视为序贯平差的阶段1,将已有SAR影像集中较新的部分SAR影像集与新增SAR影像的形变相位速率视为序贯平差的阶段2,即可利用序贯平差思想更新所有SAR影像获取时刻的形变相位速率。
对于X1和X2,已通过SBAS-InSAR求解得到其初始结果X′1和X′2:
| $ \boldsymbol{X}_1=\boldsymbol{X}_1^{\prime}+\delta \boldsymbol{X}_1, \boldsymbol{X}_2=\boldsymbol{X}_2^{\prime}+\delta \boldsymbol{X}_2 $ | (3) |
式中,δX1、δX2分别为X1、X2的改正数。
假设各观测时刻获取的SAR影像相互独立,且权矩阵为单位矩阵,利用序贯平差思想可得[6]:
| $ \begin{aligned} & {\left[\begin{array}{c} \delta \boldsymbol{X}_2 \\ \boldsymbol{X}_3 \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{Q}+\boldsymbol{B}_2^{\mathrm{T}} \boldsymbol{B}_2 & \boldsymbol{B}_2^{\mathrm{T}} \boldsymbol{C} \\ \boldsymbol{C}^{\mathrm{T}} \boldsymbol{B}_2 & \boldsymbol{C}^{\mathrm{T}} \boldsymbol{C} \end{array}\right]^{-1}\left[\begin{array}{c} \boldsymbol{B}_2^{\mathrm{T}} \boldsymbol{L}_2^{\prime} \\ \boldsymbol{C}^{\mathrm{T}} \boldsymbol{L}_2^{\prime} \end{array}\right]} \\ & \boldsymbol{Q}=\boldsymbol{B}_1^{\mathrm{T}} \boldsymbol{B}_1-\boldsymbol{B}_1^{\mathrm{T}} \boldsymbol{A}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{B}_1 \\ & \delta \boldsymbol{X}_1=-\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{B}_1 \delta \boldsymbol{X}_2 \\ & \boldsymbol{L}_2^{\prime}=\boldsymbol{L}_2-\boldsymbol{B}_2 \boldsymbol{X}_2^{\prime} \end{aligned} $ | (4) |
式中,Q为SBAS-InSAR求解中存储的协方差矩阵。
综合式(3)和式(4)即可得到新增N1景SAR影像后各相邻SAR影像获取时刻的形变相位速率,在此基础上,通过数值积分可得到更新后的形变时间序列。
2 实验验证采用模拟数据和真实数据,从解算精度和计算效率2个方面验证渐进式SBAS-InSAR的可行性与有效性。
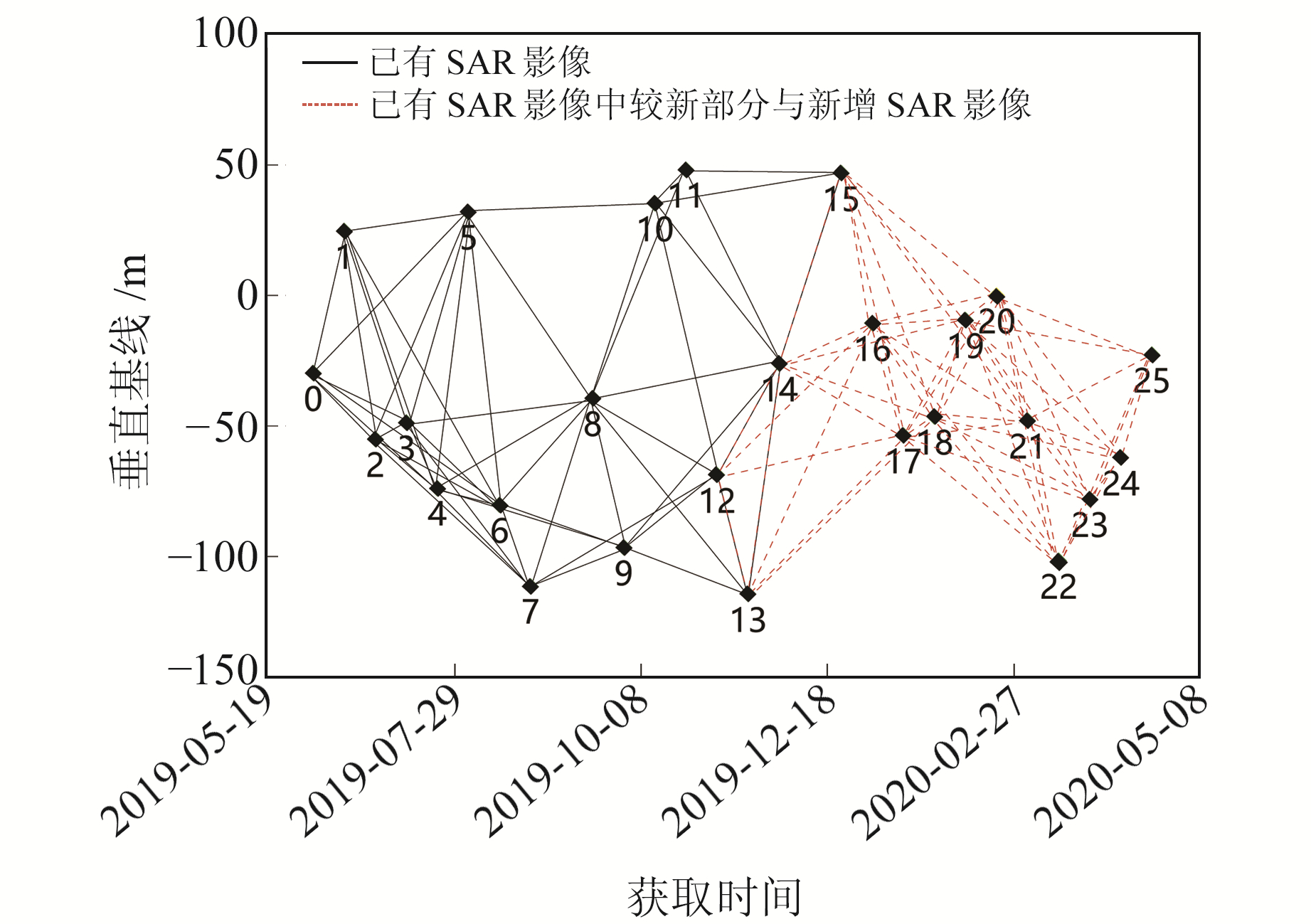
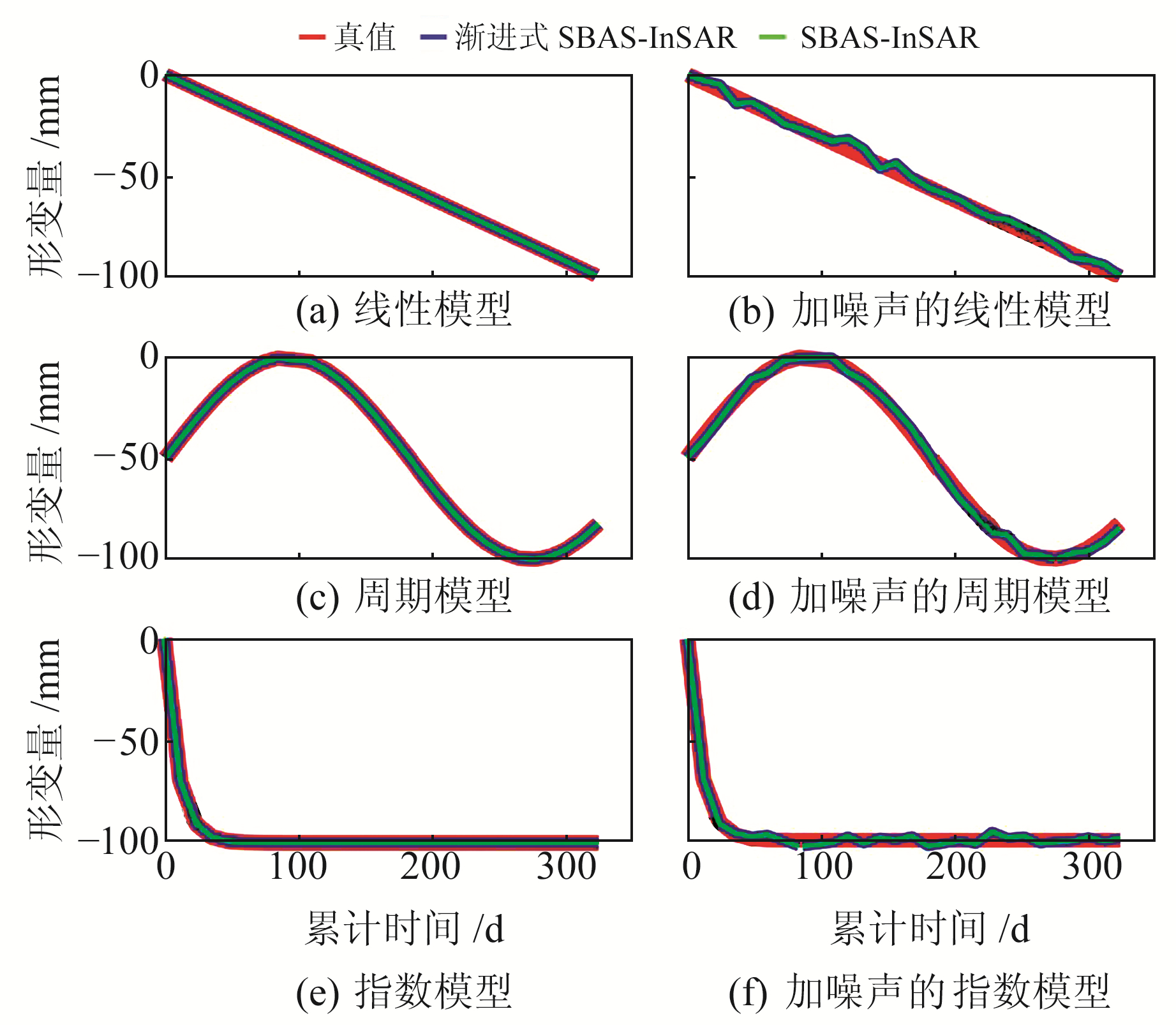
2.1 模拟数据实验以1个像元为例模拟3种形变模型,即线性模型、周期模型和指数模型。模拟时选用覆盖北京平原地区的26景SAR影像参数,假设前16景(2019-06-03~12-24)SAR影像为存档SAR影像,第17~26景(2020-01-05~04-22)为新增SAR影像,设置时空基线阈值为60 d与120 m,共形成112个干涉对,其时空基线组成如图 2所示。此外,对3种形变模型分别添加均值为0 mm、方差为1.5 mm的高斯噪声,并进行100次蒙特卡洛随机模拟。分别利用SBAS-InSAR与渐进式SBAS-InSAR求解参数,得到地表形变时间序列,图 3为添加高斯噪声与未添加噪声情况下3种形变模型对应的模拟真值、SBAS-InSAR和渐进式SBAS-InSAR获取的形变时间序列。结果显示,2种技术获取的未知参数的标准差小于1 mm,表明渐进式SBAS-InSAR与SBAS-InSAR获得的参数精度相当。
|
图 2 已有SAR影像和已有SAR影像中较新部分SAR影像与新增SAR影像的时空基线分布 Fig. 2 Spatiotemporal baseline distribution of existing SAR images and newer SAR images in existing SAR images and new SAR images |
|
图 3 3种形变模型下SBAS-InSAR和渐进式SBAS-InSAR的形变时间序列 Fig. 3 Deformation time series derived from SBAS-InSAR and progressive SBAS-InSAR with three different deformation models |
选取北京通州区、朝阳区等地面沉降严重的地区进行研究,覆盖范围约38 km×42 km(图 4)。研究区位于第四系凹陷区,受地下水水位降低及地下水不断超采的影响存在明显的地表形变[7]。利用SBAS-InSAR和渐进式SBAS-InSAR处理与分析2019-06~2020-04共26景C波段的升轨Sentinel-1A SAR影像。为去除地形和轨道误差对干涉相位的影响,同时使用欧空局提供的30 m分辨率SRTM1-DEM高程数据和精密轨道数据(定位精度优于5 cm)进行校正。

|
图 4 研究区位置 Fig. 4 Location of the study area |
假设已有SAR影像集包含16景(2019-06-03~12-24)SAR影像,设置时空基线阈值为60 d与120 m,得到54对干涉对(图 2黑色实线)。影像配准和重采样后,结合外部DEM及精密轨道数据去除地形及轨道误差,对高程误差进行建模和估算以将其扣除,采用时空域的高低通滤波去除大气延迟效应,最后利用SBAS-InSAR求解出相应时刻的形变相位值。在此基础上,逐渐新增1~10景(2020-01-05~04-22)SAR影像,并将已有SAR影像中较新部分SAR影像纳入新增SAR影像中(图 2红色虚线),采用渐进式SBAS-InSAR进行处理,获取全部影像的形变时间序列。
为分析渐进式SBAS-InSAR的精度与时间效率,同时利用SBAS-InSAR对所有SAR影像进行解算,获取其地表形变时间序列和所需时间。
3 实验结果与分析 3.1 监测结果分析 3.1.1 形变速率结果分析图 5为新增10景SAR影像时SBAS-InSAR与渐进式SBAS-InSAR分别反演得到的2019-06~2020-04北京平原地区沿雷达视线向的地表形变速率场。可以看出,研究区形变空间分布不均匀,主要集中在朝阳区与通州区交界地带,包括金盏乡、楼梓庄乡、徐辛庄镇、黑庄户乡、台湖乡、梨园、平西府镇、燕丹乡和李桥镇等地,最大形变速率约为-110 mm/a。结合图 5(a)和5(b)可知,无论是形变量级还是形变分布区域,2种技术反演得到的形变结果均具有较高的一致性。

|
图 5 年平均形变速率 Fig. 5 Annual average deformation rate |
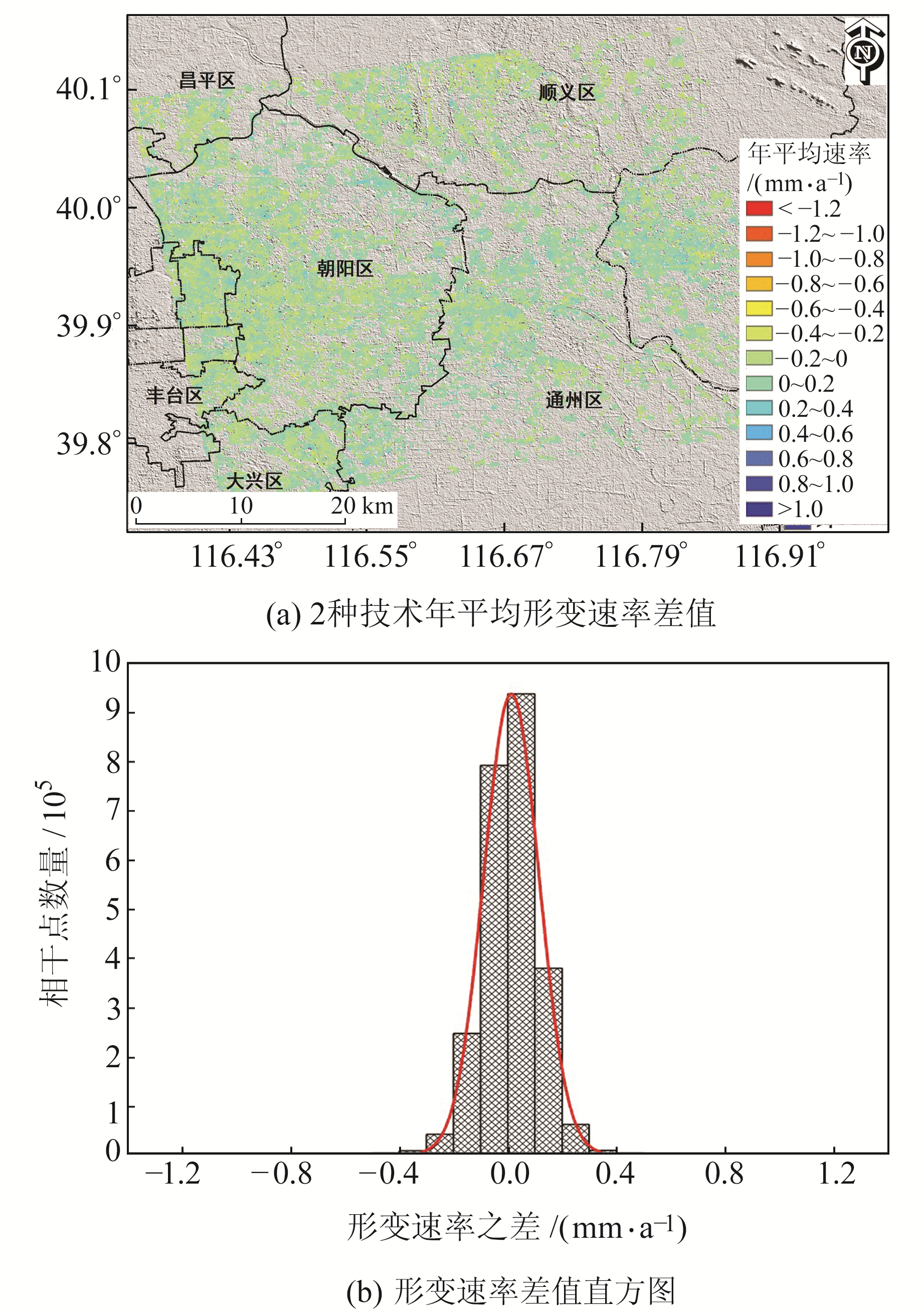
为更直观地显示本文方法的可靠性,对渐进式SBAS-InSAR与SBAS-InSAR获取的年平均形变速率作差(图 6)。可以看出,二者差值的平均值和标准差分别为0.01 mm/a和0.1 mm/a,且2种技术获取的形变速率之差的绝对值基本小于0.5 mm/a,最大不超过1.5 mm/a,表明2种技术获取的形变结果具有较高的一致性。
|
图 6 渐进式SBAS-InSAR与SBAS-InSAR年平均形变速率对比 Fig. 6 Difference of annual average deformation rate between progressive SBAS-InSAR and SBAS-InSAR |
图 7为利用渐进式SBAS-InSAR获取的形变时间序列。可以看出:1)2019-06~2020-04研究区主要形变位于朝阳区与通州区的交界处,最大累积形变量约为-106 mm。2)研究区西部及东北部表现为轻微的地面抬升现象。3)随着监测时间的累积,金盏乡、楼梓庄乡、徐辛庄镇、黑庄户乡、台湖乡和梨园形变区的累积形变量不断增加,形变范围亦不断扩大;平西府镇、燕丹乡和李桥镇形变区的累积形变量有所增加,形变范围基本不变。

|
图 7 渐进式SBAS-InSAR的形变时间序列 Fig. 7 Deformation time series of progressive SBAS-InSAR |
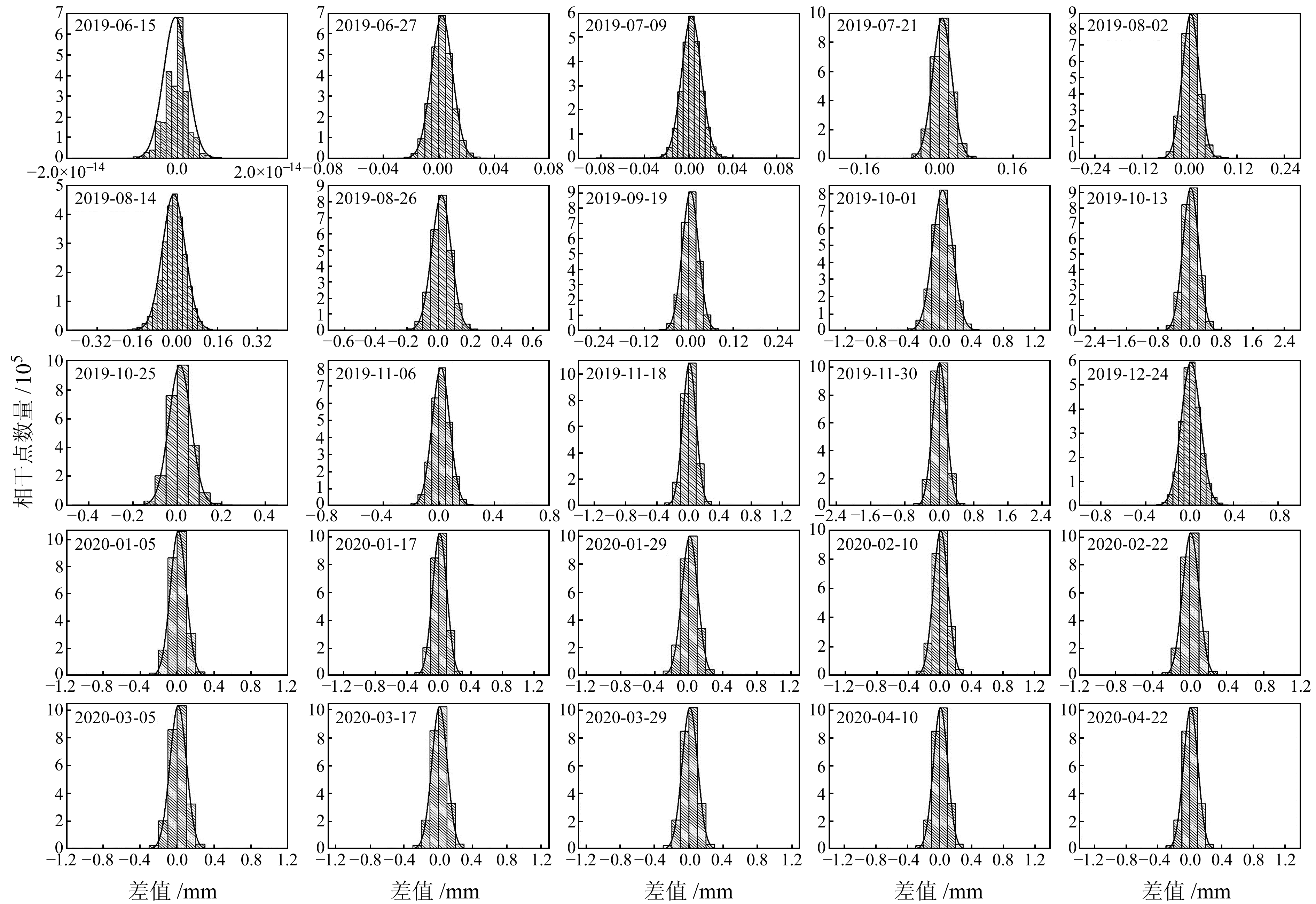
图 8为渐进式SBAS-InSAR与SBAS-InSAR获取的累积形变量之间的差异直方图。可以看出,形变差异绝对值基本小于1 mm,最大形变差异绝对值不超过3 mm,表明渐进式SBAS-InSAR获取的累积时间序列与SBAS-InSAR的监测结果具有较好的一致性。
|
图 8 SBAS-InSAR与渐进式SBAS-InSAR时间序列累积形变量之差直方图 Fig. 8 Histograms of the difference of cumulative deformation time series between SBAS-InSAR and progressive SBAS-InSAR |
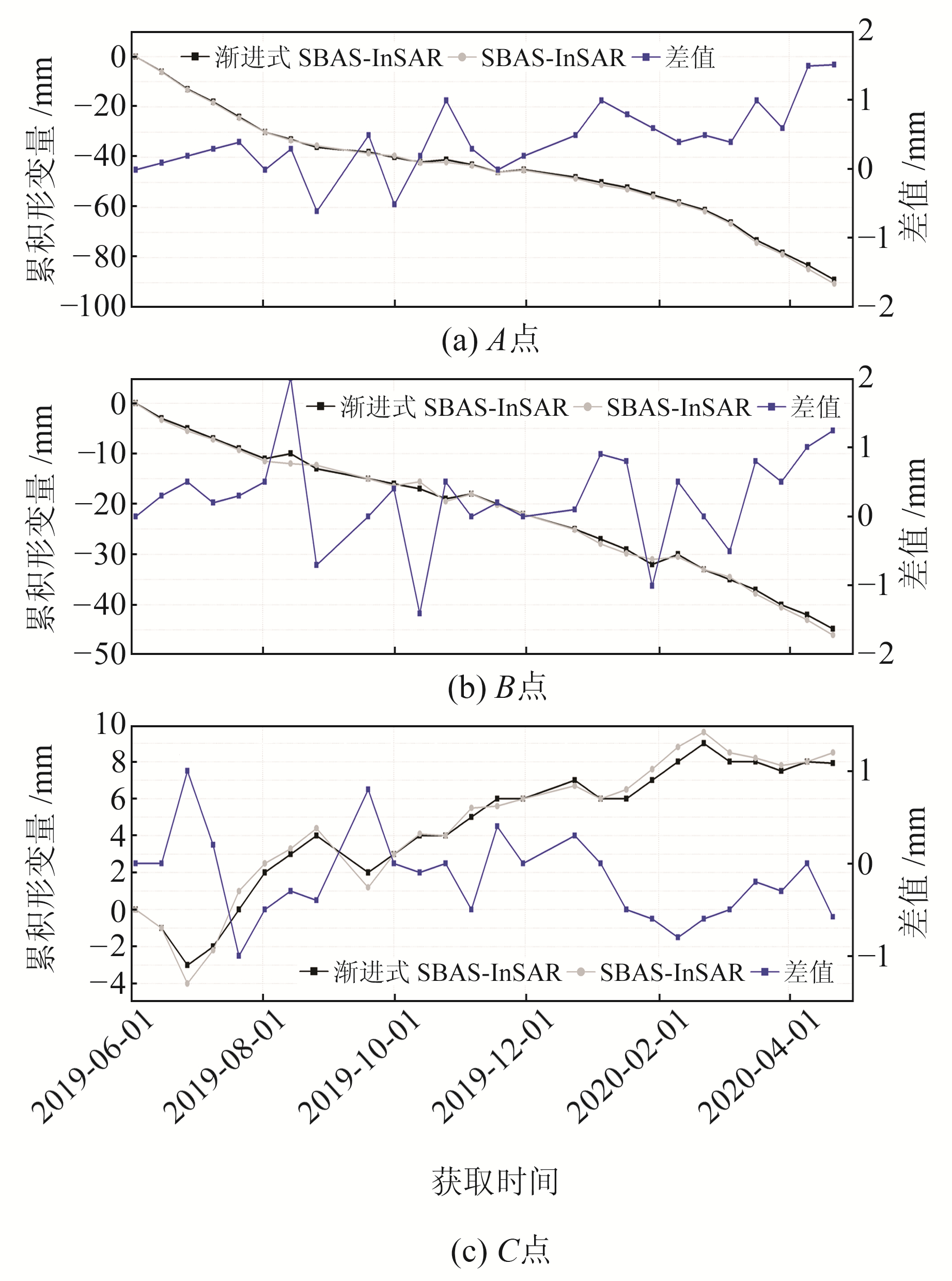
此外,选取3个特征点(A点位于快速形变区、B点位于较快速形变区、C点位于地表稳定区,位置见图 5)对2种技术获取的时间序列进行对比分析,结果如图 9所示。可以看出,3个特征点的累积形变量差值均小于2 mm,可忽略不计,表明渐进式SBAS-InSAR与SBAS-InSAR获取的累积形变结果高度吻合。
|
图 9 3个特征点的形变时间序列 Fig. 9 Deformation time series of three feature points |
为便于对比分析,采用相同的准则选取渐进式SBAS-InSAR与SBAS-InSAR的高相干点目标,故2种技术处理的高相干点数目相同。以任意一个高相干点为例,分析渐进式SBAS-InSAR与SBAS-InSAR求解所需时间。对于单个高相干点,在相同时空基线阈值下,当新增N1景SAR影像后,SBAS-InSAR需要对M+M1(M为已有数据形成的干涉对数量,M1为新增SAR影像和已有SAR影像中较新部分形成的干涉对数量)幅干涉对去除地形、纠正大气效应和轨道误差等,而渐进式SBAS-InSAR只需对M1幅干涉图进行处理。从理论上讲,当已有SAR影像很多而新增SAR影像不多时,M1≪M,因此渐进式SBAS-InSAR比SBAS-InSAR具有更高的效率。
求解形变相位值时,已知形变相位值的求解主要涉及线性方程组(式(2)和式(3))的最小二乘法计算,计算复杂度与待求解未知数的个数有关,未知数越多,计算越复杂。SBAS-InSAR需要求解N+N1景SAR影像对应的地表形变速率增量,而渐进式SBAS-InSAR则只针对新增的N1景SAR影像对应的形变速率增量进行解算,并更新已有N景SAR影像对应的地表形变速率增量,计算复杂度明显降低,计算所需存储空间更小,时效性更高。
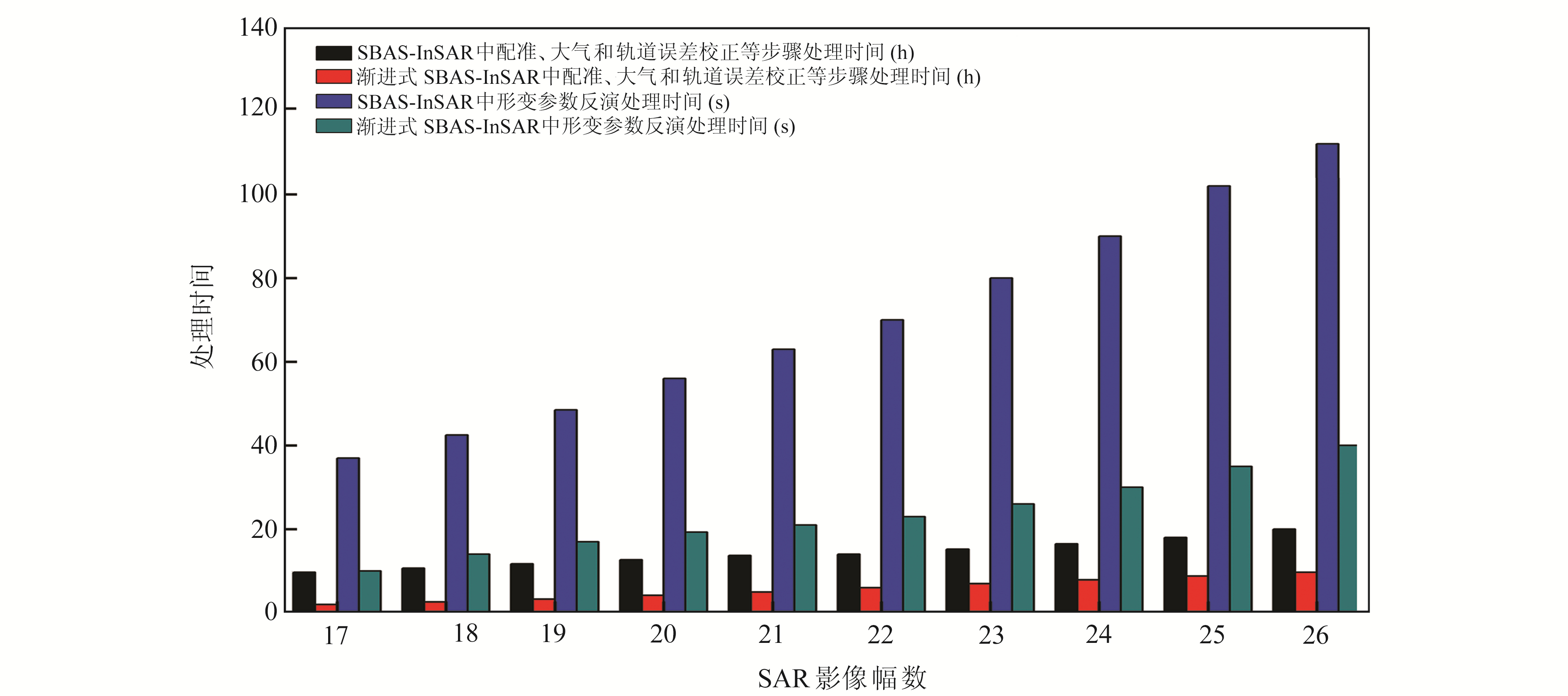
图 10为在16景SAR影像的基础上逐渐新增1~10景SAR影像分别进行渐进式SBAS-InSAR与SBAS-InSAR处理的时间成本。数据处理的计算机配置为Intel Core i7(2.60 GHz),内存32 G。从图 10可以看出,执行配准、大气和轨道误差校正等步骤时,SBAS-InSAR的处理时间约为渐进式SBAS-InSAR的2~5倍。在形变参数反演解算阶段,渐进式SBAS-InSAR一方面要引入和使用SBAS-InSAR对已有SAR影像求解的协方差矩阵,另外还要对已解算的结果进行修正与更新,故无法像前一阶段那样明显地缩短运行时间。但随着SAR影像逐渐增加,渐进式SBAS-InSAR的时间效率相较于SBAS-InSAR仍具有明显的改进,在增加第10景SAR影像时,其形变解算时间提高约66%。综上,在处理随时间动态增加的SAR影像时,渐进式SBAS-InSAR明显具有更高的时间效率。
|
图 10 渐进式SBAS-InSAR与SBAS-InSAR所需时间对比 Fig. 10 Comparison of data processing time between progressive SBAS-InSAR and SBAS-InSAR |
本文分别采用模拟数据和真实数据对渐进式SBAS-InSAR和SBAS-InSAR进行对比分析,得出如下结论:
1) 在添加高斯噪声与未添加噪声的情况下,3种不同形变模型的计算结果显示,2种技术获取的未知参数的标准差均小于1 mm,表明渐进式SBAS-InSAR与SBAS-InSAR解算精度相近。
2) 利用2019-06~2020-04的26景Sentinel-1A数据对北京平原地区的地表形变进行监测与分析,发现2种技术反演得到的地表形变速率在量级和形变区域分布上均具有较高的一致性,差值的绝对值基本小于0.5 mm/a,最大不超过1.5 mm/a。
3) 针对随时间动态增加的SAR影像,渐进式SBAS-InSAR获取形变结果所需时间仅是SBAS-InSAR的1/2~1/5,可大幅提高地表形变的计算效率。
| [1] |
Berardino P, Fornaro G, Lanari R, et al. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2 375-2 383 DOI:10.1109/TGRS.2002.803792
(  0) 0) |
| [2] |
Ansari H, Zan F, Bamler R. Sequential Estimator: Toward Efficient InSAR Time Series Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5 637-5 652 DOI:10.1109/TGRS.2017.2711037
(  0) 0) |
| [3] |
胡俊, 刘计洪, 李志伟, 等. 一种基于序贯平差的InSAR时序地表形变监测方法: CN109061641A[P]. 2018-12-21 (Hu Jun, Liu Jihong, Li Zhiwei, et al. InSAR Time Sequence Surface Deformation Monitoring Method Based on Sequential Adjustment: CN109061641A[P]. 2018-12-21)
(  0) 0) |
| [4] |
Wang B H, Zhao C Y, Zhang Q, et al. Sequential Estimation of Dynamic Deformation Parameters for SBAS-InSAR[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(6): 1 017-1 021 DOI:10.1109/LGRS.2019.2938330
(  0) 0) |
| [5] |
王辉, 曾琪明, 焦健, 等. 结合序贯平差方法监测地表形变的InSAR时序分析技术[J]. 北京大学学报: 自然科学版, 2021, 57(2): 241-249 (Wang Hui, Zeng Qiming, Jiao Jian, et al. InSAR Time Series Analysis Technique Combined with Sequential Adjustment Method for Monitoring of Surface Deformation[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2021, 57(2): 241-249)
(  0) 0) |
| [6] |
隋立芬, 刘雁雨, 王威. 自适应序贯平差及其应用[J]. 武汉大学学报: 信息科学版, 2007, 32(1): 51-54 (Sui Lifen, Liu Yanyu, Wang Wei. Adaptive Sequential Adjustment and Its Application[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 51-54)
(  0) 0) |
| [7] |
贾三满, 王海刚, 赵守生, 等. 北京地面沉降机理研究初探[J]. 城市地质, 2007, 2(1): 20-26 (Jia Sanman, Wang Haigang, Zhao Shousheng, et al. A Tentative Study of the Mechanism of Land Subsidence in Beijing[J]. City Geology, 2007, 2(1): 20-26)
(  0) 0) |
2. Faculty of Geomatics, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China;
3. Key Laboratory of Mine Environmental Monitoring and Improving around Poyang Lake, MNR, 418 Guanglan Road, Nanchang 330013, China
 2023, Vol. 43
2023, Vol. 43


