矿区开采引起的地表沉降易受多种因素影响,地表形变在时间域上通常呈现非线性特征,传统的线性模型难以描述、预测其复杂的动态变化过程。BP神经网络具有非常强大的非线性映射能力,可以进行自我学习和训练,对输入的多个影响要素进行非线性分析[1],更合理、科学地得到多个因素共同作用导致的预测结果。但BP神经网络要求训练样本质量较好,且其泛化能力不高,易陷入局部极小值[2]。鉴于卡尔曼滤波(KF)有较好的信息处理能力,本文将其与BP神经网络进行融合,构建KF-BP模型,并进一步融合AdaBoost算法,根据加权组合的方式提出AdaBoost-KF-BP强预测器模型。最后,通过MATLAB软件分别计算BP神经网络模型、KF-BP模型、AdaBoost-BP模型和AdaBoost-KF-BP模型预测矿区地表沉降的精度。
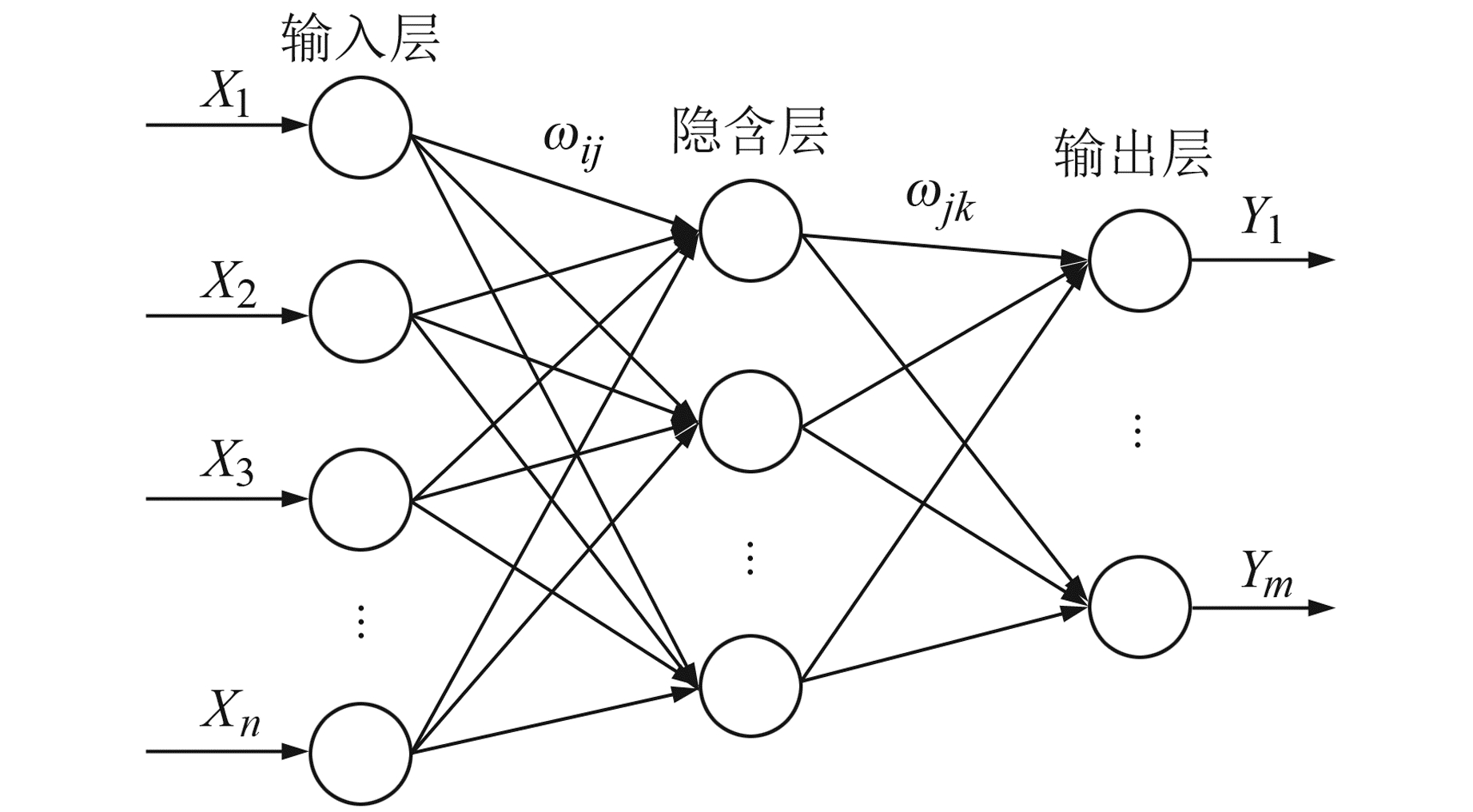
1 AdaBoost-KF-BP模型 1.1 BP神经网络BP神经网络是一种由信息正向传播和误差逆向传播2个部分组成的多层前馈网络,其本质是将输入层的数据信息通过正向传递,经隐含层计算传至输出层进行输出,再根据输出值与真实值的差值进行误差反向传播,以对网络中各层神经元的权值和阈值进行调整修改,使误差函数沿负梯度方向下降,直到输出结果达到期望目标[3]。BP神经网络可对输入的多个要素进行非线性处理分析,一般分为输入层、隐含层和输出层,其拓扑结构如图 1所示。
|
图 1 BP神经网络拓扑图 Fig. 1 Topology of BP neural network |
本文选取9种影响矿区地表沉降的因素和最大下沉值构建BP神经网络,输入层接受9种影响因素,输出层输出最大下沉值,故输入层节点数为9,输出层节点数为1。由Kolmogorov定理可确定隐含层节点数范围为[5, 14],经多次测试,当隐含层节点数为8时,训练和预测效果最佳。
1.2 KF优化BP神经网络BP神经网络对初始训练样本数据的要求较高[4],而获取矿区沉降监测数据时不可避免地会夹杂噪声数据,且作为单一预测模型,其稳定性与精度尚有优化空间。因此,本文将经典BP神经网络与KF进行融合。KF是一种最优化自回归数据的处理算法,可以应用于任何含有不确定信息且伴随各种噪声和干扰的动态系统中,根据对最新观测数据和前一时刻估计值的数据分析提出作用于系统的参数,估计出系统的历史状态和现在状态,再通过最优估计理论和滤波自身不断进行递推,对系统下一步走向作出有根据的预测[5]。KF的基本方程可分为状态方程(即动态方程)和观测方程,其离散化形式表示为:
| $ \left\{\begin{array}{l} \boldsymbol{X}_k=\boldsymbol{A} \boldsymbol{X}_{k-1}+\boldsymbol{B} \boldsymbol{u}_k+\boldsymbol{w}_k \\ \boldsymbol{Z}_k=\boldsymbol{H} \boldsymbol{X}_k+\boldsymbol{v}_k \end{array}\right. $ | (1) |
式中,Xk、Xk-1分别为k、k-1时刻的系统状态;A为状态转移矩阵;B为控制变量矩阵;uk为状态控制向量;wk为服从高斯分布的控制系统噪声,wk~N(0,Q),Q为系统噪声协方差,该状态方程可根据k-1时刻的状态和控制向量来推测k时刻的状态;Zk为测量向量;H为状态向量到测量向量的转换矩阵;vk为测量噪声,vk~N(0,R),R为测量噪声的协方差。针对本文原始数据,经过多次试错调参发现,当Q=1、R=1时,KF优化BP神经网络的效果最佳。
KF算法可分为预测阶段和更新阶段。其中,预测阶段:
| $ \hat{\boldsymbol{X}}_{\bar{k}}=\boldsymbol{A} \hat{\boldsymbol{X}}_{k-1}+\boldsymbol{B} \boldsymbol{u}_k $ | (2) |
| $ \boldsymbol{P}_{\bar{k}}=\boldsymbol{A P}_{k-1} \boldsymbol{A}_k^{\mathrm{T}}+Q $ | (3) |
更新阶段:
| $ \boldsymbol{K}_k=\frac{\boldsymbol{P}_{\bar{k}} \boldsymbol{H}^{\mathrm{T}}}{\boldsymbol{H} \boldsymbol{P}_{\bar{k}} \boldsymbol{H}^{\mathrm{T}}+R} $ | (4) |
| $ \hat{\boldsymbol{X}}_k=\hat{\boldsymbol{X}}_{\bar{k}}+\boldsymbol{K}_k\left(\boldsymbol{Z}_k-\boldsymbol{H} \hat{\boldsymbol{X}}_{\bar{k}}\right) $ | (5) |
| $ \boldsymbol{P}_k=\left(\boldsymbol{I}-\boldsymbol{K}_k \boldsymbol{H}\right) \boldsymbol{P}_{\bar{k}} $ | (6) |
式中,
在预测阶段,根据前一时刻的状态估计值推算当前时刻的状态变量先验估计值和误差协方差先验估计值;更新阶段则负责通过先验估计和新的测量变量来完成后验估计的构造与改进。因此,KF算法是一个递归的预测-校正方法。
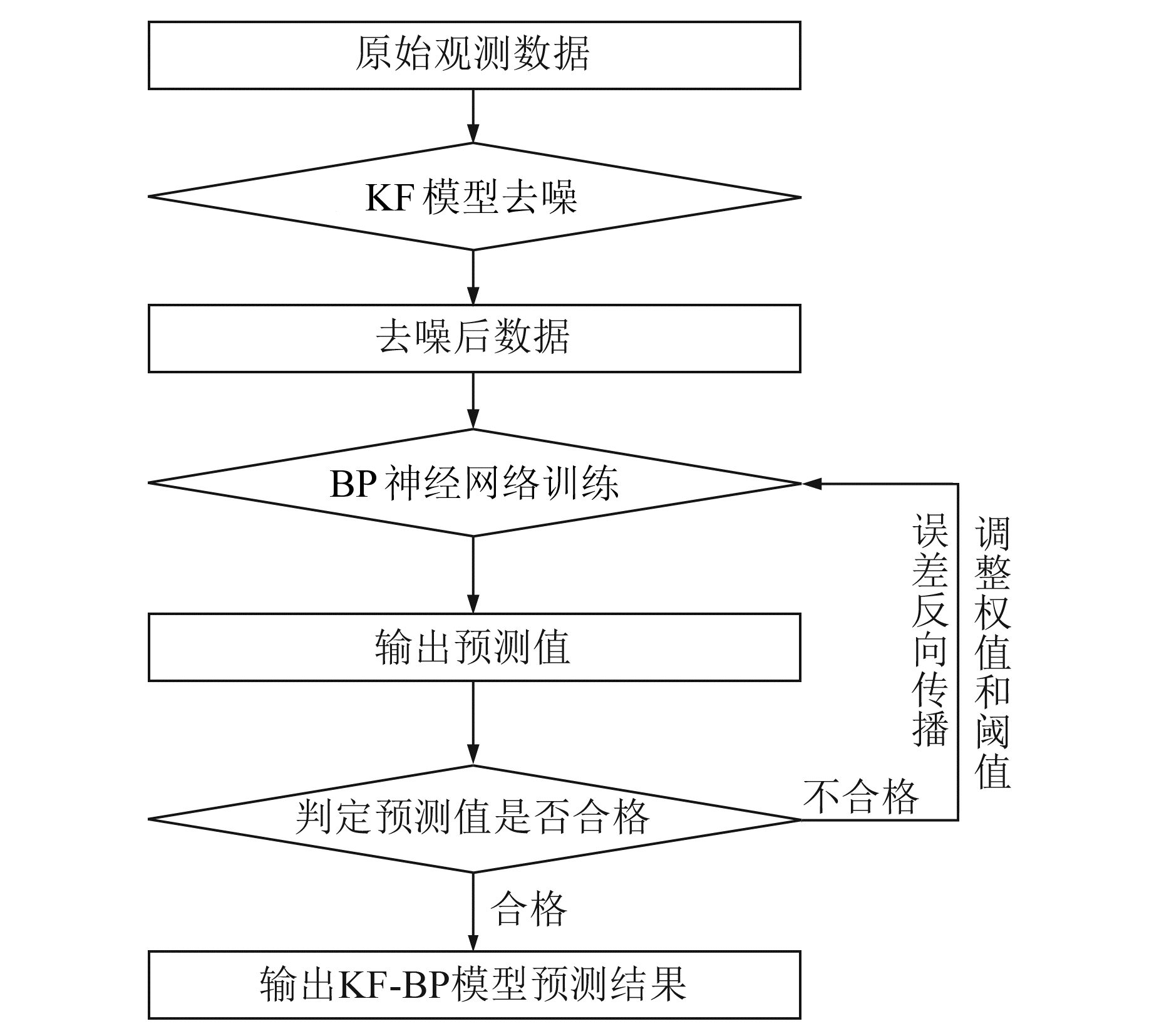
在实际矿区沉降预测工作中,KF-BP模型的作用机理是通过KF算法对获取的原始矿区沉降监测数据进行去噪处理,再将去噪后的数据传递到BP神经网络模型中作为训练集参与后续的处理分析[6];之后根据输出值与真实值的差值进行误差反向传播,对网络中各层神经元的权值和阈值进行调整修改,使误差函数沿负梯度方向下降,直到输出结果达到期望目标。这种方法能在一定程度上改善BP神经网络中训练学习样本的质量,因此可有效提高模型的预测精度。KF-BP组合模型预测流程如图 2所示。
|
图 2 KF-BP模型预测流程 Fig. 2 Prediction flow chart of KF-BP model |
AdaBoost算法由Boosting算法改进而来,两者核心思想均是将多个弱预测器组合成一个强预测器。不同的是,Boosting算法采用平均投票机制组合多个弱预测器,而Ada-Boost算法则重视误差较大的样本,通过改变其权重来改变样本数据分布,经过N次重复训练、测试,最终得到T个弱预测器及各自权重,根据加权组合的方式将T个弱预测器组合形成一个强预测器[7],这种方式得到的强预测器的精度更高。
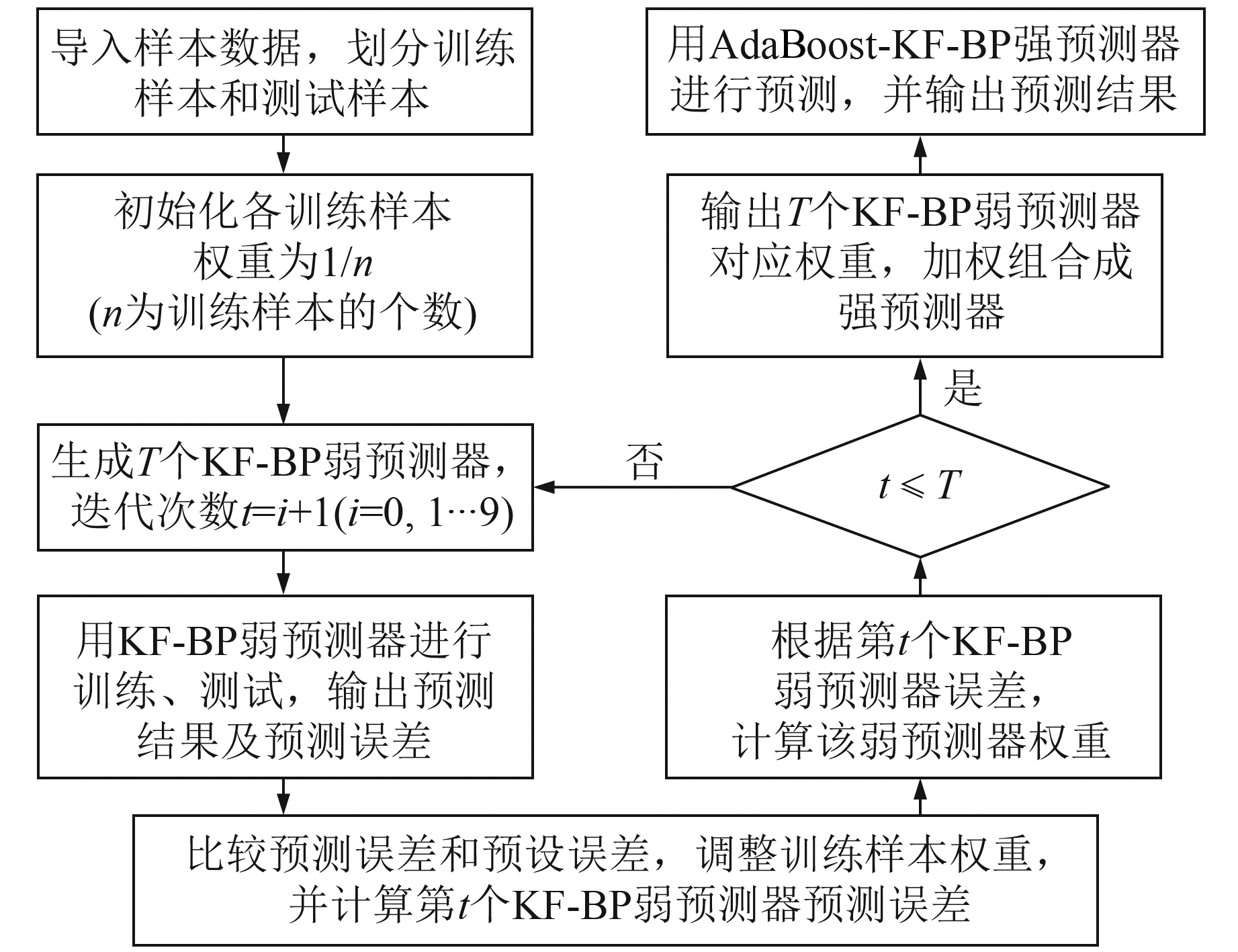
根据上述理论,AdaBoost-KF-BP模型的作用机理是将KF-BP模型视作AdaBoost算法中的弱预测器参与后续训练、预测,若预测误差达不到期望,则将该样本作为加强训练样本,调整其样本权重并计算下一个弱预测器的权重。经多次测试,根据最终的各弱预测器权重分布,将多个弱预测器组合构成一个强预测器[8]。建立AdaBoost-KF-BP模型的基本思路如图 3所示。
|
图 3 AdaBoost-KF-BP模型预测流程 Fig. 3 Prediction flow chart of AdaBoost-KF-BP model |
AdaBoost-KF-BP模型的具体步骤为:
1) 导入样本数据。划分训练样本和测试样本,初始化各训练样本权重:
| $ D_i=\frac{1}{n}, i=1, 2, \cdots, n $ | (7) |
式中,Di为第i个训练样本的初始权重,n为训练样本的个数。
2) 构建KF-BP模型。生成T个KF-BP弱预测器模型,并对样本进行训练、预测。
3) 计算KF-BP弱预测器模型预测训练样本得到的预测误差ec。
4) 比较预测误差ec与预设误差e,调整训练样本权重Di。
5) 计算第t个KF-BP弱预测器模型的权重σt:
| $ \begin{array}{c} {e_t} = \sum\limits_{i = 1}^t {{D_i}} \\ i = 1, 2, \cdots , n;t = 1, 2, \cdots , T \end{array} $ | (8) |
| $ \sigma_t=\frac{1}{2} \ln \left(\frac{1-e_t}{e_t}\right) $ | (9) |
式中,et为第t个KF-BP弱预测器模型的预测误差率;T为弱预测器的个数。返回步骤2),进行下一次迭代,直到迭代T次后,结束训练。
6) 输出AdaBoost-KF-BP强预测器模型。经T次训练,得到T组弱预测器模型及其弱预测函数ft(x),根据权重分布,将弱预测函数加权组合成强预测函数F(x):
| $ F(x) = \sum\limits_{t = 1}^T {\left[ {{\sigma _t}{f_t}(x)} \right]} $ | (10) |
已有研究表明,矿区地表沉降过程具有一定的时间性与随机性,其复杂性主要受地质和采矿等因素的影响[9]。考虑到矿区地表沉降规律受影响因素及其取值的不同而表现出较大差异性,本文选取9个主要影响因素:弹性模量、泊松比、内聚力、内摩擦角、采深、采高、倾角、覆岩平均单向抗压强度及松散层厚度,其中覆岩平均单向抗压强度和松散层厚度代表覆盖层的岩石特性和地质构造对矿区地表沉降的影响。选取某矿区40组监测点数据进行最大下沉值预测实验(实验1),样本数据如表 1所示。
|
|
表 1 实验1样本数据 Tab. 1 Sample data of experiment 1 |
地表沉降机理表明,采深对地表沉降影响较大[10],故将原始40组数据根据采深是否大于300 m分为2组进行不同采深区域的矿区最大下沉值预测实验(实验2)。通过对比实验,分析AdaBoost-KF-BP模型在不同采深区的适用性,并验证采深对地表沉陷规律的影响。实验2中,采深小于300 m区域与采深大于300 m区域的样本数据如表 2和3所示。
|
|
表 2 采深300 m以下区域的样本数据 Tab. 2 Sample data of areas with mining depth below 300 m |
|
|
表 3 采深300 m以上区域的样本数据 Tab. 3 Sample data of areas with mining depth above 300 m |
实验1中,选取表 1前30组数据作为BP神经网络模型的训练样本,后10组数据作为测试样本,使用MATLAB建立BP神经网络预测模型进行训练、预测。在BP神经网络的基础上,采用KF对原始训练样本集进行降噪处理后,再输入到BP神经网络中[11],构建KF-BP预测模型,以验证KF优化BP神经网络的可行性。将BP神经网络视作弱预测器模型,以此来构建AdaBoost-BP预测模型,分析AdaBoost算法对单一BP神经网络模型精度的提升。最终,为达到进一步优化的目的,构建AdaBoost-KF-BP组合模型,将原始样本数据输入该预测模型进行训练、预测。为更好地对比优化效果,将AdaBoost-BP模型和AdaBoost-KF-BP模型中的弱预测器个数均设置为9。
实验2也采用与实验1相同的4种模型,不同的是,分别将表 2和3前15组数据作为训练集,后5组数据作为测试集。
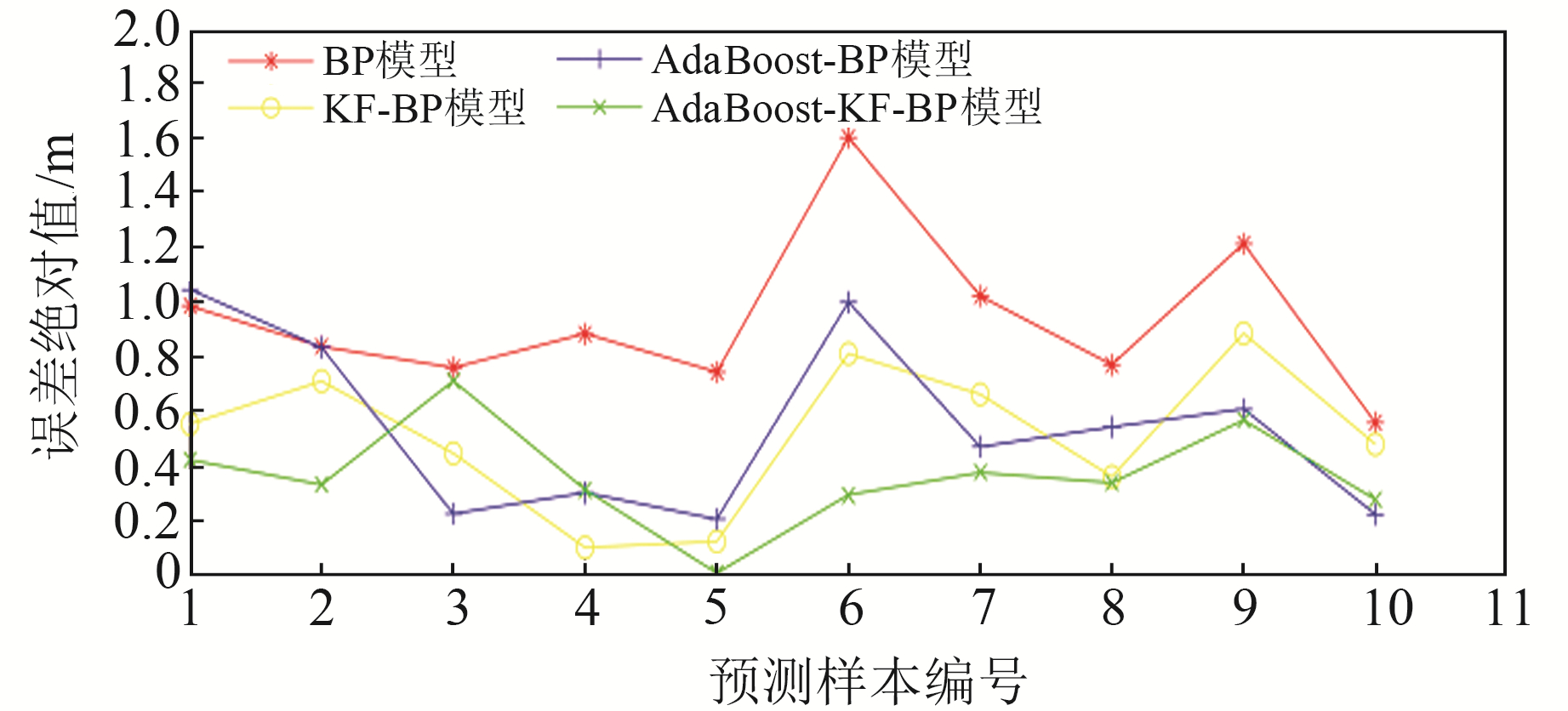
2.3 结果与分析实验1中,利用各模型预测矿区最大下沉值,并将预测误差绝对值进行对比分析,结果如图 4所示。从图 4看出,BP模型的预测精度较差,得到的误差绝对值最大达到1.600 m,最小值为0.561 m;KF-BP模型和AdaBoost-BP模型的精度相比于BP模型有所提高,两者的预测误差绝对值最小分别为0.106 m和0.209 m;AdaBoost-KF-BP模型整体的预测精度最高,其预测误差绝对值最小为0.013 m,且在10次预测实验中,AdaBoost-KF-BP模型的提升效果比KF-BP模型和AdaBoost-BP模型稳定。
|
图 4 实验1预测结果 Fig. 4 Prediction results of experiment 1 |
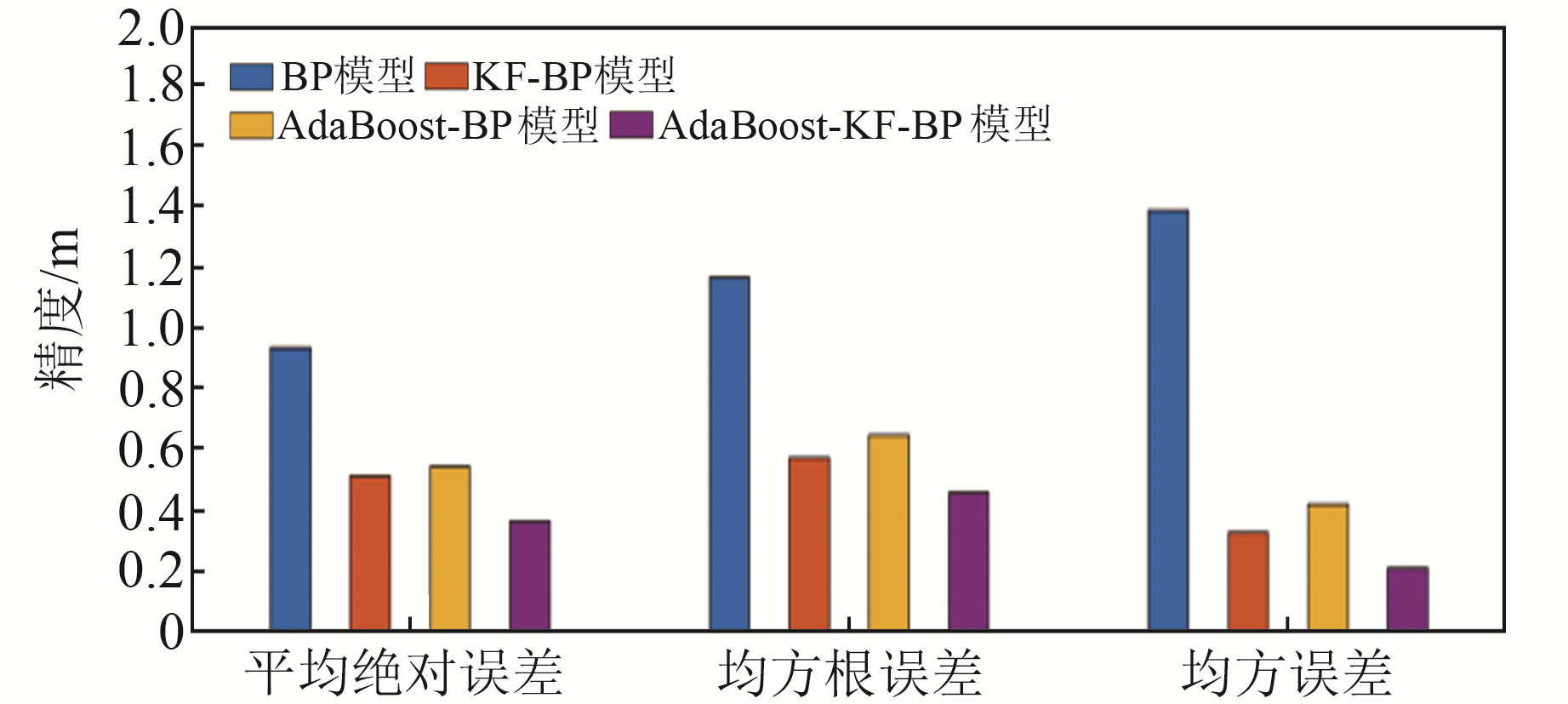
选取平均绝对误差、均方根误差和均方误差3种误差评价指标对各模型预测精度进行分析,结果见图 5和表 4。可以看出,BP模型由于网络泛化能力不高、易陷入局部极小值及初始数据中存在随机误差和噪声等原因,其各项评价指标的值最大,平均绝对误差、均方根误差和均方误差分别为0.938 m、1.166 m和1.388 m;KF-BP模型通过利用KF对数据降噪处理优化BP神经网络,其精度相比于BP模型有所改善,平均绝对误差下降到0.516 m;AdaBoost算法通过将多个弱预测器组成强预测器的方式优化BP神经网络,其平均绝对误差为0.548 m;本文改进的AdaBoost-KF-BP模型集成了KF和AdaBoost算法各自的优点,预测精度最高,且明显优于前3种预测模型,其3种精度评价指标分别为0.367 m、0.460 m和0.212 m,相比于BP神经网络模型,平均绝对误差提升60.9%。
|
图 5 实验1预测精度 Fig. 5 Prediction accuracy of experiment 1 |
|
|
表 4 实验1各模型精度对比 Tab. 4 Comparison of precision of each model in experiment 1 |
实验2的预测精度见表 5和6。对比表 5和6可以看出,AdaBoost-KF-BP模型对2个区域的预测结果的平均绝对误差分别为0.296 m和0.247 m,且采深300 m以上区域的各项评价指标的值均略低于采深300 m以下区域。该结果也验证了大采深区域的地表最大下沉速度更稳定,形变更缓慢、均匀[12],导致该区域的AdaBoost-KF-BP模型预测精度也会略有提高。在实际应用中,在对大采深区域进行矿区地表沉降预测时,可优先考虑AdaBoost-KF-BP模型。
|
|
表 5 采深300 m以下区域预测精度分析 Tab. 5 Prediction accuracy analysis of areas with mining depth below 300 m |
|
|
表 6 采深300 m以上区域预测精度分析 Tab. 6 Prediction accuracy analysis of areas with mining depth above 300 m |
1) KF-BP模型和AdaBoost-BP模型的预测精度均优于传统BP模型,而AdaBoost-KF-BP模型同时融合了KF和AdaBoost算法的优点,预测精度最高,比其他3种模型更适用于矿区地表沉降的预测。
2) 实验2中,将原始数据根据开采深度分为2组进行对比。结果表明,在采深跨度接近时,本文融合预测模型更适用于大采深区域。
3) 值得注意的是,AdaBoost-KF-BP模型在3号预测样本的精度较差,相较于BP模型提升不大,造成这种现象的原因需进行更深入的研究。
| [1] |
刘建国. 基于卡尔曼滤波的BP神经网络模型在桥梁形变中的应用: 以京沪高铁为例[D]. 西安: 长安大学, 2010 (Liu Jianguo. Based on Kalman Filtering BP Neural Network Model in Bridge Deformation Application——Take Beijing to Shanghai High-Speed Iron as an Example[D]. Xi'an: Chang'an University, 2010)
(  0) 0) |
| [2] |
邓传军, 欧阳斌, 陈艳红. 一种基于PSO-BP神经网络的建筑物沉降预测模型[J]. 测绘科学, 2018, 43(6): 27-31 (Deng Chuanjun, Ouyang Bin, Chen Yanhong. A Buliding Settlement Prediction Model Based on PSO-BP Neural Network[J]. Science of Surveying and Mapping, 2018, 43(6): 27-31)
(  0) 0) |
| [3] |
周纯择, 阳军生, 牟友滔, 等. 南昌上软下硬地层中盾构施工地表沉降的BP神经网络预测方法[J]. 防灾减灾工程学报, 2015, 35(4): 556-562 (Zhou Chunze, Yang Junsheng, Mou Youtao, et al. BP Neural Network Prediction Method for Ground Surface Settlement Caused by Shield Tunneling in Soft Layer down Laid on Hard Layer in Nanchang[J]. Journal of Disaster Prevention and Mitigation Engineering, 2015, 35(4): 556-562)
(  0) 0) |
| [4] |
林凯. 卡尔曼滤波-BP神经网络组合模型在地铁变形监测中的应用[D]. 西安: 西安科技大学, 2019 (Lin Kai. Application of Kalman Filter-BP Neural Network Combination Model in Metro Deformation Monitoring[D]. Xi'an: Xi'an University of Science and Technology, 2019)
(  0) 0) |
| [5] |
卢克东, 孟雪莹. 利用Kalman-BP综合模型进行矿区开采沉陷动态预测[J]. 北京测绘, 2020, 34(11): 1 555-1 558 (Lu Kedong, Meng Xueying. Mining Area Subsidence Dynamic Prediction Based on Kalman-BP Comprehensive Model[J]. Beijing Surveying and Mapping, 2020, 34(11): 1 555-1 558)
(  0) 0) |
| [6] |
Yang Y H, Shi Y. Application of Improved BP Neural Network in Information Fusion Kalman Filter[J]. Circuits, Systems, and Signal Processing, 2020, 39(10): 4 890-4 902 DOI:10.1007/s00034-020-01393-y
(  0) 0) |
| [7] |
潘红宇, 赵云红, 张卫东, 等. 基于AdaBoost的改进BP神经网络地表沉陷预测[J]. 煤炭科学技术, 2019, 47(2): 161-167 (Pan Hongyu, Zhao Yunhong, Zhang Weidong, et al. Prediction of Surface Subsidence with Improved BP Neural Network Based on AdaBoost[J]. Coal Science and Technology, 2019, 47(2): 161-167)
(  0) 0) |
| [8] |
Ding D H, Zhu S S. A Method of Forest-Fire Image Recognition Based on AdaBoost-BP Algorithm[J]. International Journal of Circuits, Systems and Signal Processing, 2019, 13: 312-319
(  0) 0) |
| [9] |
崔希民, 邓喀中. 煤矿开采沉陷预计理论与方法研究评述[J]. 煤炭科学技术, 2017, 45(1): 160-169 (Cui Ximin, Deng Kazhong. Research Review of Predicting Theory and Method for Coal Mining Subsidence[J]. Coal Science and Technology, 2017, 45(1): 160-169)
(  0) 0) |
| [10] |
孙超, 薄景山, 刘红帅, 等. 采空区地表沉降影响因素研究[J]. 吉林大学学报: 地球科学版, 2009, 39(3): 498-502 (Sun Chao, Bo Jingshan, Liu Hongshuai, et al. Study on Influencing Factors of Ground Settlement over Mined-out Area[J]. Journal of Jilin University: Earth Science Edition, 2009, 39(3): 498-502)
(  0) 0) |
| [11] |
李依泽, 陆超, 王印峰, 等. 基于Kalman滤波与神经网络的高精度同步时钟算法[J]. 电网技术, 2019, 43(3): 777-784 (Li Yize, Lu Chao, Wang Yinfeng, et al. A High Accuracy Synchronous Clock Algorithm Based on Kalman Filter and Neural Network[J]. Power System Technology, 2019, 43(3): 777-784)
(  0) 0) |
| [12] |
魏义强. 大采深条件下采煤活动引起的覆岩移动变形及破坏规律研究[D]. 太原: 太原理工大学, 2010 (Wei Yiqiang. Research on the Overburden Deformation and Its Damage Regular under the Conditions of a Large Mining Depth[D]. Taiyuan: Taiyuan University of Technology, 2010)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


