2. 中国科学院精密测量科学与技术创新研究院,武汉市徐东大街340号,430077;
3. 中国科学院大学地球与行星科学学院,北京市玉泉路19号甲,100049;
4. 中南民族大学资源与环境学院,武汉市民族大道182号,430074
合成孔径雷达差分干涉测量(D-InSAR)技术是目前地表形变监测的重要手段,但雷达信号在大气中传播时会受到空气中各类介质的影响,导致相位延迟或提前。对流层和电离层是大气中造成信号延迟的主要介质层,其中对流层延迟是D-InSAR形变测量最主要的误差源[1-3]。D-InSAR对流层校正方法可分为两大类,一类是通过GPS、MERIS、MODIS等外部数据建立大气误差模型[4-6],如GACOS(generic atmospheric correction online service for InSAR)系统[7-9];另一类是利用InSAR对流层延迟在时空上的统计特性,基于统计学方法来削弱其影响[10],即拟合研究区LOS向形变相位与数字高程模型(digital elevation model,DEM)[11-13]进行误差校正。
目前已有学者对GACOS与DEM数据在时序InSAR形变监测中大气校正效果进行研究[10],但是未考虑大气噪声与地形(相位-高程)函数中形变信号对拟合函数的影响,且不适用于同震形变观测。施贺青等[13]基于DEM拟合相位-高程函数并降低大气误差,但是未考虑选择不同拟合区域对拟合函数与校正精度的影响。本文从地震活动频发地区选取震级MS5.4~7.0事件。首先以精河地震为例,通过研究区数据分析得到基于外部DEM进行大气误差校正时拟合区域的选取方法,然后以外部DEM数据分别拟合与地形相关的大气误差模型和GACOS数据建立的大气误差模型进行误差校正;最后依据实验结果分析两种大气校正方法的适用性和校正精度。
1 数据源与误差分析 1.1 数据源Sentinel-1A/B为C波段SAR卫星,在高纬度地区的重访周期最短可以达到1 d[14]。本文选取10对覆盖地震影响区域的Sentinel-1A/B卫星干涉宽幅模式(IW)雷达影像(表 1),基于GMTSAR软件,采用两轨法处理SAR数据。
|
|
表 1 SAR数据基本信息 Tab. 1 Basic information of SAR data |
大气延迟误差主要来源于电离层和对流层,C波段SAR卫星受电离层干扰较小,且两次成像期间电离层延迟效应变化较小,可在数据处理过程中抵消大部分延迟信号。对流层约包含75% 的大气质量和几乎全部的大气水汽,天顶对流层总延迟(ZTD)可以表示为[15]:
| $ \begin{gathered} \mathrm{ZTD}=10^{-6} k_1 R_d \int_{h_0}^h \rho \mathrm{d} h+ \\ 10^{-6} \int_{h_0}^h\left(k_2 \frac{P_w}{T} Z_w^{-1}+k_3 \frac{P_w}{T^2} Z_w^{-1}\right) \mathrm{d} h \end{gathered} $ | (1) |
式中,Rd为干空气气体常数,ρ为干空气总质量密度,Zw为可压缩系数,Pw为水汽局部气压,T为大气温度,k1、k2、k3为大气折射常数,h0与h分别为测站与对流层顶部对应的高程。式(1)右边第1项为天顶静力学延迟(ZHD),第2项为天顶湿延迟(ZWD),SAR影像中大气延迟主要由对流层中湿延迟造成,引起的相位误差可表示为:
| $ \begin{gathered} \Delta \varphi=\varphi_1-\varphi_2= \\ \frac{4 \pi}{\lambda}\left[\left(R_1-R_2\right)+\left(\frac{{\rm ZWD}_1}{\cos \theta}-\frac{\rm ZWD_2}{\cos \theta}\right)\right] \end{gathered} $ | (2) |
式中,λ为雷达波长,θ为雷达入射角,R1和R2分别为雷达两次成像时的往返斜距,φ1和φ2分别为对应的相位。
现有研究结果表明,大气延迟与地形具有相关性[2, 10, 16]。基于InSAR技术提取形变场时,通过拟合高程与形变场大气噪声可得到噪声随高程变化的函数模型,然后扣除与地形变化相关的大气延迟信号。虽然同震形变信号远小于高程,但一般强于大气噪声,拟合大气误差函数时若未扣除形变区域,拟合函数将受到真实形变信号的显著影响。Albino等[16]基于DEM对形变场进行大气误差校正,但在拟合相位-高程函数时未分离形变信号与大气噪声,导致函数模型中包含真实形变信号的影响。
2.1 不同拟合区域参数分析为避免同震形变对拟合相位-高程函数产生影响,在拟合大气延迟信号时扣除干涉图中有明显同震形变条纹的区域,剩余相位解缠后的区域用于拟合两次SAR成像期间大气延迟信号。相位解缠共选择13个区域,其形变边界逐步扩大,如图 1(a)所示,其中黑色矩形表示选择的所有实验区相位解缠窗口,红色矩形为拟合函数时扣除的区域,面积为1 020 km2。图 1(b)为拟合区面积与相位-高程相关系数,其中横坐标表示拟合区面积。从图中可以看出,精河地震区域形变信号受大气噪声影响较大,包含大气噪声的形变信号与高程具有强相关性,相关系数绝对值最低为0.839 1,最高为0.915 7,拟合区域面积为2 760 km2时达到最大值,之后缓慢下降。为避免形变信号对标准差的影响,图 1(c)、1(d)、1(e)为去除同震影响区域的大气校正前后标准差及其差值,其中横坐标为扣除同震影响区域后的面积。从图中可以看出,大气校正前后标准差随拟合区面积增加表现出明显的变化趋势,拟合面积为2 350~2 760 km2时,校正后标准差降到最小值且校正前后标准差变化量趋近最大值,即此时校正效果最优。同时,从图 1(g)、1(h)可以看出,研究区域总面积小于3 800 km2时,大气校正后均方根下降速度较快,随后降速变缓。

|
图 1 研究区与相关参数 Fig. 1 Study area and related parameters |
通过§2.1分析可知,基于DEM数据拟合大气误差函数进行同震形变场大气校正时,其结果主要受拟合区域影响。相位-高程函数可通过同震影响区域以外的数据拟合得到,拟合大气误差时在较小范围内扩大或缩小扣除的同震影响区域(图 1(a)红色矩形区域)对误差函数模型与校正结果基本无影响。因此,拟合相位-高程函数时扣除的同震影响区域只需观察干涉图条纹进行选择。
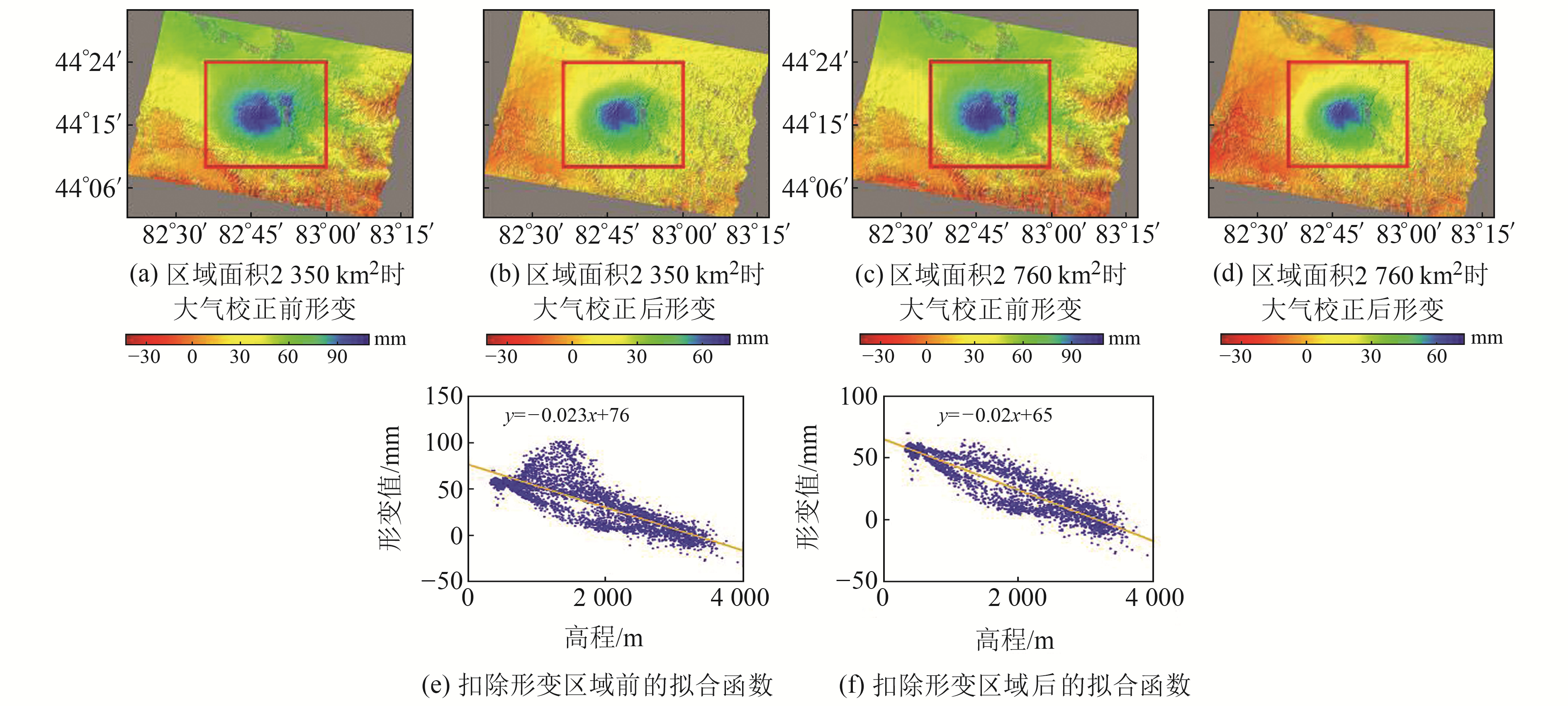
根据均方根、标准差及大气校正前后同震形变对比等综合分析可知,拟合区域面积选择在2 300~2 800 km2时,大气校正前后LOS向形变值与标准差、均方根变化均较为稳定,相关系数也接近幅值,可取得较好的大气校正效果。大气分布具有时空差异,拟合区面积大且与形变区域较远时,大气延迟随高程的变化关系与形变场中心大气分布差异性越大;拟合区面积小则相关系数低,无法准确拟合高程与形变之间的变化关系,校正后噪声同样较大。因此,根据校正前后均方根、标准差变化值及LOS向形变场综合分析可知,精河地震同震形变场拟合区域面积为2 300 ~2 800km2时噪声相对较小且变化稳定。图 2为拟合区域面积为2 350 km2和2 760 km2时大气校正前后形变场,从图中可以看出,LOS向最大形变量稳定在7.0~7.5 cm之间。
|
红色矩形为拟合相位-高程相关模型时去除的区域,红色矩形之外为拟合区域 图 2 不同拟合区校正结果 Fig. 2 Correction results of different fitting areas |
Albino等[16]基于GACOS与DEM数据对2017年印尼火山喷发前后形变进行大气校正,Bekaert等[10]通过幂律函数对大气噪声进行校正,但上述方法均未分析研究区形变在拟合误差函数时的影响。考虑到上述因素以及不同区域的地形差异,在对其余研究案例进行大气校正时,以精河地震误差函数模型的拟合区为参考,根据同震影响范围选择拟合区域。从数据处理结果可知,利用GACOS数据校正后的形变场可能会存在显著趋势,本文分别在是否设置参考点的情况下利用GACOS进行误差校正。此外,为考虑轨道误差造成的影响[17],通过上述两种方法进行大气误差校正后拟合并去除形变场趋势。
3.1 基于DEM的大气误差校正图 3为校正前后的形变场、误差模型与相位-高程线性函数。表 2为每个地震事件对应的相位-高程相关系数、标准差、均方根等参数。图 3(a)为拜城地震,对比校正前后的形变场可以看出,校正后幅值下降约3 cm,均方根下降2.6 cm。图 3(d)中大气校正之前很难分辨其形变信号,然而LOS向形变与DEM相关系数达0.8,校正后噪声大幅减小,形变量约为5 cm。图 3(e)中校正后均方根下降3.3 cm。图 3(g)中校正前断层两盘沿LOS向形变幅值为6 cm和-9 cm,校正后形变量为8 cm和-7 cm,噪声下降约2 cm,比张克亮等[18]的GNSS研究结果以及杨九元等[19]的InSAR研究结果更具可靠性。图 3(i)为近海地区,与地形无关的对流层延迟信号一般较为显著,基于DEM数据进行校正后噪声下降相对较小。图 3中其他事件的大气噪声与高程相关系数较低,基于DEM进行校正后整体均方根与标准差变化微弱。

|
图中a~j依次为表 1中序号1~10对应的地震事件;图中红色矩形为拟合相位-高程函数时扣除的主要同震影响区域,矩形以外为拟合区 图 3 基于DEM和GACOS数据大气延迟校正 Fig. 3 Atmospheric delay correction based on DEM and GACOS data |
|
|
表 2 研究区大气校正前后相关参数 Tab. 2 Related parameters before and after atmospheric correction in study area |
基于GACOS数据的校正结果如图 3中a5~j5所示,均方根及标准差等参数见表 2。为提高数据处理精度,将GACOS大气延迟信号逐像素投影至LOS向,然后分别在未设置和设置参考点的情况下进行大气校正。未设置参考点时部分研究案例校正后噪声反而增加,均方根增加值最大可达9 cm左右,校正后形变值可靠性低。根据形变场均值设置参考点或拟合趋势,校正后的形变值与现有较为可靠的研究结果相近[13, 18-19]。
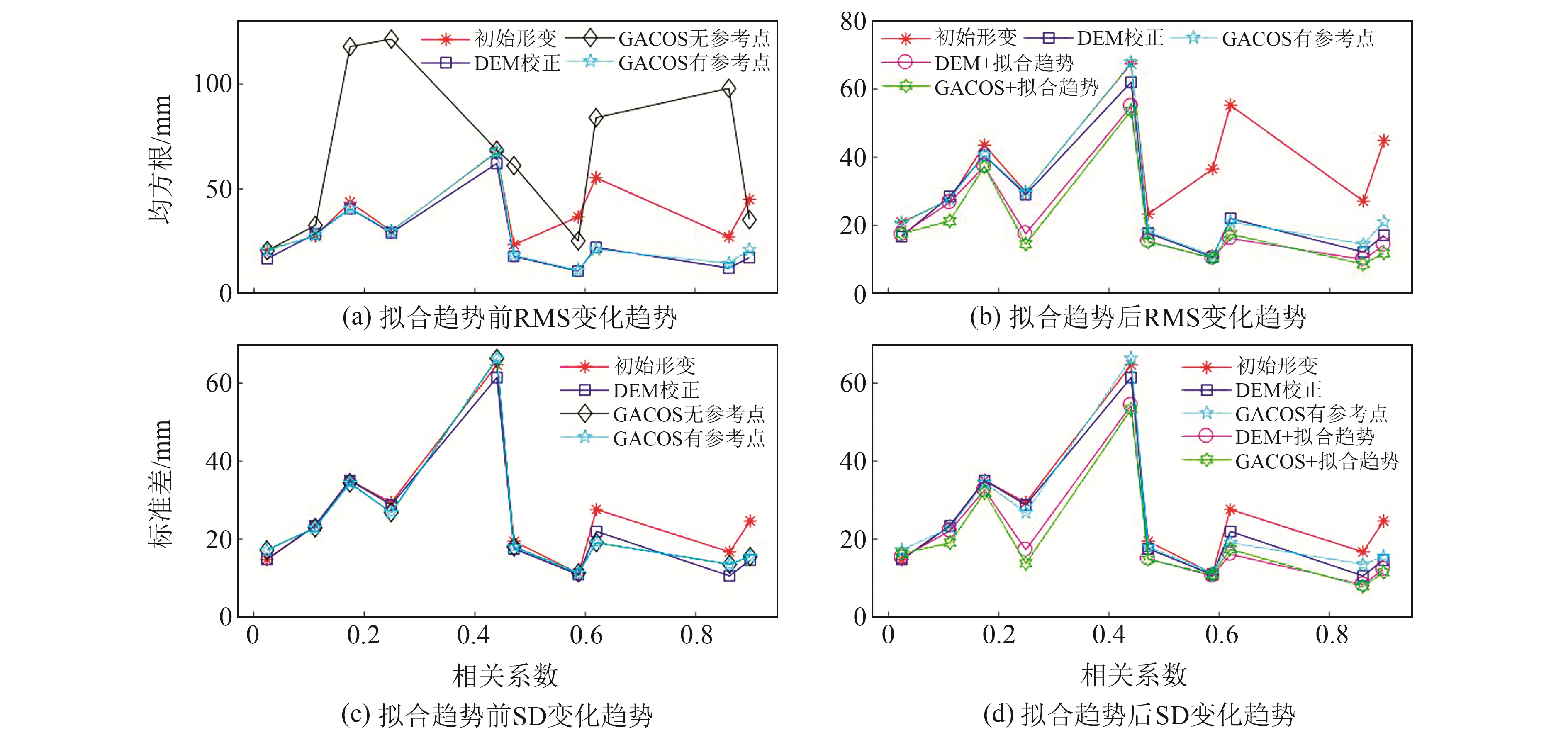
3.3 误差校正结果分析与讨论综合图 3中形变场以及图 4中校正前后参数变化趋势可知,相关系数0.45以上的地震事件基于DEM函数模型可取得较好的校正效果,均方根降幅在1~4 cm之间;相关系数大于0.8时,基于DEM数据的校正效果整体优于GACOS。由表 2和图 4可知,在相位-高程相关系数低于0.4时,DEM无法拟合可靠函数模型,而利用GACOS数据进行误差校正,均方根与标准差均下降,从形变场也可观察到噪声显著下降。相关系数为0.4~0.8时,使用GACOS校正也可达到与DEM校正相近的结果,可以使用两种方法相互验证。因此,基于两类数据进行大气误差校正时可以互补,噪声与高程相关性越强,说明地形越复杂且存在显著大气噪声,此时GACOS数据受GNSS站密度与ECMWF(European centre for medium-range weather forecasts) 等数据源精度影响,校正精度相对较低;而相关性越强,说明噪声分布更依赖于高程,只使用DEM拟合大气误差函数可获得更为精确的结果。
|
(c)中有无参考点对应的标准差一致,因此只体现出3组数据 图 4 大气校正前后参数随相关性变化趋势 Fig. 4 Variation trend of parameters with correlation before and after atmospheric correction |
本文以大气噪声显著的精河地震为例,建立基于DEM进行大气误差校正时拟合区的选取方法;然后分别基于DEM和GACOS建立的误差模型对不同地区与震级事件的LOS向形变数据进行校正,并分析校正精度和不同方法的适用性,得到以下结果:
1) 考虑到不同发震区域地形差异以及拟合区与形变区大气延迟的空间差异性,基于DEM拟合大气误差模型时,最佳拟合区并非固定值,在一定范围内均可取得较好的大气校正结果。以精河地震为例,相位-高程相关系数绝对值临近最大值且拟合区域面积在2 300~2 800 km2范围内时,校正效果整体较好。因此,本文未给出通过多次实验确定拟合面积的计算方程,而是给出相关性与校正精度随拟合区面积的变化趋势,以供拟合误差函数时参考。
2) 相位-高程相关系数绝对值大于0.4时,必须考虑大气误差对形变值的影响;相关系数小于0.4时,噪声受高程影响较小,可基于GACOS进行误差校正;相关系数为0.4~0.8时,可使用两种校正方法相互验证;相关系数大于0.8时,基于DEM校正后的均方根与标准差均低于GACOS,强相关性也表明形变场噪声分布显著依赖于高程,可单独基于DEM拟合噪声分布模型。
3) 在本文所有研究案例中,基于上述两种方法校正的数据结果在消除趋势后均方根与标准差整体下降,因此,大气校正后可通过对形变场进行多项式拟合以消除部分趋势。
| [1] |
Hanssen R F. Radar Interferometry: Data Interpretation and Error Analysis[M]. Dordrecht: Kluwer Academic Publishers, 2001
(  0) 0) |
| [2] |
Zebker H A, Rosen P A, Hensley S. Atmospheric Effects in Interferometric Synthetic Aperture Radar Surface Deformation and Topographic Maps[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B4): 7 547-7 563 DOI:10.1029/96JB03804
(  0) 0) |
| [3] |
Li Z W, Ding X L, Liu G X. Modeling Atmospheric Effects on InSAR with Meteorological and Continuous GPS Observations: Algorithms and Some Test Results[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2004, 66(11): 907-917 DOI:10.1016/j.jastp.2004.02.006
(  0) 0) |
| [4] |
Li Z H, Muller J P, Cross P, et al. Interferometric Synthetic Aperture Radar (InSAR) Atmospheric Correction: GPS, Moderate Resolution Imaging Spectroradiometer (MODIS), and InSAR Integration[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B3)
(  0) 0) |
| [5] |
Li Z H, Fielding E J, Cross P, et al. Interferometric Synthetic Aperture Radar Atmospheric Correction: GPS Topography-Dependent Turbulence Model[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B2)
(  0) 0) |
| [6] |
唐伟, 廖明生, 张丽, 等. 基于全球气象再分析资料的InSAR对流层延迟改正研究[J]. 地球物理学报, 2017, 60(2): 527-540 (Tang Wei, Liao Mingsheng, Zhang Li, et al. Study on InSAR Tropospheric Correction Using Global Atmospheric Reanalysis Products[J]. Chinese Journal of Geophysics, 2017, 60(2): 527-540)
(  0) 0) |
| [7] |
Yu C, Li Z H, Penna N T, et al. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(10): 9 202-9 222 DOI:10.1029/2017JB015305
(  0) 0) |
| [8] |
Yu C, Li Z H, Penna N T. Interferometric Synthetic Aperture Radar Atmospheric Correction Using a GPS-Based Iterative Tropospheric Decomposition Model[J]. Remote Sensing of Environment, 2018, 204: 109-121 DOI:10.1016/j.rse.2017.10.038
(  0) 0) |
| [9] |
Yu C, Penna N T, Li Z H. Generation of Real-Time Mode High-Resolution Water Vapor Fields from GPS Observations[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(3): 2 008-2 025 DOI:10.1002/2016JD025753
(  0) 0) |
| [10] |
Bekaert D P S, Hooper A, Wright T J. A Spatially Variable Power Law Tropospheric Correction Technique for InSAR Data[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(2): 1 345-1 356 DOI:10.1002/2014JB011558
(  0) 0) |
| [11] |
Li Z W, Ding X L, Huang C, et al. Modeling of Atmospheric Effects on InSAR Measurements by Incorporating Terrain Elevation Information[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2006, 68(11): 1 189-1 194 DOI:10.1016/j.jastp.2006.03.002
(  0) 0) |
| [12] |
杨成生, 张勤, 赵超英, 等. 基于地形和GPS观测的SAR干涉图大气延迟估计[J]. 大地测量与地球动力学, 2011, 31(1): 142-146 (Yang Chengsheng, Zhang Qin, Zhao Chaoying, et al. Atmospheric Delay Estimation of SAR Interferogram Based on GPS Observations and Terrain[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 142-146)
(  0) 0) |
| [13] |
施贺青, 张占彪, 陈云锅, 等. 利用InSAR数据约束反演2017年MW6.3精河地震同震破裂模型[J]. 大地测量与地球动力学, 2019, 39(11): 1 106-1 111 (Shi Heqing, Zhang Zhanbiao, Chen Yunguo, et al. Constraints on Coseismic Rupture Model of the 2017 MW6.3 Jinghe Earthquake from InSAR Data[J]. Journal of Geodesy and Geodynamics, 2019, 39(11): 1 106-1 111)
(  0) 0) |
| [14] |
Salvi S, Stramondo S, Funning G J, et al. The Sentinel-1 Mission for the Improvement of the Scientific Understanding and the Operational Monitoring of the Seismic Cycle[J]. Remote Sensing of Environment, 2012, 120: 164-174
(  0) 0) |
| [15] |
Davis J L, Herring T A, Shapiro I I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Science, 1985, 20(6): 1 593-1 607
(  0) 0) |
| [16] |
Albino F, Biggs J, Yu C, et al. Automated Methods for Detecting Volcanic Deformation Using Sentinel-1 InSAR Time Series Illustrated by the 2017-2018 Unrest at Agung, Indonesia[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(2)
(  0) 0) |
| [17] |
Zhang L, Wu J C, Ding X L, et al. The Propagation of Orbital Errors in the 3-Pass DInSAR Processing[C]. 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, 2007
(  0) 0) |
| [18] |
张克亮, 甘卫军, 梁诗明, 等. 2021年5月21日MS6.4漾濞地震GNSS同震变形场及其约束反演的破裂滑动分布[J]. 地球物理学报, 2021, 64(7): 2 253-2 266 (Zhang Keliang, Gan Weijun, Liang Shiming, et al. Coseismic Displacement and Slip Distribution of the 2021 May 21, MS6.4, Yangbi Earthquake Derived from GNSS Observations[J]. Chinese Journal of Geophysics, 2021, 64(7): 2 253-2 266)
(  0) 0) |
| [19] |
杨九元, 温扬茂, 许才军. 2021年5月21日云南漾濞MS6.4地震: 一次破裂在隐伏断层上的浅源走滑事件[J]. 地球物理学报, 2021, 64(9): 3 101-3 110 (Yang Jiuyuan, Wen Yangmao, Xu Caijun. The 21 May 2021 MS6.4 Yangbi (Yunnan) Earthquake: A Shallow Strike-Slip Event Rupturing in a Blind Fault[J]. Chinese Journal of Geophysics, 2021, 64(9): 3 101-3 110)
(  0) 0) |
2. Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China;
3. College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
4. College of Resources and Environmental Science, South-Central Minzu University, 182 Minzu Road, Wuhan 430074, China
 2023, Vol. 43
2023, Vol. 43

