2. 山东科技大学海洋科学与工程学院,青岛市前湾港路579号,266590
随着5G和物联网技术的快速发展,人们对于位置服务(location based service,LBS)[1]的应用需求日益增长。同时,由于惯性传感器逐渐集成于智能手机中,智能手机常与惯性导航技术相结合,故利用智能手机来实现行人导航定位已成为研究热点。目前,面向智能手机的室内惯性导航普遍采用行人航位推算(pedestrian dead reckoning,PDR)方法[2]。
步态检测、步长估计和航向估计是PDR的3个重要组成部分[3]。步态检测是行人航位推算的关键环节,可识别行人步频信息,并将得到的步频信息提供给步长估算,因此会对步长估计的可靠性造成影响,进而影响PDR系统的定位精度。目前,步态检测方法大多基于加速度传感器数据进行脚步探测,部分情况以角速度为辅。常用的步态检测方法如下:波峰检测法[4]原理为检测加速度周期的波峰数量,将波峰数量记为行走步数,但常存在伪波峰,会影响计步结果;零交叉法[5]常使用足部惯导,通过在脚步安装传感器采集步态信息,利用加速度或角速度信息判断零速点,缺点是不适用于智能手机;谱分析法[6]实现计步功能需要将时域信息转为频域信息,计算量大且复杂度高;有限状态机(finite state machine,FSM)方法依据加速度变化情况将1个步态周期划分为多种状态,通过各个状态之间的流转完成计步。Alzantot等[7]研究有限状态机步态检测方法,通过设定4个加速度阈值来判断起始、波峰、波谷和终止状态,但仅利用加速度阈值来识别步态普适性较差;王革超等[8]将1个步态周期划分为3个状态,提出的有限状态机法可避免阈值误判和伪波峰的干扰,但未添加其他活动状态,仅研究静止和步行状态;徐德昌等[9]提出基于6个状态的有限状态机步态检测,通过设定的阈值进行状态转换,但未验证该算法在其他活动下的检测情况。
因此,本文根据步行加速度波形“增加-波峰-下降-波谷”的特点,将步态周期划分为5个状态,并与行走过程中合加速度变化趋势对应,提出改进的FSM步态检测方法,从不同运动状态和手机模态验证该算法的有效性和适用性,进而实现二维平面内行人航位推算。
1 基于智能手机的行人航迹推算在初始位置已知情况下,利用手机采集加速度计和陀螺仪等传感器数据分析估算行人运动方向、步数和步长距离,进而估算最终位置,计算表达式为:
| $ \left\{\begin{array}{l} E_k=E_0+\sum\limits_{n=1}^k L_n \sin \theta_n \\ N_k=N_0+\sum\limits_{n=1}^k L_n \cos \theta_n \end{array}\right. $ | (1) |
式中,(E0, N0)为初始位置,(Ek, Nk)为第k步位置,L为步长,θn为航向角。
1.1 步长估计由于步长具有多样性和随机性,根据行走时加速度与步长的非线性关系,本文选择Weinberg模型[10]计算步长:
| $ L=k \cdot \sqrt[4]{a_{\max }-a_{\min }} $ | (2) |
式中,amax和amin为合加速度的最大值和最小值;k为步长参数,可通过实验测试来获取。
1.2 基于转角检测的航向估计航向估计主要使用智能手机中集成的方向传感器进行,但方向传感器比较灵敏,获取的航向角数据噪声较多。本文使用基于转角检测航向估算方法,首先利用陀螺仪输出的角速度判断行人行走时的转弯情况;然后在转弯阶段保留原始航向角数据,在无转弯情况下采用卡尔曼滤波对方向角进行修正滤波处理。
2 改进FSM步态检测 2.1 加速度数据预处理本文采用50 Hz作为手机输出频率,按式(3)计算得到合加速度模值:
| $ \mathrm{acc}=\sqrt{a_x^2+a_y^2+a_z^2} $ | (3) |
式中,acc为合加速度,ax、ay、az分别为x轴、y轴和z轴的加速度值。
本文采用窗口大小为7的滑动平均滤波法对合加速度数据进行预处理。由图 1可知,未经滤波的合加速度信号存在大量毛刺,噪声较多;滤波后的波形明显变得平滑,同时已剔除部分抖动误差,因此也更能突显其周期性。

|
图 1 加速度信号预处理 Fig. 1 Acceleration signal preprocessing |
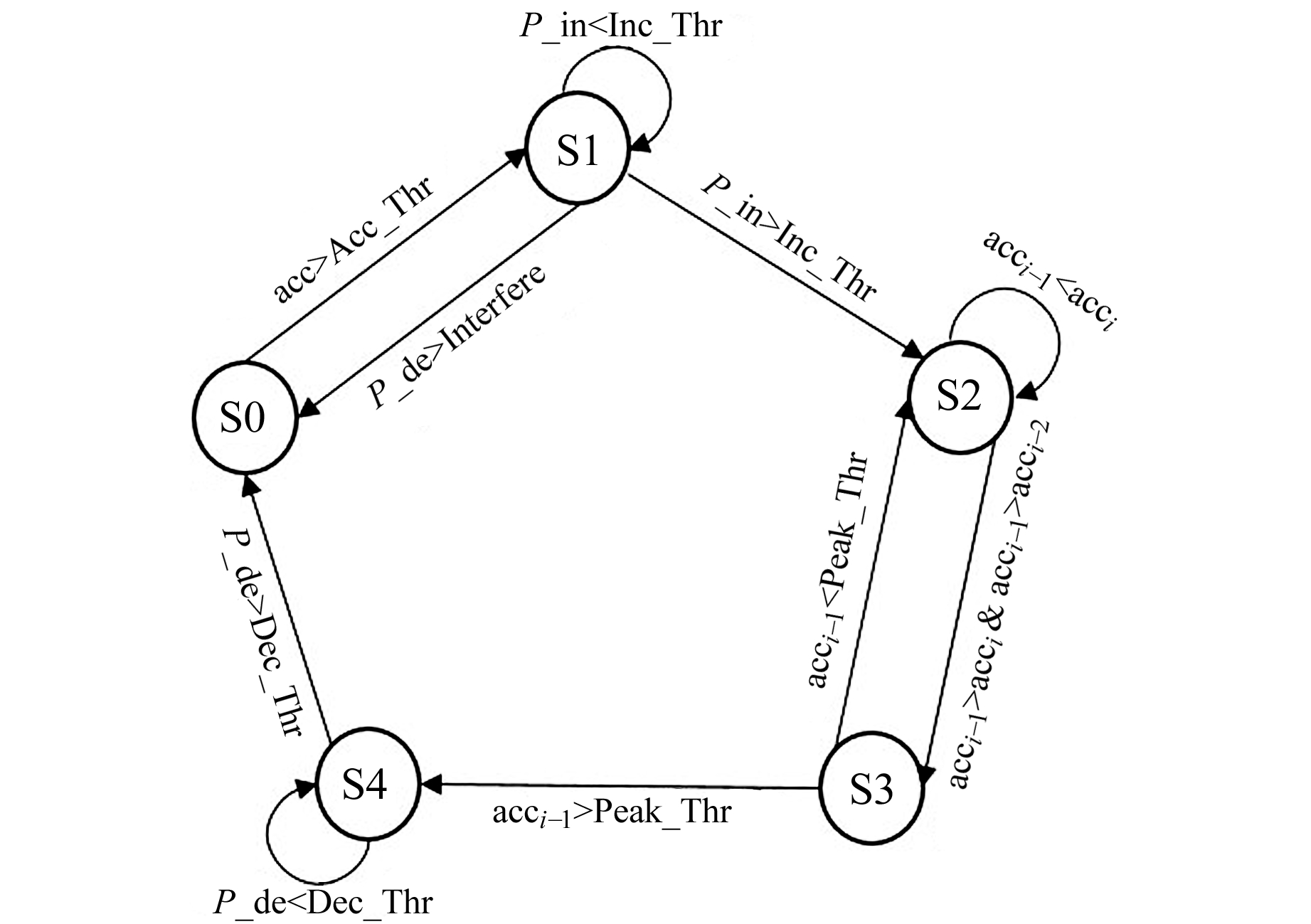
本文提出的改进FSM步态检测算法设定5个状态为一个步态周期,记为S0~S4,与步行加速度波形一一对应。由于波形趋势为增加-波峰-下降-波谷,故将S0定义为平稳状态,处于上一步结束下一步未开始的过渡阶段;S1定义为上升状态,表示用户开始起步、脚后跟逐渐抬起随之加速度不断增大的过程;S2表示寻找波峰状态,在进入上升状态后搜寻所存在的波峰;S3设定为波峰阈值判断阶段,将上一步骤寻找的波峰依次与波峰下界阈值比较,去除其中存在的伪波峰;S4定义为下降状态,表示用户脚离开地后逐渐收脚的过程。
本算法中阈值Acc_Dif表示相邻两个时刻加速度变化的阈值,Acc_Thr表示每个步态在开始进入步态检测流程的加速度阈值,Inc_Thr表示在一个步态周期中判断为上升状态的最大值,Dec_Thr表示在一个步态周期中判断为下降状态的最大值,Peak_Thr表示波峰的下界阈值,Interfere表示干扰阈值。
为描述步态周期波形的上升与下降状态,引入两个状态量P_in与P_de,每一个步态周期开始时P_in与P_de重置为0,P_in与P_de更新方法如下:
| $ \left\{\begin{array}{l} P_{-} \text {in }=P_{-} \text {in }+1, \mathrm{acc}_i-\mathrm{acc}_{i-1}>\text { Acc_Dif } \\ P_{-} \mathrm{de}=P_{-} \mathrm{de}+1, \mathrm{acc}_i-\mathrm{acc}_{i-1}<-\text { Acc_Dif } \end{array}\right. $ | (4) |
式中,P_in与P_de分别表示加速度上升与下降大于阈值Acc_Dif的次数。
改进FSM步态检测算法流程如图 2所示。
|
图 2 改进的步态检测算法流程 Fig. 2 The flow chart of improved gait detection algorithm |
有限状态机算法可描述为:
1) 开始处于S0平稳状态,如果当前加速度值大于Acc_Thr,则判定进入S1状态,同时P_in与P_de置零;
2) 在S1上升状态,引入噪声屏蔽机制,如果通过加速度计获取的数据存在较大噪声,则加速度波形会发生剧烈波动,即P_in与P_de会同时增大,由于Interfere比Inc_Thr小,会先满足P_de>Interfere,系统将返回S0平稳状态进行重新检测;
3) 在进入到上升状态后,如果P_in超过设定的上升次数阈值Inc_Thr,则系统进入S2状态,设置系统进入S3状态的触发条件为寻找到波峰即可;
4) 如步骤3)所述,在进入到下一状态后,如果Peak_Thr小于当前波峰值,则系统将进入S4状态,否则返回S2状态;
5) 在S4状态时,如果P_de不断增大直到大于Dec_Thr,则系统返回S0平稳状态,此时步数加1。
本文结合文献[8]中算法阈值设置方法,通过对比实验结果,逐步优选FSM算法中的阈值(表 1)。
|
|
表 1 步态检测算法中的经验参数 Tab. 1 Empirical parameters in gait detection algorithm |
本文以荣耀V30 Pro作为传感器数据采集测量工具,在实验过程中,实验人员平持手机放置胸前,进行步态检测实验和行人航迹定位实验。
3.1 改进FSM步态检测实验为验证改进FSM步态检测算法的计步准确率,将波峰检测法和改进的FSM算法从不同运动状态和手机模态两个角度进行实验分析。本实验波峰检测法是在传统波峰检测法基础上添加3个阈值,分别为波峰下界阈值、相邻两个波峰之间的时间差阈值和波峰波谷阈值。
为验证不同运动状态下的计步准确率,开展5组实验,分别为正常行走、快速行走、慢跑和上下楼梯,实验人员平端手机放置胸前行进60步。为避免算法存在偶然性,每组实验测试20次,实验对象为身高不同的4名用户,每组每名实验对象测试5次,求取平均值,实验结果如表 2所示。
|
|
表 2 不同运动状态下步态检测结果 Tab. 2 Gait detection results in different motion states |
根据表 2分析可知,当用户处于正常行走和快速行走两种状态时,改进的FSM步态检测算法准确率可达99%以上;对于上下楼梯实验组,该算法准确率均在98%以上,明显高于波峰检测法;当用户处于慢跑状态时,本文算法准确率仍保持在97%以上。综上可知,在不同运动状态下,改进的FSM步态检测算法精度高于波峰检测法。
通常手机模态为发消息、打电话、放置在上衣口袋和随手臂摆动。为验证该步态检测算法在不同手机模态下的识别准确率,安排两名实验对象,下文中用A和B表示,分别按照上述4种手机模态进行实验,每组每名实验对象测试5次,实验结果如表 3所示。
|
|
表 3 不同手机模态的步态检测结果 Tab. 3 Gait detection results of different mobile modes |
本次实验对改进的FSM算法在4种不同手机模态下的适用性进行研究。从表 3可以看出,在打电话、发消息和放置在上衣口袋三种状态下,改进的FSM步态检测结果平均准确率可达99%以上,但在随手臂摆动情况下,本文步态检测结果均不理想。这是由于该状态下加速度计数据是行人步行加速度与手臂摇摆加速度的合加速度,因此步态检测结果不太理想。综上可知,该算法适用于日常打电话、发消息和放置在上衣口袋,并能实现高准确率的步态检测。
3.2 行人航迹推算实验为验证本文提出的改进FSM行人航位推算方法的定位效果,实验选取东南大学四牌楼校区逸夫建筑馆一楼大厅为实验场地,实验人员平持手机放置胸前,按照实验路线A→B→C→D→A进行数据采集。从图 3可以看出,改进后的FSM算法形成的PDR轨迹路线和真实路径最接近,能显示出完整的航迹路线,特别是在拐弯处偏离程度和闭合误差较小,而波峰检测算法形成的PDR轨迹偏移程度较大。

|
图 3 PDR轨迹 Fig. 3 The trajectory of PDR |
统计上述两种算法在图 3轨迹中拐点A、B、C、D处的位置误差(表 4,单位m),由表可知,波峰检测法在第一个拐点B处的位置误差较小,在其他三处均存在较大的位置误差,4个点的平均误差为1.29 m,说明拐弯后波峰检测法容易出现步数误判,同时时间累积误差逐渐增大,导致位置误差较大;改进的FSM步态检测算法PDR平均位置误差为0.46 m,在4处参考点的位置误差均小于波峰检测法,相比于传统波峰检测法平均位置误差减小64.1%。
|
|
表 4 拐点位置误差统计 Tab. 4 Statistics of position error in inflection points |
综上可知,改进的FSM算法不仅步态识别准确率高,且航位推算的位置误差小,其PDR定位效果明显比波峰检测法定位结果更接近实际,表明本文算法具有可靠性。
4 结语针对传统波峰检测法的步态识别率低以及普适性和稳定性较差等问题,提出改进FSM步态检测的行人航位推算方法,将一个步态周期划分为5种状态并引入相邻合加速度差值和上、下坡次数阈值。为验证该算法的计步性能,将波峰检测法和改进的FSM算法分别从不同运动状态和手机模态进行实验对比分析,并绘制二维平面内行人航位推算结果图。实验结果表明:1)在不同运动状态和不同手机模态下,改进FSM步态检测的识别准确率均高于波峰检测法;2)改进FSM步态检测后航迹推算的时间累积误差减小,拐点处位置误差减小,PDR定位效果比波峰检测法定位结果更接近实际,表明本文算法具有可靠性。
| [1] |
Ashraf I, Hur S, Park Y. Smartphone Sensor Based Indoor Positioning: Current Status, Opportunities, and Future Challenges[J]. Electronics, 2020, 9(6)
(  0) 0) |
| [2] |
熊汉江, 郭胜, 郑先伟, 等. 室内行人移动行为识别及轨迹追踪[J]. 武汉大学学报: 信息科学版, 2018, 43(11): 1696-1703 (Xiong Hanjiang, Guo Sheng, Zheng Xianwei, et al. Indoor Pedestrian Mobile Activity Recognition and Trajectory Tracking[J]. Geomatics and Information Science of Wuhan University, 2018, 43(11): 1696-1703)
(  0) 0) |
| [3] |
毕京学. 智能手机Wi-Fi/PDR室内混合定位优化问题研究[J]. 测绘学报, 2021, 50(10): 1416 (Bi Jingxue. Study on Optimization Problem of Wi-Fi/PDR Indoor Hybrid Positioning on Smartphone[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(10): 1416 DOI:10.11947/j.AGCS.2021.20200408)
(  0) 0) |
| [4] |
马培兴, 王玫, 周陬, 等. 基于行人航迹推算的蓝牙峰值检测方法[J]. 计算机应用研究, 2022, 39(3): 851-856 (Ma Peixing, Wang Mei, Zhou Zou, et al. Bluetooth Peak Detection Method Based on PDR[J]. Application Research of Computers, 2022, 39(3): 851-856)
(  0) 0) |
| [5] |
Ruiz A R J, Granja F S, Honorato J C P, et al. Accurate Pedestrian Indoor Navigation by Tightly Coupling Foot-Mounted IMU and RFID Measurements[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(1): 178-189 DOI:10.1109/TIM.2011.2159317
(  0) 0) |
| [6] |
Kang X M, Huang B Q, Qi G D. A Novel Walking Detection and Step Counting Algorithm Using Unconstrained Smartphones[J]. Sensors, 2018, 18(1)
(  0) 0) |
| [7] |
Alzantot M, Youssef M. UPTIME: Ubiquitous Pedestrian Tracking Using Mobile Phones[C]. 2012 IEEE Wireless Communications and Networking Conference, Paris, 2012
(  0) 0) |
| [8] |
王革超, 梁久祯, 陈璟, 等. 加速度差分有限状态机计步算法[J]. 计算机科学与探索, 2016, 10(8): 1133-1142 (Wang Gechao, Liang Jiuzhen, Chen Jing, et al. Step Counting Algorithm Based on Finite State Machine Using Acceleration Differential[J]. Journal of Frontiers of Computer Science and Technology, 2016, 10(8): 1133-1142)
(  0) 0) |
| [9] |
徐德昌, 蔡成林, 邱云翔. 基于磁场指纹/PDR组合的室内行人定位算法[J]. 传感器与微系统, 2020, 39(6): 151-153 (Xu Dechang, Cai Chenglin, Qiu Yunxiang. Indoor Pedestrian Localization Algorithm Based on Magnetic Field Fingerprinting/PDR[J]. Transducer and Microsystem Technologies, 2020, 39(6): 151-153)
(  0) 0) |
| [10] |
Weinberg H. Using the ADXL202 in Pedometer and Personal Navigation Applications[J]. Analog Devices AN-602 Application Note, 2002, 2(2)
(  0) 0) |
2. College of Ocean Science and Engineering, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266590, China
 2023, Vol. 43
2023, Vol. 43


