兼容与互操作是未来GNSS发展的主要方向,BDS-3在设计和建设中尽可能采用与GPS和Galileo相同频点等频域参数[1]。BDS-3相比于北斗二代区域导航系统,在B1I和B3I信号基础上,新增B1C、B2a和B2b三个信号[2]。其中,B1C信号与GPS L1C和Galileo E1开放服务信号形成兼容互操作,B2a信号与GPS L5和Galileo E5a开放服务信号形成兼容互操作[3-4]。
截至2021-04,BDS-3 MEO卫星及IGSO卫星已经全部升空并提供开放服务。Yan等[5]使用全球连续监测评估系统(international GNSS monitoring and assessment system, iGMAS)数据分析BDS-3信号质量,结果表明B1C信号相比于其他BDS-3信号具有更低的载噪比,同时B2a可达到B1I和B3I信号水平。Zhang等[6]研究认为,B1C和B2a信号观测噪声低于B1I信号。对于BDS-3卫星的定轨能力,Xu等[7]评估早期BDS-3卫星的精密定轨性能,结果表明SLR(satellite laser ranging)检核残差优于7 cm。Li等[8]使用9个MGEX测站B1C/B2a数据对BDS-3 C19~C37卫星进行精密定轨,结果表明BDS-3 MEO卫星切向、法向和径向精度分别为19.2 cm、13.5 cm、5.7 cm,3D RMS为24.2 cm。总体而言,由于早期能够接收B1C/B2a信号的测站数量较少,现有文献对B1C/B2a数据精密定轨性能分析不够全面,不同文献分析结论差异较大,且缺乏B1C/B2a信号在multi-GNSS联合精密定轨中的性能分析。
为全面揭示BDS-3组网完成后B1C/B2a信号定轨性能,本文拟在数据量充足、测站全球均匀分布情况下,评估B1C/B2a单系统精密定轨性能及B1C/B2a在multi-GNSS联合精密定轨中的表现。首先进行数据收集,并介绍精密定轨和轨道精度评价相关模型及策略;然后通过48 h重叠弧段及SLR检核残差评估单BDS-3 MEO卫星基于B1C/B2a组合观测值精密定轨的轨道质量;最后对比分析仅BDS-3 MEO卫星精密定轨和加入Galileo E1/E5a信号进行联合精密定轨两种情况下B1C/B2a与B1I/B3I定轨性能。值得注意的是,由于GPS可发射L1C和L5信号的卫星较少,因此本文研究不包含GPS卫星。
1 数据收集卫星在轨跟踪与精密定轨是保障卫星系统安全性和可用性的核心,精密定轨测站的正确选取是保证轨道精度的重要前提[9]。截至2021-06,武汉大学IGS数据中心包含B1C和B2a信号的MGEX测站数已超过110个,测站数足够且分布均匀。本文收集2021-05-01~06-30 MGEX测站观测数据,对BDS-3 MEO卫星使用B1C/B2a组合观测值单系统精密定轨及Galileo+BDS-3 MEO联合精密定轨的性能进行评估。
2 精密定轨原理与解算策略GNSS卫星精密定轨可以理解为利用大量观测值建立与初始轨道参数的联系,以此对轨道参数初值进行精化处理,得到相对最优的初值,然后通过数值积分方式获得任意时刻卫星的位置和速度[10-11]。
2.1 观测模型本文GNSS精密定轨采用无电离层组合模型消除一阶电离层延迟,基本观测模型如下:
| $ \begin{gathered} P_{\mathrm{IF}}=\frac{f_1^2 \cdot P_1-f_2^2 \cdot P_2}{f_1^2-f_2^2}=\rho+c\left(\delta t_{\mathrm{r}}-\delta t^{\mathrm{s}}\right)+ \\ T+\delta m+c\left[d_{\mathrm{r}}(t)-d^{\mathrm{s}}\left(t-\tau_{\mathrm{r}}^{\mathrm{s}}\right)\right]+\varepsilon P_{\mathrm{IF}} \end{gathered} $ | (1) |
| $ \begin{gathered} \phi_{\mathrm{IF}}=\frac{f_1^2 \cdot \phi_1-f_2^2 \cdot \phi_2}{f_1^2-f_2^2}= \\ \rho+c\left(\delta t_{\mathrm{r}}-\delta t^{\mathrm{s}}\right)+T+\lambda_{\mathrm{IF}} b_{\mathrm{IF}}+\delta m+\varepsilon \phi_{\mathrm{IF}} \end{gathered} $ | (2) |
式中,Pi和ϕi分别代表第i个频率上伪距和载波原始观测值,PIF和ϕIF分别代表伪距和载波相位的无电离层组合观测值,bIF代表观测值模糊度,ρ代表卫星与测站接收机之间的几何距离,c代表光速,δtr和δts分别代表接收机和卫星钟差,dr(t)代表接收机端硬件延迟,ds代表卫星端硬件延迟,τrs代表信号在卫星和接收机上的传播时间,t为观测时间,εPIF和εϕIF分别代表两种组合观测值的观测噪声,T代表对流层延迟,δm代表多路径效应,λIF代表载波波长。利用式(1)和式(2)进行批处理最小二乘估计或序贯最小二乘求解,即可得到精确的轨道初始参数。
2.2 轨道积分轨道积分的主要功能是在已知卫星某一时刻的位置、速度和光压参数情况下进行数值积分,得到任意时刻卫星的位置和速度。求解卫星参数的数值方法分为单步法和线性多步法,单步法中Runge-Kutta方法主要用于线性多步法的起步算法,轨道积分中单步法及多步法具体公式参考文献[10]。
2.3 轨道精度评定方法定轨结果精度评定采用内符合的重叠弧段互差和外符合的SLR精度检核两种方法进行。
1) 重叠弧段互差。一般用来评估轨道内部的一致性,也可通过对比两个重叠弧段之间轨道的切向(A)、法向(C)、径向(R)和3D RMS互差值来评定轨道质量。计算公式如下:
| $ \left\{\begin{array}{l} \sigma_{\mathrm{RMS}}^i=\sqrt{\sigma_R^{j^2}+\sigma_A^{j^2}+\sigma_C^{j^2}} \\ \sigma_R^j=\sqrt{\sum\limits_{i=0}^n \mathrm{~d} R_i^{j^2} / n} \\ \sigma_A^j=\sqrt{\sum\limits_{i=0}^n \mathrm{~d} A_i^{j^2} / n} \\ \sigma_C^j=\sqrt{\sum\limits_{i=0}^n \mathrm{~d} C_i^{j^2} / n} \end{array}\right. $ | (3) |
式中,σRMSi表示卫星综合A、C和R三个方向精度得到的3D RMS值,j表示卫星号,n表示历元总数,σRj、σAj及σCj表示重叠弧段在R、A及C方向的偏差平均值,dRij、dAij及dCij表示重叠弧段在第i个历元R、A及C方向的偏差。
2) SLR精度检核。通过激光测距得到地面站到卫星激光反射器的距离检核卫星轨道的径向精度。公式如下:
| $ \sigma=O-C $ | (4) |
式中,σ为SLR检核残差,C为通过激光检核站高精度坐标和轨道估计结果计算的星地距离,O为SLR实际观测值。
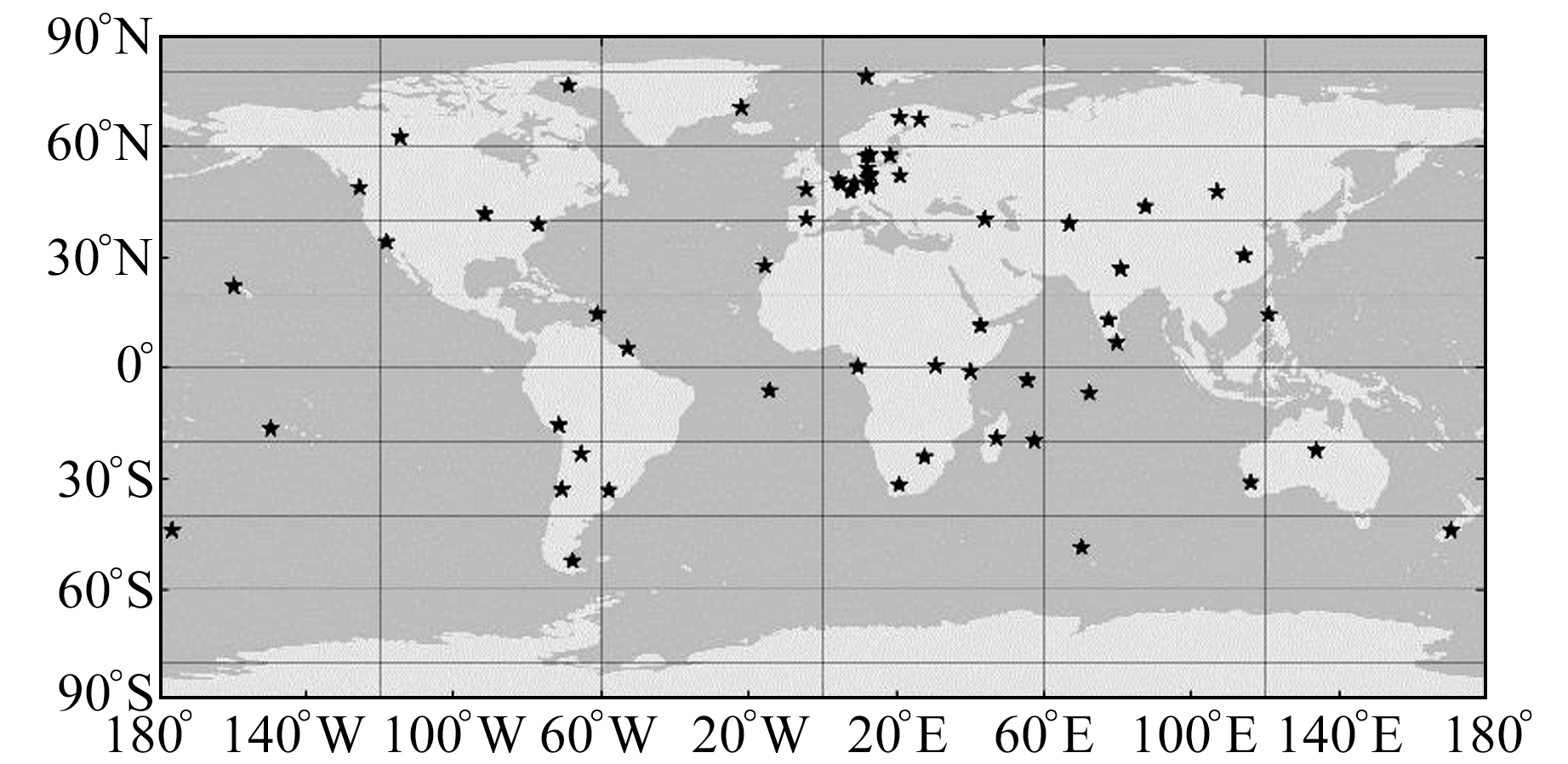
2.4 解算策略本文选择69个全球均匀分布的MGEX测站(图 1)参与精密定轨。BDS-3观测值采用B1C/B2a和B1I/B3I两种无电离层组合观测值,Galileo采用E1/E5a无电离层组合观测值。表 1为精密定轨策略的详细信息,包括观测模型和动态模型。
|
图 1 精密定轨测站分布 Fig. 1 Distribution of stations for precise orbit determination |
|
|
表 1 数据处理策略与相关模型描述 Tab. 1 Description of data processing strategies and related models |
值得说明的是,虽然采用ECOM1模型进行精密定轨能够得到良好的GPS轨道精度,但是Galileo卫星和BDS-3 MEO卫星采用ECOM1模型进行精密定轨时,其SLR残差均随距角变化而出现系统性变化问题。因此,对Galileo卫星与BDS-3 MEO卫星分别采用Montenbruck等[12]和Yan等[13]构建的先验光压模型。
3 实验分析 3.1 B1C/B2a精密定轨结果本节分析利用B1C/B2a组合观测值得到的轨道精度,采用48 h重叠弧段互差和SLR残差对轨道精度进行评估。
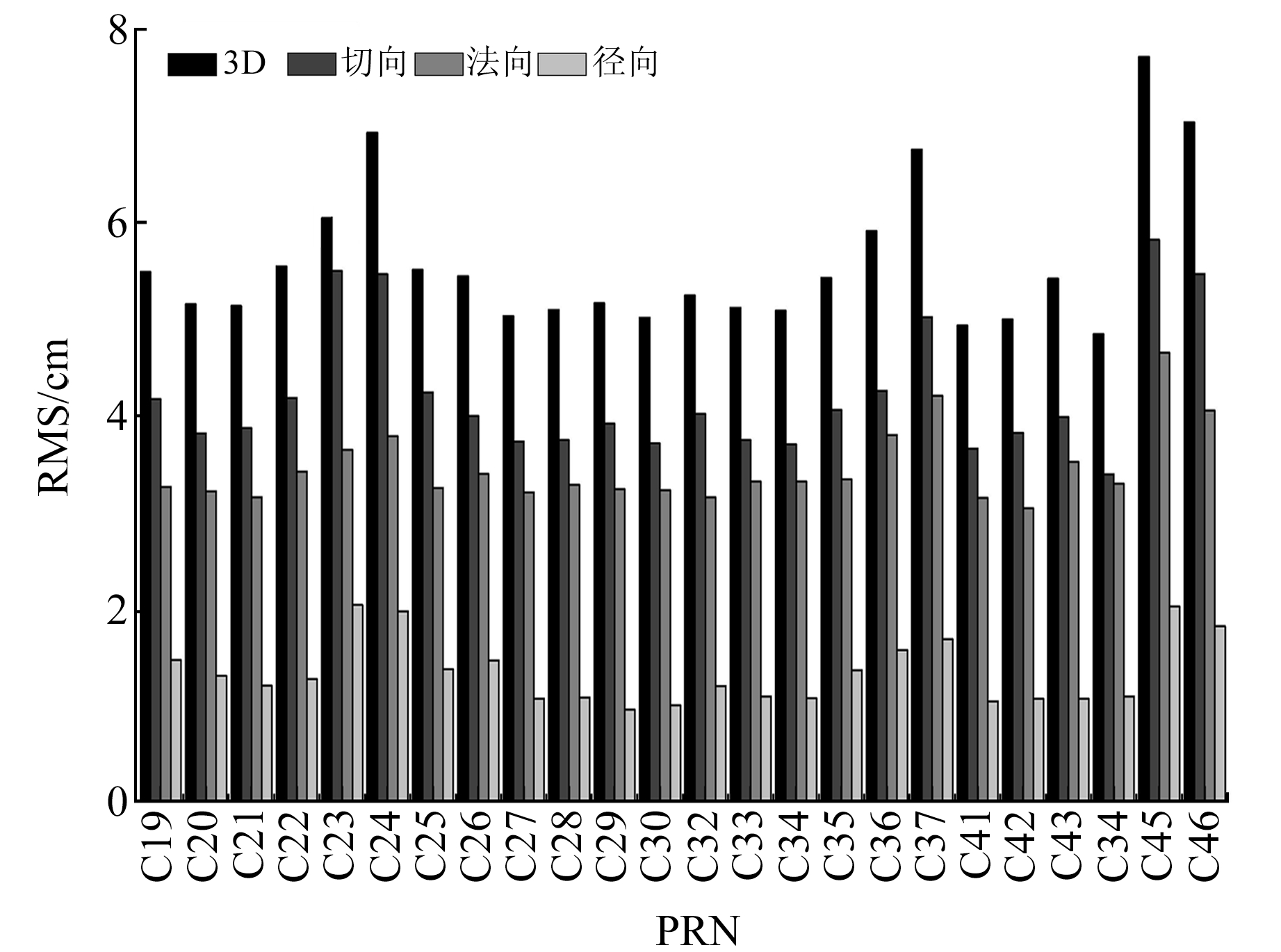
图 2为重叠弧段互差平均值,从图中可以看出,轨道径向互差值远小于轨道切向和法向互差值,24颗BDS-3 MEO卫星轨道切向互差值均优于5 cm,法向互差值优于4 cm,径向互差值优于2 cm,3D RMS值优于7 cm。
|
图 2 基于B1C/B2a组合观测值的BDS-3 MEO卫星48 h重叠弧段互差3D、切向、法向及径向平均值 Fig. 2 Mean RMS of 48 h overlapping arc difference of BDS-3 MEO satellites in along-track, cross-track, radial and 3D directions using combined observations of B1C/B2a |
表 2(单位cm)为24颗MEO卫星重叠弧段切向、法向、径向及3D RMS平均值。由表可知,基于B1C/B2a组合观测值进行精密定轨时,BDS-3 MEO卫星重叠弧段切向、法向、径向及3D RMS平均值分别为4.21 cm、3.45 cm、1.26 cm及5.51 cm。
|
|
表 2 基于B1C/B2a组合观测值的BDS-3 MEO卫星48 h重叠弧段互差3D、切向、法向及径向平均值 Tab. 2 Mean RMS of 48 h overlapping arc difference of BDS-3 MEO satellites in along-track, cross-track, radial and 3D directions using combined observations of B1C/B2a |
SLR残差检核中BDS-3 MEO卫星LRA偏移量采用北斗办公室发布的卫星参数,详细数据见表 3(单位m)。SLR观测数据由ILRS(international laser ranging service)公开提供。
|
|
表 3 BDS-3卫星激光反射器阵列(LRA)偏移量 Tab. 3 Offset of BDS-3 satellite laser retroreflector array(LRA) |
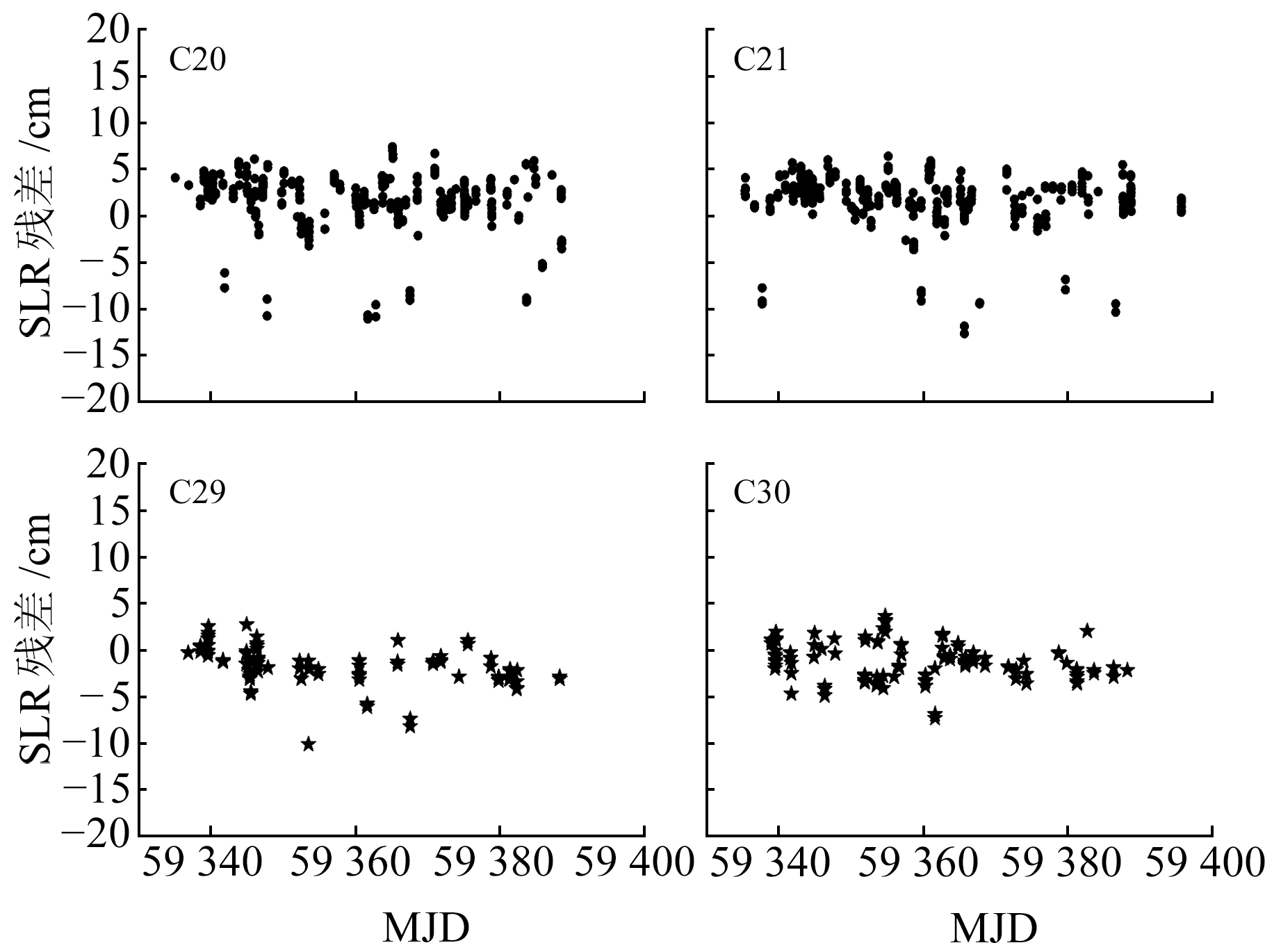
图 3为4颗BDS-3卫星SLR检核残差(五角星为CAST卫星,圆点为SECM卫星),从图中可以看出,SLR残差多数在10 cm以内。
|
图 3 基于B1C/B2a信号的BDS-3 MEO SLR残差 Fig. 3 BDS-3 MEO SLR residual using B1C/B2a signal |
表 4(单位cm)为SLR残差的平均值、标准差、均方根误差及总观测数,对于C20、C21、C29、C30卫星,其SLR检核残差RMS值分别为3.32 cm、3.25 cm、2.79 cm、2.24 cm,SECM卫星SLR检核残差优于CAST卫星。这可能是由于采用的先验光压模型更适用于SECM卫星。
|
|
表 4 基于B1C/B2a信号定轨SLR检核精度 Tab. 4 SLR check accuracy of POD results using B1C/B2a signal |
由于BDS-3保留B1I和B3I信号,且目前各分析中心提供的BDS-3轨道产品均是基于B1I和B3I信号,本节基于相同的定轨策略使用B1I/B3I组合观测值进行精密定轨,并将B1C/B2a和B1I/B3I组合观测值精密定轨结果进行比较。
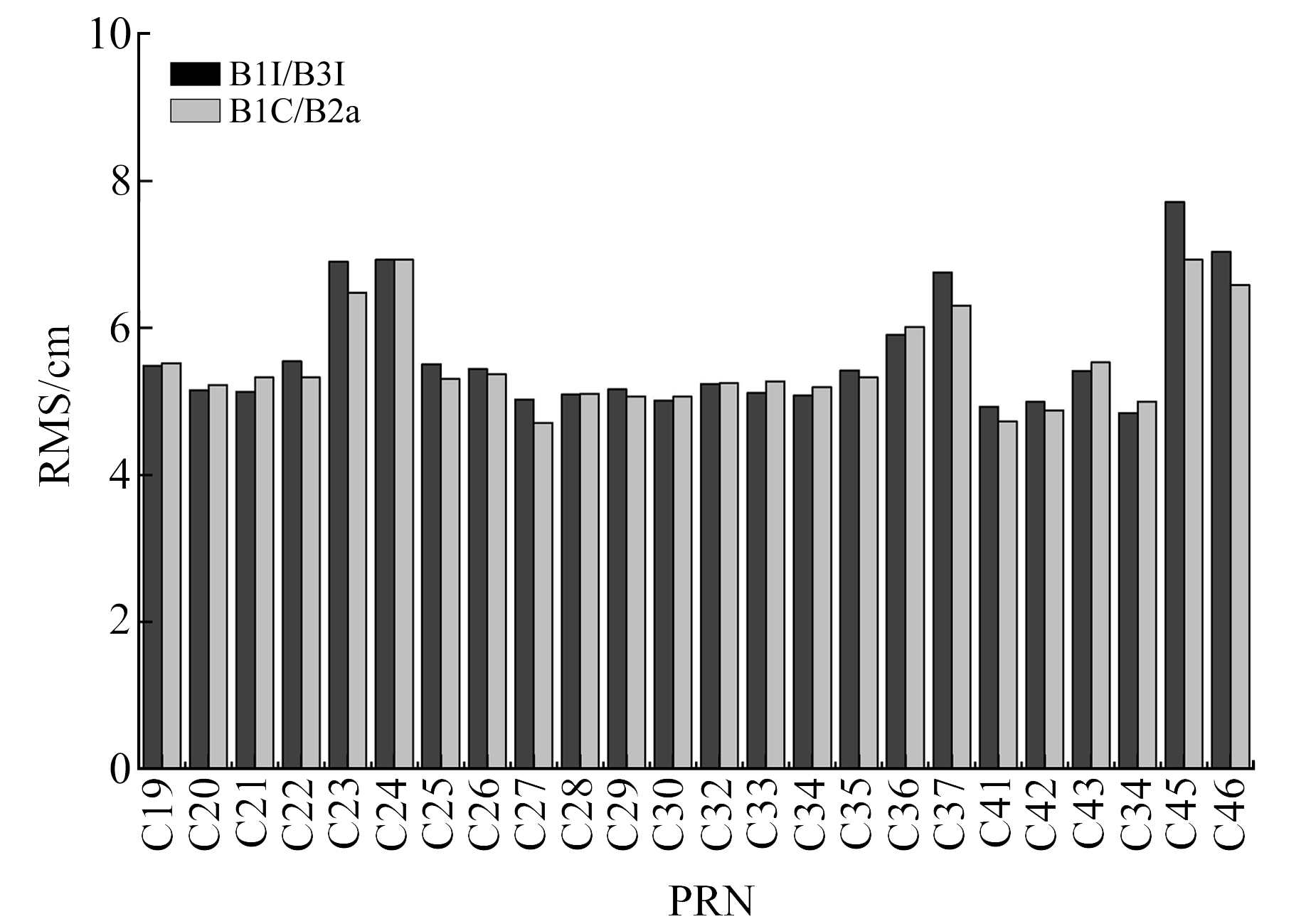
图 4为B1C/B2a与B1I/B3I组合观测值解算的精密轨道产品重叠弧段互差,从图中可以看出,大多数BDS-3 MEO卫星两种定轨精度基本一致,但对于C23、C37、C45、C46卫星而言,使用B1C/B2a组合观测值明显优于B1I/B3I组合观测值。
|
图 4 仅BDS-3 MEO单系统定轨情况下新老信号48 h重叠弧段互差3D RMS平均值 Fig. 4 Mean values of 3D RMS of 48 h overlapping arc difference of old and new signals of only BDS-3 MEO system orbit determination |
表 5(单位cm)为基于B1C/B2a与B1I/B3I组合观测值精密定轨重叠弧段互差。结果显示,基于B1I/B3I组合观测值进行精密定轨时,BDS-3 MEO卫星重叠弧段切向、法向、径向及3D RMS平均值分别为4.22 cm、3.45 cm、1.34 cm及5.61 cm,两种组合观测值重叠弧段互差在3D方向、切向、法向和径向上分别相差0.10 cm、0.11 cm、0.00 cm和0.08 cm。
|
|
表 5 基于B1C/B2a及B1I/B3I精密定轨重叠弧段互差 Tab. 5 Overlapping arc differences based on B1C/B2a and B1I/B3I signals |
表 6(单位cm)为基于B1C/B2a与B1I/B3I组合观测值精密定轨SLR检核残差的平均值、标准差、均方根误差,对于C20、C21、C29、C30卫星,其SLR检核残差RMS值分别为3.31 cm、3.21 cm、2.76 cm、2.40 cm,两种组合观测值SLR检核残差RMS值分别为-0.01 cm、-0.03 cm、-0.03 cm和-0.04 cm。
|
|
表 6 基于B1C/B2a及B1I/B3I信号SLR检核精度比较 Tab. 6 Comparison of orbit SLR check accuracy based on B1C/B2a and B1I/B3I signals |
综合48 h重叠弧段和SLR检核残差结果可知,在BDS-3 MEO单系统定轨情况下,新老信号定轨结果精度相差不超过1 mm,定轨性能基本相当。
3.3 Multi-GNSS精密定轨结果对比本节对比BDS-3基于B1C/B2a和B1I/B3I组合观测值与Galileo E1/E5a组合观测值进行multi-GNSS联合精密定轨结果。测站选择与仅BDS-3 MEO卫星精密定轨一致,所有测站均可接收Galileo E1和E5a信号,解算策略见表 1。
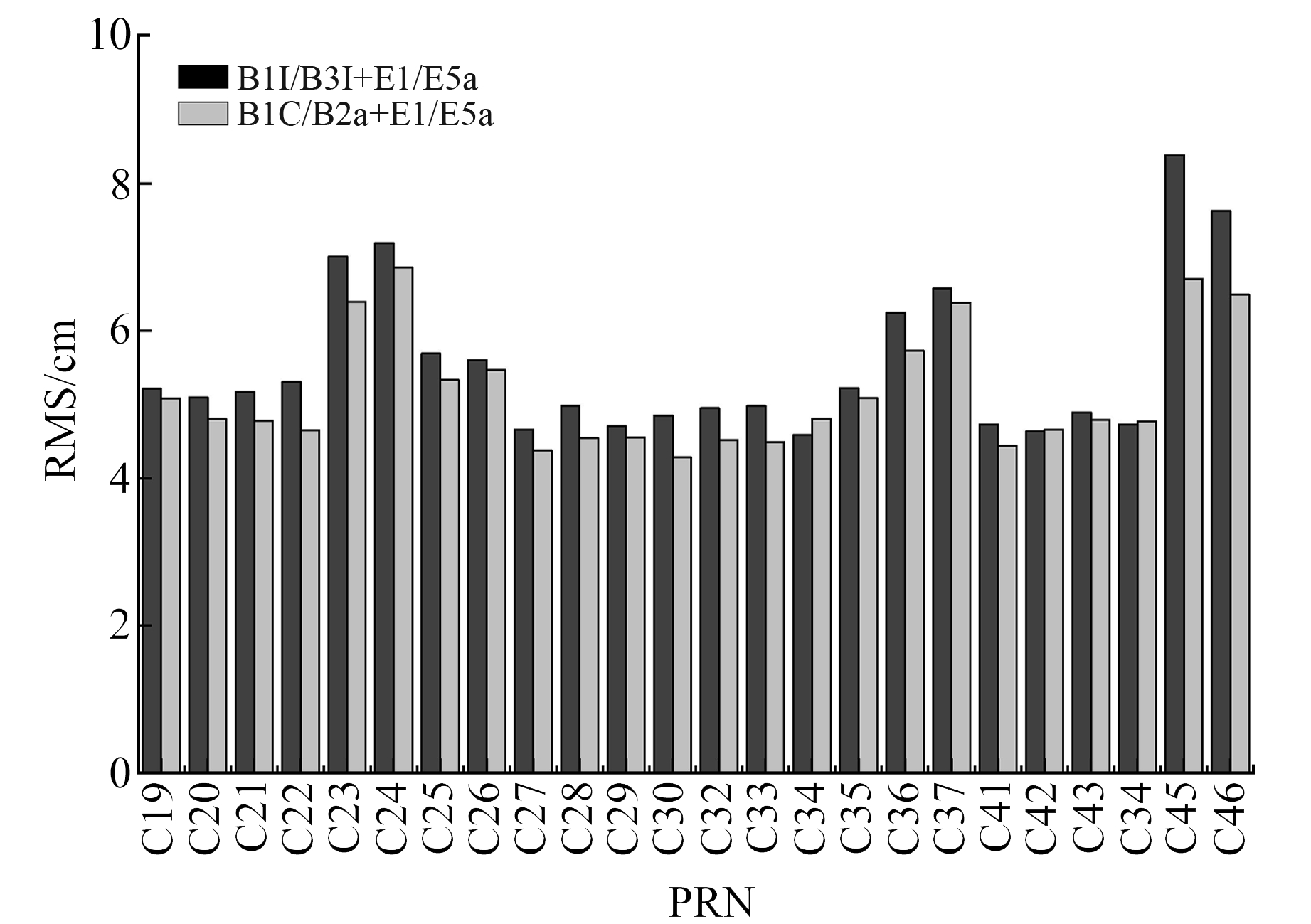
图 5为B1C/B2a及B1I/B3I组合观测值与Galileo E1/E5a组合观测值联合精密定轨结果,从图中可以看出,前者相比于后者大多数BDS-3 MEO卫星轨道质量得到提升,仅C34、C42、C44卫星出现略微下降。
|
图 5 BDS-3新老信号联合Galileo E1/E5a信号定轨重叠弧段互差 Fig. 5 The POD overlapping arc difference of old and new BDS-3 signals combined with Galileo E1/E5a signal |
表 7(单位cm)为仅BDS-3 MEO卫星精密定轨结果和BDS-3 MEO+Galileo联合精密定轨结果,从表中可以看出,BDS-3卫星在BDS-3 MEO+Galileo联合精密定轨时,B1C/B2a相较于B1I/B3I联合精密定轨在3D方向、切向、法向和径向上分别提高0.38 cm、0.30 cm、0.21 cm和0.10 cm,提高率分别为6.86%、7.00%、6.31%和8.62%;当仅BDS-3 MEO定轨时,B1C/B2a与B1I/B3I轨道精度基本相当。
|
|
表 7 BDS-3 MEO卫星两种情况下定轨重叠弧段互差 Tab. 7 The POD overlapping arc difference of BDS-3 MEO satellites under two cases |
为验证Galileo卫星在两种情况下的定轨精度,表 8(单位cm)为本文在两种情况下解算的Galileo轨道与CODE(center for orbit determination in Europe)事后精密轨道产品互差值。由表可知,Galileo卫星在BDS-3 MEO+Galileo联合精密定轨时,如采用B1I/B3I组合观测值,其轨道重叠弧段3D RMS为5.15 cm,在切向、法向和径向分量上分别为3.45 cm、2.90 cm和2.50 cm;当BDS-3采用B1C/B2a组合观测值时,其轨道重叠弧段3D RMS为4.90 cm,在切向、法向和径向分量上分别为3.14 cm、2.81 cm和2.50 cm。后者相比于前者,在3D方向、切向、法向和径向上分别提高0.25 cm、0.34 cm、0.09 cm和0.00 cm。这表明在BDS-3+Galileo联合定轨情况下,BDS-3 MEO使用B1C/B2a组合观测值相比于使用B1I/B3I组合观测值,能得到更高质量的Galileo卫星轨道产品。
|
|
表 8 Galileo卫星两种情况下POD结果与CODE事后轨道产品互差比较 Tab. 8 Comparison of Galileo satellite POD results with CODE final products under two cases |
1) 仅BDS-3 MEO情况下,使用B1C/B2a新信号进行精密定轨,24颗BDS-3 MEO卫星48 h重叠弧段切向互差值均优于5 cm,法向互差值优于4 cm,径向互差值优于2 cm,3D RMS值优于7 cm。SLR检核残差表明,CAST卫星径向精度优于4 cm,SECM卫星优于3 cm。
2) 在相同测站、仅BDS-3 MEO卫星参与精密定轨情况下,48 h重叠弧段结果表明,B1C/B2a组合观测值精密定轨相较于B1I/B3I在3D方向、切向、法向和径向上分别相差0.10 cm、0.11 cm、0.00 cm和0.08 cm。SLR检核残差RMS值在C20、C21、C29及C30卫星分别相差-0.01 cm、-0.03 cm、-0.03 cm和-0.04 cm。综合48 h重叠弧段和SLR检核残差结果可知,在BDS-3 MEO单系统定轨情况下,新老信号定轨性能基本相当。
3) 当加入Galileo E1/E5a进行联合精密定轨时,BDS-3新信号相比于老信号,MEO轨道在3D方向、切向、法向和径向上分别提升0.38 cm、0.30 cm、0.21 cm和0.10 cm,3D RMS值提高明显,提高率为6.86%。Galileo轨道在3D方向、切向、法向和径向上分别提高0.25 cm、0.34 cm、0.09 cm和0.00 cm。BDS-3 MEO与Galileo轨道质量均得到提升。目前各分析中心对于BDS-3产品仍基于B1I/B3I进行解算,随着B1C/B2a数据逐步稳定,可以考虑常态化进行B1C/B2a轨道解算。
| [1] |
杨元喜, 陆明泉, 韩春好. GNSS互操作若干问题[J]. 测绘学报, 2016, 45(3): 253-259 (Yang Yuanxi, Lu Mingquan, Han Chunhao. Some Notes on Interoperability of GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 253-259)
(  0) 0) |
| [2] |
李涌涛, 李建文, 潘林, 等. 北斗三号新信号B1C和B2a观测数据质量分析评估[J]. 地球科学进展, 2018, 33(11): 1 161-1 168 (Li Yongtao, Li Jianwen, Pan Lin, et al. Quality Assessment of the Beidou-3 New Signal B1C and B2a Observation Data[J]. Advances in Earth Science, 2018, 33(11): 1 161-1 168)
(  0) 0) |
| [3] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测——试验验证数据分析[J]. 中国科学: 地球科学, 2018, 48(5): 584-594 (Yang Yuanxi, Xu Yangyin, Li Jinlong, et al. Progress and Performance Evaluation of Beidou Global Navigation Satellite System: Data Analysis Based on BDS-3 Demonstration System[J]. Science China: Earth Sciences, 2018, 48(5): 584-594)
(  0) 0) |
| [4] |
Xiao W, Liu W X, Sun G F. Modernization Milestone: Beidou M2-S Initial Signal Analysis[J]. GPS Solutions, 2016, 20(1): 125-133 DOI:10.1007/s10291-015-0496-7
(  0) 0) |
| [5] |
Yan X Y, Huang G W, Zhang Q, et al. Early Analysis of Precise Orbit and Clock Offset Determination for the Satellites of the Global Beidou-3 System[J]. Advances in Space Research, 2019, 63(3): 1 270-1 279 DOI:10.1016/j.asr.2018.10.038
(  0) 0) |
| [6] |
Zhang Y Z, Kubo N, Chen J P, et al. Initial Positioning Assessment of BDS New Satellites and New Signals[J]. Remote Sensing, 2019, 11(11)
(  0) 0) |
| [7] |
Xu X L, Wang X L, Liu J N, et al. Characteristics of BD3 Global Service Satellites: POD, Open Service Signal and Atomic Clock Performance[J]. Remote Sensing, 2019, 11(13)
(  0) 0) |
| [8] |
Li R, Wang N B, Li Z S, et al. Precise Orbit Determination of BDS-3 Satellites Using B1C and B2a Dual-Frequency Measurements[J]. GPS Solutions, 2021, 25(3)
(  0) 0) |
| [9] |
张睿. BDS精密定轨关键技术研究[J]. 测绘学报, 2018, 47(9): 1 290 (Zhang Rui. Research on Key Technologies of BDS Precise Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(9): 1 290)
(  0) 0) |
| [10] |
赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004 (Zhao Qile. Research on Precision Orbit Determination Theory and Software of both GPS Naviagation Constellation and LEO Satellites[D]. Wuhan: Wuhan University, 2004)
(  0) 0) |
| [11] |
楼益栋. 导航卫星实时精密轨道与钟差确定[D]. 武汉: 武汉大学, 2008 (Lou Yidong. Research on Real-Time Precise GPS Orbit and Clock Offset Determination[D]. Wuhan: Wuhan University, 2008)
(  0) 0) |
| [12] |
Montenbruck O, Steigenberger P, Hugentobler U. Enhanced Solar Radiation Pressure Modeling for Galileo Satellites[J]. Journal of Geodesy, 2015, 89(3): 283-297 DOI:10.1007/s00190-014-0774-0
(  0) 0) |
| [13] |
Yan X Y, Liu C C, Huang G W, et al. A Priori Solar Radiation Pressure Model for Beidou-3 MEO Satellites[J]. Remote Sensing, 2019, 11(13)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


