2. 广西建设职业技术学院土木工程学院,南宁市罗文大道33号,530007
针对卫星广播星历提供的钟差数据精度较低、难以满足精密单点定位(PPP)需求,国际GNSS服务(IGS)组织于2000年开始提供高精度的卫星钟差产品。但这些产品是基于采样间隔的离散化序列结果,以离散形式表述和服务的卫星钟差,随着采样间隔增加,占用的存储空间也会增加,并未充分发挥卫星钟差中显著的规律性变化特性。因此,研究一种以参数方式代替序列化数值的方法,以减少产品存储空间,并充分利用卫星钟差的显著特性十分必要。目前,国内外钟差研究中常用的模型有一次多项式模型、二次多项式模型、灰色模型以及自回归滑动平均模型(ARIMA)等[1-6],其中一、二次多项式模型可高精度地表示卫星钟差短时间内的变化,而卫星钟差中除一、二次项的变化趋势外,还存在一些显著的周期项变化[7-11]。
本文通过对2021年(GPS周2 138~2 190)IGS BDS-3精密钟差数据进行分析,在二次多项式拟合残差基础上采用快速傅里叶变换(FFT)方法分析残差的周期特性[12-13],构造高精度卫星钟差模型化函数,并在研究BDS-3卫星原子钟特性基础上实现高精度、长时间模型化,以分析其在PPP中的性能。
1 模型分析星载原子钟在运行过程中会出现频率漂移现象,给后续定位产生很大影响。卫星时钟最常见的误差模型为n阶多项式模型,其表达式为:
| $ \operatorname{clk}(t)=a_0+\sum\limits_{k=1}^n\left(a_k \times t^k\right) $ | (1) |
式中,a0为常数项,ak(k=1~n)为k阶多项式系数,clk(t)为t时刻卫星钟差。在卫星导航文件中,通常采用相位、频率、频漂3个因素作为二次多项式系数来对钟差进行拟合。研究表明,卫星钟差具有明显的周期特性,可通过傅里叶变换进行频谱分析来提取卫星钟差的周期项。对于离散型傅里叶级数,其表达式为:
| $ X(k)=\sum\limits_{n=0}^{N-1} x(n) \mathrm{e}^{-\frac{i 2 \pi}{k} k n} $ | (2) |
式中,X(k)为k时段的频谱值,x(n)为拟合残差序列,i为虚数单位,e为自然底数,n为残差序列号,N为残差序列个数。在实际计算中,采用快速傅里叶变换进行频谱分析,根据频谱即可确定周期项。基于频谱分析得到的周期项对钟差进行建模,构造钟差序列结合二次多项式的周期项模型:
| $ \begin{gathered} \operatorname{clk}(t)=a_0+\sum\limits_{k=1}^2\left(a_k \times t^k\right)+ \\ \sum\limits_{m=1}^n A_m \times \sin \left(\frac{2 \pi}{T_m} t+\Phi_m\right) \end{gathered} $ | (3) |
式中,n为周期项个数,Tm为周期,Am为振幅,Φm为初始相位,a0、ak为多项式系数。
2 数据处理利用2021年(GPS周2 138~2 190)IGS采样间隔为30 s的BDS-3最终卫星精密钟差产品进行分析。首先通过快速傅里叶方法分析卫星钟的周期项,然后在BDS-3原子钟周期特性基础上进行模型化效果分析,以构建高精度、长时间的卫星钟差模型化函数,并采用5个IGS站数据分析其PPP性能。5个IGS站分布如图 1所示。

|
图 1 5个IGS站分布 Fig. 1 Distribution of 5 IGS stations |
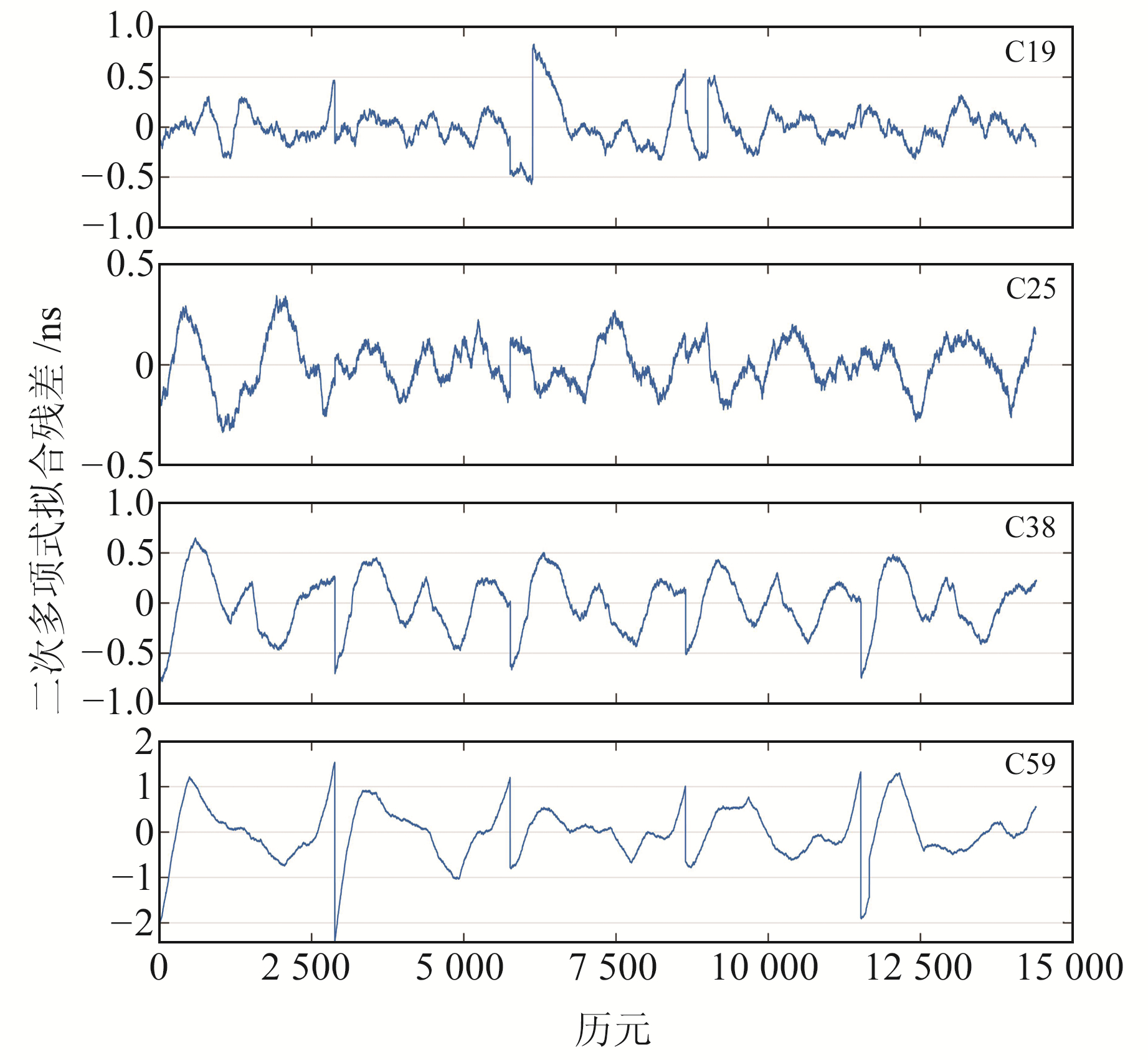
以C19(MEO)、C25(MEO)、C38(IGSO)、C59(GEO)4颗卫星的钟差数据为例,分析二次多项式拟合残差特性。图 2为4颗卫星2021-07-01~05共5 d的IGS最终钟差数据文件去除趋势项后的拟合残差,采样间隔为30 s,共14 400个历元。由图 2可知,去除二次多项式趋势后的拟合残差具有明显的周期变化特性,表明BDS-3钟差除二次多项式趋势外还具有一定的周期特征,这些周期特性对于高精度卫星钟差模型化具有重要意义。
|
图 2 C19、C25、C38和C59卫星二次拟合残差 Fig. 2 Quadratic fitting residuals of C19, C25, C38 and C59 satellites |
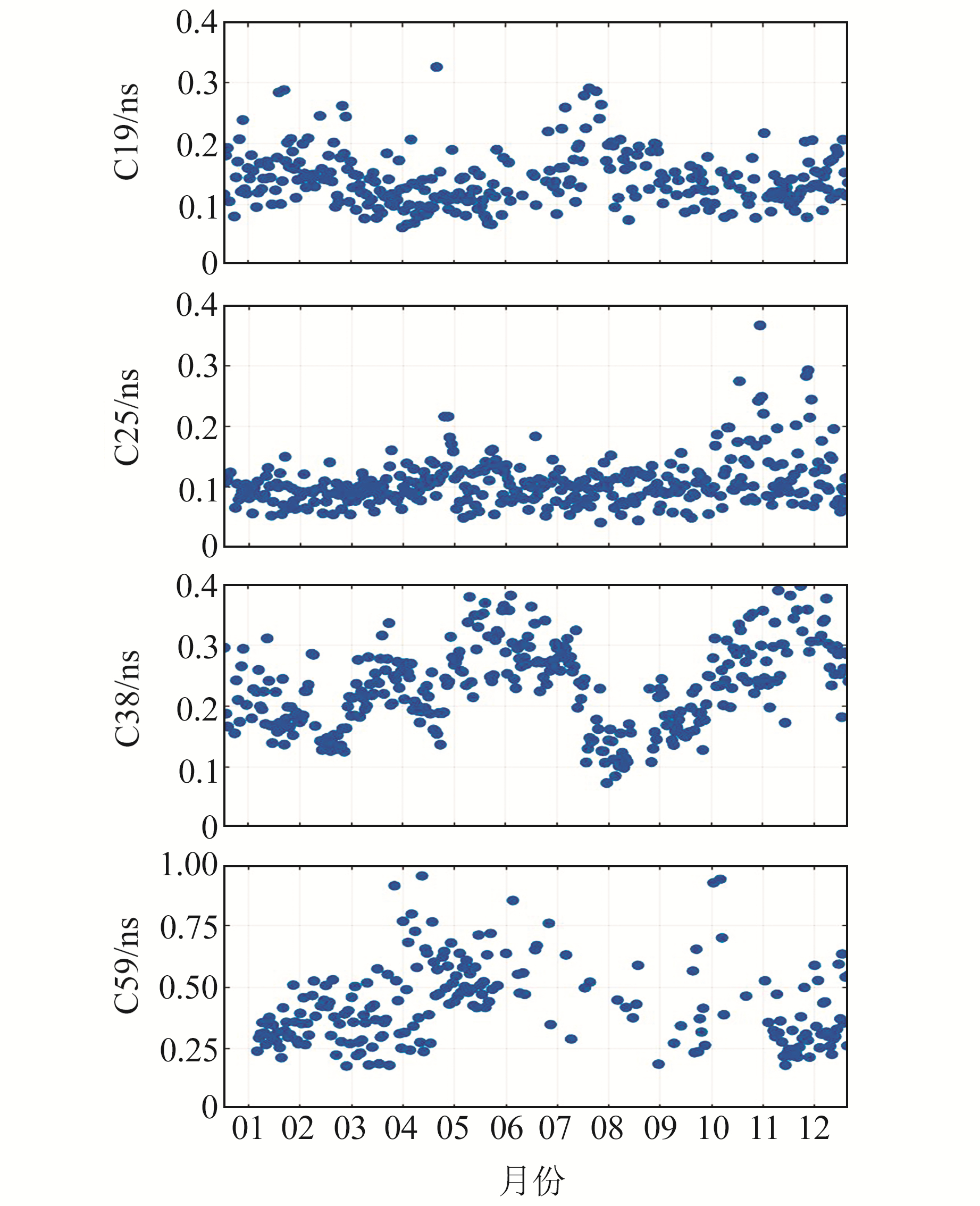
计算所有卫星1 a残差的单日均方根,统计年平均值,结果如表 1所示。图 3为C19、C25、C38、C59卫星2021年单日二次多项式拟合残差RMS结果,图中横坐标为相应月份。结合表 1和图 3可以看出,MEO卫星的拟合残差较小,C19和C25卫星的二次多项式拟合残差分别为0.14 ns和0.11 ns左右,而C38(IGSO)卫星的拟合残差约为0.24 ns,GEO卫星的拟合残差较大,C59卫星的拟合残差为0.34 ns左右。
|
|
表 1 BDS-3卫星二次拟合残差RMS年均值 Tab. 1 Annual average residual RMS of quadratic fitting of BDS-3 satellites |
|
图 3 C19、C25、C38和C59卫星二次多项式单日拟合残差RMS Fig. 3 Single-day residual RMS of quadratic polynomials fitting of C19, C25, C38 and C59 satellites |
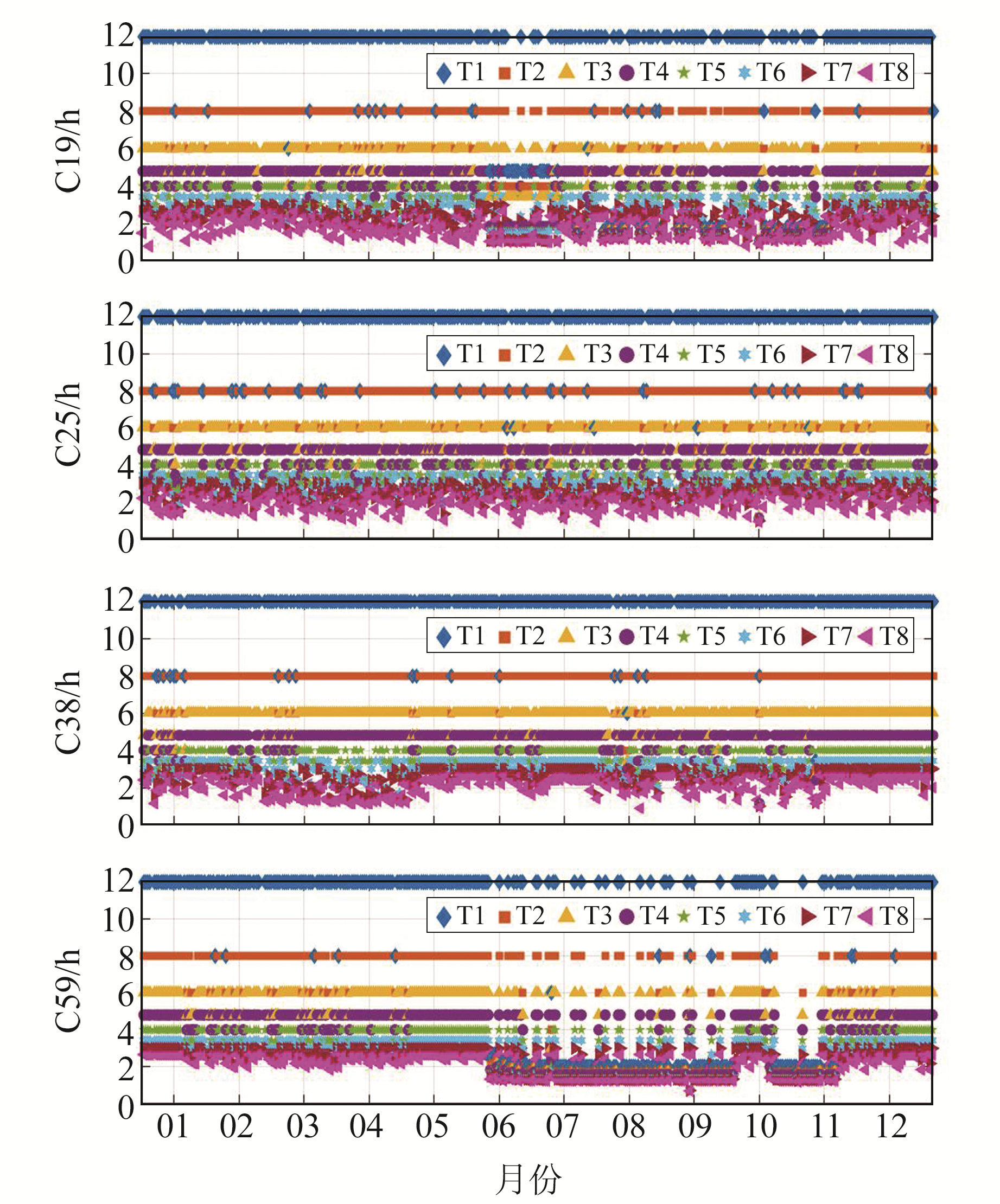
由§2.1可知,BDS-3卫星原子钟不仅含有二次多项式趋势,还存在一定周期性。对二次多项式的拟合残差进行频谱分析,运用快速傅里叶变换将残差序列转换到频率域,并对数据幅值波形进行分析,找出卫星钟差存在的周期规律,以进行周期项分析。为分析残差序列的周期特征,对2021年IGS最终精密钟差数据进行频谱分析,图 4为C19、C25、C38、C59四颗卫星每日前8个周期的结果,从图中可以看出,卫星在不同天内表现出的周期性有所差别,可能是由于接收到BDS-3信号的测站分布不均匀,导致钟差数据存在部分历元缺失所致。因此,在构造附加周期项函数模型时,需考虑不同卫星在不同时间具有不同主周期的特性。表 2为BDS-3所有卫星1 a内最常见的8个显著周期,从表中可以看出,不同轨道和星载原子钟类型卫星在周期上无较大差别,常见的周期有12 h(每天2个周期)、8 h(每天3个周期)、6 h(每天4个周期)、4.8 h及4 h等,这些周期均比较稳定,接近卫星轨道的运行周期。但也存在如2.7 h、2.4 h等小周期,无法与轨道周期耦合,说明还有部分其他因素可能会影响卫星时钟或信号,可能与太阳光照的热变化、卫星内部硬件、不同轨道平面及复杂空间环境有关[14-16]。
|
图 4 C19、C25、C38和C59卫星1 a单日周期 Fig. 4 Single-day periods of satellite clock for C19, C25, C38 and C59 satellites in one year |
|
|
表 2 BDS-3卫星8个显著周期信息 Tab. 2 Information of eight significant periods of BDS-3 satellites |
根据卫星钟的主要周期项,对每日卫星钟差产品进行模型化分析,计算基于二次多项式附加表 2中前4个周期、前6个周期及8个周期后函数的拟合残差及其1 a每日残差RMS,结果见图 5。从图中可以看出,对于卫星钟差去除二次项趋势后残差的周期特性,加入周期项改正模型可提高对钟差数据的拟合精度,且随着加入周期项数的增加,拟合精度也在提高。但根据对拟合残差周期特性的分析可知,除前几个较为稳定的主周期外,还存在不稳定的小周期,因此加入的周期项数过多,可能会带来误差影响,对拟合精度的提高无明显作用。由图 5可知,附加8个周期的模型拟合精度最高,相比多项式拟合精度提高约70%,适合参数化BDS-3卫星钟差。

|
图 5 BDS-3卫星二次多项式附加4个周期、6个周期及8个周期的年均拟合残差RMS Fig. 5 Annual average residual RMS of quadratic polynomial fitting of BDS-3 satellites with 4 periods, 6 periods and 8 periods |
对建模后的钟差数据进行PPP计算,并与原始IGS精密钟差数据进行比较,分析其定位精度。利用基于不同模型化函数生成的24 h参数化卫星钟差产品,对PPP性能进行测试,统计5个IGS站2021-07-31参数化卫星钟差和IGS钟差的静态和动态PPP结果,数据采样间隔为30 s,截止高度角为10°,使用B1和B3观测的无电离层组合,并对地潮、天线相位中心偏移和地转等影响进行修正,分析定位误差及收敛时间,其中收敛时间定义为在N、E、U三方向连续的估计坐标误差小于10 cm时所经过的时间。根据估计历元坐标误差计算PPP结果的RMS误差,图 6为静态PPP在三方向的平均收敛时间,24 h静态和动态PPP误差的平均RMS如图 7所示。由图 6和图 7可知,模型化产品的静态定位结果可达cm级,但其收敛时间比IGS序列化产品长。二次多项式模型化由于忽略卫星钟差存在的周期性特征,在定位精度和收敛时间上均最差,附加8个周期项的模型化处理结果优于其他模型,但比IGS序列化产品略差,尤其是在U方向收敛时间方面。上述结果表明,BDS-3卫星钟差的模型化服务方法仍需改进。

|
图 6 静态PPP处理的平均收敛时间 Fig. 6 Average convergence time of static PPP processing |

|
图 7 静态和动态定位精度 Fig. 7 Static and kinematic positioning accuracy |
卫星钟差是影响卫星定位精度的重要因素之一,研究其特性并进行高精度估计和服务是GNSS系统的重要工作。目前,精确的卫星钟差由IGS组织提供,并以离散序列形式存储,这会占据大量内存空间,而采用高精度模型化函数系数代替时钟序列可简化服务模式。本文基于2021年BDS-3卫星钟差数据,通过对卫星钟差序列进行建模,分析BDS-3卫星钟特点,得出以下结论:
1) 卫星钟差在去除二次多项式趋势后具有明显的周期性规律,经过傅里叶变换后可得到12 h、8 h、6 h、4.8 h等较稳定的主要周期项,另外还存在不太稳定的小周期项。
2) 结合卫星钟存在的周期特性,构造不同的高精度模型化函数。结果表明,加入周期改正的模型化精度比二次多项式高,附加8个周期项的模型精度相比二次多项式提高约70%。
3) 将模型化后的钟差数据应用于PPP处理中,其定位结果均能达到cm级,其中附加8个周期项的模型函数优于其他2种函数,但收敛时间均比IGS最终钟差产品慢。模型化钟差数据在PPP处理中的精度略差于IGS钟差序列结果,但模型化钟差数据可极大减小产品存储空间。
| [1] |
王宇谱. GNSS星载原子钟性能分析与卫星钟差建模预报研究[J]. 测绘学报, 2018, 47(7): 1 026 (Wang Yupu. Research on Modeling and Prediction of the Satellite Clock Bias and Performance Evaluation of GNSS Satellite Clocks[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 1 026)
(  0) 0) |
| [2] |
Xi C, Cai C L, Li S M, et al. Long-Term Clock Bias Prediction Based on an ARMA Model[J]. Chinese Astronomy and Astrophysics, 2014, 38(3): 342-354 DOI:10.1016/j.chinastron.2014.07.010
(  0) 0) |
| [3] |
黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报: 信息科学版, 2008, 33(5): 496-499 (Huang Guanwen, Zhang Qin, Xu Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 496-499)
(  0) 0) |
| [4] |
杨定江, 马泽林, 李卓凡, 等. 顾及周期项的北斗卫星钟差建模与预报[J]. 北京测绘, 2020, 34(6): 819-824 (Yang Dingjiang, Ma Zelin, Li Zhuofan, et al. Modeling and Forecasting of Beidou Satellite Clock Error Considering Periodic Items[J]. Beijing Surveying and Mapping, 2020, 34(6): 819-824 DOI:10.19580/j.cnki.1007-3000.2020.06.020)
(  0) 0) |
| [5] |
Huang G W, Cui B B, Zhang Q, et al. An Improved Predicted Model for BDS Ultra-Rapid Satellite Clock Offsets[J]. Remote Sensing, 2018, 10(1)
(  0) 0) |
| [6] |
王利, 张勤, 黄观文, 等. 基于指数平滑法的GPS卫星钟差预报[J]. 武汉大学学报: 信息科学版, 2017, 42(7): 995-1 001 (Wang Li, Zhang Qin, Huang Guanwen, et al. GPS Satellite Clock Bias Prediction Based on Exponential Smoothing Method[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 995-1 001)
(  0) 0) |
| [7] |
毛亚, 王潜心, 胡超, 等. BDS-3卫星钟差特性分析[J]. 武汉大学学报: 信息科学版, 2020, 45(1): 53-61 (Mao Ya, Wang Qianxin, Hu Chao, et al. Analysis of the Characterization for BDS-3 Satellite Clock Error[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1): 53-61)
(  0) 0) |
| [8] |
王宁, 王宇谱, 李林阳, 等. BDS星载原子钟频率稳定性分析[J]. 武汉大学学报: 信息科学版, 2017, 42(9): 1 256-1 263 (Wang Ning, Wang Yupu, Li Linyang, et al. Stability Analysis of the Space-Borne Atomic Clock Frequency for BDS[J]. Geomatics and Information Science of Wuhan University, 2017, 42(9): 1 256-1 263)
(  0) 0) |
| [9] |
王宇谱, 陈正生, 李伟杰, 等. BDS卫星钟差短期预报性能分析[J]. 大地测量与地球动力学, 2017, 37(5): 450-456 (Wang Yupu, Chen Zhengsheng, Li Weijie, et al. Analyzing the Short-Term Prediction Performance of BDS Satellite Clock Bias[J]. Journal of Geodesy and Geodynamics, 2017, 37(5): 450-456 DOI:10.14075/j.jgg.2017.05.003)
(  0) 0) |
| [10] |
Xie X, Geng T, Zhao Q L, et al. Performance of BDS-3: Measurement Quality Analysis, Precise Orbit and Clock Determination[J]. Sensors, 2017, 17(6): 1 233-1 240 DOI:10.3390/s17061233
(  0) 0) |
| [11] |
周佩元, 杜兰, 路余, 等. 多星定轨条件下北斗卫星钟差的周期性变化[J]. 测绘学报, 2015, 44(12): 1 299-1 306 (Zhou Peiyuan, Du Lan, Lu Yu, et al. Periodic Variations of Beidou Satellite Clock Offsets Derived from Multi-satellite Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1 299-1 306)
(  0) 0) |
| [12] |
胡广书. 数字信号处理: 理论、算法与实现[M]. 北京: 清华大学出版社, 2003 (Hu Guangshu. Theory, Algorithm and Implementation of Digital Signal Processing[M]. Beijing: Tsinghua University Press, 2003)
(  0) 0) |
| [13] |
Li H J, Liao X L, Li B F, et al. Modeling of the GPS Satellite Clock Error and Its Performance Evaluation in Precise Point Positioning[J]. Advances in Space Research, 2018, 62(4): 845-854 DOI:10.1016/j.asr.2018.05.025
(  0) 0) |
| [14] |
Senior K L, Ray J R, Beard R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12: 211-225 DOI:10.1007/s10291-008-0089-9
(  0) 0) |
| [15] |
Li H J, Zhou X H, Wu B. Fast Estimation and Analysis of the Inter-Frequency Clock Bias for Block ⅡF Satellites[J]. GPS Solutions, 2013, 17(3): 347-355 DOI:10.1007/s10291-012-0283-7
(  0) 0) |
| [16] |
Ye Z, Li H J, Wang S J. Characteristic Analysis of the GNSS Satellite Clock[J]. Advances in Space Research, 2021, 68(8): 3 314-3 326 DOI:10.1016/j.asr.2021.06.030
(  0) 0) |
2. School of Civil Engineering, Guangxi Polytechnic of Construction, 33 Luowen Road, Nanning 530007, China
 2023, Vol. 43
2023, Vol. 43


