近年来,随着观测仪器的大量布设和震例资料的不断累积,地震前兆异常研究获得越来越多的关注,其中破年变异常研究较为普遍[1-2]。该类异常过去主要以人工判别为主,为提升客观性,相关学者开展定量提取算法研究,以正常年变背景拟合为基础,提出包括距平法、最小二乘法、分段最小二乘法、滑动傅里叶方法和奇异谱分析方法等典型算法[3-5]。其中,距平法、最小二乘法构建的背景年变时序相对固定,无法适应变化的背景年变;分段最小二乘法通过分段形式解决背景年变变化问题,但会在分段点处引入阶跃;滑动傅里叶方法对非正/余弦波及非平稳时序周期成分的识别不太稳定;奇异谱分析方法存在相移现象,且处理过程中部分参数需要根据实际情况进行交互设置,不利于自动化业务应用。在预报效能定量评估方面,目前的主要依据包括有震报准率、无震报准率、漏报率、虚报率、时空占有率等参数,对上述参数进行适当组合,形成R值评分、Molchan图表法、接收者操作特性(ROC)曲线等评估方法[6-8]。虽然上述方法的侧重点不同,但相互之间具有一定的关联,在实际预报业务中得到广泛应用。
本文提出一种基于时频分析方法的破年变信息分离提取流程,并基于双向非对称阈值策略,结合R值评分及Molchan图表法构建预测指标确定和效能定量评估方法。以新疆库尔勒水平摆倾斜北南测项的处理分析为例,介绍该方法的实际应用过程。
1 破年变信息提取及预测指标效能评估方法 1.1 基于时频分析方法的破年变信息提取流程时频分析方法在多组分信号非稳态时频演化过程研究中具备优势,比较适合破年变信息的分离和提取。本文将时频分析类方法中应用相对广泛的S变换方法[9]作为流程构建基础,该方法具有良好的时频聚集性和时频分辨率。具体步骤如下:
1) S变换处理。在去台阶、去突跳点、缺数插值等预处理基础上,针对日值采样数据进行数据筛选,选择观测时长较长且年变显著的数据用于S变换计算(基于频段幅值比进行年变显著程度的定量评估)。为降低边界效应,对数据两侧进行数据总长度7.5%的扩边处理。
2) 信息指标建立。基于计算结果建立2个信息指标,分别为年频段归一化平均幅度(ANA)和其他频段归一化平均幅度(ONA)。具体定义如下:
| $ y(t) = \frac{1}{{{\mathop{\rm num}\nolimits} }}\sum\limits_{T = {T_1}}^{{T_2}} | S(t, T)| $ | (1) |
| $ {y_{{\rm{norm }}}}(t) = \frac{{y(t) - \overline y }}{y} $ | (2) |
式中,S(t, T)为S变换结果,t为观测时间,T为信号周期,num为累加的不同周期信号个数,
预测指标确定和效能评估最常用的方法为R值评分法。R值为扣除随机概率后的预报成功率,R=0表示预报无效。当同样的R值基于的地震次数不同时,信度也不同,因此还需要考虑R0值。当R值大于R0值时可认为,该R值至少有97.5%的置信度[10]。Molchan图表法同样考虑了漏报率、预报占时率等要素,可通过概率增益、显著性水平等要素对模型预测能力展开进一步评价。
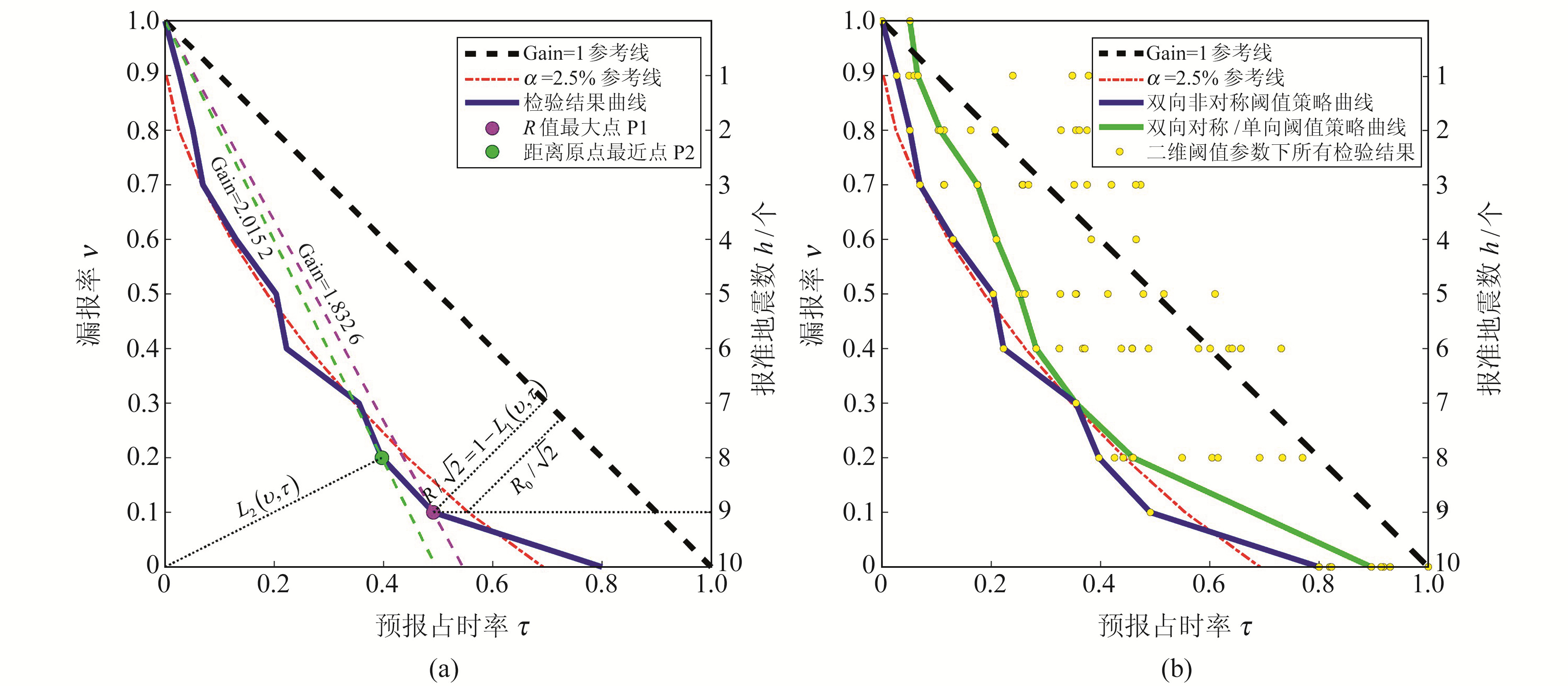
综上所述,动态设置一系列异常阈值,利用漏报率、预报占时率建立坐标,可生成Molchan曲线。基于该曲线可确定特定规则下(特定震级范围、预报范围及预报时窗)的相对最优阈值,即同时考虑距对角线最远点P1及距原点最近点P2,从中选择概率增益更大点对应的阈值参数(概率增益Gain=有震报准率/预报占时率,可反映与随机概率相比目前概率的提升倍数)。P1实际对应R值最大点,即漏报率、预报占时率L1范数最小点,P2则对应漏报率、预报占时率L2范数最小点。当Molchan曲线点位于显著性水平α=2.5%参考线左侧时,表示该点对应的R值大于R0值(图 1(a))。采用双向非对称二维阈值策略(信息指标小于负向阈值Th1或大于正向阈值Th2,均被判定为异常,Th2>Th1),可充分考虑正向、负向异常差异性。同一漏报率可能会对应多个预报占时率,需从中选择预报占时率最小时所对应的阈值参数组合。常用的双向对称阈值、单向阈值等一维参数均为该策略的特例,因此基于双向非对称阈值策略获得的阈值参数预测效能最优(图 1(b))。按照震级档对空间范围、预报时窗等参数进行调整,重复上述相对最优参数指标计算过程,对比不同参数组合下的R值,选择最大值对应的空间范围、预报时窗、阈值参数作为该震级档的最优预测指标。若R值相同,则可进一步依据高概率增益、低显著性水平进行筛选。
|
图 1 预测指标确定和效能评估定量方法原理 Fig. 1 Quantitative methods for predictor determination and efficacy assessment |
新疆库尔勒台周边中强地震相对较多,以该台站水平摆倾斜北南测项为例,介绍上述方法的实际应用过程。使用数据时段为2008-01-01~2022-02-22(图 2(a)),该数据频段幅值比为2.02,具备相对清晰的年变背景(图 2(b))。

|
图 2 新疆库尔勒台水平摆倾斜北南测项观测曲线及年变显著程度检测 Fig. 2 The NS component of the horizontal pendulum tiltmeter in the Korla station in Xinjiang and the detection of significant degree of annual variation |
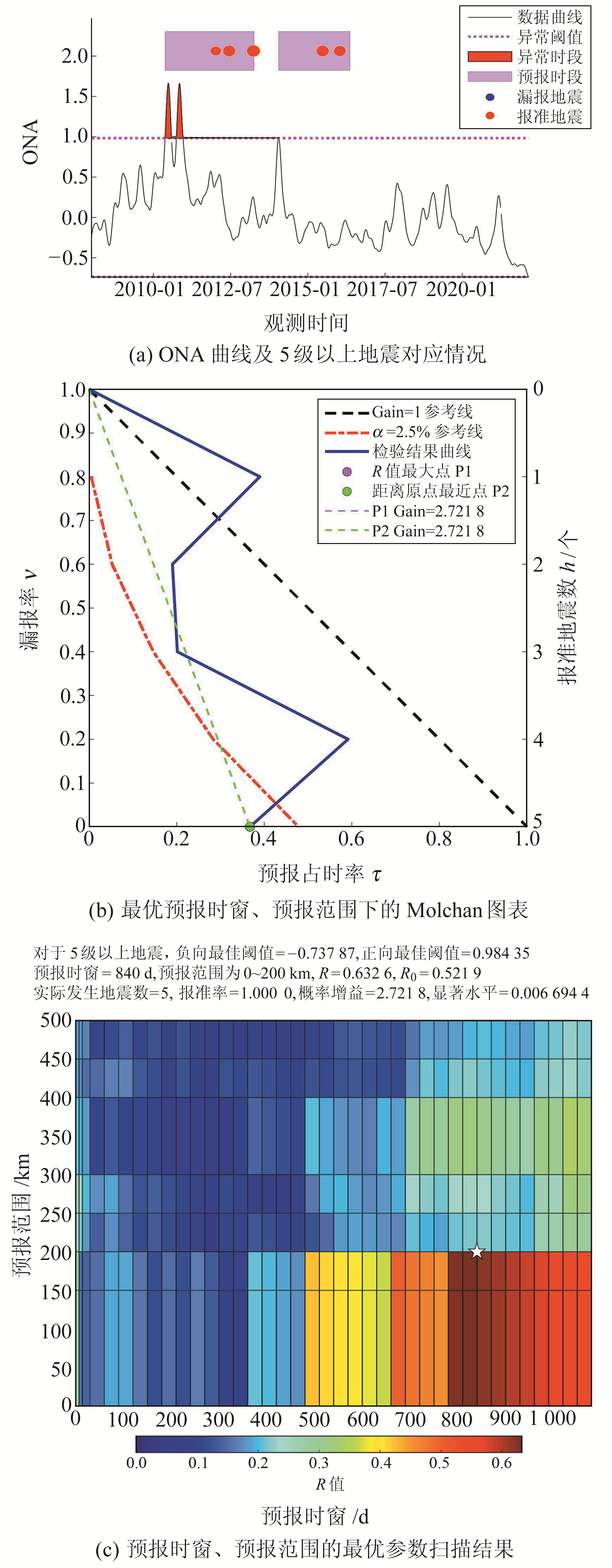
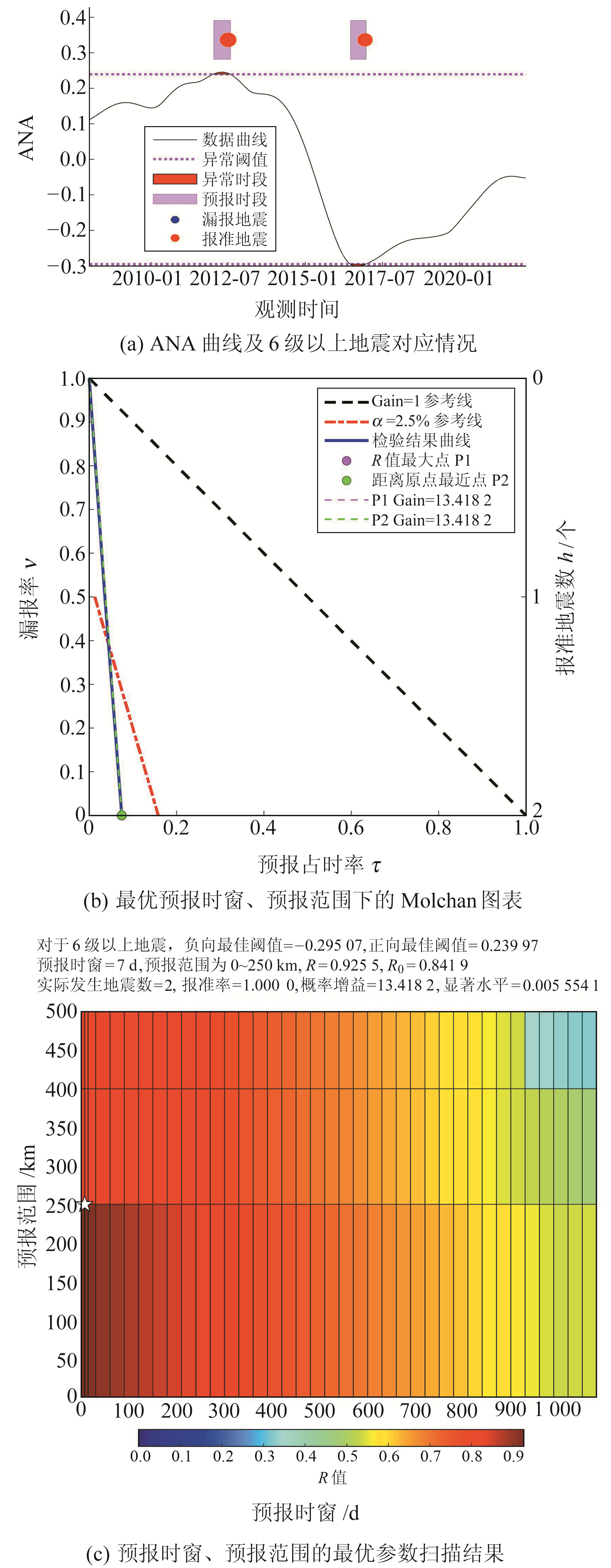
图 3(a)、图 4(a)分别为其他频段归一化平均幅度ONA(周期为14~500 d)以及年频段归一化平均幅度ANA(周期为250~500 d)曲线图。ONA可显示短周期信号的变化情况,由图 3(a)可见,2015年之前周期信号变化相对剧烈,2015年之后变化相对减缓;ANA可反映背景年变信号演化过程,由图 4(a)可见,ANA指标幅度缓慢增大,并在2012-07前后达到峰值,之后逐渐减小,2016-08前后再次缓慢增大。基于该信息,根据M≥5和M≥6两个震级档开展预测指标确定和效能评估。图 3(c)和图 4(c)为不同预报时窗、不同空间范围下相对最优阈值组合对应的R值分布情况,白色五角星为最优空间范围和预报时窗所处位置。
|
图 3 库尔勒台站周边ONA信息的5级以上地震预测指标及对应效能 Fig. 3 Forecasting index and corresponding performance of ONA information for M≥5 earthquakes around the Korla station |
|
图 4 库尔勒台站周边ANA信息的6级以上地震预测指标及对应效能 Fig. 4 Forecasting index and corresponding performance of ANA information for M≥6 earthquakes around the Korla station |
由图 3、4可见,5级以上地震的ANA和ONA信息最优预报范围均在200 km以内,最优预报时窗分别为930 d和840 d。最优预测指标均可正确预测观测期间发生的5次5级以上地震(2012-01-08和硕5.0级、2012-06-15轮台5.4级、2013-03-29昌吉5.6级、2015-06-25托克逊5.4级和2016-01-14轮台5.3级地震),2种信息最优指标的R值均大于R0值,统计意义上可信度较高。ONA信息最优预测指标对应的预报占时率和显著性水平更低,R值和概率增益更高,预测效能相对更优。
6级以上地震的ANA和ONA信息最优预报范围均在250 km以内,且最优预报时窗均为7 d。最优预测指标均可正确预测观测期间发生的2次6级以上地震(2012-06-30新源6.6级和2016-12-08呼图壁6.2级地震)。由于该时段内发震次数较少,对应的R0值较高,因此只有当ANA信息最优指标的R值大于R0值时,才会在统计意义上有较高的可信度。ONA信息最优指标对应的预报占时率较高,导致R值偏低,未通过显著性水平2.5%的检验。
3 结语本文基于S变换时频分析方法,构建破年变信息分离提取新流程,该流程在提供短周期信号(ONA)的同时还可提供背景年变信号(ANA)的演化过程。采用双向非对称二维阈值策略,结合R值评分及Molchan图表法重新构建预测指标确定及效能评估流程。阈值参数空间扩展及评估因素的增加使得获取的指标相对更优、评估更加合理。新疆库尔勒水平摆倾斜北南测项的实际应用效果较好,该测项ANA对台站周边250 km内6级以上地震具有较好的预测效能,ONA则对200 km范围内5级以上地震具有相对更优的预测效果。
需要说明的是,本文方法获得的预测指标均基于概率统计,该类指标大多会面临地震样本数较少导致的稳定性问题,且单个地震实况不一定与整体概率预测结果一致,因此在实际震情研判过程中还需要综合考虑多方面因素。此外,为提升预测指标的合理性,后续可围绕干扰排除、震例相关性等进行更深入的研究。
| [1] |
刘琦, 闫伟, 李智蓉, 等. 南北地震带定点形变前兆异常指标初建[J]. 地震, 2016, 36(4): 76-88 (Liu Qi, Yan Wei, Li Zhirong, et al. Preliminary Anomaly Index of Precursory Fix-Point Deformation in the North-South Seismic Belt[J]. Earthquake, 2016, 36(4): 76-88)
(  0) 0) |
| [2] |
孙小龙, 王俊, 向阳, 等. 基于《中国震例》的地下流体异常特征统计分析[J]. 地震, 2016, 36(4): 120-130 (Sun Xiaolong, Wang Jun, Xiang Yang, et al. Statistical Characteristics of Subsurface Fluid Precursors Based on Earthquake Cases in China[J]. Earthquake, 2016, 36(4): 120-130 DOI:10.3969/j.issn.1000-3274.2016.04.010)
(  0) 0) |
| [3] |
苑争一, 闫伟, 牛安福, 等. 定点形变破年变异常自动识别应用研究[J]. 地震研究, 2020, 43(2): 394-401 (Yuan Zhengyi, Yan Wei, Niu Anfu, et al. Application Research on Automatic Identification of Annual Cycle Breaking Anomalies in the Fixed-Point Deformation[J]. Journal of Seismological Research, 2020, 43(2): 394-401 DOI:10.3969/j.issn.1000-0666.2020.02.023)
(  0) 0) |
| [4] |
王维, 李鸿宇, 叶碧文, 等. 形变观测序列变振幅年周期探测方法研究[J]. 大地测量与地球动力学, 2020, 40(1): 7-10 (Wang Wei, Li Hongyu, Ye Biwen, et al. Research on the Method for Annual Period Detection of Variable Amplitude for the Time Series of Deformation[J]. Journal of Geodesy and Geodynamics, 2020, 40(1): 7-10)
(  0) 0) |
| [5] |
Yu Z N, Hattori K, Zhu K G, et al. Detecting Earthquake-Related Anomalies of a Borehole Strain Network Based on Multi-Channel Singular Spectrum Analysis[J]. Entropy, 2020, 22(10): 1 086 DOI:10.3390/e22101086
(  0) 0) |
| [6] |
马宏生, 刘杰, 吴昊, 等. 基于R值评分的年度地震预报能力评价[J]. 地震, 2004, 24(2): 31-37 (Ma Hongsheng, Liu Jie, Wu Hao, et al. Scientific Evaluation of Annual Earthquake Prediction Efficiency Based on R-Value[J]. Earthquake, 2004, 24(2): 31-37)
(  0) 0) |
| [7] |
Molchan G M. Earthquake Prediction as a Decision-Making Problem[J]. Pure and Applied Geophysics, 1997, 149(1): 233-247 DOI:10.1007/BF00945169
(  0) 0) |
| [8] |
Mandrekar J N. Receiver Operating Characteristic Curve in Diagnostic Test Assessment[J]. Journal of Thoracic Oncology, 2010, 5(9): 1 315-1 316
(  0) 0) |
| [9] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the Complex Spectrum: The S Transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1 001
(  0) 0) |
| [10] |
国家地震局科技监测司. 地震学分析预报方法程式指南[M]. 北京: 地震出版社, 1990 (Department of Science and Technology Monitoring, National Earthquake Administration. Program Guide for Seismological Analysis and Prediction Methods[M]. Beijing: Seismological Press, 1990)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

