2. 自然资源部大地测量数据处理中心,西安市友谊东路334号,710054;
3. 自然资源部第二地形测量队,西安市测绘路6号,710054
为满足社会发展需要,我国建立了新一代中国似大地水准面模型CQG2000。21世纪初,陈俊勇等[1-3]和晁定波[4]基于地面重力、卫星测高、船测重力等数据,采用EGM96全球重力场,建立重力似大地水准面模型。利用高程异常控制网对其进行拟合纠正,获取15′×15′分辨率的似大地水准面模型,其中102°E以东地区中误差小于±0.3 m,102°E以西、36°N以北地区中误差小于±0.4 m,102°E以西、36°N以南地区中误差小于±0.6 m。近年来,各省市陆续建立了高精度、高分辨率的区域似大地水准面模型[5-11]。虽然高精度似大地水准面模型能够满足精度要求,但高程转换计算量巨大。以1 ∶10 000图幅为例,单个图幅的高程基准转换通常需要几十万到上百万个要素点,然而图幅高程基准转换所需的高程精度却较低,在遥感行业,精度一般为dm级甚至m级[12-13]。区域似大地水准面在地球表面空间域内变化较缓,但在地形剧烈变化区域或地类变化过渡区域的变化较为明显。梯度作为数值变化的表征量,可以反映数值在一定区域内变化的大小、方向。CQG2000的梯度用格网点在经、纬度方向上的高程异常空间变化率表示,该数值可以量化不同比例尺图幅内高程异常的变化幅度,可用于分析图幅内平均高程异常对不同比例尺高程精度的适用性。此外,CQG2000的梯度也能反映我国大陆范围内重力场的空间变化特性,有助于解译地球内部质量分布等相关问题。
基于此,本文利用梯度定量描绘CQG2000在全国范围空间域内的变化趋势,分析CQG2000在空间域中的相关性,为建立实用化区域似大地水准面模型提供基础数据,同时也为深入解释似大地水准面变化机理提供科学依据。
1 梯度模型及计算方法 1.1 梯度模型区域似大地水准面受地球质量分布的影响,在平原、丘陵及高山区的变化趋势不同,变化剧烈区域的结果可能未达到行业应用的精度标准。为更好地表述区域似大地水准面格网模型变化,引入梯度函数,即格网点(B, L) 处的梯度:
| $ \begin{aligned} & \operatorname{grad} f(B, L)=\frac{\partial f}{\partial B} \boldsymbol{i}+\frac{\partial f}{\partial L} \boldsymbol{j}= \\ & \frac{\zeta_{m+1, n}-\zeta_{m, n}}{\Delta B} \boldsymbol{i}+\frac{\zeta_{m, n+1}-\zeta_{m, n}}{\Delta L} \boldsymbol{j} \end{aligned} $ | (1) |
式中,f(B, L) 为区域似大地水准面模型,B、L为纬度和经度,ΔB、ΔL为纬度、经度方向上的分辨率,m、n为格网模型的行、列数,i、j为梯度矢量的分量方向。
对比分析多种方法发现,三阶反距离平方权差分方法计算效果较好[14]。因此,本文采用坡度的三阶反距离权差分方法计算CQG2000格网点的梯度数值。
1.2 三阶反距离平方权差分方法采用三阶反距离平方权差分方法选取3×3的移动窗口,计算似大地水准面规则格网点的梯度(图 1),即
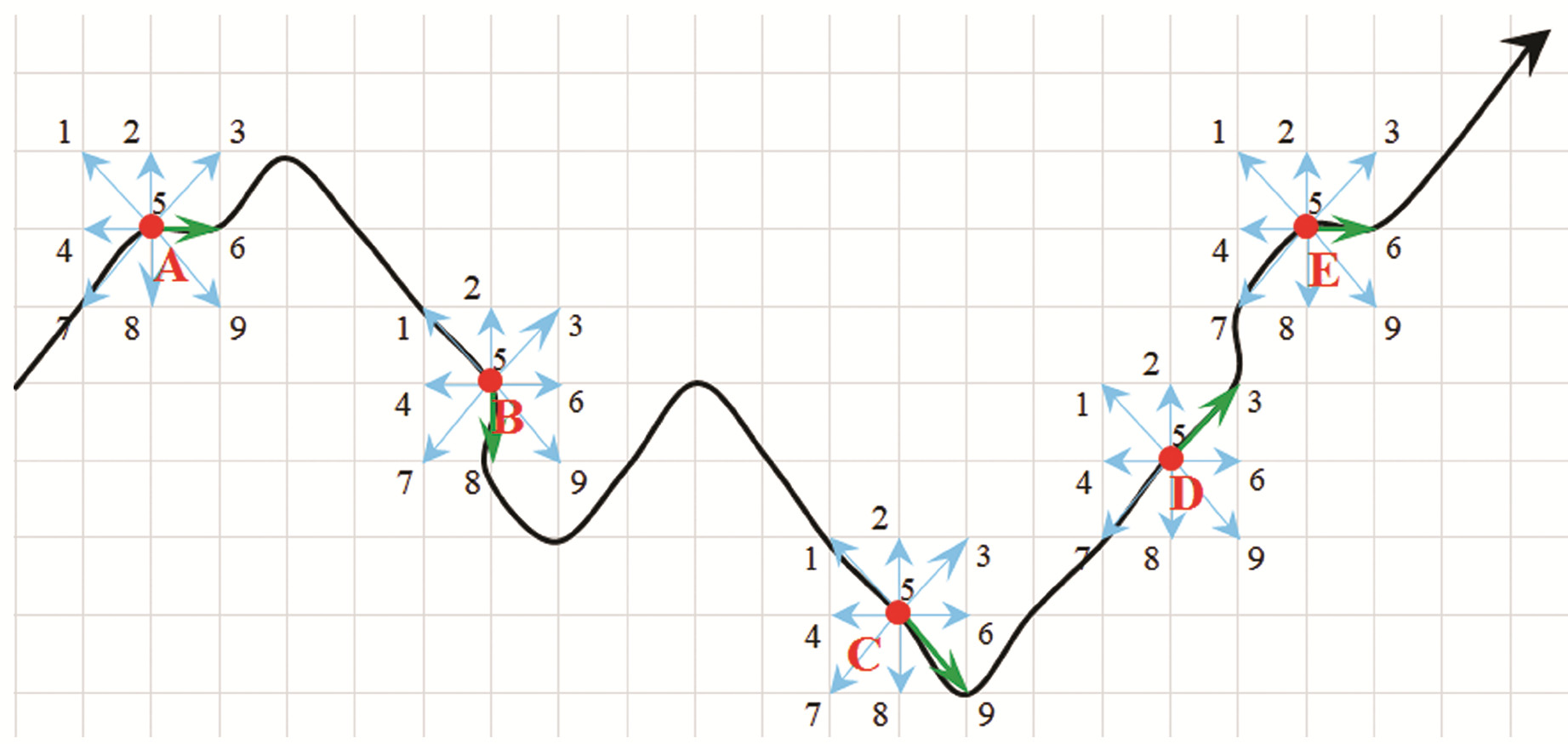
|
图 1 梯度计算示意图 Fig. 1 Schematic diagram of gradient calculation |
| $ f_B=\frac{\partial f}{\partial B}=\frac{\zeta_7-\zeta_1+2\left(\zeta_8-\zeta_2\right)+\zeta_9-\zeta_3}{8 \Delta B} $ | (2) |
| $ f_L=\frac{\partial f}{\partial L}=\frac{\zeta_3-\zeta_1+2\left(\zeta_6-\zeta_4\right)+\zeta_9-\zeta_7}{8 \Delta L} $ | (3) |
式中,fB、fL为纬度、经度方向上的梯度分量,ΔB、ΔL为纬度、经度方向上的分辨率,ζ1~ζ9分别为9个格网点的高程异常值。
梯度方位角α为:
| $ \alpha = \frac{3}{2}{\rm{ \mathit{ π} }} + {\rm{arctan}}\left( {\frac{{{f_L}}}{{{f_B}}}} \right) - \frac{1}{2}{\rm{ \mathit{ π} }}\frac{{{f_B}}}{{\left| {{f_B}} \right|}} $ | (4) |
假设在3×3的窗口内,区域似大地水准面可以表示为曲面ζk=f(Bk, Lk),且三阶连续可微,按泰勒级数展开并取至三次项,即
| $ \begin{gathered} f(B+\Delta B, L)=f(B, L)+f_B(B, L) \Delta B+ \\ f^{\prime \prime}{ }_B(B, L) \frac{(\Delta B)^2}{2}+f^{\prime \prime \prime}{ }_B\left(\zeta_B, L\right) \frac{(\Delta B)^3}{3 !} \end{gathered} $ | (5) |
| $ \begin{gathered} f(B-\Delta B, L)=f(B, L)-f_B(B, L) \Delta B+ \\ f^{\prime \prime}{ }_B(B, L) \frac{(\Delta B)^2}{2}-f^{\prime \prime \prime}{ }_B\left(\gamma_B, L\right) \frac{(\Delta B)^3}{3 !} \end{gathered} $ | (6) |
式中,
在8个格网点处按泰勒级数展开,整理后的fB为:
| $ \begin{array}{c} {f_B} = \left\{ {\frac{{2\left( {{\zeta _8} - {\zeta _2}} \right) + \left( {{\zeta _7} - {\zeta _1}} \right) + \left( {{\zeta _9} - {\zeta _3}} \right)}}{{8\Delta B}} + } \right.\\ \frac{{2\left( {{\rm{d}}{\zeta _8} - {\rm{d}}{\zeta _2}} \right) + \left( {{\rm{d}}{\zeta _7} - {\rm{d}}{\zeta _1}} \right) + \left( {{\rm{d}}{\zeta _9} - {\rm{d}}{\zeta _3}} \right)}}{{8\Delta B}} - \\ \frac{{{{(\Delta B)}^2}}}{{8 \times 3!}}\left[ {2\left( {{f^{\prime \prime \prime }}_B\left( {{\zeta _B}, L} \right) - {f^{\prime \prime \prime }}_B\left( {{\gamma _B}, L} \right)} \right) + } \right.\\ \left( {{f^{\prime \prime \prime }}_B\left( {{\zeta _B}, L - \Delta L} \right) - {f^{\prime \prime \prime }}_B\left( {{\gamma _B}, L - \Delta L} \right)} \right) + \\ \left. {\left. {\left( {{f^{\prime \prime \prime }}_B\left( {{\zeta _B}, L + \Delta L} \right) - {f^{\prime \prime \prime }}_B\left( {{\gamma _B}, L + \Delta L} \right)} \right)} \right]} \right\} \end{array} $ | (7) |
令MB、ML为
| $ \begin{array}{c} {f_B} = \left\{ {\frac{{2\left( {{\zeta _8} - {\zeta _2}} \right) + \left( {{\zeta _7} - {\zeta _1}} \right) + \left( {{\zeta _9} - {\zeta _3}} \right)}}{{8\Delta B}} + } \right.\\ \frac{{2\left( {{\rm{d}}{\zeta _8} - {\rm{d}}{\zeta _2}} \right) + \left( {{\rm{d}}{\zeta _7} - {\rm{d}}{\zeta _1}} \right) + \left( {{\rm{d}}{\zeta _9} - {\rm{d}}{\zeta _3}} \right)}}{{8\Delta B}} - \\ \left. {\frac{{{{(\Delta B)}^2}}}{{8 \times 3!}}\left( {4{M_B} + 2{M_B} + 2{M_B}} \right)} \right\} = \\ \left\{ {\frac{{2\left( {{\zeta _8} - {\zeta _2}} \right) + \left( {{\zeta _7} - {\zeta _1}} \right) + \left( {{\zeta _9} - {\zeta _3}} \right)}}{{8\Delta B}} + } \right.\\ \frac{{2\left( {{\rm{d}}{\zeta _8} - {\rm{d}}{\zeta _2}} \right) + \left( {{\rm{d}}{\zeta _7} - {\rm{d}}{\zeta _1}} \right) + \left( {{\rm{d}}{\zeta _9} - {\rm{d}}{\zeta _3}} \right)}}{{8\Delta B}} - \\ \left. {\frac{{{{(\Delta B)}^2}}}{{3!}}{M_B}} \right\} \end{array} $ | (8) |
式中,fB一般取式(8)第1项,第2、3项为数据误差及其他误差。
同理可得fL为:
| $ \begin{gathered} f_L=\left\{\frac{2\left(\zeta_6-\zeta_4\right)+\left(\zeta_3-\zeta_1\right)+\left(\zeta_9-\zeta_7\right)}{8 \Delta L}+\right. \\ \frac{2\left(\mathrm{~d} \zeta_6-\mathrm{d} \zeta_4\right)+\left(\mathrm{d} \zeta_3-\mathrm{d} \zeta_1\right)+\left(\mathrm{d} \zeta_9-\mathrm{d} \zeta_7\right)}{8 \Delta L}- \\ \left.\frac{(\Delta L)^2}{3 !} M_L\right\} \end{gathered} $ | (9) |
假设区域似大地水准面格网点中误差为σζ,MB、ML中误差相等且均为M,则σfB为:
| $ \begin{gathered} \sigma_{f_B}^2=\left(\frac{1}{8 \Delta B}\right)^2\left[4 \sigma_\zeta^2+4 \sigma_\zeta^2+\sigma_\zeta^2+\sigma_\zeta^2+\sigma_\zeta^2+\sigma_\zeta^2\right]+ \\ \left(\frac{(\Delta B)^2}{3 !}\right)^2 M^2=\frac{12 \sigma_\zeta^2}{64(\Delta B)^2}+\frac{(\Delta B)^4 M^2}{36}= \\ \frac{3 \sigma_\zeta^2}{16(\Delta B)^2}+\frac{(\Delta B)^4 M^2}{36} \end{gathered} $ | (10) |
同理可得σfL为:
| $ \sigma_{f_L}^2=\frac{3 \sigma_{\xi}^2}{16(\Delta L)^2}+\frac{(\Delta L)^4 M^2}{36} $ | (11) |
由于M数值较小,因此式(10)、(11)中的第2项可以忽略。
根据误差传播定律,由式(4)、(10)、(11)推导出梯度方位角误差σα为:
| $ \begin{gathered} \sigma_\alpha^2=\left(\frac{f_L}{f_B^2+f_L^2}\right)^2 \sigma_{f_B}^2+\left(\frac{f_B}{f_B^2+f_L^2}\right)^2 \sigma_{f_L}^2= \\ \frac{f_L^2 \sigma_{f_B}^2+f_B^2 \sigma_{f_L}^2}{\left(f_B^2+f_L^2\right)^2} \end{gathered} $ | (12) |
梯度计算精度主要受区域似大地水准面精度、区域似大地水准面曲面离散化精度、格网分辨率等因素影响。CQG2000梯度的分辨率较低,为5′×5′(约10 km×10 km),无法准确表示高程异常极值点,相邻格网点的高程异常差一般为cm级甚至dm级。为有效表示梯度数值,本文采用经、纬度方向上单位弧长的高程异常变化(单位为m/(′))进行计算。在梯度相关精度计算中,需将该单位换算成长度单位m(约1 800 m)。将梯度分量均值
为更加精细地描绘CQG2000的空间域变化,在计算梯度时,对原有15′×15′分辨率的模型进行双线性内插处理成5′×5′分辨率的格网模型(忽略内插误差影响)。按照§1.3中公式计算格网点梯度数值及方向,获取全国似大地水准面的梯度,如图 2所示。同时,根据表 1、2中的全国梯度信息,按照CQG2000精度划分的3个区域范围统计102°E以东(区域1),102°E以西、36°N以北(区域2)和102°E以西、36 °N以南(区域3)3个区域的梯度分量精度和梯度方位角平均精度,结果见表 3、图 2。
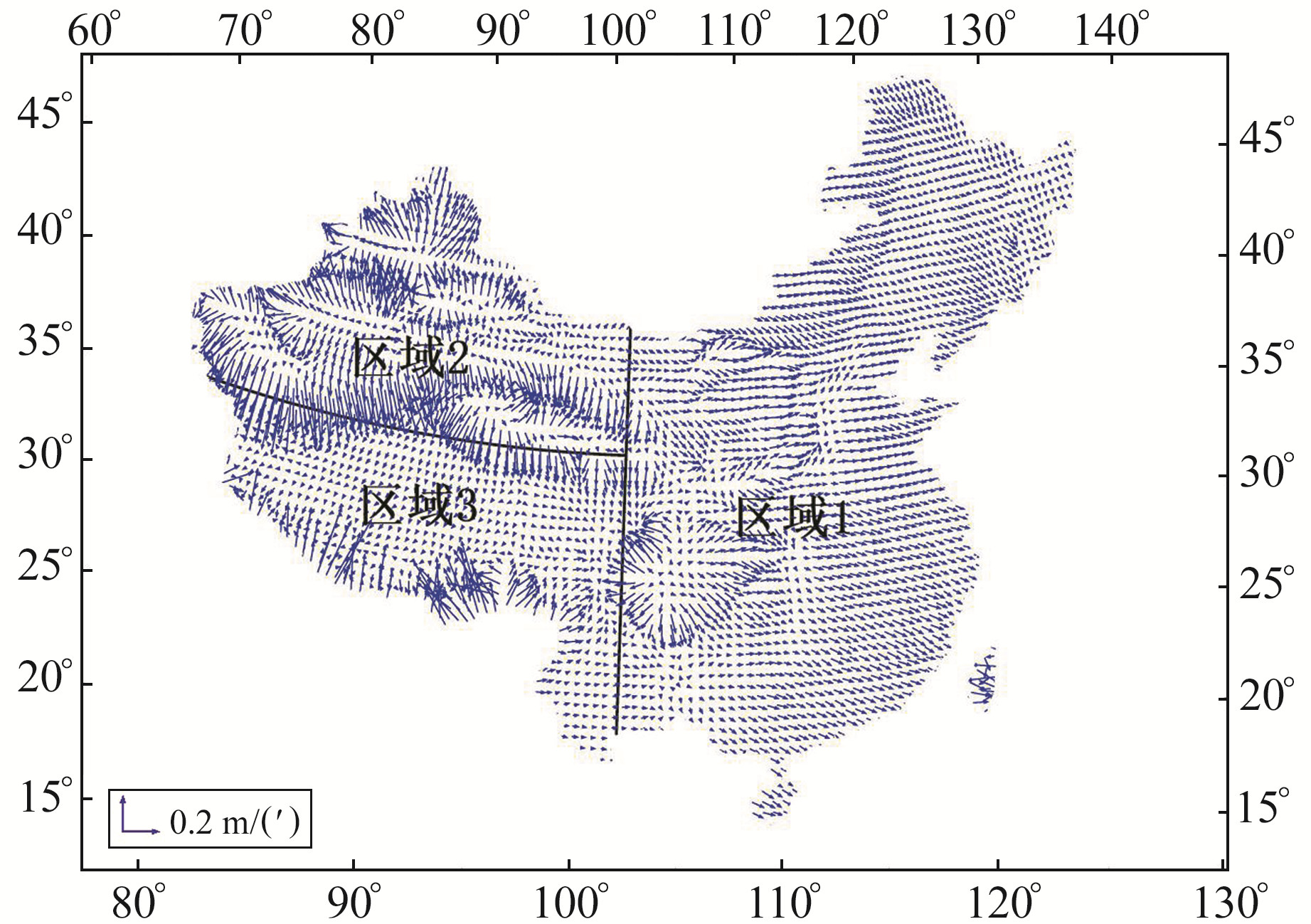
|
图 2 CQG2000的梯度分布 Fig. 2 The distribution of gradient for CQG2000 |
|
|
表 1 CQG2000的梯度数值 Tab. 1 Gradient value for CQG2000 |
|
|
表 2 CQG2000的梯度方位角 Tab. 2 Gradient azimuth for CQG2000 |
|
|
表 3 CQG2000的梯度精度 Tab. 3 Gradient accuracy for CQG2000 |
1) 102°E以东地区CQG2000的梯度方位角方向主要为东,量级小于0.2 m/(′),且变化平缓。其中,东北地区、华南地区梯度方向主要为东南,角度约为东向南45°;30°~40°N区间内的梯度方位角方向为正东。102°E以西地区CQG2000梯度在不同地类区域的方向不同,且梯度数值变化幅度较大。
2) 我国东部、西北、西南地区的梯度分量精度σfB、σfL随似大地水准面格网点精度σζ的增大而增大,随分辨率的增大而减小。西南地区σα误差最大,为50.1°;西北地区σα误差最小,为16.4°。造成上述差异的主要原因为梯度方位角精度σα主要受梯度分量及其精度的影响,较小的梯度数值变化会导致较大的梯度方位角精度变化。进一步说明,相比于梯度分量精度σfB、σfL,梯度方位角误差σα对梯度方位角α更加敏感。
3) 新疆北部与南部、青海、成都平原等地存在多个梯度扩散中心,区域似大地水准面格网点高程异常值由中心向四周逐渐增大;喜马拉雅山脉、新疆中部地区出现区域似大地水准面梯度会聚现象;河西走廊也出现区域似大地水准面梯度会聚现象,甘南西部梯度方向为正南,同时顺时针旋转;宁夏南部、甘肃东北部地区区域似大地水准面梯度方向为正东,同时逆时针旋转。喜马拉雅山脉、新疆南部昆仑山脉等地的区域似大地水准面梯度数值较大,最大值位于西藏墨脱县(0.625 m/(′));青藏高原绝大部分区域的区域似大地水准面梯度较小,变化较平缓。
4) CQG2000梯度变化剧烈区域与我国大山脉走向一致,说明区域似大地水准面与地球内部质量分布密切相关。在喜马拉雅山、昆仑山、天山、秦岭等山脉区域,区域似大地水准面变化速度较大,梯度数值变化为小-大-小。
5) CQG2000自身精度为dm级,实际分辨率为15′×15′。虽然区域似大地水准面梯度精度不高,但能整体反映我国范围内似大地水准面空间域的变化特征。此外,CQG2000梯度与全国范围内的垂线偏差分布[15]一致, 仅在西藏东南部地区存在一定差异, 可能是该区域缺乏重力等基础资料、似大地水准面精度较低所致。
6) 由于CQG2000是利用EGM96参考重力场模型获取高精度重力似大地水准面, 再通过GNSS水准点纠正融合得到, 因此重力似大地水准面梯度与似大地水准面梯度的总体趋势一致二者系统偏差较小, 梯度大小与方向差异也较小CQG2000梯度与高精度EGM2008重力场模型梯度在我国中东地区的差异较小, 在喜马拉雅山、昆仑山、天山、秦岭等山脉区域存在一定差异, 最大差值位于喜马拉雅山地区, 约为0.18m/('), 可能是CQG2000在该区域缺乏基础资料所致。
3 结语梯度信息可反映我国似大地水准面CQG2000在空间域内的整体变化情况,描述不同范围内高程异常变化的量级和方向,可为建立行业所需的实用化模型提供基础数据。整体上看,东北地区CQG2000梯度方位角方向为正东且运动规律与地壳水平运动趋势一致;西部地区梯度方位角方向随地形分布逐渐变化,梯度剧烈变化区域与昆仑山等大山脉走向一致。本文可为进一步开展地球动力学机理研究提供科学依据。此外,高分七号等遥感卫星能够开展大范围1 ∶10 000立体测图工作,满足各行业对高精度产品的需求,但如何综合利用区域似大地水准面及梯度信息快速、高效地实现卫星遥感影像数据处理的高程自动化转换,是下一步的研究重点。
| [1] |
陈俊勇, 李建成, 宁津生, 等. 中国似大地水准面[J]. 测绘学报, 2002, 31(增1): 1-6 (Chen Junyong, Li Jiancheng, Ning Jinsheng, et al. On a Chinese New Quasi Geoid[J]. Acta Geodaetica et Cartogrphica Sinica, 2002, 31(S1): 1-6)
(  0) 0) |
| [2] |
陈俊勇, 李建成, 晁定波, 等. 我国海域大地水准面的计算及其与大陆大地水准面拼接的研究和实施[J]. 地球物理学报, 2003, 46(1): 31-35 (Chen Junyong, Li Jiancheng, Chao Dingbo, et al. Geoid Determination on China Sea and Its Merge with the Geoid in Chinese Mainland[J]. Chinese Journal of Geophysics, 2003, 46(1): 31-35)
(  0) 0) |
| [3] |
陈俊勇, 李建成, 宁津生, 等. 全国及部分省市地区高精度高分辨率似大地水准面的研究和实施[J]. 测绘通报, 2005(5): 1-5 (Chen Junyong, Li Jiancheng, Ning Jinsheng, et al. Study and Implementation of Geoid Model with High Precision and High Resolution in China and Its some Provinces and Cities[J]. Bulletin of Surveying and Mapping, 2005(5): 1-5 DOI:10.3969/j.issn.0494-0911.2005.05.001)
(  0) 0) |
| [4] |
晁定波. 关于我国似大地水准面的精化及有关问题[J]. 武汉大学学报: 信息科学版, 2003, 28(增1): 110-114 (Chao Dingbo. Refinement of Quasi-Geoid in China and Relevant Problems[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 110-114)
(  0) 0) |
| [5] |
张全德, 郭春喜, 王斌, 等. 华北地区似大地水准面精化[J]. 测绘通报, 2007(7): 13-15 (Zhang Quande, Guo Chunxi, Wang Bin, et al. Determination of Quasi-Geoid in North China Region[J]. Bulletin of Surveying and Mapping, 2007(7): 13-15)
(  0) 0) |
| [6] |
张全德, 郭春喜, 王斌, 等. 华东、华中区域似大地水准面精化[J]. 地理信息世界, 2007, 14(5): 21-26 (Zhang Quande, Guo Chunxi, Wang Bin, et al. The Quasi-Geoid Refining in East and Middle China Area[J]. Geomatics World, 2007, 14(5): 21-26)
(  0) 0) |
| [7] |
张全德, 郭春喜, 王斌. 浙闽赣区域似大地水准面精化[J]. 测绘科学, 2007, 32(1): 11-13 (Zhang Quande, Guo Chunxi, Wang Bin. Improvement of Regional Quasi-Geoid in Zhe Min Gan[J]. Science of Surveying and Mapping, 2007, 32(1): 11-13)
(  0) 0) |
| [8] |
Zhang C Y, Dang Y M, Jiang T, et al. Heterogeneous Gravity Data Fusion and Gravimetric Quasigeoid Computation in the Coastal Area of China[J]. Marine Geodesy, 2017, 40(2-3): 142-159
(  0) 0) |
| [9] |
佟洞, 李昱春, 宋玉兵. 江苏省陆海统一测绘基准的建设探讨[J]. 现代测绘, 2017, 40(4): 49-52 (Tong Dong, Li Yuchun, Song Yubing. Discussion on Land and Sea Unified Mapping Benchmark Construction in Jiangsu Province[J]. Modern Surveying and Mapping, 2017, 40(4): 49-52)
(  0) 0) |
| [10] |
董明旭, 李建成, 华亮春, 等. 湖南省似大地水准面2017模型及精度分析[J]. 大地测量与地球动力学, 2019, 39(1): 66-71 (Dong Mingxu, Li Jiancheng, Hua Liangchun, et al. Hunan 2017 GNSS Gravity Quasi-Geoid Model and Its Precision Analysis[J]. Journal of Geodesy and Geodynamics, 2019, 39(1): 66-71)
(  0) 0) |
| [11] |
赵亮, 杜玉祥, 周星. 甘肃省新似大地水准面精化模型精度分析[J]. 测绘标准化, 2020, 36(4): 5-10 (Zhao Liang, Du Yuxiang, Zhou Xing. Accuracy Analysis of New Quasi-Geoid Refinement Model in Gansu Province[J]. Standardization of Surveying and Mapping, 2020, 36(4): 5-10)
(  0) 0) |
| [12] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB 35650-2017国家基本比例尺地图测绘基本技术规定[S]. 北京: 中国标准出版社, 2017 (General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization and Administration of the People's Republic of China. GB 35650-2017 Basic Specifications for Surveying and Mapping of National Fundamental Scale Maps[S]. Beijing: Standards Press of China, 2017)
(  0) 0) |
| [13] |
中华人民共和国住房和城乡建设部. CJJ/T 73-2010国家基本比例尺地图测绘基本技术规定[S]. 北京: 中国建筑工业出版社, 2010 (Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical Code for Urban Surveying Using Satellite Positioning System[S]. Beijing: China Architecture and Building Press, 2010)
(  0) 0) |
| [14] |
刘学军, 龚健雅, 周启鸣, 等. 基于DEM坡度坡向算法精度的分析研究[J]. 测绘学报, 2004, 33(3): 258-263 (Liu Xuejun, Gong Jianya, Zhou Qiming, et al. A Study of Accuracy and Algorithms for Calculating Slope and Aspect Based on Grid Digital Elevation Model(DEM)[J]. Acta Geodaetica et Cartogrphica Sinica, 2004, 33(3): 258-263)
(  0) 0) |
| [15] |
自然资源部大地测量数据处理中心. 全国垂直形变分析研究报告[R]. 西安, 2018 (Geodetic Data Processing Center, MNR. Research on Vertical Deformation Analysis in Chinese Mainland[R]. Xi'an, 2018)
(  0) 0) |
2. Geodetic Data Processing Center, MNR, 334 East-Youyi Road, Xi'an 710054, China;
3. The Second Topographic Surveying Brigade, MNR, 6 Cehui Road, Xi'an 710054, China
 2023, Vol. 43
2023, Vol. 43


