2. 国家基础地理信息中心测绘基准部,北京市莲花池西路28号,100830
北京时间2021-05-22 02:04,青海省果洛藏族自治州玛多县发生MW7.3地震[1-2],震中(34.598°N、98.251°E)位于玛多县以南38 km处,处于青藏高原北部巴颜喀拉地块内部的北部边缘,以及东昆仑南部约70 km的甘德-玛多断裂带上。震源深度约10 km,断层走向约92°,倾角约67°,朝向为S,破裂断层走向近EW。美国地质调查局USGS公布此次地震为具有显著拉张分量的左旋走滑地震事件,而GCMT公布此次地震为接近纯左旋走滑事件,二者存在较大差异[3-4]。玛多地震是中国大陆继汶川MW8.0地震后发生的最大地震,震级大、震源浅,造成震中附近房屋、道路、桥梁等基础设施不同程度的隆起或坍塌。由于地震所处的巴颜喀拉块体边缘断裂带的构造变形控制着地块整体向东运动,与边缘地震的发生息息相关,因此对边缘历史地震的分布特征进行研究,有助于深入了解玛多地震的孕震机制以及巴颜喀拉块体边缘强震的活动特征。
随着GNSS软硬件的快速发展,科研工作者可在震后第一时间解算GNSS数据,对地震发生机制以及周围地表影响作出快速响应。玛多地震发生后,本课题组迅速响应,组织野外考察队赶赴现场进行GNSS观测。本文以此次观测的GNSS站点、周边CORS站和中国大陆构造环境监测网络(以下简称陆态网络)共40个连续运行站的数据为约束,构建三维有限元模型,分析和探讨玛多地震同震形变特征,评估周边地区的地震危险性。
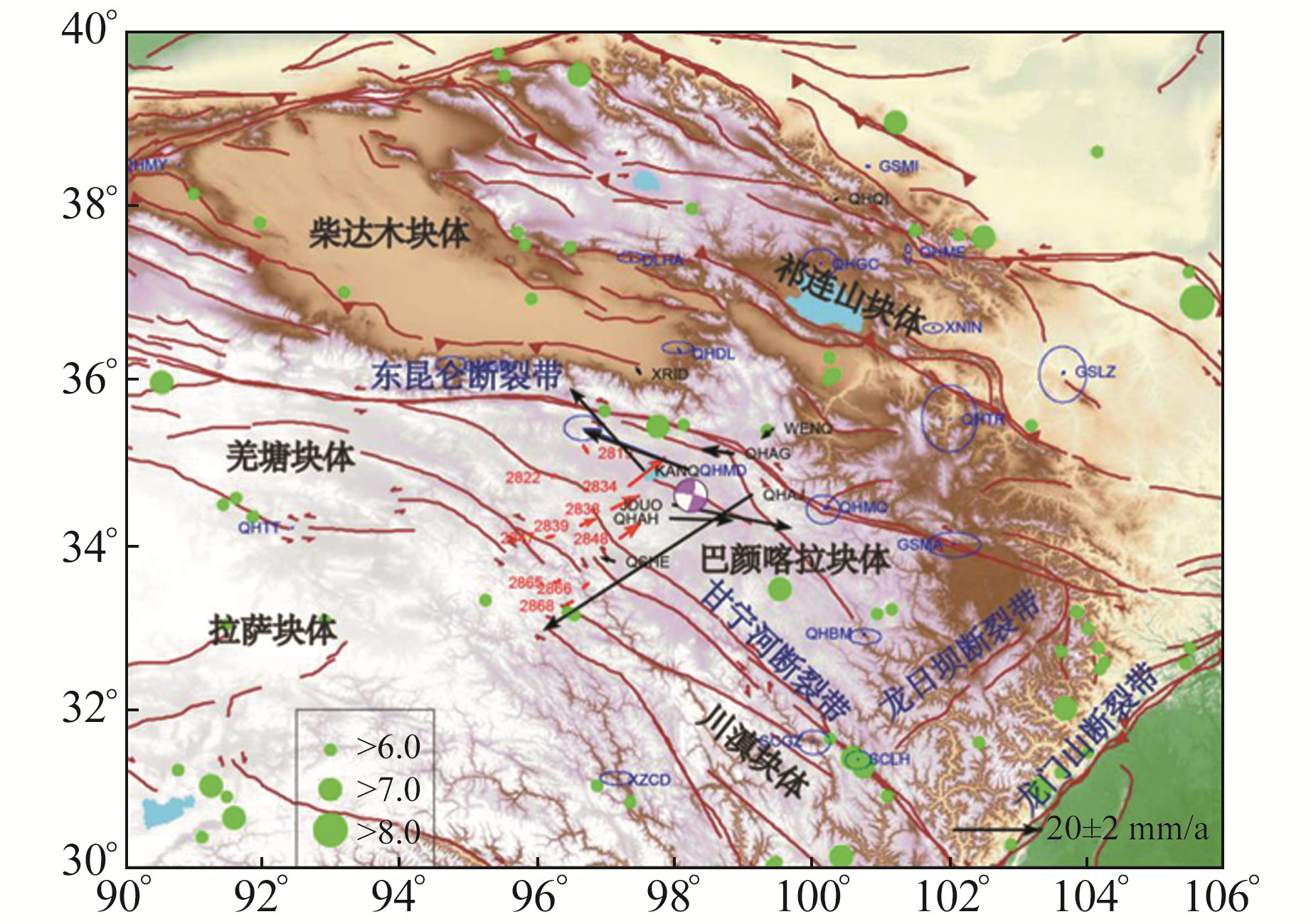
1 数据获取与解算策略本文使用的GNSS站均分布在距震中800 km范围内,均匀覆盖震中区域(图 1)。距离震中最近的站点为青海玛多站(QHMD),距离震中约38 km;最远的为青海茫崖站(QHMY),距离震中约790 km。40个测站中12个测站的GNSS形变结果来自文献[5];10个测站的形变结果来自课题组对以往GNSS站进行的重复性观测,观测时间为震前2020年doy180~186、doy239~250、doy254~256以及震后2021年doy162~172;18个测站的形变结果来自陆态网络。
|
图 1 玛多MW7.3地震同震形变场及青藏高原主要活动断裂和历史地震 Fig. 1 The coseismic deformation field of Madoi MW7.3 earthquake and major active faults and historical earthquakes in the Tibetan plateau |
GNSS站和陆态网络共28个测站的数据均由Bernese 5.2软件[6]解算得到。由于Bernese 5.2软件基线解算模式的精度高于单点定位精度,且定位结果与初始坐标精度有关,因此为保证单日解精度的可靠性,首先用精密单点定位获取cm或mm级(与数据质量有关)的单日解作为初始值,然后采用基线解算模型对中国及周边IGS核心站进行约束,解算得到ITRF2014框架下精度为mm级的单日解。在解算过程中,轨道和钟差数据均采用IGS发布的最终产品。以CODE中心发布的全球电离层模型为基础进行高阶电离层改正,相同频率不同码以及不同频率之间存在的偏差采用CODE中心每月发布的码差分偏差数据进行校正,数据采样率为30 s,卫星截止高度角为5°。天线相位中心偏差采用绝对天线相位中心模型进行改正。利用各站点的多天单日解组成三维时间序列,分别拟合地震前后的时间序列,得到高精度同震形变场(图 1)。
2 三维有限元模型的构建为模拟玛多地震同震地壳形变,采用Abaqus软件构建弹性三维有限元模型[7],该软件能够根据弹性断层错动、粘弹性松弛和孔隙回弹引起的地表形变进行正演模拟,还可以对不同区域(细化到每个单元)赋予不同物质属性进行模拟。首先在长2 000 km、宽2 000 km、深400 km的三维几何模型的基础上,建立长200 km、宽33.3 km、走向N103°E的断层,断层中心为34.575 7°N、98.251 7°E;然后对三维几何模型进行网格划分,在保证解算精度的前提下提高计算效率。采用四面体单元划分网格,根据距断层距离的远近设置单元大小,单元长度由近及远逐渐增大,从断层面及附近单元长度的4 km逐步增大至最远处的80 km,从而得到包括400个子断层、95 571个单元、139 667个节点数的精细三维有限元模型(图 2)。为验证模型的准确性,将其与弹性半空间Okada模型[8]进行比较。有限元模型的初始条件为零位移,在后续分析过程中,假设整个模型均处于弹性状态(泊松比为0.25,杨氏模量为75 GPa),即上表面不加任何应力,处于自由状态。将远场(即模型侧面和底面)设置为零位移状态,依次在每一个子断层的走滑和倾滑方向上加载单位位移,解算由子断层错动引起的地表各节点位移。通过内插方法得到GNSS站位移,从而获得用于断层滑动分布反演的格林函数:

|
图 2 玛多地震三维有限元模型 Fig. 2 Three-dimensional finite element model for Madoi earthquake |
| $ \frac{\partial}{\partial x_j}\left[G(x)\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right]+\frac{\partial}{\partial x_j}\left[\lambda(x) \frac{\partial u_k}{\partial x_k}\right] \delta_{i j}=0 $ | (1) |
式中,u为位移;x为走滑或倾滑方向位移;在三维模型中,指数i、j分别为x、y、z方向上的分量;k为3个分量方向的位移总和;G和λ分别为剪切模量和拉梅常数;δij为狄拉克函数。
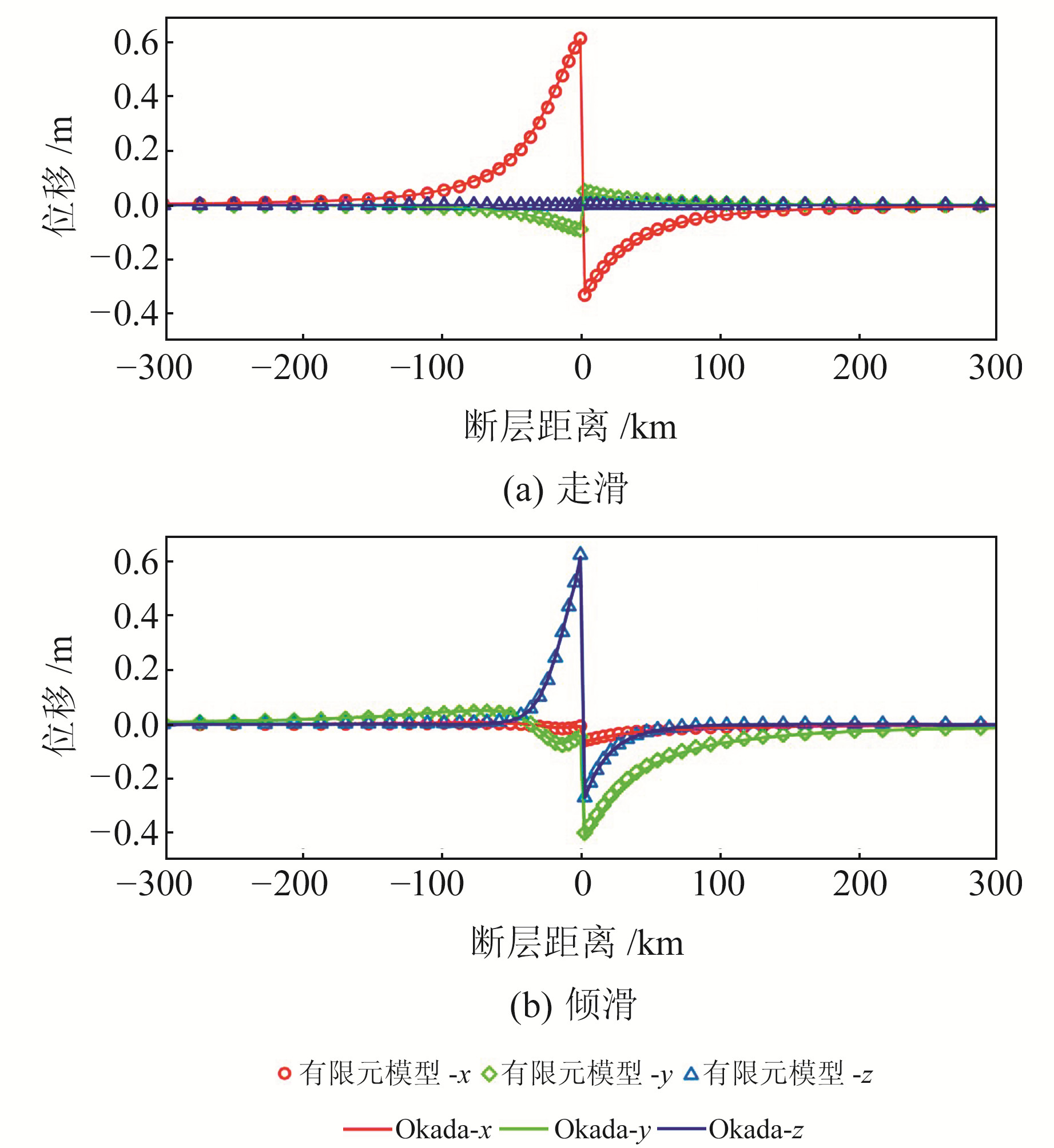
为验证本文模型和分析方法的准确性,分别采用Okada模型和有限元模型,在断层走滑和倾滑方向上加载单位位移,并将其与经过断层中心并垂直于断层的剖面投影到地表的节点位移进行对比(图 3)。由图可见,无论是断层单位走滑还是倾滑,采用有限元模型和Okada方法解算出的地表位移结果均相同,验证了本文模型的准确性。
|
图 3 断层单位走滑/倾滑错动引起的地表位移 Fig. 3 The surface displacements caused by unit strike/dip dislocation on the fault |
在走滑和倾滑方向上依次对子断层加载单位错动,得到GPS站点的位移,即通过有限元模型获取格林函数。断层滑动分布公式为:
| $ \boldsymbol{G} \boldsymbol{m}=\boldsymbol{d} $ | (2) |
式中,G为综合格林函数;m和d分别为断层滑动分布和GNSS观测到的同震位移。系数Gij为GNSS站点j上节点对i加载单位位错而产生的位移,根据最小二乘原理可求得断层滑动分布。为验证利用最小二乘法反演有限元模型中断层滑动分布的可靠性,本文对玛多地震的断层面赋予初始滑动分布值,如图 4(a)所示,其中白色代表滑动值为1 m,黑色代表滑动值为0 m。首先利用初始滑动分布模型(图 4(a))正演得到分布在震源近场和远场上的20个虚拟GNSS站点同震位移场,然后利用最小二乘原理和网格搜索法反复调试平滑因子,反演出断层最优滑动分布,如图 4(b)所示。结果表明,模拟得到的滑动分布与真实值(给予每个子断层的单位错动)在近地表的一致性较好,同震凹凸体主要分布在接近地面的断层面上。该结果验证了采用最小二乘原理和网格搜索法反演断层滑动分布的准确性。

|
图 4 断层位错模型和滑动分布 Fig. 4 The fault dislocation model and slip distribution |
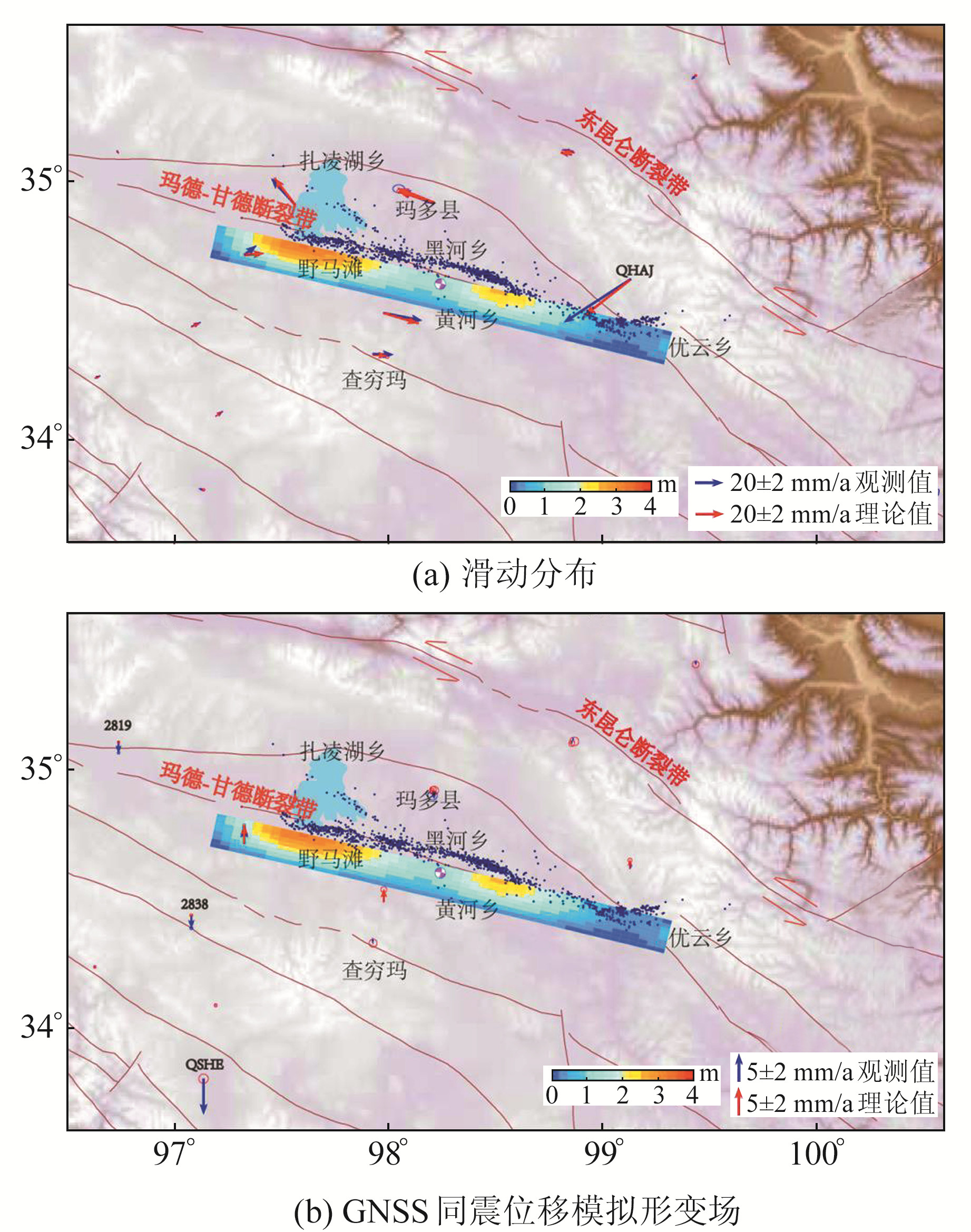
首先基于建立的三维有限元模型,利用400个子断层的单位走滑和倾滑错动引起的GPS点位移计算得到综合格林函数;然后根据最小二乘原理加入平滑因子进行网格搜索,反演断层同震滑动分布模型;最后根据滑动分布估计GNSS站点的同震理论位移,将与观测值最接近的理论值视为最优滑动分布。因篇幅有限,本文仅给出最优滑动分布以及根据最优滑动分布解算得到的GNSS近场同震形变理论值(图 5)。由图可见,远场GNSS同震形变观测值不足1 cm,与理论值的差异为mm级。根据反演得到的滑动分布可以看出,本文构建的玛多地震断层破裂区与余震精定位位置[9]一致,反演长度(200 km)大于实际破裂长度(约160 km)。地震引起的破裂主要分布在野马滩和黄河乡附近,破裂长度分别约为3.4 m和2.5 m,野马滩大桥在地震中坍塌。本文模型与中国地震局地质研究所采用InSAR构建的滑动分布模型吻合较好,但与美国地质调查局USGS以及北京大学张勇工作组的滑动分布模型相差较大[3],可能是因为地质所采用的InSAR数据以及本文采用的GNSS数据均覆盖玛多地震震源区域,可以更好地约束玛多地震的断层几何形状以及同震滑动分布;而其他2种模型则采用相对稀疏的全球地震波数据,且缺乏近场约束。
|
图 5 玛多地震滑动分布及GNSS同震位移模拟形变场 Fig. 5 Coseismic slip distrubution and GNSS coseismic displacements field for Madoi earthquake |
GNSS同震形变的水平和高程方向上的理论值与观测值总体上保持一致,二者的差值称为残差。就GNSS水平位移场(图 5(a))而言,距离震源较近的站点QHAJ残差最大(17 cm),可能是存在观测误差或者几何模型不够精细所致,最小残差不足1 cm。从同震水平形变的观测值和理论值可以看出,玛多地震是以左旋走滑为主的破裂事件,远场GNSS站同震水平位移和垂向位移相对较小,仅为0.1~3 cm,说明玛多地震对周围地表的影响随震中距的增大迅速衰减。在GNSS同震形变高程方向上(图 5(b)),距离震源较近的GNSS站点理论值与观测值相差较小,而距离震源较远的QSHE、2838和2819测站,模拟值接近于0,观测值和模拟值相差较大,残差最大为5.2 cm。根据玛多地震震级和同震形变的水平位移场分布可知,地震对较远GNSS站点的位移影响非常有限,理论上垂向同震位移接近于0。2819和2838测站属于流动观测站,解算得到的垂向同震位移分别为1.9 cm和2.3 cm,误差均为0.4 cm,该误差可能与观测天数较少有关。QSHE测站同震形变结果来自文献[5],垂向同震位移为6.9 cm,解算精度为0.8 cm,解算值和理论值不符,可能与观测数据较少或者观测环境不佳[5]有关。
4 结语根据GNSS数据获取同震形变场,构建玛多地震三维有限元模型,并用弹性半空间Okada模型验证其准确性。通过调节滑动因子进行网格搜索,反演玛多地震同震滑动分布。结果表明,地震引起的破裂主要分布在野马滩和黄河乡附近,滑动值分别为3.4 m和2.5 m,与中国地震局地质研究所得到的滑动分布结果相似。地质所采用的InSAR数据和本文采用的GNSS数据均能较好地覆盖震中附近区域,二者采用不同的大地测量观测数据反演得到类似的断层滑动模型,说明本文反演结果具有可靠性。滑动分布解算得到的GNSS同震形变理论值与观测值拟合较好,再次证明本文模型的合理性和准确性。本文对于玛多地震后续研究和该地区内部结构及其他地震的断层滑动分布构造等研究具有重要的理论价值和应用意义,也可为相关研究提供重要的数据参考。
| [1] |
张彩红, 谭凯, 王东振, 等. 利用GPS高频信号分析玛多地震产生的动态位移特征[J]. 大地测量与地球动力学, 2022, 42(3): 231-233 (Zhang Caihong, Tan Kai, Wang Dongzhen, et al. Analysis on the Features of Dynamic Displacements Caused by Madoi Earthquake Based on GPS High Rate Signal[J]. Journal of Geodesy and Geodynamics, 2022, 42(3): 231-233)
(  0) 0) |
| [2] |
Chen H, Qu C Y, Zhao D Z, et al. Rupture Kinematics and Coseismic Slip Model of the 2021 MW7.3 Madoi(China) Earthquake: Implications for the Seismic Hazard of the Kunlun Fault[J]. Remote Sensing, 2021, 13(16)
(  0) 0) |
| [3] |
杨君妍, 孙文科, 洪顺英, 等. 2021年青海玛多7.4级地震的同震变形分析[J]. 地球物理学报, 2021, 64(8): 2671-2683 (Yang Junyan, Sun Wenke, Hong Shunying, et al. Coseismic Deformation Analysis of the 2021 Qinghai Madoi M7.4 Earthquake[J]. Chinese Journal of Geophysics, 2021, 64(8): 2671-2683)
(  0) 0) |
| [4] |
詹艳, 梁明剑, 孙翔宇, 等. 2021年5月22日青海玛多MS7.4地震深部环境及发震构造模式[J]. 地球物理学报, 2021, 64(7): 2232-2252 (Zhan Yan, Liang Mingjian, Sun Xiangyu, et al. Deep Structure and Seismogenic Pattern of the 2021.5.22 Madoi(Qinghai) MS7.4 Earthquake[J]. Chinese Journal of Geophysics, 2021, 64(7): 2232-2252)
(  0) 0) |
| [5] |
李志才, 丁开华, 张鹏, 等. GNSS观测的2021年青海玛多地震(MW7.4)同震形变及其滑动分布[J]. 武汉大学学报: 信息科学版, 2021, 46(10): 1489-1497 (Li Zhicai, Ding Kaihua, Zhang Peng, et al. Coseismic Deformation and Slip Distribution of 2021 MW7.4 Madoi Earthquake from GNSS Observation[J]. Geomatics and Information Science of Wuhan University, 2021, 46(10): 1489-1497)
(  0) 0) |
| [6] |
张彩红, 谭凯, 杨少敏. Bernese软件评估北斗静态定位精度[J]. 大地测量与地球动力学, 2015, 35(2): 183-185 (Zhang Caihong, Tan Kai, Yang Shaomin. Evaluation of the Precision of Static Positioning with BDS Based on Bernese Software[J]. Journal of Geodesy and Geodynamics, 2015, 35(2): 183-185)
(  0) 0) |
| [7] |
Masterlark T, Feigl K L, Haney M, et al. Nonlinear Estimation of Geometric Parameters in FEMs of Volcano Deformation: Integrating Tomography Models and Geodetic Data for Okmok Volcano, Alaska[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B2)
(  0) 0) |
| [8] |
Okada Y. Surface Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1135-1154
(  0) 0) |
| [9] |
王未来, 房立华, 吴建平, 等. 2021年青海玛多MS7.4地震序列精定位研究[J]. 中国科学: 地球科学, 2021, 51(7): 1193-1202 (Wang Weilai, Fang Lihua, Wu Jianping, et al. Study on the Precise Location of Madoi MS7.4 Earthquake Sequence in Qinghai Province in 2021[J]. Science China: Earth Science, 2021, 51(7): 1193-1202)
(  0) 0) |
2. Geodesy Datum Department, National Geomatics Center of China, 28 West-Lianhuachi Road, Beijing 100830, China
 2023, Vol. 43
2023, Vol. 43

