据美国地质调查局USGS测定,2021-07-29 06:15(UTC时)美国阿拉斯加州以南海域发生MW8.2地震,震中位于55.364°N、157.888°W,震源深度35.0 km。阿拉加斯南部位于北美板块和太平洋板块的交界处,太平洋板块以约55.0 mm/a的速度向北美板块俯冲[1],使得该区域的地震和火山等构造运动十分频繁。阿拉斯加MW8.2地震震中位于太平洋板块向北美板块俯冲的阿留申俯冲带东段,该段构造运动以垂直岛弧走向的板块会聚和太平洋板块向北美大陆岩石圈的俯冲为主。Global CMT测定的震源机制解(图 1)表明,此次地震为低倾角逆冲型破裂事件,地震释放的地震矩约为2.96×1021Nm。
|
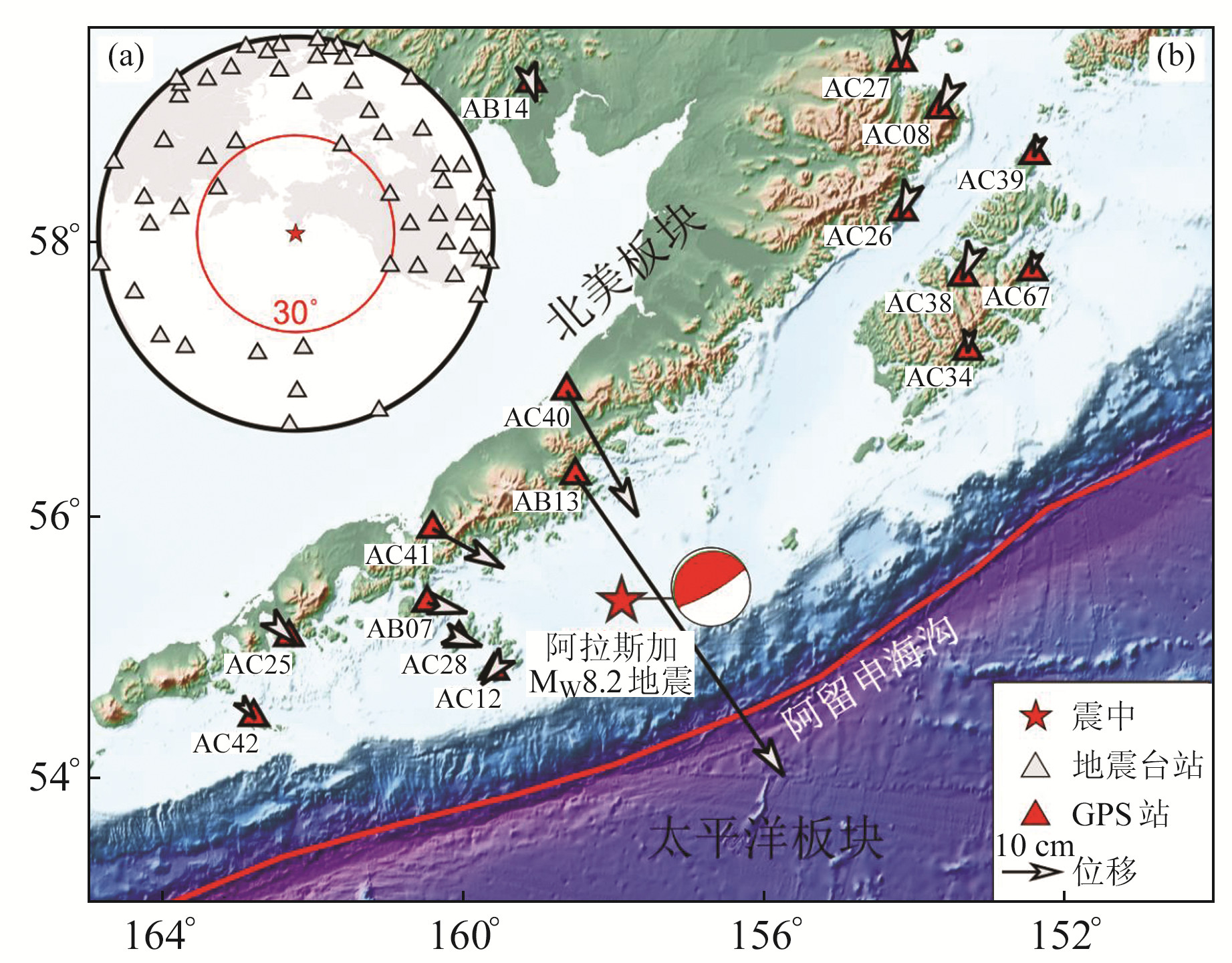
图 1 构造背景 Fig. 1 Tectonic setting |
震源参数是对复杂震源性质的参数化、定量化描述,准确测定震源参数是认识地震发生、发展过程的主要方式,有助于揭示震源区域变形的动力学成因、孕震机制及应力变化状态。近年来,地震震源破裂研究主要分为地震的震源机制解和震源破裂过程2部分[2],地震的破裂过程是评估地震影响范围、了解强地面震动(peak-ground-velocity, PGV和peak-ground-accumulation, PGA)情况、调查地表破裂特征,以及计算库仑应力场和同震、震后形变的基础[3-4]。此外,反演地震发生时断层的位错滑动,也有助于从地震的运动学特征和震区的孕震背景2方面来探讨地震的发生机理[5-6]。
阿拉斯加半岛和阿留申群岛的GPS站记录到此次地震引起的地表形变,为反演该地震的震源破裂模型提供了宝贵的近场形变数据约束;全球地震台网(global seismic network, GSN)为此次研究提供了优质的远场体波资料。为研究阿拉斯加MW8.2地震的震源破裂特征,本文以近场GPS形变和远场地震波为约束,基于Slab2.0模型[7]构建震源位错模型,反演此次地震的震源破裂过程,并讨论海洋俯冲带地震断层破裂特点、地表变形特征及其物理过程。
1 数据 1.1 GPS观测数据不同类型的数据对震源破裂参数的敏感性不同,在计算发震断层的位置、走向以及断层面上的位移解析度等方面,大地测量数据的精度较高。本文采用的是美国内华达大地测量实验室(NGL)发布的阿拉斯加MW8.2地震GPS同震位移数据,该数据是地震发生次日采用5 min采样率的时间序列计算得到的结果。根据GPS站点的震中距对数据进行初步分析后,选取阿拉斯加半岛和阿留申群岛上16个GPS站点的同震形变观测数据进行计算。观测站点的位置分布及其同震位移如图 1所示,其中,AB13站点距离震中最近,观测到的同震位移最大,东西向和南北向同震位移分别约为24.7 cm和35.7 cm。整体上看,距离震中越近的站点,其位移量越大,位移量随着震中距的增加快速减小,且同震水平位移都指向震源方向。地表位移指向震源破裂集中区的特点符合逆冲地震位错理论模型。
1.2 远场地震数据震源参数的精确度取决于观测数据的丰富程度和信噪比大小。早期震源参数的确定主要依赖于地震波资料,由于垂向P波资料具有震相单纯、初动易于辨认、时间窗截取相对容易、受其他震相干扰小等优点,因此利用该资料可得到较好的反演结果。全球地震台网由装备宽频带数字地震仪器的永久地震台站均匀布设而成,本文从GSN(http://ds.iris.edu/)中选取震中距在30°~90°范围内的远场体波数据,该震中距范围内的直达P波主要在物质相对均匀的地幔中传播,受介质结构非均匀性的影响较小,且震相清晰干净,易于识别。分析台站数据的信噪比和方位角分布情况后,共挑选出57个台站的直达P波数据(图 1(a))。利用SAC(seismic analysis code)软件对波形数据进行去仪器响应、剪切、滤波等处理,频率范围选择0.005~0.5 Hz,波形长度为150 s(直达P波到时前20 s和后130 s)。
2 震源破裂滑动分布反演 2.1 地震位错反演模型的构建由于较大地震的震源破裂尺度也相对较大,因此无法再将震源看作单纯点源[6]。假如将地震断层面近似看作平面,则有限断层反演方法可根据地震断层的产状将断层面划分为若干矩形块,每个矩形块代表一个子断层或子事件,每个子事件的震源时间函数(或地震矩释放过程)可看作由若干个一定“形状”的时间窗组成,需要指定或搜索时间窗的宽度[2, 6, 8]。子断层的滑动角是未知量,由走滑和倾滑方向的滑动量大小约束[9]。由于此次地震发生在俯冲带上,属于逆冲型破裂事件,因此可将断层的滑动方向约束在90° ± 45°的范围内。本文基于Slab2.0模型给出的阿拉斯加地区太平洋板块俯冲几何数据,参考USGS有限断层破裂模型的破裂范围后,构建2021年阿拉斯加MW8.2地震的曲面断层几何模型,设置断层的长度为280 km,宽度为200 km。对断层模型进行约8.0 km的等间隔划分,共划分为35×25个子断层,每个子断层的震源时间函数由2个三角形函数表示,每个三角形函数的时间窗长为2.0 s,即每个子断层破裂持续时间跨度最大为3.0 s。确定断层模型的几何参数后,建立断层面上滑动参数与观测数据之间的线性关系。在解算各子断层的滑动量或标量地震矩参数时,除了要考虑理论计算结果同观测数据的拟合程度,还需要考虑滑动分布粗糙度,即
| $ \begin{gathered} \|w(\boldsymbol{G} \cdot \boldsymbol{M}-\boldsymbol{D})\|^2+ \\ \beta^2\|\boldsymbol{L} \cdot \boldsymbol{M}\|^2=\text { minmum } \end{gathered} $ | (1) |
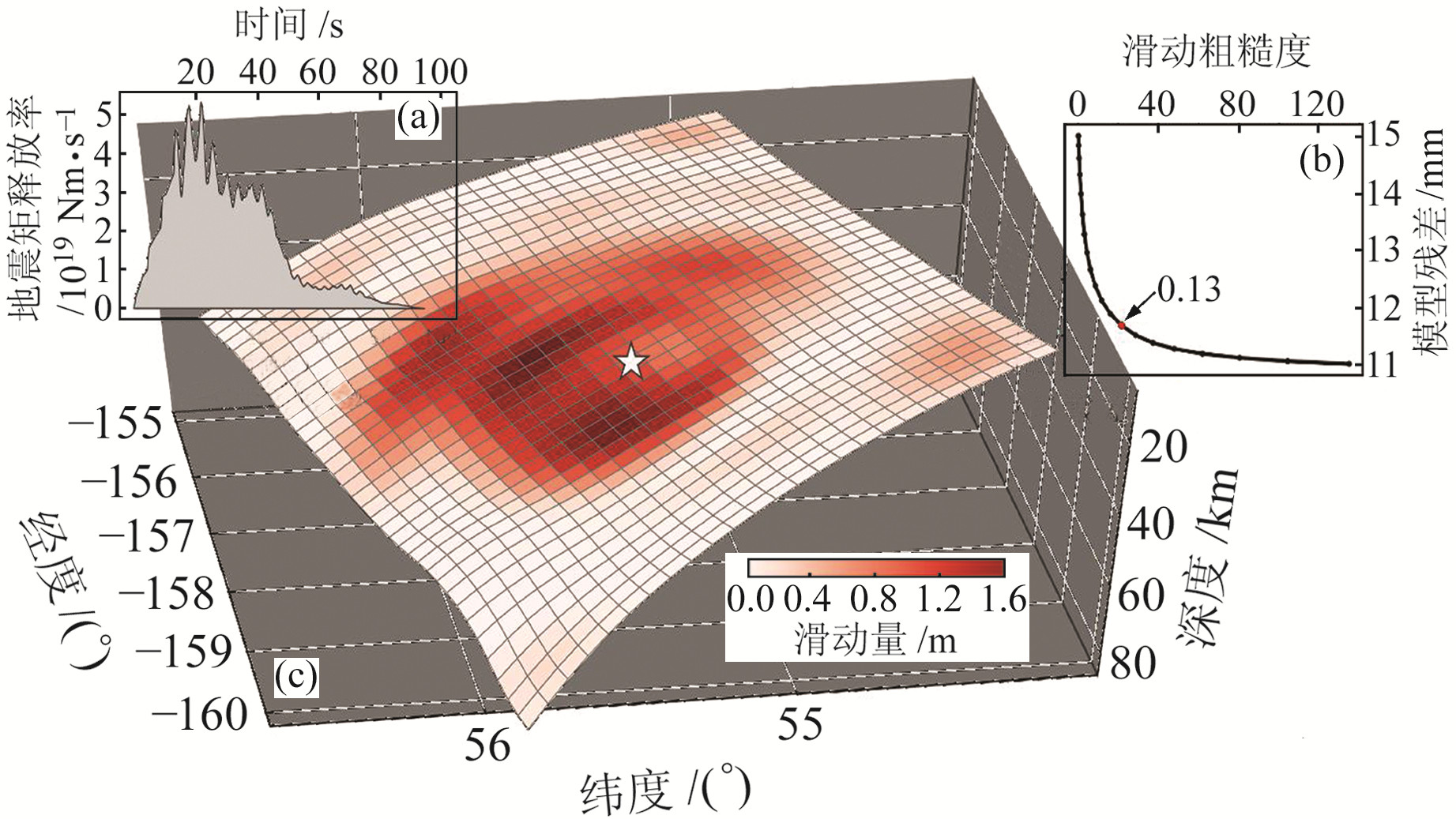
式中,D为观测值;M为滑动量或地震矩,G为格林函数,G·M为模拟值;w为观测值权重,单一类型数据的w=1;L为拉普拉斯二阶差分算子;β为平滑因子。远场P波格林函数的计算工具(hudson96)和近场GPS格林函数计算工具(hstat96)由CPS(computer program in seismology) 提供。远场P波格林函数的震源时间函数时间窗长为1.0 s,采用AK135一维地球速度模型表示;近场GPS格林函数采用Crust1.0地壳速度结构表示。本文联合近场GPS形变和远场直达P波反演2021年阿拉斯加MW8.2地震震源破裂过程,由于GPS精度较高,因此其权重被设置为1.0;地震波权重通过搜索确定,搜索范围为0.1~1.0,间隔为0.1,最优权重为0.5。平滑因子β由模型的粗糙度和残差的折合曲线共同确定,本文最优平滑因子为0.13(图 2(b))。
|
图 2 2021年阿拉斯加MW8.2地震震源破裂过程 Fig. 2 Rupture process of the 2021 AlaskaMW8.2 earthquake |
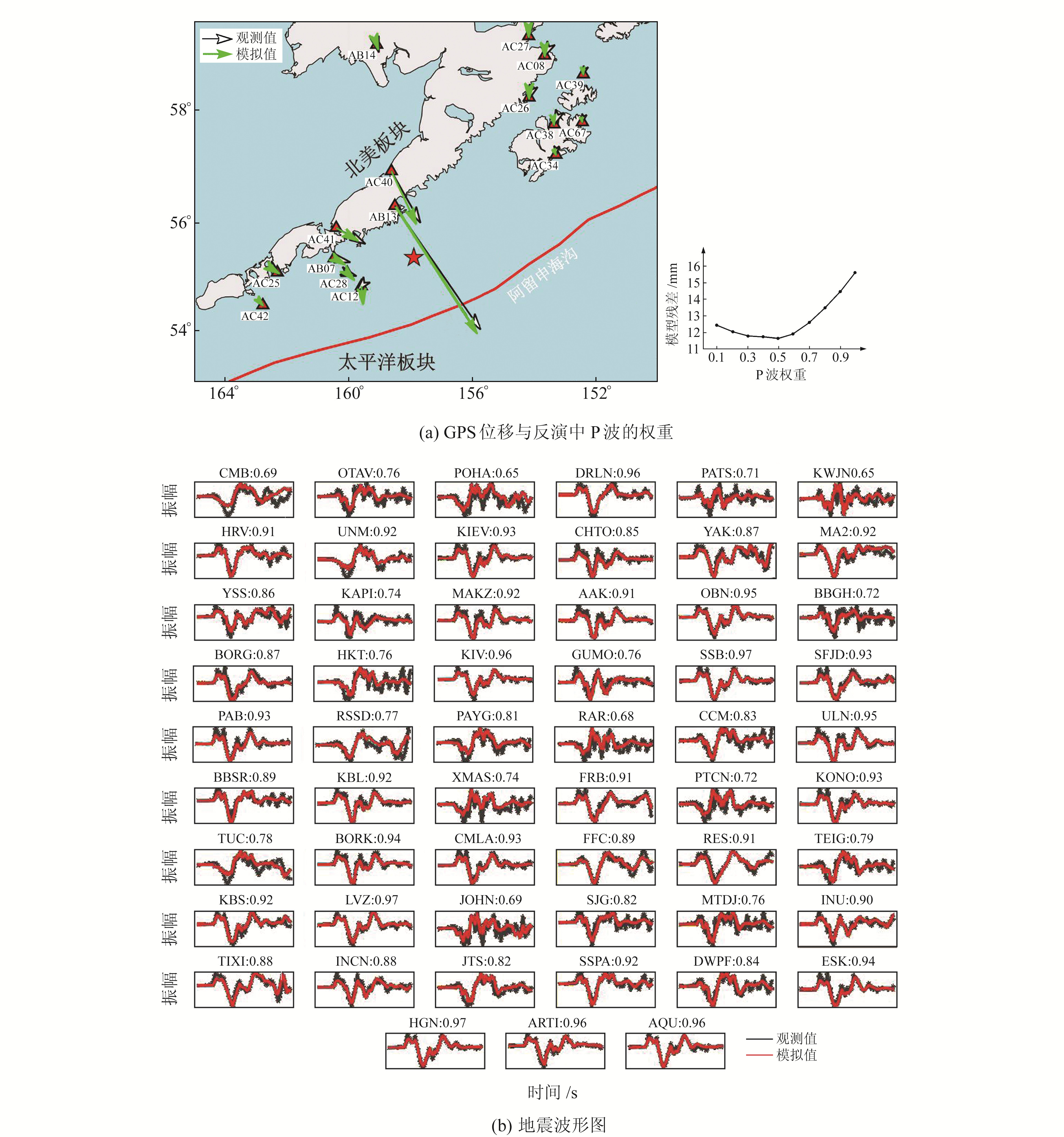
震源破裂过程的最优解如图 2所示,观测值和模拟值的符合度如图 3所示。由图 3可见,模拟值和观测值基本吻合,即破裂模型可以合理解释观测数据,本文反演获得的地震破裂滑动分布模型具有可靠性。此次阿拉斯加MW8.2地震的最大滑动量约为1.87 m,释放的地震矩约为1.59×1021 Nm,上述结果与USGS有限断层反演结果相近。地震持续时间约100 s,能量释放主要集中在前50 s。本文反演的地震断层滑动分布与USGS利用地震波快速反演得到的结果存在一定差异,这是因为USGS有限断层模型的断层滑动分布缺少近场数据的约束,滑移量大的子断层集中在震中附近,滑动方向基本垂直于岛弧走向。本文地震破裂滑动分布反演结果显示,此次阿拉斯加MW8.2地震的断层破裂并非以震中为中心对称分布,而是主要发生在震中的北东侧,发震断层的西南端并未发生明显滑移。相比于USGS单一平面模型,基于Slab2.0曲面模型构建的同震破裂滑动分布模型的子断层走向和倾角是变化的,因此得到的破裂区比USGS的破裂区更深。GPS近场数据的加入丰富了破裂细节,进而分辨出3个破裂集中区。
|
图 3 模拟值和观测值 Fig. 3 Simulation and observed values |
本文以GPS近场形变和远场P波资料为约束,利用Slab2.0模型构建断层几何模型,反演阿拉斯加MW8.2地震的震源破裂过程。相比于USGS单一平面模型,本文模型子断层的走向和倾角是变化的。反演结果显示,断层破裂并非以震中为中心对称分布,而是自震中沿断层向NEE延伸,破裂主要发生在震中的北东侧,发震断层的西南端未发生明显滑移。GPS近场数据的加入丰富了破裂细节,进而分辨出3个破裂集中区,震源破裂持续时间约100 s,释放的地震矩约为1.59×1021 Nm。同震形变整体上符合海沟特大地震的逆冲断层弹性回跳理论模式[10]。受到断层闭锁的影响,太平洋板块俯冲北美板块,使得上盘北美板块受到长时间持续挤压,地震发生瞬间转变为拉张松弛状态。
| [1] |
Finzel E S, Flesch L M, Ridgway K D. Kinematics of a Diffuse North America-Pacific-Bering Plate Boundary in Alaska and Western Canada[J]. Geology, 2011, 39(9): 835-838 DOI:10.1130/G32271.1
(  0) 0) |
| [2] |
Kikuchi M, Kanamori H. Inversion of Complex Body Waves-Ⅲ[J]. Bulletin of the Seismological Society of America, 1991, 81(6): 2335-2 350 DOI:10.1785/BSSA0810062335
(  0) 0) |
| [3] |
Olson A H, Apsel R J. Finite Faults and Inverse Theory with Applications to the 1979 Imperial Valley Earthquake[J]. Bulletin of the Seismological Society of America, 1982, 72(6A): 1969-2 001 DOI:10.1785/BSSA07206A1969
(  0) 0) |
| [4] |
King G C, Stein R S, Lin J. Static Stress Changes and the Triggering of Earthquakes[J]. Bulletin of the Seismological Society of America, 1994, 84: 935-953
(  0) 0) |
| [5] |
Zhang L F, Li J G, Liao W L, et al. Source Rupture Process of the 2015 Gorkha, Nepal MW 7.9 Earthquake and Its Tectonic Implications[J]. Geodesy and Geodynamics, 2016, 7(2): 124-131 DOI:10.1016/j.geog.2016.03.001
(  0) 0) |
| [6] |
Kikuchi M, Yamanaka Y, Abe K, et al. Source Rupture Process of the Papua New Guinea Earthquake of July 17, 1998 Inferred from Teleseismic Body Waves[J]. Earth, Planets and Space, 1999, 51(12): 1 319-1 324 DOI:10.1186/BF03351605
(  0) 0) |
| [7] |
Hayes G P, Moore G L, Portner D E, et al. Slab2, a Comprehensive Subduction Zone Geometry Model[J]. Science, 2018, 362(6 410): 58-61
(  0) 0) |
| [8] |
Li Q, Tan K, Wang D Z, et al. Joint Inversion of GNSS and Teleseismic Data for the Rupture Process of the 2017 MW6.5 Jiuzhaigou, China, Earthquake[J]. Journal of Seismology, 2018, 22(3): 805-814 DOI:10.1007/s10950-018-9733-1
(  0) 0) |
| [9] |
Xu C, Liu Y, Wen Y, et al. Coseismic Slip Distribution of the 2008 MW7.9 Wenchuan Earthquake from Joint Inversion of GPS and InSAR Data[J]. Bulletin of the Seismological Society of America, 2010, 100(5B): 2736-2749 DOI:10.1785/0120090253
(  0) 0) |
| [10] |
Hyndman R D, Wang K. Thermal Constraints on the Zone of Major Thrust Earthquake Failure: The Cascadia Subduction Zone[J]. Journal of Geophysical Research: Solid Earth, 1993, 98(B2): 2039-2060 DOI:10.1029/92JB02279
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

