大地测量中不同大地坐标系间的转换可通过三维七参数模型实现:选择一定数量且分布较为均匀的公共点数据求取坐标转换参数,建立坐标系间的转换关系。通常基于最小二乘原理,以转换残差加权平方和最小为目标条件进行平差计算。由于2000国家大地坐标系的精度比传统参心坐标系高1~2个数量级[1],因此对已有参心坐标系成果进行转换时,需要考虑参心坐标系下坐标成果存在的误差。
总体最小二乘法(TLS)能够求解受随机误差影响的变量误差模型(EIV),由于系数矩阵中各随机元素的精度不同,因此TLS可进一步扩展为加权总体最小二乘法(WTLS)。WTLS常用的求解方法是基于拉格朗日乘数法的条件极值建立的迭代算法[2]。目前,WTLS方法已被广泛应用于坐标转换、高程拟合、线性回归等[3-5]。由于EIV模型假定系数矩阵中每个元素都存在误差,而三维七参数转换模型的系数矩阵中存在常数项,因此可设置系数矩阵协因数阵相应元素为0,进而使常数项元素改正数为0。但上述方法无法解决系数矩阵中存在重复元素的问题。部分变量误差模型(Partial EIV)对EIV模型进行了扩展,使得系数矩阵中部分元素存在误差,进而形成统一的模型形式[6]。
采用Partial EIV模型的加权总体最小二乘法WTLS能够提高三维七参数的精度,但在对参数进行转换时,待转换坐标的误差是未知的。基于此,本文采用RBF神经网络建立源坐标系坐标的误差分布模型,从而更有效地发挥七参数加权总体最小二乘解的作用。
1 三维坐标转换的加权总体最小二乘法WTLS 1.1 三维坐标转换模型不同空间直角坐标系转换的布尔莎模型为:
| $ \begin{gathered} {\left[\begin{array}{c} X^{\mathrm{T}} \\ Y^{\mathrm{T}} \\ Z^{\mathrm{T}} \end{array}\right]=\left[\begin{array}{c} \Delta X_0 \\ \Delta Y_0 \\ \Delta Z_0 \end{array}\right]+} \\ (1+m)\left[\begin{array}{ccc} 1 & \varepsilon_Z & -\varepsilon_Y \\ -\varepsilon_Z & 1 & \varepsilon_X \\ \varepsilon_Y & -\varepsilon_X & 1 \end{array}\right]\left[\begin{array}{l} X^{\mathrm{S}} \\ Y^{\mathrm{S}} \\ Z^{\mathrm{S}} \end{array}\right] \end{gathered} $ | (1) |
式中,(XS, YS, ZS)为源坐标系下的坐标,(XT, YT, ZT)为目标坐标系下的坐标,ΔX0、ΔY0、ΔZ0为3个平移参数,εX、εY、εZ为3个旋转参数,m为尺度参数。
令a1=m+1、a2=a1εX、a3=a1εY、a4=a1εZ,则式(1)可改写为:
| $ \begin{matrix} \overset{{\boldsymbol{y}}}{\mathop{\left[ \begin{matrix} X_{1}^{y} \\ Y_{1}^{\text{T}} \\ Z_{1}^{\text{T}} \\ \vdots \\ X_{n}^{\text{T}} \\ Y_{n}^{\text{T}} \\ Z_{n}^{\text{T}} \\ \end{matrix} \right]}}\, = \\ \overset{{\boldsymbol{A}}}{\mathop{\left[ \begin{matrix} 1 & 0 & 0 & X_{1}^{\text{S}} & 0 & -Z_{1}^{\text{S}} & Y_{1}^{\text{S}} \\ 0 & 1 & 0 & Y_{1}^{\text{S}} & Z_{1}^{\text{S}} & 0 & -X_{1}^{\text{S}} \\ 0 & 0 & 1 & Z_{1}^{\text{S}} & -Y_{1}^{\text{S}} & X_{1}^{\text{S}} & 0 \\ {} & {} & {} & {} & \vdots & {} & {} \\ 1 & 0 & 0 & X_{n}^{\text{S}} & 0 & -Z_{n}^{\text{S}} & Y_{n}^{\text{S}} \\ 0 & 1 & 0 & Y_{n}^{\text{S}} & Z_{n}^{\text{S}} & 0 & -X_{n}^{\text{S}} \\ 0 & 0 & 1 & Z_{n}^{\text{S}} & -Y_{n}^{\text{S}} & X_{n}^{\text{S}} & 0 \\ \end{matrix} \right]}}\, \overset{{\boldsymbol{x}}}{\mathop{\left[ \begin{matrix} \Delta {{X}_{0}} \\ \Delta {{Y}_{0}} \\ \Delta {{Z}_{0}} \\ {{a}_{1}} \\ {{a}_{2}} \\ {{a}_{3}} \\ {{a}_{4}} \\ \end{matrix} \right]}}\, \\ \end{matrix} $ | (2) |
式中,n为控制点个数。
根据最小二乘原理VTQy-1V=min,式(2)解为:
| $ \boldsymbol{x}_{\mathrm{LS}}=\boldsymbol{x}_0+\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{Q}_y^{-1}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{Q}_y^{-1}\left(\boldsymbol{y}-\boldsymbol{A} \boldsymbol{x}_0\right) $ | (3) |
式中,x0为参数近似值,Qy为观测值向量协因数阵。
1.2 Partial EIV模型的加权总体最小二乘法考虑到系数矩阵受随机误差影响,且存在非随机元素或重复随机元素,需采用Partial EIV模型[6]:
| $ \left\{\begin{array}{l} \boldsymbol{y}-\boldsymbol{e}_y=\left(\boldsymbol{x}^{\mathrm{T}} \otimes \boldsymbol{I}_n\right)(\boldsymbol{h}+\boldsymbol{B} \overline{\boldsymbol{a}}) \\ \boldsymbol{a}-\boldsymbol{e}_a=\overline{\boldsymbol{a}} \\ \operatorname{vec}(\boldsymbol{A})=\boldsymbol{h}+\boldsymbol{B} \boldsymbol{a} \end{array}\right. $ | (4) |
式中,⊗为克罗内克积运算,a为系数矩阵A中非重复随机元素的t维列向量,a为真值,ea为随机误差,h为系数矩阵A中的非随机元素和0组成的nm维列向量,B为系数矩阵A中与随机元素有关的(nm×t)维固定矩阵,In为(n×n)维单位矩阵。随机模型为:
| $ \boldsymbol{e}=\left[\begin{array}{l} \boldsymbol{e}_y \\ \boldsymbol{e}_a \end{array}\right] \sim N\left(\left[\begin{array}{l} 0 \\ 0 \end{array}\right], \sigma_0^2\left[\begin{array}{cc} \boldsymbol{Q}_y & 0 \\ 0 & \boldsymbol{Q}_a \end{array}\right]\right) $ | (5) |
其中,Qa为系数向量a的协因数阵。
令
1) 设置初值:x(0)=xLS,ea(0)=0。
2) 求参数更新值:
3) 更新参数:
三维坐标转换的Partial EIV模型中,向量h和固定矩阵B为[9]:
| $ \boldsymbol{h}=\left[\begin{array}{c} \boldsymbol{h}_1 \\ \boldsymbol{h}_2 \\ \vdots \\ \boldsymbol{h}_7 \end{array}\right], \boldsymbol{B}=\left[\begin{array}{c} \boldsymbol{B}_1 \\ \boldsymbol{B}_2 \\ \vdots \\ \boldsymbol{B}_7 \end{array}\right] $ | (6) |
式中,
RBF神经网络是一种3层前馈局部逼近网络,将输入层数据非线性变化到高维空间的隐含层中,实现低维度空间内线性不可分问题在高维度空间内的线性可分,再将隐含层线性变换到输出层中[10]。
通常选用高斯函数作为径向基函数的激活函数:
| $ \varphi_j(\boldsymbol{X})=\exp \left(-\frac{\left\|\boldsymbol{X}-\mu_j\right\|^2}{2 \sigma_j^2}\right) $ | (7) |
式中,φj(X)为隐含层第j个神经元的输出值,X为输入向量,μj为隐含层神经元中心参数,σj为高斯函数的扩展参数。
输出层估计值为:
| $ y_k=\sum\limits_{j=1}^m w_{k j} \varphi_j(\bf{X}) $ | (8) |
式中,wkj为输出层第k个神经元与隐含层第j个神经元之间的权重。
对于坐标改正数,可建立隐含层有m个神经元的(3×m×3)神经网络。
2.2 组合解法的建立使用Partial EIV模型的加权总体最小二乘法求解三维坐标转换参数,在考虑系数矩阵误差的情况下,求出七参数以及源坐标的改正数。由于使用七参数进行转换时无法确定待转换坐标的误差大小,因此本文基于RBF神经网络建立源坐标的误差分布模型,从而更有效地发挥加权总体最小二乘法对七参数求解的作用。
具体流程如图 1所示,算法步骤如下:

|
图 1 组合方法坐标转换流程 Fig. 1 Coordinate transformation process of composite method |
1) 根据§1.1中公式,利用重合点坐标计算七参数加权最小二乘解,并将其作为初值;
2) 根据§1.2中迭代过程计算Partial EIV模型的加权总体最小二乘解;
3) 利用步骤2)计算出的源坐标系坐标改正数训练RBF神经网络;
4) 基于RBF神经网络计算的待转换点坐标改正数,利用Partial EIV模型的加权总体最小二乘法求出的七参数进行转换。
3 实验分析本文选取某地81个同时具有1980西安坐标系和2000国家大地坐标系成果坐标的重合点数据,利用其中69个点计算模型参数,12个点作为检核点,分别计算最小二乘解LS、加权总体最小二乘解WTLS、Partial EIV模型的加权总体最小二乘解PWTLS,并检验本文提出的PWTLS+RBF组合方法的有效性。
表 1(单位m)为3种七参数解算模型的单位权中误差,可以看出,相比于经典最小二乘平差LS,考虑系数矩阵中存在误差的WTLS单位权中误差提高了29%,考虑系数矩阵中存在相关元素的PWTLS单位权中误差提高了55%。
|
|
表 1 单位权中误差 Tab. 1 Unit weight mean square error |
表 2(单位m)为3种求解参数方法的内符合精度,可以看出,PWTLS的内符合精度略高于LS,但低于WTLS。这是因为WTLS未考虑系数矩阵中的重复元素,所以能够自由调节改正数以满足目标函数。
|
|
表 2 内符合精度比较 Tab. 2 Comparison of internal coincidence accuracy |
表 3(单位m)为3种方法的外符合精度比较,由表可见,3种方法的外符合精度均相同,这主要是因为3种方法求出的七参数值差异较小,所以在未知检核点坐标误差的情况下,求解出的转换残差基本相同。而本文提出的PWTLS+RBF组合方法首先利用RBF神经网络计算检核点的坐标误差,然后根据PWTLS方法计算的转换参数进行转换,因此外符合精度较高。
|
|
表 3 外符合精度比较 Tab. 3 Comparison of external coincidence accuracy |
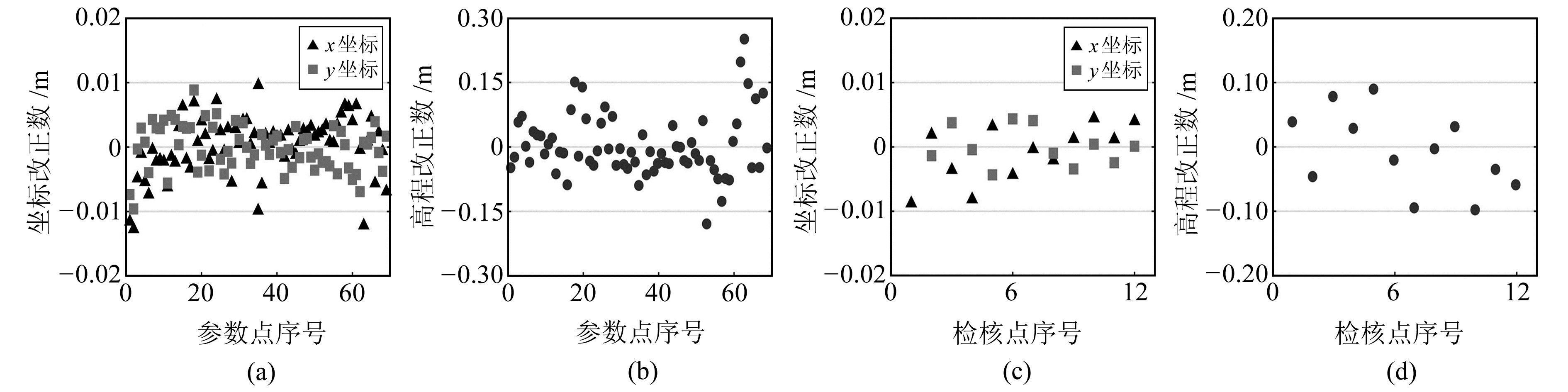
图 2(a)、(b)为PWTLS方法直接解算得到的参数点源坐标改正数,以此为训练样本对RBF神经网络进行训练;图 2(c)、(d)为利用训练完成的RBF神经网络检核点源坐标改正数,对源坐标进行改正后再根据七参数进行转换的过程图,转换结果如图 3所示。
|
图 2 源坐标改正数 Fig. 2 Correction of source coordinate |
|
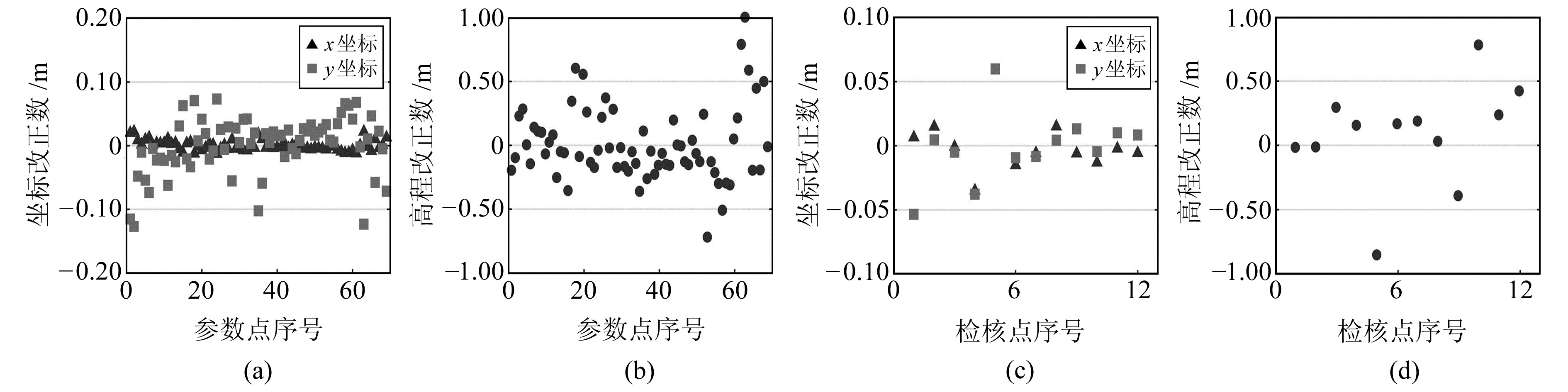
图 3 PWTLS+RBF组合法转换残差 Fig. 3 Residuals of coordinate transformation method combining PWTLS and RBF |
由图 3(a)、(b)可见,PWTLS+RBF组合法计算参数点高斯投影平面坐标残差的绝对值小于0.1 m,大地高残差的绝对值小于0.5 m;由图 3(c)、(d)可见,PWTLS+RBF组合法检核点高斯投影平面坐标残差的绝对值小于0.05 m,大地高残差的绝对值小于0.5 m,说明重合点的大地高精度较低。
4 结语本文顾及源坐标误差对转换参数求解的影响,对比分析LS、WTLS、PWTLS方法对七参数求解的不同影响。为解决实际转换过程中待转换坐标误差未知的问题,提出PWTLS+RBF组合坐标转换方法。实验结果表明,PWTLS能够更好地解决转换模型系数矩阵中同时存在常数元素和重复元素的问题,单位权中误差和内符合精度均小于LS,且源坐标改正数较WTLS更加合理。PWTLS+RBF方法能够使PWTLS求解参数得到有效使用,提高其在实际应用中的转换精度。
| [1] |
程鹏飞, 成英燕, 秘金钟, 等. 国家大地坐标系建立的理论与实践[M]. 北京: 测绘出版社, 2017 (Cheng Pengfei, Cheng Yingyan, Bei Jinzhong, et al. Theory and Practice for Establishment of National Geodetic Coordinate System[M]. Beijing: Surveying and Mapping Press, 2017)
(  0) 0) |
| [2] |
Shen Y Z, Li B F, Chen Y. An Iterative Solution of Weighted Total Least-Squares Adjustment[J]. Journal of Geodesy, 2011, 85(4): 229-238 DOI:10.1007/s00190-010-0431-1
(  0) 0) |
| [3] |
方兴, 曾文宪, 刘经南, 等. 三维坐标转换的通用整体最小二乘算法[J]. 测绘学报, 2014, 43(11): 1139-1143 (Fang Xing, Zeng Wenxian, Liu Jingnan, et al. A General Total Least Squares Algorithm for Three-Dimensional Coordinate Transformations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1139-1143)
(  0) 0) |
| [4] |
赵辉, 张书毕, 张秋昭. 基于加权总体最小二乘法的GPS高程拟合[J]. 大地测量与地球动力学, 2011, 31(5): 88-90 (Zhao Hui, Zhang Shubi, Zhang Qiuzhao. GPS Height Fitting of Weighted Total Least-Squares Adjustment[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 88-90)
(  0) 0) |
| [5] |
王乐洋, 孙坚强. 总体最小二乘回归预测模型的方差分量估计[J]. 武汉大学学报: 信息科学版, 2021, 46(2): 280-288 (Wang Leyang, Sun Jianqiang. Variance Components Estimation for Total Least-Squares Regression Prediction Model[J]. Geomatics and Information Science of Wuhan University, 2021, 46(2): 280-288)
(  0) 0) |
| [6] |
Xu P L, Liu J N, Shi C. Total Least Squares Adjustment in Partial Errors-in-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675 DOI:10.1007/s00190-012-0552-9
(  0) 0) |
| [7] |
王乐洋, 余航, 陈晓勇. Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22-29 (Wang Leyang, Yu Hang, Chen Xiaoyong. An Algorithm for Partial EIV Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22-29)
(  0) 0) |
| [8] |
姚宜斌, 孔建. 顾及设计矩阵随机误差的最小二乘组合新解法[J]. 武汉大学学报: 信息科学版, 2014, 39(9): 1028-1032 (Yao Yibin, Kong Jian. A New Combined LS Method Considering Random Errors of Design Matrix[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1028-1032)
(  0) 0) |
| [9] |
邱德超, 鲁铁定. 基于Partial EIV模型的三维坐标转换参数求解方法[J]. 江西科学, 2017, 35(3): 355-359 (Qiu Dechao, Lu Tieding. Three-Dimensional Coordinate Conversion Parameters Method Based on Partial EIV Model[J]. Jiangxi Science, 2017, 35(3): 355-359)
(  0) 0) |
| [10] |
袁德宝, 张建, 赵传武, 等. 基于改进RBF神经网络的GNSS高程拟合[J]. 大地测量与地球动力学, 2020, 40(3): 221-224 (Yuan Debao, Zhang Jian, Zhao Chuanwu, et al. GNSS Height Fitting Based on Improved RBF Neural Network[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 221-224)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


