星基增强系统(SBAS)可提升导航系统定位精度和完好性,该系统主要通过地球静止轨道卫星GEO向用户播发星历改正数和完好性信息,进而为用户端提供完好性服务。目前处于正式运行状态的SBAS包括美国的WASS(wide area augmentation system)、欧洲的EGNOS(European geostationary navigation overlay service)、日本的MSAS(MTSAT satellite-based augmentation system) 和印度的GAGAN(GPS aided GEO augmentation navigation),另外俄罗斯的SDCM(system for differential corrections and monitoring)、韩国的KASS(Korean augmentation satellite system)等SBAS也处于发展之中。我国的BDSBAS作为北斗系统的七大服务之一,在系统建设、服务测试、国际标准化等各方面都取得巨大进展,并将在国家“十四五”规划中发挥更加重要的作用[1]。
目前BDSBAS增强信号正处于测试阶段,各方面的性能还有待完善[2-3],官方也未明确给出最基本的BDSBAS服务范围,这就导致用户无法确定自己所处的位置能否使用BDSBAS,进而限制了BDSBAS的推广应用,因此确定BDSBAS的服务范围具有重要的现实意义。
WAAS和EGNOS已在官网上明确公布服务范围:WAAS基于不同的用户服务等级,根据完好性参数计算出相应的保护级,并根据保护级给出具体服务范围[4];EGNOS利用现有基准站,在有效的导航定位精密进近(precision approach,PA)结果下,在水平导航系统误差(horizontal navigation system error,HNSE)优于3 m、垂直导航系统误差(vertical navigation system error,VNSE)优于4 m的双重约束下确定其服务范围[5]。其他增强系统仅给出大致的服务范围,缺少明确的报告或者数据支撑。此外,由于SBAS服务范围研究的文献资料相对较少,因此本文基于BDSBAS现阶段发展情况,提出一种基于单频(single frequence,SF) SBAS完好性参数99.9%包络概率要求的SBAS服务范围确定方法。首先利用欧洲EGNOS实际播发的完好性参数信息推算EGNOS服务范围;然后将其与实际服务范围进行比较,验证本文方法的合理性;最后对我国BDSBAS服务范围进行推算,给出BDSBAS的初步服务范围。本文将对BDSBAS服务范围的确定提供理论依据,并促进BDSBAS服务性能的提升。
1 SBAS服务范围确定的基本原理 1.1 UDRE参数包络在高斯分布中,3.29倍中误差分位数处对应的分布概率为99.9%,可以理解为当修正误差在用户位置上的投影值分布符合高斯模型时,UDRE(user differential range error)理论上可以包络住99.9%的修正误差投影值。因此,在卫星测距误差评估中,UDRE对轨道/钟差修正误差最差投影值的包络概率需要达到99.9%,才能满足SBAS完好性风险检验。
1.1.1 增强轨道/钟差计算首先利用接收的导航电文计算卫星位置和钟差,然后利用星基增强电文中的轨道/钟差改正数对卫星位置和钟差进行修正,得到增强后的轨道/钟差结果。具体步骤如下:
1) 利用导航电文计算卫星在地心地固坐标系中的位置和钟差[XE YE ZE BE]。
2) 利用星基增强电文计算轨道/钟差改正数。慢变改正数信息包括卫星星历慢变改正数和卫星时钟慢变改正数,在单频增强电文中,慢变改正数信息由电文25播发。
卫星星历慢变改正数的计算公式为:
| $ \begin{gathered} {\left[\delta x_{k} \;\delta y_{k} \;\delta z_{k}\right]^{\mathrm{T}}=} \\ {\left[\begin{array}{lll} \delta x & \delta y & \delta z \end{array}\right]^{\mathrm{T}}+\left[\begin{array}{lll} {\delta} \dot{x} & \delta \dot{y} & \delta \dot{z} \end{array}\right]^{\mathrm{T}}\left(t-t_0\right)} \end{gathered} $ | (1) |
式中, [δxk δyk δzk]T为当前时刻轨道改正数,[δx δy δz]T为轨道偏差,
卫星时钟慢变改正数的计算公式为:
| $ \delta \Delta t_{\mathrm{SV}}(t)=\delta a_{\;f 0}+\delta a_{\;f 1}\left(t-t_0\right)+\delta a_{\;f G 0} $ | (2) |
式中,t为当前时刻,δΔtSV(t)为当前时刻时钟改正数,δaf0为时钟偏差,δaf1为时钟偏差变化率,t0为改正数参考时刻,δafG0为GLONASS卫星改正参数(在电文12中播发,非GLONASS卫星的δafG0=0)。
3) 利用改正数对卫星位置和钟差进行修正:
| $ \begin{aligned} & {\left[\begin{array}{llll} X_{\mathrm{C}} & Y_{\mathrm{C}} & Z_{\mathrm{C}} & B_{\mathrm{C}} \end{array}\right]^{\mathrm{T}}=\left[\begin{array}{llll} X_{\mathrm{E}} & Y_{\mathrm{E}} & Z_{\mathrm{E}} & B_{\mathrm{E}} \end{array}\right]^{\mathrm{T}}+} \\ &\;\;\;\;\;\;\;\;\;\; {\left[\delta x_{k} \;\delta y_{k} \;\delta z_{k} \;\delta \cdot \;t_{\mathrm{SV}} \;* \;c\right]^{\mathrm{T}}} \\ & \end{aligned} $ | (3) |
式中,[XC YC ZC BC]T为t时刻改正后的增强轨道/钟差。
1.1.2 UDRE参数包络概率首先将改正后的增强轨道/钟差分别与事后精密轨道/钟差产品作差,得到修正误差,然后将修正误差投影至格网点上,判断UDRE是否对修正残差形成包络。统计目标区域格网点的UDRE包络概率,并确定包络概率大于99.9%的区域。具体步骤如下:
1) 将修正后的卫星位置和钟差分别与精密卫星轨道和钟差作差:
| $ \begin{aligned} & \;\;\;\;\;\;\;\;\;\; {[\Delta X \;\Delta Y \;\Delta Z \;\Delta B]^{\mathrm{T}}=} \\ & {\left[\begin{array}{llll} X_{\mathrm{C}} & Y_{\mathrm{C}} & Z_{\mathrm{C}} & B_{\mathrm{C}} \end{array}\right]^{\mathrm{T}}-\left[\begin{array}{llll} X_{\mathrm{P}} & Y_{\mathrm{P}} & Z_{\mathrm{P}} & B_{\mathrm{P}} \end{array}\right]^{\mathrm{T}}} \\ & \end{aligned} $ | (4) |
式中,[XC YC ZC BC]T为时刻t改正后的卫星位置和钟差,[XP YP ZP BP]T为时刻t精密卫星轨道和钟差,[ΔX ΔY ΔZ ΔB]T为二者的差值。
2) 修正残差在格网点位置上的投影为:
| $ \Delta R=[\Delta X \; \Delta Y \; \Delta Z \; \Delta B]^{\mathrm{T}} \cdot \boldsymbol{l} $ | (5) |
式中,l为卫星到格网点的单位方向矢量。
3) 统计目标区域格网点的UDRE包络概率,并确定包络概率大于99.9%的区域S(UDRE):
| $ \mathrm{S}_{(\mathrm{UDRE})}=S\left(P\left(\sigma_{\mathrm{UDRE}} \geqslant \Delta R\right) \geqslant 99.9 \%\right) $ | (6) |
式中,σUDRE为UDREI对应的UDRE值,对应关系如表 1[6-7]所示;P(·)为包络概率。
|
|
表 1 UDRE与量化值对应表 Tab. 1 Correspondence table between UDRE and quantized value |
由表 1可见,UDRE与σUDRE存在如下关系:
| $ \mathrm{UDRE}=3.29 \sigma_{i, \mathrm{UDRE}} $ |
与UDRE参数类似,在电离层延迟误差评估中,通常认为电离层网格点垂直延迟误差(grid ionospheric vertical error,GIVE)对修正误差的包络率需达到99.9%,才能满足SBAS完好性风险检验。
SBAS为每个电离层格网点(ionsopheric grid point,IGP)播发GIVE和电离层格网点垂直延迟值,以确保电离层改正数的准确性。在GIVE性能分析过程中,计算全球电离层格网模型的电离层延迟量,将其与SBAS电文中提供的对应IGP处的电离层延迟作差,得到电离层误差,并统计GIVE对该差值的包络概率。若实际使用的格网点密度高于全球电离层格网模型或增强星历播发的格网点密度,则可以利用平面几何内插法对全球电离层格网模型增强电文的GIVE和电离层延迟进行内插,进而计算GIVE的包络概率。具体步骤如下:
1) 计算服务区域内IGP增强电文电离层延迟量IC和GIVE值,计算对应IGP的全球电离层格网模型电离层延迟量I。若有必要,还需进行平面几何内插。
2) 计算电离层改正数与电离层延迟的差值ΔI:
| $ \Delta I=\mathrm{IC}-I $ | (7) |
3) 统计目标区域内格网点的GIVE包络概率,并确定包络概率大于99.9%的区域S(GIVE):
| $ S_{(\mathrm{GIVE})}=S\left(P\left(\sigma_{\mathrm{GIVE}} \geqslant \Delta I\right) \geqslant 99.9 \%\right) $ | (8) |
式中,σGIVE为GIVEI对应的GIVE值,对应关系如表 2[6]所示;P(·)为包络概率。
|
|
表 2 GIVE与量化值对应表 Tab. 2 Correspondence table between GIVE and quantized value |
由表 2可见,GIVE与σGIVE存在如下关系:
| $ \mathrm{GIVE}=3.29 \sigma_{i, \mathrm{GIVE}} $ | (9) |
为保证用户端的完好性,避免完好性风险事件的发生,SF SBAS播发的完好性参数(UDRE、GIVE)通常需要以99.9%的概率对相应的改正数修正残差形成包络。基于此,本文提出一种确定SBAS服务范围的方法,具体步骤如下:
1) 选定SBAS初步服务区域。
2) 解算当前历元GNSS卫星轨道和钟差修正残差以及UDRE信息。
3) 以5°×5°的经纬度差对目标区域进行分割,计算每个历元、每颗卫星在每个格网点上的轨道/钟差综合误差[7],并判断UDRE对轨道/钟差综合误差是否形成包络。统计目标区域内格网点UDRE包络概率,并确定包络概率大于99.9%的区域。
4) 计算目标区域电离层延迟误差值和GIVE信息。本文计算周期为5 min(SBAS电离层信息5 min播发一次),判断GIVE对电离层延迟误差是否形成包络。统计包络概率大于99.9%的区域和GIVE有效格网点概率(当前时刻格网点有计算结果定义为有效)。
5) 对99.9%包络要求下的完好性参数UDRE和GIVE的公共区域进行叠加,并确定最终的SBAS服务区域。
2 SBAS服务范围验证 2.1 数据来源本文采集西安某单位楼顶2020-12-04原始观测电文开展SBAS服务范围确定实验。接收机型号为Septentrio PolaRx5,使用天线为NovAtel GNSS-750。外部文件包括IGS服务中心发布的全球广播星历文件、事后精密轨道/钟差产品、天线相位中心改正文件和全球电离层格网模型文件等。由于西安本地可以接收到EGNOS电文信号,且EGNOS官方网站(https://www.essp-sas.eu)已公布其服务范围,因此本文利用EGNOS电文数据开展SBAS服务范围验证实验,并通过BDSBAS电文数据的解算结果,对BDSBAS服务范围进行初步分析,进而为行业用户使用BDSBAS服务提供参考。
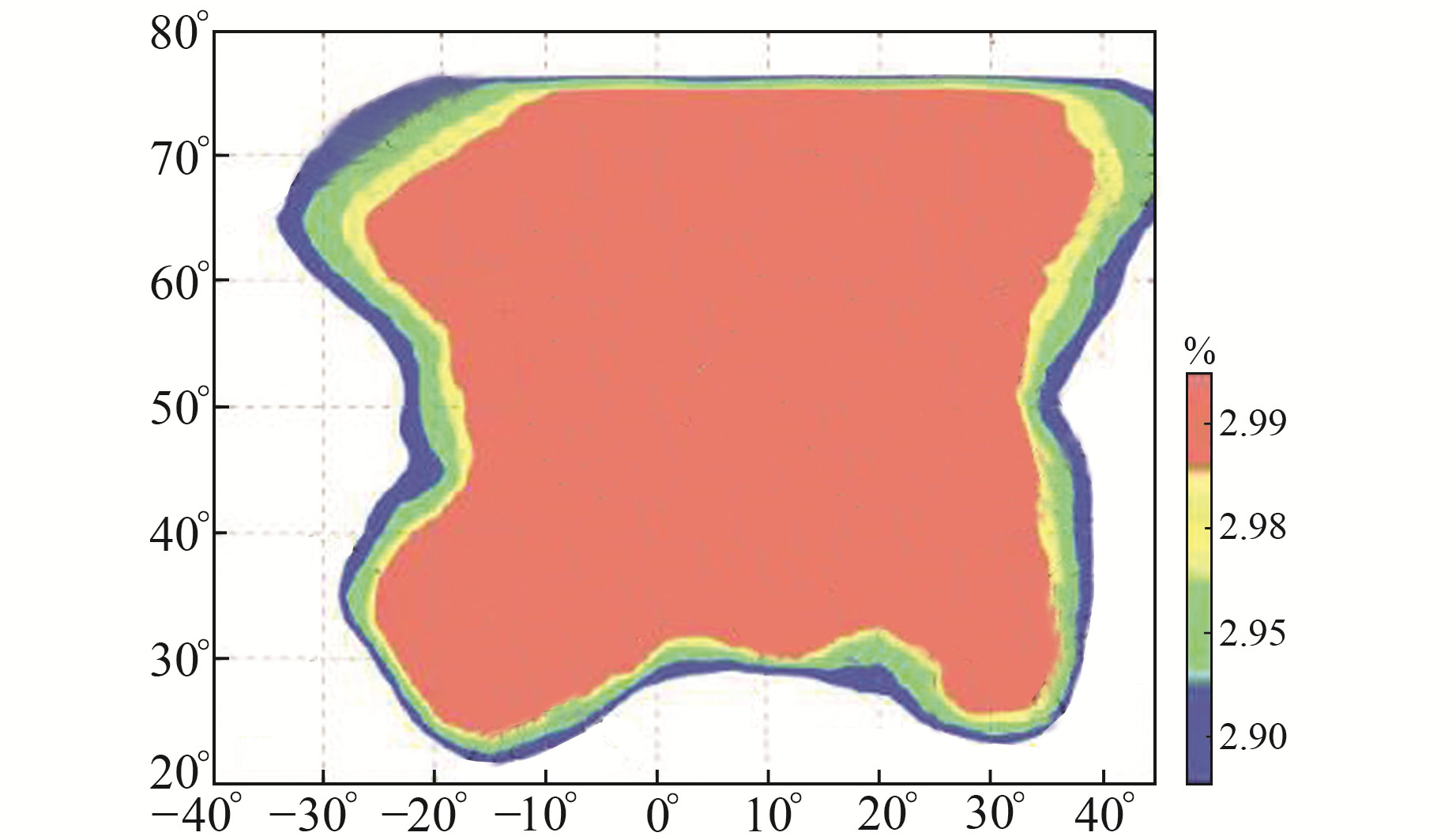
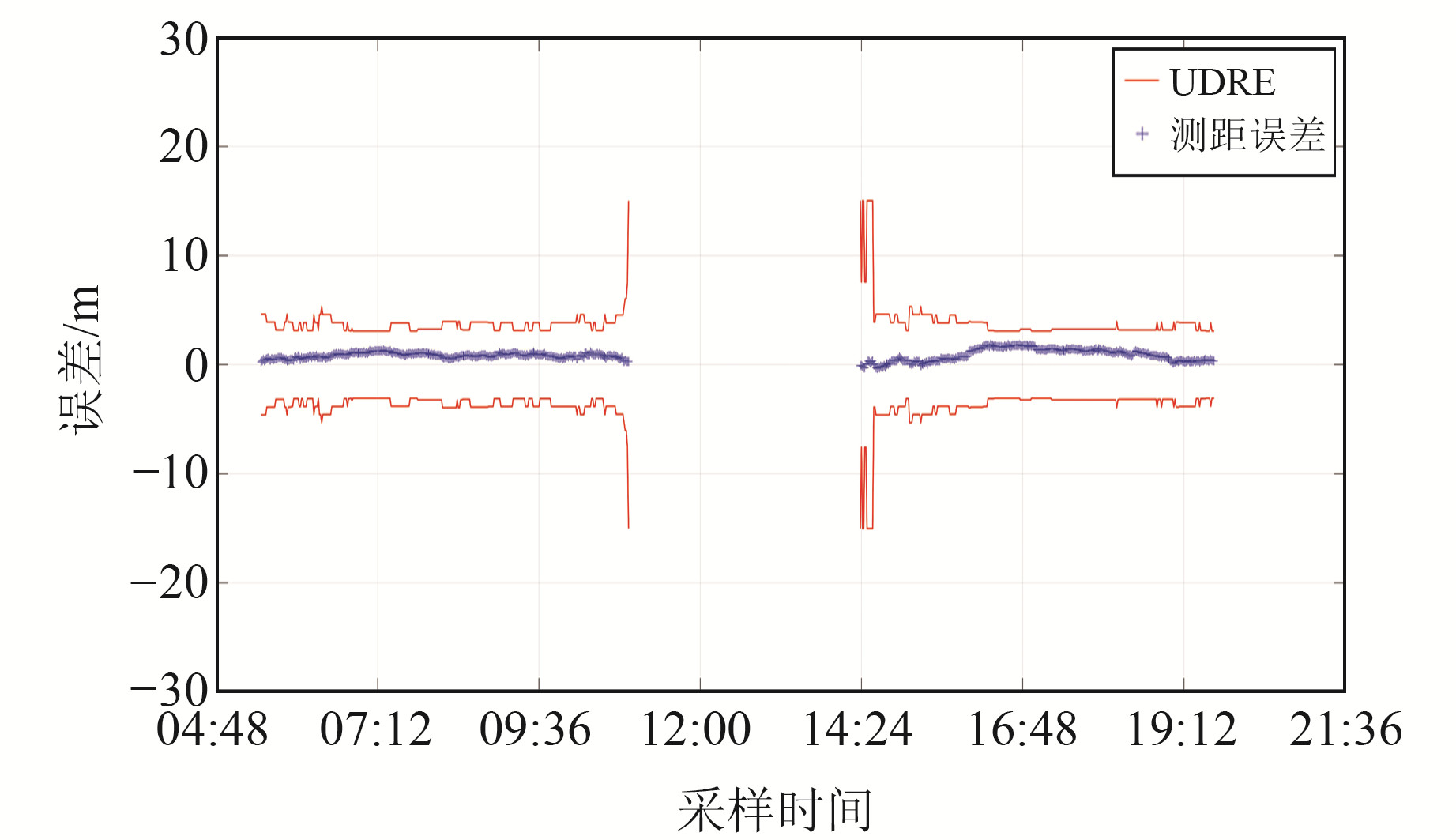
2.2 EGNOS服务范围验证在验证EGNOS服务范围时,将目标区域定为45°W~60°E、20°~80°N,基于实际接收的EGNOS PRN 126增强电文以及外部基准文件,利用自编软件对EGNOS完好性参数包络结果进行计算。图 1为目标区域EGNOS UDRE包络概率图,可以看出,UDRE的包络概率均达到99.9%以上,表明EGNOS轨道/钟差参数在目标区域内能够满足用户需求。此外,除当天未播发的PRN11和PRN14号卫星外,UDRE对其他各卫星的最大投影误差均可实现100%包络。图 2和图 3为EGNOS增强GPS PRN19和PRN23号卫星的UDRE误差包络序列,可以看出,观测弧段内UDRE对2颗卫星的最大投影误差均可实现100%包络。值得注意的是,卫星出入境时UDRE参数较大,即用户端的完好性风险较大,这与导航卫星出入境时卫星观测数据质量较差有关[8]。
|
图 1 EGNOS UDRE包络概率 Fig. 1 EGNOS UDRE envelope probability |
|
图 2 EGNOS增强GPS PRN 19号卫星UDRE包络序列 Fig. 2 UDRE envelope sequence of EGNOS enhanced GPS PRN 19 |

|
图 3 EGNOS增强GPS PRN 23号卫星UDRE包络序列 Fig. 3 UDRE envelope sequence of EGNOS enhanced GPS PRN 23 |
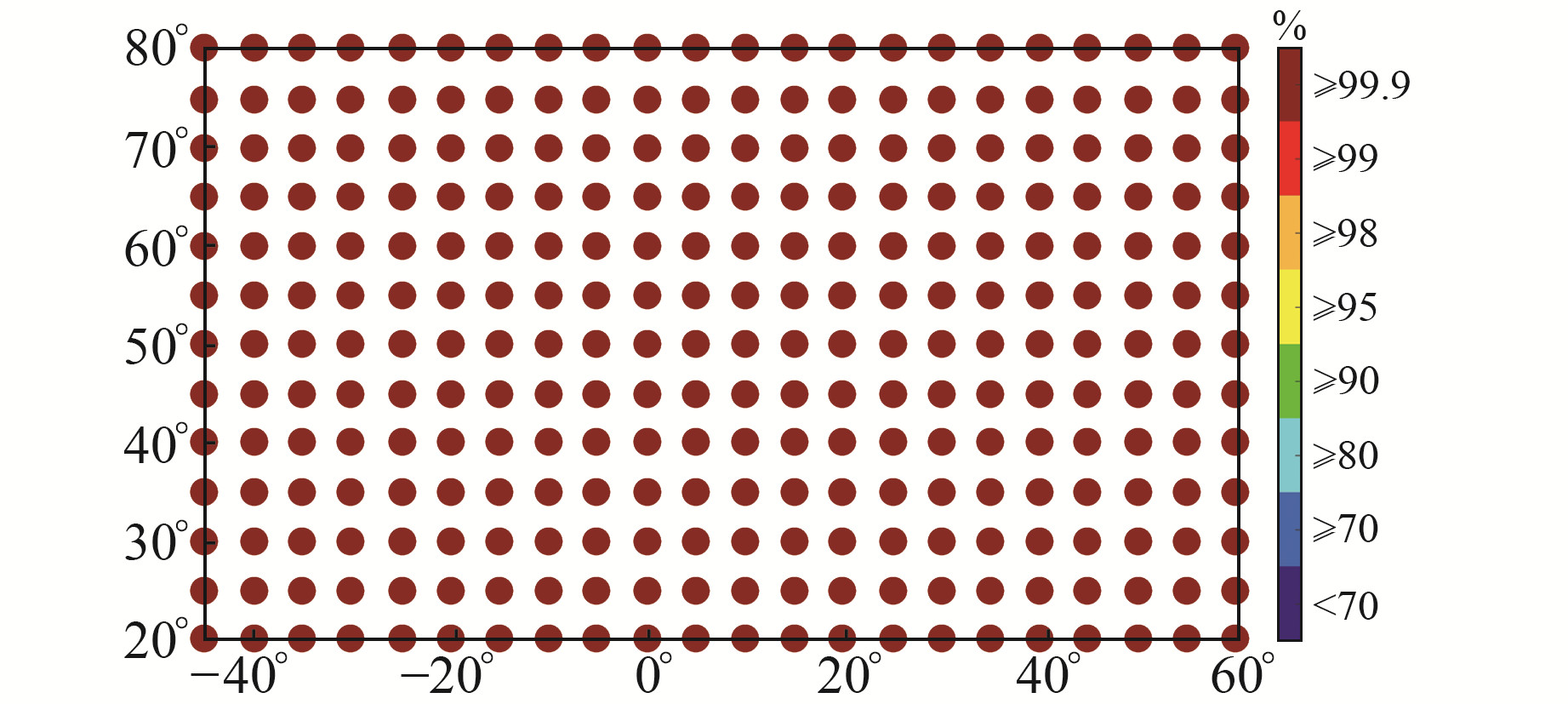
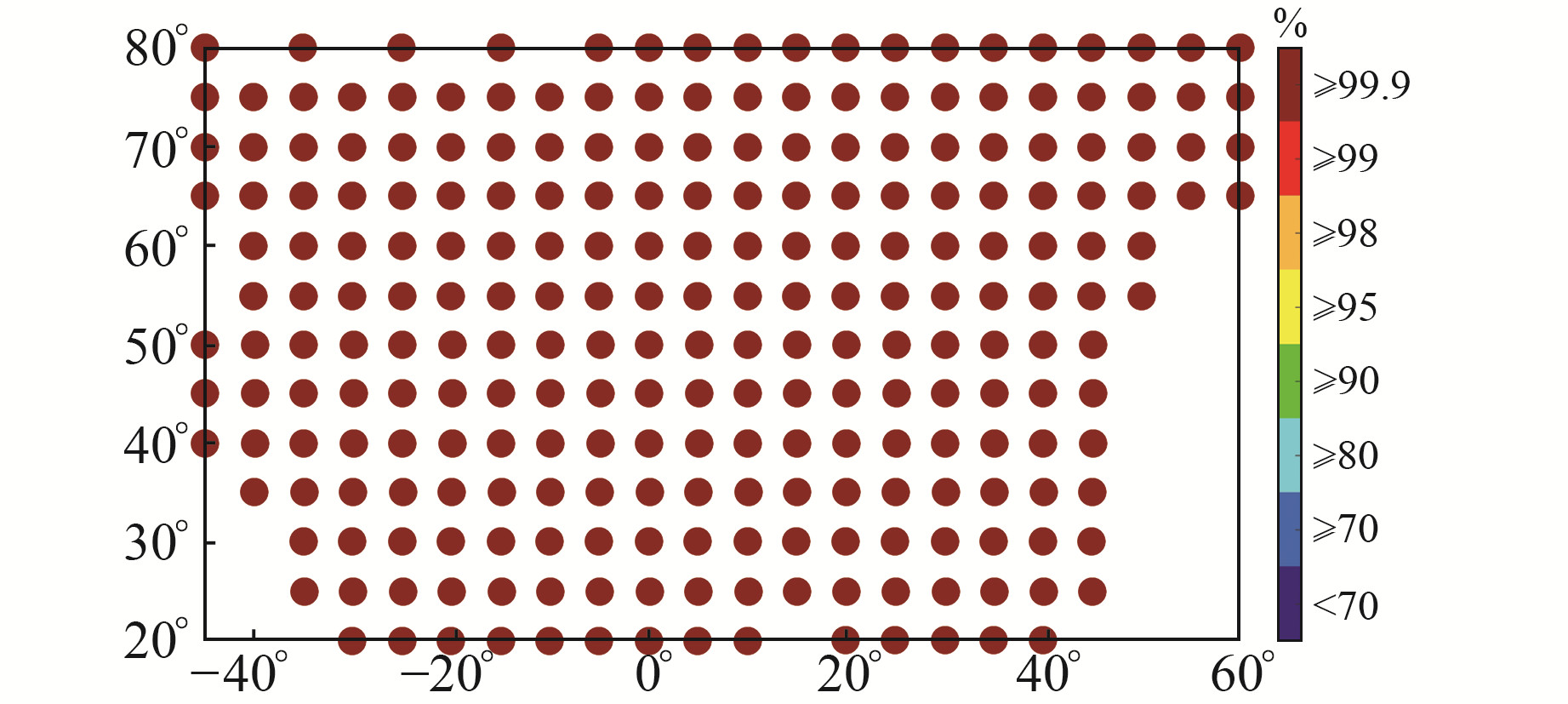
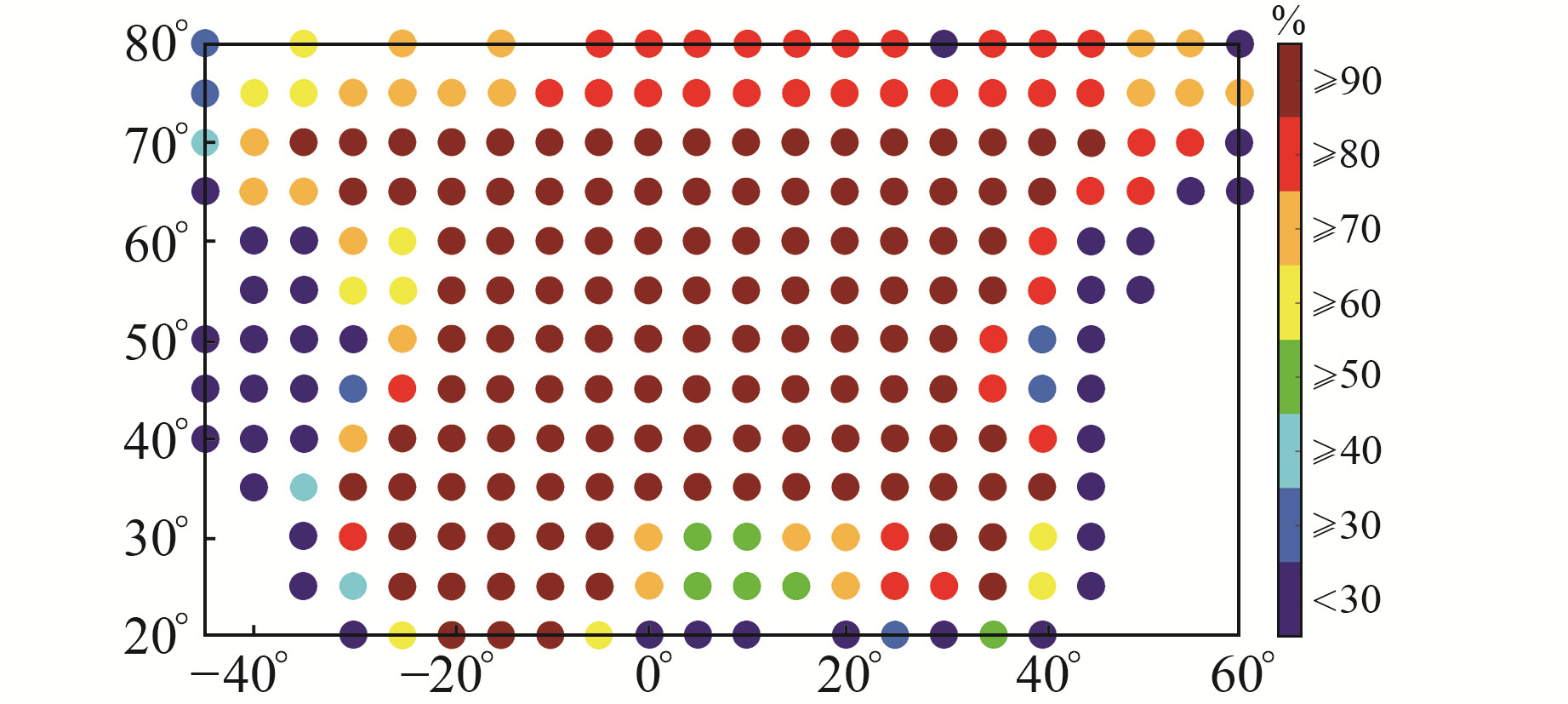
图 4和图 5分别为EGNOS GIVE包络概率和有效格网概率。由图 4可见,目标区域中GIVE可对电离层延迟误差形成100%包络;由图 5可见,目标区域边缘的有效格网概率逐渐降低,该现象主要与基准站的分布有关:越靠近边缘地区,EGNOS基准站越少,相应格网点生成有效电离层改正数的频率越低,进而影响到EGNOS服务的连续性和完好性。
|
图 4 EGNOS GIVE包络概率 Fig. 4 EGNOS GIVE envelope probability |
|
图 5 EGNOS GIVE有效格网概率 Fig. 5 EGNOS GIVE effective grid probability |
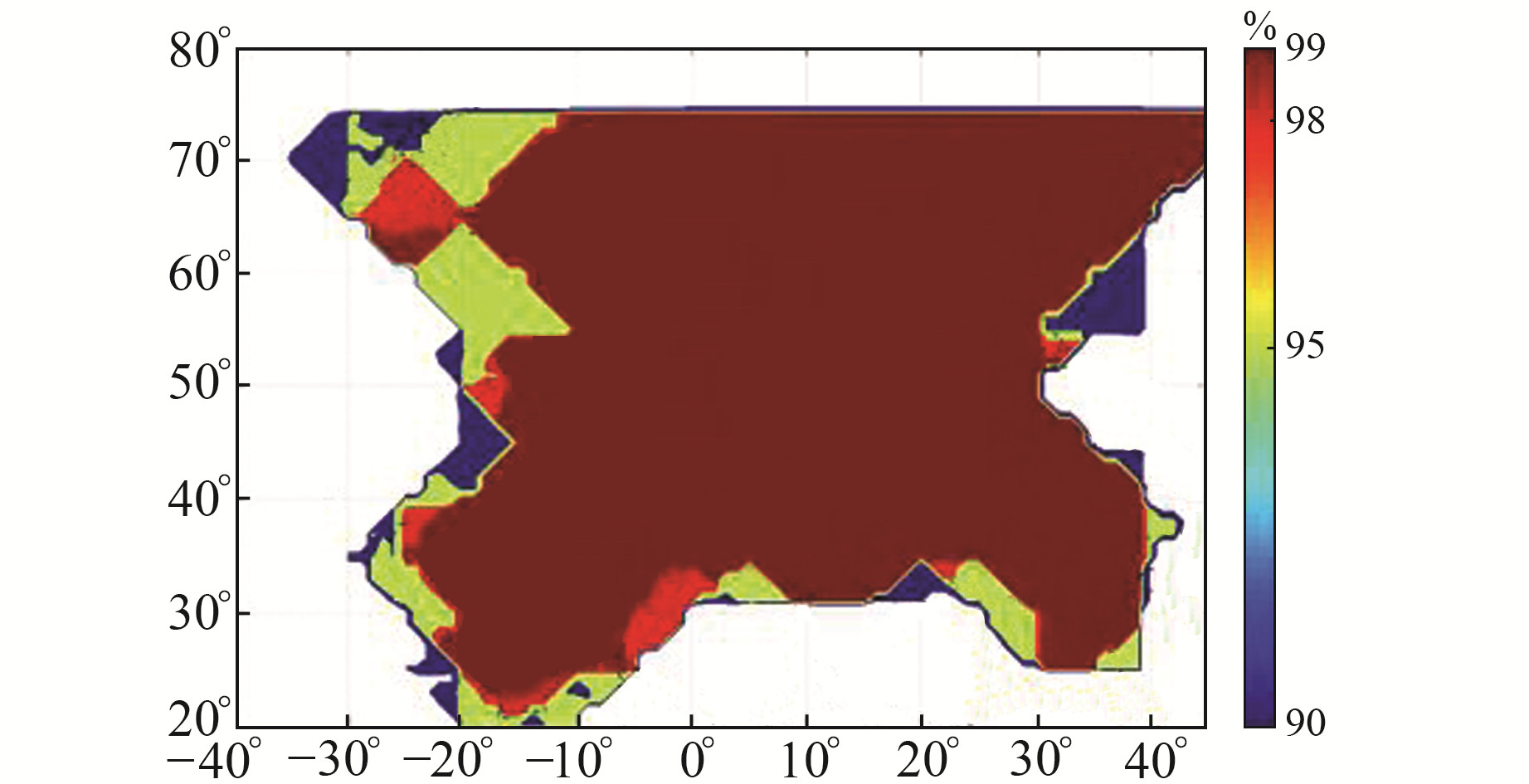
综合考虑EGNOS完好性参数UDRE/GIVE99.9%包络概率要求和GIVE有效格网概率后,最终推算的服务范围结果如图 6所示,EGNOS官方公布的服务范围如图 7所示[5]。可以看出,2种结果大致相同,但也存在部分差异,主要是因为SBAS增强电文以5°的格网点区间播发电离层参数信息时,会出现不平滑拟合现象。由此可见,本文提出的SBAS服务范围确定方法有效。
|
图 6 基于完好性要求叠加的EGNOS服务范围 Fig. 6 EGNOS service range based on superposition of integrity requirements |
2.3 BDSBAS服务范围初步分析
基于本文提出的SBAS服务范围确定方法,对BDSBAS的服务范围进行初步研究。本文将目标区域设定为60°~140°E、10°~60°N,在此区域内对BDSBAS完好性参数包络情况进行计算。图 8为目标区域BDSBAS UDRE包络概率图,可以看出,UDRE均达到99.9%以上,表明BDSBAS轨道/钟差参数能够满足用户需求,且UDRE对目标区域内大部分卫星最大投影误差均可实现100%包络。图 9和图 10分别为BDSBAS增强GPS PRN19和PRN23号卫星的UDRE误差包络序列,可以看出,BDSBAS在卫星可见弧段内播发的UDRE变化不大,未出现EGNOS随出入境逐渐变化的情况。PRN23号卫星在可见弧段内的包络概率为99.68%,在卫星出境时未形成包络,原因有2方面:一是目标区域边缘地区距离BDSBAS基准站点较远,其轨道/钟差改正数在边缘区域的服务效果较差;二是卫星出入境时用户观测数据质量较差,系统播发的轨道/钟差改正数较大,但播发的相应UDRE值却较小。目标区域内其他几颗未形成包络的卫星与PRN23号卫星情况相似,建议在UDRE参数播发的过程中,能够在卫星出入境时作一些策略调整,使其更符合实际情况。

|
图 8 BDSBAS UDRE包络概率 Fig. 8 BDSBAS UDRE envelope probability |

|
图 9 BDSBAS增强GPS PRN 19号卫星UDRE包络序列 Fig. 9 UDRE envelope sequence of BDSBAS enhanced GPS PRN 19 |

|
图 10 BDSBAS增强GPS PRN 23号卫星UDRE包络序列 Fig. 10 UDRE envelope sequence of BDSBAS enhanced GPS PRN 23 |
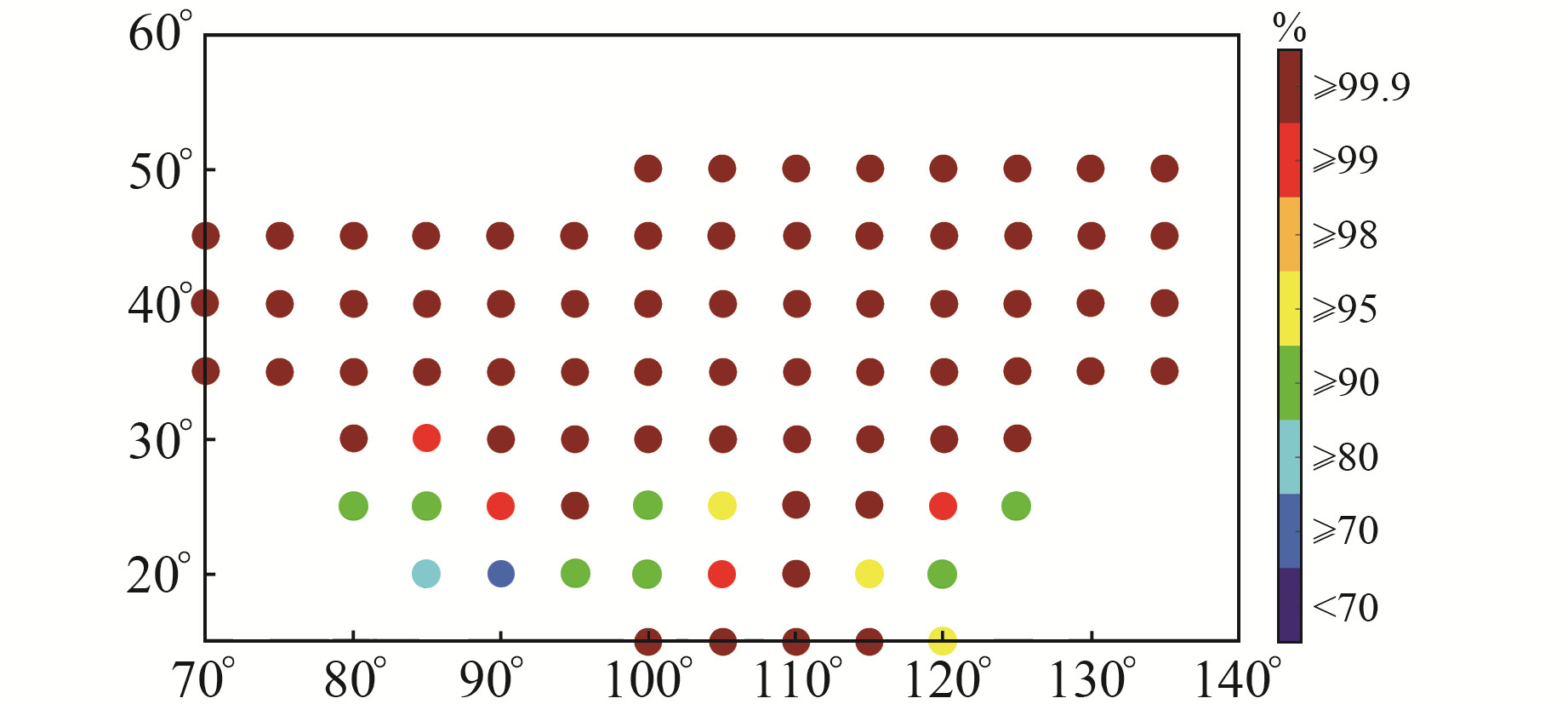
图 11和图 12分别为BDSBAS GIVE包络概率图和有效格网概率图。由图 11可见,GIVE可对中国大陆大部分区域的电离层延迟误差形成100%包络。由于西南地区存在电离层延迟误差较大或BDSBAS监测站分布较少等问题,GIVE在该区域未达到99.9%以上的概率包络,目标区域的高纬度地区和沿海地区未播发电离层改正数。由图 12可见,与EGNOS情况相似,BDSBAS目标区域边缘有效格网概率逐渐降低,该现象也是边缘地区基准站分布较少所致。
|
图 11 BDSBAS GIVE包络概率 Fig. 11 BDSBAS GIVE envelope probability |

|
图 12 BDSBAS GIVE有效格网概率 Fig. 12 BDSBAS GIVE effective grid probability |
综合考虑BDSBAS完好性参数UDRE/GIVE 99.9%包络概率要求和GIVE有效格网概率后,得到BDSBAS初步服务范围如图 13所示。由图可见,BDSBAS能够较好地为用户提供完好性服务。此外,建议BDSBAS在我国西南、西北、东北等地提高电离层参数播发性能,或进行合理选址建站,从而扩大并提高相应地区的完好性服务。

|
图 13 基于完好性要求叠加的BDSBAS服务范围 Fig. 13 BDSBAS service range based on superposition of integrity requirements |
本文首先对SF SBAS完好性参数(UDRE、GIVE)的验证方法进行介绍,然后在99.9%的完好性参数包络概率约束下对相应改正数修正残差形成包络,提出一种确定SBAS服务范围的方法。通过实际数据采集,对欧洲EGNOS播发的完好性信息进行分析。结果表明,本文方法推算出的EGNOS服务范围与其公布的服务范围基本一致,验证了本文方法的可行性。最后基于本文方法的原理和步骤,对BDSBAS的服务范围进行分析,初步给出BDSBAS服务范围,为行业用户使用BDSBAS服务提供参考。本文方法能够为BDSBAS服务范围的确定提供研究思路和理论依据,促进BDSBAS服务性能的提升。
| [1] |
RTCA. Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment[Z]. 2006
(  0) 0) |
| [2] |
戴凯阳, 李保东, 张键. 北斗三号新体制信号数据质量分析与接收机性能评估[J]. 现代导航, 2020, 11(2): 105-108 (Dai Kaiyang, Li Baodong, Zhang Jian. New Signal Data Quality Analysis and Receiver Performance Evaluation of BDS-3[J]. Modern Navigation, 2020, 11(2): 105-108)
(  0) 0) |
| [3] |
郭树人, 刘成, 高为广, 等. 卫星导航增强系统建设与发展[J]. 全球定位系统, 2019, 44(2): 1-12 (Guo Shuren, Liu Cheng, Gao Weiguang, et al. Construction and Development of Satellite Navigation Augmentation Systems[J]. GNSS World of China, 2019, 44(2): 1-12)
(  0) 0) |
| [4] |
黄双临, 辛洁, 王冬霞, 等. 星基增强系统电文及播发特性研究[J]. 数字通信世界, 2019(2): 4-6 (Huang Shuanglin, Xin Jie, Wang Dongxia, et al. Research on Propagating Message and Strategy of Satellite-Based Augmentation System[J]. Digital Communication World, 2019(2): 4-6)
(  0) 0) |
| [5] |
孟祥广, 孙越强, 白伟华, 等. 北斗卫星广播星历精度分析[J]. 大地测量与地球动力学, 2016, 36(10): 870-873 (Meng Xiangguang, Sun Yueqiang, Bai Weihua, et al. Precision Analysis of Beidou Satellites Broadcast Ephemeris[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 870-873)
(  0) 0) |
| [6] |
邵搏, 耿永超, 丁群, 等. 国际星基增强系统综述[J]. 现代导航, 2017, 8(3): 157-161 (Shao Bo, Geng Yongchao, Ding Qun, et al. Summarize of International Satellite Based Augmentation System[J]. Modern Navigation, 2017, 8(3): 157-161)
(  0) 0) |
| [7] |
王君君, 李锐, 程军, 等. SBAS完好性评估方法研究[J]. 现代导航, 2019, 10(4): 235-240 (Wang Junjun, Li Rui, Cheng Jun, et al. Research on Integrity Evaluation Method of SBAS[J]. Modern Navigation, 2019, 10(4): 235-240)
(  0) 0) |
| [8] |
中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件星基增强服务信号BDSBAS-B1C(1.0版)[Z]. 2020 (China Satellite Navigation Office. Beidou Navigation Satellite System Signal in Space Interface Control Document Satellite Based Augmentation System Service Signal BDSBAS-B1C(Version 1.0)[Z]. 2020)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43