2. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079;
3. 山东理工大学建筑工程学院,山东省淄博市新村西路266号,255000
BDS-2/3采用双频伪距观测量和双频载波相位观测量进行伪距单点定位(SPP)和精密单点定位(PPP),其理论方法和实现算法已经成熟[1-3]。然而,目前最常用的双频消电离层组合(IF)方法虽然可以消除一阶项电离层误差[4],但在解算过程中会出现卫星端与接收机端间的硬件延迟,且地面接收机在接收信号时也会存在由天线和仪器设备等造成的测距码偏差,上述偏差统称为观测量码偏差[5-6]。观测量码偏差一直是精密定位研究中的热点,通常将差分定位解算中的观测量偏差称为差分码偏差DSB或DCB,将IF组合定位解算中的观测量偏差称为ISB[7-8],国内外学者在观测量码偏差方面做了大量研究[9-14]。
近年来,随着各系统支持频点的不断增多,DCB的估计与改正步骤也日趋繁琐,有学者提出一种新的码偏差估计方法OSB[5]。相较于DCB,OSB的估计、使用过程较为简单,但其发展较晚、相关研究较少[6, 15]。基于此,本文首先介绍OSB估计的理论方法;然后利用武汉大学(WHU)发布的OSB产品对BDS-2/3各卫星各频点的OSB估计值进行稳定性分析;最后结合国际GNSS监测评估系统(iGMAS)实测数据,分析OSB改正对BDS-2/3的B1I/B3I旧频点和B1C/B2a新频点组合下SPP和PPP精度的影响。本文研究对于提升BDS-2/3精密定位服务性能具有重要意义。
1 OSB估计模型与稳定性分析 1.1 OSB估计模型在估计各卫星各频点的OSB前,首先需要估计卫星端与接收机端之间的DCB,然后对DCB估计值施加约束,计算出各卫星各频点的OSB。在忽略多路径误差和观测噪声误差的情况下,卫星与接收机之间的原始伪距观测方程为:
| $ \left\{\begin{array}{c} P_{\mathrm{r}, x}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+I_{\mathrm{r}, x}^{\mathrm{s}}+T_{\mathrm{r}}^{\mathrm{s}}+c \cdot \\ \quad\left(\mathrm{d} t_{\mathrm{r}}-\mathrm{d} t^{\mathrm{s}}\right)+B_{\mathrm{r}, x}+B_x^{\mathrm{s}} \\ P_{\mathrm{r}, y}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+I_{\mathrm{r}, y}^{\mathrm{s}}+T_{\mathrm{r}}^{\mathrm{s}}+c \cdot \\ \quad\left(\mathrm{d} t_{\mathrm{r}}-\mathrm{d} t^{\mathrm{s}}\right)+B_{\mathrm{r}, y}+B_y^{\mathrm{s}} \end{array}\right. $ | (1) |
式中,Pr, xs和Pr, ys分别为频点x和y的伪距观测值;ρrs为站星之间的几何距离;Ir, xs和Ir, ys分别为测距码x和y的电离层延迟;Trs为对流层延迟;c为光速;dtr和dts分别为接收机端和卫星端的钟差;Br, x、Br, y、Bxs和Bys分别为与接收机端和卫星端相关的OSB延迟量[14-15]。
通过区分2频点之间的伪距观测量,可以得到无几何组合观测量GF:
| $ \begin{gathered} P_{\mathrm{r}, \mathrm{GF}}^{\mathrm{s}}=P_{\mathrm{r}, x}^{\mathrm{s}}-P_{\mathrm{r}, y}^{\mathrm{s}}=40.3\left(\frac{1}{f_x^2}-\frac{1}{f_y^2}\right) \cdot \\ \mathrm{STEC}_{\mathrm{r}}^{\mathrm{s}}+B_{r, x}-B_{\mathrm{r}, y}+B_x^{\mathrm{s}}-B_y^{\mathrm{s}} \end{gathered} $ | (2) |
式中,STECrs为卫星到接收机的信号传播路径上的倾斜总电子含量;fx和fy分别为频点对应的频率。令DCBr, xy=Br, x-Br, y,DCBxys=Bxs-Bys,则有:
| $ \begin{gathered} \mathrm{DCB}_{\mathrm{r}, x y}^{\mathrm{s}}=\mathrm{DCB}_{\mathrm{r}, x y}+\mathrm{DCB}_{x y}^{\mathrm{s}}= \\ B_{\mathrm{r}, x}-B_{\mathrm{r}, y}+B_x^s-B_y^s \end{gathered} $ | (3) |
式中,DCBr, xys为频率x和y及卫星端和接收机端的码偏差量。DCB值主要与仪器硬件设备有关,通常认为1 a内的DCB值是稳定的[5, 12]。
由于式(3)中的各偏差值不可分离,因此完成DCB估计后需要在计算过程中施加一些与IGS官方约束相一致的约束条件。首先对Bxs进行约束,假设每个星座下卫星端码偏差是稳定的,则有:
| $ \frac{1}{N_x} \sum\limits_{i=1}^{N_x} B_x^{\mathrm{s}}=0 $ | (4) |
式中,Nx为1 a内观测到的频点x卫星总数。认为双频IF组合下卫星端2频点的码偏差IF组合以及接收机端2频点的码偏差IF组合均为0,则有:
| $ \left\{\begin{array}{l} \frac{f_x^2}{f_x^2-f_y^2} B_x^{\mathrm{s}}-\frac{f_y^2}{f_x^2-f_y^2} B_y^{\mathrm{s}}=0 \\ \frac{f_x^2}{f_x^2-f_y^2} B_{\mathrm{r}, x}-\frac{f_y^2}{f_x^2-f_y^2} B_{\mathrm{r}, y}=0 \end{array}\right. $ | (5) |
通过式(5)的模型方法和约束条件,可以估计出各卫星各频点1 a内的OSB值。
1.2 BDS-2/3卫星OSB稳定性分析目前,中国科学院(CAS)、武汉大学(WHU)、欧洲定轨中心(CODE)及德国航空航天中心(DLR)等多家单位发布了OSB估计产品,但由于卫星刚组网成功且稳定运行不久,目前仅有CAS和WHU 2家单位的产品向外发布。本文利用WHU发布的2020-10-07(doy281/MJD59 129)~2022-02-06(doy037/MJD59 616)共计488 d的产品进行BDS-2/3各频点OSB稳定性分析。
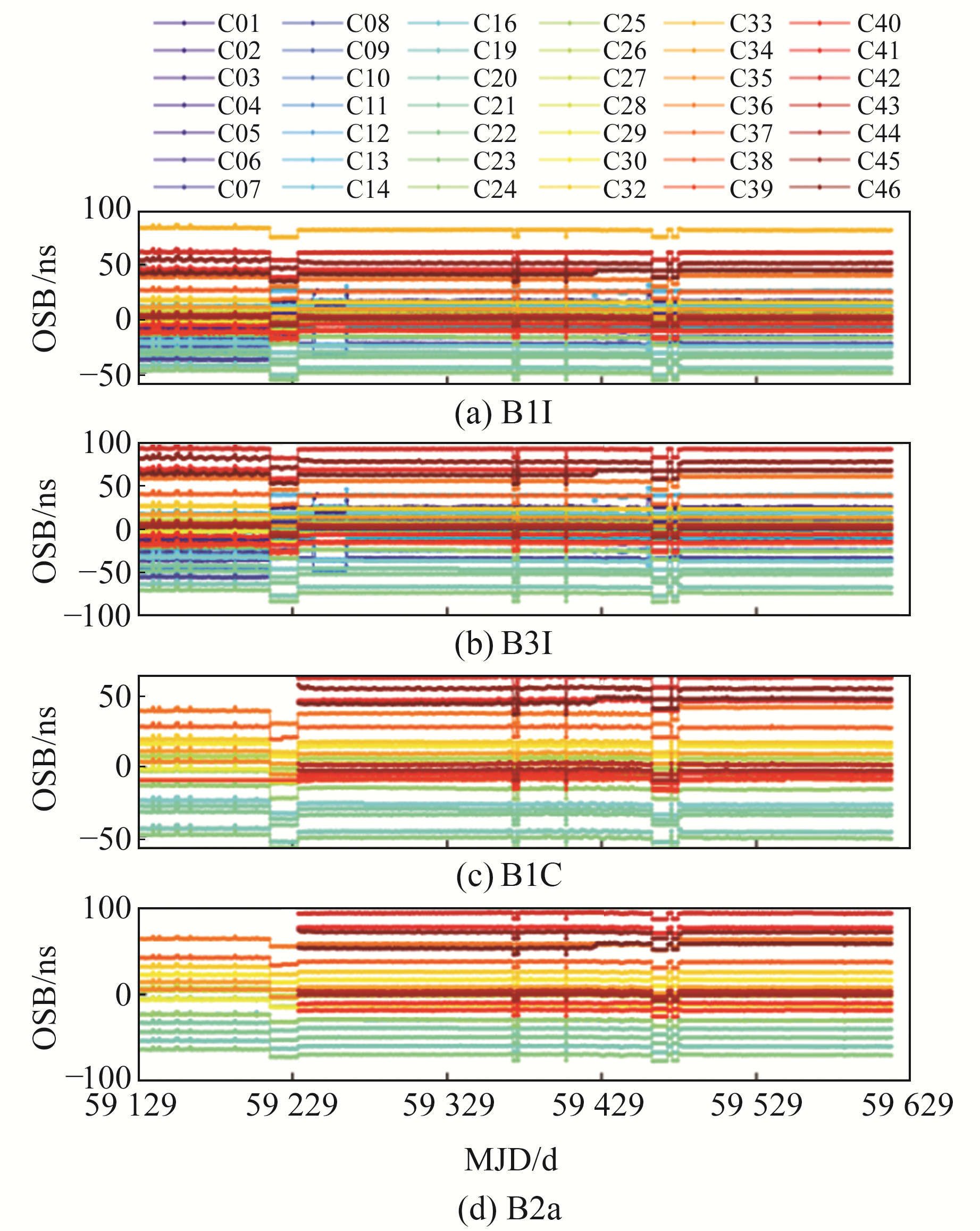
图 1为BDS-2/3卫星播发B1I、B3I、B1C和B2a频点的OSB改正数时间序列,可以看出,各频点的OSB改正值为-70~100 ns,各频点的OSB估计数值较为稳定,无明显波动。从数值上看,由OSB引起的等效距离误差可达10 m量级,因此精密定位时必须将此误差考虑在内。个别时段会出现明显的跳变现象,原因可能是BDS卫星未参与当日OSB解算,导致估计观测量偏差时采用了零均值基准约束。当参与解算的卫星数量发生改变时,约束条件也随之变化,使得原先所有卫星的OSB日解值整体发生常数跳变。从图 1还可以看出,OSB值与卫星类型有关,BDS-2卫星B1I和B3I频点的OSB估计值偏低,BDS-3卫星B1C和B2a频点的OSB值各不相同。
|
图 1 各频点OSB值时间序列 Fig. 1 Time series of OSB values at each frequency |
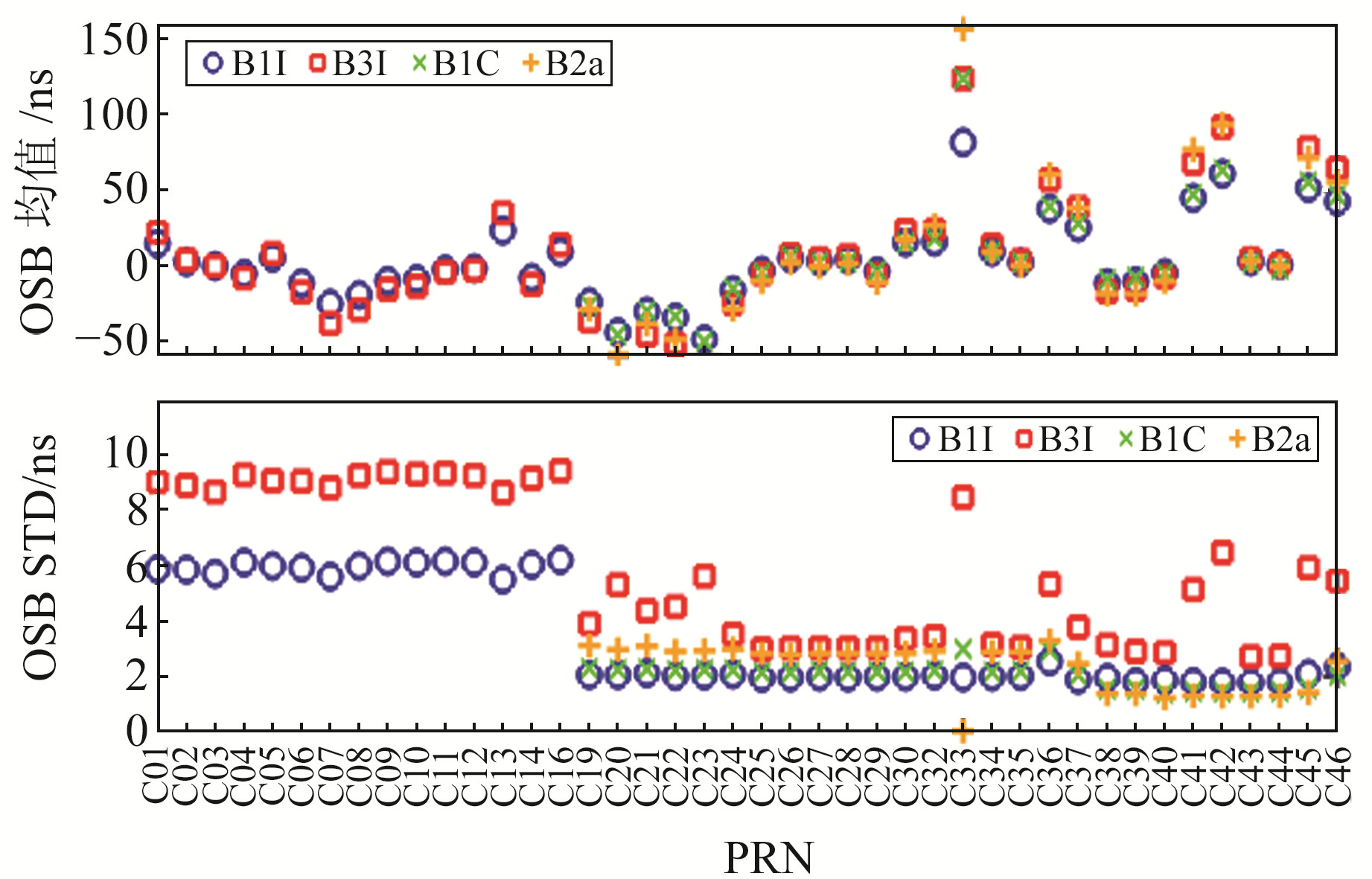
图 2为BDS-2/3各卫星各频点的均值和STD值,可以看出,BDS-2卫星播发的B1I和B3I频点的OSB均值相差不大,整体稳定在-50~50 ns之间;而BDS-3卫星播发的B1I、B3I、B1C和B2a频点的大部分OSB均值都稳定在某个常数值内,只有个别OSB估计均值存在差异,如C33卫星,这也说明OSB估计值与卫星和接收机的硬件设备有关。从各卫星OSB估计STD值可以明显看出,BDS-2卫星B1I和B3I频点OSB估计值STD精度较低,说明OSB稳定性较差,但各卫星的精度较为稳定,没有较大跳变。其中,BDS-2卫星B1I频点OSB估计STD值约为6 ns,B3I频点OSB估计STD值约为9 ns。对于BDS-3卫星4个频点而言,B1I、B1C和B2a频点OSB估计STD精度较高,均稳定在3 ns以内;而BDS-3部分卫星B3I频点的OSB估计值稳定性较差。综上所述,WHU发布的BDS-2/3卫星B1I、B3I、B1C和B2a各频点的OSB估计值STD精度分别为3.41 ns、5.87 ns、2.04 ns和2.32 ns,其中新频点B1C和B2a的OSB稳定性较好。
|
图 2 BDS-2/3各卫星各频点OSB均值和STD值 Fig. 2 OSB mean value and STD value of each satellite at each frequency point of BDS-2/3 |
为评估OSB改正对BDS-2/3卫星新旧频点SPP及PPP精度和收敛时间的影响,本文选择8个能够接收到BDS-2/3卫星所有频点的iGMAS测站(BJF1、CHU1、GUA1、KUN1、LHA1、SHA1、WUH1及XIA1)实测数据。为避免偶然性,时间跨度选为2022-01-01~31共31 d,BDS-2/3的广播星历和精密星历由武汉大学IGS分析中心提供。首先利用自行编写的软件对各个测站的观测数据进行OSB改正;然后利用日本东京海洋大学T.TAKASU开源发布的RTKLIB软件对OSB改正前后的BDS-2/3数据进行SPP和PPP解算;最后将iGMAS官方发布的测站坐标作为真值,分析OSB改正前后对解算结果的影响。具体解算策略见表 1。
|
|
表 1 精密定位处理策略 Tab. 1 Precision positioning processing strategy |
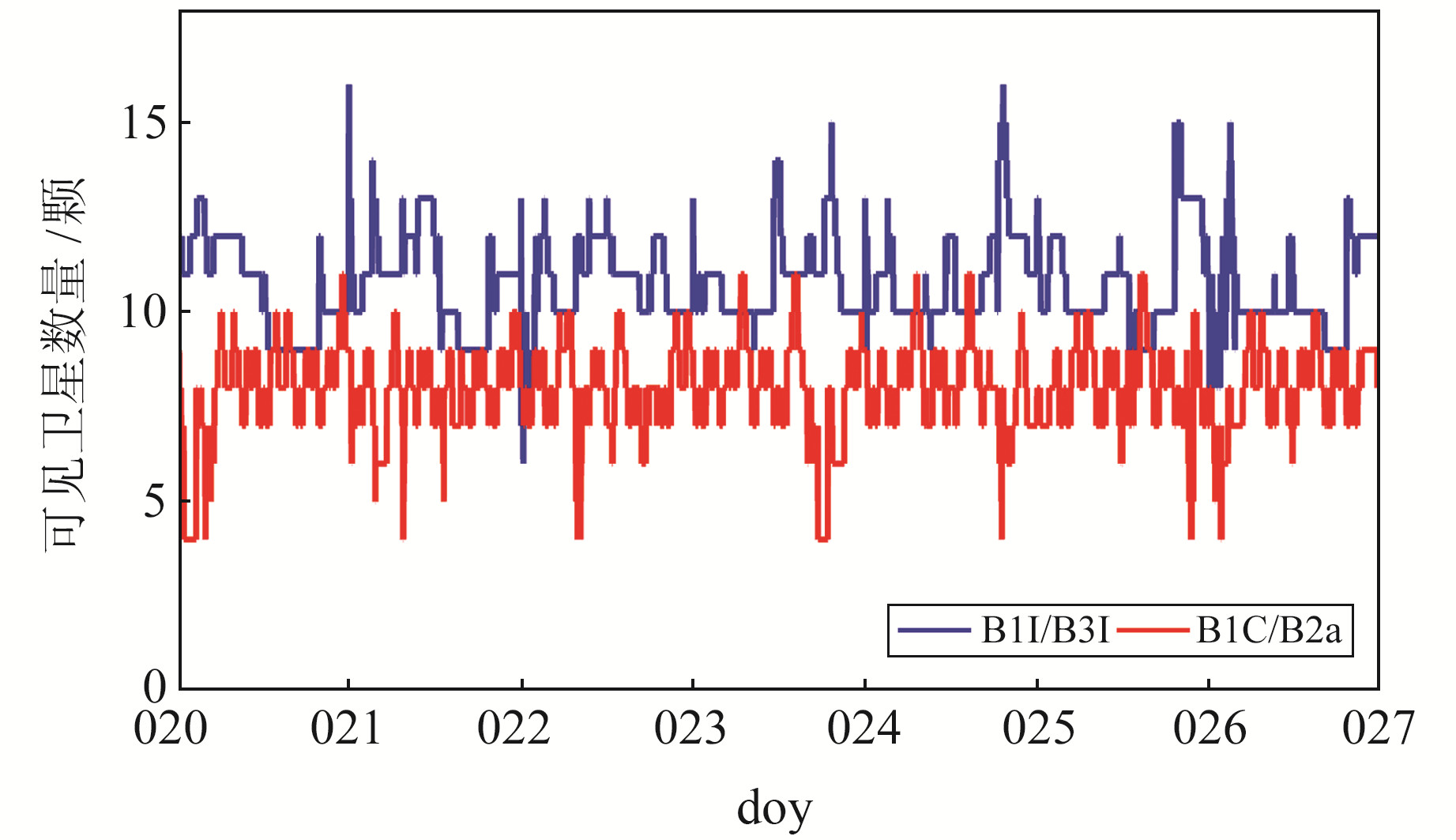
首先统计能够观测到的B1I/B3I和B1C/B2a频点的可见卫星数量,图 3为2022-01-07~13 iGMAS拉萨跟踪站(LHA1)所观测到的各频点卫星数量。目前BDS卫星已建网完成,地面接收机可以稳定接收到约12个B1I/B3I频点的BDS-2/3卫星及8个B1C/B2a频点的BDS-3卫星,均满足SPP和PPP的定位需求。
|
图 3 可见卫星数量 Fig. 3 Number of visible satellite |
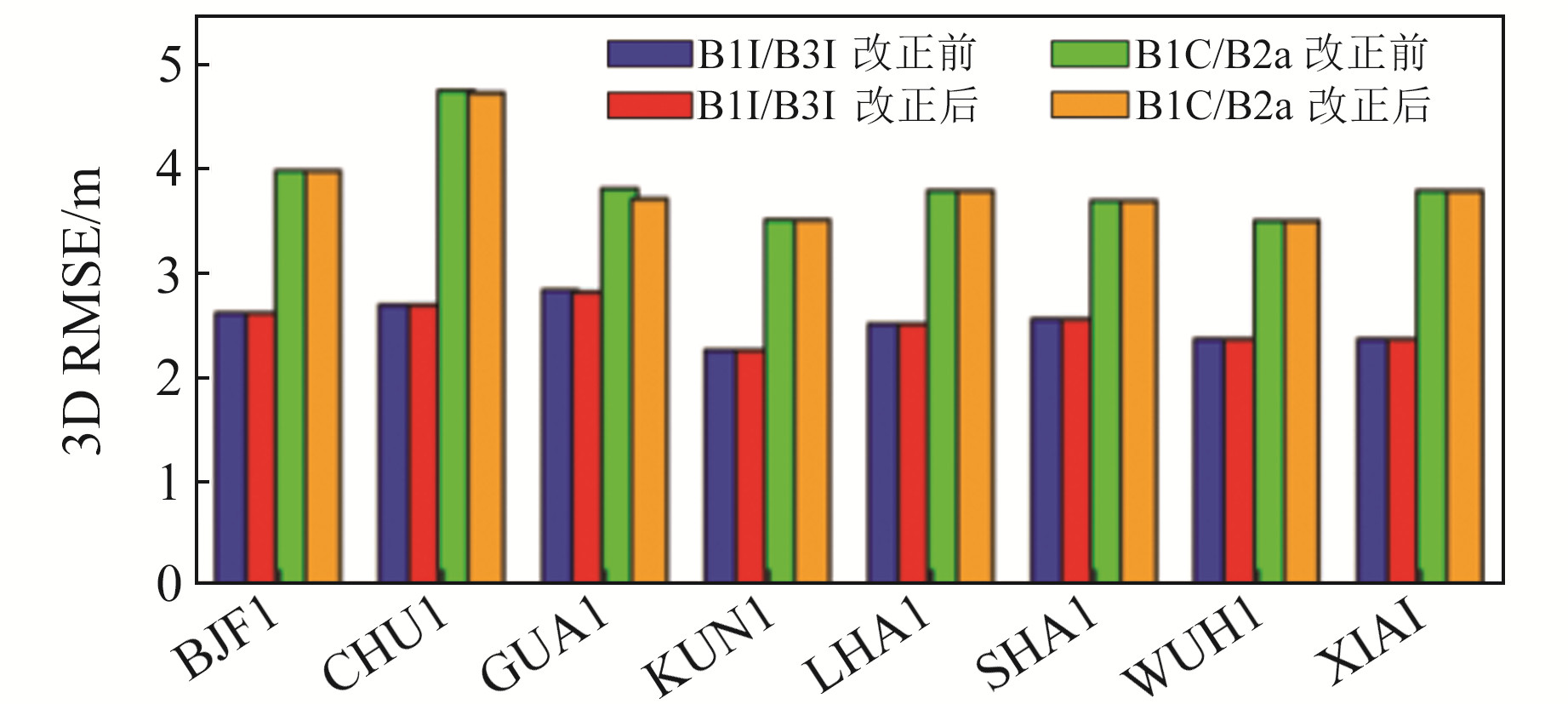
计算OSB改正前后8个iGMAS测站31 d内B1I/B3I组合和B1C/B2a组合的SPP,各测站在3D方向上的RMSE精度统计见图 4。可以看出,OSB改正对SPP解算精度的提升并不明显,可能是因为BDS卫星的星历精度较差,SPP解算中OSB改正所提升的精度被星历引起的误差所吸收。从双频组合的SPP精度对比可以看出,改正后B1I/B3I组合的SPP精度可达2.53 m,而B1C/B2a组合的SPP精度仅为3.84 m。二者精度相差较大,原因可能是B1I/B3I的观测卫星数量相对较多,卫星空间分布的几何结构较好,在解算时坐标参数的计算精度更高。通过对比可以看出,部分测站的解算精度较低,这可能与测站环境和测站接收信号的观测质量有关。
|
图 4 OSB改正前后SPP精度 Fig. 4 SPP accuracy before and after OSB correction |
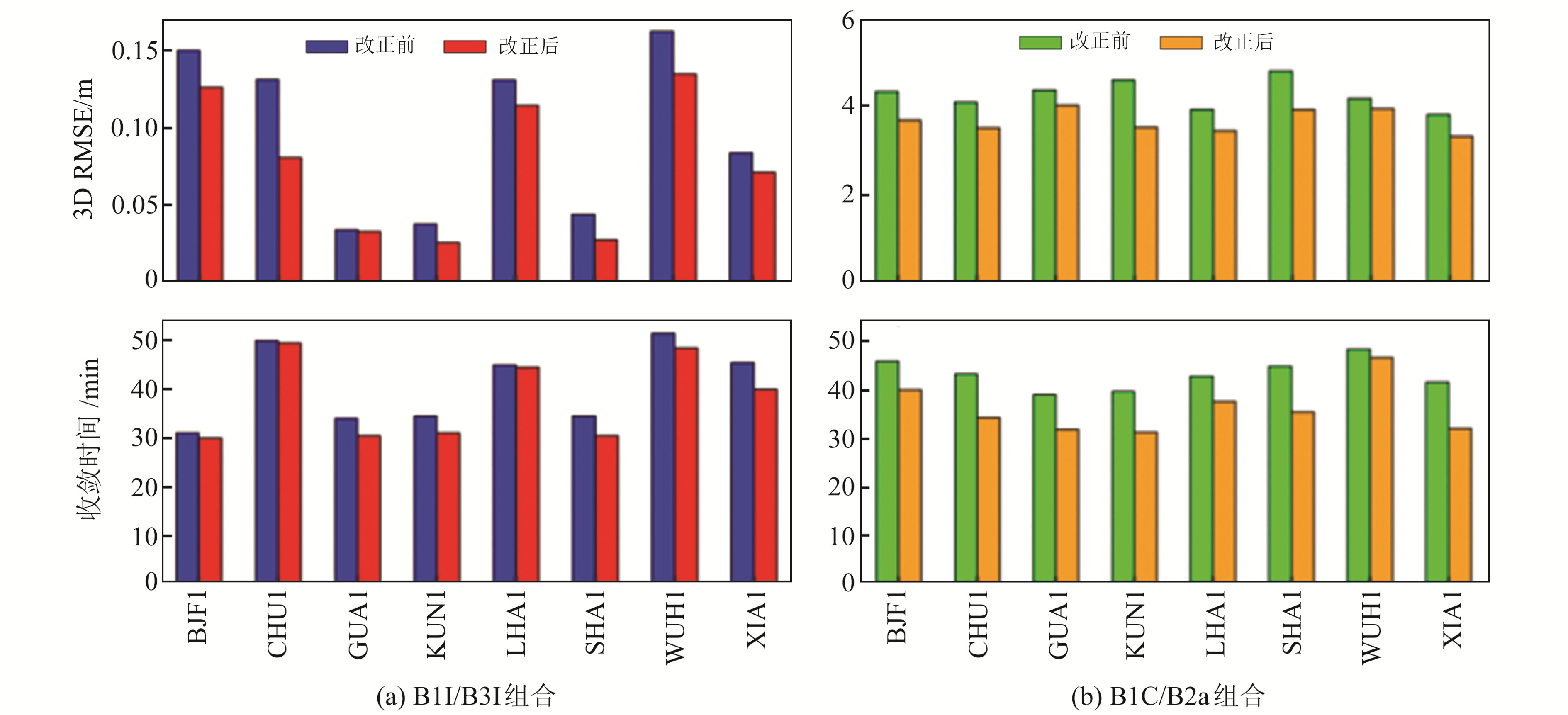
在PPP解算方面,OSB改正前后8个iGMAS测站31 d内B1I/B3I组合和B1C/B2a组合的收敛时间和3D方向上的RMSE精度统计见图 5。由图 5(a)可知,OSB改正对BDS-2/3卫星B1I/B3I旧频点组合的PPP精度影响较为明显,改正前各测站PPP定位精度在3D方向上的RMSE约为9.7 cm,收敛时间约为41 min;改正后各测站PPP定位精度在3D方向上的RMSE约为7.7 cm,提升约20.6%,收敛时间约为38 min,提升约7.3%。由于B1I/B3I解算时利用的BDS-2地球同步轨道(GEO)卫星的轨道精度较低,因此会影响PPP精度、收敛时间及OSB改正效果。
|
图 5 各测站OSB改正前后PPP精度和收敛时间 Fig. 5 PPP accuracy and convergence time before and after OSB correction at each station |
由图 5(b)可见,OSB改正前B1C/B2a新频点组合各测站PPP精度约为4.2 cm,收敛时间约为43 min;OSB改正后定位精度约为3.7 cm,提升约11.9%,收敛时间约为36 min,提升约16.3%。由于BDS-3卫星均为中轨道(MEO)卫星,相比于GEO卫星具有更好的轨道精度,且运行更加稳定,因此虽然整体上接收B1C/B2a频点的卫星数量少于B1I/B3I,但B1C/B2a的PPP结果更优且更加稳定。从SPP和PPP的解算结果来看,OSB改正对PPP定位性能的影响较大,因此在利用BDS-2/3数据进行PPP解算时需进行OSB改正。
3 结语1) BDS-2/3卫星B1I、B3I、B1C和B2a各频点的OSB估计均值为-80~70 ns,STD精度分别为3.41 ns、5.87 ns、2.04 ns和2.32 ns,BDS不同类型卫星在不同频点上的OSB值也各不相同。综合来看,B1C和B2a频点的稳定性较好。
2) 在SPP方面,OSB改正对B1I/B3I组合和B1C/B2a组合的定位精度影响并不明显。OSB改正后,B1I/B3I组合和B1C/B2a组合的SPP精度分别为2.53 m和3.84 m。
3) 在PPP方面,OSB改正对B1I/B3I组合和B1C/B2a组合的定位精度影响较为明显。对于B1I/B3I组合而言,PPP精度和收敛时间分别提升20.6%和7.3%;B1C/B2a组合的PPP精度和收敛时间分别提升11.9%和16.3%。
本文仅分析BDS-2/3卫星4个频点的OSB改正情况,随着能够接收BDS信号的测站数量不断增多,OSB估计精度也随之提高。此外,随着地面测站的增多,BDS-2/3卫星的精密轨道精度不断提高,SPP和PPP精度也会得到进一步提升。为增加数据观测量,需采用多系统PPP模式进行GNSS定位,后续将进一步研究GNSS多系统OSB改正对动态PPP精度的影响及实时OSB产品的生成。
致谢: 感谢武汉大学IGS分析中心和iGMAS分析中心提供的帮助和数据支持。
| [1] |
张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256 (Zhang Xiaohong, Zuo Xiang, Li Pan, et al. Convergence Time and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250-256)
(  0) 0) |
| [2] |
赵文. 北斗2/3联合精密单点定位关键技术研究[D]. 武汉: 武汉大学, 2020 (Zhao Wen. Research on Key Technology of Combined Beidou-2 and Beidou-3 Precise Point Positioning[D]. Wuhan: Wuhan University, 2020)
(  0) 0) |
| [3] |
蔡洪亮, 孟轶男, 耿长江, 等. 北斗三号全球导航卫星系统服务性能评估: 定位导航授时、星基增强、精密单点定位、短报文通信与国际搜救[J]. 测绘学报, 2021, 50(4): 427-435 (Cai Hongliang, Meng Yinan, Geng Changjiang, et al. BDS-3 Performance Assessment: PNT, SBAS, PPP, SMC and SAR[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(4): 427-435)
(  0) 0) |
| [4] |
Wilson B M, Yinger C, Feess W, et al. New and Improved: The Broadcast Interfrequency Biases[J]. GPS World, 1999, 10(9): 56-66
(  0) 0) |
| [5] |
Villiger A, Schaer S, Dach R, et al. Determination of GNSS Pseudo-Absolute Code Biases and Their Long-Term Combination[J]. Journal of Geodesy, 2019, 93(9): 1487-1500 DOI:10.1007/s00190-019-01262-w
(  0) 0) |
| [6] |
Deng Y F, Guo F, Ren X D, et al. Estimation and Analysis of Multi-GNSS Observable-Specific Code Biases[J]. GPS Solutions, 2021, 25(3): 1-13
(  0) 0) |
| [7] |
Paziewski J, Wielgosz P. Accounting for Galileo-GPS Inter-System Biases in Precise Satellite Positioning[J]. Journal of Geodesy, 2015, 89(1): 81-93 DOI:10.1007/s00190-014-0763-3
(  0) 0) |
| [8] |
Sanz J, Miguel J J, Rovira-Garcia A, et al. GPS Differential Code Biases Determination: Methodology and Analysis[J]. GPS Solutions, 2017, 21(4): 1549-1561 DOI:10.1007/s10291-017-0634-5
(  0) 0) |
| [9] |
Wanninger L. Carrier-Phase Inter-Frequency Biases of GLONASS Receivers[J]. Journal of Geodesy, 2012, 86(2): 139-148 DOI:10.1007/s00190-011-0502-y
(  0) 0) |
| [10] |
樊家琛, 吴晓莉, 李宇翔, 等. 基于三频数据的北斗卫星导航系统DCB参数精度评估方法[J]. 中国空间科学技术, 2013, 33(4): 62-70 (Fan Jiachen, Wu Xiaoli, Li Yuxiang, et al. COMPASS Satellites DCB Parameter Accuracy Assessment Based on Tri-Frequency Data[J]. Chinese Space Science and Technology, 2013, 33(4): 62-70)
(  0) 0) |
| [11] |
李子申, 王宁波, 袁运斌. 多模多频卫星导航系统码偏差统一定义与处理方法[J]. 导航定位与授时, 2020, 7(5): 10-20 (Li Zishen, Wang Ningbo, Yuan Yunbin. A Unified Definition and Processing Method of Observable-Specific Signal Biases for Multi-Mode and Multi-Frequency Global Navigation Satellite System[J]. Navigation Positioning and Timing, 2020, 7(5): 10-20)
(  0) 0) |
| [12] |
Montenbruck O, Hauschild A, Steigenberger P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation, 2014, 61(3): 191-201
(  0) 0) |
| [13] |
Wang Q S, Jin S G, Yuan L L, et al. Estimation and Analysis of BDS-3 Differential Code Biases from MGEX Observations[J]. Remote Sensing, 2019, 12(1): 68
(  0) 0) |
| [14] |
Dai P P, Xing J P, Ge Y L, et al. The Effect of BDS-3 Time Group Delay and Differential Code Bias Corrections on Positioning[J]. Applied Sciences, 2020, 11(1): 104
(  0) 0) |
| [15] |
Wang N B, Li Z S, Duan B B, et al. GPS and GLONASS Observable-Specific Code Bias Estimation: Comparison of Solutions from the IGS and MGEX Networks[J]. Journal of Geodesy, 2020, 94(8): 1-15
(  0) 0) |
2. GNSS Research Center, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. School of Civil and Architectural Engineering, Shandong University of Technology, 266 West-Xincun Road, Zibo 255000, China
 2023, Vol. 43
2023, Vol. 43


