2. 苏州科技大学北斗导航与环境感知研究中心,苏州市学府路99号,215009;
3. 中国科学院空天信息创新研究院,北京市邓庄南路9号,100094
精密单点定位(PPP)是一种基于单台接收机多频载波相位观测值的GNSS高精度定位技术[1-2]。PPP技术需要诸如IGS、JPL和WUH等分析机构向全球用户提供精密星历和钟差等产品[3],国内外众多学者已就此展开大量研究[4-5]。与GNSS网解方式相比,PPP技术具有操作简单、效率高和成本低等优点[6],获取测站坐标的同时还可以获得对流层延迟(ZTD)和电离层延迟等大气延迟参数[7-8]。ZTD与大气可降水量(PWV)关系密切,可反映大气中水汽含量,因此高精度ZTD对于天气预报和气候变化分析等具有一定的应用价值和现实意义[9]。
自PPP技术问世以来,已有众多研究机构开发出了许多可解算得到ZTD的PPP软件和在线解算系统[10]。李冉等[11]利用RTKLib解算赤道及120°E附近的GNSS数据,分析经纬度对PPP定位精度的影响;王挥云[12]基于APPS、CSRS-PPP、GAPS和MagicGNSS等平台解算部分IGS站的ZTD,其研究结果与IGS-ZTD的一致性较高;杨军建等[13]基于APPS、MagicGNSS和CSRS-PPP分析ZTD精度发现,CSRS-PPP在收敛前存在较大误差,收敛后的ZTD结果较为可靠,APPS和MagicGNSS的ZTD精度较高且较为稳定。
上述研究主要分析不同软件的ZTD精度,鲜有不同地理位置及季节变化对PPP-ZTD精度影响的研究。因此,本文基于RTKLib、MagicGNSS、CSRS-PPP和华测(CGline)4类PPP软件,评估不同时空条件下(测站位置和季节)的PPP-ZTD精度。
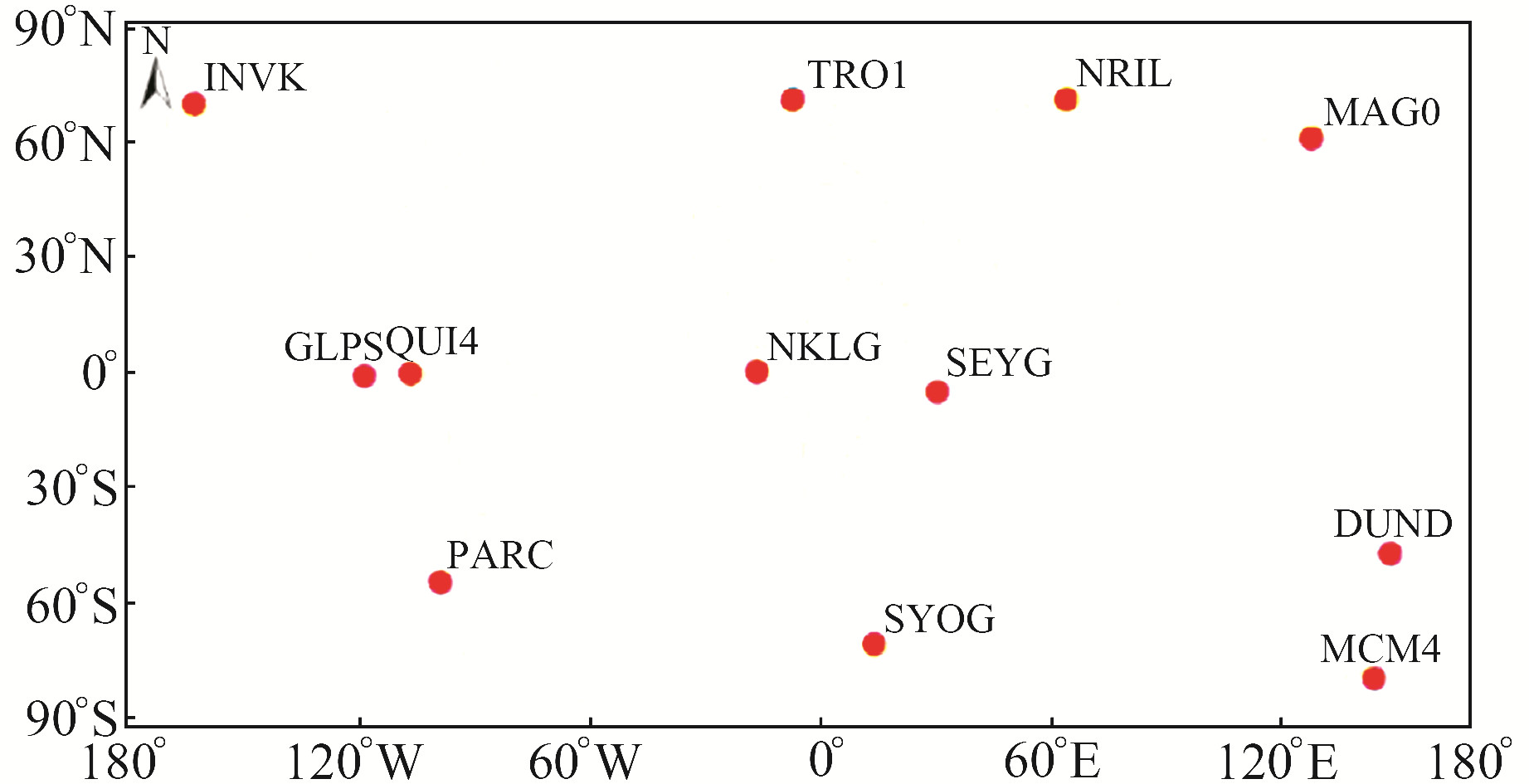
1 数据来源及统计方法 1.1 数据来源本文GNSS数据来源于武汉大学IGS分析中心(http://www.igs.gnsswhu.cn)。选取北半球的INVK、MAG0、NRIL、TRO1测站、赤道地区的GLPS、NKLG、QUI4、SEYG测站、南半球的DUND、MCM4、PARC、SYOG测站进行分析。RTKLib选取上述IGS测站2020年春、夏、秋、冬各连续7 d的GNSS数据进行解算;在线PPP解算系统选取上述IGS测站2020年春、夏、秋、冬各1 d的GNSS数据进行解算。上述实验均以IGS-ZTD公布值作为参考。图 1为IGS测站分布情况。
|
图 1 IGS站分布 Fig. 1 Distribution of IGS stations |
本文采用平均值(bias)和均方根误差(RMSE)评价各软件PPP-ZTD与IGS-ZTD参考值之间的偏离程度,采用相关系数(R)反映2组变量之间的相关性。公式如下:
| $ \text { bias }=\frac{\sum\limits_{i=1}^n\left(\mathrm{ZTD}_{\mathrm{PPP}}-\mathrm{ZTD}_{\mathrm{IGS}}\right)}{n} $ | (1) |
| $ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^n\left(\mathrm{ZTD}_{\mathrm{PPP}}-\mathrm{ZTD}_{\mathrm{IGS}}\right)^2}{n}} $ | (2) |
| $ R(\mathrm{ZTD})=\frac{\operatorname{cov}(\mathrm{PPP}, \mathrm{IGS})}{\sqrt{\operatorname{var}[\mathrm{PPP}] \operatorname{var}[\mathrm{IGS}]}} $ | (3) |
式中,n为对应的ZTD历元数,cov(PPP, IGS)为对应软件PPP-ZTD与IGS-ZTD的协方差,var[PPP]为PPP-ZTD的方差,var[IGS]为IGS-ZTD的方差。
2 数据处理方法 2.1 RTKLib与在线PPP解算系统RTKLib利用RTKPOST后处理程序实现相对定位、标准单点定位及PPP等多种定位模式[14]。由于进行RTKLib的PPP解算前需要进行模糊度收敛,其PPP-ZTD在起始2 h内误差较大,因此在前向滤波模式下,本文取2~24h的ZTD作为有效统计数据。此外,本文将后向滤波0~2 h的RTKLib-ZTD、前向和后向滤波2~22 h的RTKLib-ZTD平均值以及前向滤波22~24 h的RTKLib-ZTD作为组合滤波的最终RTKLib-ZTD,各自统计前向滤波和组合滤波的PPP-ZTD精度。为获得最优精度的RTKLib-ZTD,需要修改高度角、载波相位偏差的过程噪声及测量噪声等数据[10-11]。
CSRS-PPP是加拿大国土资源部提供的在线PPP解算平台[15],该系统从2003年开始提供服务,可以在静态或动态模式下解算双频GNSS数据。CSRS-PPP使用由IGS提供的精密卫星轨道和钟差,通过后向滤波模式解算并获得最优的ZTD时间序列。
MagicGNSS是西班牙GMV航空航天和国防公司提供的在线PPP处理系统,可以处理GPS、GLONASS、Galileo和Beidou等GNSS数据,用户可选用IGS或GMV提供的精密卫星轨道和钟差,在静态或动态模式下处理GNSS数据。
CGline是华测自主研发的一套在线解算平台,旨在为用户提供高精度PPP解算服务,具有交互简单、作业高效、精度高等优点。
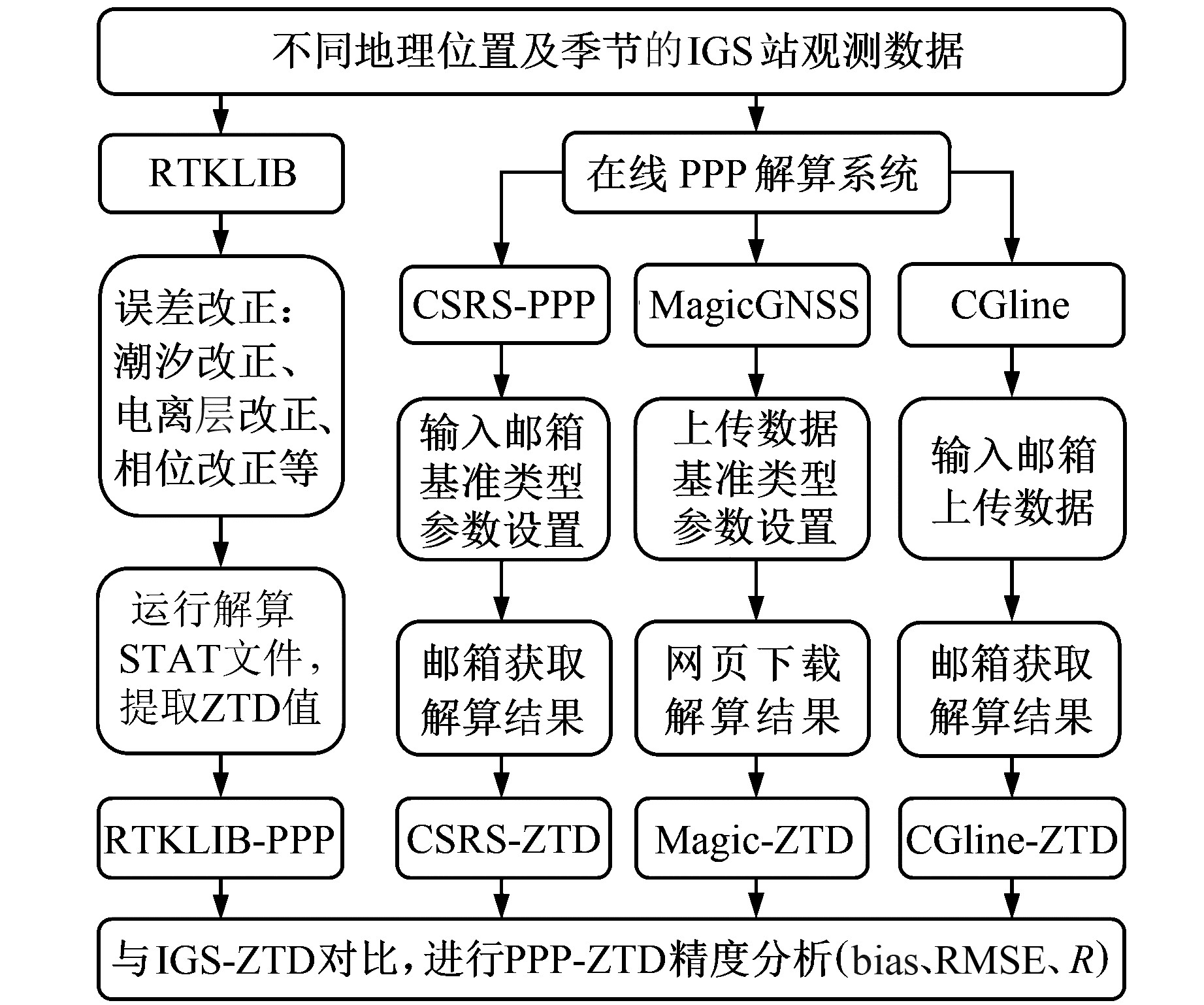
2.2 PPP-ZTD数据处理方法RTKLib需要RINEX标准格式观测值、广播星历、精密卫星轨道、精密卫星钟差、DCB、EOP和误差项改正等数据,其中误差改正包括地球潮汐、电离层、对流层、卫星及接收机相位中心偏差等,RTKPOST中STAT文件可获取RTKLib-ZTD。CSRS-PPP系统会返回CLK、POS、SUM、TRO、Excel和PDF等文件,ZTD以图片形式展示在PDF文件中;MagicGNSS系统会返回CLK、SNX和PDF等文件,ZTD以图片形式展示在PDF文件中;CGline会返回POS、STAT和EST等文件,STAT文件中包含采样间隔为30 s的ZTD。图 2为上述4类PPP平台的ZTD解算流程。
|
图 2 PPP-ZTD解算流程 Fig. 2 Solution process of PPP-ZTD |
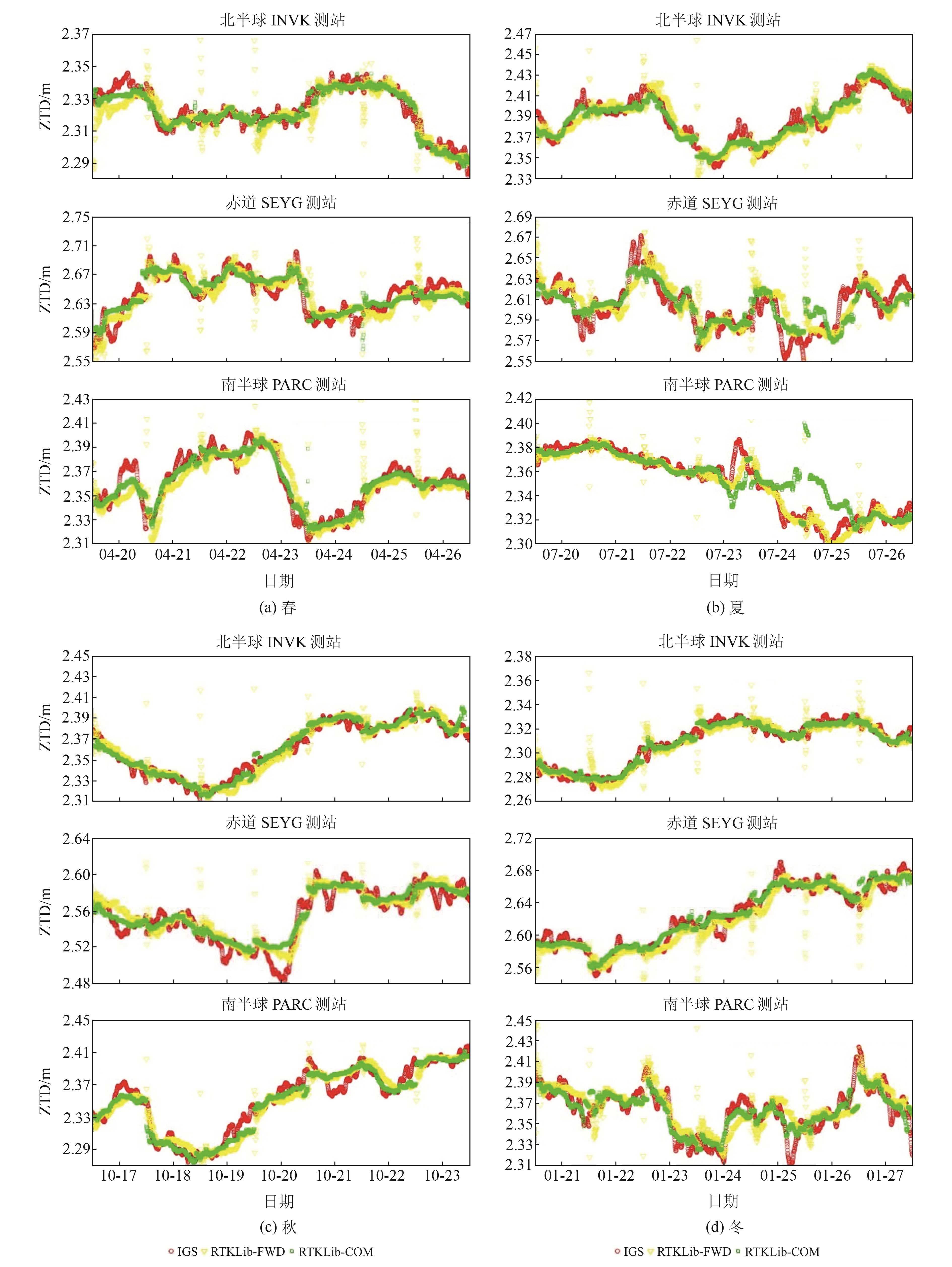
图 3为北半球、赤道、南半球各1个IGS测站的四季ZTD时序变化。由图可知,南北半球IGS测站的RTKLib-ZTD与IGS-ZTD较为接近,而赤道附近IGS测站的RTKLib-ZTD偏差较大,其中组合滤波(RTKLib-COM)的吻合程度优于前向滤波(RTKLib-FWD)。
|
图 3 各测站春、夏、秋、冬的PPP-ZTD时序变化 Fig. 3 PPP-ZTD temporal variations in spring, summer, autumn and winter at different stations |
表 1(单位mm)为北半球、赤道和南半球的IGS站RTKLib-ZTD精度统计,表 2(单位mm)为不同季节的IGS站RTKLib-ZTD精度统计。由表 1、2可知,不同地理位置、不同季节的组合滤波平均RMSE为8.7 mm,前向滤波的平均RMSE为9.1 mm。整体上看,组合滤波的解算精度优于前向滤波。由表 1可见,组合滤波模式下不同地理位置的ZTD精度由高到低依次为:北半球(5.8 mm)、南半球(9.6 mm)和赤道(10.7 mm)。赤道附近的IGS站RMSE略大,这是因为赤道附近水汽含量大,致使ZTD误差也偏大。由表 2可见,组合滤波模式下不同季节的ZTD精度由高到低依次为:夏季(7.9 mm)、春季(8.3 mm)、秋季(8.4 mm)和冬季(10.2 mm)。整体上看,组合滤波和前向滤波的大部分RMSE优于1 cm,满足后处理和实时应用需求。
|
|
表 1 不同地理位置IGS测站RTKLib-ZTD精度 Tab. 1 Accuracy of IGS station RTKLib-ZTD at different locations |
|
|
表 2 不同季节IGS测站RTKLib-ZTD精度 Tab. 2 Accuracy of IGS station RTKLib-ZTD in different seasons |
图 4为北半球、赤道和南半球各1个IGS测站的四季PPP-ZTD时序变化。由图可知,3种软件的PPP-ZTD与IGS-ZTD整体变化趋势吻合度较高。其中,CSRS-PPP与MagicGNSS的ZTD与IGS-ZTD吻合度较高,CGline的南、北半球ZTD与IGS-ZTD较为吻合,赤道附近的PPP-ZTD与IGS-ZTD存在较小偏差。相较于RTKLib-ZTD,不同季节下在线PPP解算系统的ZTD与IGS-ZTD更加吻合,说明季节变化对在线PPP解算系统的精度影响较小。

|
图 4 各测站春、夏、秋、冬的PPP-ZTD时序变化 Fig. 4 PPP-ZTD temporal variations in spring, summer, autumn and winter at different stations |
表 3(单位mm)为3类PPP在线软件在不同位置下的ZTD精度统计表。由表可见,不同地理位置下CSRS-PPP的ZTD与IGS-ZTD的平均相关系数为0.83,解算精度由高到低依次为:北半球(4.1 mm)、南半球(6.2 mm)和赤道(7.2 mm);MagicGNSS的ZTD与IGS-ZTD的平均相关系数为0.75,精度由高到低依次为:北半球(6.0 mm)、南半球(6.4 mm)和赤道(6.8 mm);CGline的ZTD与IGS-ZTD的平均相关系数为0.71,精度由高到低依次为北半球(7.1 mm)、南半球(7.9 mm)和赤道(11.1 mm)。整体上看,CSRS-PPP和MagicGNSS解算的ZTD精度均在1 cm以内,CGline在赤道附近的ZTD偏差略大。
|
|
表 3 3类PPP在线软件不同位置的ZTD精度对比 Tab. 3 Comparative of ZTD accuracy at different locations of three online PPP softwares |
表 4(单位mm)为4类PPP软件的各季节ZTD精度统计。由表可见,CSRS-PPP、MagicGNSS的ZTD与IGS-ZTD最为接近,解算精度均在6.2 mm以内,CGline的ZTD精度均在9.1 mm以内,RTKLib的ZTD精度在10.1 mm以内。PPP-ZTD精度由高到低依次为CSRS-PPP(5.40 mm)、MagicGNSS(5.94 mm)、RTKLib(8.69 mm)和CGline(8.74 mm)。
|
|
表 4 4类PPP软件各季节的ZTD平均RMSE Tab. 4 Average RMSE of ZTD of four PPP softwares in different season |
1) 4类PPP软件的ZTD精度由高到低依次为CSRS-PPP(5.40 mm)、MagicGNSS(5.94 mm)、RTKLib(8.69 mm)和CGline(8.74 mm)。其中RTKLib的组合滤波精度优于前向滤波,组合滤波的平均RMSE为8.7 mm,前向滤波的平均RMSE为9.1 mm,二者大部分PPP-ZTD的RMSE优于1 cm,满足后处理和实时应用需求。
2) 不同地理位置下CSRS-PPP、MagicGNSS、RTKLib和CGline的ZTD精度由高到低均为北半球、南半球和赤道,其中赤道地区CGline-ZTD的RMSE超过1 cm。
3) RTKLib-ZTD受季节影响较大,精度由高到低依次为夏季(7.9 mm)、春季(8.3 mm)、秋季(8.4 mm)和冬季(10.2 mm);而不同季节对在线PPP解算系统的ZTD精度影响较小。
| [1] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017 DOI:10.1029/96JB03860
(  0) 0) |
| [2] |
Héroux P, Kouba J. GPS Precise Point Positioning with a Difference[J]. Geomatics, 1995, 13-15
(  0) 0) |
| [3] |
Kouba J, Héroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28 DOI:10.1007/PL00012883
(  0) 0) |
| [4] |
Bock H, Hugentobler U, Springer T A, et al. Efficient Precise Orbit Determination of LEO Satellites Using GPS[J]. Advances in Space Research, 2002, 30(2): 295-300 DOI:10.1016/S0273-1177(02)00298-3
(  0) 0) |
| [5] |
Gao Y, Abdel-Salam M, Chen K, et al. Point Real-Time Kinematic Positioning[M]. Berlin: Springer, 2005
(  0) 0) |
| [6] |
关小果, 柴洪洲, 韩世静, 等. 基于系统间交叉验证的海上精密单点定位质量检核方法[J]. 大地测量与地球动力学, 2021, 41(12): 1235-1240 (Guan Xiaoguo, Chai Hongzhou, Han Shijing, et al. Quality Check Method for Marine Precise Point Positioning Based on Cross Validation between Systems[J]. Journal of Geodesy and Geodynamics, 2021, 41(12): 1235-1240 DOI:10.14075/j.jgg.2021.12.006)
(  0) 0) |
| [7] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays Onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [8] |
Rocken C, Hove T, Johnson J V, et al. GPS/STORM—GPS Sensing of Atmospheric Water Vapor for Meteorology[J]. Journal of Atmospheric and Oceanic Technology, 1995, 12(3): 468-478 DOI:10.1175/1520-0426(1995)012<0468:GSOAWV>2.0.CO;2
(  0) 0) |
| [9] |
李黎, 匡翠林, 朱建军, 等. 基于实时精密单点定位技术的暴雨短临预报[J]. 地球物理学报, 2012, 55(4): 1129-1136 (Li Li, Kuang Cuilin, Zhu Jianjun, et al. Rainstorm Nowcasting Based on GPS Real-Time Precise Point Positioning Technology[J]. Chinese Journal of Geophysics, 2012, 55(4): 1129-1136 DOI:10.6038/j.issn.0001-5733.2012.04.008)
(  0) 0) |
| [10] |
KačmaAřík M. Retrieving of GNSS Tropospheric Delays from RTKLIB in Real-Time and Post-Processing Mode[M]. Berlin: Springer, 2017
(  0) 0) |
| [11] |
李冉, 何丽娜. 基于RTKLIB的精密单点定位精度分析[J]. 勘察科学技术, 2019, 225(4): 14-18 (Li Ran, He Lina. Precision Analysis of Precise Point Positioning Based on RTKLIB[J]. Site Investigation Science and Technology, 2019, 225(4): 14-18 DOI:10.3969/j.issn.1001-3946.2019.04.003)
(  0) 0) |
| [12] |
王挥云. 4种在线PPP服务系统定位精度分析[J]. 测绘通报, 2016, 472(7): 66-69 (Wang Huiyun. Positioning Accuracy Analysis Obtained from Four Online PPP Services[J]. Bulletin of Surveying and Mapping, 2016, 472(7): 66-69)
(  0) 0) |
| [13] |
杨军建, 姚宜斌, 许超钤, 等. 不同在线PPP技术得到的ZTD对比与精度分析[J]. 测绘地理信息, 2015, 40(6): 11-14 (Yang Junjian, Yao Yibin, Xu Chaoqian, et al. Accuracy Analysis of ZTD Obtained from Different GPS Online Post-Processing Services[J]. Journal of Geomatics, 2015, 40(6): 11-14)
(  0) 0) |
| [14] |
杜石, 黄观文, 葛玉龙, 等. BNC/RTKLIB/PPPWIZARD实时精密单点定位服务性能评估[J]. 大地测量与地球动力学, 2021, 41(2): 125-130 (Du Shi, Huang Guanwen, Ge Yulong, et al. Performance Evaluation of BNC/RTKLIB/PPPWIZARD Real-Time Precise Point Positioning Service[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 125-130)
(  0) 0) |
| [15] |
Tetreault P, Kouba J, Heroux P, et al. CSRS-PPP: An Internet Service for GPS User Access to the Canadian Spatial Reference Frame[J]. Geomatica, 2005, 59(1): 17-28
(  0) 0) |
2. Research Center of Beidou Navigation and Environmental Remote Sensing, Suzhou University of Science and Technology, 99 Xuefu Road, Suzhou 215009, China;
3. Aerospace Information Research Institute, CAS, 9 South-Dengzhuang Road, Beijing 100094, China
 2023, Vol. 43
2023, Vol. 43

