2. 北斗导航应用技术协同创新中心,郑州市科学大道62号,450001
在目前诸多GNSS定位模糊度求解方法中,以降相关思想为核心的LAMBDA算法应用最为广泛[1-2]。LAMBDA算法解算模糊度的步骤主要包括:模糊度降相关、模糊度搜索和模糊度检验。其中,模糊度降相关过程涉及大量矩阵运算,耗时较长。为此,学者们进行了大量研究:Chang等[3]和Borno等[4]分别利用贪心算法和部分元素降相关方法对LAMBDA算法进行改进;Liu等[5]通过上下三角过程构造联合去相关算法,降低模糊度之间的相关性;徐琦等[6]通过对比分析认为,联合去相关法的处理成功率高于迭代法;Xu[7]使用Cholesky分解构建整数高斯矩阵,结果表明,在高维情况下分解得到的浮点解协方差矩阵条件数最小;陈树新[8]以降低协方差矩阵的条件数为准则,提出一种性能更加优越的模糊度去相关算法;Liu等[9]通过三次差分测量得到模糊度浮动解,通过降低模糊度协方差矩阵的维数对搜索空间进行去相关处理,克服了Z变换可能带来的矩阵病态分解,减少了20%的解算时间。还有学者研究不同的排序算法对降相关性能的影响[10-14]。Hassibi等[15]将格理论中的规约算法Lenstra-Lenstra-Lovász(LLL)应用于模糊度降相关的研究中,此后大量学者对LLL算法进行了详细研究与分析,并开展相应的改进和优化[16-22]。
综上可知,减少矩阵的复杂运算是提高降相关效率的重要手段之一。LAMBDA算法的模糊度降相关过程主要包括Cholesky分解和矩阵降相关2个步骤。其中,传统Cholesky分解过程复杂,会造成大量计算冗余;矩阵降相关过程主要为条件方差排序计算,每次排序计算都需要对非主对角元素进行降相关处理,涉及大量复杂运算。基于此,本文提出一种分块最小二乘模糊度降相关(BLAMBDA)算法:采用条件方差分块算法优化降相关过程,对条件方差矩阵进行分块,减少条件方差排序次数,并在此基础上对Cholesky分解公式进行整合,减少Cholesky分解过程中的数乘运算。
1 整数最小二乘去相关算法模型假设
| $ \min\limits _a(\hat{\boldsymbol{a}}-\boldsymbol{a})^{\mathrm{T}} \boldsymbol{Q}_\hat{a}^{-1}(\hat{\boldsymbol{a}}-\boldsymbol{a}), \boldsymbol{a} \in \boldsymbol{Z}^n $ | (1) |
式中,a为模糊度整数候选向量。
针对最小二乘估计问题,LAMBDA算法采用整数高斯变换(Z变换)对
| $ \min\limits _z(\boldsymbol{z}-\hat{\boldsymbol{z}})^{\mathrm{T}} \boldsymbol{Q}_{\hat{z}}^{-1}(\boldsymbol{z}-\hat{\boldsymbol{z}}), \boldsymbol{z} \in \boldsymbol{Z}^n $ | (2) |
| $ \boldsymbol{z}=\boldsymbol{Z}^{\mathrm{T}} \boldsymbol{a}, \hat{\boldsymbol{z}}=\boldsymbol{Z}^{\mathrm{T}} \hat{\boldsymbol{a}}, \boldsymbol{Q}_{\hat{z}}=\boldsymbol{Z}^{\mathrm{T}} \boldsymbol{Q}_{\hat{a}} \boldsymbol{Z} $ | (3) |
式中,Z为幺模矩阵,即矩阵的行列式为1且矩阵Z的元素均为整数。矩阵的构造要满足以下2个要求[3]:1)更新得到的
| $ \bar{d}_1 \geqslant \bar{d}_2 \geqslant \cdots \geqslant \bar{d}_n $ | (4) |
利用下三角Cholesky对
| $ \boldsymbol{Q}_{\hat{a}}=\boldsymbol{L}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{L}, \boldsymbol{Q}_{\hat{z}}=\boldsymbol{Z}^{\mathrm{T}} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{L} \boldsymbol{Z}=\overline{\boldsymbol{L}}^{\mathrm{T}} \overline{\boldsymbol{D}} \overline{\boldsymbol{L}} $ | (5) |
式中,
| $ \left\{\begin{array}{l} \left|\bar{l}_{i, j}\right| \leqslant 0.5, i>j \\ \bar{d}_i+\bar{l}_{i+1, i}^2 \bar{d}_{i+1} \geqslant \bar{d}_{i+1} \end{array}\right. $ | (6) |
式中,
为满足式(4),LAMBDA算法在条件方差交换时需按照从后往前的顺序排列。当遇到判别交换的条件方差dk和dk+1相差过大时,dk+1、dk+2及之前的交换过程可能不再满足条件,需要对其进行再次交换,此过程会发生大量重复交换的情况,并增加元素降相关的运算时间。基于此,本文对条件方差矩阵进行分块处理,使条件方差在块内交换,通过改变交换维数和方式来减少条件方差的交换次数,并对Cholesky分解过程进行优化处理,提出改进的LAMBDA算法。
首先,对式(5)LTDL分解中的D矩阵进行分块处理:
| $ \boldsymbol{D}=\left[\begin{array}{llll} \boldsymbol{R}_1 & & & \\ & \ddots & & \\ & & \boldsymbol{R}_{m-1} & \\ & & & \boldsymbol{R}_m \end{array}\right] $ | (7) |
将n维矩阵D分成m块(R1,R2, …,Rm),前(m-1)块的大小为k,Rm的大小为r=n-(m-1)k, r为不足分块大小的部分。任意分块Ri(1≤i≤m)和Rm可表示为:
| $ \boldsymbol{R}_i=\left[\begin{array}{llll} d_{(i-1) k+1} & & & \\ & \ddots & & \\ & & d_{(i-1) k+k-1} & \\ & & & d_{i k} \end{array}\right] $ | (8) |
| $ \boldsymbol{R}_m=\left[\begin{array}{llll} d_{(m-1) k+1} & & \\ & \ddots & & \\ & & d_{(i-1) k+r, -1} & \\ & & & d_n \end{array}\right] $ | (9) |
BLAMBDA算法若不满足式(6),则仅在各分块内进行交换。由于各分块的维数较低,因此在分块内更容易满足式(4),使得各分块条件方差交换次数之和远小于LAMBDA算法降相关过程中条件方差的交换次数,减少了大量矩阵运算和高斯变换过程。以di和di+1进行一次条件方差交换为例,减少的计算过程公式推导如下:
| $ \begin{aligned} \boldsymbol{Q}_{\hat{a}}=\boldsymbol{L}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{L}= & {\left[\begin{array}{lll} \boldsymbol{L}_{11}^{\mathrm{T}} & \boldsymbol{L}_{21}^{\mathrm{T}} & \boldsymbol{L}_{31}^{\mathrm{T}} \\ & \boldsymbol{L}_{22}^{\mathrm{T}} & \boldsymbol{L}_{32}^{\mathrm{T}} \\ & & \boldsymbol{L}_{33}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{lll} \boldsymbol{D}_1 & & \\ & \boldsymbol{D}_2 & \\ & & \boldsymbol{D}_3 \end{array}\right] \times } \\ & {\left[\begin{array}{lll} \boldsymbol{L}_{11} & & \\ \boldsymbol{L}_{21} & \boldsymbol{L}_{22} & \boldsymbol{L}_{31} \end{array}\right] } \end{aligned} $ | (10) |
令
| $ \boldsymbol{p}=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right], \boldsymbol{P}_{i, i-1}=\left[\begin{array}{lll} \boldsymbol{I}_{i-1} & & \\ & \boldsymbol{p} & \\ & & \boldsymbol{I}_{n-i-1} \end{array}\right] $ | (11) |
则有:
| $ \begin{aligned} & \boldsymbol{P}_{i, i+1}^{\mathrm{T}} \boldsymbol{Q}_{\hat{a}} \boldsymbol{P}_{i, i+1}=\left[\begin{array}{ccc} \boldsymbol{L}_{11}^{\mathrm{T}} & \overline{\boldsymbol{L}}_{21}^{\mathrm{T}} & \boldsymbol{L}_{31}^{\mathrm{T}} \\ & \overline{\boldsymbol{L}}_{22}^{\mathrm{T}} & \overline{\boldsymbol{L}}_{23}^{\mathrm{T}} \\ & & \boldsymbol{L}_{33}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{lll} \boldsymbol{D}_1 & & \\ & \overline{\boldsymbol{D}}_2 & \\ & & \boldsymbol{D}_3 \end{array}\right] \times \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[\begin{array}{lll} \bf{L}_{11} & & \\ \overline{\boldsymbol{L}}_{21} & \overline{\boldsymbol{L}}_{22} & \\ \boldsymbol{L}_{31} & \overline{\boldsymbol{L}}_{32} & \boldsymbol{L}_{33} \end{array}\right]} \\ & \end{aligned} $ | (12) |
式中,
在各分块内完成交换后,需要对相邻块进行条件方差交换,完成条件方差的块传递。相邻块条件方差交换条件为:
| $ \begin{gathered} \delta\left(d_{(i-1) k+1} \times d_{(i-1) k+2} \times \cdots \times d_{i k}\right)> \\ d_{i k+1} \times d_{i k+2} \times \cdots \times d_{(i+1) k} \end{gathered} $ | (13) |
式中,δ为条件约束因子,其大小决定了相邻块是否需要使用相邻块传递的对称旋转策略[3]。
当相邻块不满足式(13)时,需要对Ri的第1个元素d(i-1)k+1和Ri+1的最后1个元素d(i+1)k进行交换。当Ri中的条件方差远小于Ri+1时,需使用一次对称旋转策略,此过程会使2分块内的条件方差大致按降序排列;否则仅对Ri和Ri+1的相邻元素dik和dik+1作比较交换处理,实现相邻块的交换传递。交换公式为:
| $ \bar{d}_{i k}=\frac{d_{i k}}{\bar{d}_{i k+1}} d_{i k+1} $ | (14) |
| $ \bar{d}_{i k+1}=d_{i k}+l_{i+1}^2 d_{i k+1} $ | (15) |
虽然在块之间的传递过程中使用对称旋转策略会增加部分计算量,但该计算量远小于条件方差交换过程中减少的计算量。
在减少条件方差交换的同时,为减少元素降相关次数,BLAMBDA算法在各分块间进行条件方差交换前,仅对L矩阵的次对角线元素进行整数高斯变换。当没有条件方差需要交换时,对L矩阵的非主次对角元素进行降相关处理。
为进一步减少BLAMBDA算法的矩阵运算耗时,对LAMBDA算法的分解算法进行优化,即(ModifyLTDL,MLTDL)。优化策略如下:
| $ \boldsymbol{Q}_{\hat{a}}=\left[\begin{array}{ll} \boldsymbol{Q} & \boldsymbol{q}^{\mathrm{T}} \\ \boldsymbol{q} & \boldsymbol{q}_n \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{L}^{\mathrm{T}} & \boldsymbol{l}^{\mathrm{T}} \\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} \boldsymbol{D} & 0 \\ 0 & \boldsymbol{d}_n \end{array}\right]\left[\begin{array}{cc} \boldsymbol{L} & 0 \\ \boldsymbol{l} & 1 \end{array}\right] $ | (16) |
式中,
| $ \boldsymbol{q}_n=\boldsymbol{d}_n, \boldsymbol{q}^{\mathrm{T}}=\boldsymbol{l}^{\mathrm{T}} \boldsymbol{d}_n, \boldsymbol{l}=\boldsymbol{q} / \boldsymbol{d}_n $ | (17) |
| $ \boldsymbol{Q}=\boldsymbol{Q}-\boldsymbol{l}^{\mathrm{T}} \boldsymbol{d}_n \boldsymbol{l}=\boldsymbol{L}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{L} $ | (18) |
将式(17)代入式(18)中,得:
| $ \boldsymbol{Q}=\boldsymbol{Q}-\boldsymbol{q}^{\mathrm{T}} \boldsymbol{l}=\boldsymbol{L}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{L} $ | (19) |
从式(16)~(19)可以看出,该迭代过程中没有开平方根运算,且式(19)在式(18)的基础上减少了数乘运算。
3 实验验证与分析本文利用MATLAB 2014构建算法的仿真实验平台,基于Visual Studio 2019 C语言进行实验的整体解算。计算机系统为Windows 10,处理器为8 GB内存的Intel(R) Core(TM) i7-8550U CPU@1.80 GHz 1.99 GHz。在实际解算过程中,基于RTKLIB进行基线解算,短基线的双差模糊度整体高于中长、长基线的双差模糊度。实测实验以代表性实测数据(长、中长、短基线)为例进行深入分析,具有更强的说服力。
3.1 仿真实验分析仿真实验的方差协方差矩阵不依赖于特定卫星和接收机的几何构图及定权方式,能更全面地检验BLAMBDA算法。构造方法如下:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{a}}=100 \times \operatorname{randn}(n, 1) \\ \boldsymbol{Q}_{\hat{a}}=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}, \boldsymbol{A}=\operatorname{randn}(n, n) \end{array}\right. $ | (20) |
式中,randn(n, 1)为随机函数生成的符合正态分布的n个随机数。
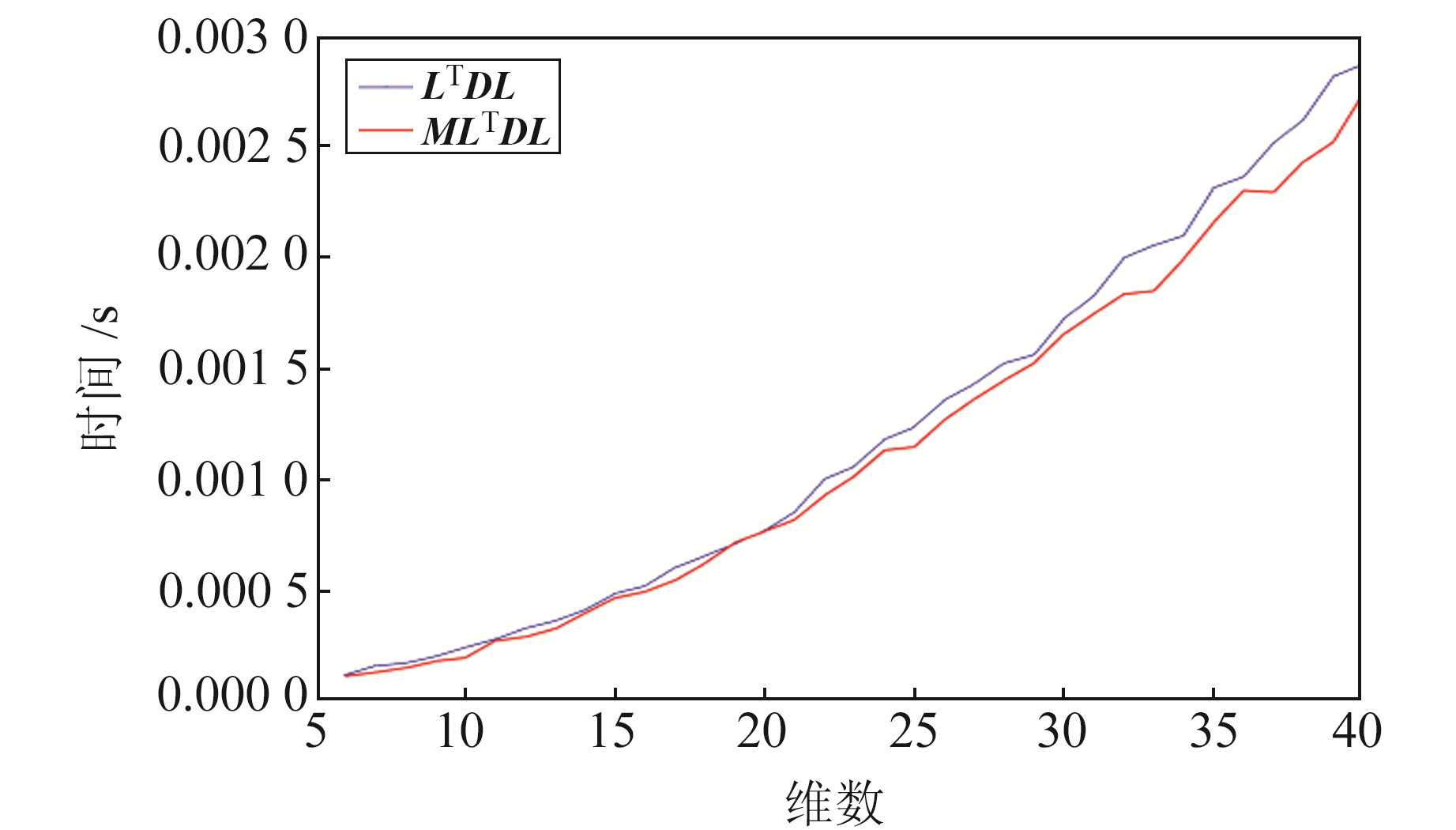
首先对2种LTDL分解方法进行仿真实验,仿真维数为6~40维。为避免偶然性,对每组仿真数据的2种分解方式各模拟100次,求取时间的平均值。图 1为BLAMBDA算法中改进后的MLTDL分解算法与LAMBDA算法中LTDL分解算法的解算时间对比。
|
图 1 2种分解算法的平均运行时间 Fig. 1 Average running time of two decomposition algorithms |
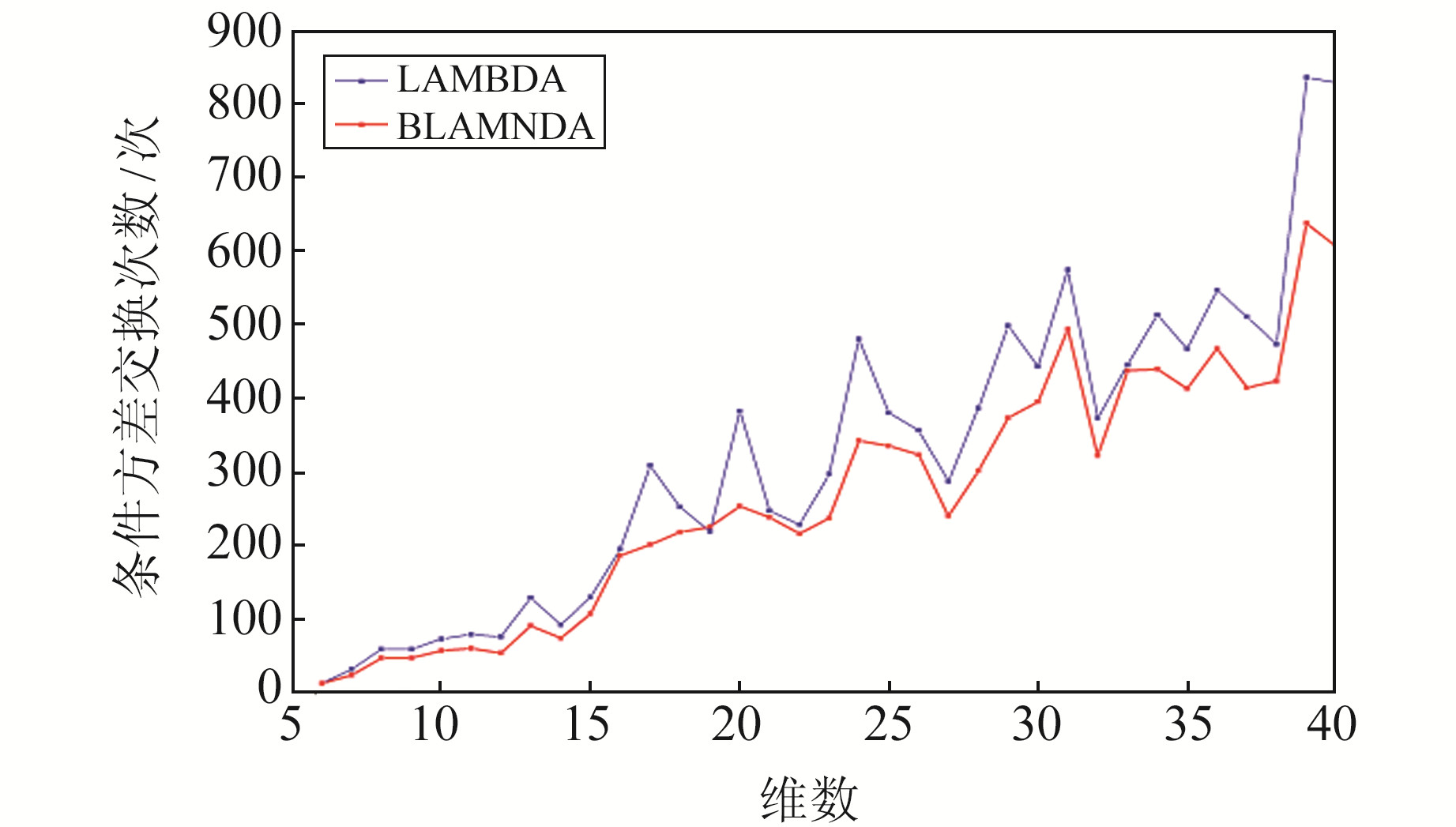
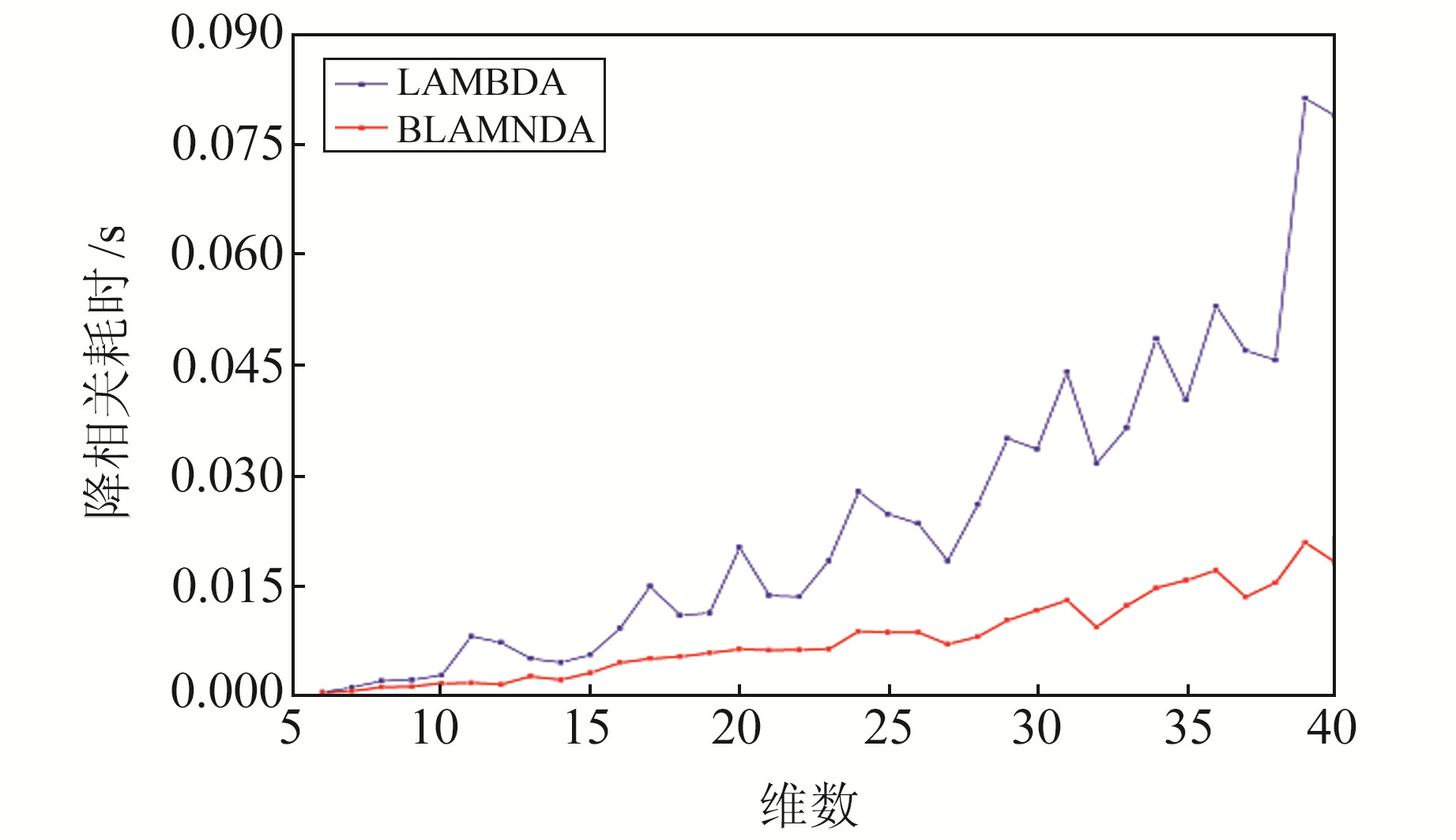
为更直观地说明BLAMBDA算法能够减少条件方差交换次数,仅对条件方差矩阵进行分块处理,模拟方式与图 1相同,实验结果如图 2所示。BLAMBDA算法和LAMBDA算法整体降相关耗时对比如图 3所示。
|
图 2 2种算法条件方差交换次数对比 Fig. 2 Comparison of conditional variance switching times between two algorithms |
|
图 3 2种算法降相关耗时对比 Fig. 3 Time consumption of decorrelation of two algorithms |
由图 1可见,LTDL分解算法具有可行性,说明减少矩阵的数乘可以明显提高矩阵分解效率。由图 2可见,相较于LAMBDA算法,BLAMBDA分块算法具有明显的优越性。由图 3可见,总体上看,BLAMBDA算法在去相关耗时效率上优于LAMBDA算法。
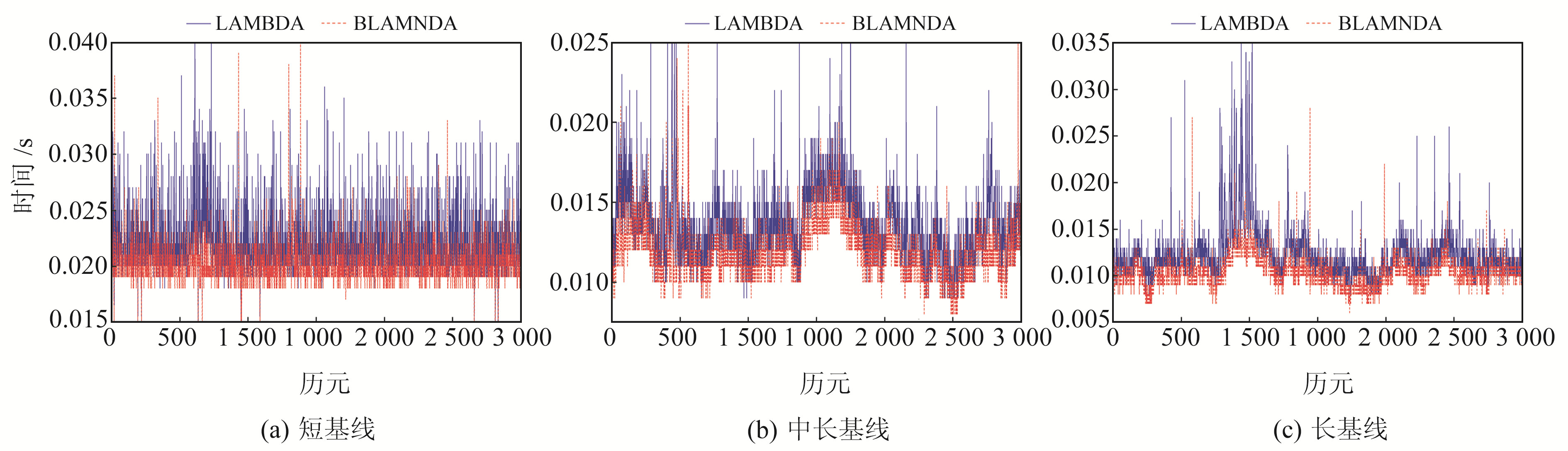
3.2 实测实验实测实验分为3组:1)短基线组采用1组和芯星通UB4B0-MINI板卡采集的静态观测数据,基线长89.83 m,采样间隔为1 s,截取3 000个历元进行实验分析;2)中长基线组采用武汉大学IGS数据中心下载的香港地区HKSL和HKWS测站的IGS数据,2站构成的基线长度为42.51 km,采样间隔为30 s;3)长基线组采用武汉大学IGS数据中心下载的香港地区HKSL测站和上海SHAO测站的IGS数据,2站构成的基线长度为1 216.01 km,采样间隔为30 s。本文所使用的数据包括星历数据和观测数据,且均为标准RINEX格式。为保证实验的合理性,BLAMBDA算法和LAMBDA算法均采用SEVB搜索算法进行降相关处理[3]。本实验基于RTKLIB的源代码进行数据处理, 实际解算过程中对2种算法的固定模糊度进行对比发现,二者结果一致性较高。本文提出的算法与RTKLIB源代码中的LAMBDA算法具有一致性,在此基础上采用GPS、BDS、Galileo、GLONASS等多系统数据进行整周模糊度融合解算,3种基线解算时间对比情况如图 4所示,耗时概率分布如图 5所示。
|
图 4 3种基线解算时间对比 Fig. 4 Comparison of three baseline calculation time |
|
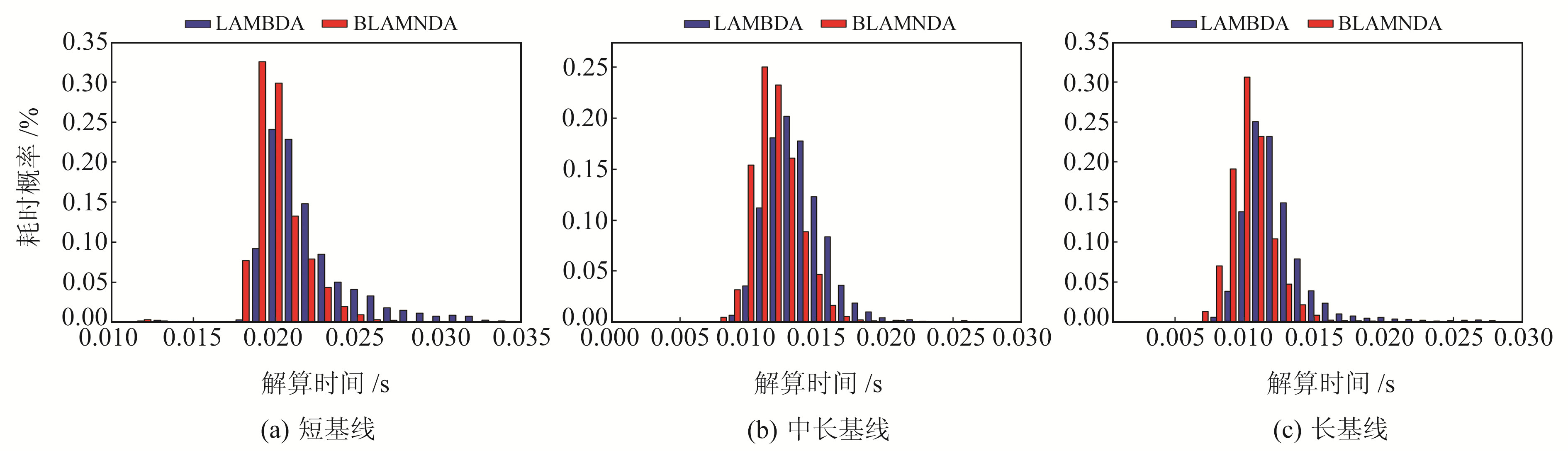
图 5 3种基线解算时间耗时概率对比分布 Fig. 5 Probability distribution of three baseline calculation time |
由图 4可见,BLAMBDA算法的解算时间明显短于LAMBDA算法。由于中长、长基线的采样间隔为30 s,而短基线的时间间隔为1 s,中长、长基线的观测时间长于短基线,因此图 4(a)的时间波动比图 4(b)、(c)的平缓。此外,短基线的双差模糊度维数整体高于中长、长基线,双差模糊度维数越高,BLAMBDA算法对时间效率的提升越明显。
由图 5(a)可见,LAMBDA算法在0.021~0.035 s内的解算耗时概率明显高于BLAMBDA算法,BLAMBDA算法的解算耗时大都集中在0.020 s左右;由图 5(b)、(c)可见,中长基线和长基线的BLAMBDA算法解算耗时与LAMBDA算法相比方差较小,解算耗时分布更加集中。LAMBDA算法存在高耗时的现象,而BLAMBDA算法在某种程度上弥补了这一缺陷。由此可以看出,BLAMBDA算法不仅在解算效率上优于LAMBDA算法,而且具有更好的稳定性。
4 结语为解决LAMBDA算法模糊度去相关过程计算量过大的问题,引入条件方差矩阵分块方法,并对分解算法进行改进,提出BLAMBDA算法。仿真与实测实验结果表明,BLAMBDA算法求解模糊度的整体效率高于LAMBDA算法。各历元解算耗时大小的概率分布表明,BLAMBDA算法的计算稳定性优于LAMBDA算法。
在BLAMBDA算法中,对条件方差矩阵进行分块处理,可以进一步提高模糊度的解算效率,这将是BLAMBDA算法下一步的研究重点。
| [1] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70: 65-82 DOI:10.1007/BF00863419
(  0) 0) |
| [2] |
Teunissen P J G. Integer Aperture GNSS Ambiguity Resolution[J]. Artificial Satellites, 2003, 38(3): 79-88
(  0) 0) |
| [3] |
Chang X W, Yang X, Zhou T. MLAMBDA: A Modified LAMBDA Method for Integer Least-Squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565 DOI:10.1007/s00190-005-0004-x
(  0) 0) |
| [4] |
Borno M A, Chang X W, Xie X H. On 'Decorrelation' in Solving Integer Least-Squares Problems for Ambiguity Determination[J]. Survey Review, 2014, 46(334): 37-49 DOI:10.1179/1752270612Y.0000000029
(  0) 0) |
| [5] |
Liu L T, Hsu H T, Zhu Y Z, et al. A New Approach to GPS Ambiguity Decorrelation[J]. Journal of Geodesy, 1999, 73(9): 478-490 DOI:10.1007/PL00004003
(  0) 0) |
| [6] |
徐琦, 杨艳玲, 李宏力. 基于LAMBDA方法的模糊度解算研究[J]. 测绘与空间地理信息, 2019, 42(2): 162-165 (Xu Qi, Yang Yanling, Li Hongli. Research on Ambiguity Resolution Based on LAMBDA Method[J]. Geomatics and Spatial Information Technology, 2019, 42(2): 162-165)
(  0) 0) |
| [7] |
Xu P L. Random Simulation and GPS Decorrelation[J]. Journal of Geodesy, 2001, 75: 408-423 DOI:10.1007/s001900100192
(  0) 0) |
| [8] |
陈树新. GPS整周模糊度动态确定的算法及性能研究[D]. 西安: 西北工业大学, 2002 (Chen Shuxin. A Study of the Algorithm and Its Performance for GPS Ambiguity Resolution on the Fly[D]. Xi'an: Northwestern Polytechnical University, 2002)
(  0) 0) |
| [9] |
Liu Z K, Huang S J. Research on Ambiguity Resolution Aided with Triple Difference[J]. Journal of Systems Engineering and Electronics, 2008, 19(6): 1 090-1 096 DOI:10.1016/S1004-4132(08)60202-9
(  0) 0) |
| [10] |
崔立鲁, 许文超, 邹正波, 等. 顾及病态转换矩阵的整周模糊度去相关迭代算法[J]. 科学技术与工程, 2019, 19(16): 21-25 (Cui Lilu, Xu Wenchao, Zou Zhengbo, et al. Integer Ambiguity Drop Decorrelation Iteration Algorithm Based on Ill-Pose Transformation Matrix[J]. Science Technology and Engineering, 2019, 19(16): 21-25)
(  0) 0) |
| [11] |
卢立果, 刘万科, 鲁铁定, 等. GNSS模糊度降相关性能的条件方差平稳度评价法[J]. 测绘学报, 2020, 49(8): 955-964 (Lu Liguo, Liu Wanke, Lu Tieding, et al. Conditional Variance Stationarity Evaluation Method for GNSS Ambiguity Decorrelation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(8): 955-964)
(  0) 0) |
| [12] |
蒋涅, 裴炳南, 张豪生. 一种改进的整周模糊度去相关算法[J]. 电光与控制, 2020, 27(1): 37-41 (Jiang Nie, Pei Bingnan, Zhang Haosheng. An Improved Integer Ambiguity Decorrelation Algorithm[J]. Electronics Optics and Control, 2020, 27(1): 37-41)
(  0) 0) |
| [13] |
鲁铁定, 汪鑫, 卢立果, 等. 排序对模糊度解算中降相关性能的影响分析[J]. 大地测量与地球动力学, 2020, 40(5): 470-475 (Lu Tieding, Wang Xin, Lu Liguo, et al. Analysis of the Influence of Sorting on Decorrelation Performance in the Ambiguity Solution[J]. Journal of Geodesy and Geodynamics, 2020, 40(5): 470-475)
(  0) 0) |
| [14] |
鲁铁定, 汪鑫, 鲁春阳. 一种改进的GNSS高维模糊度快速降相关算法[J]. 大地测量与地球动力学, 2021, 41(5): 511-515 (Lu Tieding, Wang Xin, Lu Chunyang. An Improved GNSS High-Dimensional Ambiguity Fast Decorrelation Algorithm[J]. Journal of Geodesy and Geodynamics, 2021, 41(5): 511-515)
(  0) 0) |
| [15] |
Hassibi A, Boyd S. Integer Parameter Estimation in Linear Models with Applications to GPS[J]. IEEE Transactions on Signal Processing, 1998, 46(11): 2938-2 952
(  0) 0) |
| [16] |
Lenstra A K, Lenstra Jr H W, Lovász L. Factoring Polynomials with Rational Coefficients[J]. Mathematische Annalen, 1982, 261(4): 515-534
(  0) 0) |
| [17] |
Lannes A. On the Theoretical Link between LLL-Reduction and LAMBDA-Decorrelation[J]. Journal of Geodesy, 2013, 87(4): 323-335
(  0) 0) |
| [18] |
Grafarend E W. Mixed Integer-Real Valued Adjustment (IRA) Problems: GPS Initial Cycle Ambiguity Resolution by Means of the LLL Algorithm[J]. GPS Solutions, 2000, 4(2): 31-44
(  0) 0) |
| [19] |
刘经南, 于兴旺, 张小红. 基于格论的GNSS模糊度解算[J]. 测绘学报, 2012, 41(5): 636-645 (Liu Jingnan, Yu Xingwang, Zhang Xiaohong. GNSS Ambiguity Resolution Using the Lattice Theory[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 636-645)
(  0) 0) |
| [20] |
谢恺, 柴洪洲, 范龙, 等. 一种改进的LLL模糊度降相关算法[J]. 武汉大学学报: 信息科学版, 2014, 39(11): 1363-1368 (Xie Kai, Chai Hongzhou, Fan Long, et al. An Improved LLL Ambiguity Decorrelation Algorithm[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1363-1368)
(  0) 0) |
| [21] |
范龙. 基于格理论的GNSS模糊度估计方法研究[D]. 郑州: 信息工程大学, 2013 (Fan Long. Research on Method of Integer Ambiguity Estimation with Lattice Theory[D]. Zhengzhou: Information Engineering University, 2013)
(  0) 0) |
| [22] |
卢立果. GNSS整数最小二乘模糊度解算理论与方法研究[J]. 测绘学报, 2017, 46(9): 1204 (Lu Liguo. Study on Theory and Method of GNSS Integer Least Squares Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1204)
(  0) 0) |
2. Collaborative Innovation Center of BDS Research Application, 62 Kexue Road, Zhengzhou 450001, China
 2023, Vol. 43
2023, Vol. 43


