常用的GNSS时间序列粗差剔除方法主要有3σ法、中位数(MAD)法、四分位距(inter quartile range,IQR)法等[1-6],但这3种方法都有一个共同的缺陷——数据剔除的效果在很大程度上受限于数据长度,以至于无法把握真实的数据趋势[7]。为解决这个问题,可以采用滑动窗口的方式一段一段地剔除数据,但这会增加更多的限制,而且还会受到窗口选取的影响。
本文针对窗口难以选取的问题提出一种基于小波分析的一阶导数粗差剔除法,经过仿真模型及实际验证,解决了传统粗差探测算法在数据处理中的过剔除现象,在小波分析过程中能准确提取到信号的真实形变趋势,尽可能多地区分出粗差点;同时,在粗差点采用广义延拓插值补点,兼顾了监测数据的连续性。
1 GNSS形变监测时间序列的粗差数据处理方法 1.1 基于小波分析的一阶导数粗差剔除法基于小波分析的一阶导数粗差剔除法步骤如下:
1) 首先引入一阶导数分析信号趋势项。将信号求一阶导数后,会得到类似高尺度下的小波系数,借用小波阈值的思想,原本小波阈值函数是将信号中低幅值的小波系数进行过滤,现在则认为大于阈值的一阶导数点是粗差点。
2) 利用小波原有的minimaxi法则求出阈值,以分离异常导数值,这里采用经验方程。如果要达到更好的效果,可以在阈值的设定方面进行拓展,这与小波阈值的设计相同,将其标志成为异常点,大部分异常点会在此被剔除。阈值计算公式为:
| $ \lambda=\left\{\begin{array}{l} \sigma\left(0.3936+0.1829 \log _2 N\right), N>32 \\ 0, N<32 \end{array}\right. $ | (1) |
式中,
3) 将剔除后的数据只进行1次3σ剔除,此处也可以选取大一点的判决门限(如5σ等)防止剔除了有用信号。
4) 最后借用小波分析的手段对数据进行粗差剔除,其主要方式是通过小波分解得到低频趋势项,将原信号和低频趋势项作差得到残差。考虑到重复计算趋势项会大幅增加计算量,这里只求1次趋势项,对获取到的残差进行拉依达准则(3σ准则)计算。将异常点置0(这里的异常点指的是偏离趋势项的异常值),残差就会慢慢向0收缩,最后将残差为0对应的原始信号点进行剔除。
1.2 形变监测缺失数据的广义延拓插值法粗差剔除后,原始信号中会存在信号间断及数据缺失,为使监测数据连续,需要进行插值运算,本文采用广义延拓插值法进行数据填补。广义延拓吸取现有插值法和拟合法的长处与特点,采用分片光滑的做法,利用延拓域构建单元域拟合函数,并锁定单元域边界节点,以逼近最好效果。
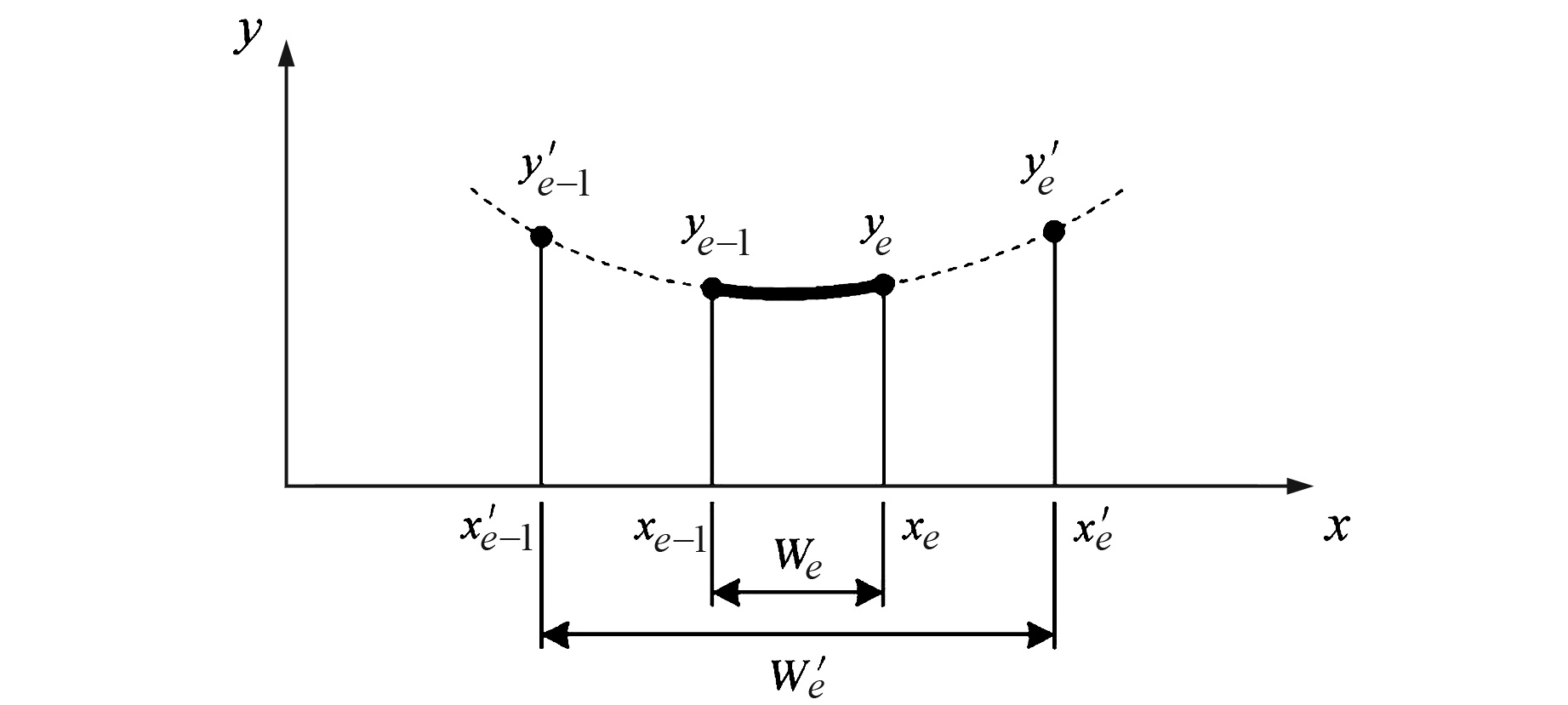
首先将每段被剔除的集合作为单元域We,向两边扩展一定长度作为延拓域W′e。
单元域We中有r个剔除点,满足xr∈[xe-1, xe],延拓域W′e中有s个节点,满足xs∈[x′e-1, x′e],如图 1所示。
|
图 1 延拓域及相应函数值 Fig. 1 Continuation domain and corresponding function value |
在延拓域构建逼近函数ye(x):
| $ y_e(x)=\sum\limits_{j=1}^v a_j g_j(x), x \in\left[x_{e-1}, x_e\right] $ | (2) |
式中,aj(j=1, 2, …, v) 为待定系数,gj(j=1, 2, …, v) 为We上的一组基函数,v为逼近函数项数,且满足r < v < s,求解待定系数时,将x取值扩展为[x′e-1, x′e]。本文采用二次多项式作为基函数拟合曲线。
建立广义延拓逼近内插模型:
| $ \left\{\begin{array}{l} \min I\left(a_1, a_2, \cdots, a_j\right)=\min \sum\limits_{i=1}^s\left[a_j g_j\left(x_i\right)-y_i\right]^2 \\ \text { s.t. }\left\{\begin{array}{l} a_j g_j\left(x_{e-1}\right)=y_{e-1} \\ a_j g_j\left(x_e\right)=y_e \end{array}\right. \end{array}\right. $ | (3) |
式中,I(a1, a2, …, aj)为逼近函数与先验值的误差。
单元域We因粗差剔除导致数据缺失,需要通过单元域外的数据对整个延拓域W′e进行拟合,以记录单元域内每一个残缺点的数值。在此基础上,保证单元域外的点全部固定,延拓域的所有点经过广义延拓模型反复迭代,直到获得残缺点的稳定值。
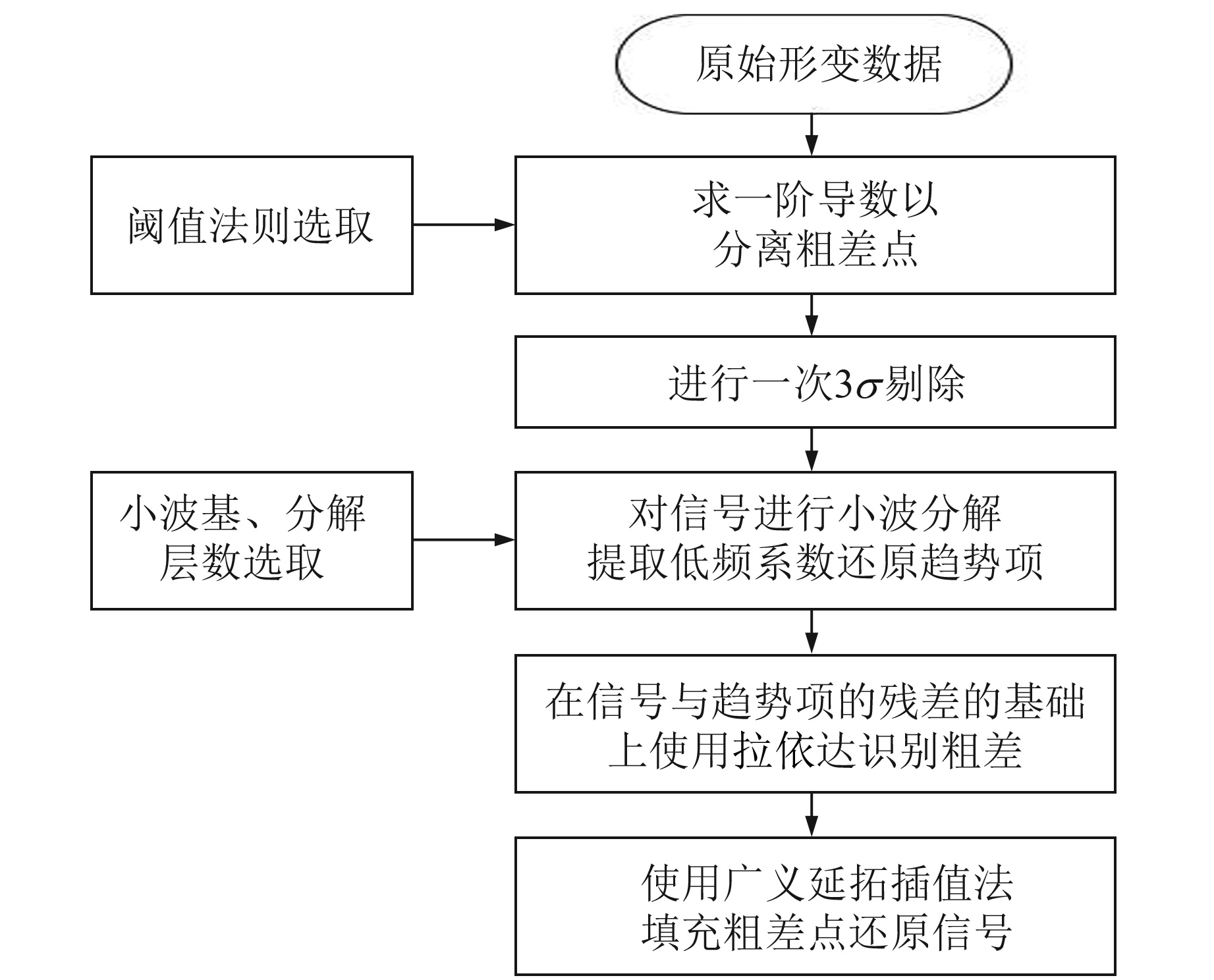
综上,本文GNSS形变时间序列粗差数据处理流程见图 2。
|
图 2 数据处理流程 Fig. 2 Data processing flow |
为验证新算法的有效性,模拟GNSS形变的坐标时间序列,其原始表达式为:
| $ \begin{gathered} S(t)=4 \sin \left(\frac{\pi}{400} t\right) \sin \left(\frac{\pi}{125} t\right)+ \\ 2 \sin \left(\frac{\pi}{300} t\right)+\sin \left(\frac{2 \pi}{65} t\right)+0.0015 t \end{gathered} $ | (4) |
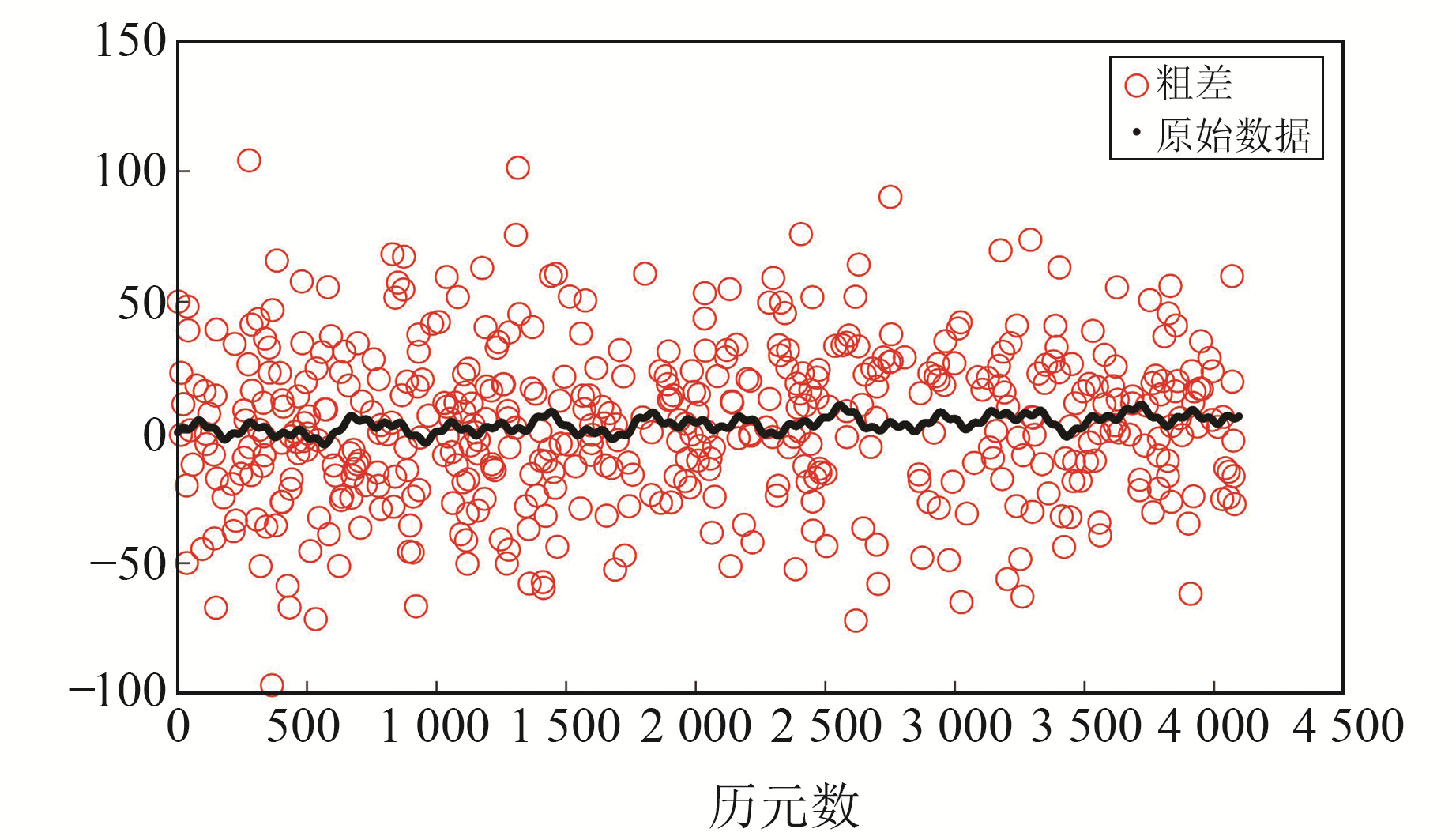
采样频率为1 Hz,取4 096个历元,考虑到实际形变监测过程中粗差数量多、分布范围广,在原始信号中添加10倍标准差的粗差点,粗差点数为500个,占比为12.22%(图 3)。采用3σ法、MAD法、四分位距法和一阶导数小波剔除法进行对比,小波基选择为db1~db5,分别作1~8层分解并计算剔除率,仿真次数为10 000次,结果见表 1和2。
|
图 3 原始数据及全部粗差 Fig. 3 Raw data and all gross errors |
|
|
表 1 常规粗差剔除法的剔除率 Tab. 1 Rejection rate of conventional gross error elimination method |
|
|
表 2 一阶导数小波剔除法在不同小波分解情况的剔除率 Tab. 2 The rejection rate of the first-order derivative wavelet removal method in different wavelet decomposition conditions |
从表 2可见,除db1外其他几种小波使用效果基本相似,说明对粗差影响最大的是分解层数。由于增加小波分解层数会大幅增加运算量,即可以随意选取一组小波基作一层分解,本文后续都采用基函数db4进行一层分解。
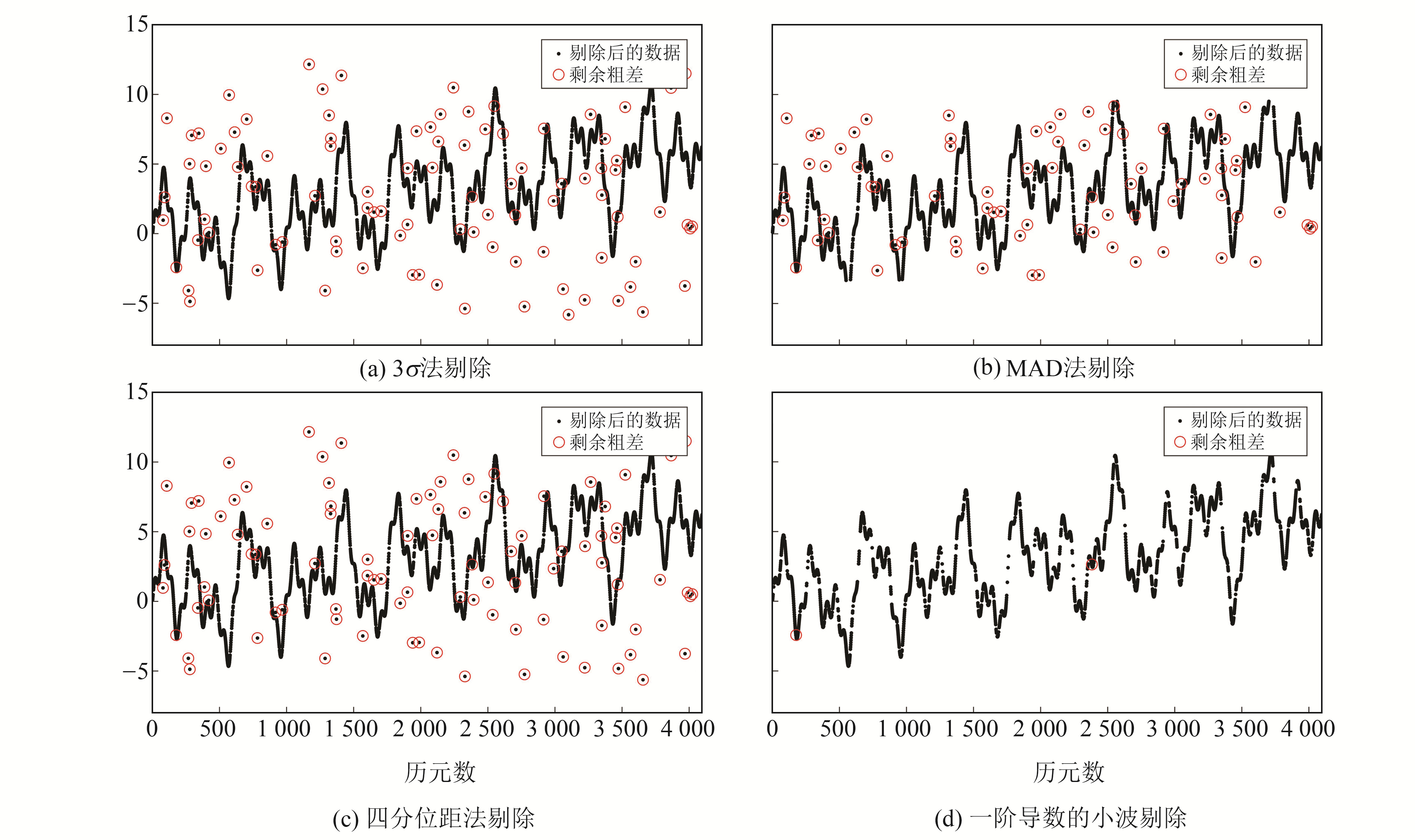
4种粗差剔除法效果对比见图 4,可以看出,一阶导数的小波剔除率远高于其他3种传统粗差剔除算法,几乎能探测到所有的粗差点。最后将图 4(d)剔除后的信号分别进行广义延拓插值、分段三次样条插值(spline)、相邻非缺失值的线性插值(linear)、保形分段三次样条插值(pchip)及修正Akima三次Hermite插值(makima),并对比原始信号计算RMSE来评价插值效果,结果如表 3所示。可以看出,广义延拓插值效果优于其余插值方法,故将其应用于后续计算。
|
图 4 4种粗差剔除法剔除效果 Fig. 4 Four gross error elimination methods |
|
|
表 3 插值精度对比 Tab. 3 Interpolation accuracy comparison |
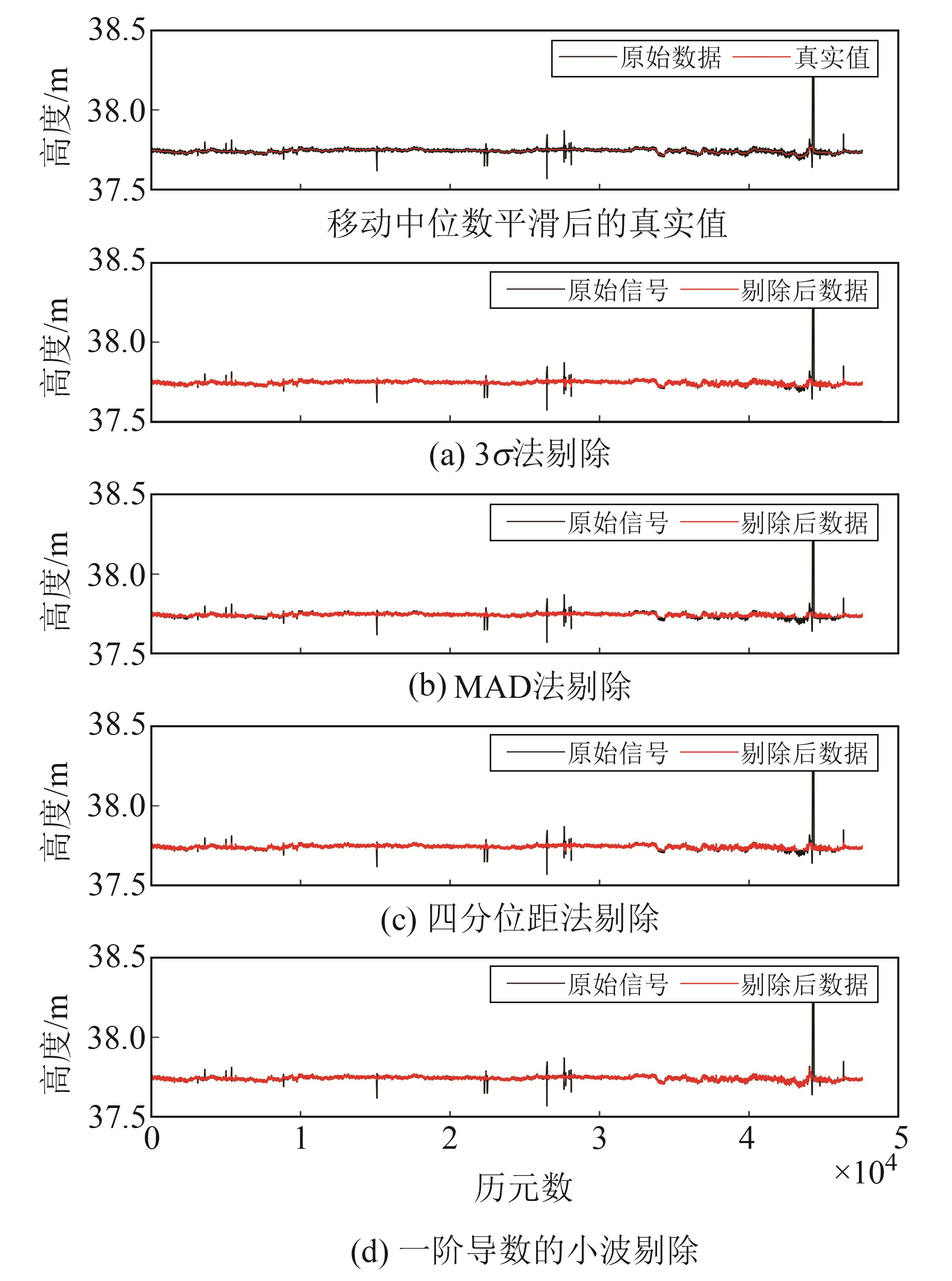
本文使用富阳市金鑫广场桁架张拉测试时的数据,时间跨度为2020-10-26~27,共47 561个历元。监测拆除施工辅助支架桁架下沉时高度数据的变化情况,现场遍布高压电线和信号基站,使监测设备终端接收信号产生干扰,造成原始数据存在许多粗差点,真实波形难以观察。由于真实信号未知,对原始含噪数据采用移动中位数进行平滑处理,得到近似的真实信号,窗口长度为200。
从图 5(a)~5(c)可以看出,传统粗差算法难以准确还原信号的原有趋势,而一阶导数的小波剔除法保留了信号的有用成分。为达到较好的剔除效果,3种传统算法每次需要剔除1个点后再重新将剩余数据进行相同的操作,4种粗差剔除算法运行时间结果见表 4。
|
图 5 金鑫广场桁架形变监测数据及粗差剔除效果 Fig. 5 Jinxin square truss deformation monitoring data and gross error removal effect |
|
|
表 4 算法执行速度 Tab. 4 Algorithm execution speed |
由于MAD法和四分位距法需要计算中位数和百分位数,所以花费时间较多,而本文提出的新算法所用时间仅是3σ法的0.01倍。粗差剔除的正确性会影响到插值算法的效果,故将4组算法得到的剔除数据与原始数据进行精度对比,并挑选精度最高的进行广义延拓插值,以补充剔除位置的数据。
由于真实信号采用的是原始信号平滑滤波后的数据,因此除了RMSE外,同时使用均值偏离量u作为精度评价指标,其计算公式为:
| $ u=\left|\frac{\sum\limits_{i=1}^q s(i)}{q}-\frac{\sum\limits_{i=1}^p s^{\prime}(i)}{p}\right| $ | (5) |
式中,s为平滑滤波后的真实信号近似,s′为经过粗差剔除后剩余的信号,q和p分别为2个信号的总长度。
从表 5可见,前4种算法的RMSE较为接近,说明这4种算法都可以剔除影响较大的误差。3σ法、MAD法和四分位距法存在过剔除现象,所以剔除后信号的均值与真实值存在较大的偏离,而一阶导数小波剔除法能够避免窗口的选取,经过广义延拓插值后与真实值仅存在约0.03 mm的偏离。
|
|
表 5 精度对比 Tab. 5 Comparison of precision |
针对GNSS形变监测的传统粗差探测算法性能受限于数据长度的问题,提出基于小波分析的一阶导数粗差剔除法。采用原始信号的一阶导数来区分正常波动和粗差异常,可以有效避免窗口数据的选择,而且只进行1次一阶导数的剔除,大幅减少了计算量;同时,在粗差点采用广义延拓插值补点,保证了监测数据的连续性。经实例验证,本文算法的计算效率和准确度都较传统算法有较大提升。
| [1] |
Tao Y, Liu C, Liu C Y, et al. Empirical Wavelet Transform Method for GNSS Coordinate Series Denoising[J]. Journal of Geovisualization and Spatial Analysis, 2021, 5(1)
(  0) 0) |
| [2] |
张恒璟, 程鹏飞. 基于GPS高程时间序列粗差的抗差探测与插补研究[J]. 大地测量与地球动力学, 2011, 31(4): 71-75 (Zhang Hengjing, Cheng Pengfei. Study on Robust Detection and Interpolation from Gross Errors of GPS Height Time Series[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 71-75)
(  0) 0) |
| [3] |
徐洪钟, 吴中如, 李雪红, 等. 基于小波分析的大坝变形观测数据的趋势分量提取[J]. 武汉大学学报: 工学版, 2003, 36(6): 5-8 (Xu Hongzhong, Wu Zhongru, Li Xuehong, et al. Abstracting Trend Component of Dam Observation Data Based on Wavelet Analysis[J]. Engineering Journal of Wuhan University, 2003, 36(6): 5-8)
(  0) 0) |
| [4] |
黄立人, 韩月萍, 高艳龙, 等. GNSS连续站坐标的高程分量时间序列在地壳垂直运动研究中应用的若干问题[J]. 大地测量与地球动力学, 2012, 32(4): 10-14 (Huang Liren, Han Yueping, Gao Yanlong, et al. Several Issues in Application of Elevation Component Time Series of GNSS CORS in Vertical Crustal Movement Studying[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 10-14 DOI:10.3969/j.issn.1671-5942.2012.04.003)
(  0) 0) |
| [5] |
舒颖. GPS坐标时间序列粗差剔除方法比较分析[J]. 导航定位学报, 2021, 9(4): 79-85 (Shu Ying. Comparative Analysis on Outlier Elimination Methods for GPS Coordinate Time Series[J]. Journal of Navigation and Positioning, 2021, 9(4): 79-85)
(  0) 0) |
| [6] |
吴浩, 卢楠, 邹进贵, 等. GNSS变形监测时间序列的改进型3σ粗差探测方法[J]. 武汉大学学报: 信息科学版, 2019, 44(9): 1282-1288 (Wu Hao, Lu Nan, Zou Jingui, et al. An Improved 3σ Gross Error Detection Method for GNSS Deformation Monitoring Time Series[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1282-1288)
(  0) 0) |
| [7] |
王威, 许芬, 王宇谱. 一种基于小波分析的卫星钟差数据粗差处理方法[J]. 大地测量与地球动力学, 2021, 41(6): 623-627 (Wang Wei, Xu Fen, Wang Yupu. A Preprocess Method for Gross Error Detection Based on Wavelet Analysis[J]. Journal of Geodesy and Geodynamics, 2021, 41(6): 623-627)
(  0) 0) |
| [8] |
王宇谱. GNSS星载原子钟性能分析与卫星钟差建模预报研究[D]. 郑州: 信息工程大学, 2017 (Wang Yupu. Research on Modeling and Prediction of the Satellite Clock Bias and Performance Evaluation of GNSS Satellite Clocks[D]. Zhengzhou: Information Engineering University, 2017)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

