2. 西南科技大学土木工程与建筑学院,四川省绵阳市青龙大道中段59号, 621010
目前,建筑物变形预测方法以统计学方法和人工智能算法为主。其中,统计学方法是在对变形数据进行分析处理的基础上,提取其中的规律性信息,并利用确定的数学模型对其建模,常用的有ARMA、ARIMA等时间序列模型及灰色理论模型和卡尔曼滤波等[1-2]。不同于统计学方法,人工智能算法不需要建立精确的数学模型,直接采用数据驱动的方式将时间序列中的变形信息转化为网络结构参数,通过自适应自学习能力对未来的变形趋势进行预测,经典的人工智能算法包括反向传播(back propagation, BP)神经网络[3]、长短时记忆神经网络(long short-term memory neural network, LSTM)[4]和支持向量机(support vector machine, SVM)[5]等方法。其中,BP神经网络具有任意非线性函数逼近能力,其预测性能优于时间序列模型;而SVM采用核函数的方式将低维空间中的非线性问题转化为高维空间中的线性问题,从而提升模型的计算效率及对小样本、非线性问题的适应能力。但BP神经网络和LSTM神经网络的预测性能受网络初值影响较大,且对噪声敏感[6]。
针对建筑物变形数据非平稳和波动性特征,本文基于分解-预测-重构的思想,提出一种基于分数阶傅里叶变换(FrFT)和支持向量机(SVM)的组合预测模型,用于建筑变形趋势预测。实验结果表明,该组合模型相对于单一预测模型能够获得更高的预测精度。
1 组合预测模型建筑物的变形过程具有非线性、非平稳和波动性特征,单一模型无法在预测过程中准确捕捉这些信息,因此预测精度不高,且噪声稳健性较差。本文结合FrFT处理非平稳时间序列的优势和SVM对小样本、非线性问题的泛化能力,提出一种FrFT-SVM建筑物变形组合预测模型。该组合预测模型首先利用FrFT将复杂时间序列分解为多个简单子序列,同时引入相关向量机(relevance vector machine, RVM)自动确定最优FrFT阶次,并利用SVM对每个子序列分别进行建模预测;同时为了提升预测性能,提出一种改进的果蝇优化算法(improved fruit fly optimization algorithm, IFOA)对SVM核参数和惩罚因子进行全局寻优;最后将每个子序列的预测结果进行综合叠加,得到最终预测结果。
1.1 基于FrFT的变形时间序列分解FrFT又称为广义傅里叶变换,在保留传统傅里叶变换性质的同时又具备其特有优势,能够同时对时域和频域信息进行分析处理,是非线性、非平稳时间序列分析的强有力工具[7]。
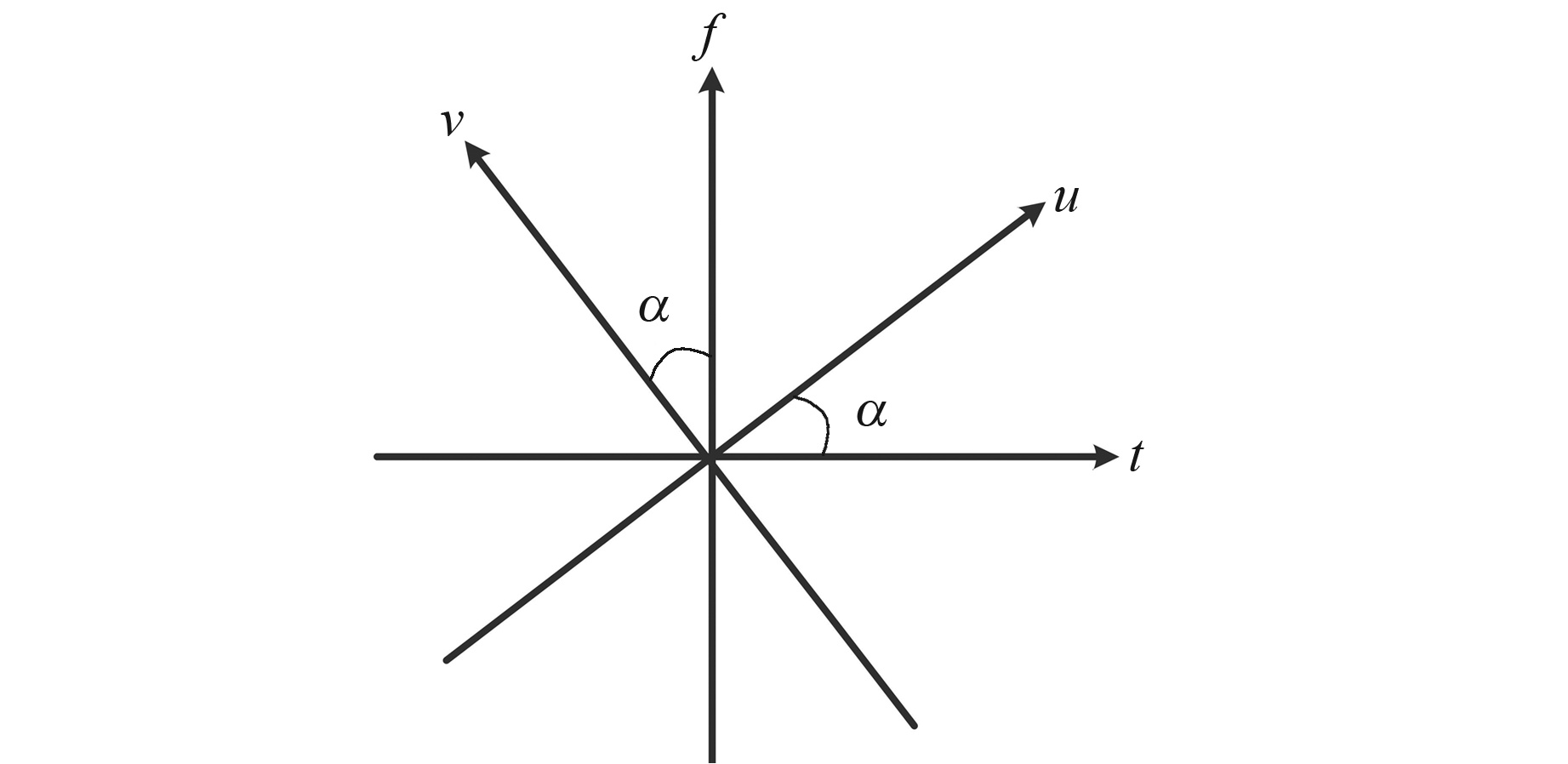
图 1在时间-频率二维坐标平面中给出传统傅里叶变换和FrFT之间的关系示意图,其中横坐标代表时间t,纵坐标表示频率f。传统傅里叶变换可以看作是将时间轴按逆时针方向旋转π/2,得到频率轴的一种线性变化,即在(t, f)二维平面内的一种时间序列分析手段;而FrFT可以看作是将时间序列沿逆时针方向旋转任意α角度,得到分数谱f(u)和F(v)的过程,随着α的取值从0变化到π/2,FrFT可以呈现出时间序列从时域向频域逐渐转变的过程。对于(t, f)平面内的非平稳信号,通过将其转换到合适的(u, v)平面能够有效消除交叉项。
|
图 1 FrFT与传统傅里叶变换关系示意图 Fig. 1 Schematic diagram of the relationship between FrFT and traditional Fourier transform |
对于连续时间序列f(t),对其进行p阶FrFT变换的表达式为:
| $ f_p(u)=\int_{-\infty}^{+\infty} K_p(u, t) f(t) \mathrm{d} t $ | (1) |
式中,
由于实际工程实践中处理的都是经采样后的离散序列,因此要对式(1)进行离散化处理,从而得到离散分数阶傅里叶变换(discrete FrFT, DFrFT)。常用的一种FrFT离散化方法为Ozaktas采样方法,首先对原始信号进行时域展开,然后根据Shannon采样定理进行插值,最后得到FrFT的离散化处理结果。对式(1)展开得:
| $ \begin{gathered} f_p(u)=\sqrt{\frac{1-\mathrm{j} \cot t}{2 \pi}} \exp \left[\mathrm{j} \pi u^2 \cot \alpha\right] \times \\ \int_{-\infty}^{+\infty} f(t) \exp \left[\mathrm{j} \pi t^2 \cot \alpha\right] \exp [-\mathrm{j} 2 \pi u t \csc \alpha] \mathrm{d} t \end{gathered} $ | (2) |
利用Shannon定理对式(2)中积分项f(t)exp[jπt2cotα]进行插值处理,可将其转化为:
| $ \begin{array}{c} f(t) \exp \left[\mathrm{j} \pi t^2 \cot \alpha\right]=\sum\limits_{n=-N}^N f\left(\frac{n}{2 \Delta x}\right) \times \\ \exp \left[\frac{\mathrm{j} \pi(\cot \alpha) n^2}{(2 \Delta x)^2}\right] \sin c\left[2 \Delta x\left(t-\frac{n}{2 \Delta x}\right)\right] \end{array} $ | (3) |
最后,将式(3)代入式(2),得到原始时间序列f(t)的p阶DFrFTfp(m)为:
| $ \begin{gathered} f_p(m)=\frac{A_a}{2 \Delta x} \exp \left\{\frac{\mathrm{j} \pi[\cot \alpha-\csc \alpha] m^2}{(2 \Delta x)^2}\right\} \times \\ \sum\limits_{n=-N}^N \exp \left[\frac{\mathrm{j} \pi(\cot \alpha)(m-n)^2}{(2 \Delta x)^2}\right] \times \\ \exp \left\{\frac{\mathrm{j} \pi[\cot \alpha-\csc \alpha] n^2}{(2 \Delta x)^2}\right\} f\left(\frac{n}{2 \Delta x}\right) \end{gathered} $ | (4) |
式中,n和m分别为原始时间序列和p阶DFrFT的采样点数,N为时间序列总长度,1/Δx为时间序列采样间隔。
1.2 最优FrFT阶次的确定根据式(1)~式(4),当DFrFT阶次p=0时,得到的结果为原始时间序列;当p=1时,得到的结果为原始时间序列的频谱。利用DFrFT进行时间序列分析时,通常将p的取值在0.1~0.9范围内按0.1间隔进行遍历,分别得到不同阶次的DFrFT结果。遍历方法虽然简单,但是得到的DFrFT中有些阶次会获得较好的时-频能量聚集特点,能够有效反映时间序列的趋势性和周期性等有用信息,另外一些阶次(例如噪声分量)能量会均匀分布在整个平面内,不包含对趋势预测的有用信息,因此需要一种方法能够自动确定DFrFT中的最优阶次。
相关向量机(relevance vector machine, RVM)是一种贝叶斯框架下的最优分类器,与SVM类似,RVM同样采用核函数的方式将低维空间中的非线性问题映射为高维空间中的线性问题,但同时又具备特有的优势:1)RVM通过引入共轭先验分布的方式增加了模型的稀疏性,因而具有自动特征选择能力;2)RVM模型将特征选择与分类器设计统一为同一个优化问题,具备更强的泛化能力;3)RVM能够提供概率式预测结果,相当于提供了更多的信息;4)RVM核函数的选择不受摩西准则约束。
将原始变形时间序列经过DFrFT分解所得0.1~0.9阶子序列记为{xp}p=19,将其作为RVM的输入特征向量,利用RVM进行特征选择的过程即可等价于最优阶次选择的过程。RVM分类函数可以表示为:
| $ y(x, w)=\sum\limits_{p=1}^9 w_p K\left(x, x_p\right)+\varepsilon $ | (5) |
式中,K(x, xp)为核函数,wp代表不同的权重,ε为0均值高斯白噪声(方差为τ-1)。
RVM通过向分类模型中引入Sigmoid函数的方式实现对目标值的概率预测,此时输入特征向量的似然函数可以表示为:
| $ \begin{gathered} p(t \mid w)= \\ \prod\limits_{p=1}^9 \sigma\left[y\left(x_p, w\right)\right]^{t_n}\left[1-\sigma\left[y\left(x_p, w\right)\right]\right]^{1-t_p} \end{gathered} $ | (6) |
式中,tp为xp对应的类别标号。
为了构建完整的贝叶斯框架,对模型权值wp引入先验分布,常用的分布形式为高斯分布,即假设wn服从0均值、方差为α-1的高斯分布。由于高斯分布的共轭先验分布为伽马分布,因此采用伽马分布定义α-1和τ-1的超先验值:
| $ \begin{aligned} & p(\alpha)=\prod\limits_{i=0}^N \operatorname{Gamma}\left(\alpha_i \mid a, b\right) \\ & p(\tau)=\operatorname{Gamma}(\tau \mid c, d) \end{aligned} $ | (7) |
式中,Gamma(τ|c, d)=Γ(c)-1dcτc-1e-dτ,
上述RVM模型常用的求解方法为变分贝叶斯期望最大(variational bayesian expectation maximization, VBEM)算法[ 8],在求解过程中会发现,大部分α会随着迭代的进行逐渐趋于无穷大,对应的w则趋于0,从而实现了权值向量的稀疏化;迭代终止时,不为0的权值对应的特征向量即为要选择的特征。
1.3 改进的IFOA-SVM预测模型对FrFT分解得到的子序列建立SVM回归模型并进行预测,SVM回归模型具有预测精度高、算法复杂度低及适合于小样本应用等众多优点,利用SVM对变形时间序列进行回归预测的模型可以表示为:
| $ y=\boldsymbol{\omega}^{\mathrm{T}} \varphi(x)+b $ | (8) |
式中,φ(x)为非线性映射函数,ω为权值,b为线性偏移量。
SVM采用结构风险最小化准则,将式(8)中模型参数ω和b的求解过程转化为如下优化问题:
| $ \left\{\begin{array}{l} \min \left[\frac{1}{2} \boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\omega}+c \sum\limits_{i=1}^l\left(\xi_i+\xi_i^*\right)\right] \\ \text { s. t. }\left\{\begin{array}{l} y_i-\boldsymbol{\omega} \varphi\left(x_i\right)-b \leqslant \varepsilon+\xi_i^* \\ \boldsymbol{\omega} \varphi\left(x_i\right)+b-y_i \leqslant \varepsilon+\xi_i \\ \xi_i, \xi_i^* \geqslant 0 \end{array}\right. \end{array}\right. $ | (9) |
式中,c为非负惩罚因子,ε为模型不敏感参数,ξi和ξi*为非负松弛因子,l为训练样本数量。
采用拉格朗日乘子法将式(9)转化为:
| $ \left\{\begin{array}{l} \max \left[\begin{array}{l} \sum\limits_{i=1}^l\left(\eta_i-\eta_i^*\right) y_i-\frac{1}{2} \sum\limits_{i=1}^l \sum\limits_{j=1}^l\left(\eta_i-\eta_i^*\right) \times \\ K\left(x_i, x_j\right)-\sum\limits_{i=1}^l\left(\eta_i+\eta_i^*\right) \varepsilon \end{array}\right] \\ \text { s. t. }\left\{\begin{array}{l} \sum\limits_{i=1}^l\left(\eta_i-\eta_i^*\right)=0 \\ 0 \leqslant \eta_i \leqslant c, 0 \leqslant \eta_i^* \leqslant c \end{array}\right. \end{array}\right. $ | (10) |
式中,ηi和ηi*为拉格朗日乘子;K(xi, xj)为核函数,广泛使用的一种核函数形式为径向基核函数,其定义为:
| $ K\left(x_i, x_j\right)=\exp \left[-\frac{\left\|x_i-x_j\right\|^2}{2 \gamma^2}\right] $ | (11) |
式中,γ为核参数。
对式(10)进行求解,可以得到最终的SVM回归模型:
| $ f(x)=\sum\limits_{i=1}^l\left(\eta_i-\eta_i^*\right) K\left(x_i, x_j\right)+b $ | (12) |
SVM回归模型的预测精度和泛化能力与惩罚因子c及核参数γ的取值密切相关,目前常用的交叉验证法存在运算量大、自动化程度不高等问题。因此,本文将果蝇优化算法(fruit fly optimization algorithm, FOA)[9]与SVM相结合,利用FOA的全局搜索能力对SVM参数进行寻优,提升模型预测性能。同时,考虑到传统FOA采用固定搜索步长,在迭代过程中存在灵活性不足的问题,提出自适应搜索步长方法对其进行改进,得到IFOA算法。利用IFOA算法对SVM进行优化的步骤为:
1) 初始化SVM回归模型,设定惩罚因子与核参数的取值范围。
2) 设置果蝇种群数量N和最大迭代次数T,将惩罚因子c和核参数γ作为果蝇群体的位置坐标,即
| $ \left\{\begin{array}{l} X_{\mathrm{axis}}=c \\ Y_{\mathrm{axis}}=\gamma \end{array}\right. $ | (13) |
3) 根据式(14)随机赋予果蝇个体搜寻食物的方向和位置:
| $ \left\{\begin{array}{l} X_i=X_{\mathrm{axis}}+R(i) \\ Y_i=Y_{\mathrm{axis}}+R(i) \end{array}\right. $ | (14) |
式中,
4) 计算当前果蝇个体与原点之间的距离Di及对应味道浓度判定值Pi:
| $ \left\{\begin{array}{l} D_i=\sqrt{X_i^2+Y_i^2} \\ P_i=\frac{1}{D_i} \end{array}\right. $ | (15) |
5) 利用Pi计算得到果蝇所在位置的味道浓度值Si,将当前果蝇群体中味道浓度值最小的果蝇作为最优个体,并记录Si和对应的位置坐标[Xi, Yi]。
6) 重复上述步骤,并记录每次迭代过程中最优个体的味道浓度值和空间位置信息,即
| $ \left\{\begin{array}{l} X_i=X_{i_{-} \text {best }} \\ Y_i=Y_{i_{-} \text {best }} \\ S_i=S_{i_{-} \text {best }} \end{array}\right. $ | (16) |
式中,(Xi_best, Yi_best)为第i次迭代果蝇群体中最优个体所处位置,Si_best为对应的味道浓度值。
7) 当迭代次数达到最大值T时,步骤6)记录数据中最小浓度值对应的位置信息即为SVM的最优参数组合,即
| $ \left\{\begin{array}{l} c_{\mathrm{opt}}=X_{\mathrm{best}} \\ \gamma_{\mathrm{opt}}=Y_{\mathrm{best}} \end{array}\right. $ | (17) |
根据上述分析可知,对于给定变形监测时间序列s,首先利用FrFT对其进行分解,得到0.1~0.9阶子序列{xp}p=19,即
| $ \boldsymbol{x}_p=\operatorname{DFrFT}(s)_p, p=0.1 \sim 0.9 $ | (18) |
利用RVM对FrFT进行阶次选择,得到最优阶次FrFT子序列xi, xj, … xl, i, j, l∈[1, 9];利用IFOA-SVM对每个子序列分别进行建模预测,得到每个子序列的预测结果
| $ \tilde{\boldsymbol{s}}=\tilde{\boldsymbol{x}}_i+\tilde{\boldsymbol{x}}_j+\cdots+\tilde{\boldsymbol{x}}_l $ | (19) |
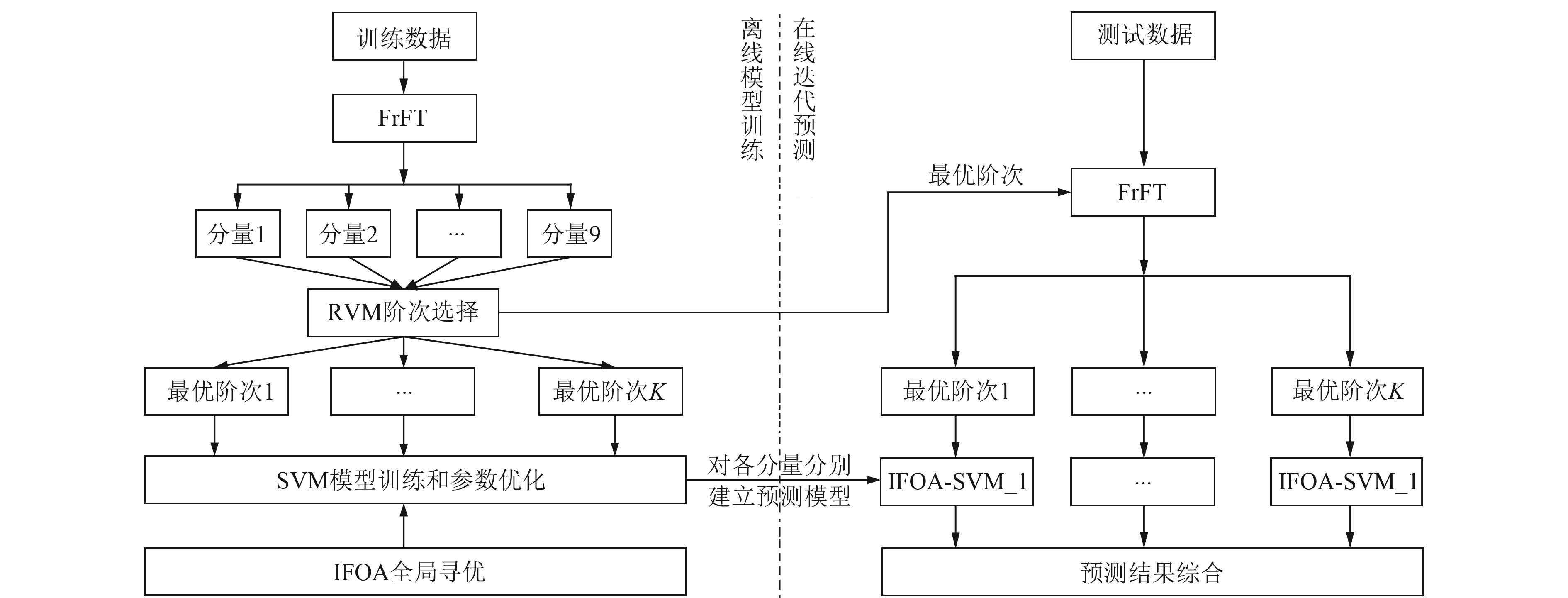
组合预测模型首先对时间序列进行0.1~0.9阶次的FrFT分解,并结合RVM的稀疏性和特征选择能力实现对最优K个FrFT阶次的选取,将原始时间序列转化为K个不同时频尺度下的子序列,实现序列关键信息的有效提取;然后分别采用SVM对各个子序列进行训练建模,并通过IFOA算法优化模型参数;最后通过对测试数据的预测结果进行叠加综合,得到实际的预测结果。本文组合模型的算法流程如图 2所示,具体步骤可以总结为:
|
图 2 组合预测模型流程 Fig. 2 Flow chart of combined forecasting model |
1) 将建筑物变形时间序列划分为训练集和测试集;初始化模型参数:FrFT阶次p=0.1, …, 0.9,SVM惩罚因子c及核参数γ的取值区间,果蝇种群数量N和最大迭代次数T;
2) 在离线模型训练阶段,利用FrFT对时间序列进行分解,并结合RVM特征选择获取最优阶次对应的子序列,利用IFOA选取各子序列的最优参数,训练SVM模型;
3) 在在线迭代预测阶段,利用FrFT方法和步骤2)得到的最优阶次,获得K个最优子序列,利用训练阶段获得的最优IFOA-SVM回归模型,对每个子序列进行预测,最后根据式(19)对各子序列预测值进行综合累加,得到真实的建筑物变形预测值。
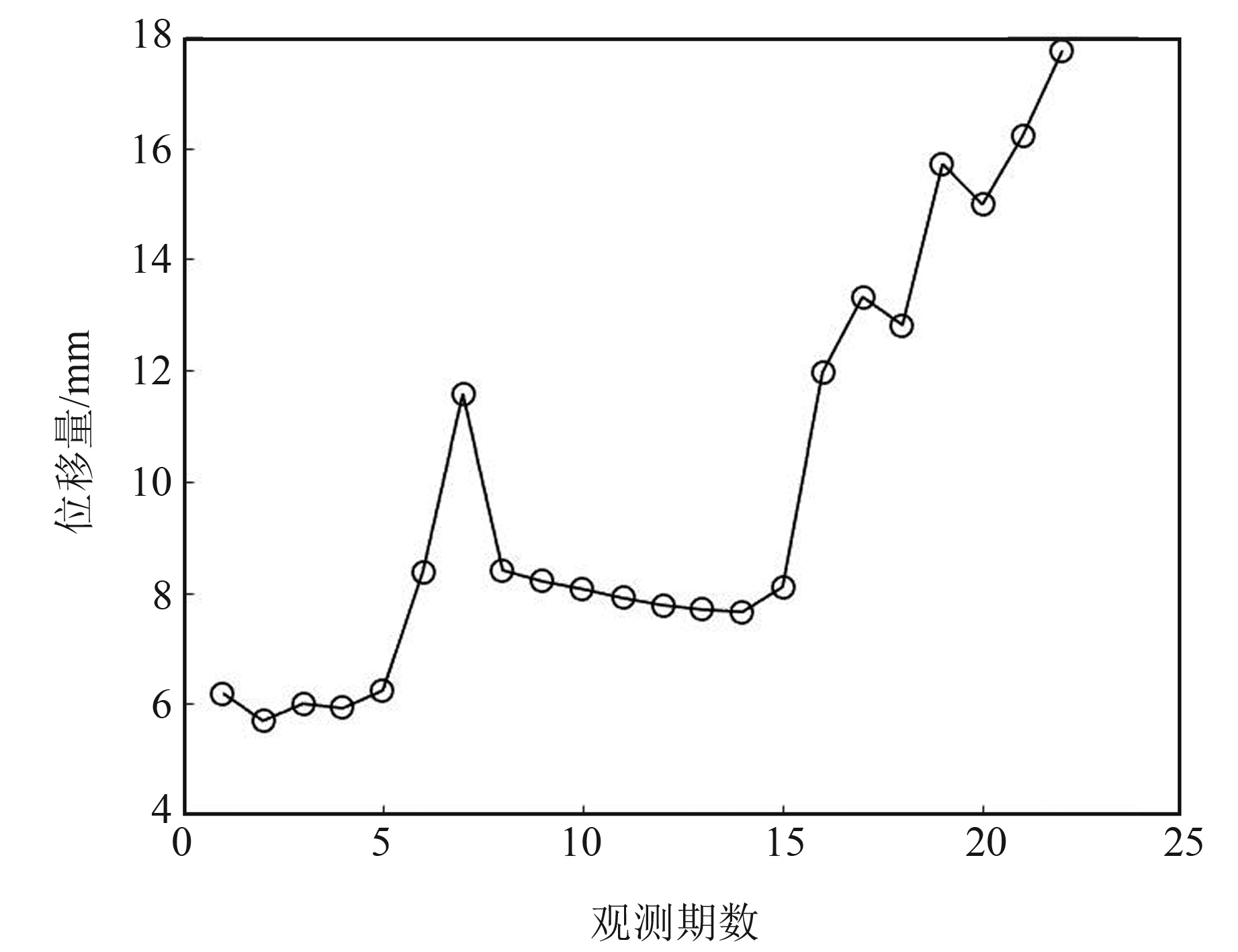
2 实验及结果分析 2.1 实验数据及模型评估指标为验证本文组合预测模型在实际使用过程中的预测性能,选用我国西南地区某混凝土大坝2003-01~2005-02期间水平位移数据开展实验,采样检测1月/期。该大坝总共布设6个水平位移监测点,经过数据分析发现各监测点的水平位移变化规律大致相同,因此本文选择具有代表性的3号监测点记录的数据进行分析(图 3)。可以看出,在前5期和第8~15期观测周期内,大坝位移变化较为平缓,其余时间变化较大,呈现出典型的非线性、非平稳和波动性特征。
|
图 3 大坝变形原始时间序列 Fig. 3 Original time series of dam deformation |
为定量评估本文组合模型的变形预测精度,采用预测值与真实值之间的相对误差(relative error, RE)和均方根误差(root mean square error, RMSE)作为评估指标:
| $ \mathrm{RE}=\frac{y_i-\tilde{y}_i}{y_i} \times 100 \% $ | (20) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(y_i-\tilde{y}_i\right)^2} $ | (21) |
式中,yi为第i期水平位移实际测量值,
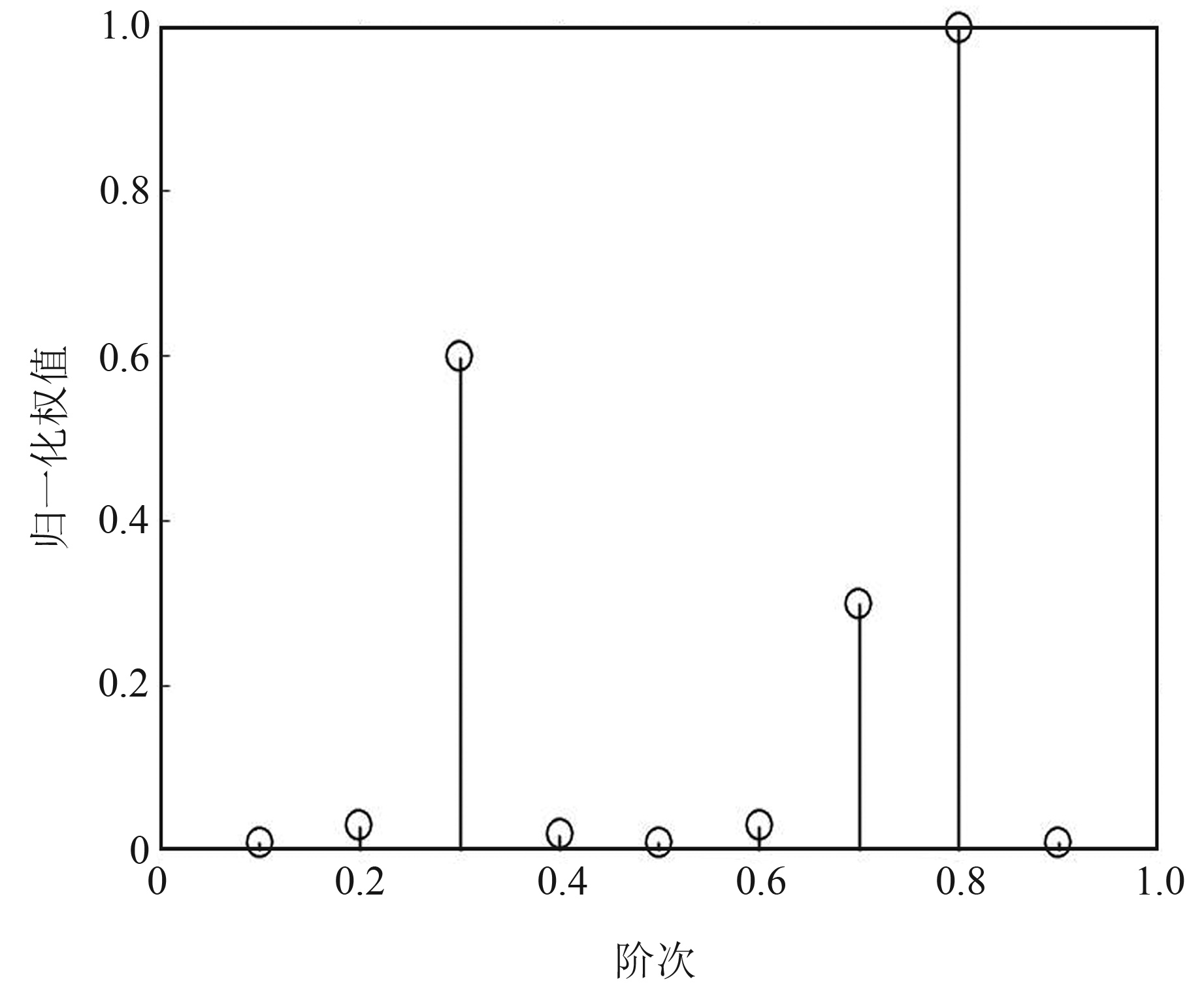
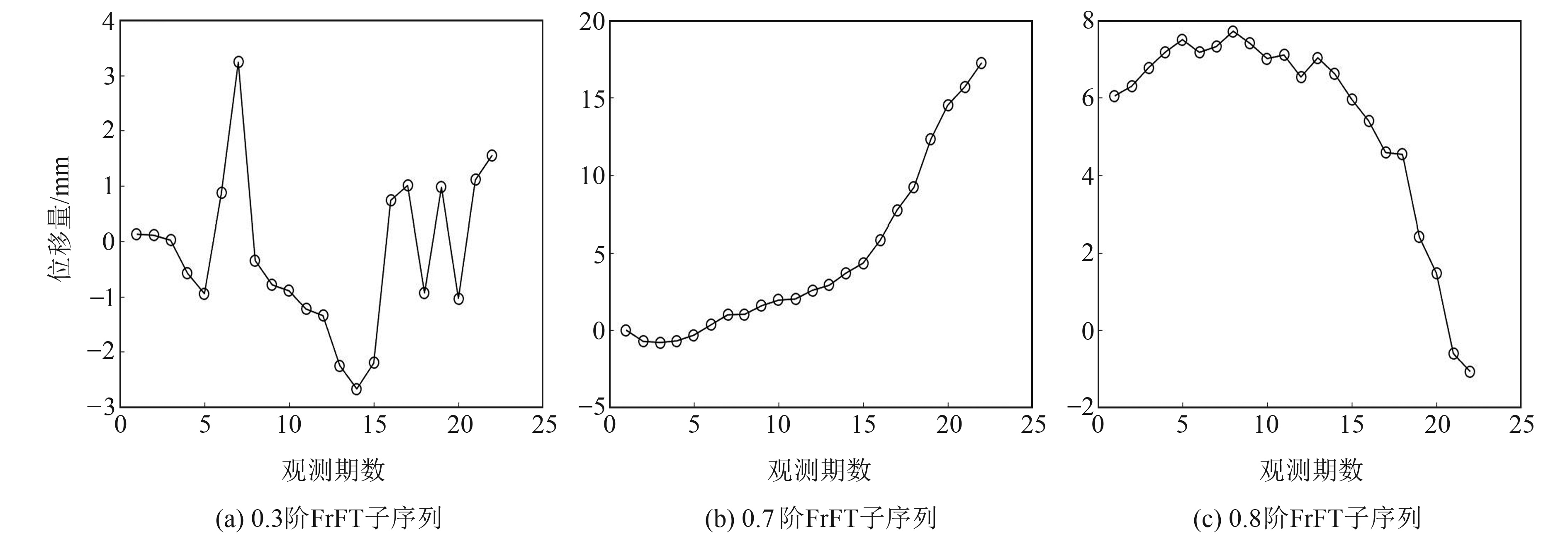
根据图 2所示流程,首先需要对变形时间序列进行0.1~0.9阶次的FrFT分解,并结合RVM的稀疏性和特征选择能力实现对最优K个FrFT阶次的选取。图 4给出利用VBEM算法求解RVM模型,在迭代终止时权值向量的取值结果,可以看出,经RVM特征选择后,阶次为0.3、0.7和0.8的3个子序列对应的权值较大,其余阶次子序列对应的权值均接近于0。图 5给出0.3阶、0.7阶和0.8阶子序列波形,对比图 4和5可以看出,RVM选出的3个子序列都包含了原始序列中的不同维度信息:0.3阶子序列波形变化比较剧烈,且数据之间的关联性较弱,反映出原始序列中的波动性特性;0.7阶子序列呈现出较明显的上升趋势,反映原始序列中的趋势性信息;0.8阶子序列表现出一定的周期性,反映原始序列中隐含的周期性信息。上述结果表明,经过FrFT分解后,每个子序列都从不同维度反映了原始序列中的变形信息,对原始序列进行FrFT分解的过程有效弱化了对不同信息进行分析时的相互干扰和相互影响,且每个子序列的波形变化曲线相对于原始曲线更加简单平滑,降低了后续预测模型的复杂度。
|
图 4 RVM阶次选择结果 Fig. 4 Order selection results of RVM |
|
图 5 FrFT分解结果 Fig. 5 FrFT decomposition results |
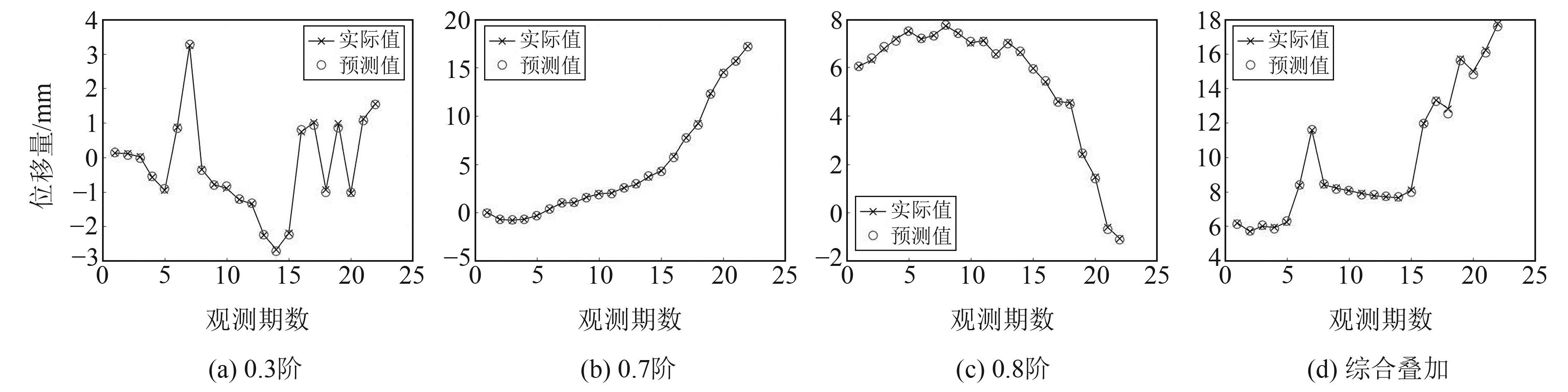
根据图 2所示算法流程,在FrFT完成时间序列分解后,利用IFOA-SVM对每个子序列分别进行建模预测。实验中,将前12期数据作为训练样本用于IFOA-SVM建模和参数优化,剩余9期数据作为测试样本,得到的预测结果如图 6(a)~6(c)所示,图 6(d)给出对每个子序列结果综合叠加后得到的最终预测结果。
|
图 6 组合模型预测结果 Fig. 6 Predictionresults of the combined model |
从图 6可以看出,组合模型通过FrFT分解能够深度挖掘数据中隐含的物理规律信息,使分解后的每个子序列呈现出较为简单平滑的变化趋势,从而明显降低后续预测难度,提升预测性能。根据式(20)和式(21)可以计算得到预测结果的最大RE为1.33%,RMSE为0.072 9。
2.3 与其他预测方法比较分析表 1给出在相同条件下分别采用组合预测模型、SVM、GM(1, 1)和LSTM四种模型进行预测得到的结果和对应的预测残差。对表 1所示结果进行分析可知,传统灰色GM(1, 1)预测模型在初期能够获得较高的预测精度,但随着预测时间的增长,其预测性能出现了较大波动,预测模型的最大RE为8.46%,RMSE为0.634 1;SVM模型的预测精度要略高于GM(1, 1)模型,其预测结果的最大RE为3.17%,RMSE为0.343 3;LSTM在进行变形预测时会加入对前期位移数据的回忆,具备动态预测能力,因此相对于GM(1, 1)模型和SVM模型的预测性能出现明显提升,其预测结果的最大RE为2.65%,RMSE为0.230 8,能够满足实际工程应用要求的预测精度,而本文组合模相对于LSTM模型性能提升超过120%,具有更好的应用前景。
|
|
表 1 不同方法的预测结果 Tab. 1 Prediction results of different methods |
建筑物变形数据是一种典型的非线性、非平稳和波动性时间序列,传统基于单一模型的预测方法由于无法充分挖掘数据中的隐含信息,存在预测精度低、噪声稳健性差的问题。本文基于分解-预测-重构的思路,利用FrFT结合RVM将复杂变形数据分解为K个结构简单子序列,进而利用IFOA-SVM对每个子序列进行建模预测,通过叠加综合获得最终预测结果。实验结果表明,组合预测方法能够获得更高的预测精度和噪声稳健性,相对于单一模型具有更为广阔的应用前景。
| [1] |
杨小虎, 朱庆伟, 沈宇恒, 等. 改进灰色时序模型在建筑物变形监测中的应用[J]. 西安科技大学学报, 2020, 40(5): 919-926 (Yang Xiaohu, Zhu Qingwei, Shen Yuheng, et al. Application of Improved Grey-Time Series Model in Monitoring Building Deformation[J]. Journal of Xi'an University of Science and Technology, 2020, 40(5): 919-926)
(  0) 0) |
| [2] |
袁德宝, 张振超, 张军, 等. 最优化分数阶算子EGM(1, 1)模型在变形监测预报中的应用[J]. 大地测量与地球动力学, 2020, 40(4): 331-334 (Yuan Debao, Zhang Zhenchao, Zhang Jun, et al. Application of Optimized Fractional Order EGM(1, 1) Model in Deformation Monitoring and Forecasting[J]. Journal of Geodesy and Geodynamics, 2020, 40(4): 331-334)
(  0) 0) |
| [3] |
刘晶磊, 张国朋, 张冲冲, 等. 基于误差分级迭代法的基坑变形预测[J]. 科学技术与工程, 2021, 21(14): 5822-5827 (Liu Jinglei, Zhang Guopeng, Zhang Chongchong, et al. Research on Deformation Prediction of Foundation Pit Based on Error Grading Iterative Method[J]. Science Technology and Engineering, 2021, 21(14): 5822-5827 DOI:10.3969/j.issn.1671-1815.2021.14.025)
(  0) 0) |
| [4] |
Xing Y, Yue J P, Chen C. Interval Estimation of Landslide Displacement Prediction Based on Time Series Decomposition and Long Short-Term Memory Network[J]. IEEE Access, 2019(8): 3187-3196
(  0) 0) |
| [5] |
牛景太. 基于奇异谱分析与PSO优化SVM的混凝土坝变形监控模型[J]. 水利水电科技进展, 2020, 40(6): 60-65 (Niu Jingtai. Dam Deformation Monitoring Model Based on Singular Spectrum Analysis and SVM Optimized by PSO[J]. Advances in Science and Technology of Water Resources, 2020, 40(6): 60-65)
(  0) 0) |
| [6] |
Wei B W, Yuan D Y, Li H K, et al. Combination Forecast Model for Concrete Dam Displacement Considering Residual Correction[J]. Structural Health Monitoring, 2019, 18(1): 232-244
(  0) 0) |
| [7] |
陶然, 齐林, 王越. 分数阶Fourier变换的原理与应用[M]. 北京: 清华大学出版社, 2004 (Tao Ran, Qi Lin, Wang Yue. Theory and Applications of the Fractional Fourier Transform[M]. Beijing: Tsinghua University Press, 2004)
(  0) 0) |
| [8] |
Nielsen F B. Variational Approach to Factor Analysis and Related Models[D]. Denmark: Technical University of Denmark, 2003
(  0) 0) |
| [9] |
王岩, 张波, 薛博. 基于FOA-SVM的中文文本分类方法研究[J]. 四川大学学报: 自然科学版, 2016, 53(4): 759-763 (Wang Yan, Zhang Bo, Xue Bo. Research on Chinese Classification Based on FOA-SVM[J]. Journal of Sichuan University: Natural Science Edition, 2016, 53(4): 759-763)
(  0) 0) |
2. School of Civil Engineering and Architecture, Southwest University of Science and Technology, 59 Mid-Qinglong Road, Mianyang 621010, China
 2022, Vol. 42
2022, Vol. 42


