2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
随着科技发展,运用全球导航卫星系统(global navigation satellite system, GNSS)采集地理数据已成为空间大地测量领域的一种重要手段[1]。但通过GNSS技术所获取的高程是以WGS84参考椭球面为基准的大地高,如何将大地高转换为实际工程中常用的正常高已成为国内外学者的重要研究课题[2]。为获取高精度GNSS高程异常值以进行大地高与正常高之间的转换,建立符合实际值的高程异常拟合模型尤为重要。重力模型法是国内外常用的方法,但由于国内高精度的重力模型还未完善,难以在实际工程中应用。常用的高程异常拟合法还有加权最小二乘法、多面函数法、移动曲面法等[3-4],但这些方法的数值模型是基于假定的似大地水准面,因此存在模型误差。
近年来,许多学者利用BP神经网络法的非线性自适应、分布式运算容错性高、具备自学习能力且无模型误差等特性,将其运用在各个领域,并取得了一定成果。研究表明,BP神经网络用于GNSS高程拟合时具备良好的精度[5],当测区内已知的GNSS水准点分布较均匀且数量较少时,BP神经网络拟合法可作为首选拟合方法[6]。然而由于BP神经网络自身的梯度下降机制,在网络结构复杂、隐含层数较多等条件下存在梯度消失的问题,且其网络权值是通过沿局部改善的方向进行调整的,算法本身也易陷入局部极值。若能解决上述问题,GNSS高程拟合精度在理论上将得到进一步提高[7]。MVO算法作为一种元启发式优化算法,可在全局空间多个区域内寻求最优解,且具备收敛速度快的特性[8]。本文采用MVO算法求取BP神经网络各层之间较优的神经元阈值与连接权,对BP神经网络进行优化,并建立基于MVO算法的BP神经网络高程异常拟合模型,从而提高GNSS高程异常拟合精度,为GNSS高程异常拟合提供一种新方法。
1 MVO-BP神经网络拟合预测模型 1.1 多元宇宙优化算法多元宇宙优化算法(MVO)全局寻优能力强且收敛速度快,适用于多个领域[9]。MVO可模拟多元宇宙中物体由高膨胀率宇宙传递到低膨胀率宇宙的过程,通过多元宇宙中白洞、黑洞、虫洞的交互作用找出具备最佳膨胀率的宇宙,多元宇宙中每个宇宙均可视为优化问题的候选解,宇宙中的物体即为候选解的变量,求解最优宇宙的过程即为算法迭代寻优过程,多元宇宙在初始化后经历多个周期的演化,最终可得到最优解。实现步骤如下:
1) 初始化多元宇宙种群数n,当前演化周期T,最大演化周期Tmax,用于启动迭代寻优,则多元宇宙矩阵可表示为:
| $ \boldsymbol{U}=\left[\begin{array}{c} \boldsymbol{U} \\ \boldsymbol{U}_2 \\ \vdots \\ \boldsymbol{U}_n \end{array}\right]=\left[\begin{array}{cccc} x_1^1 & x_1^2 & \cdots & x_1^d \\ x_2^1 & x_2^2 & \cdots & x_2^d \\ \vdots & \vdots & \vdots & \vdots \\ x_n^1 & x_n^2 & \cdots & x_n^d \end{array}\right] $ | (1) |
式中,Ui=[xi1, xi2, …, xid] 表示第i个宇宙,对应的空间维度为d,则xij表示第i个宇宙的第j个物体。多元宇宙种群数n通常取值为10~40,若所需优化问题的参数较多,可适当增加多元宇宙种群数n,有利于全局寻优。初始状态下当前演化周期T取值为1,最大演化周期Tmax表示算法所设置的主循环最大迭代次数,以保证在演化周期T达到Tmax前完成收敛。
2) 初始化旅程距离速率TDR,可定义对当前最佳宇宙进行局部搜索的精确度,表达式为:
| $ \mathrm{TDR}=1-\frac{T^{1 / p}}{T_{\max }^{1 / p}} $ | (2) |
式中,p为TDR的限制参数,p值越大TDR递增速度越快,p值一般取为常数6。TDR随演化周期T的递增而线性递减,从而可进行精度更高的局部搜索。
3) 初始化虫洞存在概率WEP的表达式为:
| $ \mathrm{WEP}=\mathrm{WEP}_{\min }+T \times\left(\frac{\mathrm{WEP}_{\max }-\mathrm{WEP}_{\min }}{T_{\max }}\right) $ | (3) |
式中,WEPmin为WEP最小值,WEPmax为WEP最大值,WEPmin和WEPmax分别取值0.2和1,表示虫洞的最小存在概率和最大存在概率分别为20%和100%,以保证各个宇宙均有可能存在虫洞。由式(3)可知,演化周期T越长,虫洞存在概率越大,虫洞的存在使各个宇宙在不考虑膨胀率的情况下也能进行物体传递,可为多元宇宙提供更复杂的演化方向。
4) 计算每个宇宙膨胀率并归一化,表达式为:
| $ x_i^j=\left\{\begin{array}{l} x_i^j, \text { roulette }() \geqslant \operatorname{NI}\left(\boldsymbol{U}_i\right) \\ x_k^j, \text { roulette }()<\operatorname{NI}\left(\boldsymbol{U}_i\right) \end{array}\right. $ | (4) |
式中,roulette()为遵循轮盘赌机制生成的[0, 1]范围内的随机数;NI (Ui) 为第i个宇宙的归一化膨胀率,在新一轮迭代开始时,归一化膨胀率NI (Ui) 随着U的变动重新进行计算;xkj表示经轮盘赌机制选择的第k个宇宙的第j个物体,由于其膨胀率较大,该物体将通过黑洞/白洞轨道传递至当前最佳宇宙。
5) 由WEP与TDR参数构建虫洞机制,该机制可保证各个宇宙均有机会与当前最优宇宙进行物体传递,从而丰富宇宙演化的多样性,避免算法陷入局部最优,表达式为:
| $ R_j=\left(\mathrm{ub}_j-1 \mathrm{~b}_j\right) \times \text { roulette }()+1 \mathrm{b}_j $ | (5) |
| $ x_i^j = \left\{ \begin{array}{l} \left\{ \begin{array}{l} {x_j} + {\rm{ IDR }} \times {R_j}, {\rm{ roulette( )}} \le 0.5\\ {x_j} - {\rm{ TDR }} \times {R_j}, {\rm{ roulette }}() > 0.5 \end{array} \right.\\ \ \ \ \ {\rm{ roulette }}() < {\rm{ WEP}}\\ x_i^j, {\rm{ roulette }}() \ge {\rm{WEP }} \end{array} \right. $ | (6) |
式中,xj为当前最优宇宙的变量,ubj与lbj为变量xj的上界与下界。
6) 在一个演化周期T内,由i=1开始执行虫洞影响下的个体行为,单个个体行为完成时i+1,直到i=n时完成一个演化周期,计算并更新当前最佳宇宙位置,此时T+1。若T < Tmax,则重复步骤2)~5)迭代流程,每次迭代完成后当前演化周期T+1,直到T=Tmax时多元宇宙演化完成,输出当前最优宇宙及其最佳膨胀度。
1.2 BP神经网络BP神经网络是一种基于输出误差逆向传播的多层前馈神经网络,由输入层、隐含层、输出层构成基本的网络拓扑结构,不同层的神经元互相连接形成映射通道,各层间的连接权与神经元阈值决定映射效果,在此基础上输出值的误差在神经网络中逆向传播,从而逐渐修正神经网络的各项参数。典型的BP神经网络模型如图 1所示。

|
图 1 BP神经网络模型 Fig. 1 BP neural network model |
图 1中x、y、z分别为输入值、中间值及输出值,其中输入层神经元数为n,隐含层神经元数为m,输出层神经元数为l,输出值的目标值为tar(tar维度为l)。设输入层到隐含层的神经元正向映射函数为f1,隐含层到输出层的神经元正向映射函数为f2,则:
| $ z_k=f_2\left(\sum\limits_{j=1}^h w_{j k} f_1\left(\sum\limits_{i=1}^n w_{i j} x_i-\alpha\right)-\beta\right) $ | (7) |
式中,输入值xi在神经网络中经历2次正向映射,最终求得输出值zk,wij为输入层与隐含层的连接权,wjk为隐含层与输出层的连接权,α为隐含层神经元阈值,β为输出层神经元阈值。此时神经网络输出误差为:
| $ \delta=\frac{1}{2} \sum\limits_{k=1}^m\left(\operatorname{tar}_k-z_k\right)^2 $ | (8) |
式中,tark为目标值。若δ不满足精度要求,则误差以梯度下降的方式在神经网络中逆向传播,从而逐渐更新神经网络的各项参数;若在经历多次迭代后δ满足精度要求,则视为神经网络训练完成。
1.3 MVO优化BP神经网络原理BP神经网络的训练会以误差梯度下降的方式更新网络参数,当模型复杂时可能会造成梯度消失,从而使模型无法收敛。另外,由于网络的权值是通过沿局部改善的方向逐渐进行调整的,会使算法陷入局部极值,权值收敛到局部极小点,从而导致网络训练失败。此外,BP神经网络对初始网络权重非常敏感,以不同权重初始化网络,往往会收敛于不同的局部极小值。为此,本文利用MVO算法可在全局空间多个区域内寻求最优解的特性,优化BP神经网络的连接权和神经元阈值,进而采用优化后的连接权和神经元阈值进行BP神经网络模型训练,从而提高算法收敛速度和拟合预测精度。图 2为MVO-BP算法流程。
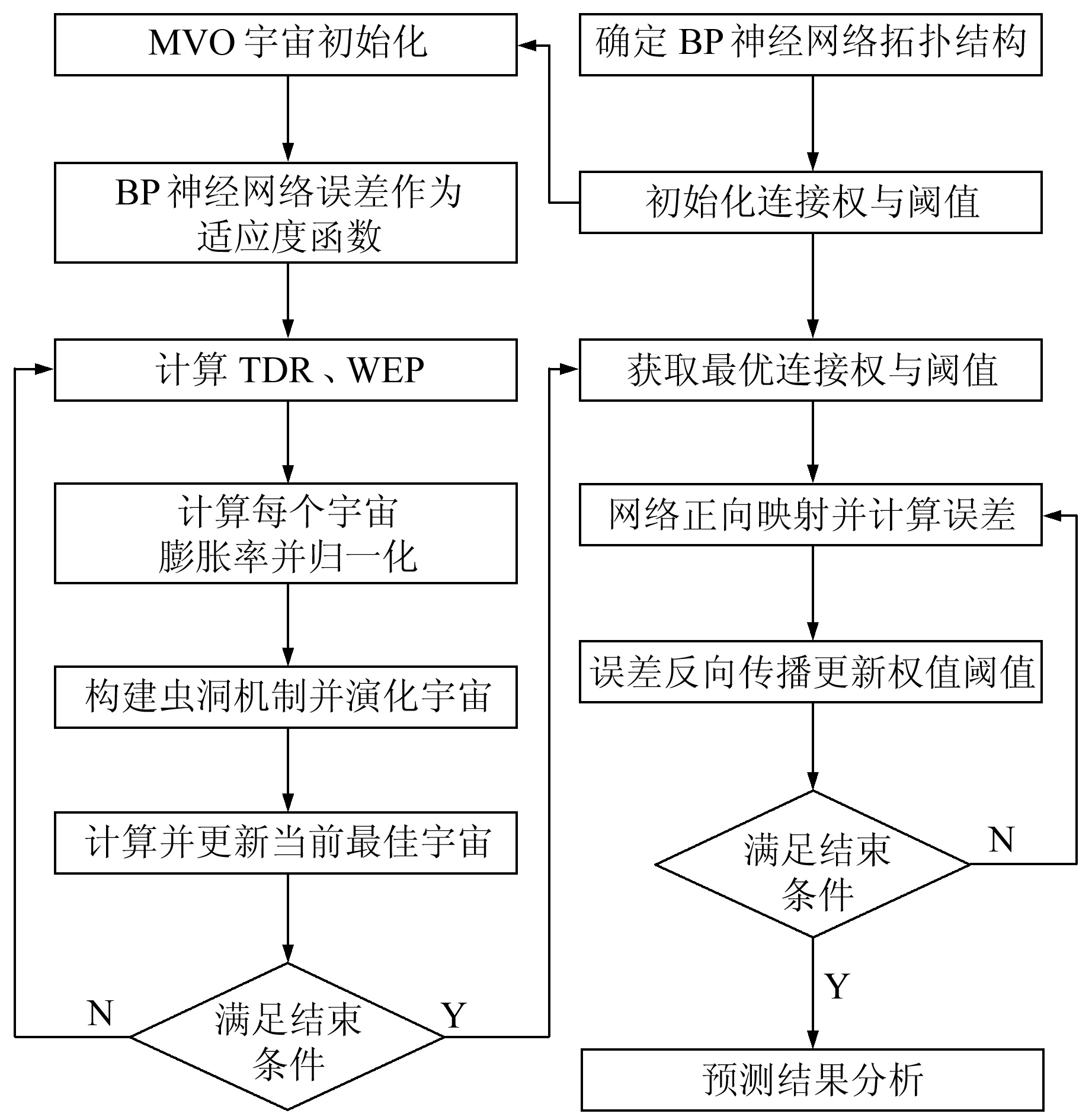
|
图 3 MVO-BP算法流程 Fig. 3 Flow chart of MVO-BP algorithm |
以GNSS高程异常拟合为例构建MVO-BP拟合预测模型,模型建立步骤如下:
1) 确定网络结构。假设有n个GNSS高程异常样本点,则训练样本数据组为P={P1, P2, …, Pn},其中Pi={xi, yi, hi},将训练样本点的平面坐标(xi, yi) 作为训练输入值,将对应点的高程异常hi作为训练输出的目标值,则可确定输入层神经元节点数为2,输出层神经元节点数为1。隐含层节点一般为1~15范围内的自然数,本文通过枚举法选择具有最小均方根误差的隐含层节点数,确定隐含层节点数为5。
2) 数据预处理。将训练样本数据组P归一化到[0, 1]区间,得到初始化的BP神经网络连接权与神经元阈值数组U。
3) 多元宇宙初始化。基于数组U初始化多元宇宙种群数n、当前演化周期T、最大演化周期Tmax,由式(2)和式(3)初始化旅程距离速率TDR与虫洞存在概率WEP。
4) 构建多元宇宙演化机制。由式(4)构建多元宇宙物体通过黑洞/白洞轨道传递机制,由式(6)构建多元宇宙物体通过虫洞传递机制。
5) 多元宇宙演化。在MVO迭代周期内,以BP神经网络的连接权与神经元阈值作为多元宇宙待优化数组 U ,以BP神经网络训练集与测试集整体均方误差的平均值作为MVO适应度函数,计算每个宇宙的膨胀率(适应度),并根据白洞/黑洞轨道及虫洞机制持续更新当前最佳宇宙位置,若达到最大迭代数Tmax,则输出当前最优宇宙,即优化后的数组 U 。
6) BP神经网络训练。采用包含最优连接权与阈值的数组 U 及归一化后的样本数据P进行训练,若训练结果小于训练目标最小误差,或达到设定的最大训练次数,则视为神经网络训练完成。
7) 插值预测。步骤1)~6)已完成MVO-BP神经网络的拟合预测模型构建,在训练好的模型中输入测区内任意待预测点的平面坐标(x, y),即可求得其高程异常值。
2 工程实例分析为验证MVO-BP算法在GNSS高程拟合中的有效性及其在不同地形的适用性,分别选取两个地貌特征不同的测区进行算例分析,其中算例1为地貌相对平坦的沿海带状区域,算例2为地势复杂且包含喀斯特地貌的内陆面状区域。
2.1 沿海带状区域 2.1.1 数据来源采用2006年杭州跨海大桥工程实例中39个GNSS水准重合点进行算例分析(三等及以上水准测量精度要求)[10]。点位整体呈带状分布,长度约为36 km,宽度约为30 m。选取其中28个点进行拟合建模处理,选取11个GNSS水准重合点作为高程异常拟合的外部检查点,点位分布情况见图 3。由于参与建模的点较少,将多元宇宙种群数n设置为10,为保证计算结果收敛前尚未达到最大演化周期,最大演化周期Tmax设置为30。图 4为MVO收敛曲线,由图可知,在演化周期为25之前算法已初步收敛。
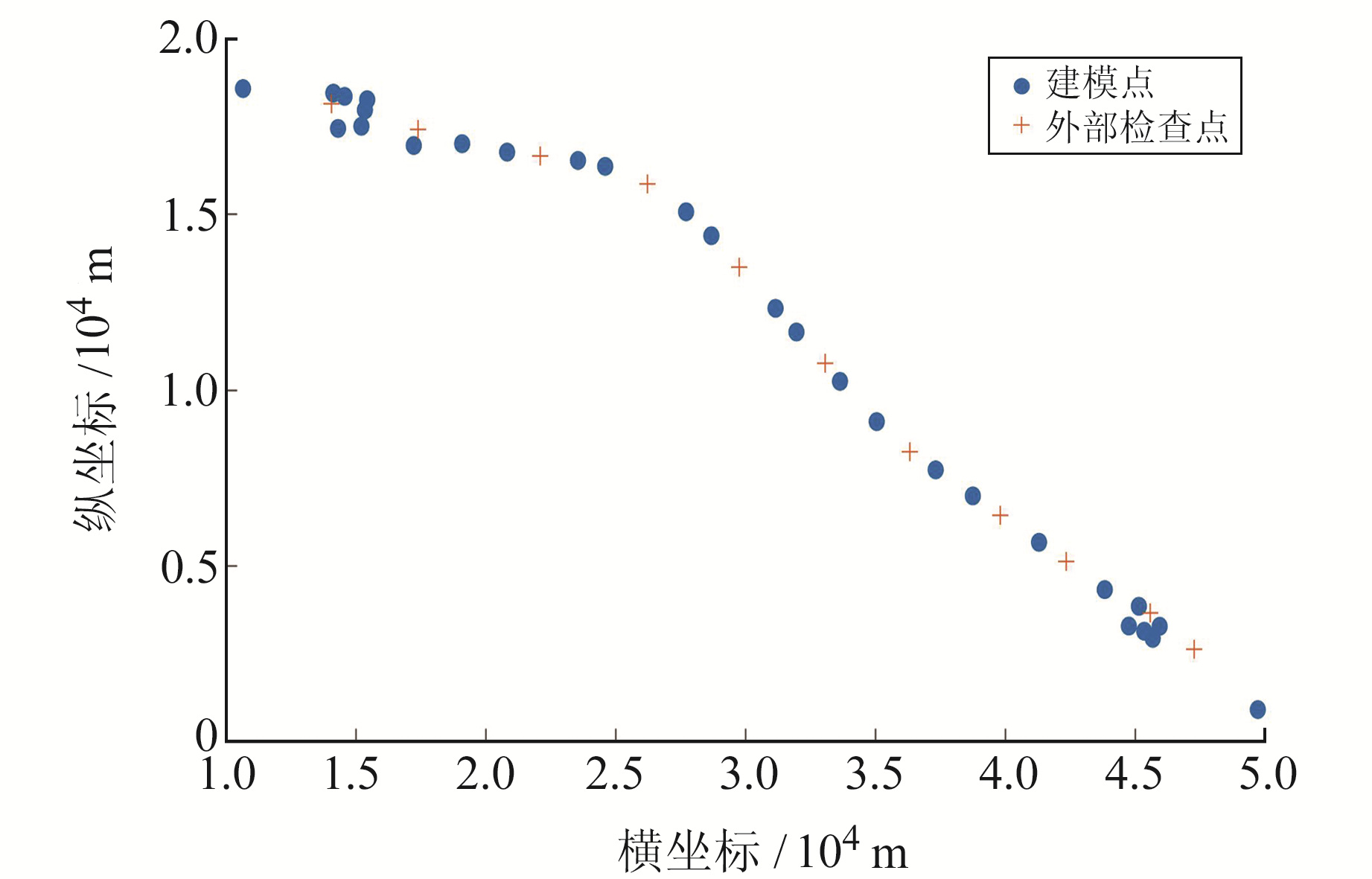
|
图 3 带状区域点位分布 Fig. 3 Point distribution of the banded area |
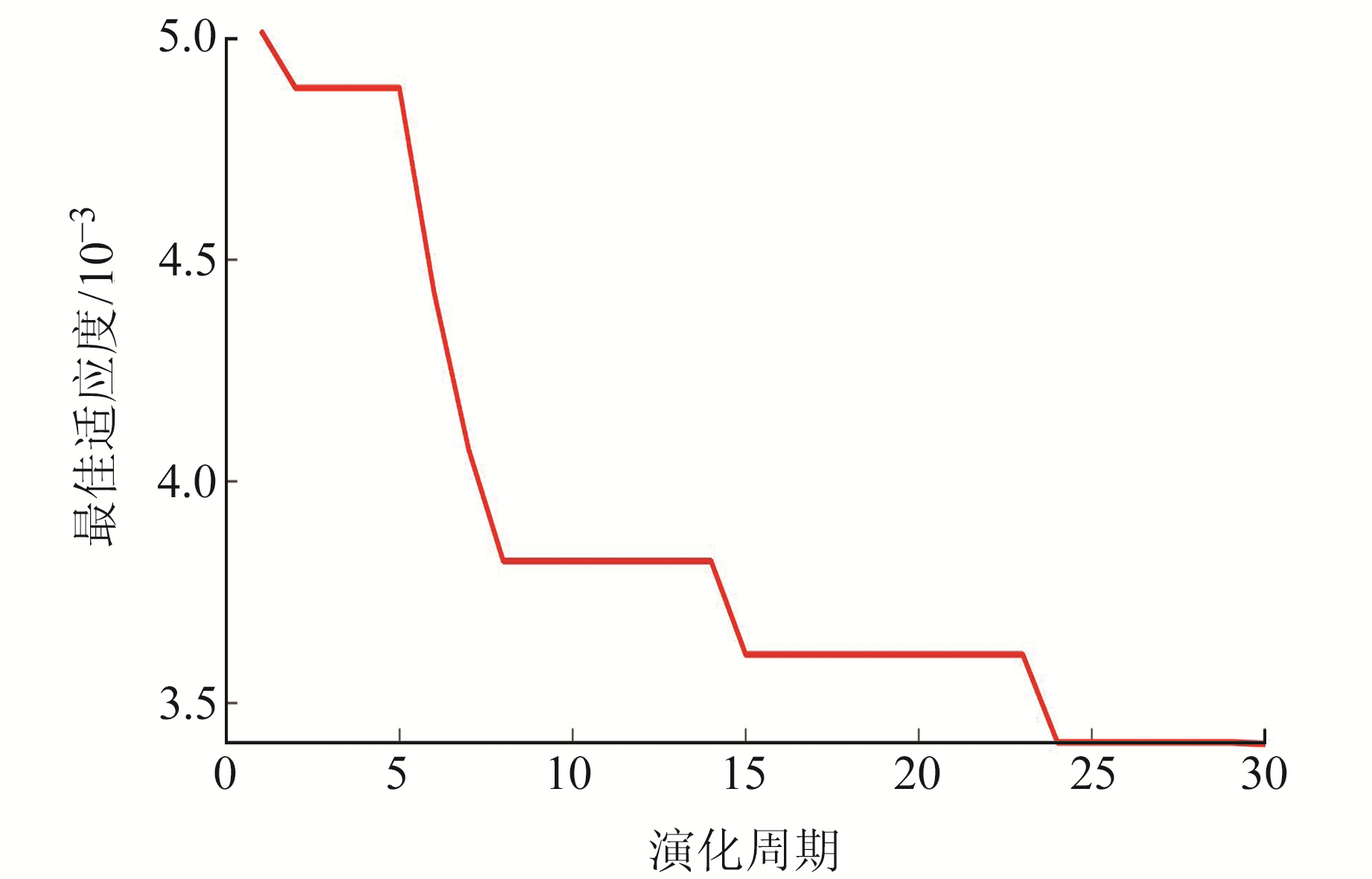
|
图 4 MVO收敛曲线 Fig. 4 MVO convergence curve |
为比较MVO-BP神经网络算法与其他常规算法的优劣,验证MVO-BP高程异常拟合模型的拟合精度及有效性,使用相同数据,将其与常规的BP神经网络及常用的多面函数法进行对比分析,并分别统计采用3种方法得到的高程异常值与残差,结果见表 1。
|
|
表 1 不同拟合模型检核点的预测结果 Tab. 1 The prediction results of checkpoints of different fitting models |
由表 1可知,多面函数法残差变化区间为-3.0~3.3 cm,常规BP神经网络残差变化区间为-2.4~3.1 cm,MVO-BP神经网络残差变化区间为-1.8~2.3 cm。相比之下,MVO-BP神经网络法拟合残差变化区间较小,外符合精度较高。图 5为3种方法的高程异常值柱状图,可直观分析其变化趋势。
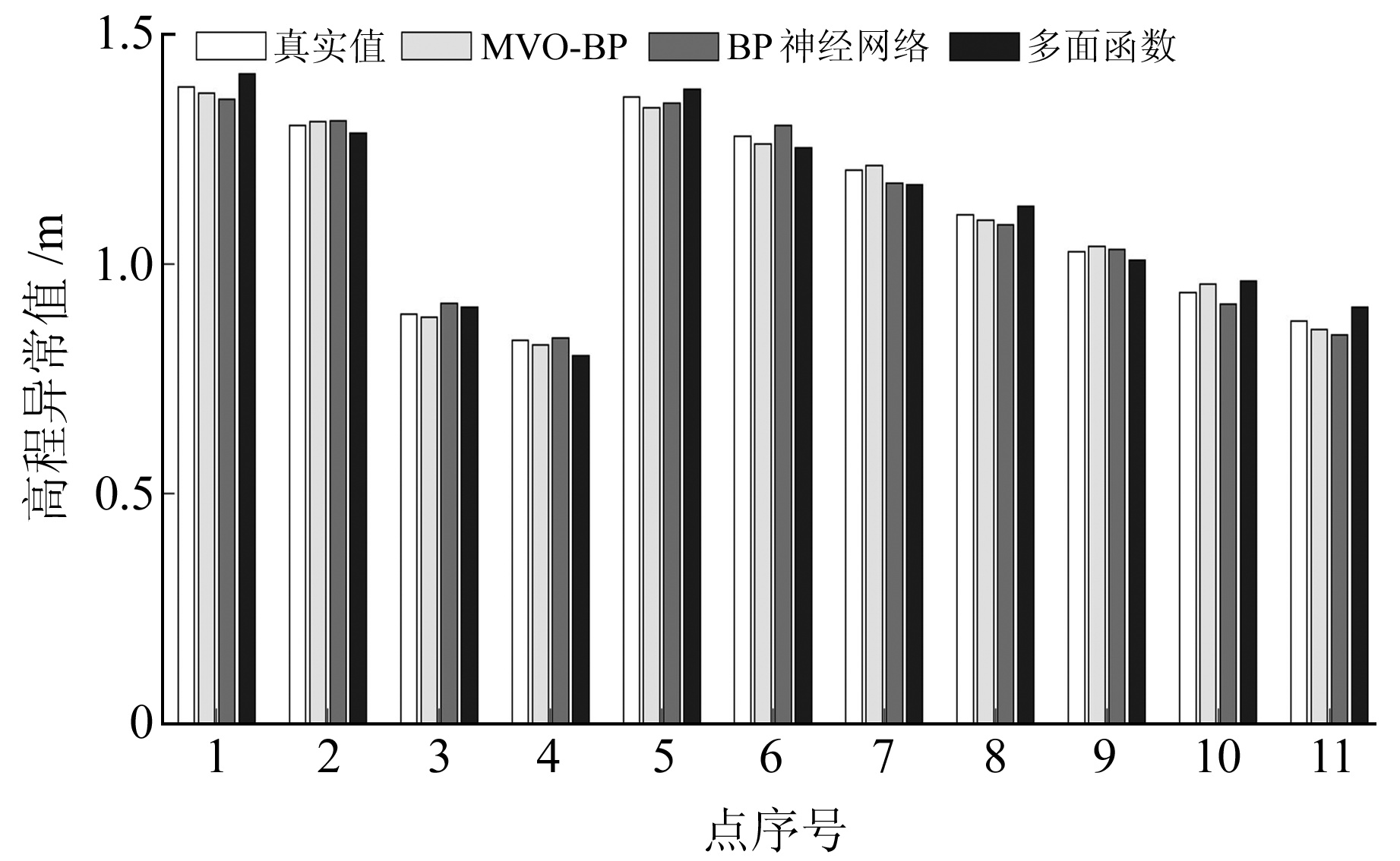
|
图 5 不同方法的高程异常预测值对比 Fig. 5 Comparison of elevation anomaly prediction values of different methods |
结合表 1与图 5可知,3种方法对于5号点与11号点预测值与真实值的误差均相对较大,其中5号点与最近2个建模点的总间距为3 219.5 m,11号点与最近2个建模点的总间距为4 473.0 m,二者均大于其他检查点,可能是这两个点与建模点间距较远导致预测精度偏低。而相比于传统的BP神经网络与多面函数法,在11个检核点中MVO-BP法有9个点的高程异常预测值与真实值最为接近,表明BP神经网络在经过MVO优化后精度有所提高,整体上MVO-BP法高程异常拟合结果的可靠性更高。
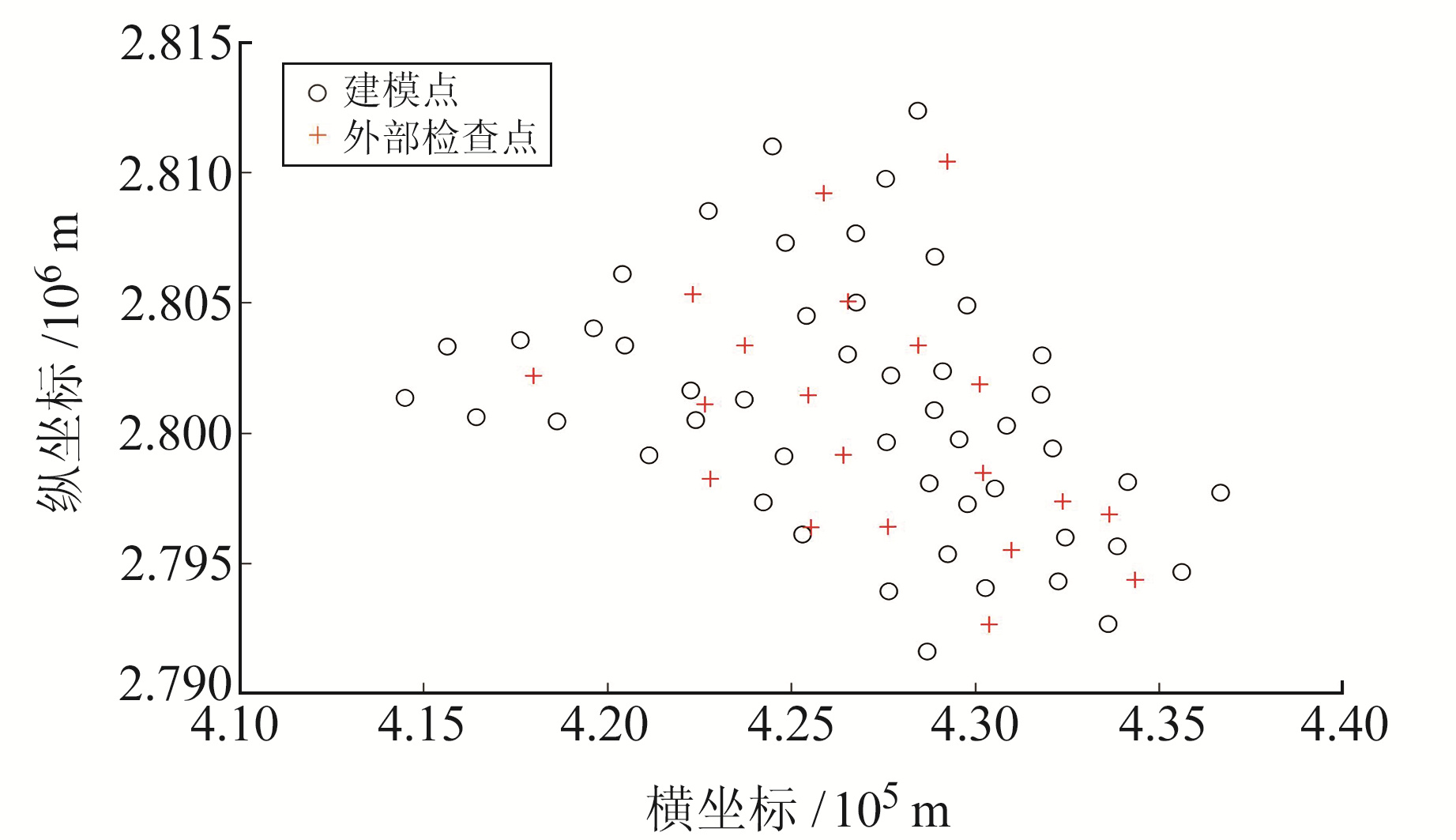
2.2 内陆面状地区 2.2.1 数据来源为进一步验证本文算法在地貌复杂的面状区域的有效性,采用广西桂林市某区域(喀斯特地貌)74个GNSS水准点重合点进行算例分析(四等及以上水准测量精度要求),重合点点位分布较均匀(图 6),间隔2~2.5 km,覆盖面积约300 km2。均匀选取54个重合点进行拟合建模处理,另外选取20个符合水准测量精度要求的点位作为高程异常拟合的外部检查点。
|
图 6 面状区域的点位分布 Fig. 6 Point distributionof the planar region |
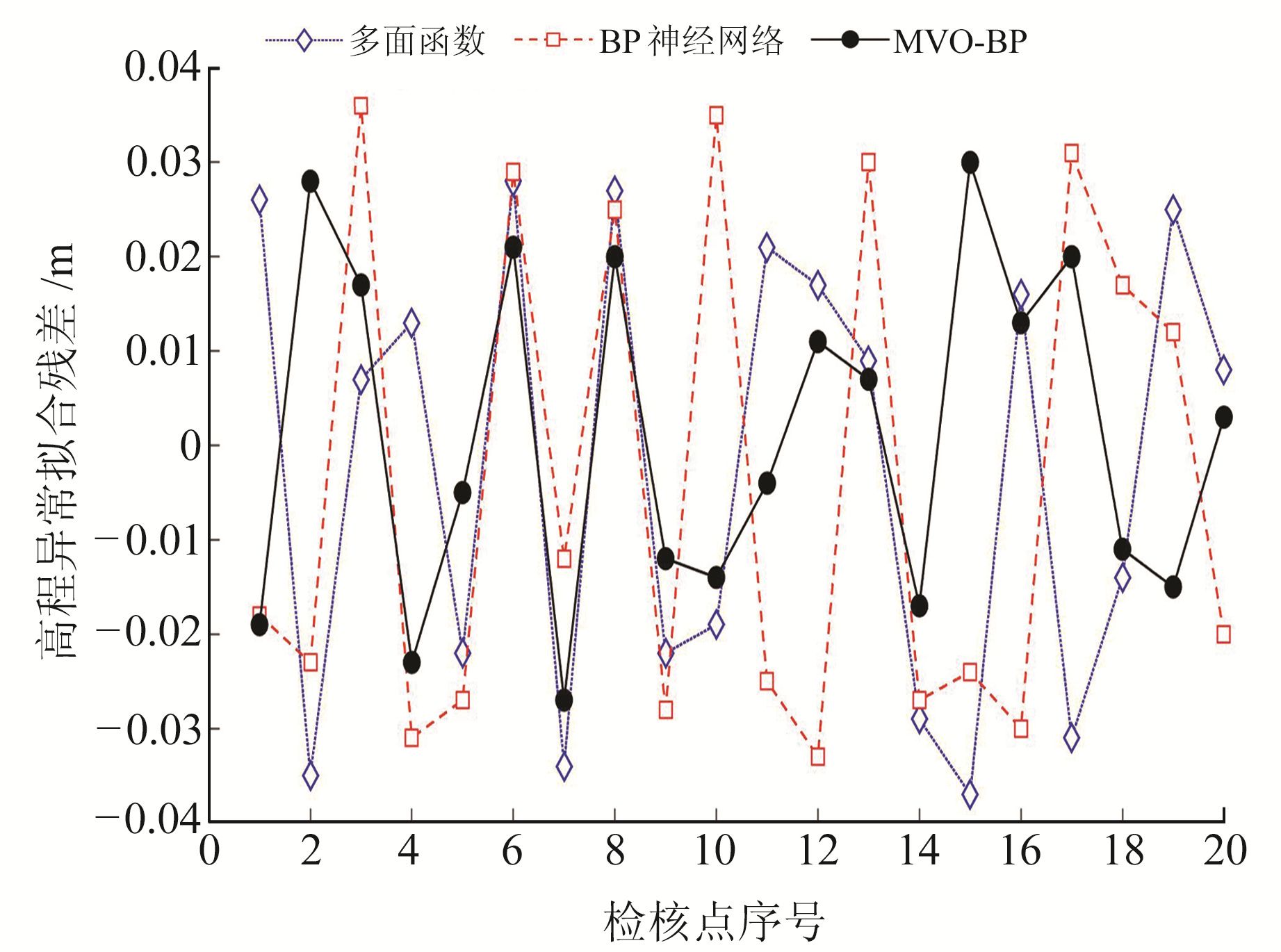
由于建模点数较多,为保证算法收敛,将多元宇宙种群数n设置为20,最大演化周期为30,构建内陆面状地区的MVO-BP神经网络高程异常拟合模型,并求得外部检核点的高程异常预测值,同时分别统计MVO-BP神经网络、BP神经网络及多面函数法预测值与真实值的残差,结果见表 2。为直观了解3种不同方法应用于内陆面状区域的高程异常拟合结果,绘制残差折线图(图 7)。
|
|
表 2 不同拟合模型检核点的预测结果 Tab. 2 The prediction results of checkpoints of different fitting models |
|
图 7 不同方法的检核点残差 Fig. 7 Check point residuals of different methods |
结合图 7与表 2可知,在本算例中多面函数法残差变化区间为-0.037~0.028 m,精度略高于常规BP神经网络法;而MVO-BP神经网络法残差变化区间为-0.027~0.030 m,波动范围最小。在3种方法中MVO-BP神经网络法的外符合精度最高,达到±1.76 cm,这主要是因为MVO算法优化了BP神经网络的连接权和神经元阈值,可避免神经网络误差反向传播时梯度消失和陷入局部最小值的情况,从而提高MVO-BP的高程异常拟合精度。
结合表 1可以看出,BP神经网络法与MVO-BP神经网络法在地貌复杂的内陆面状区域的高程异常拟合精度低于沿海带状区域;而多面函数法与MVO-BP法在算例2中均取得了良好的高程异常拟合精度,其中MVO-BP法在算例2中的精度比常规BP神经网络法提高33.6%,表明在MVO算法的优化下,BP神经网络应对复杂情况的适用性与精度得到了提高。
3 结语本文提出一种基于MVO的BP神经网络优化方法(MVO-BP),利用具备全局快速寻优特性的MVO算法求取BP神经网络各层之间可靠的神经元阈值与连接权,从而使神经网络预测模型具备更高的精度。利用实际数据,将本文算法与常规BP神经网络法及常用的多面函数法进行对比,经统计分析发现,MVO-BP神经网络法的精度优于其他两种方法,但本文方法所需设置的初始参数较多,应合理选择初始参数以避免对结果产生较大影响。本文验证了MVO-BP神经网络算法在GNSS高程拟合中的有效性及其在不同地形中的适用性,可提供一种高程异常拟合新方法。
| [1] |
江博. 科技创新驱动: 我国北斗卫星导航与位置服务产业发展策略研究[D]. 武汉: 武汉大学, 2018 (Jiang Bo. Science and Technology Innovation Driven: Research on the Development Strategy of the Beidou Satellite Navigation and Position Service Industry in China[D]. Wuhan: Wuhan University, 2018)
(  0) 0) |
| [2] |
赫林, 李建成, 褚永海. 联合GRACE/GOCE重力场模型和GPS/水准数据确定我国85高程基准重力位[J]. 测绘学报, 2017, 46(7): 815-823 (He Lin, Li Jiancheng, Chu Yonghai. Evaluation of the Geopotential Value for the Local Vertical Datum of China Using GRACE/GOCE GGMS and GPS/Leveling Data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 815-823)
(  0) 0) |
| [3] |
谭江涛, 王章朋, 钟波, 等. 多面函数参数自适应选取方法在GPS高程拟合中的应用[J]. 大地测量与地球动力学, 2020, 40(8): 832-837 (Tan Jiangtao, Wang Zhangpeng, Zhong Bo, et al. Application of Self-Adaptive Parameter Selection for Multiquadric Function in GPS Elevation Fitting[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 832-837)
(  0) 0) |
| [4] |
任超, 梁月吉, 蓝岚, 等. 不同组合方法对GPS高程拟合的影响[J]. 大地测量与地球动力学, 2015, 35(6): 1036-1040 (Ren Chao, Liang Yueji, Lan Lan, et al. Influence of Different Combination Methods of GPS Elevation Fitting[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 1036-1040)
(  0) 0) |
| [5] |
彭中波, 高阳. BP神经网络在水下地形高程拟合的应用[J]. 重庆交通大学学报: 自然科学版, 2018, 37(11): 64-68 (Peng Zhongbo, Gao Yang. Application of BP Neural Network in Elevation Fitting of Underwater Terrain[J]. Journal of Chongqing Jiaotong University(Natural Science), 2018, 37(11): 64-68)
(  0) 0) |
| [6] |
张炎. 基于ABC-FOA-LSSVM的GNSS高程拟合方法研究[D]. 桂林: 桂林理工大学, 2020 (Zhang Yan. Research on GNSS Height Fitting Method Based on ABC-FOA-LSSVM[D]. Guilin: Guilin University of Technology, 2020)
(  0) 0) |
| [7] |
袁德宝, 张建, 赵传武, 等. 基于改进RBF神经网络的GNSS高程拟合[J]. 大地测量与地球动力学, 2020, 40(3): 221-224 (Yuan Debao, Zhang Jian, Zhao Chuanwu, et al. GNSS Height Fitting Based on Improved RBF Neural Network[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 221-224)
(  0) 0) |
| [8] |
潘魏. 多元宇宙优化算法及应用研究[D]. 南宁: 广西民族大学, 2017 (Pan Wei. The Research of Multi-Verse Optimization Algorithm and Its Application[D]. Nanning: Guangxi University for Nationalities, 2017)
(  0) 0) |
| [9] |
Mirjalili S, Mirjalili S M, Hatamlou A. Multi-Verse Optimizer: A Nature-Inspired Algorithm for Global Optimization[J]. Neural Computing and Applications, 2016, 27(2): 495-513
(  0) 0) |
| [10] |
杨天宇. 基于BP神经网络的GPS高程拟合及其在杭州湾跨海大桥中的应用[D]. 成都: 西南交通大学, 2006 (Yang Tianyu. The GPS Height Fitting Based on BP Neural Network and Its Application in Hangzhou Gulf Bridge[D]. Chengdu: Southwest Jiaotong University, 2006)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2022, Vol. 42
2022, Vol. 42


