2. 长安大学地学与卫星大数据研究中心,西安市雁塔路126号,710054
精确认知和改正观测误差有助于提升全球卫星导航系统GNSS的服务性能。其中,导航卫星天线相位中心偏差改正模型PCC会对卫星轨道、钟差、参考框架尺度、测站坐标及天顶对流层延迟等产生系统性影响[1]。卫星精密轨道确定的动力学模型基于质心系统,而观测值则以天线相位中心为参考点。在进行高精度定轨定位时,需要将载波和码的观测值统一归算到卫星质心上,因此导航卫星PCC改正是前提条件之一[2],而PCC改正由天线相位中心偏差PCO和天线相位中心变化PCV构成。自1996年起,相对相位中心模型被广泛应用于GNSS数据处理,然而该类模型仅采用与卫星类型相关的PCO,忽略了卫星端PCV,由此引起的参考框架尺度存在超过1 ppb的系统偏差[1, 3]。为解决这一问题,国际GNSS服务组织IGS于2006年起采用绝对相位中心模型[4],并不定期发布通用天线格式ANTEX文件。由于缺乏卫星厂商提供的PCC改正值,早期GPS和GLONASS的PCC协议值均由地面观测数据在轨估计得到,并固定到IGS或国际地球参考框架ITRF中[5]。针对我国北斗卫星导航系统BDS,特别是北斗二号卫星,国内外学者对接收机和卫星端PCC标定方法[6-7]及其对定轨定位的影响[8-10]等进行了深入探讨。
为促进GNSS高精度数据处理和应用,新兴的卫星导航系统,如欧盟的Galileo和中国的BDS等,均以官方发布了包括天线相位中心文件在内的卫星元数据。中国卫星导航系统管理办公室CSNO授权发布的北斗三号BDS-3天线相位中心文件包含4个公开服务OS频点(B1I:1 561.098 MHz;B3I:1 268.52 MHz;B1C:1 575.42 MHz;B2a:1 176.45 MHz)的卫星PCO官方发布值,而PCV尚未公布,其中B1I/B3I为北斗二号历史频点,B1C/B2a为北斗三号新频点。有研究表明,CSNO发布的北斗三号PCO与IGS14框架尺度保持较好的一致性[11],然而由于历史数据交换等原因,目前IGS采用的北斗三号卫星PCO协议值仍基于非官方推荐值[12]。尽管卫星端PCO可基于地面台站数据进行校正,但由于该参数与对流层延迟、测站高度和接收机端PCO高度耦合,较难获得稳定独立的解算结果[13],高精度定轨和定位PCC信息的不一致将限制北斗服务性能的进一步提升。针对此问题,本文对比基于IGS和CSNO北斗三号PCO改正模型的差异,探求PCO模型差异和不同频点观测值组合对精密定轨定位的影响,并通过实测数据进行分析和验证。
1 卫星天线相位中心模型卫星PCO是卫星质心到天线平均相位中心的偏差值。卫星星固坐标系的原点位于卫星质心,Z轴指向地心,Y轴为卫星太阳帆板的旋转轴,X、Y与Z轴构成右手坐标系。因此,PCO可由x向偏差(x-offset)、y向偏差(y-offset)、z向偏差(z-offset)3个分量进一步表述。由于星固系Z轴(天线方向)始终指向地心,所以PCO的z向通常被称为竖直方向PCO,X轴和Y轴天线相位中心偏差称为水平方向PCO。考虑到最终的几何观测值为星地距离,进一步引入星固系与惯性系的转换矩阵,其数学模型可表示为:
| $ \boldsymbol{r}^{\mathrm{s} \text { ant }}=\boldsymbol{r}^{\mathrm{s}}+\boldsymbol{R}_{\mathrm{srf} \rightarrow \mathrm{cis}} \boldsymbol{P} $ | (1) |
式中,rs, ant为卫星天线相位中心在惯性坐标系的向量,rs为卫星质心在惯性系下的向量,P=[x-offset y-offset z-offset]T为卫星星固坐标系下的PCO向量,Rsrf→cis为星固坐标系到惯性坐标系的旋转矩阵。在不考虑PCV影响的情况下,可利用卫星PCO改正观测值,进而构建观测方程。
由于CSNO和IGS发布的PCO改正值包含北斗三号卫星不同频点的模型值,在实际数据处理时可分别对2个频点的观测数据进行PCO改正,然后进行无电离层(ionosphere-free, IF)组合。为了方便对比,将单频点PCO进行B1I/B3I及B1C/B2a组合,限于篇幅,本文仅展示IGS协议值导出的PCO模型,其具体数值如表 1(单位mm)所示。考虑到北斗三号卫星包含地球静止轨道(GEO)、倾斜地球同步轨道(IGSO)和中圆轨道(MEO),且上述卫星由中国空间技术研究院(CAST)和中国科学院微小卫星创新研究院(SECM)分别负责研发制造,本文将其归为MEO-CAST、MEO-SECM和IGSO-CAST三个卫星类别。由于北斗三号GEO卫星(C59)仅播发B1I和B3I两个频点,因此本文的分析和对比仅针对北斗三号IGSO和MEO卫星。
|
|
表 1 基于IGS协议值导出的B1I/B3I和B1C/B2a无电离层PCO模型 Tab. 1 B1I/B3I and B1C/B2a ionosphere-free PCO models derived based on IGS conventional values |
为进一步对比CSNO与IGS的PCO模型,给出两者基于B1I/B3I和B1C/B2a组合的PCO差异情况,如图 1所示,按照制造厂商和运行轨道分别统计出MEO-CAST、MEO-SECM和IGSO-CAST卫星的均值,结果如表 2(单位mm)所示。由图 1和表 2可知:1)针对同一类型无电离层组合PCO改正值,CSNO与IGS水平方向PCO的差异不显著,除C25-C26、C45-C46和C34-C35外其余均在20 mm以内,相比于MEO,IGSO卫星水平方向PCO差异更小。对于垂直方向PCO,多数卫星差异在100 mm以内,其统计均值MEO-CAST卫星约为60 mm、MEO-SECM卫星小于10 mm、IGSO-CAST卫星为20~30 mm。采用B1I/B3I无电离层组合CSNO与IGS PCO模型的差异与采用B1C/B2a无电离层组合CSNO与IGS PCO模型的差异变化趋势较为一致。2)基于相同PCO改正文件,MEO-CAST卫星与MEO-SECM卫星在竖直方向PCO的差异显著,但两者在水平方向PCO的差异均值小于5 mm。此外,采用B1I/B3I无电离层组合和B1C/B2a无电离层组合的MEO PCO模型相较于IGSO卫星差异更小,CAST IGSO卫星B1I/B3I和B1C/B2a在竖直方向PCO的差异接近200 mm,表明北斗三号MEO和IGSO卫星平台或星上荷载存在差异。
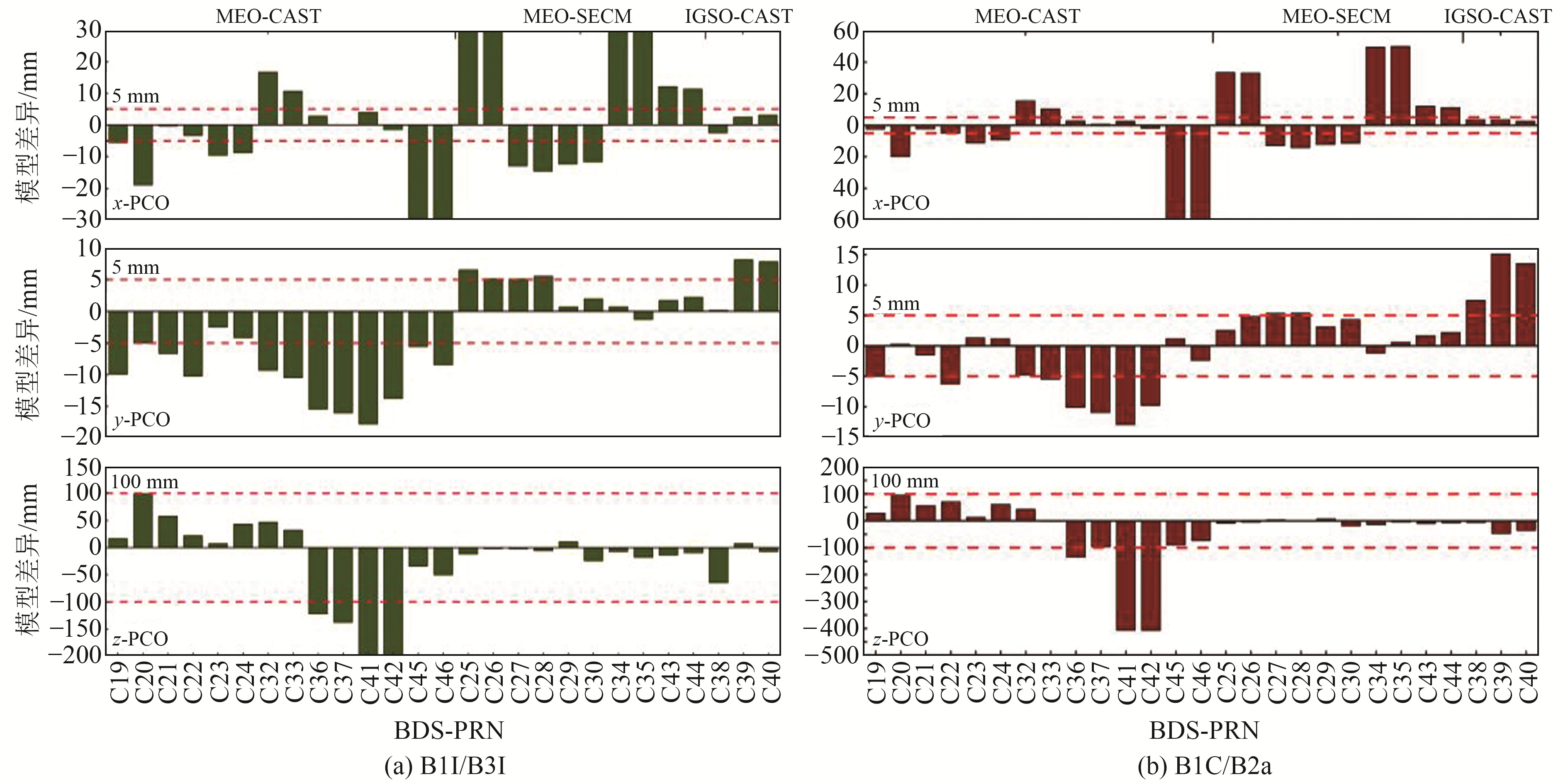
|
图 1 CSNO和IGS天线相位中心改正模型差异 Fig. 1 Differences between CSNO and IGS antenna phase center correction models |
|
|
表 2 基于B1I/B3I和B1C/B2a的IGS与CSNO PCO模型差异统计 Tab. 2 PCO models difference statistics between IGS and CSNO based on B1I/B3I and B1C/B2a |
自2020年北斗三号开通全球服务以来,包括IGS和iGMAS在内的地面设备持续更新接收机硬件版本(如TRIMBLE Alloy、Javad TRE_3和Septentro POLARX5等),以实现对北斗三号卫星的跟踪观测。截至2020年底,iGMAS所有地面站均具备北斗三号跟踪观测能力,IGS也已有超过200个测站公开北斗三号数据。然而,大多数IGS测站仅在B1I和B3I两个频点跟踪北斗三号卫星,无B1C和B2a观测值。因此,为了保证B1C/B2a和B1I/B3I对比实验的一致性,本文仅选取同时具备北斗三号卫星4个OS频点观测数据的地面跟踪站,其中包含全球IGS-MGEX和iGMAS共约75个测站,测站分布如图 2所示。2021-01-01~31北斗三号卫星对上述地面测站的每日平均观测值个数如图 3所示,由图可见,新发射的北斗三号卫星(如C38-C47)对应的观测值明显少于其他卫星。以300 s为采样间隔,多数MEO卫星的日平均地面观测数约为5 000个,而新近发射的MEO卫星个数仅为其1/2。尽管北斗三号C38-C40三颗IGSO卫星受益于亚太地区的覆盖能力,其地面观测值数量仍少于早期发射的MEO卫星。这表明部分地面测站接收机具备了北斗三号卫星的跟踪能力,但其接收机版本仍需进一步更新,以保证充分的观测通道,实现对全部北斗三号卫星的跟踪。
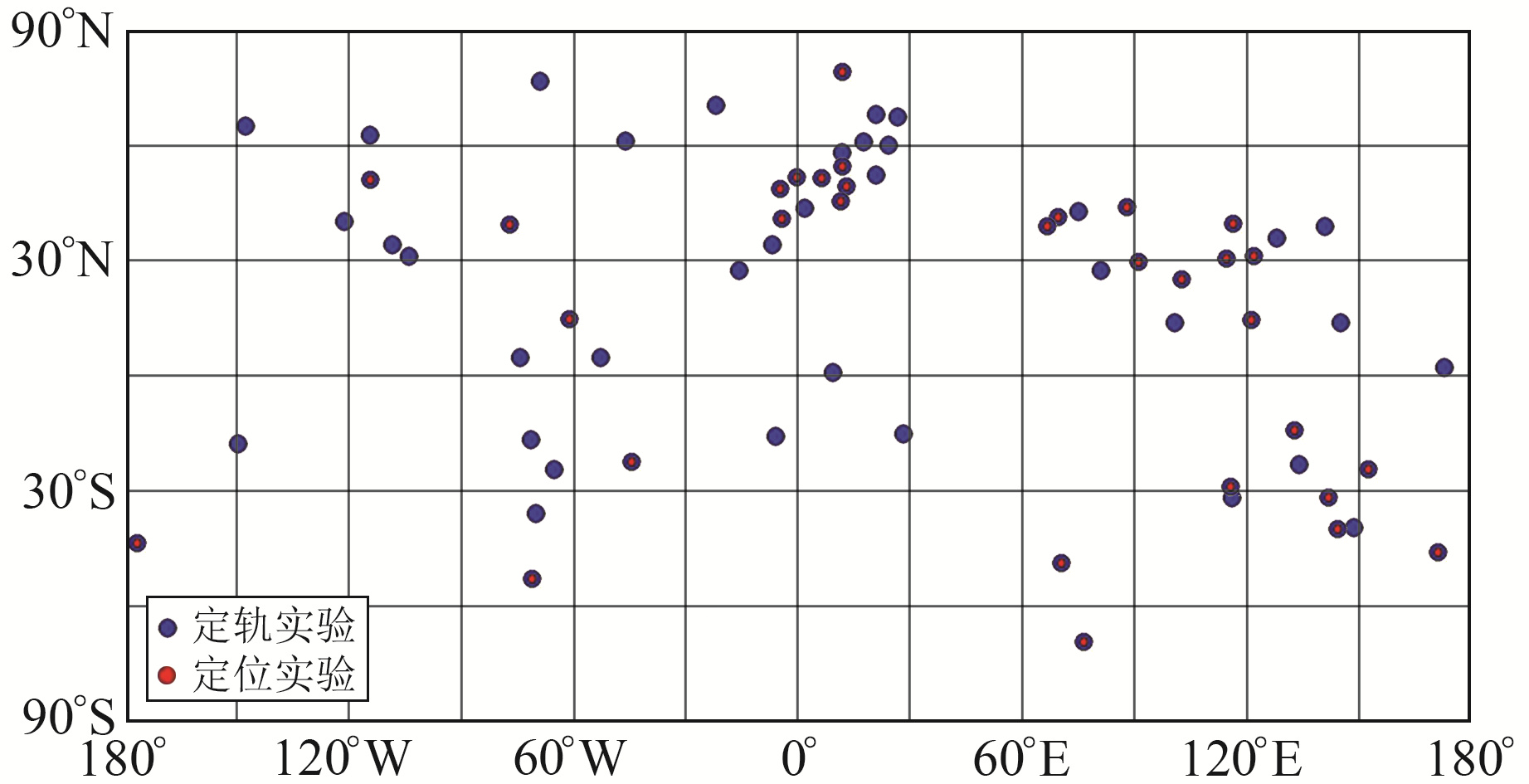
|
图 2 北斗三号卫星精密定轨及定位实验站点分布 Fig. 2 BDS-3 satellite precision orbit determination and positioning site distribution |
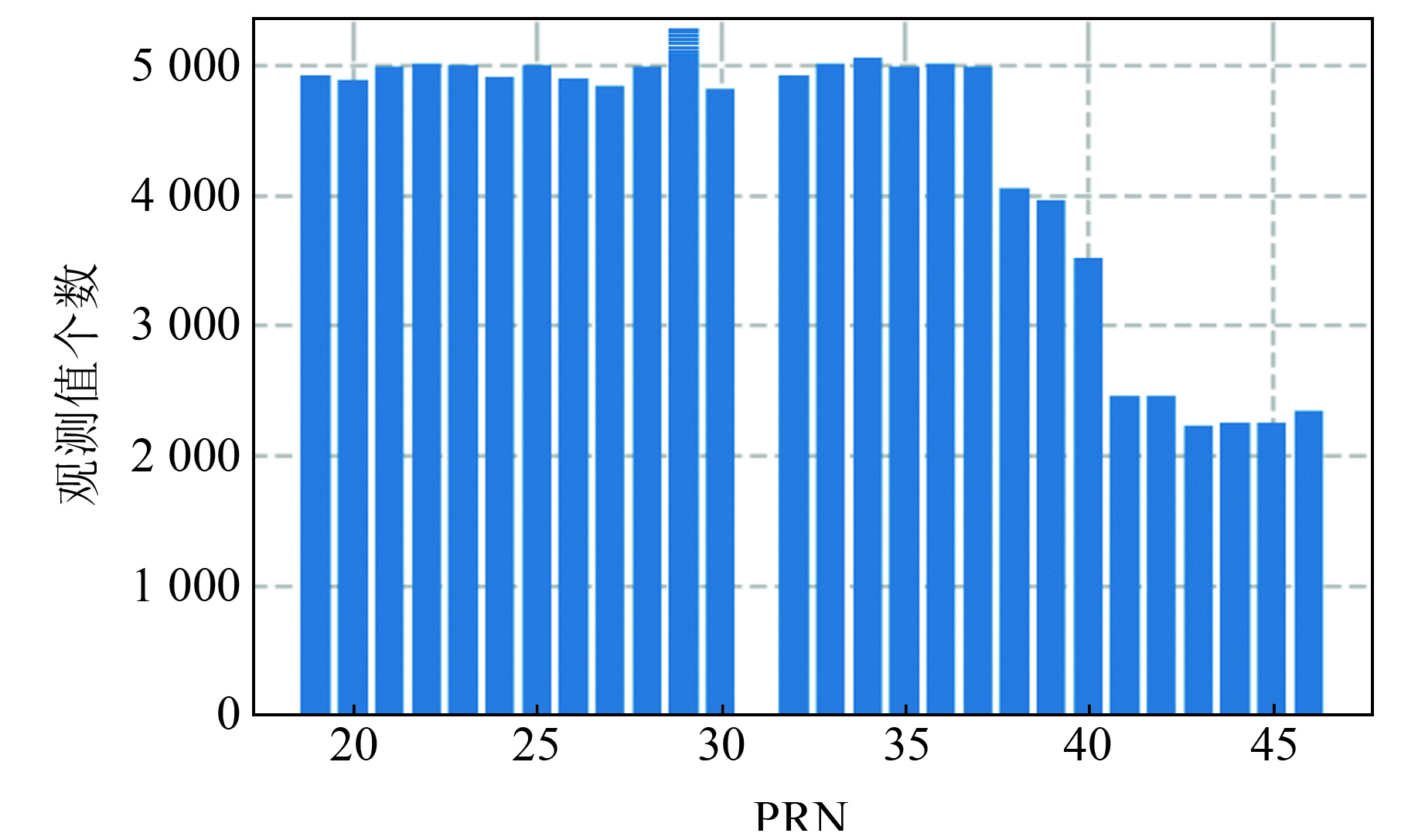
|
图 3 北斗三号卫星2021年年积日1~31的平均观测值个数 Fig. 3 Average number of observations of doy 1~31 in 2021 for BDS-3 satellites |
本文数据处理基于PANDA(position and navigation data analyst)软件的改进版本,卫星定轨所采用的观测数据采样间隔为300 s,截止高度角为10°,定轨弧长为1 d。除地球重力场、N体引力和地球固体潮等保守力摄动外,考虑的非引力模型包括太阳光压模型和地球反照辐射压。考虑到先验光压模型可以提升定轨性能,本文在精密定轨时采用了5参数ECOM+先验光压模型[14]。在观测模型方面,低阶电离层延迟可通过双频IF组合消除,测站天顶对流层延迟采用先验模型改正和参数估计方法,湿延迟在天顶方向每2 h估计1次。测站坐标依据IGS及iGMAS周解的snx文件坐标进行紧约束。表 3为本文采用的具体定轨策略。
|
|
表 3 精密定轨策略 Tab. 3 Precision orbit determination setting strategies |
为分析和验证PCO对精密定轨和定位的影响,本文共设计4组对照实验:1)基于IGS PCO模型的B1I/B3I频点IF组合观测模型定轨(S1);2)基于IGS PCO模型的B1C/B2a频点IF组合观测模型定轨(S2);3)基于CSNO PCO模型的B1I/B3I频点IF组合观测模型定轨(S3);4)基于CSNO PCO模型的B1C/B2a频点IF组合观测模型定轨(S4)。卫星定轨验后残差作为常用的内符合检核手段,常用作定轨精度评定的指标,观测值噪声、多径误差及未被有效吸收的轨道动力学模型和几何观测模型误差均会在定轨验后残差中体现。基于上述4组对照实验,本文将BDS-3卫星的载波相位残差(LC)和伪距残差(PC)汇总,并按照卫星生产厂商和类型给出形影伪距残差和载波残差RMS值,其结果如表 4(单位mm)所示。
|
|
表 4 北斗三号卫星定轨PC和LC验后残差RMS Tab. 4 Beidou-3 satellite orbiting PC and LC post-check residual RMS |
对比基于相同观测值频点的实验结果(S1/S3或S2/S4)可以看出,相较于IGS,CSNO PCO模型LC和PC的定轨残差统计值均有所改善,但改善程度不显著。伪距PC验后残差差异最大为3 mm,载波LC验后残差差异最大为0.2 mm。考虑到定轨过程中卫星钟差、模糊度、动力学参数和测站坐标等作为未知数解算,上述待估参数均会吸收各类几何观测误差,因此尽管采用CSNO PCO模型的定轨验后残差略小,但相较于IGS,其残差改善不显著。
对比基于相同PCO模型的不同观测值频点实验结果(S1/S2或S3/S4)可以看出,PC或LC的残差统计值主要受无电离层组合系数量值的影响。需要注意的是,尽管验后残差统计值明显与无电离层组合系数相关,但其同时也受具体频点观测噪声的影响,而不同频点伪距观测值噪声水平与卫星信号调制方式、信号强度和环境等因素相关,因此不同频点伪距观测值相较于载波噪声水平存在差别。统计结果表明,基于B1C/B2a观测值的定轨残差均显著优于B1I/B3I。
除定轨验后残差,轨道相邻2 d重叠弧段(也称轨道天不连续性或轨道闭合差)是轨道精度检核的常用方式,其计算方式为直接对相邻2 d子夜点处解算的轨道作差。图 4为各卫星重叠弧段在轨道切向、法向及径向的RMS值,其统计结果如表 5(单位mm)所示。综合图 4和表 5可知,北斗三号MEO卫星的重叠弧段轨道精度优于IGSO卫星。一方面是由于北斗三号卫星的观测值数量相对较少,其观测值几何强度受限(图 3);另一方面是因为IGSO较高的轨道高度导致其相较于MEO天底角范围更小,参数相关性更强,轨道参数与其他待估参数更难分离。
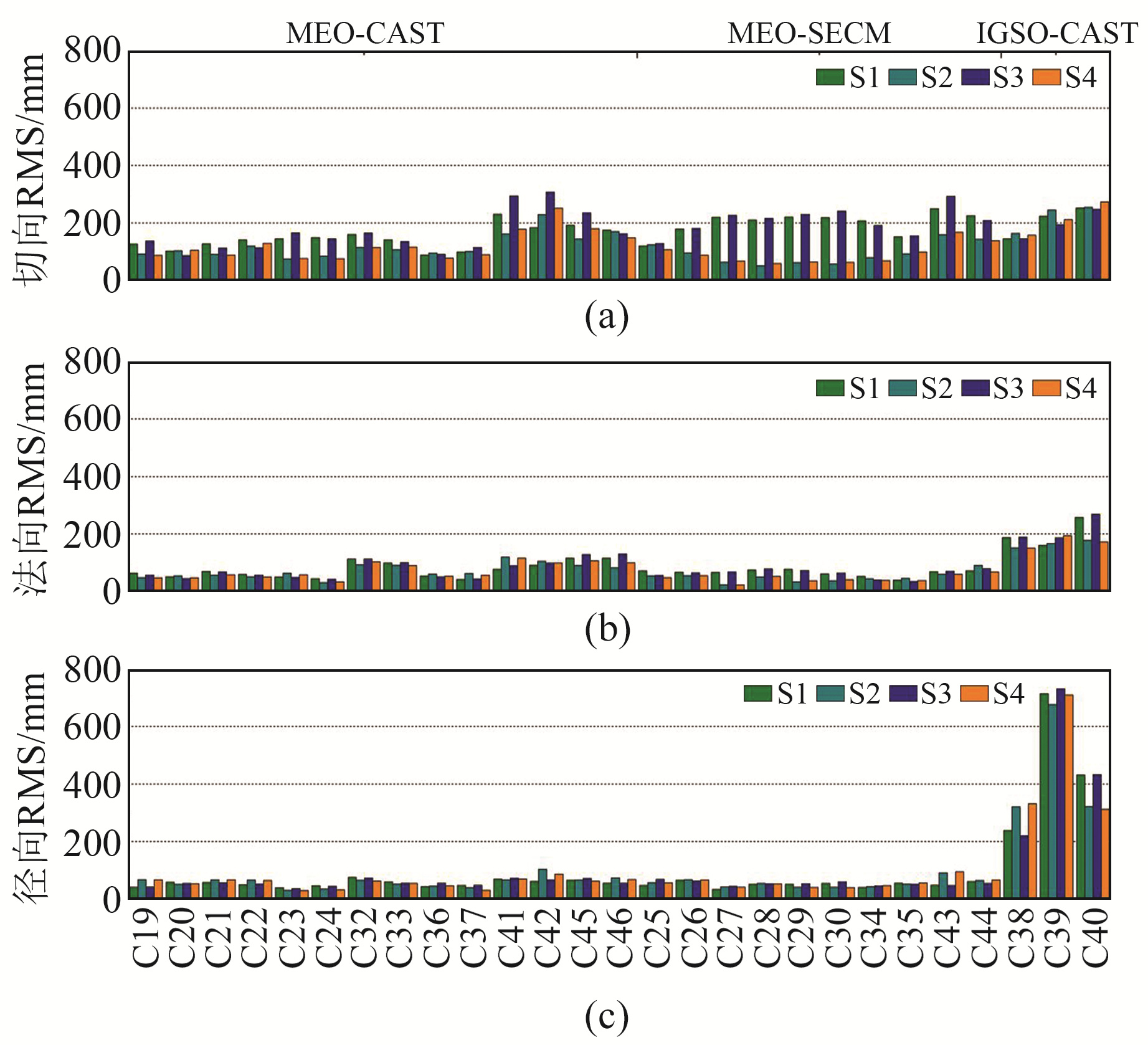
|
图 4 北斗三号卫星相邻2 d的重叠弧段轨道差异 Fig. 4 Overlapping arc segment orbit differences between two days adjacent of the BDS-3 satellite |
|
|
表 5 BDS-3各类型卫星相邻2 d的重叠弧段轨道RMS均值 Tab. 5 RMS mean values of overlapping arc orbits for two days adjacent to each type of BDS-3 satellite |
对比基于相同观测值频点的轨道重叠弧段结果(S2/S4)可以发现,相较于IGS协议值,CSNO PCO模型可以获得更优的定轨精度。对比基于相同PCO模型的不同观测值频点轨道重叠弧段结果发现,B1C/B2a无电离层组合的重叠弧段精度明显优于B1I/B3I无电离层组合,这与验后残差的结论一致。综上所述,无论是采用IGS还是CSNO的PCO模型,相较于B1I/B3I,基于B1C/B2a解算的轨道MEO-CAST和MEO-SECM卫星轨道重叠弧段3D RMS提升幅度约为20%和56%。该结果相较于文献[15]的提升幅度更加显著,原因是本文与其在定轨弧长和测站数量等定轨策略上存在差异。对比S1和S3的轨道重叠弧段精度可以看出,尽管IGSO-CAST轨道径向精度稍有减小,但3D RMS提升约10 cm。值得一提的是,相较于B1I/B3I,MEO-SECM卫星在采用B1C/B2a频点观测值后,其轨道切向精度显著提升超过50%,与MEO-CAST卫星同一量级。考虑到轨道切向精度与水平方向PCO相关,有必要对B1I/B3I频点的MEO-SECM卫星水平方向PCO值精度进行进一步核验,以探求造成该现象的其他可能原因。
为进一步验证PCO对北斗三号卫星精密定位的影响,本文基于S1~S4四套精密轨道和卫星精密钟差产品,设计了5组北斗三号单系统静态PPP实验方案,如表 6(单位cm)所示。其中,P1~P4与定轨实验中的S1~S4对应,考虑到PPP过程中可能存在与定轨解算所使用的PCO不一致的情况,本文额外设计了对照实验P5,其定位采用的是CSNO PCO模型,而轨道钟差解算则基于IGS PCO模型。IGS测站坐标真值来源于IGS发布的坐标周解文件,iGMAS测站采用iGMAS发布的坐标周解文件。研究表明,iGMAS站坐标综合解和IGS产品处于同一水平[16],表 7为静态PPP的具体解算策略。
|
|
表 6 5组静态PPP实验方案和定位误差RMS统计 Tab. 6 Five groups of static PPP experimental protocols and positioning error RMS values statistics |
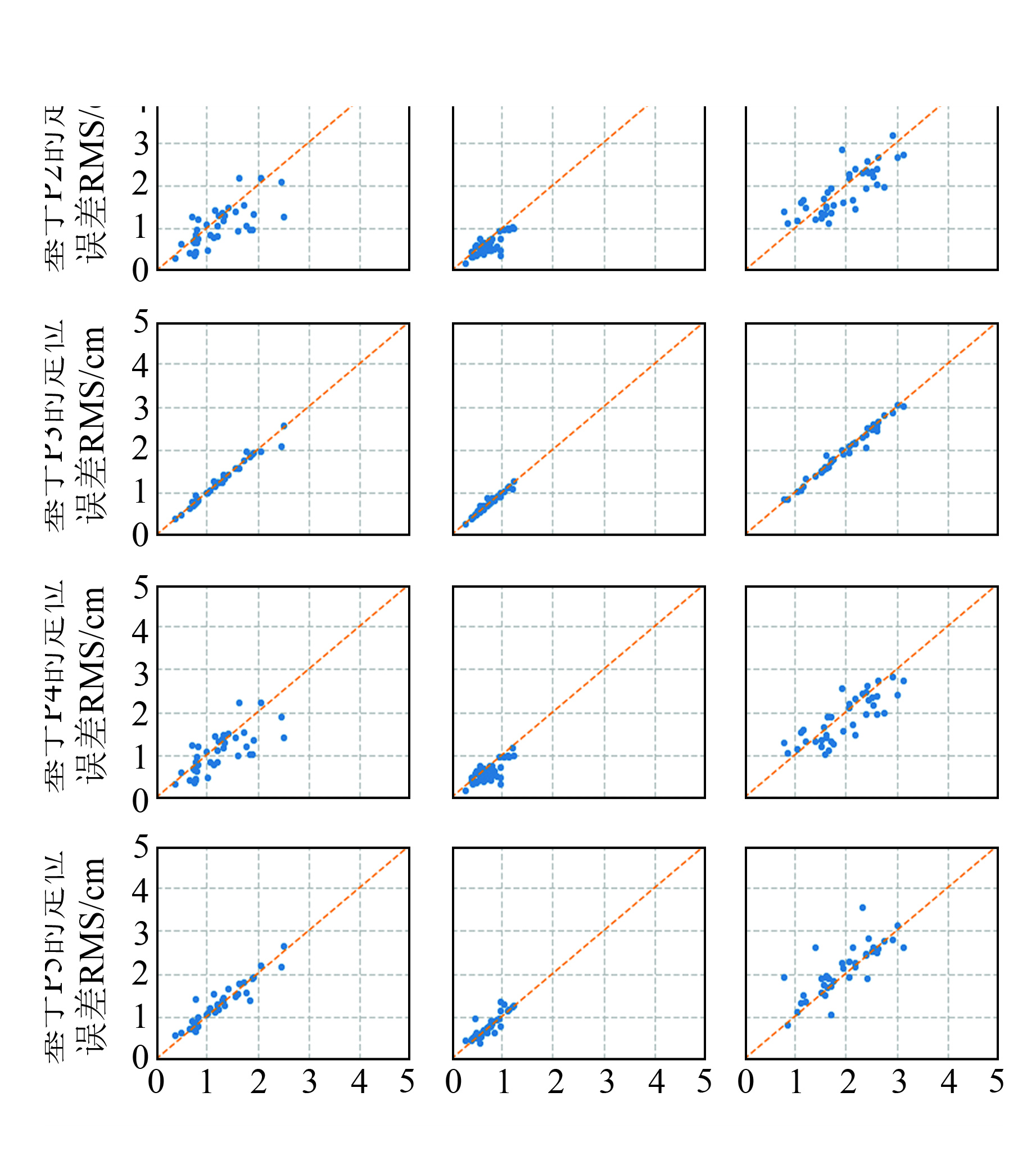
图 5以P1定位误差为参考,给出了P2~P5静态定位误差RMS分布,由图可见,静态定位精度与定轨精度符合性较好。对比P1/P3及P2/P4可以发现,基于相同观测值频点组合,采用IGS与CSNO发布的PCO,其对静态PPP精度的影响约为0.5 mm,差异主要表现在U方向上,且基于CSNO PCO发布值的坐标解算精度更优。此外,基于相同频点观测值组合的定位误差分布更为集中。对比基于相同PCO模型不同观测值频点组合的PPP实验结果(P1/P2及P3/P4)可以看出,基于B1C/B2a的定轨结果更优。以P1为参考,P4的坐标在E、N和U方向上的精度分别提升5%、13%和14%。而当采用与定轨不一致的轨道钟差产品时,其定位影响在U方向上的精度最大可超过5 mm,统计均值约2 mm。需要注意的是,为了保证定轨实验的一致性,本文轨道解算仅采用了约75个支持4个北斗三号OS频点的测站,通过增加地面测站数量、优化其分布并考虑PPP模糊度固定等方式,进一步提升定轨和定位精度。
|
图 5 基于P1~P5的静态定位误差RMS Fig. 5 Static positioning error RMS based on P1~P5 |
|
|
表 7 北斗三号静态精密单点定位处理策略 Tab. 7 BDS-3 static precision single-point positioning processing strategy |
1) CSNO和IGS PCO模型差异为cm级,且主要集中在竖直方向PCO上,个别卫星差异可达20 cm。
2) 在定轨验后残差方面,相较于PCO差异的影响,观测值频点的选择对定轨残差的影响更显著,主要由观测值频点无电离层组合系数的放大倍数决定,基于CSNO B1C/B2a PCO模型的定轨残差最小。
3) 在轨道重叠弧段精度方面,利用CSNO PCO发布值可以获得更优的定轨精度,且基于B1C/B2a的定轨精度明显优于B1I/B3I,这与验后残差的结论一致。
4) 在静态精密单点定位方面,与定轨验后残差结论类似,相较于CSNO和IGS PCO模型差异的影响,B1C/B2a与B1I/B3I观测值频点的选择对定位影响更显著。尽管两者的PCO模型差异对轨道影响达cm级,但该误差大部分被钟差吸收,因此对精密定位影响不显著。以基于IGS B1I/B3I PCO模型为参考,CSNO B1C/B2a PCO模型定位坐标在E、N、U方向上的统计精度分别提升约5%、13%、14%。此外,精密定轨和精密定位若采用不一致的PCO模型,其对坐标在U方向的定位精度平均影响超过2 mm,在实际数据处理时需要避免该问题。
| [1] |
Zhu S Y, Massmann F H, Yu Y, et al. Satellite Antenna Phase Center Offsets and Scale Errors in GPS Solutions[J]. Journal of Geodesy, 2003, 76(11-12): 668-672 DOI:10.1007/s00190-002-0294-1
(  0) 0) |
| [2] |
Zhao Q L, Guo J, Wang C, et al. Precise Orbit Determination for BDS Satellites[J]. Satellite Navigation, 2022
(  0) 0) |
| [3] |
Ge M, Gendt G, Dick G, et al. Impact of GPS Satellite Antenna Offsets on Scale Changes in Global Network Solutions[J]. Geophysical Research Letters, 2005, 32(6)
(  0) 0) |
| [4] |
Schmid R, Rothacher M, Thaller D, et al. Absolute Phase Center Corrections of Satellite and Receiver Antennas[J]. GPS Solutions, 2005, 9(4): 283-293 DOI:10.1007/s10291-005-0134-x
(  0) 0) |
| [5] |
李晓波, 王小亚, 任金卫. GNSS天线相位中心偏差与变化精确标定方法研究[J]. 天文学进展, 2012, 30(4): 501-517 (Li Xiaobo, Wang Xiaoya, Ren Jinwei. Research on Calibration Methods of GNSS Antenna Phase Center Offsets and Variations[J]. Progress in Astronomy, 2012, 30(4): 501-517)
(  0) 0) |
| [6] |
胡志刚. 北斗卫星导航系统性能评估理论与试验验证[D]. 武汉: 武汉大学, 2013 (Hu Zhigang. Beidou Navigation Satellite System Performance Assessment Theory and Experimental Verification[D]. Wuhan: Wuhan University, 2013)
(  0) 0) |
| [7] |
苏牡丹, 赵齐乐, 郭靖, 等. 接收机端天线相位中心标定及其对北斗导航卫星精密定轨的影响[J]. 测绘学报, 2018, 47(增1): 78-85 (Su Mudan, Zhao Qile, Guo Jing, et al. Phase Center Calibration for Receiver Antenna and Its Impact on Precise Orbit Determination of BDS Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(S1): 78-85)
(  0) 0) |
| [8] |
涂锐, 黄观文, 邹顺. 天线相位中心偏差变化及改正模型对精密单点定位精度的影响[J]. 大地测量与地球动力学, 2010, 30(3): 113-117 (Tu Rui, Huang Guanwen, Zou Shun. Study on Impact of Antenna Phase Center Offsets Variation and Their Correction Models on GPS Precise Point Positioning Accuracy[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 113-117)
(  0) 0) |
| [9] |
谷世铭, 党亚民, 王虎, 等. 北斗天线相位中心偏差改正对精密单点定位的影响[J]. 测绘通报, 2020(1): 66-70 (Gu Shiming, Dang Yamin, Wang Hu, et al. The Effect of Beidou Antenna Phase Center Offsets and Variations Correction on Precise Single Point Positioning[J]. Bulletin of Surveying and Mapping, 2020(1): 66-70)
(  0) 0) |
| [10] |
张勤, 燕兴元, 黄观文, 等. 北斗卫星天线相位中心改正模型精化及对精密定轨和定位影响分析[J]. 测绘学报, 2020, 49(9): 1101-1111 (Zhang Qin, Yan Xingyuan, Huang Guanwen, et al. Refinement of Beidou Satellite Antenna Phase Center Correction Model and Its Impact on Precision Orbit Determination and Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1101-1111)
(  0) 0) |
| [11] |
Qu Z Y, Guo J, Zhao Q L. Phase Center Corrections for BDS IGSO and MEO Satellites in IGb14 and IGSR3 Frame[J]. Remote Sensing, 2021, 13(4): 745
(  0) 0) |
| [12] |
Geng J H, Guo J, Wang C, et al. Satellite Antenna Phase Center Errors: Magnified Threat to Multi-Frequency PPP Ambiguity Resolution[J]. Journal of Geodesy, 2021, 95(6): 1-18
(  0) 0) |
| [13] |
Xia F Y, Ye S R, Chen D Z, et al. Estimation of Antenna Phase Center Offsets for Beidou IGSO and MEO Satellites[J]. GPS Solution, 2020, 24(4): 1-15
(  0) 0) |
| [14] |
王晨. 北斗导航卫星光压模型构建与精化研究[D]. 武汉: 武汉大学, 2019 (Wang Chen. Solar Radiation Pressure Modelling for Beidou Navigation Satellites[D]. Wuhan: Wuhan University, 2019)
(  0) 0) |
| [15] |
Li R, Wang N B, Li Z S, et al. Precise Orbit Determination of BDS-3 Satellites Using B1C and B2a Dual-Frequency Measurements[J]. GPS Solutions, 2021, 25(3): 1-14
(  0) 0) |
| [16] |
陈国, 魏娜, 赵齐乐, 等. 多分析中心站坐标产品的综合方法研究[J]. 武汉大学学报: 信息科学版, 2019, 44(9): 1289-1295 (Chen Guo, Wei Na, Zhao Qile, et al. Research on the Combination of Station Coordinate Products Derived from Multiple Analysis Centers[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1289-1295)
(  0) 0) |
2. Big Data Center for Geosciences and Satellites(BDCGS), Chang'an University, 126 Yanta Road, Xi'an 710054, China
 2022, Vol. 42
2022, Vol. 42


