2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 西部矿产资源与地质工程教育部重点实验室,西安市雁塔路126号,710054
全球导航卫星系统GNSS观测数据的实时获取定位结果被广泛应用于辅助驾驶、行人导航、位置分享、消防减灾等领域[1]。2016-05谷歌公司在Android N操作系统上提供了访问GNSS原始观测数据的接口,给基于智能手机GNSS导航定位技术的研究提供了新的机遇。此后,国内外众多学者对智能手机接收的GNSS数据进行了质量评估,并对其定位性能进行了测试分析[2-3]。智能手机GNSS定位模块采用线性极化天线及低成本芯片,已有研究表明,对低成本多系统GNSS芯片而言,由于不同GNSS信号体制及抗多径能力的不同,不同GNSS的数据质量可能会呈现显著差异[4-6]。
随着GNSS的不断完善与发展,对多系统进行组合与兼容成为导航定位的主要方法。与单系统相比,多系统可以提供更加充足的可视卫星数量,极大提高导航定位的精度与可靠性。在进行多系统组合定位时,准确确定卫星的随机模型是实现多系统高精度定位的前提。大量学者基于与高度角相关的随机模型,对GNSS多系统组合定位时的系统间权比进行了研究[7-8]。
为提升智能手机的定位效果,本文基于华为P30手机采集到的GPS/BDS/GLONASS/Galileo观测数据,首先对其伪距噪声进行评估,并在此基础上对四系统组合定位的随机模型及GNSS多系统手机定位效果进行分析。本文相关评估结果对于智能手机的高可靠性定位研究具有一定的参考价值。
1 GPS/BDS/GLONASS/Galileo伪距单点定位模型 1.1 多系统伪距单点定位函数模型考虑到各系统时间基准的差异,将GPS系统作为参考基准,则GPS/BDS/GLONASS/Galileo组合伪距单点定位的函数模型[9]为:
| $ \left\{\begin{array}{l} P^{\mathrm{G}}=R^{\mathrm{G}}+c \mathrm{~d} t_{\mathrm{r}}^{\mathrm{G}}-c \mathrm{~d} t_{\mathrm{s}}^{\mathrm{G}}+d_{\text {trop }}^{\mathrm{G}}+d_{\text {ion }}^{\mathrm{G}}+\varepsilon^{\mathrm{G}} \\ P^{\mathrm{G}}=R^{\mathrm{C}}+c \mathrm{~d} t_{\mathrm{r}}^{\mathrm{G}}-c \mathrm{~d} t_{\mathrm{r}}^{\mathrm{C}, \mathrm{G}}-c \mathrm{~d} t_{\mathrm{s}}^{\mathrm{C}}+ \\ \quad d_{\text {trop }}^{\mathrm{C}}+d_{\text {ion }}^{\mathrm{C}}+\varepsilon^{\mathrm{C}} \\ P^{\mathrm{R}}=R^{\mathrm{R}}+c \mathrm{~d} t_{\mathrm{r}}^{\mathrm{G}}-c \mathrm{~d} t_{\mathrm{r}}^{\mathrm{R}, \mathrm{G}}-c \mathrm{~d} t_{\mathrm{s}}^{\mathrm{R}}+ \\ \quad d_{\text {trop }}^{\mathrm{R}}+d_{\text {ion }}^{\mathrm{R}}+\varepsilon^{\mathrm{R}} \\ P^{\mathrm{E}}=R^{\mathrm{E}}+c \mathrm{~d} t_{\mathrm{r}}^{\mathrm{G}}-c \mathrm{~d} t_{\mathrm{r}}^{\mathrm{E}, \mathrm{G}}-c \mathrm{~d} t_{\mathrm{s}}^{\mathrm{E}}+ \\ \quad d_{\text {trop }}^{\mathrm{E}}+d_{\text {ion }}^{\mathrm{E}}+\varepsilon^{\mathrm{E}} \end{array}\right. $ | (1) |
式中,G、C、R、E分别为GPS、BDS、GLONASS、Galileo卫星;P为伪距;c为真空光速;R为卫星到接收机间的几何距离;dtrG为GPS卫星的接收机钟差,在伪距单点定位中通常作为白噪声参数进行估计;dtrC, G、dtrR, G、dtrE, G分别为BDS、GLONASS、Galileo相较于GPS的系统间时间偏差;dts为卫星钟差;dtrop、dion和ε分别为对流层延迟、电离层延迟和码伪距噪声。
1.2 多系统伪距定位随机模型GNSS定位的随机模型常采用高度角随机模型和信噪比模型[10]。对于测量型接收机而言,采用多系统进行单点定位时通常忽略系统间信号质量的差异,因此可直接采用这两种模型;对于智能手机而言,由于天线和芯片的结构及成本受限较大,不同GNSS信号体制不同,其信号质量可能存在显著差异。常用的GNSS信号噪声评估方法主要有多路径公式法、零基线单差残差法、四次差法、码减载波法等[11]。智能手机单频数据无法使用双频多路径公式,同时由于手机天线内置,难以精准构建零基线/短基线,本文采用四次差法评估不同系统的伪距噪声。四次差法计算相对简便,可较好地消除几何距离、接收机钟差及大气误差的影响,算法原理如下[12]:
| $ \nabla P^{j, k}(t)=\rho^{j, k}+c \mathrm{~d} t_r^{j, k}+d_{\text {ion }}+d_{\text {trop }}+\varepsilon_P^{j, k} $ | (2) |
式中,▽为星间单差算法因子,j、k分别为非参考星和参考星,P为伪距观测值,ρ为卫星到测站的几何距离,c为真空光速,dtr为卫星钟差,dion和dtrop分别为电离层延迟和对流层延迟,ε为伪距观测噪声。式(2)可以消除接收机钟差的影响,对星间单差伪距噪声进行历元间三次差,可消除系统偏量,得到伪距噪声量。考虑到采样率为1 Hz,因此四次差最终可简化为:
| $ \begin{gathered} D=\nabla P^{j, k}(t)-3 \nabla P^{j, k}(t-1)+ \\ 3 \nabla P^{j, k}(t-2)-\nabla P^{j, k}(t-3) \end{gathered} $ | (3) |
式中,D为四次差伪距噪声,P为伪距观测值。根据误差传播定律[12],四次差伪距噪声中误差σD与伪距噪声中误差σL的关系如下:
| $ \sigma_L=\frac{1}{2 \sqrt{10}} \sigma_D $ | (4) |
本文设计静态和动态2种实验,静态实验点位于校内操场中央,在P30手机附近架设一台中海达测量型接收机进行同步静态观测,该接收机支持GPS L1/L2、BDS B1/B2、GLONASS G1/G2、Galileo E1/E5a,观测时长约6 h。动态实验是将华为P30手机与测量型接收机一起放置于小推车上,沿学校田径场推行30 min左右,将测量型接收机的RTK定位结果作为参考基准。
本文在进行伪距单点定位解算时,采用四系统L1波段的伪距观测值,电离层误差采用Klobuchar模型进行改正,对流层误差采用Saastamotion模型进行改正,并在定位前采用Grubbs准则探测粗差,进行验后伪距噪声检验,信噪比阈值设置为25 dB-Hz,截止高度角设置为15°。为探究优化的随机模型对定位结果的影响,本文采用4种不同的随机模型进行单点定位实验:高度角定权(方案1)、高度角定权+系统间加权(方案2)、信噪比定权(方案3)、信噪比定权+系统间加权(方案4)。其中,高度角与信噪比模型前文已介绍,系统间加权模型则根据前文得到的GPS、BDS、GLONASS、Galileo伪距噪声中误差平方之比的倒数进行定权,对传统的随机模型进行优化。
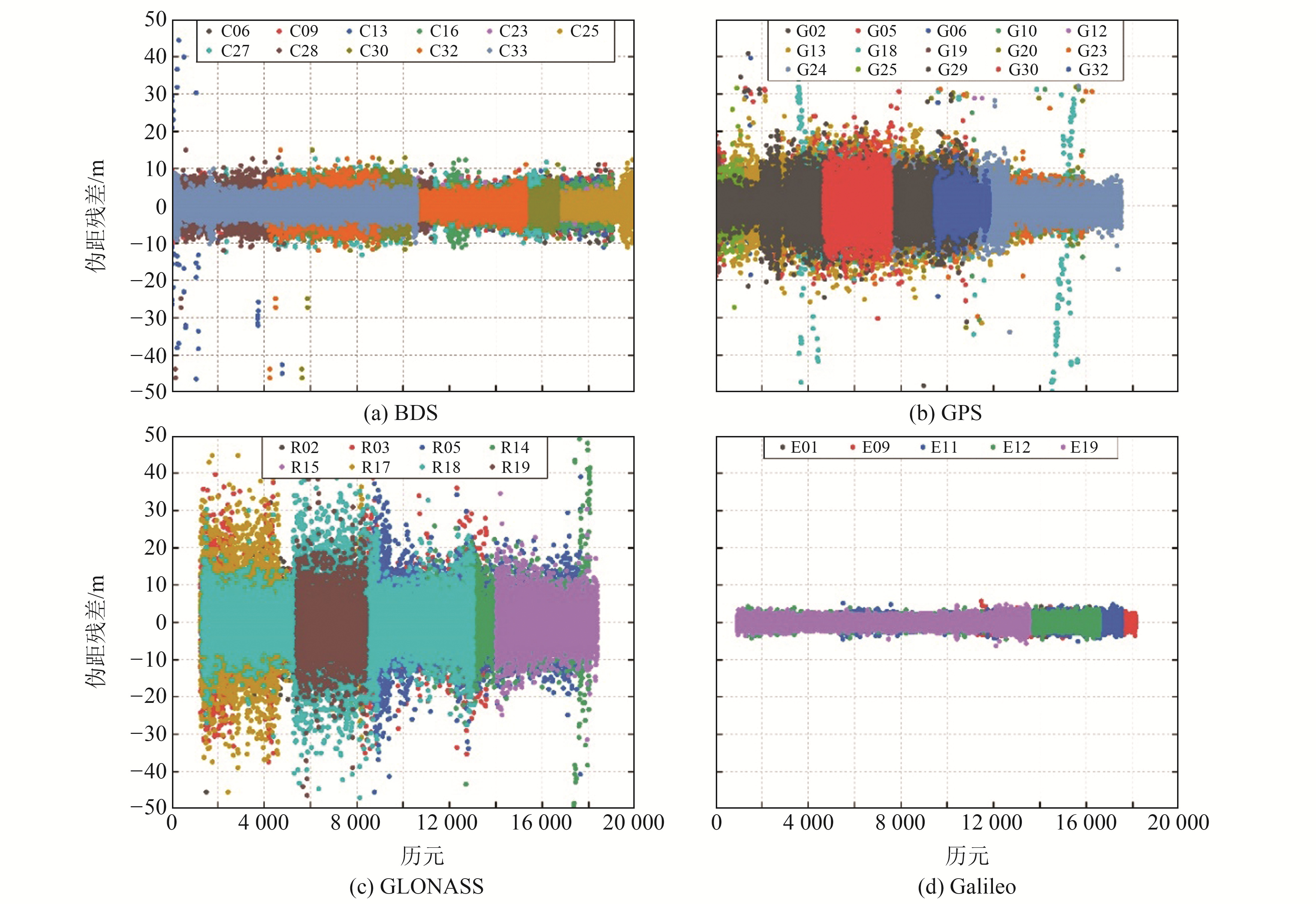
2.2 四次差伪距噪声分析利用四次差法计算华为P30手机的伪距精度,由图 1可见,BDS的四次差伪距噪声大部分在15 m以内;GPS伪距噪声较大,绝大多数集中在20 m以内;GLONASS大部分在30 m以内;Galileo大部分在5 m以内。将观测值的四次差结果作为原始观测值噪声进行统计可得,BDS、GPS、GLONASS、Galileo的伪距噪声中误差分别为2.75 m、5.30 m、7.92 m和1.07 m。P30手机四系统的伪距质量差异显著,因此采用多系统智能手机数据进行定位时,需进行系统间加权。
|
图 1 华为P30四次差伪距噪声 Fig. 1 The fourth difference pseudorange residual of Huawei P30 |
由华为P30手机四系统观测值伪距噪声分析结果可知,不同系统间的伪距噪声差异较大,仅利用传统的定权方法无法完全反映不同系统观测值的实际精度,因此需要根据伪距噪声情况在先验定权的基础上对不同系统的权比进行确定,以提高伪距精度高的系统所占的权比。根据不同系统间伪距噪声方差的倒数之比确定不同系统间定权的数值,各定权方案计算结果如表 1所示。
|
|
表 1 不同方案的定权方法 Tab. 1 Weighting methods of different schemes |
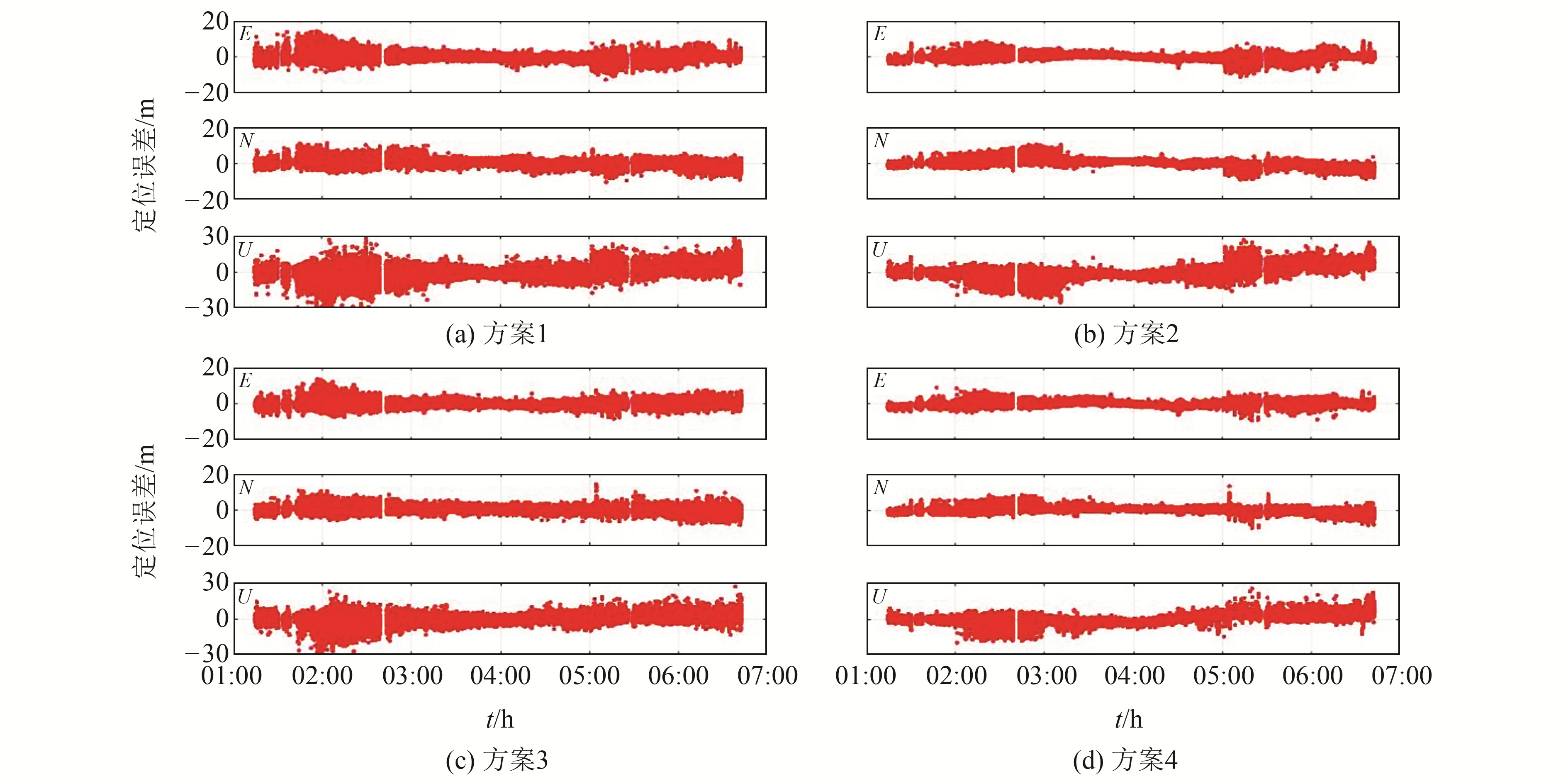
采用4种方案对静态模式下采集的数据进行处理,结果如图 2及表 2(单位m)所示。由图 2可见,与方案1和3相比,方案2和4在2:00~3:00时段内的定位误差显著减小。结合表 2的定位结果可见,无论是采用信噪比加权模型还是高度角加权随机模型,进行系统间加权后,单点定位模式在E、N、U方向上的定位中误差均有所减小。采用高度角加权时,进行系统间加权后,其在E、N、U方向上的定位精度分别提升了18.94%、6.79%、5.08%;而采用信噪比加权并进行系统间加权后,其在E、N、U方向上的定位精度分别提升了36.12%、25.79%、31.30%。
|
图 2 静态环境不同方案下的手机定位结果 Fig. 2 Smartphone positioning results under different schemes in static environment |
|
|
表 2 不同方案下的手机静态定位精度 Tab. 2 Smartphone static positioning accuracy under different schemes |
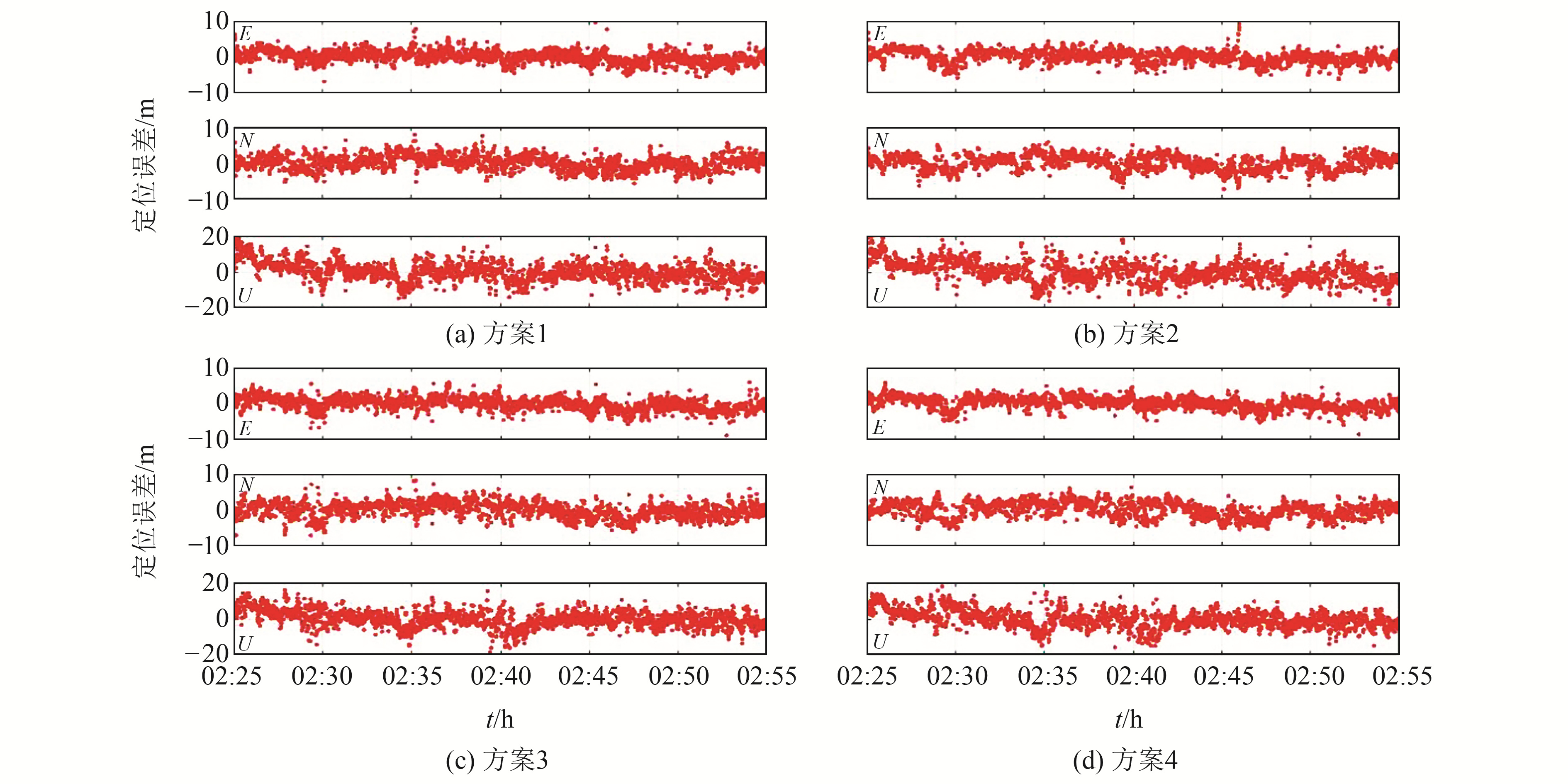
使用上述定位方法对华为P30手机采集的GNSS数据进行动态单点定位实验。图 3为方案4的手机单点定位结果与测量型接收机RTK结果对比,图中绿色轨迹为RTK参考定位结果,黄-红色轨迹为手机单点定位结果,可以看到,整体轨迹吻合度较高。计算不同方案下的手机定位误差,结果如图 4和表 3(单位m)所示。由图表可见,单点定位模式下,采用优化的随机模型后定位精度显著提高。采用高度角加权时,进行系统间加权后,其在E、N、U方向上的定位精度分别提升了20.33%、10.63%、4.41%;而采用信噪比加权并进行系统间加权后,其在E、N、U方向上的定位精度分别提升了25.73%、12.37%、24.73%。

|
图 3 方案4定位结果与测量型接收机RTK结果对比 Fig. 3 Comparison between the results of pseudorange differential positioning of mobile phone and RTK results of measurement receiver |
|
图 4 动态环境不同方案下的手机定位精度 Fig. 4 Smartphone positioning results under different schemes in dynamic environment |
|
|
表 3 不同方案下的手机动态定位精度 Tab. 3 Smartphone kinematic positioning accuracy under different schemes |
1) 华为P30智能手机不同系统卫星观测值的伪距噪声差异较大,GPS、BDS、GLONASS、Galileo的观测值伪距噪声中误差分别为5.30 m、2.75 m、7.92 m和1.07 m,BDS和Galileo卫星的伪距观测值精度明显优于GPS和GLONASS。
2) 采用信噪比+系统间随机模型进行定位实验,并与传统的高度角模型进行对比。在静态模式下,伪距单点定位精度在E、N、U方向上分别提升了36.12%、25.79%、31.30%;在动态模式下,伪距单点定位精度在E、N、U方向上分别提升了25.73%、12.37%、24.73%。
| [1] |
Paziewski J D. Recent Advances and Perspectives for Positioning and Applications with Smartphone GNSS Observations[J]. Measurement Science and Technology, 2020, 31(9)
(  0) 0) |
| [2] |
Robustelli U, Baiocchi V, Pugliano G. Assessment of Dual Frequency GNSS Observations from a Xiaomi Mi 8 Android Smartphone and Positioning Performance Analysis[J]. Electronics, 2019, 8(1): 91 DOI:10.3390/electronics8010091
(  0) 0) |
| [3] |
刘万科, 史翔, 朱锋, 等. 谷歌Nexus 9智能终端原始GNSS观测值的质量分析[J]. 武汉大学学报: 信息科学版, 2019, 44(12): 1749-1756 (Liu Wanke, Shi Xiang, Zhu Feng, et al. Quality Analysis of Raw GNSS Observation of Google Nexus 9 Smart Tablet Terminal[J]. Geomatics and Information Science of Wuhan University, 2019, 44(12): 1749-1756)
(  0) 0) |
| [4] |
Lachapelle G, Gratton P. GNSS Precise Point Positioning with Android Smartphones and Comparison with High Performance Receivers[C]. 2019 IEEE International Conference on Signal, Information and Data Processing, Chongqing, 2019
(  0) 0) |
| [5] |
郭斐, 吴维旺, 张小红, 等. Android智能手机实时精密单点定位软件实现及精度分析[J]. 武汉大学学报: 信息科学版, 2021, 46(7): 1053-1062 (Guo Fei, Wu Weiwang, Zhang Xiaohong, et al. Realization and Precision Analysis of Real-Time Precise Point Positioning with Android Smartphones[J]. Geomatics and Information Science of Wuhan University, 2021, 46(7): 1053-1062)
(  0) 0) |
| [6] |
汪亮, 李子申, 周凯, 等. 面向Android智能终端的多模GNSS实时非差精密定位[J]. 导航定位与授时, 2019, 6(3): 1-10 (Wang Liang, Li Zishen, Zhou Kai, et al. Multi-GNSS Real-Time Un-Differecced Precise Positioning for Android Smart Devices[J]. Navigation Positioning and Timing, 2019, 6(3): 1-10)
(  0) 0) |
| [7] |
吴桂栋. GPS/COMPASS组合系统单点定位随机模型算法研究[D]. 合肥: 合肥工业大学, 2014 (Wu Guidong. Algorithm Research on Stochastical Model for GPS/COMPASS Combined System's Point Positioning[D]. Hefei: Hefei University of Technology, 2014)
(  0) 0) |
| [8] |
史翔. 基于智能手机GNSS观测值的连续平滑定位算法[D]. 武汉: 武汉大学, 2019 (Shi Xiang. Continuous Smoothing Positioning Algorithm Based on GNSS Observations of Smartphones[D]. Wuhan: Wuhan University, 2019)
(  0) 0) |
| [9] |
Pan L, Cai C, Santerre R, et al. Performance Evaluation of Single-Frequency Point Positioning with GPS, GLONASS, Beidou and Galileo[J]. Survey Review, 2017, 49(354): 197-205 DOI:10.1080/00396265.2016.1151628
(  0) 0) |
| [10] |
Hartinger H, Brunner F K. Variances of GPS Phase Observations: The SIGMA-ε Model[J]. GPS Solutions, 1999, 2(4): 35-43 DOI:10.1007/PL00012765
(  0) 0) |
| [11] |
高晓, 戴吾蛟, 李施佳. 高精度GPS/BDS兼容接收机内部噪声检测方法研究[J]. 武汉大学学报: 信息科学版, 2015, 40(6): 795-799 (Gao Xiao, Dai Wujiao, Li Shijia. Interior Performance Test of High Precision GPS/BDS Compatible Receivers[J]. Geomatics and Information Science of Wuhan University, 2015, 40(6): 795-799)
(  0) 0) |
| [12] |
李征航. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2013 (Li Zhenghang. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2013)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Key Laboratory of Western China's Mineral Resources and Geological Engineering, Ministry of Education, 126 Yanta Road, Xi'an 710054, China
 2022, Vol. 42
2022, Vol. 42


