2. 航天晨光股份有限公司,南京市天元中路188号,211100;
3. 北京理工大学化学与化工学院,北京市中关村南大街5号,100081
CNS抗干扰能力强,误差不随时间积累,精度高达角秒级[1],在航天飞机、载人飞船及深空探测等领域得到广泛应用[2];同时,SINS和CNS都是完全自主的导航系统,将二者组合也是目前的研究重点。组合导航系统的滤波方法主要分为线性和非线性,其中线性滤波方法以常规卡尔曼滤波为代表,而非线性滤波方法包括扩展卡尔曼滤波(EKF)、不敏卡尔曼滤波(UKF)及粒子滤波(PF)等。相对于扩展卡尔曼滤波和粒子滤波,不敏卡尔曼滤波因具有精度高及易于实现的特点而得到广泛应用[3]。
目前,基于UKF的GNSS/SINS组合导航系统得到深入研究,主要原因是其速度和位置的样本点、均值及方差较容易生成,且可通过线性叠加产生[4-6];由于姿态角不是普通的矢量,故对基于UKF的CNS/SINS组合导航系统的研究相对繁琐[7-8]。本文将UKF方法运用于CNS/SINS组合导航系统中,建立其非线性状态方程及线性量测方程,并提出了一种基于UKF的CNS/SINS组合导航系统滤波算法。
1 基于UKF的组合导航滤波模型 1.1 标准UKF简介考虑如下形式的n维离散时间非线性系统:
| $ \left\{\begin{array}{l} \boldsymbol{X}_k=f\left(\boldsymbol{X}_{k-1}, \boldsymbol{u}_k, \boldsymbol{W}_k, k\right) \\ \boldsymbol{Z}_k=h\left(\boldsymbol{X}_{k-1}, \boldsymbol{V}_k, k\right) \end{array}\right. $ | (1) |
式中,f(·)、h(·)为非线性函数;k为离散时刻;Xk为k时刻的系统状态,假设其方差矩阵为Pk;uk为系统确定性输入项;Zk为量测值;Wk和Vk分别为系统噪声和量测噪声,其方差矩阵分别为Qk和Rk。
由式(1)可知,标准UKF算法包含初始化、样点计算、时间更新、量测更新及滤波更新等过程。因式(1)中状态方程及量测方程均为典型的非线性方程,故UKF中的时间更新及量测更新过程也是典型的非线性运算,算法复杂度高。同时,标准UKF算法将系统状态向量、系统噪声和量测噪声增广为系统状态,也进一步增大了滤波算法的运算量。
1.2 CNS/SINS组合导航系统滤波模型结合式(1)的非线性系统模型,基于CNS/SINS组合导航系统的UKF算法,以导航参数直接作为被估计的状态,采用捷联惯性导航系统的机械编排方程作为状态方程,且状态方程无需进行线性化处理。选取N、E、U地理坐标系作为导航坐标系,惯导系统采取指北方位机械编排的形式,其状态方程可表示为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot X}}(t) = f\left( {\mathit{\boldsymbol{X}}(t), \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}}, {\mathit{\boldsymbol{f}}^{\rm{b}}}, t} \right)\\ \mathit{\boldsymbol{X}}(t) = {\left[ {\begin{array}{*{20}{l}} \gamma &\theta &\varphi &{{v_E}}&{{v_N}}&{{v_U}}&\lambda &L&H \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (2) |
式中,X(t) 为系统状态向量,9个参数中γ、θ、φ分别表示横滚角、俯仰角和航向角,vE、vN、vU分别表示E向速度、N向速度和U向速度,λ、L、H分别表示经度、纬度和高度;ωibb为陀螺仪输出;fb为加速度计输出;t为时间。
依据SINS工作原理,展开式如下:
| $ \left\{ \begin{array}{l} \left[ {\Delta {\mathit{\boldsymbol{\theta }}_j}} \right] = \int_{{t_1}}^{{t_2}} \mathit{\boldsymbol{M}} \left( {\mathit{\boldsymbol{\omega }}_{ib}^b - \mathit{\boldsymbol{C}}_{n, j - 1}^b\mathit{\boldsymbol{\omega }}_{in, j - 1}^b + {\mathit{\boldsymbol{b}}_{g, j}}} \right){\rm{d}}t = \left[ {\begin{array}{*{20}{c}} 0&{ - \Delta {\theta _{x, j}}}&{ - \Delta {\theta _{y, j}}}&{ - \Delta {\theta _{z, j}}}\\ {\Delta {\theta _{x, j}}}&0&{\Delta {\theta _{z, j}}}&{ - \Delta {\theta _{y, j}}}\\ {\Delta {\theta _{y, j}}}&{ - \Delta {\theta _{z, j}}}&0&{\Delta {\theta _{x, j}}}\\ {\Delta {\theta _{z, j}}}&{\Delta {\theta _{y, j}}}&{ - \Delta {\theta _{x, j}}}&0 \end{array}} \right]\\ {\mathit{\boldsymbol{q}}_{k, j}} = {{\rm{e}}^{0.5\left[ {\Delta {{\bf{ \pmb{\mathsf{ θ}} }}_j}} \right]}}{\mathit{\boldsymbol{q}}_{k - 1, j}} = {\left[ {\begin{array}{*{20}{l}} {{q_0}}&{{q_1}}&{{q_2}}&{{q_3}} \end{array}} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{C}}_{n, j}^b = \left[ {\begin{array}{*{20}{c}} {q_1^2 + q_0^2 - q_3^2 - q_2^2}&{2\left( {{q_1}{q_2} - {q_0}{q_3}} \right)}&{2\left( {{q_1}{q_3} - {q_0}{q_2}} \right)}\\ {2\left( {{q_1}{q_2} - {q_0}{q_3}} \right)}&{q_0^2 + q_2^2 - q_3^2 - q_1^2}&{2\left( {{q_2}{q_3} - {q_0}{q_1}} \right)}\\ {2\left( {{q_1}{q_3} - {q_0}{q_2}} \right)}&{2\left( {{q_2}{q_3} - {q_0}{q_1}} \right)}&{q_3^2 + q_0^2 - q_2^2 - q_1^2} \end{array}} \right]\\ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_{k, j}} = {\mathit{\boldsymbol{v}}_{k - 1, j}} + \left[ {\mathit{\boldsymbol{C}}_{n, j}^b\left( {{\mathit{\boldsymbol{f}}^b} + {\mathit{\boldsymbol{b}}_{a, j}}} \right) + {\mathit{\boldsymbol{g}}^n} - \left( {2\mathit{\boldsymbol{\omega }}_{ie}^n + \mathit{\boldsymbol{\omega }}_{en, j}^n} \right){\mathit{\boldsymbol{v}}_{k - 1, j}}} \right]\Delta t}\\ {{\mathit{\boldsymbol{p}}_{k, j}} = {\mathit{\boldsymbol{p}}_{k - 1, j}} + {\mathit{\boldsymbol{v}}_{k, j}}\Delta t} \end{array} \end{array} \right. $ | (3) |
式中,q为姿态四元数;Cnb为姿态矩阵;v和p分别为三维速度和三维位置向量;其他参数详见文献[5]。
CNS的输出可转换为地理坐标系下的横滚角、俯仰角及航向角,故选取CNS输出作为观测量,则系统的量测方程可表示为:
| $ \left\{\begin{array}{l} \boldsymbol{Z}(t)=\boldsymbol{H}(t) \boldsymbol{X}(t)+\boldsymbol{V}(t) \\ \boldsymbol{Z}(t)=\left[\begin{array}{lll} \gamma & \theta & \varphi \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{H}(t)=\left[\begin{array}{ll} \boldsymbol{I}_{3 \times 3} & \bf{0}_{3 \times 6} \end{array}\right] \end{array}\right. $ | (4) |
对式(2)和式(4)进行离散化处理,可以得到离散化的状态方程及量测方程,且假设导航系统的先验状态、过程噪声方差和测量噪声方差相互独立。
1.3 CNS/SINS组合导航的简化UKF算法基于式(2)和式(4)可以看出,CNS/SINS组合导航系统具有状态方程非线性而量测方程线性的特点,为此仅将系统状态向量和系统噪声增广为状态向量[9],则简化的系统增广状态向量为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}^a} = {\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{X}}&\mathit{\boldsymbol{W}} \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{\chi }}^a} = {\left[ {\begin{array}{*{20}{l}} {{{\left( {{\mathit{\boldsymbol{\chi }}^X}} \right)}^{\rm{T}}}}&{{{\left( {{\mathit{\boldsymbol{\chi }}^W}} \right)}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (5) |
式中,χa、χX和χW分别为Xa、X和W的样点,其维数分别定义为La、Lx和Lw,且La=Lx+Lw。
步骤1):初始化。
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\widehat X}}}_0} = E\left[ {{\mathit{\boldsymbol{X}}_0}} \right]}\\ {{\mathit{\boldsymbol{P}}_0} = E\left[ {\left( {{\mathit{\boldsymbol{X}}_0} - {{\mathit{\boldsymbol{\widehat X}}}_0}} \right){{\left( {{\mathit{\boldsymbol{X}}_0} - {{\mathit{\boldsymbol{\widehat X}}}_0}} \right)}^{\rm{T}}}} \right]}\\ {\mathit{\boldsymbol{\widehat X}}_0^a = E\left[ {{\mathit{\boldsymbol{X}}^a}} \right] = {{\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\widehat X}}_0^{\rm{T}}\quad {\bf{0}}} \end{array}} \right]}^{\rm{T}}}}\\ \begin{aligned} \mathit{\boldsymbol{P}}_0^a &= E\left[ {{\mathit{\boldsymbol{X}}^a}} \right] = E\left[ {\left( {\mathit{\boldsymbol{X}}_0^a - \mathit{\boldsymbol{\widehat X}}_0^a} \right) \times } \right.\\ &\left. {{{\left( {\mathit{\boldsymbol{X}}_0^a - \mathit{\boldsymbol{\widehat X}}_0^a} \right)}^{\rm{T}}}} \right] = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{P}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{Q}} \end{array}} \right] \end{aligned} \end{array}} \right. $ | (6) |
步骤2):样点计算。
| $ \left\{\begin{array}{l} \boldsymbol{\chi}_{0, k-1}^a=\hat{\boldsymbol{X}}_{k-1}^a \\ \boldsymbol{\chi}_{i, k-1}^a=\hat{\boldsymbol{X}}_{k-1}^a+\left(\sqrt{n \bf{P}_{k-1}^a}\right)_i, \\ \quad i=1, \cdots, L_a \\ \boldsymbol{\chi}_{i, k-1}^a=\hat{\boldsymbol{X}}_{k-1}^a-\left(\sqrt{n \bf{P}_{k-1}^a}\right)_i, \\ \quad i=L_a+1, \cdots, 2 L_a \end{array}\right. $ | (7) |
| $ \left\{\begin{array}{l} \boldsymbol{W}_0^m=\frac{\lambda}{L_a+\lambda} \\ \boldsymbol{W}_0^c=\frac{\lambda}{L_a+\lambda}+\left(1-\alpha^2+\beta\right) \\ \boldsymbol{W}_i^m=W_i^c=\frac{1}{2\left(L_a+\lambda\right)}, i=1, \cdots, 2 L_a \end{array}\right. $ | (8) |
其中,λ=α2(n+κ)-La,α、β和κ为比例因子。
步骤3):时间更新。
| $ \left\{\begin{array}{l} \boldsymbol{\chi}_{i, k \mid k-1}^X=f\left(\boldsymbol{\chi}_{i, k-1}^X, \boldsymbol{\omega}_{\mathrm{ib}}^{\mathrm{b}}, \boldsymbol{f}^{\mathrm{b}}, \boldsymbol{\chi}_{i, k-1}^W\right) \\ \hat{\boldsymbol{X}}_{k \mid k-1}=\sum\limits_{i=0}^{2 L_a} \boldsymbol{W}_i^m \boldsymbol{\chi}_{i, k \mid k-1}^X \end{array}\right. $ | (9) |
| $ \begin{aligned} \boldsymbol{P}_{k \mid k-1}= & \sum\limits_{i=0}^{2 L_a} \boldsymbol{W}_i^c\left[\boldsymbol{\chi}_{i, k \mid k-1}^X-\hat{\boldsymbol{X}}_{k \mid k-1}\right] \times \\ & {\left[\boldsymbol{\chi}_{i, k \mid k-1}^X-\hat{\boldsymbol{X}}_{k \mid k-1}\right]^{\mathrm{T}} } \end{aligned} $ | (10) |
步骤4):量测更新。
根据式(4),CNS量测样点
| $ \hat{\boldsymbol{Z}}_{k \mid k-1}=\sum\limits_{i=0}^{2 L_a} \boldsymbol{W}_i^m \hat{\boldsymbol{Z}}_{i, k \mid k-1}=\boldsymbol{H} \hat{\boldsymbol{X}}_{k \mid k-1} $ | (11) |
而
| $ \begin{gathered} \boldsymbol{P}_{Z Z}=\sum\limits_{i=0}^{2 L_a} \boldsymbol{W}_i^c\left[\hat{\boldsymbol{Z}}_{i, k \mid k-1}-\hat{\boldsymbol{Z}}_{k \mid k-1}\right]\left[\hat{\boldsymbol{Z}}_{i, k \mid k-1}-\hat{\boldsymbol{Z}}_{k \mid k-1}\right]^{\mathrm{T}} \\ +\boldsymbol{R}=\sum\limits_{i=0}^{2 L_a} \boldsymbol{W}_i^c \boldsymbol{H}\left[\boldsymbol{X}_{i, k \mid k-1}^X-\hat{\boldsymbol{X}}_{k \mid k-1}\right]\left[\boldsymbol{X}_{i, k \mid k-1}^X-\right. \\ \left.\hat{\boldsymbol{X}}_{k \mid k-1}\right]^{\mathrm{T}} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}=\boldsymbol{H} \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R} \end{gathered} $ | (12) |
同理,有:
| $ \boldsymbol{P}_{X Z}=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} $ | (13) |
步骤5):滤波更新。
| $ \left\{\begin{array}{l} \boldsymbol{K}_k=\boldsymbol{P}_{X Z} \boldsymbol{P}_{Z Z}^{-1} \\ \hat{\boldsymbol{X}}_k=\hat{\boldsymbol{X}}_{k \mid k-1}+\boldsymbol{K}_k\left(\boldsymbol{Z}_k-\hat{\boldsymbol{Z}}_{k \mid k-1}\right) \\ \boldsymbol{P}_k=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{K}_k \boldsymbol{P}_{Z Z} \boldsymbol{K}_k^{\mathrm{T}}=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{K}_k \boldsymbol{P}_{X Z}^{\mathrm{T}} \end{array}\right. $ | (14) |
对比标准UKF算法,简化UKF算法的计算复杂度得到了降低。
2 组合导航系统中姿态融合的设计与位置和速度不同,计算姿态与真实姿态之间的误差不能通过简单的线性减法来实现,必须借助于捷联姿态误差分析原理进行。在捷联式惯性导航系统中,用数字平台坐标系模拟导航坐标系,由于平台有误差,故数字平台坐标系(n′)和导航坐标系(n)之间存在着平台角误差,将这种平台角误差写成列向量,可表示为[12]:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^n} = {\left[ {\begin{array}{*{20}{l}} {{\varphi _x}}&{{\varphi _y}}&{{\varphi _z}} \end{array}} \right]^{\rm{T}}} $ | (15) |
式中,φx、φy和φz分别为x、y和z方向平台角误差。则2个坐标系之间的转换矩阵为:
| $ \boldsymbol{C}_n^{n^{\prime}}=\left[\begin{array}{ccc} 1 & \varphi_z & -\varphi_y \\ -\varphi_z & 1 & \varphi_x \\ \varphi_y & -\varphi_x & 1 \end{array}\right] $ | (16) |
对捷联式系统计算的姿态阵为:
| $ \hat{\boldsymbol{C}}_b^n=\boldsymbol{C}_b^{n^{\prime}}=\boldsymbol{C}_b^n \boldsymbol{C}_n^{n^{\prime}} $ | (17) |
即
| $ \boldsymbol{C}_n^{n^{\prime}}=\left(\boldsymbol{C}_b^n\right)^{-1} \hat{\boldsymbol{C}}_b^n=\boldsymbol{C}_n^b\left[\hat{\boldsymbol{C}}_n^b\right]^{\mathrm{T}}=\boldsymbol{C}_n^b\left[\boldsymbol{C}_{n^{\prime}}^b\right]^{\mathrm{T}} $ | (18) |
UKF算法中,位置、速度及IMU噪声的样点可以通过式(7)进行简单的线性叠加得到,并且位置和速度对应的协方差矩阵也可通过式(10)计算得到。根据捷联导航原理可知,为避免姿态计算过程中出现奇点(即方程退化的问题),需要通过四元数乘法或方向余弦矩阵等算法来计算姿态角,是典型的非线性计算。为此,本文以方向余弦矩阵为工具,计算姿态角样点、均值和方差,具体过程如下。
1) 假设初始姿态向量(即第1个姿态采样点)为a0=[γ0 θ0 φ0]T,其对应的姿态矩阵为Cbn0 (假设n0为某一数字平台坐标系):
| $ \boldsymbol{C}_{n_0}^b=\left[\boldsymbol{C}_{b^0}^{n^0}\right]^{\mathrm{T}}=\left[\begin{array}{ccc} \cos \gamma_0 \cos \varphi_0+\sin \gamma_0 \sin \theta_0 \sin \varphi_0 & -\cos \gamma_0 \sin \varphi_0+\sin \gamma_0 \sin \theta_0 \cos \varphi_0 & -\sin \gamma_0 \cos \theta_0 \\ \cos \theta_0 \sin \varphi_0 & \cos \theta_0 \cos \varphi_0 & \sin \theta_0 \\ \sin \gamma_0 \cos \varphi_0-\cos \gamma_0 \sin \theta_0 \sin \varphi_0 & -\sin \gamma_0 \sin \varphi_0-\cos \gamma_0 \sin \theta_0 \cos \varphi_0 & \cos \gamma_0 \cos \theta_0 \end{array}\right] $ | (19) |
2) 根据式(7)中
3) 基于步骤1)与步骤2),得到分布在姿态角a0两边的2La个样点所对应的方向余弦矩阵为Cbnj= Cbn0Cnjn0,进行姿态计算可得围绕a0的另外2La个姿态样点。至此,得到姿态角的初始2La+1个样点,在第1次滤波开始前,依据捷联惯导系统的工作原理依次进行位置、速度及姿态样点的计算。第1次滤波按照式(9)~式(14)进行,滤波结束后按照下述步骤进行姿态均值和方差的计算。
4) 假设滤波结束后经过校正的姿态角向量(即新1轮的第1个姿态样点)对应的方向余弦矩阵为Cbn0,姿态均值对应的方向余弦矩阵为Cnb,并选取Cnb= Cbn0,类似地,利用后面2La个姿态样点Cbnj依次计算出2La个平台角误差向量φj对应的转换矩阵为Cnjn0=[Cbn0]TCbnj。
5) 平台角误差向量φj的均值可表示为
6) 在计算UKF的状态误差一步协方差矩阵Pk|k-1时,对姿态部分用φj、φ分别取代式(10)中的
根据上述分析可知,CNS/SINS组合导航系统在进行姿态融合时,量测值一步预测误差
| $ \boldsymbol{C}_n^{n^{\prime}}=\boldsymbol{C}_{b(k)}^n\left[\boldsymbol{C}_{n^{\prime}(k \mid k-1)}^b\right]^{\mathrm{T}} $ | (20) |
根据式(16)的定义,可以得到量测值一步预测误差为:
| $ \left(\boldsymbol{Z}_k-\hat{\boldsymbol{Z}}_{k \mid k-1}\right) \triangleq\left[\begin{array}{l} \boldsymbol{C}_n^{n^{\prime}}(2, 3) \\ \boldsymbol{C}_n^{n^{\prime}}(3, 1) \\ \boldsymbol{C}_n^{n^{\prime}}(1, 2) \end{array}\right] $ | (21) |
式中,Cnn′(2, 3) 为矩阵Cnn′的第2行第3列元素,以此类推。
3 仿真结果及分析 3.1 仿真条件设定飞行器初始经度、纬度和高度分别为118°、29°、50 m,初始航向角、俯仰角和横滚角分别为90°、0°和0°,飞行时间为3 600 s,捷联解算周期为0.02 s,滤波周期为1 s。滤波初始参数设置如下:三维位置误差均为5 m,三维速度误差均为0.1 m/s,三维姿态角误差均为0.5°;陀螺随机游走驱动噪声及陀螺白噪声均为1°/h,加速度计随机游走驱动噪声及陀螺白噪声均为10-4g;CNS测角误差为300″,其采样周期为1 s。系统仿真在MATLAB7.1环境下进行,仿真轨迹如图 1所示。
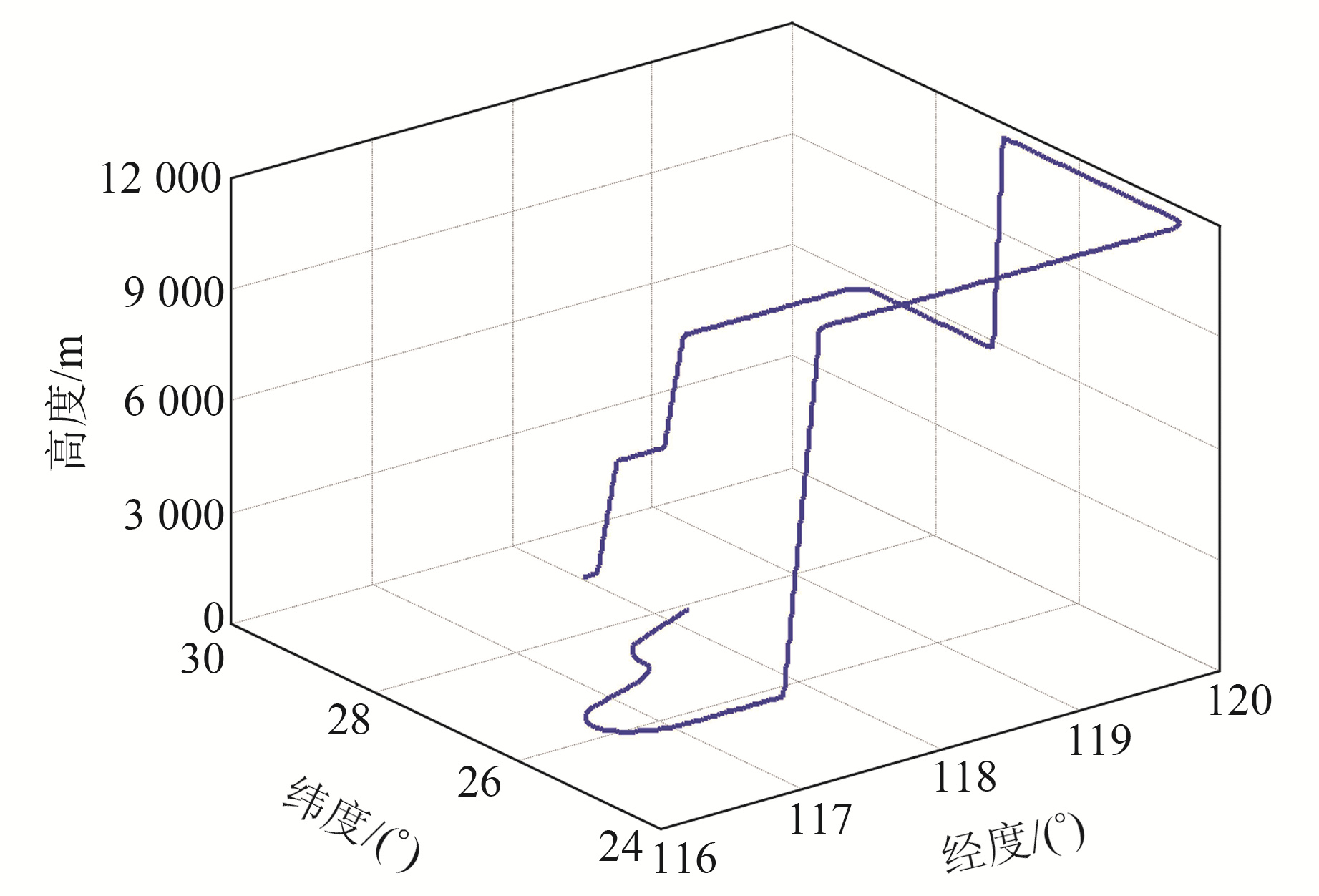
|
图 1 载体飞行轨迹 Fig. 1 Flight trajectory of carrier |
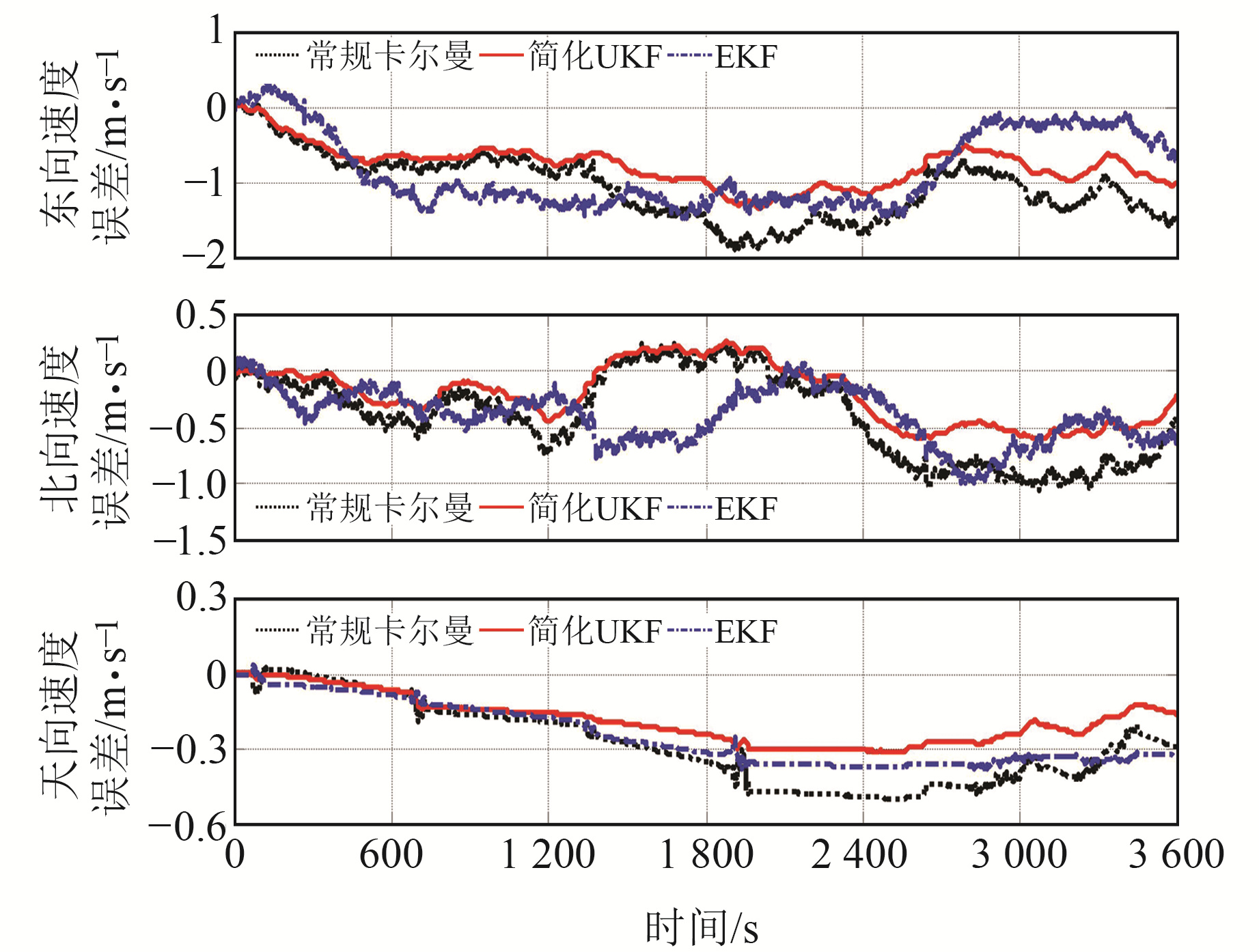
根据仿真初始条件的设定,对于相同导航传感器仿真的原始数据,本文分别进行了基于下述滤波模型的仿真实验:1)基于常规卡尔曼滤波[7-8];2)基于简化UKF算法;3)基于EKF算法[13]。图 2~4分别给出3组仿真实验结果的位置误差、速度误差及姿态误差对比曲线,可以看出,3种算法均可有效抑制位置及速度的发散,使姿态角处于收敛状态,且本文简化UKF算法的效果要优于常规卡尔曼滤波及EKF算法。

|
图 2 位置误差曲线对比 Fig. 2 Position error curve |
|
图 3 速度误差曲线对比 Fig. 3 Velocity error curve |

|
图 4 姿态误差曲线对比 Fig. 4 Attitude error curve |
为更加具体形象地说明3种滤波算法对姿态角的滤波效果,表 1给出实验结果数据统计的对比分析。可以看出,简化UKF算法的姿态角滤波精度比EKF算法提高了约9%,比常规卡尔曼滤波算法提高了约14%。
|
|
表 1 姿态均方误差统计对比 Tab. 1 Statistical comparison of attitude RMS errors |
为研究本文算法对滤波器初始三维姿态角误差的敏感度,分别在初始三维姿态角误差为1°及300″的情况下,对三维姿态角的均方差(即平台角误差)进行仿真,时长为600 s。图 5给出了平台角误差的协方差仿真曲线,可以看出,在2种滤波器初始三维姿态角误差的条件下,本文算法得到的平台角误差协方差曲线完全重合,即本文算法对滤波器初始三维姿态角误差的敏感度极低。为对滤波器初始阶段协方差曲线的细节有更完全的描述,仅取图 5中1~4 s时间段进行对比,具体如图 6所示。可以看出,在2种初始条件下,经过3次滤波后本文算法得到的平台角误差协方差曲线完全重合,进一步说明了本文算法对滤波器初始三维姿态角误差的鲁棒性极高。
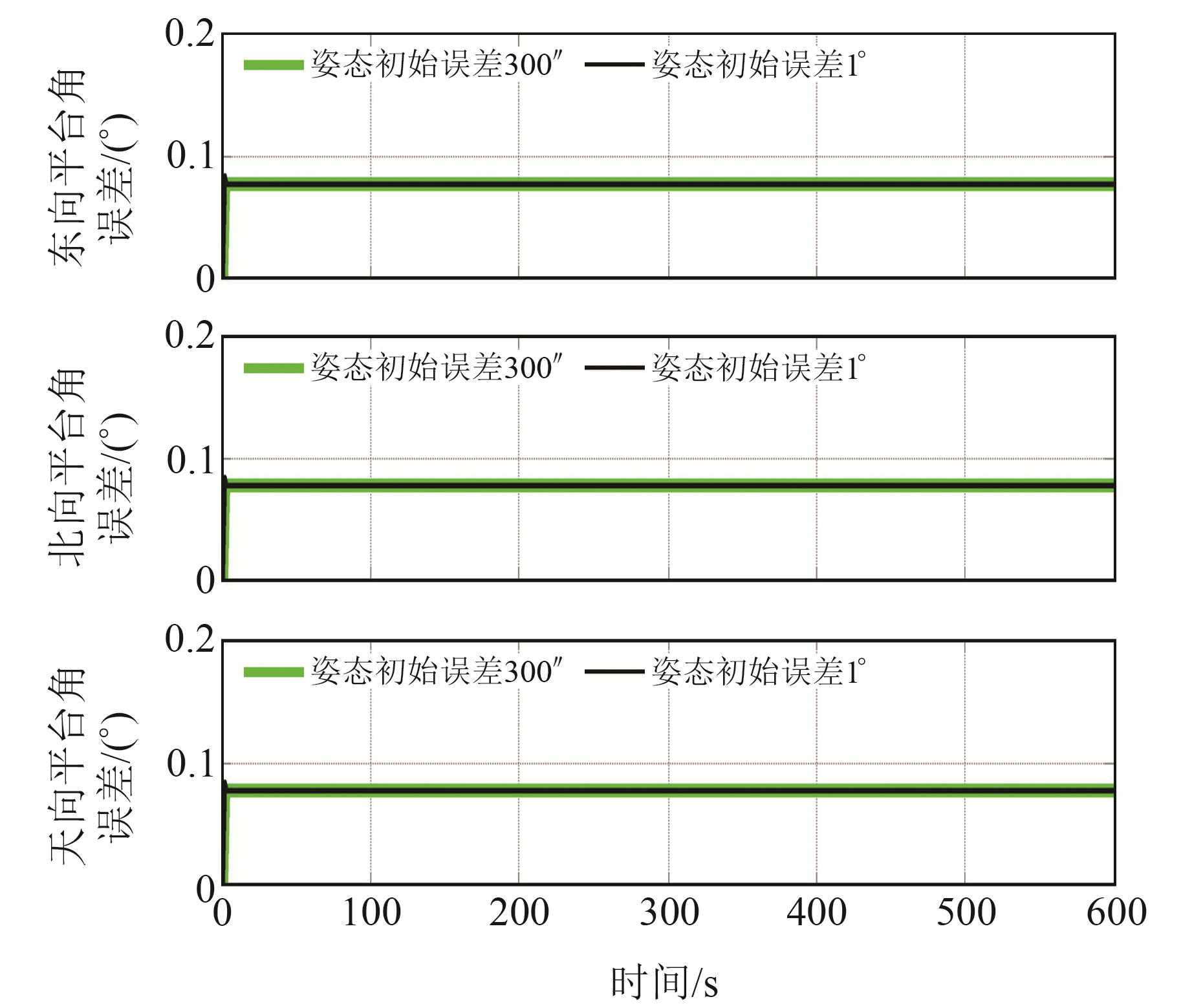
|
图 5 不同滤波器初始姿态误差角条件下的平台误差角协方差对比曲线 Fig. 5 Platform angle error covariance contrast curve under the condition of different filter initial attitude error |
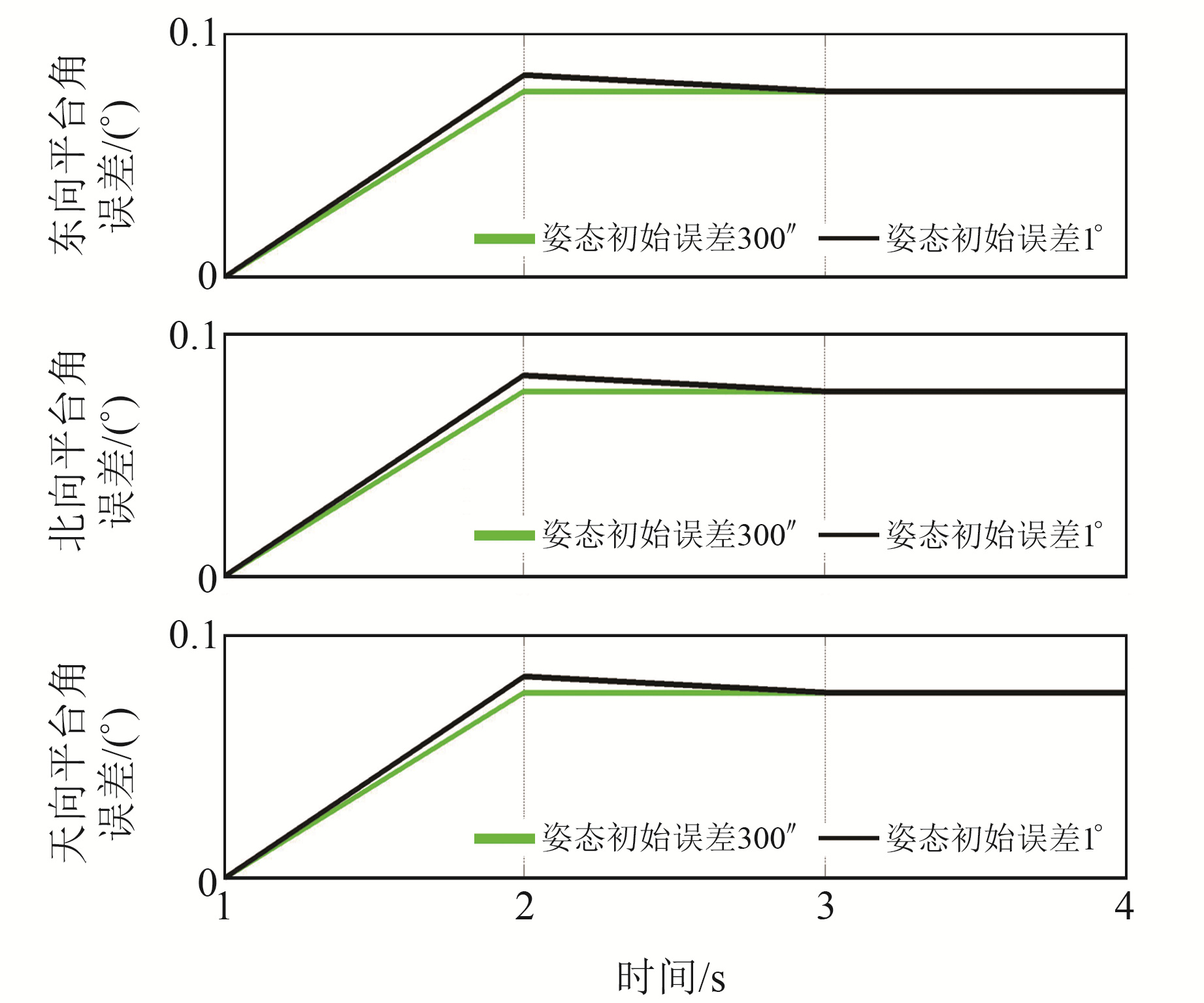
|
图 6 图 5中起始时间段内的平台角误差协方差对比曲线 Fig. 6 Platform angle error covariance contrast curve during the starting period of Fig. 5 |
基于图 2~4的仿真实验,对标准UKF算法及本文简化UKF算法的计算量进行对比分析。从表 2可以看出,简化UKF算法的计算时间比标准UKF算法减少了18.5%,有效地降低了算法的复杂度。
|
|
表 2 算法计算量分析 Tab. 2 Statistical comparison of experimental results |
CNS/SINS组合导航系统采用姿态融合的方式,其状态方程具有强非线性、量测方程具有线性的特点。当采用UKF算法对系统进行滤波时,由于姿态角样点、样点均值和样点方差的生成不同于以往GNSS/SINS组合导航系统模式,本文首先对标准UKF算法进行简化,在生成姿态角样点的基础上,借助于平台角误差这一概念设计了姿态角样点均值及方差的生成过程;同样,借助于平台角误差,设计了量测更新过程中的量测一步预测误差生成过程。仿真结果表明,本文算法具有比常规卡尔曼滤波及EKF算法更高的导航精度,同时本文算法对滤波器初始三维姿态角误差具有更高的鲁棒性。
| [1] |
Wang K D, Zhu T Q, Qin Y J, et al. Integration of Star and Inertial Sensors for Spacecraft Attitude Determination[J]. Journal of Navigation, 2017, 70(6): 1335-1348 DOI:10.1017/S0373463317000339
(  0) 0) |
| [2] |
房建成. 天文导航原理及应用[M]. 北京: 北京航空航天大学出版社, 2006 (Fang Jiancheng. Principle and Application of Celestial Navigation[M]. Beijing: Beihang University Press, 2006)
(  0) 0) |
| [3] |
西蒙. 最优状态估计: 卡尔曼, H∞及非线性滤波[M]. 张勇刚, 李宁, 奔粤阳, 译. 北京: 国防工业出版社, 2012 (Simon D. Optimal State Estimation—Kalman, H∞, and Nonlinear Approaches[M]. Zhang Yonggang, Li Ning, Ben Yueyang, translate. Beijing: National Defense Industry Press, 2012)
(  0) 0) |
| [4] |
李荣冰, 刘建业, 赖际舟, 等. Sigma-Point直接式卡尔曼滤波惯性组合导航算法[J]. 控制与决策, 2009, 24(7): 1018-1022 (Li Rongbing, Liu Jianye, Lai Jizhou, et al. Sigma-Point Direct Kalman Filtering Algorithm for Inertial Integrated Navigation System[J]. Control and Decision, 2009, 24(7): 1018-1022 DOI:10.3321/j.issn:1001-0920.2009.07.011)
(  0) 0) |
| [5] |
马晓杰, 林雪原, 孙巧妍, 等. 一种改进的UKF滤波算法在BDS/SINS组合导航系统中的应用研究[J]. 大地测量与地球动力学, 2021, 41(4): 351-356 (Ma Xiaojie, Lin Xueyuan, Sun Qiaoyan, et al. Improved UKF Algorithmfor BDS/SINS Integrated Navigation System[J]. Journal of Geodesy and Geodynamics, 2021, 41(4): 351-356)
(  0) 0) |
| [6] |
韩厚增, 王坚. 自适应UKF在GNSS/INS紧组合导航中的应用研究[J]. 大地测量与地球动力学, 2013, 33(6): 98-102 (Han Houzeng, Wang Jian. Study on Adaptive Unscented Kalman Filter and Its Application to GNSS/INS Tightly Coupled Navigation[J]. Journal of Geodesy and Geodynamics, 2013, 33(6): 98-102)
(  0) 0) |
| [7] |
Hu H D, Huang X L. SINS/CNS/GPS Integrated Navigation Algorithm Based on UKF[J]. Journal of Systems Engineering and Electronics, 2010, 21(1): 102-109 DOI:10.3969/j.issn.1004-4132.2010.01.017
(  0) 0) |
| [8] |
孟阳, 高社生, 高兵兵, 等. 基于UKF的INS/GNSS/CNS组合导航最优数据融合方法[J]. 中国惯性技术学报, 2016, 24(6): 746-751 (Meng Yang, Gao Shesheng, Gao Bingbing, et al. UKF-Based Optimal Data Fusion Method for Integrated INS/GNSS/CNS[J]. Journal of Chinese Inertial Technology, 2016, 24(6): 746-751)
(  0) 0) |
| [9] |
潘加亮, 熊智, 王丽娜, 等. 一种简化的发射系下SINS/GPS/CNS组合导航系统无迹卡尔曼滤波算法[J]. 兵工学报, 2015, 36(3): 484-491 (Pan Jialiang, Xiong Zhi, Wang Lina, et al. A Simplified UKF Algorithm for SINS/GPS/CNS Integrated Navigation System in Launch Inertial Coordinate System[J]. Acta Armamentarii, 2015, 36(3): 484-491 DOI:10.3969/j.issn.1000-1093.2015.03.016)
(  0) 0) |
| [10] |
Gupta M, Behera L, Subramanian V K, et al. A Robust Visual Human Detection Approach with UKF-Based Motion Tracking for a Mobile Robot[J]. IEEE Systems Journal, 2015, 9(4): 1362-1375
(  0) 0) |
| [11] |
Julier S J, Uhlmann J K. Unscented Filtering and Nonlinear Estimation[J]. Proceedings of the IEEE Aerospace and Electronic Systems, 2004, 92(3): 401-422
(  0) 0) |
| [12] |
袁信, 俞济祥, 陈哲. 导航系统[M]. 北京: 航空工业出版社, 1993 (Yuan Xin, Yu Jixiang, Chen Zhe. Navigation System[M]. Beijing: Aviation Industry Press, 1993)
(  0) 0) |
| [13] |
Kim J, Vaddi S S, Menon P K, et al. Comparison between Nonlinear Filtering Techniques for Spiraling Ballistic Missile State Estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 313-328
(  0) 0) |
2. Aerosun Corporation, 188 Mid-Tianyuan Road, Nanjing 211100, China;
3. School of Chemistry and Chemical Engineering, Beijing Institute of Technology, 5 South-Zhongguancun Street, Beijing 100081, China
 2022, Vol. 42
2022, Vol. 42


