2. 航天晨光股份有限公司,南京市天元中路188号,211100;
3. 北京理工大学化学与化工学院,北京市中关村南大街5号,100081
无迹卡尔曼滤波(unscented Kalman filter,UKF)采用不敏变换原理,是一种基于确定性样点计算的非线性滤波方法,相对于扩展卡尔曼滤波(extended Kalman filter,EKF)及粒子滤波(particle filter,PF)算法,具有计算精度高、算法便于实现的优点,在目标跟踪、组合导航等领域得到较深入的研究[1-2]。目前,对于UKF算法的研究大多局限于线性滤波的范畴[3-4],并未发挥出UKF非线性滤波的优势。
GNSS/CNS/SINS组合导航系统作为一种辅助信息源全面的多传感器组合导航系统[5-6],以状态方程线性化为基础,常用的滤波方法为联邦卡尔曼滤波[7]。本文针对GNSS/CNS/SINS组合导航系统,引入序贯卡尔曼滤波思想,提出一种多传感器组合导航系统的序贯UKF最优融合算法。
1 组合导航系统非线性模型一般情况下,非线性系统的离散模型表示为:
| $ \left\{\begin{array}{l} \boldsymbol{X}_k=f\left(\boldsymbol{X}_{k-1}, \boldsymbol{u}_k, \boldsymbol{W}_k, k\right) \\ \boldsymbol{Z}_k=h\left(\boldsymbol{X}_{k-1}, \boldsymbol{V}_k, k\right) \end{array}\right. $ | (1) |
式中,f(·)、h(·) 为非线性函数;Xk为系统状态向量,其方差矩阵为Pk;k为当前离散时刻;uk为系统确定性控制项或输入项;Zk为根据辅助导航传感器而确定的量测向量;Wk和Vk分别为过程噪声向量和量测噪声向量,其方差矩阵分别为Qk和Rk。
基于非线性滤波模型的GNSS/CNS/SINS组合导航系统直接选取导航参数作为被估计的状态,采用捷联惯性导航系统的力学方程作为状态方程,选取N、E、U地理坐标系作为导航坐标系,其状态方程可表示为[8]:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot X}}(t) = f\left( {\mathit{\boldsymbol{X}}(t),\mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}},{\mathit{\boldsymbol{f}}^{\rm{b}}},t} \right)}\\ {\mathit{\boldsymbol{X}}(t) = {{\left[ {\begin{array}{*{20}{l}} \gamma &\theta &\varphi &{{v_E}}&{{v_N}}&{{v_U}}&\lambda &L&H \end{array}} \right]}^{\rm{T}}}} \end{array}} \right. $ | (2) |
式中,X(t) 为系统状态向量,包含9个导航参数:横滚角、俯仰角和航向角(γ、θ、φ),E向速度、N向速度和U向速度(vE、vN、vU),经度、纬度和高度(λ、L、H);ωibb、fb分别为陀螺仪及加速度计的原始输出;t为时间。
选取CNS输出的三维姿态作为观测量,相应的量测方程可表示为:
| $ \left\{\begin{array}{l} \boldsymbol{Z}^1(t)=\boldsymbol{H}_1(t) \boldsymbol{X}(t)+\boldsymbol{V}_1(t) \\ \boldsymbol{Z}^1(t)=\left[\begin{array}{lll} \gamma & \theta & \varphi \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{H}_1(t)=\left[\begin{array}{ll} \boldsymbol{I}_{3 \times 3} & \mathbf{0}_{3 \times 6} \end{array}\right] \end{array}\right. $ | (3) |
同理,选取GNSS输出的三维位置、三维速度作为观测量时,有相应的量测方程:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{Z}}^2}(t) = {\mathit{\boldsymbol{H}}_2}(t)\mathit{\boldsymbol{X}}(t) + {\mathit{\boldsymbol{V}}_2}(t)\\ {\mathit{\boldsymbol{Z}}^2}(t) = {\left[ {\begin{array}{*{20}{l}} {{v_E}}&{{v_N}}&{{v_U}}&\lambda &L&H \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{H}}_2}(t) = \left[ {\begin{array}{*{20}{l}} {{{\bf{0}}_{6 \times 3}}}&{{\mathit{\boldsymbol{I}}_{6 \times 6}}} \end{array}} \right] \end{array} \right. $ | (4) |
假设系统的先验状态、过程噪声及测量噪声相互独立,测量噪声向量Vj(t) 的方差矩阵为Rj(t)(j=1, 2)。对式(2)~(4)进行离散化,即可得到其离散化的非线性模型。
2 组合导航UKF算法的简化标准UKF算法针对的是状态方程及量测方程均为非线性的系统模型,而式(2)建立了非线性状态方程,式(3)、式(4)建立了线性量测方程,且量测噪声是加性的。下面以Z(t)= H(t)X(t)+V(t) 涵盖式(3)、式(4)两个量测方程,以方便问题的讨论。
2.1 组合导航标准UKF算法存在的问题在标准UKF算法中,通常将系统状态、过程噪声和量测噪声扩展成增广状态向量Xa:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}^a} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}^{\rm{T}}}}&{{\mathit{\boldsymbol{W}}^{\rm{T}}}}&{{\mathit{\boldsymbol{V}}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{\chi }}^a} = {\left[ {\begin{array}{*{20}{l}} {{{\left( {{\mathit{\boldsymbol{\chi }}^X}} \right)}^{\rm{T}}}}&{{{\left( {{\mathit{\boldsymbol{\chi }}^W}} \right)}^{\rm{T}}}}&{{{\left( {{\mathit{\boldsymbol{\chi }}^V}} \right)}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (5) |
式中,χa为Xa的样点向量。假设χX、χW和χV(Xk、Wk和Vk) 的维数分别为LX、Lw、Lv,则χa(Xa) 的维数n=Lx+Lw+Lv,且La=Lx+Lw。
标准UKF算法的样点个数为2n+1,复杂度为O[(2n+1)3];另,标准UKF算法将不敏变换(unsensitive transformation,UT)应用于状态方程与量测方程,使计算量进一步加大。显然,当Lx、Lw、Lv的值较高时,标准UKF运算量的增加非常显著,对于系统的实时性不利[9]。
同样,在标准UKF算法中,量测更新过程通过对2n+1个样点进行非线性计算后,将运算结果线性叠加,该过程的计算量较大。当量测方程是线性且量测噪声是加性时,可以对标准UKF算法进行简化,无需对状态量进行增广,以减少运算量[9]。
2.2 简化UKF的设计增广状态向量可简化为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}^a} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}^{\rm{T}}}}&{{\mathit{\boldsymbol{W}}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{\chi }}^a} = {\left[ {\begin{array}{*{20}{l}} {{{\left( {{\mathit{\boldsymbol{\chi }}^X}} \right)}^{\rm{T}}}}&{{{\left( {{\mathit{\boldsymbol{\chi }}^W}} \right)}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (6) |
式中,χa的维数定义为La,即La=Lx+Lw。具体计算步骤如下。
1) 初始化:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\widehat X}}}_0} = E\left[ {{\mathit{\boldsymbol{X}}_0}} \right]}\\ {{\mathit{\boldsymbol{P}}_0} = E\left[ {\left( {{\mathit{\boldsymbol{X}}_0} - {{\mathit{\boldsymbol{\widehat X}}}_0}} \right){{\left( {{\mathit{\boldsymbol{X}}_0} - {{\mathit{\boldsymbol{\widehat X}}}_0}} \right)}^{\rm{T}}}} \right]}\\ {\mathit{\boldsymbol{\widehat X}}_0^a = E\left[ {{\mathit{\boldsymbol{X}}^a}} \right] = {{\left[ {\mathit{\boldsymbol{\widehat X}}_0^{\rm{T}}\quad {\bf{0}}} \right]}^{\rm{T}}}}\\ \begin{aligned} \mathit{\boldsymbol{P}}_0^a &= E\left[ {{\mathit{\boldsymbol{X}}^a}} \right] = E\left[ {\left( {\mathit{\boldsymbol{X}}_0^a - \mathit{\boldsymbol{\widehat X}}_0^a} \right) \times } \right.\\ & \left. {{{\left( {\mathit{\boldsymbol{X}}_0^a - \mathit{\boldsymbol{\widehat X}}_0^a} \right)}^{\rm{T}}}} \right] = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{P}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{Q}} \end{array}} \right] \end{aligned} \end{array}} \right. $ | (7) |
2) 样点计算:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\chi }}_{0, k - 1}^a = \mathit{\boldsymbol{\widehat X}}_{k - 1}^a}\\ \begin{array}{l} \mathit{\boldsymbol{\chi }}_{i, k - 1}^a = \mathit{\boldsymbol{\widehat X}}_{k - 1}^a + {\left( {\sqrt {{L_a}\mathit{\boldsymbol{P}}_{k - 1}^a} } \right)_i}, \\ \ \ \ \ i = 1, \cdots , {L_a} \end{array}\\ \begin{array}{l} \mathit{\boldsymbol{\chi }}_{i, k - 1}^a = \mathit{\boldsymbol{\widehat X}}_{k - 1}^a - {\left( {\sqrt {{L_a}\mathit{\boldsymbol{P}}_{k - 1}^a} } \right)_i}, \\ \ \ \ \ i = {L_a} + 1, \cdots , 2{L_a} \end{array} \end{array}} \right. $ | (8) |
| $ \left\{\begin{array}{l} \boldsymbol{W}_0^m=0 \\ \boldsymbol{W}_0^c=2 \\ \boldsymbol{W}_i^m=\boldsymbol{W}_i^c=\frac{1}{2 L_a}, i=1, \cdots, 2 L_a \end{array}\right. $ | (9) |
3) 时间更新:
| $ \left\{\begin{array}{l} \boldsymbol{\chi}_{i, k \mid k-1}^X=f\left(\boldsymbol{\chi}_{i, k-1}^X, \boldsymbol{\chi}_{i, k-1}^W\right) \\ \hat{\boldsymbol{X}}_{k \mid k-1}=\sum\limits_{i=0}^{2 L_a} \boldsymbol{W}_i^m \boldsymbol{\chi}_{i, k \mid k-1}^X \end{array}\right. $ | (10) |
| $ \begin{aligned} \boldsymbol{P}_{k \mid k-1}= & \sum\limits_{i=0}^{2 L_a} W_i^c\left[\boldsymbol{\chi}_{i, k \mid k-1}^X-\hat{\boldsymbol{X}}_{k \mid k-1}\right] \times \\ & {\left[\boldsymbol{\chi}_{i, k \mid k-1}^X-\hat{\boldsymbol{X}}_{k \mid k-1}\right]^{\mathrm{T}} } \end{aligned} $ | (11) |
4) 量测更新:
| $ \hat{\boldsymbol{Z}}_{k \mid k-1}=\boldsymbol{H} \hat{\boldsymbol{X}}_{k \mid k-1} $ | (12) |
| $ \left\{\begin{array}{l} \boldsymbol{P}_{Z Z}=\boldsymbol{H P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R} \\ \boldsymbol{P}_{X Z}=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} \end{array}\right. $ | (13) |
5) 滤波更新:
| $ \left\{\begin{array}{l} \boldsymbol{K}_k=\boldsymbol{P}_{X Z} \boldsymbol{P}_{Z Z}^{-1} \\ \hat{\boldsymbol{X}}_k=\hat{\boldsymbol{X}}_{k \mid k-1}+\boldsymbol{K}_k\left(\boldsymbol{Z}_k-\hat{\boldsymbol{Z}}_{k \mid k-1}\right) \\ \boldsymbol{P}_k=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{K}_k \boldsymbol{P}_{Z Z} \boldsymbol{K}_k^{\mathrm{T}}=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{K}_k \boldsymbol{P}_{\mathrm{X}}^{\mathrm{T}} \end{array}\right. $ | (14) |
为了将UKF算法应用于多传感器组合导航系统,最直观的方法是借鉴集中式卡尔曼滤波器,即将所有传感器的量测信息在一步量测更新中同时加以处理。该方法的优点是便于工程实现,但缺点在于一旦某个传感器失效,错误数据将污染整个滤波器,同时引起计算量增加、容错性差及通信负担重等新问题。为了解决该问题,可借鉴分布式滤波、序贯滤波等思想。
为此,本文将序贯卡尔曼滤波算法与简化UKF算法进行融合,进而得到适用于多传感器组合导航系统的序贯UKF算法。具体步骤如下。
1) 初始化:与式(7)相同。
2) 样点计算:与式(8)、式(9)相同。
3) 时间更新:与式(10)、式(11)相同。
4) 量测更新:
| $ \hat{\boldsymbol{Z}}_{k \mid k-1}^j=\boldsymbol{H}_j \hat{\boldsymbol{X}}_k^{j-1} $ | (15) |
| $ \left\{\begin{array}{l} \boldsymbol{P}_{Z Z}^j=\boldsymbol{H}_j \boldsymbol{P}_k^{j-1}\left(\boldsymbol{H}_j\right)^{\mathrm{T}}+\boldsymbol{R}_j \\ \boldsymbol{P}_{X Z}^j=\boldsymbol{P}_k^{j-1}\left(\boldsymbol{H}_j\right)^{\mathrm{T}} \end{array}\right. $ | (16) |
式中,j=1, 2,
5) 滤波更新:
| $ \left\{\begin{array}{l} \boldsymbol{K}_k^j=\boldsymbol{P}_{\mathrm{XZ}}^j\left(\boldsymbol{P}_{Z Z}^j\right)^{-1} \\ \hat{\boldsymbol{X}}_k^j=\hat{\boldsymbol{X}}_k^{j-1}+\boldsymbol{K}_k^j\left(\boldsymbol{Z}_k^j-\hat{\boldsymbol{Z}}_{k \mid k-1}^j\right) \\ \boldsymbol{P}_k^j=\boldsymbol{P}_k^{j-1}-\boldsymbol{K}_k^j \boldsymbol{P}_{Z Z}^j\left(\boldsymbol{K}_k^j\right)^{\mathrm{T}}=\boldsymbol{P}_k^{j-1}-\boldsymbol{K}_k^j\left(\boldsymbol{P}_{\mathrm{XZ}}^j\right)^{\mathrm{T}} \end{array}\right. $ | (17) |
式中,Pk= Pk2和
以飞行器作为仿真对象,飞行器航迹包括加速、爬升、旋转、降落等阶段,飞行时间为3 600 s,初始经度、纬度和高度分别为118°E、29°N、50 m,方向正北,水平姿态角为0°,捷联解算周期为0.02 s,滤波周期为1 s。滤波初始参数如下:三维位置误差均为5 m,三维速度误差均为0.1 m/s,三维姿态角误差均为0.5°,设置传感器精度如表 1所示。
|
|
表 1 仿真参数 Tab. 1 Simulation parameters |
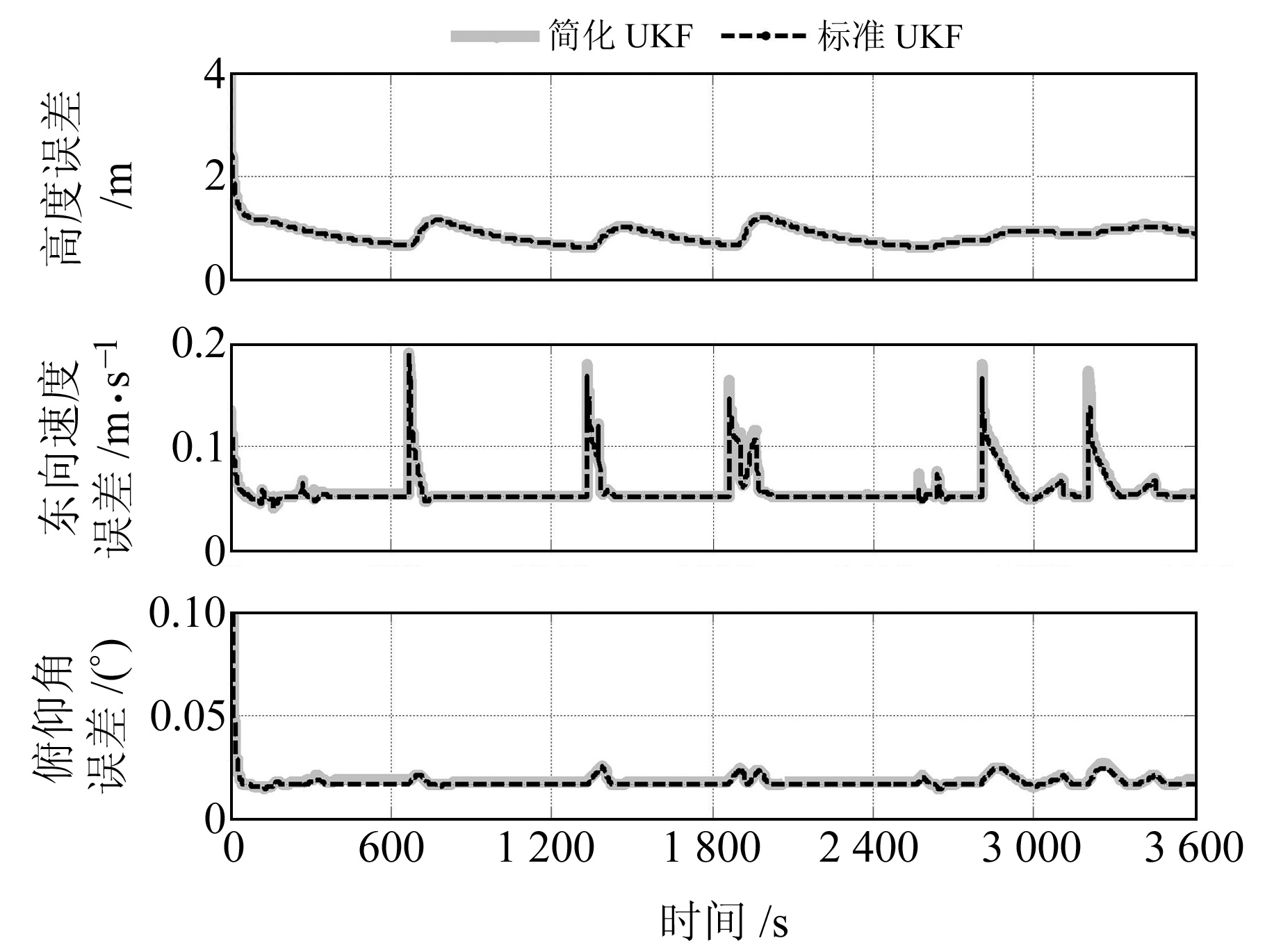
采用协方差分析法来评估标准UKF算法及简化UKF算法的估计精度,图 1给出部分导航参数误差对应的估计误差协方差曲线。可以看出,基于标准UKF算法与简化UKF算法的各导航参数估计误差的协方差曲线基本重合,即二者具有相同的滤波精度。
|
图 1 导航参数估计误差的协方差曲线 Fig. 1 Covariance curve of parameter estimation error |
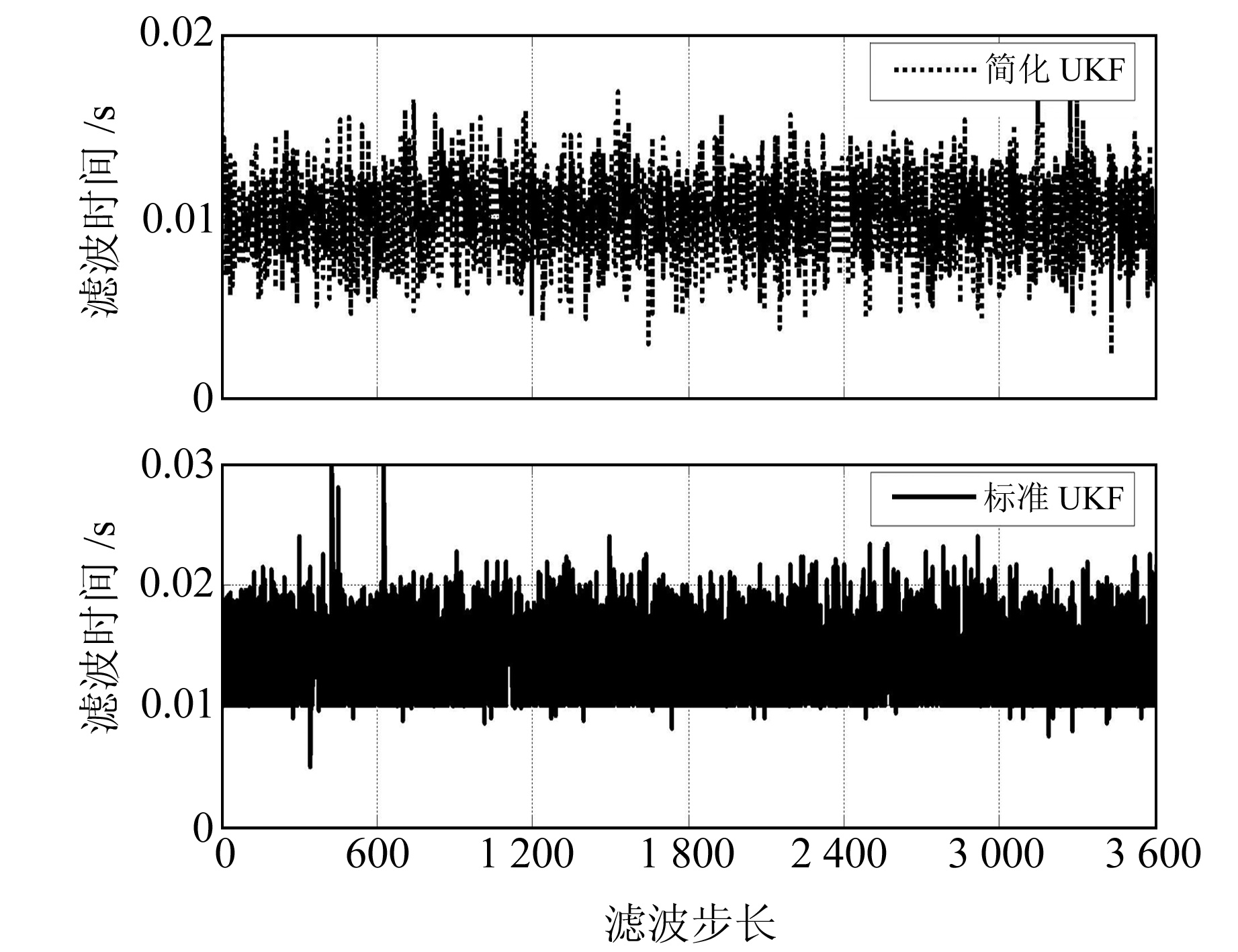
为比较标准UKF算法与简化UKF算法计算的复杂度,图 2列出二者的滤波时间对比。经统计,简化UKF算法最大滤波时间及平均滤波时间分别为0.016 0 s和0.011 0 s;而标准UKF算法最大滤波时间及平均滤波时间分别为0.030 0 s和0.013 5 s。考虑到捷联解算周期为0.02 s,简化UKF算法更容易保证系统的实时性,其计算时间比标准UKF算法减少约18%,运算量更小。
|
图 2 标准UKF与简化UKF的滤波时间对比 Fig. 2 Filtering time comparison between standard UKF and simplified UKF |
在以上分析的基础上,对GNSS/CNS/SINS多传感器组合导航系统进行序贯UKF算法实验。
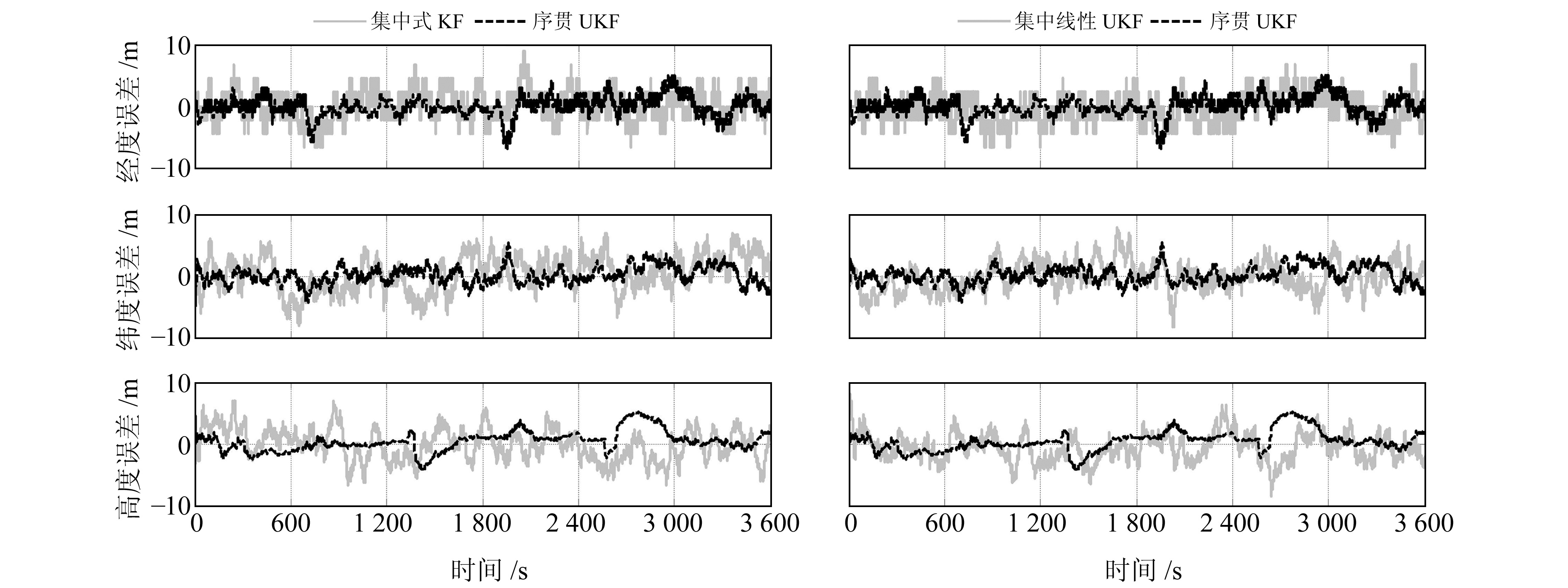
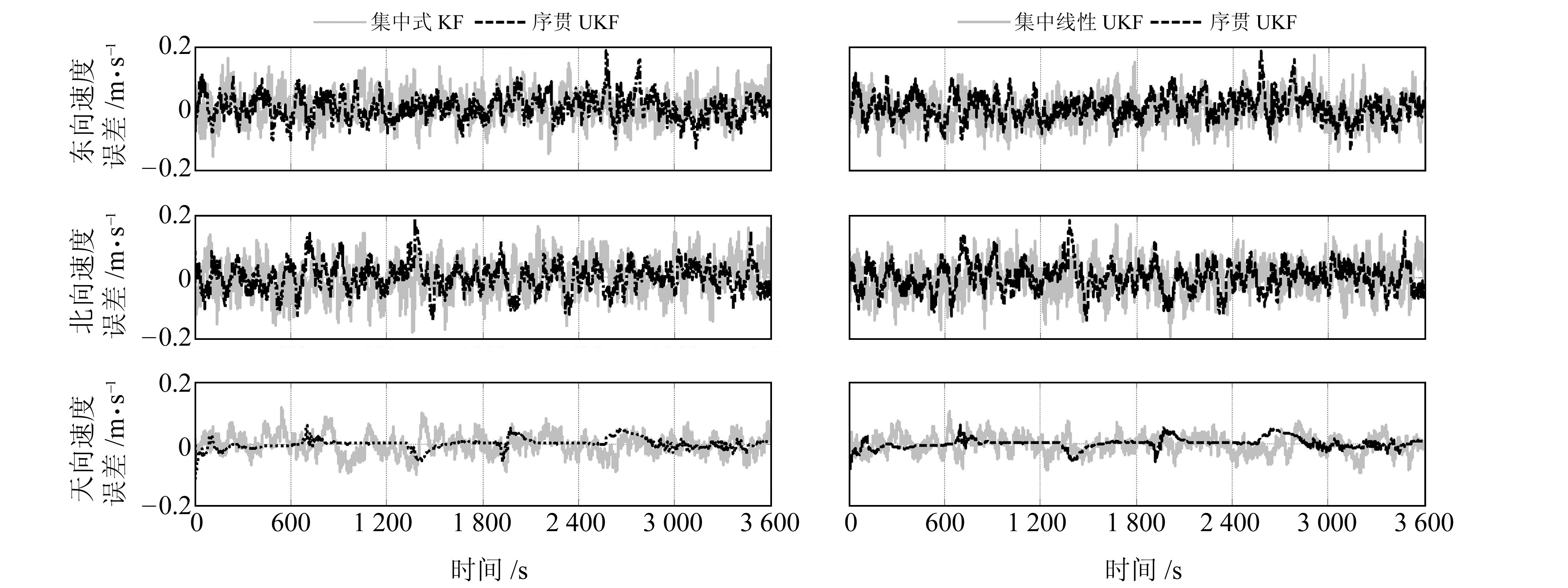
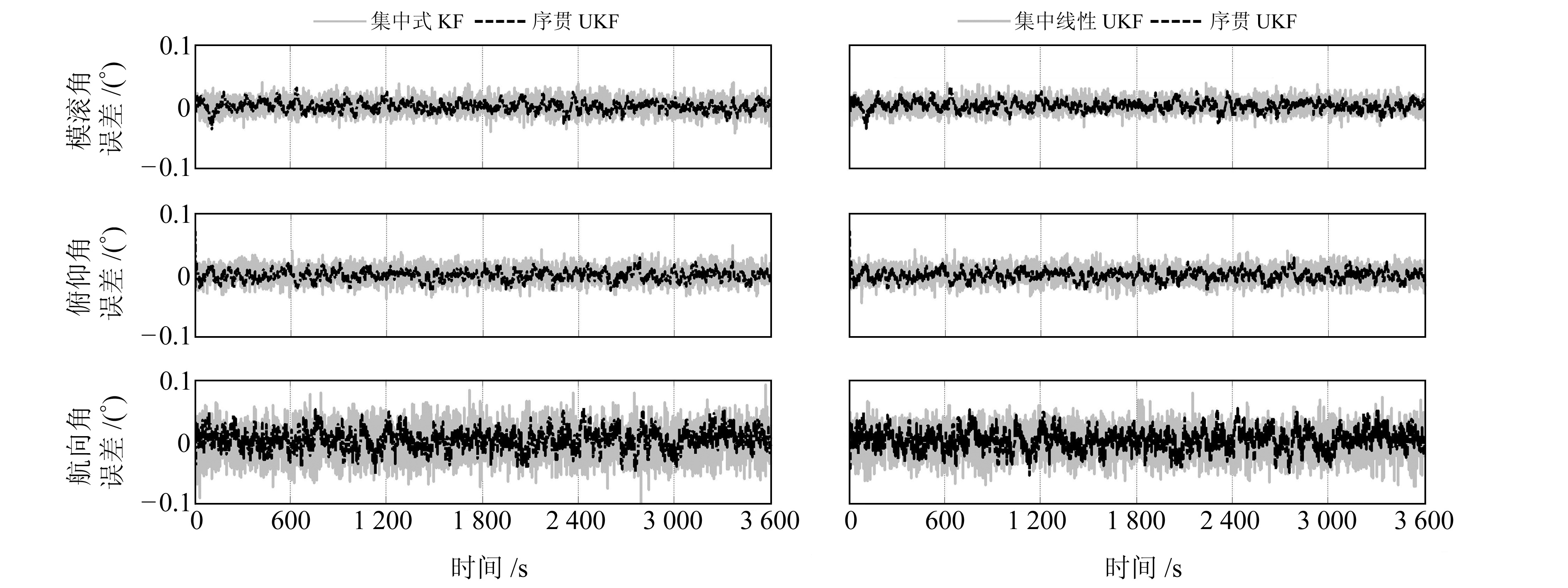
为验证本文算法的有效性,基于相同导航传感器仿真原始数据,分别进行3种滤波方案的处理:1) 集中式线性卡尔曼滤波方法(简称集中式KF算法);2)基于文献[3-4, 8]的集中UKF(简称集中线性UKF算法);3)本文算法(简称序贯UKF算法)。图 3~5为采用上述3种滤波算法求解得到的位置、速度及姿态误差曲线。
|
图 3 位置误差曲线对比 Fig. 3 Position error curve comparison |
|
图 4 速度误差曲线对比 Fig. 4 Speed error curve comparison |
|
图 5 姿态误差曲线对比 Fig. 5 Attitude error curve comparison |
根据图 3~5得到各导航参数的均方根误差(RMSE)统计结果如表 2所示,可以看出,相对于集中线性UKF算法及集中式KF算法,序贯UKF算法可分别降低32%和40%的位置误差,13.5%、19%的速度误差及20.3%、25.8%的姿态误差。
|
|
表 2 组合导航各参数均方根误差对比 Tab. 2 Comparison of RMSE of navigation parameters |
针对GNSS/CNS/SINS多传感器组合导航系统,在建立非线性状态方程及线性量测方程的基础上,设计简化UKF算法,降低标准UKF算法的计算量;通过引入序贯卡尔曼滤波原理,提出多传感器组合导航系统的序贯UKF最优融合算法。仿真实验结果表明,该算法不仅具有较低的计算量,同时具有较高的滤波精度,可为动态环境下多传感器组合导航系统的非线性估计提供一种有效的解决方法。
| [1] |
Xiong H L, Bian R C, Li Y J, et al. Fault-Tolerant GNSS/SINS/DVL/CNS Integrated Navigation and Positioning Mechanism Based on Adaptive Information Sharing Factors[J]. IEEE Systems Journal, 2020, 14(3): 3744-3754 DOI:10.1109/JSYST.2020.2981366
(  0) 0) |
| [2] |
曹娟娟, 房建成, 盛蔚, 等. 低成本多传感器组合导航系统在小型无人机自主飞行中的研究与应用[J]. 航空学报, 2009, 30(10): 1923-1929 (Cao Juanjuan, Fang Jiancheng, Sheng Wei, et al. Study and Application of Low-Cost Multi-Sensor Integrated Navigation for Small UAV Autonomous Flight[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1923-1929 DOI:10.3321/j.issn:1000-6893.2009.10.022)
(  0) 0) |
| [3] |
乔玉新, 林雪原, 张吉松, 等. 发射系下的SINS/CNS/GNSS组合导航UKF滤波算法[J]. 中国空间科学技术, 2021, 41(5): 103-109 (Qiao Yuxin, Lin Xueyuan, Zhang Jisong, et al. UKF Filtering Algorithm for SINS/CNS/GNSS Integrated Navigation in Launch Inertial Coordinate System[J]. Chinese Space Science and Technology, 2021, 41(5): 103-109)
(  0) 0) |
| [4] |
占荣辉, 张军, 欧建平. 非线性滤波理论与目标跟踪应用[M]. 北京: 国防工业出版社, 2013 (Zhan Ronghui, Zhang Jun, Ou Jianping. Nonlinear Filtering Theory with Target Tracking Application[M]. Beijing: National Defense Industry Press, 2013)
(  0) 0) |
| [5] |
Hu H D, Huang X L. SINS/CNS/GPS Integrated Navigation Algorithm Based on UKF[J]. Journal of Systems Engineering and Electronics, 2010, 21(1): 102-109 DOI:10.3969/j.issn.1004-4132.2010.01.017
(  0) 0) |
| [6] |
Ullah I, Shen Y, Su X, et al. A Localization Based on Unscented Kalman Filter and Particle Filter Localization Algorithms[J]. IEEE Access, 2019(8): 2233-2246
(  0) 0) |
| [7] |
Nowak T, Eidloth A. Dynamic Multipath Mitigation Applying Unscented Kalman Filters in Local Positioning Systems[C]. The 3rd European Wireless Technology Conference, Paris, 2010
(  0) 0) |
| [8] |
张闯, 赵修斌, 庞春雷, 等. SINS/GNSS/CNS组合导航自适应容错联邦滤波方法[J]. 控制理论与应用, 2019, 36(9): 1469-1476 (Zhang Chuang, Zhao Xiubin, Pang Chunlei, et al. Adaptive Fault Tolerance Federated Filter Method for SINS/GNSS/CNS Integrated Navigation[J]. Control Theory and Applications, 2019, 36(9): 1469-1476)
(  0) 0) |
| [9] |
周朋进, 吕志伟, 丛佃伟, 等. 改进的STUKF及其在多传感器信息融合中的应用[J]. 测绘科学技术学报, 2018, 35(4): 355-360 (Zhou Pengjin, Lü Zhiwei, Cong Dianwei, et al. An Improved Strong Tracking UKF Algorithm and Its Application in Multi-Sensor Information Fusion[J]. Journal of Geomatics Science and Technology, 2018, 35(4): 355-360)
(  0) 0) |
2. Aerosun Corporation, 188 Mid-Tianyuan Road, Nanjing 211100, China;
3. School of Chemistry and Chemical Engineering, Beijing Institute of Technology, 5 South-Zhongguancun Street, Beijing 100081, China
 2022, Vol. 42
2022, Vol. 42


