2. 应急管理部国家自然灾害防治研究院,北京市安宁庄路1号,100085;
3. 青海省地震局湟源地震台,西宁市波航乡,812199
目前,钻孔应变观测已成为地壳形变观测的一种重要手段,在地震监测预测领域发挥着重要作用。在我国的130多个钻孔应变观测站点中,绝大多数为“十五”期间规划、在2010年之前安装,这些仪器的数据采样率较低,均为分钟采样。利用这些分钟值数据,一些学者研究了不同地震的同震响应能力、同震应变阶跃、地震发震断层和发震构造等[1-3],由于受采样率低的限制,得到的研究成果相对有限,也制约了钻孔应变观测的进一步发展。近年来,高采样率四分量钻孔应变观测逐渐发展,产出了高采样率的观测数据,一些学者也利用这些高采样率数据开展相关研究[4-5],但这些研究都只采用了一种采样率数据,没有进行多种采样率数据的对比分析[6]。
通过2017~2020年陆续在青海湟源、甘肃高台等10个台站升级原YRY-4型四分量钻孔应变仪的数据采集器,提高采样率,产出4种不同采样率(分钟值、1 sps、10 sps和100 sps)数据,为研究不同采样率记录的同震波形提供了基础数据。需要说明的是,这4种不同采样率数据是由仪器厂家提供的数据采集器自动产出的原始数据,而非后续由更高采样率数据通过降采样产出。2021-05-22青海玛多M7.4地震也为开展4种不同采样率的钻孔应变数据观测同震变化的对比分析提供了很好的震例。本文基于该地震,主要以湟源台为例进行不同采样率下四分量钻孔应变观测同震变化的综合分析,探寻不同采样率四分量应变观测记录同震变化的特征,为未来定点形变站网规划中提高仪器采样率提供依据,也为正确使用不同采样率的观测数据提供说明和参考。
1 观测概况和数据目前,国内的四分量钻孔应变观测仪器主要有3种:RZB型、YRY-4型和SKZ-3型,观测原理基本相同,其观测的理论公式均为:
| $ s_\theta=A\left(\varepsilon_1+\varepsilon_2\right)+B\left(\varepsilon_1-\varepsilon_2\right) \cos 2(\theta-\emptyset) $ | (1) |
式中,ε1和ε2为水平主应变,Sθ为钻孔θ方向的孔径相对变化,Ø为ε1的方位角,系数A和B分别为套筒内、外径和围岩、填充水泥及套筒材料的杨氏模量和泊松比的函数。四分量钻孔应变仪的探头置于井下完整的基岩中,与孔壁耦合,探头中有4个水平放置的元件,相邻2个元件之间的夹角皆为45°,用来测量4个方向孔径的相对变化,这里按顺时针方向分别记为S1、S2、S3和S4。
玛多M7.4地震震中附近YRY-4型四分量钻孔应变观测台站空间分布如图 1所示,其中青海湟源和甘肃高台2个台站为高采样测点,台站距离该地震震中分别约345 km和552 km。本文主要以最近的湟源台为例进行不同采样率下四分量钻孔应变观测同震变化的综合分析,分钟值、1 sps、10 sps和100 sps四种不同采样率记录的玛多M7.4地震的同震变化曲线如图 2所示,均记录到了明显的同震变化,其中分钟值记录的波形信息明显不如其他3种采样率记录的波形信息丰富。

|
图 1 玛多M7.4地震震中附近YRY-4型四分量钻孔应变观测台站 Fig. 1 Maduo M7.4 earthquake and nearby YRY-4 borehole strainmeter stations |

|
图 2 湟源台钻孔应变记录的M7.4地震原始观测曲线 Fig. 2 Original observation curves of M7.4 earthquake recorded by borehole strainmeter at Huangyuan station |
四分量钻孔应变仪构成2组互相正交的孔径相对变化观测分量,根据式(1),任意选择一个元件的孔径相对变化测值,记为S1,依次顺时针转动45°,有元件测值S2、S3和S4。当探头与围岩的耦合处于理想状态时,理论上,任意2个互相正交方向的测值之和应相等:
| $ S_1+S_3=S_2+S_4 $ | (2) |
式(2)表达的关系式为四分量钻孔应变观测的一个重要特性[7],但是这4组测值实际上并不完全符合这个关系,而是有一定的误差,但大多数情况下,这个误差不会影响公式两边数值曲线的形态。
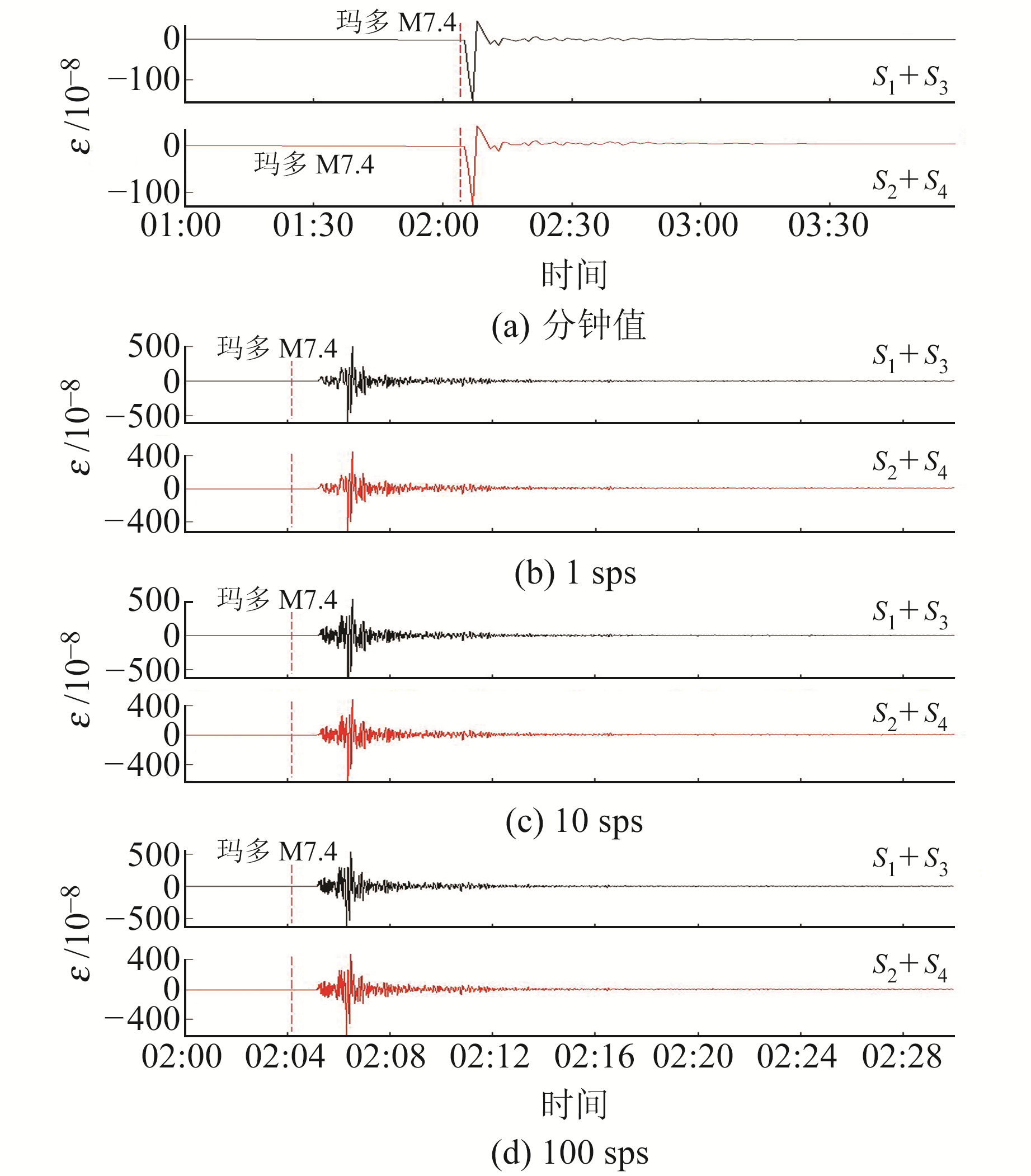
湟源台4种采样率分别记录的M7.4地震2组面应变(本文中2组面应变指的是S1+S3和S2+S4两组观测面应变)的同震观测曲线如图 3所示,各采样率的2组面应变变化形态基本一致,但变化幅度上有所差别,分钟值、1 sps、10 sps和100 sps观测的S1+S3的应变变化幅度分别为200×10-8、1 107×10-8、1 164×10-8、1 180×10-8,S2+S4的应变变化幅度分别为170×10-8、963×10-8、1 121×10-8、1 113×10-8。分钟值记录的应变变化幅度与其他3种较高采样相比差别较大,这也证明了分钟值记录地震波信息的能力不足,用分钟值数据研究同震变化幅度时将会产生信度不高的结果;不同采样率下,S1+S3的应变变化幅度均大于S2+S4的应变变化幅度;随着采样率提高,记录的2组面应变变化的幅度呈增大趋势,这证明了采样率越高,记录应变地震波信息的能力越强,但10 sps和100 sps记录的结果相差不大,这也说明10 sps已基本上记录了比较全面的应变地震波信息。
|
图 3 湟源台不同采样率下钻孔应变记录的M7.4地震面应变观测曲线 Fig. 3 Surface strain curves of M7.4 earthquake recorded by different sampling rates at Huangyuan station |
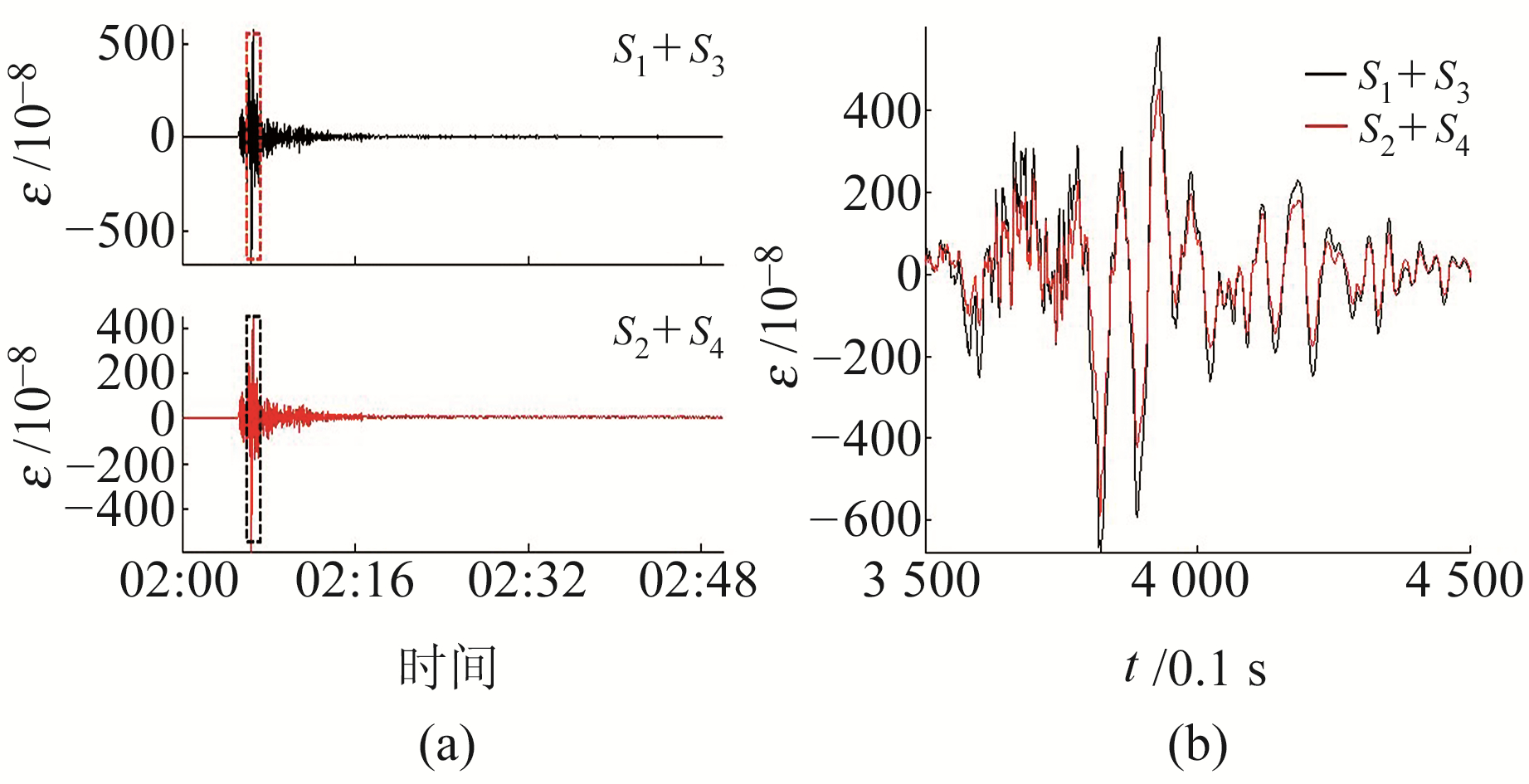
为更清晰地辨别2组面应变的一致性变化,以10 sps采样为例重新绘制图 3(c),方框选中部分(图 4(a))放大如图 4(b)所示,2组面应变地震波曲线基本重合,且可清晰地辨别出S1+S3的应变变化幅度大于S2+S4的应变变化幅度;另外,经过对1 sps和100 sps采样的观测数据作同样分析,也可得到类似的结果。这也初步说明在高采样率情况下,四分量钻孔应变观测的应变地震波符合四分量钻孔应变观测的自检特性。
|
图 4 10 sps采样记录的2组面应变 Fig. 4 Two sets of surface strain recorded by 10 sps sampling |
对于四分量钻孔应变观测,可通过2组面应变的相关系数来衡量观测数据的自检性能。根据式(2),等式两边可视为四分量钻孔应变观测的2组面应变,分别记为S13(S1与S3之和)和S24(S2与S4之和),2组面应变可计算一组相关系数,其计算公式为[8]:
| $ \begin{gathered} r= \\ \frac{\sum S_{13} S_{24}-\frac{\sum S_{13} \sum S_{24}}{N}}{\sqrt{\left(\sum S_{13}^2-\frac{\left(\sum S_{13}\right)^2}{N}\right)\left(\sum S_{24}^2-\frac{\left(\sum S_{24}\right)^2}{N}\right)}} \end{gathered} $ | (3) |
式中,r表示相关系数,N表示数据个数。
利用式(3)分别计算2个台站4种采样率记录的玛多M7.4地震同震时段2组面应变的相关系数(表 1)。从结果可知,1 sps结果的相关性最高,10 sps和100 sps的相关系数接近,但低于分钟值和1 sps的结果,这可能与更高采样率的观测数据记录到的高频噪声信息更多有关;另外,进一步分析认为,分钟值的相关系数之所以低于1 sps,可能与分钟值记录的应变地震波时段内样本数据过少有关,进行相关系数计算时用到了180个分钟值数据,而使用了1 800个1 sps采样数据。4种采样率下2组面应变均具有较强的相关性,相关系数均近乎等于1。这些定量分析的结果进一步说明,在不同采样率下,四分量钻孔应变观测的玛多M7.4地震的应变地震波均符合四分量钻孔应变观测的自检特性,说明四分量钻孔应变观测数据的信度较高。
|
|
表 1 2组面应变相关系数 Tab. 1 Correlation coefficient of two sets of surface strain |
地震发生时,钻孔应变仪会记录到同震变化,震级越大,同震变化越明显,且在观测曲线上可能会产生一种明显的阶跃变化,此种阶跃变化即为同震应变阶,国内外诸多学者曾对同震应变阶进行过相关研究[1-2, 9]。
根据同震应变阶的定义和研究,以湟源台第4分量(S4)分钟值和10 sps采样为例绘制了如图 5所示的同震应变阶曲线。可以看出,其应变阶的变化性质一致,2者均为张性应变阶;其变化大小也相当,均约为(8~9)×10-8。据此方法,统计了如表 2所示的4种采样各分量和2组面应变记录的本次地震同震应变阶,并进行对比分析。结果显示,同分量4种采样的应变阶变化性质一致,变化大小相当;不同分量4种采样的应变阶变化性质、大小不一样;2组面应变的应变阶的变化性质一致,变化大小差别较大,应是观测点接收到地震波发生瞬时震颤,破坏了元件、钢筒、水泥和岩石之间的相对均匀介质的耦合状态,但这和采样率无关。另外,对高台观测的同震应变阶也进行了分析,得到相同的结果。综合分析认为,对于四分量钻孔应变记录的同震应变阶,其变化性质和变化幅度与采样率关系不大,所以分钟值记录的应变地震波的波形信息虽缺失严重,但对于同震应变阶的研究与分析已足够,没有必要在该研究中使用高采样率观测数据。

|
图 5 湟源台分钟采样和10 sps采样记录的同震应变阶(S4) Fig. 5 Coseismic strain steps (S4) recorded by minute sampling and 10 sps sampling at Huangyuan station |
|
|
表 2 不同采样率的同震应变阶 Tab. 2 Coseismic strain steps of different sampling rates |
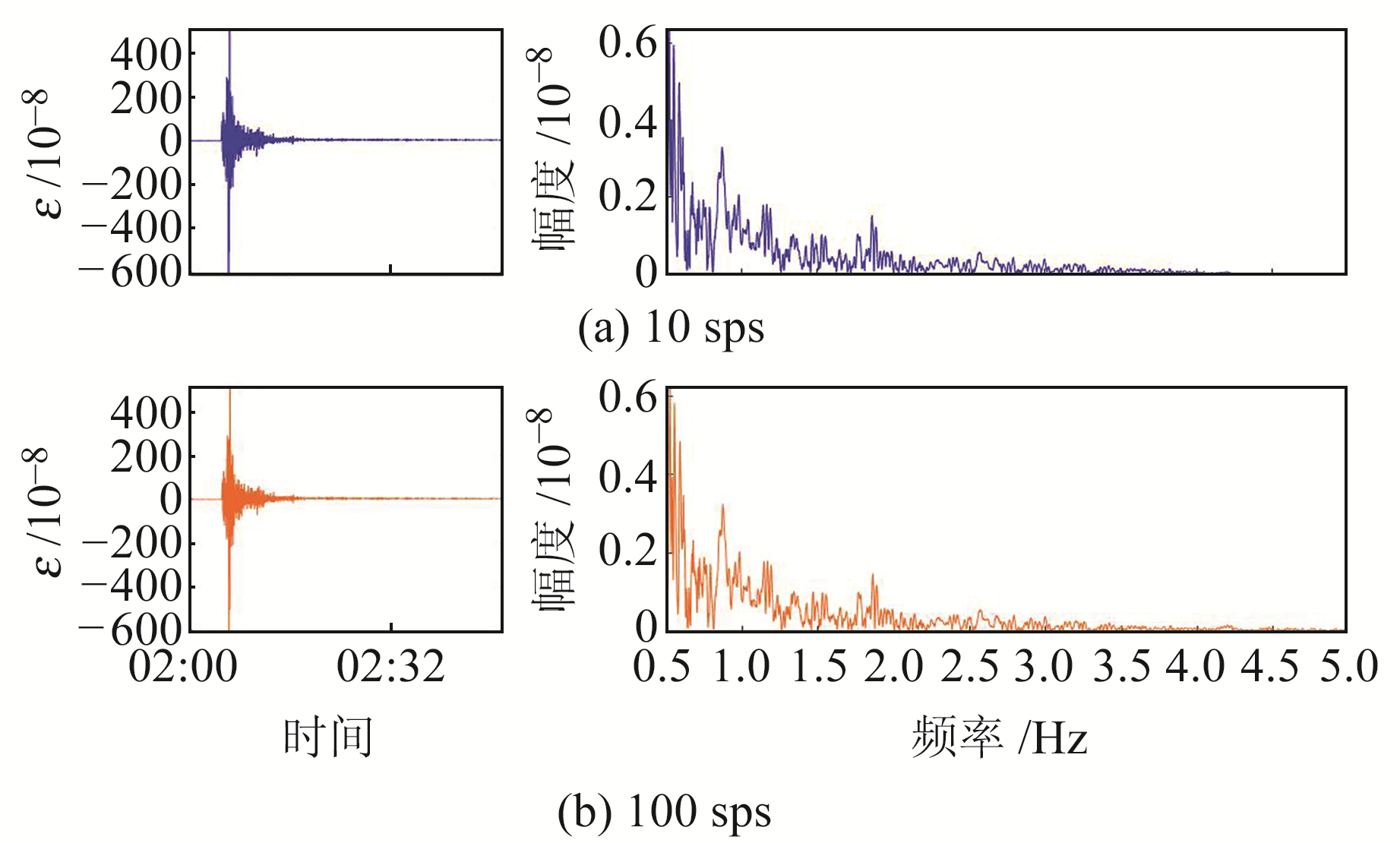
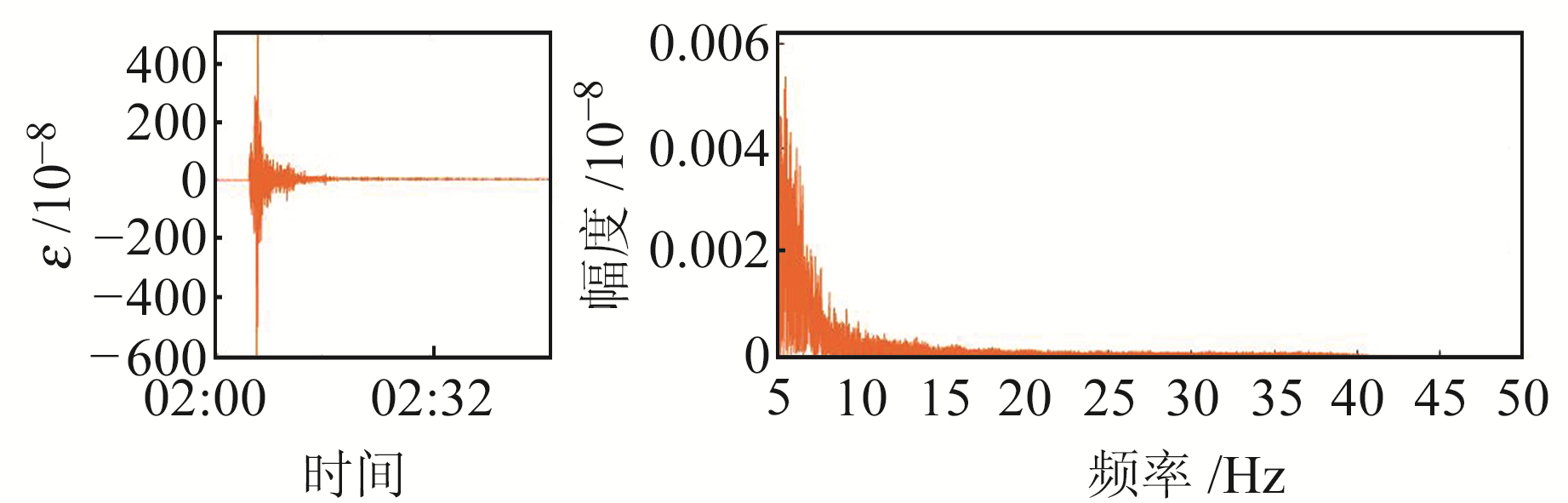
采用快速傅里叶变换和短时傅里叶变换分析方法,分别对4种采样的观测数据进行幅频分析和时频分析。为整体反映四分量观测数据信息,以面应变S作为研究数据分别给出幅频分析和时频分析结果,其中S=(S1+S3+S2+S4)/2。首先对研究数据进行幅频分析,图 6显示的是0~0.5 Hz频段4种采样率下面应变的傅里叶振幅谱,与其他采样相比,分钟值数据记录的信息有限,只能记录到0~0.008 Hz频段的信息,信息缺失严重;在0~0.5 Hz频段,1 sps、10 sps和100 sps采样的频谱几乎一致,只有1 sps在0.4~0.45 Hz频段与其他2种稍有差别;在该频段,4种采样记录的振幅大体一致,最大振幅约为4×10-8。图 7显示的是0.5~5 Hz频段,可以看出,分钟值和1 sps采样已记录不到该频段信息,10 sps和100 sps采样的频谱在该频段也基本一致,但2种采样记录的振幅与0~0.5 Hz频段相比大幅度减小,最大振幅仅约为0.6×10-8。图 8显示的是5~50 Hz频段,可以看出,除了100 sps采样,其他3种采样已记录不到该频段的信息;在该频段,100 sps采样在5~15 Hz频段的记录还算相对明显,但与0~5 Hz频段相比振幅已变得非常小,仅为0.001~0.006×10-8;15 Hz以上频段已非常不清晰,难以从中分离出研究地震的有效信息。

|
图 6 0~0.5 Hz频段4种采样率下面应变的傅里叶振幅谱 Fig. 6 Fourier amplitude spectrum of surface strain at four sampling in 0-0.5 Hz |
|
图 7 0.5~5 Hz频段10 sps和100 sps采样面应变的傅里叶振幅谱 Fig. 7 Fourier amplitude spectrum of surface strain at 10 sps and 100 sps sampling in 0.5-5 Hz |
|
图 8 5~50 Hz频段100 sps采样面应变的傅里叶振幅谱 Fig. 8 Fourier amplitude spectrum of surface strain at 100 sps sampling in 5-50Hz |
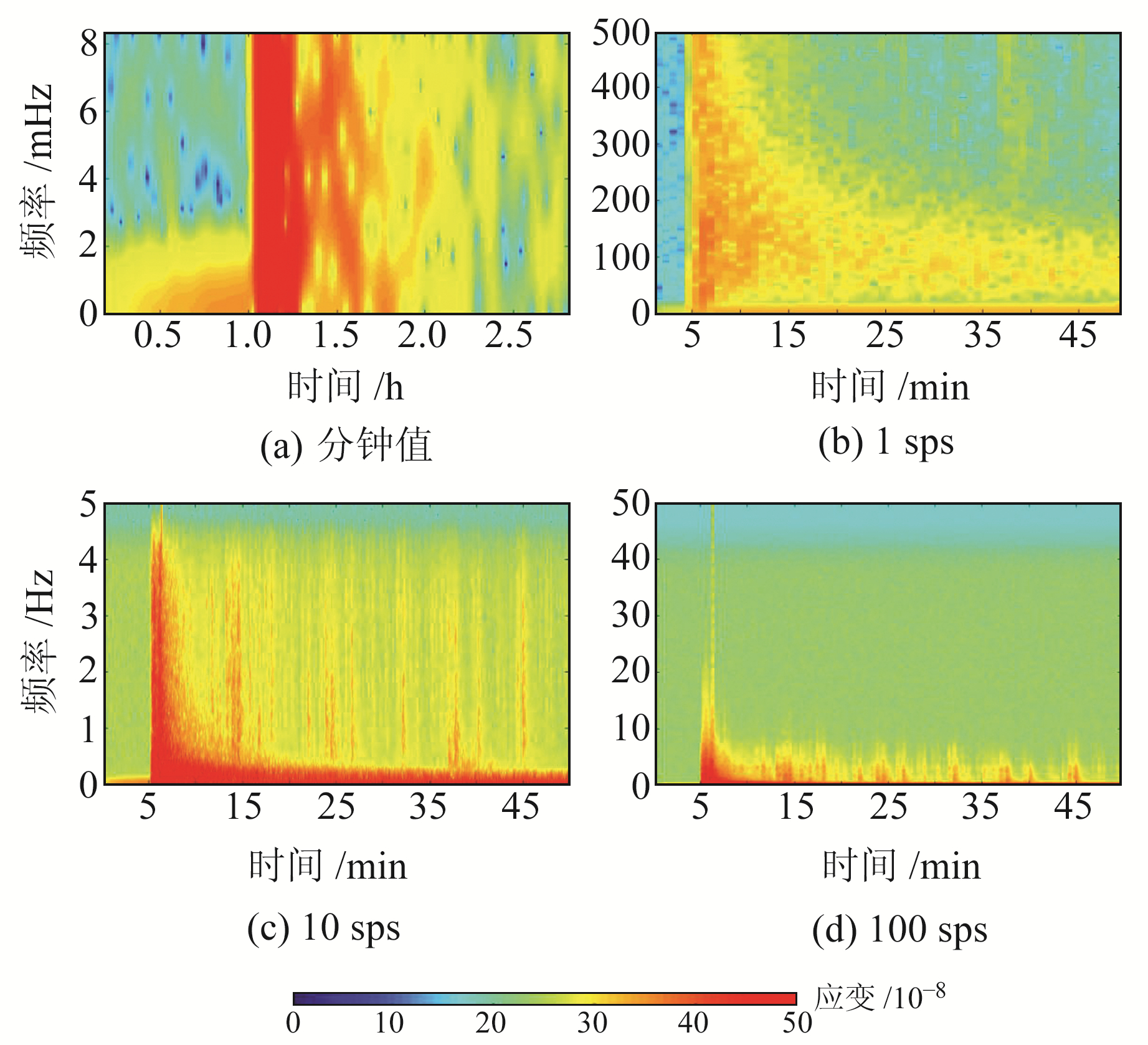
同样,采用短时傅里叶变换分析方法对研究数据进行时频分析。需要说明的是,为获取足够的样本数进行分析,分钟值数据选取地震前后3 h数据,其他3种采样选取地震前后50 min数据。图 9为4种采样率下面应变的时频分析结果,可以看出:1)分钟采样的时频谱显示,低于3 mHz的信号为背景信号,在分钟采样记录能力的0~8 mHz频段,震后1 h内,除背景信息外,也一直记录到了3~8 mHz频段的主震和余震信息,随着时间推移,也能偶尔记录到频率较高的余震信号;2)1 sps记录的0.2~0.5 Hz同震信号在15 min后逐渐减弱,主震的地震波信号和余震信号混叠;3)10 sps和100 sps采样可记录到清晰的主震和余震信息,这些信息的频段主要集中在0~4.5 Hz,但与10 sps采样相比,100 sps采样记录信号的能力并未显著提高,只是多记录到了少许4.5~8 Hz频段能量稍弱的信息;4)与幅频特性类似,100 sps采样在0~5 Hz频段记录的主震和余震信息最清晰,也能记录到5~10 Hz频段的信息,但记录不到大于10 Hz频段的余震信息。
|
图 9 4种采样率下面应变的傅里叶时频谱 Fig. 9 Fourier time spectrum of surface strain at four sampling rates |
整体分析可知,分钟值数据记录的地震信息有限,同震信号缺失严重;随着采样率提高,仪器记录的此次玛多地震主震和余震信息更丰富,但与10 sps采样相比,100 sps采样记录信号的能力并未显著提高,说明10 sps采样记录的地震信息已足够丰富,也间接说明了湟源台YRY-4型四分量钻孔应变仪器的整体频率响应可高至10Hz左右。另外,对震中距较远的高台地震台的记录也作了同样分析,得到的结果基本一致,但由于震中距较大、地震波衰减,高台记录的高频信息要比湟源台记录的高频信息少。
3 结语1) 分钟采样记录的应变变化曲线形态、变化幅度和傅里叶振幅谱等与其他3种较高采样结果相比差别较大,分钟采样记录的地震波信息缺失严重,若用分钟值数据进行地震波初动、同震变化幅度、同震变化定震级等研究将会得到信度较低的结论;采样率越高,四分量钻孔应变观测记录应变地震波信息的能力越强,但100 sps采样和10 sps采样记录的结果相差不大,10 sps采样已记录到比较全面的应变地震波信息。
2) 4种采样记录的玛多M7.4地震同震变化的2组面应变均具有较强的相关性,在不同采样率情况下,四分量钻孔应变观测的应变地震波均符合四分量钻孔应变观测的自检特性。但是,观测点接收到地震波发生瞬时震颤,破坏了元件、钢筒、水泥和岩石之间的相对均匀介质的耦合状态,引起2组面应变应变阶的变化性质或变化幅度差别较大,差别大小和破坏状态有关,所以大多数情况下,2组面应变的同震应变阶不符合四分量钻孔应变观测的自检特性。
3) 四分量钻孔应变记录的同震应变阶的变化性质和变化幅度与采样率关系不大,分钟值记录的应变地震波的波形信息虽缺失严重,但对于同震应变阶的研究与分析已足够,没有必要使用更高采样率的数据。
4) 基于钻孔应变仪器及数据处理技术的发展现状,过高的数据采样率将会提高对数据存储和网络传输的要求,对社会资源是一种浪费。因此,未来增设四分量钻孔应变仪时,应将现有分钟采样率提高,但也要适度,1 sps采样已足够满足同震变化的分析与研究;对于地震重点危险区内有特殊研究或观测需要的测点,采样率可提高至10~20 sps(美国PBO观测项目钻孔应变仪采样率为20 sps,可与其保持一致);如与测震观测进行联合分析,可提高至与测震观测的采样率一致。
| [1] |
邱泽华, 石耀霖. 地震造成远距离应力阶变的观测实例[J]. 中国科学D辑: 地球科学, 2003, 33(增1): 60-64 (Qiu Zehua, Shi Yaolin. Observation Examples of Long-Distance Stress Gradient Caused by Earthquakes[J]. Science in China Series D: Earth Sciences, 2003, 33(S1): 60-64)
(  0) 0) |
| [2] |
唐磊, 邱泽华, 郭燕平, 等. 日本9.0级地震引起的应变阶分析[J]. 地震地磁观测与研究, 2011, 32(6): 13-16 (Tang Lei, Qiu Zehua, Guo Yanping, et al. An Analysis on Strain Step Caused by MS9.0 Earthquake in Japan[J]. Seismological and Geomagnetic Observation and Research, 2011, 32(6): 13-16)
(  0) 0) |
| [3] |
卜祝源, 李玉江, 唐磊, 等. 基于钻孔应变观测约束的2016年新疆呼图壁M6.2地震的发震断层研究[J]. 地震研究, 2021, 44(1): 64-71 (Bu Zhuyuan, Li Yujiang, Tang Lei, et al. Seismogenic Fault of the 2016 Hutubi M6.2 Earthquake Constraint from the Borehole Strain Observations[J]. Journal of Seismological Research, 2021, 44(1): 64-71)
(  0) 0) |
| [4] |
范智旎, 万永革. 应变仪记录的印尼苏门答腊海域7.8级地震的同震信号研究[J]. 大地测量与地球动力学, 2020, 40(8): 849-853 (Fan Zhini, Wan Yongge. Study on Co-Seismic Signal of the M7.8 Earthquake in Sumatra, Indonesia, Recorded by Strainmeter[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 849-853)
(  0) 0) |
| [5] |
李富珍, 任天翔, 池顺良, 等. 基于钻孔应变观测资料分析远震造成的动态库仑应力变化[J]. 地球物理学报, 2021, 64(6): 1 949-1 974 (Li Fuzhen, Ren Tianxiang, Chi Shunliang, et al. The Dynamic Coulomb Stress Changes Caused by Remote Earthquakes Based on the Borehole Strainmeter Data[J]. Chinese Journal of Geophysics, 2021, 64(6): 1 949-1 974)
(  0) 0) |
| [6] |
薛兵. 关于地震观测系统中滤波器的讨论[J]. 地震, 2021, 41(1): 40-50 (Xue Bing. Discussion on Filters in Earthquake Observation Instruments[J]. Earthquake, 2021, 41(1): 40-50)
(  0) 0) |
| [7] |
邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 2005, 25(1): 118-122 (Qiu Zehua, Shi Yaolin, Ouyang Zuxi. Relative In-Situ Calibration of 4-Component Borehole Strain Observation[J]. Journal of Geodesy and Geodynamics, 2005, 25(1): 118-122)
(  0) 0) |
| [8] |
唐磊, 邱泽华, 宋茉. 钻孔四分量应变观测自检内精度分析[J]. 大地测量与地球动力学, 2010, 30(增2): 36-39 (Tang Lei, Qiu Zehua, Song Mo. Self-Test Accuracy of 4-Component Borehole Strain Observation[J]. Journal of Geodesy and Geodynamics, 2010, 30(S2): 36-39)
(  0) 0) |
| [9] |
邱泽华, 石耀霖. 观测应变阶在地震应力触发研究中的应用[J]. 地震学报, 2004, 26(5): 481-488 (Qiu Zehua, Shi Yaolin. Application of Observed Strain Steps to the Study of Remote Earthquake Stress Triggering[J]. Acta Seismologica Sinica, 2004, 26(5): 481-488)
(  0) 0) |
2. National Institute of Natural Hazards, MEM, 1 Anningzhuang Road, Beijing 100085, China;
3. Huangyuan Seismic Station of Qinghai Earthquake Agency, Bohang Town, Xining 812199, China
 2022, Vol. 42
2022, Vol. 42

