近年来,随着中国基础建设的蓬勃发展,各种复杂的大型工程建筑体日益增多[1],但施工条件和施工质量难以准确监测监控,高层建筑和大型设备设施坍塌事件时有发生,往往造成严重的人员伤亡和财产损失。如何减少这类事故的发生,已迫在眉睫。
形变数据监测是衡量建筑物结构安全稳定性的标尺[2],所以大力开展形变实时监测系统以及险情预警研究势在必行,这样有利于施工人员及时发现施工建筑存在的隐患,进而提高建筑物的安全性。然而在实际监测过程中,由于受到各种外界因素的影响,形变监测数据往往存在不稳定因素,如存在许多跳变点和尖峰,以及各时段的数据之间存在非线性、随机性[3]等情况,因此有必要关注沉降数据的去噪问题。
现今应用于形变监测的手段包括GNSS技术、常规大地测量、InSAR方法及其他专用测量技术[4],本文以钢架结构建筑物为例,采用GNSS技术获取监测站的实时差分定位(RTK)数据,开展将安全监测数据作精准测量数据处理的探索。目前在去噪处理方面使用的方法主要有傅里叶变换、经验模态分解、小波神经网络[5]等。考虑到CEEMD适用于非平稳信号的分析及小波分析在信号去噪方面的优良性能,本文采用CEEMD分解和小波变换混合去噪,降低数据处理过程产生的误差,提高信号还原精度。经仿真和实际验证,该方法适用于钢架监测数据的分析和处理,能够很好地反映出信号特征,避免有效信号的损失。
1 混合去噪方法 1.1 CEEMD分解Huang等[6]展示了一种崭新的时频分析手段——希尔伯特-黄变换(Hilbert-Huang transform,HHT)。该方法首先采用EMD(empirical mode decomposition)算法筛选非平稳信号,依据其信号特征自适应地分解成为一系列IMF分量及一个残余量;然后再对各个IMF分量进行希尔伯特变换,其结果能真实反映信号能量在时间及各尺度上的分布规律。传统的时频分析技术需要一定先验知识才能得到优良效果[7-8],可能还会受限于信号的线性及平稳性;EMD无须预先设定任何基函数,在理论上可以应用于任何信号的分解,其分解基于信号本身极值点的分布。但间断信号、脉冲干扰和噪声等成分会造成信号的间歇,这势必影响极值点的选取,由错误包络求得的IMF分量就会存在模态混叠问题,使IMF失去具体的物理意义。
Wu等[9]依据白噪声功率谱密度平均分布的特性提出一种噪声辅助分析方法(EEMD),其主要原理是在原始噪声信号中人为添加白噪声,为抵消白噪声带来的影响需要增加集合平均次数,这无疑增加了计算代价甚至可能带来误差。不仅如此,对白噪声幅度的考量也至关重要,当数值不满足要求时无法克服模态混叠。Yeh等[10]在2010年基于EEMD提出了互补集合经验模态分解(complementary EEMD,CEEMD),为减少EEMD残留的白噪声,取两次原始信号作为一组分别添加互为相反数的辅助白噪声,组与组之间相互独立,显著降低了集合平均次数,同时能减少分解迭代次数、提高计算效率,克服了EEMD分解完备性差、重构误差大的缺陷。
CEEMD分解主要依赖于EMD分解,共分为3个步骤:
1) 假定初始信号为x(t),在信号中添加正随机白噪声ξ0ui(t)和负随机白噪声-ξ0ui(t),得到xqi(t):
| $ \begin{gathered} x_q^i(t)=x(t)+(-1)^q \xi_0 u_i(t) \\ i=1,2, \cdots, L \quad q=1,2 \end{gathered} $ | (1) |
式中,ui(t) 是第i次添加的白噪声;ξ0是噪声幅度,一般为0.1~0.2倍信号标准差。
2) 对信号xqi(t)分别进行EMD分解,得到相应的IMFq, ki(t) 和残波rqi(t):
| $ x_q^i(t)=\sum\limits_{k=1}^K {\rm{IMF}}_{q, k}^i(t)+r_q^i(t) $ | (2) |
式中,k为本征模函数的阶数。
3) 重复步骤1)和2),直到i达到设定的正负白噪声的次数2M,然后对经过2M次EMD分解得到的IMFq, ki(t) 进行集合平均:
| $ \begin{gathered} \overline{{\mathrm{IMF}}_k}(t)= \\ \frac{1}{2 M} \sum\limits_{i=1}^M\left({\rm{IMF}}_{1, k}^i(t)+{\rm{IMF}}_{2, k}^i(t)\right) \end{gathered} $ | (3) |
各阶IMF分量集合平均后即为CEEMD分解的结果。
1.2 改进小波阈值去噪小波变换作为当代流行的时频分析方法,具备多尺度、去相关等性质[9],特别是对随机噪声的抑制效果良好。小波变换涉及到基函数选取,以及阈值函数、阈值规则和分解层数的选择。Dohono[10]于1995年提出阈值去噪方法,认为含噪信号在各尺度的分量其信噪能量是分离的,存在一个与小波系数w有关的临界阈值λ,当w>λ时,认为此时信号占据主要部分,需要保留;当w≤λ时,认为此时噪声为主体,应当将其舍弃,这便是硬阈值函数的由来。软阈值不是仅对噪声进行抑制,而是根据阈值的大小对小波系数进行向零逼近,最后对各个尺度下滤波信号进行重构,获得降噪信号。小波阈值去噪基本步骤如下:
1) 选取合理的分解层数和基函数,对原始含噪信号进行小波分析,获取低频系数和高频细节分量。
2) 对小波系数进行阈值处理,选择合适的阈值规则,采用全局阈值或分层阈值的方式,经由小波阈值函数的滤波保留期望的小波分量。
3) 利用小波逆变换重构各尺度分量,得到去噪信号。
硬阈值、软阈值方法是常用的阈值处理手段。硬阈值的函数表达式为:
| $ \hat{w}_{j, k}=\left\{\begin{array}{l} w_{j, k},\left|w_{j, k}\right|>\lambda \\ 0,\left|w_{j, k}\right| \leqslant \lambda \end{array}\right. $ | (4) |
软阈值函数的表达式为:
| $ \hat{w}_{j, k}=\left\{\begin{array}{l} {\rm{sign}}\left(w_{j, k}\right)\left(\left|w_{j, k}\right|-\lambda\right),\left|w_{j, k}\right|>\lambda \\ 0,\left|w_{j, k}\right| \leqslant \lambda \end{array}\right. $ | (5) |
硬阈值在阈值点存在突变点,函数值不连续,导致信号产生振荡,光滑度下降;而软阈值虽然没有间断点,但是处理前后的小波系数会存在恒定偏差,这将影响到信号的重构相似度。为克服以上两种方法的缺陷,在此提出新的阈值函数方法。
改进阈值函数的表达式为:
| $ \hat{w}_{j, k}=\left\{\begin{array}{l} u w_{j, k}+(1-u) {\rm{sign}}\left(w_{j, k}\right) \cdot \\ \quad\left(\left|w_{j, k}\right|-\frac{\lambda}{\log _2\left(2+t\left(\left|w_{j, k}\right|-\lambda\right)\right)}\right), \\ \left|w_{j, k}\right|>\lambda \\ 0,\left|w_{j, k}\right| \leqslant \lambda \end{array}\right. $ | (6) |
式中,

|
图 1 改进阈值函数与软、硬阈值函数 Fig. 1 Improved threshold function and soft and hard threshold functions |
对于含噪的形变监测信号,当有用信号含量比较低时,若采用小波阈值去噪,极大可能会将隐匿于大量噪声中的低幅值有用信号一并去除。如单纯使用CEEMD分解去噪时,通常根据相关性法则,在剔除噪声的过程中,含有最多噪声成分的高频IMF分量首先被剔除[8],这样会丧失高频有效信息。本文提出的方法是力图用CEEMD分解联合小波阈值去噪来处理钢架监测数据中的误差,弥补单一方法处理形变监测数据时存在的不足,提高监测精度。用混合方法进行去噪处理主要步骤如下:
1) 直接对含噪信号x(t) 进行CEEMD分解,得到各个IMF分量
2) 对各尺度IMF进行改进的小波阈值去噪;
3) 将滤波后的IMF分量
| $ x^{\prime}(t)=\sum\limits_{K=1}^K \overline{{\mathrm{IMF}}_k^{\prime}}(t)+r(t) $ | (7) |
按照正常EMD分解重构的流程,会将各个IMF分量作自相关,与含噪信号的自相关曲线进行对比分析,根据经验筛选处理后的IMF分量。由于随机噪声的自相关曲线是一个尖峰,而兴趣信号具备一定宽度的自相关主瓣,IMF分量自相关的表现会依据所含信号和噪声能量的比例逼近信号或噪声。本文对全部IMF分量作小波阈值去噪,不用考虑IMF分量的选择。
2 仿真实验为模拟长时间形变数据,采用MATLAB自带的Blocks标准测试信号,调节因子N取16,在原始信号中添加信噪比为-5 dB的白噪声还原真实的噪声环境。原始信号和带噪信号如图 2所示。

|
图 2 原始信号及带噪信号 Fig. 2 Original and noisy signals |
分别对带噪的信号进行EMD、CEEMD分解,CEEMD每次叠加白噪声的幅度ξ0选取为0.2倍的含噪信号标准差,循环叠加次数为100。由图 3可见,CEEMD分解能够有效处理模态混叠问题,而其效果取决于噪声幅度的选取。幅值过小的白噪声无法抵消环境噪声的影响,幅值过大的白噪声会直接导致原始信号失真。本文在此未检验白噪声幅值的影响。

|
图 3 带噪信号的EMD和CEEMD分解 Fig. 3 EMD and CEEMD decompositionof noisy signal |
为验证混合算法的可行性,针对原始信号分别进行3组实验,方案如下:1)直接进行软阈值和硬阈值去噪,统一选择极大极小规则进行分层阈值去噪,小波基函数为sym5,分解层数为5;2)对原始信号进行EMD和CEEMD分解重构,这里舍弃了IMF1至IMF4的分量,得到最优效果;3)在CEEMD分解的基础上保留所有IMF成分,采用改进阈值函数对每一个IMF成分进行去噪,其中改进阈值函数中t选为0.2,再采用软、硬阈值进行对比实验,最终去噪效果见图 4。
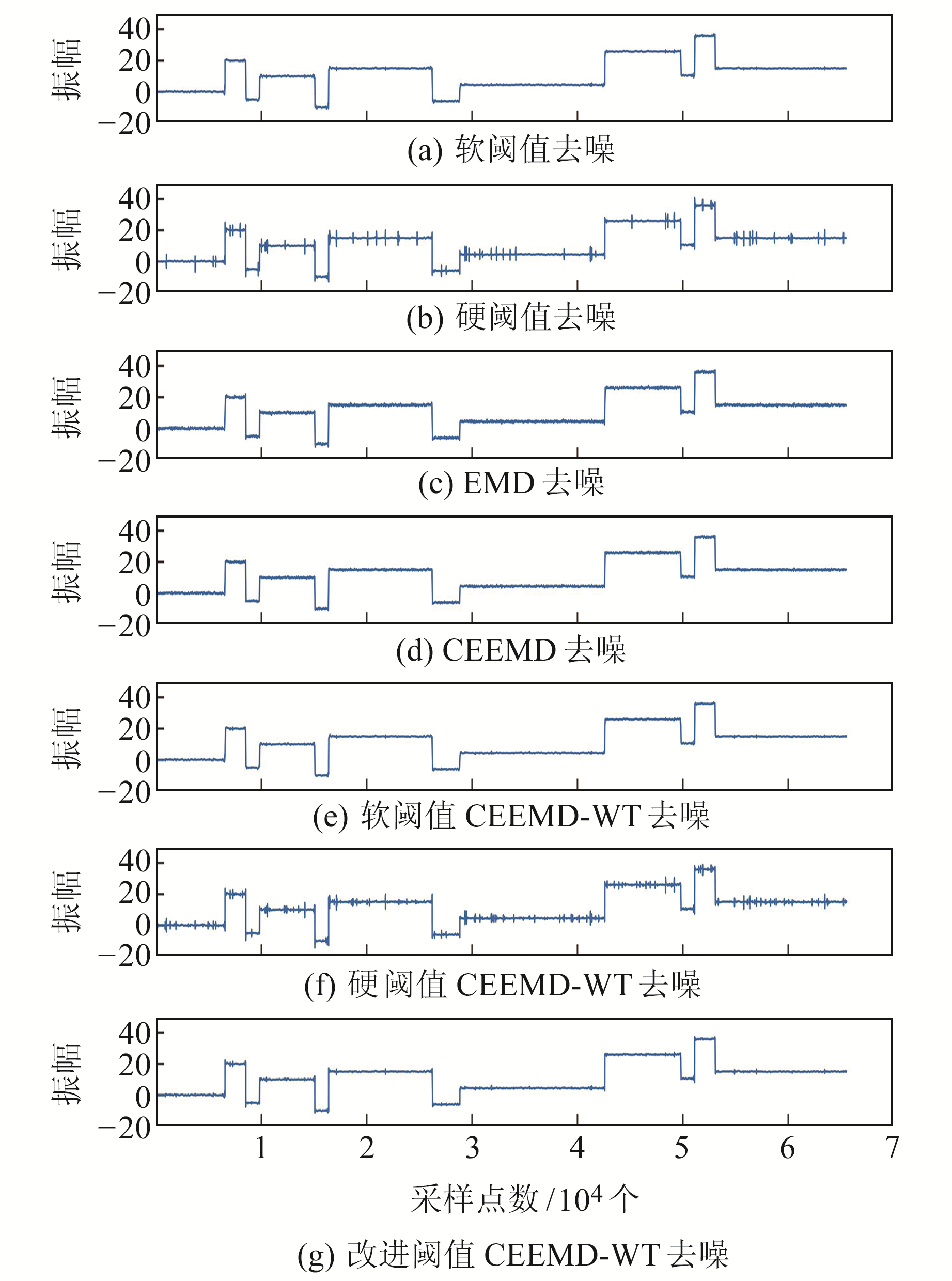
|
图 4 Blocks信号去噪效果 Fig. 4 Blocks signal denoising effect |
这里采用信噪比SNR和均方根误差RMSE衡量算法优劣:
| $ {\mathrm{SNR}}=10 \ln \left[\frac{\sum\limits_{t=1}^N s^2(t)}{\sum\limits_{t=1}^N\left(s(t)-x^{\prime}(t)\right)^2}\right] $ | (8) |
| $ {\mathrm{RMSE}}=\sqrt{\frac{1}{N} \sum\limits_{t=1}^N\left(s(t)-x^{\prime}(t)\right)^2} $ | (9) |
式中,s(t) 为原始信号,x′(t) 为去噪信号。
图 4(a)和(b)反映了硬阈值和软阈值的缺陷,硬阈值滤除噪声的同时也滤除了低幅度的有效信号,软阈值把各个小波系数按照阈值进行缩减。图 4(c)和(d)显示,直接舍弃近似无关的IMF分量,带来的误差会更加明显。图 4(e)和(f)将软阈值和硬阈值混合到CEEMD分解中,相比单纯使用软阈值或硬阈值,信噪比得到提高。图 4(g)改进阈值能够调节小波系数的衰减程度,克服了软、硬阈值的弊端,虽然波形上存在一些毛刺,但从表 1可知其性能优于其他两种混合算法。
|
|
表 1 Blocks信号去噪后的SNR、RMSE Tab. 1 SNR and RMSE of Blocks signal after denoising |
为验证混合算法在钢架结构沉降数据处理中的可行性,于2020-10-26~27在杭州富阳市金鑫广场进行桁架张拉测试。监测位置为图 5(a)红色箭头所指处,位于桁架中部略偏右,测试内容主要是监测施工辅助支架拆除过程中桁架下沉高度数据的变化情况。图 5(b)是金鑫广场桁架总体结构及张拉部位示意图,主要监测4个圆管柱上的斜拉索张拉过程中钢结构的形变情况,及撑架卸载过程中桁架的下沉情况。

|
图 5 金鑫广场桁架张拉测试 Fig. 5 Truss tension test in Jinxin square |
测试结果如图 6所示(数据监测频率为2 Hz),其中黑色部分:共9 772个数据,监测时间为2020-10-26 16:06~17:26,持续时间约1.3 h,为绳索张拉到50%张力过程;红色部分:共23 808个数据,监测时间为2020-10-27 8:00~11:25,持续时间约3.3 h,为绳索张拉到80%张力过程;蓝色部分:共13 610个数据,监测时间为2020-10-27 12:42~14:37,持续时间约1.9 h, 为切割掉下面支撑架过程。
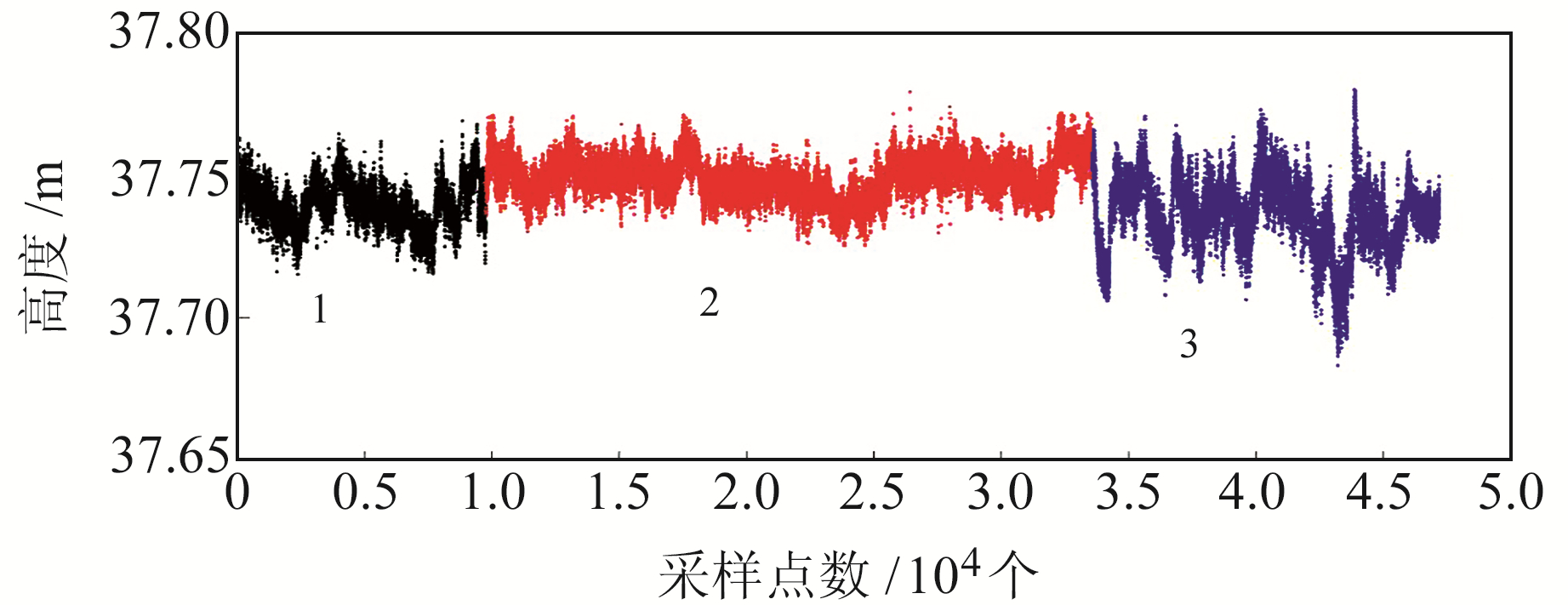
|
图 6 金鑫广场桁架监测原始数据 Fig. 6 Truss monitoring raw data in Jinxin square |
原始数据处理过程中,小波阈值去噪的基函数改为sym7、分解层数改为7。图 7是金鑫广场桁架高程变化,通过改进阈值CEEMD-WT降噪后,显著提高了信号分辨率。经表 2实例再次验证,混合算法降噪效果更为理想,较表现最好的硬阈值去噪方法均方根差下降0.7 mm。
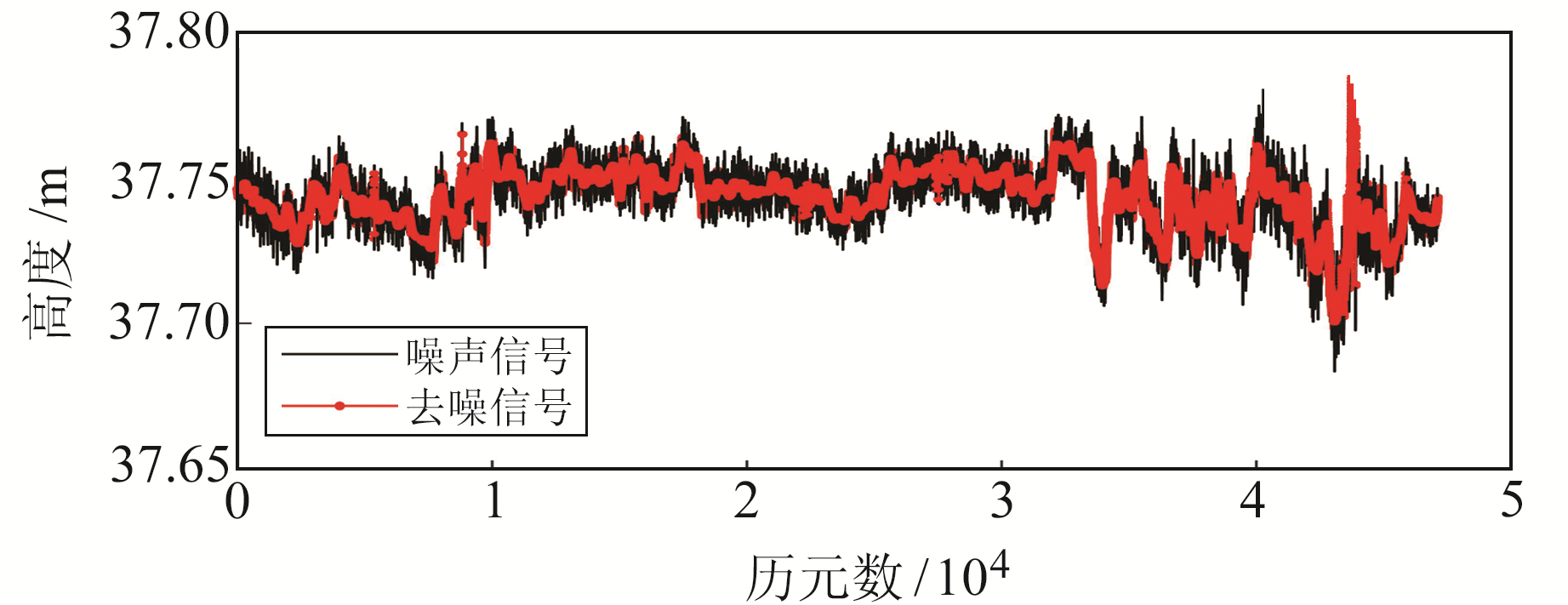
|
图 7 金鑫广场钢结构测高图 Fig. 7 Elevation change map of truss in Jinxin square |
|
|
表 2 钢架结构监测数据去噪后的SNR、RMSE Tab. 2 SNR and RMSE of steel frame structure monitoring data after denoising |
本文在固有的模态分解和小波阈值去噪的基础上构建了互补集合经验模态分解和改进小波阈值函数的混合去噪算法,首先对含噪信号作CEEMD分解,将各个IMF进行改进小波阈值的降噪,最后还原成降噪后的信号。其中,改进的小波阈值函数很好地缓解了软阈值对恒定偏差的影响,也规避了硬阈值阈值点的间断性。经过仿真及实例验证,改进后的混合算法相比单一的模态分解或传统小波阈值去噪方法精度至少提高0.7 mm,该算法可以有效处理形变监测中带来的噪声问题。
| [1] |
周吕, 文学霖, 杨飞, 等. 微变形雷达系统超高层建筑物变形监测[J]. 测绘通报, 2018(增1): 176-178 (Zhou Lü, Wen Xuelin, Yang Fei, et al. Deformation Monitoring of Super High-Rise Buildings in Micro-Deformation Radar System[J]. Bulletin of Surveging and Mapping, 2018(S1): 176-178)
(  0) 0) |
| [2] |
姚习红, 陈浩, 加松, 等. 三维激光扫描建筑信息建模技术在超高层钢结构变形监测中的应用[J]. 工业建筑, 2019, 49(2): 189-193 (Yao Xihong, Chen Hao, Jia Song, et al. Application of 3D Laser Scanning and Bim Technology in Deformation Monitoring of Super High-Rise Steel Structures[J]. Industrial Construction, 2019, 49(2): 189-193)
(  0) 0) |
| [3] |
Niu Y B, Ye Y, Zhao W J, et al. Identifying Modal Parameters of a Multispan Bridge Based on High-Rate GNSS-RTK Measurement Using the CEEMD-RDT Approach[J]. Journal of Bridge Engineering, 2021, 26(8)
(  0) 0) |
| [4] |
Zhong W, Zhang T J, Chen J, et al. Seasonal Deformation Monitoring over Thermokarst Landforms Using Terrestrial Laser Scanning in Northeastern Qinghai-Tibetan Plateau[J]. International Journal of Applied Earth Observation and Geoinformation, 2021, 103
(  0) 0) |
| [5] |
Sun M C, Xu W Y, Wang H L, et al. A Novel Hybrid Intelligent Prediction Model for Valley Deformation: A Case Study in Xiluodu Reservoir Region, China[J]. Computers, Materials and Continua, 2020, 66(1): 1 057-1 074 DOI:10.32604/cmc.2020.012537
(  0) 0) |
| [6] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995 DOI:10.1098/rspa.1998.0193
(  0) 0) |
| [7] |
Bagaria R, Wadhwani S, Wadhwani A K. Bone Fractures Detection Using Support Vector Machine and Error Backpropagation Neural Network[J]. Optik, 2021, 247
(  0) 0) |
| [8] |
杨涛, 乐友喜, 曾贤德, 等. 基于自相关函数特性的CEEMD全局阈值去噪方法研究[J]. 地球物理学进展, 2018, 33(4): 1 622-1 628 (Yang Tao, Yue Youxi, Zeng Xiande, et al. Research on CEEMD Global Threshold Denoising Method Based on Autocorrelation Function[J]. Progress in Geophysics, 2018, 33(4): 1 622-1 628)
(  0) 0) |
| [9] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41 DOI:10.1142/S1793536909000047
(  0) 0) |
| [10] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156 DOI:10.1142/S1793536910000422
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

