诸多研究表明,在大震发生前,孕震区附近地壳应力逐渐集中并导致地下介质物理性质发生变化。当地壳应力积累到一定程度时,岩石可能会出现微破裂和塑性化、塑性硬化、相变等一系列现象,从而引起不同类型地震波传播速度的变化。因此,地震波波速比通常被地球物理学家用来研究地壳介质的物性[1-5]。关于波速比变化的研究,传统方法往往是收集地震观测得到的海量P波、S波到时数据,比如通过和达法比对拟合得到波速比信息[6],其结果反映的是记录台站到震中这段距离的地壳介质的平均波速比情况。同时,台站分布对传统方法计算结果有较大影响,当地震台站分布不均匀、包围性差时,只能计算出局部区域的波速比值,难以准确反映震中集中区地下介质情况。
双差波速比的计算思路是限定震群集中活动区域,将距离同一台站相近的2个地震组成地震对,基于P波、S波到时双差,扣除地震射线的相同路径,从而获得震群型地震震中集中区波速比值的理想结果[7-9]。2017-02-14开始,长岛地区出现小震密集活动,并逐渐形成爆发式震群活动,截至2018-09长岛震群共记录到可定位地震2 800余次。本文以2017~2018年长岛震群为研究对象,选取ML2.0以上地震波形和震相数据,采用双差波速比方法对该区域波速比值进行计算,并开展特征分析。
1 方法原理双差波速比计算方法是在一个小的震群集中区内,采用多次地震事件来测定波速比的方法。对于一对地震事件(地震1和地震2),震中位置很近,有N个地震台站同时记录到该地震对,且该对地震的距离相对于台站震中距来说足够小,则认为地震速度局部恒定,地震波波前近似于平面,该地震对到集中区外同一地震台站的射线路径是一致的[7, 9],如图 1所示。P波、S波走时差可表示为:
| $ \delta T_{\mathrm{P}}^i=T_{\mathrm{P} 2}^i-T_{\mathrm{P} 1}^i=\frac{\delta l_{\mathrm{P}}^i}{V_{\mathrm{P}}} $ | (1) |
| $ \delta T_{\mathrm{S}}^i=T_{\mathrm{S} 2}^i-T_{\mathrm{S} 1}^i=\frac{\delta l_{\mathrm{S}}^i}{V_{\mathrm{S}}} $ | (2) |
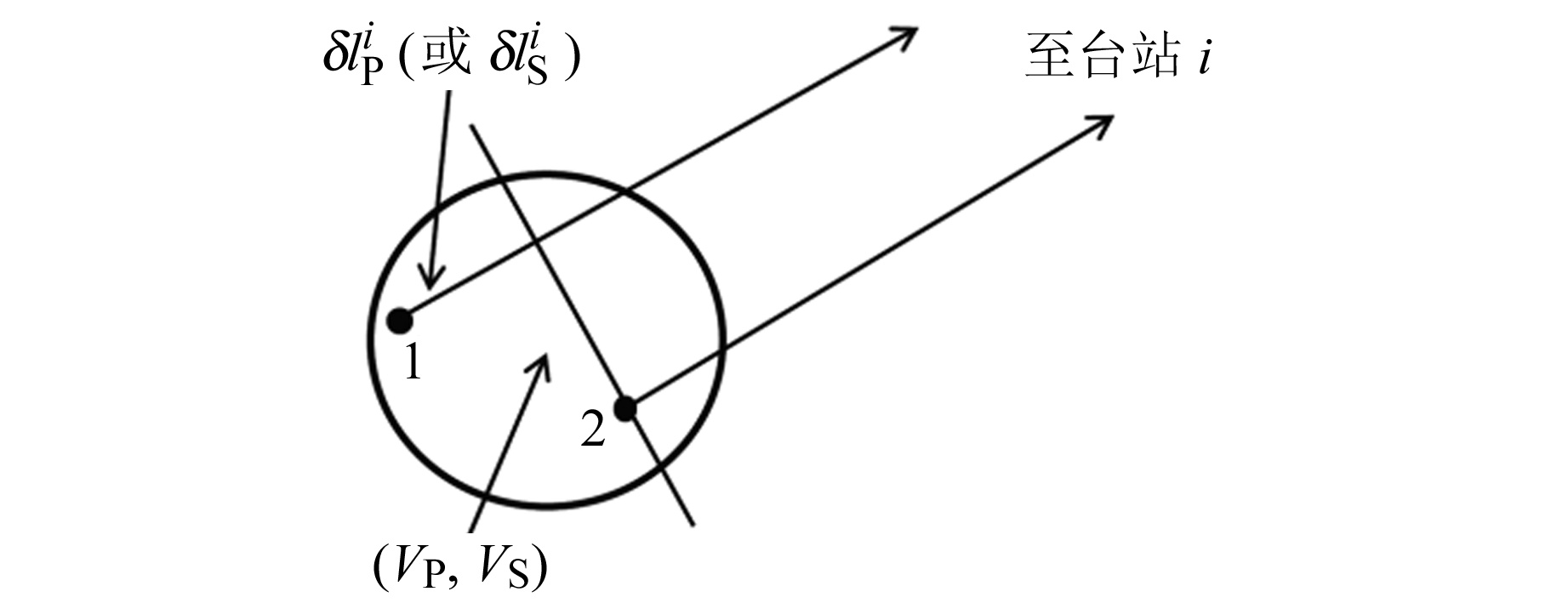
|
图 1 双差波速比原理示意图 Fig. 1 The schematic diagram of calculation the double-difference wave velocity ratio |
式中,δTPi、δTSi分别为P波、S波走时差,TP1i、TP2i、TS1i、TS2i分别为2个地震到台站i的P波、S波走时,δlPi、δlSi分别为2个地震到台站i的P波、S波路径之差,VP、VS分别为地震区的P波、S波速度。对于该地震对,认为P波、S波射线路径是一致的,即δlPi=δlSi,则可以用P波、S波走时差来估计波速比值:
| $ \frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}=\frac{\delta T_{\mathrm{S}}^i}{\delta T_{\mathrm{P}}^i} $ | (3) |
对于一组记录台站,可以获得一组(δTPi,δTSi)值(i=1, 2, …, n),由于不知道准确的发震时刻,不能准确获得地震走时T,所以用地震到时t来代替。对于第i个地震台站,2个地震的P波到时之差可表示为:
| $ \begin{gathered} \delta t_{\mathrm{P}}^i=t_{\mathrm{P} 2}^i-t_{\mathrm{P} 1}^i=\left(t_{02}+T_{\mathrm{P} 2}^i\right)- \\ \left(t_{01}+T_{\mathrm{P} 1}^i\right)=\delta t_0+\delta T_{\mathrm{P}}^i \end{gathered} $ | (4) |
式中,t01、t02分别为地震事件1和2的发震时刻。则式(3)可表示为:
| $ \frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}=\frac{\delta T_{\mathrm{S}}^i}{\delta T_{\mathrm{P}}^i}=\frac{\delta t_{\mathrm{S}}^i-\delta t_0}{\delta t_{\mathrm{P}}^i-\delta t_0} $ | (5) |
将式(5)转化成P波、S波到时差的关系式:
| $ \delta t_{\mathrm{S}}^i=\left(\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\right) \delta t_{\mathrm{P}}^i+\delta t_0\left(1-\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\right) $ | (6) |
根据式(6),同一对地震针对不同地震台站可以得到一组公式,平均值为:
| $ \overline{\delta t_{\mathrm{S}}}=\left(\frac{V_{\mathrm{P}}}{V_{\mathrm{s}}}\right) \overline{\delta t_{\mathrm{P}}}+\delta t_0\left(1-\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\right) $ | (7) |
由式(6)和式(7)可以得到:
| $ \delta t_{\mathrm{S}}^i-\overline{\delta t_{\mathrm{S}}}=\left(\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\right)\left(\delta t_{\mathrm{P}}^i-\overline{\delta t_{\mathrm{P}}}\right) $ | (8) |
令
| $ \hat{\delta} t_{\mathrm{S}}^i=\left(\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\right) \hat{\delta} t_{\mathrm{P}}^i $ | (9) |
即一组地震的不同事件对,可得到一组
长岛地区地处环渤海区域,地质结构复杂,以西侧的郯庐断裂带营口-潍坊段为界,与渤海湾盆地相邻[10],主要受到NNE向郯庐断裂带及其分支NW向张家口-蓬莱断裂带2个方向上的构造控制[11-12]。2017-02-14长岛地区出现一轮密集地震活动,2017-03-03突然爆发,2017-08-29在震群活动有明显减弱的基础上,小震活动再次爆发形成新的震群,新震中集中区较原震群南迁数千米,为便于区分,分别称其为长岛北震群及长岛南震群。截至2018-09-05,2个震群区域内的小震活动基本趋于背景活动水平。根据山东台网给出的定位目录,长岛北震群共记录到可定位地震2 499次,其中3.0~3.9级地震42次,4.0~4.9级地震4次,最大为2017-03-03发生的4.5级主震;长岛南震群共记录到可定位地震308次,其中2.0~2.9级地震27次,3.0~3.9级地震1次,最大为2017-11-20发生的3.0级地震。参考整个震群的震级-频度关系结果(图 2(a)),取最小完整性震级为ML2.0,2个震群2.0级以上地震的震中分布和M-T分别如图 2(b)和图 3所示。
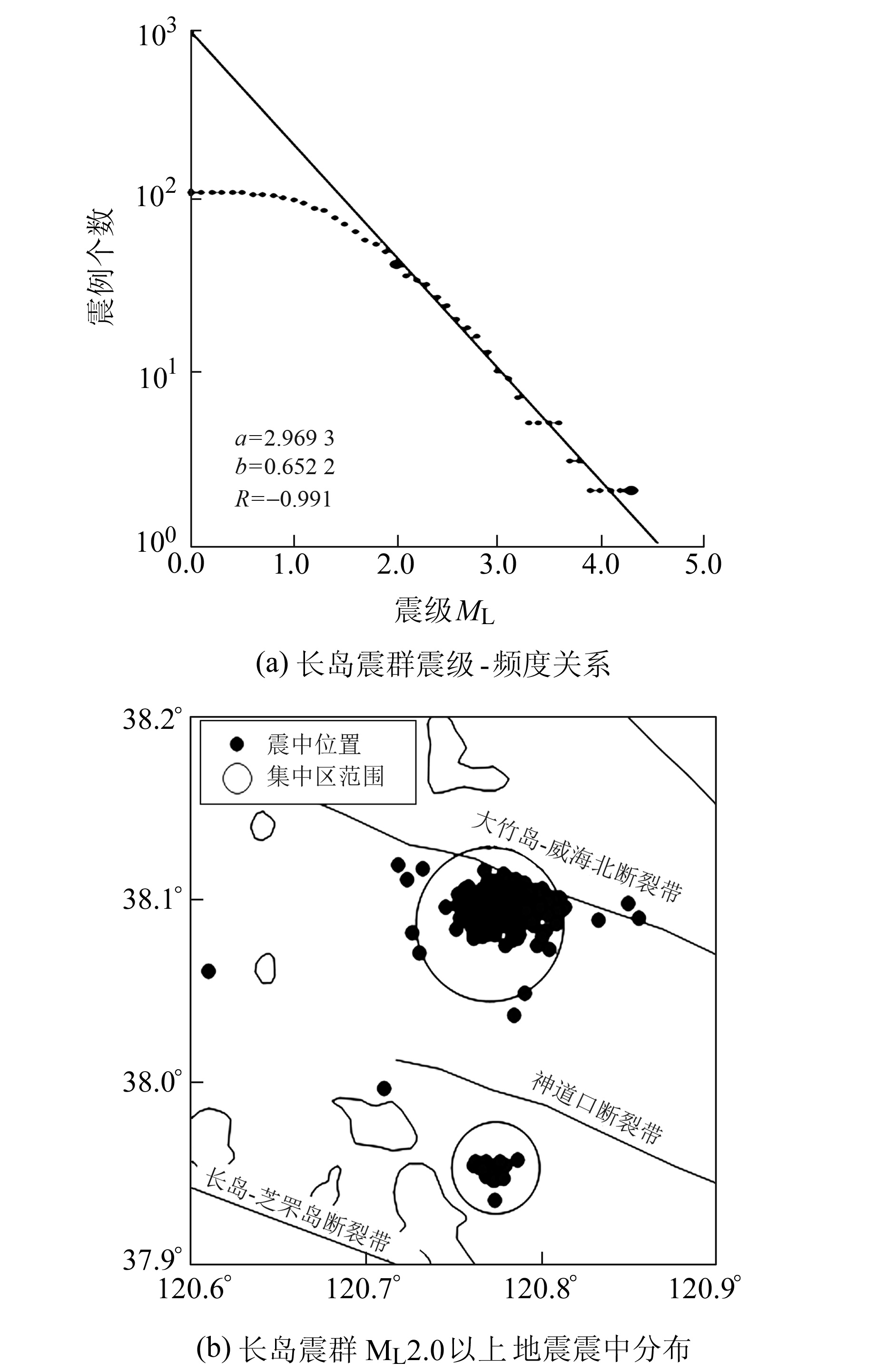
|
图 2 长岛震群ML2.0以上地震震中分布和震级-频度关系 Fig. 2 The epicenter distributions of ML≥2.0 earthquakes within Changdao earthquake swarms and magnitude-frequency diagram |
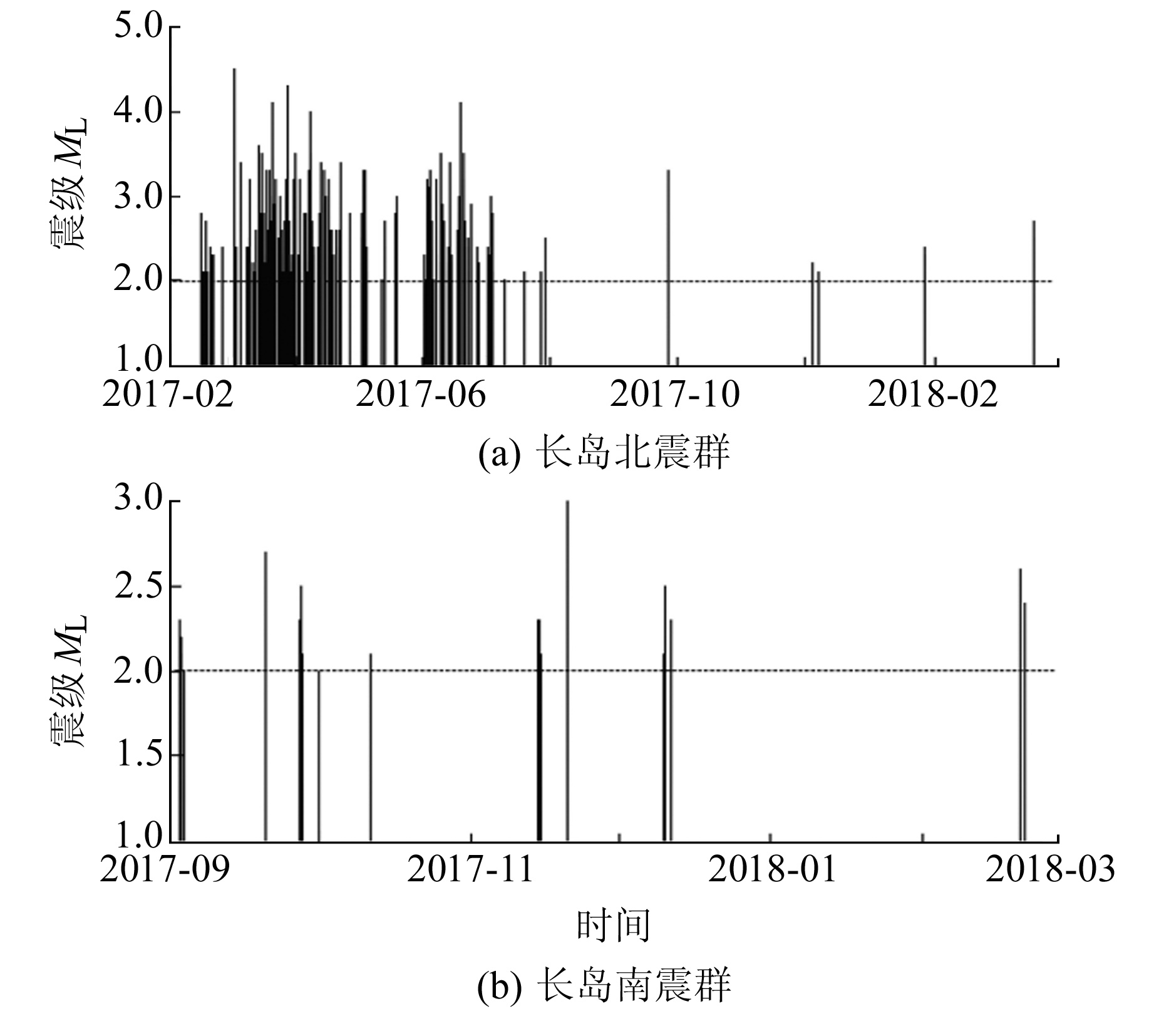
|
图 3 长岛地区北、南震群2.0级以上地震M-T图 Fig. 3 The M-T diagrams of ML≥2.0 earthquakes within northern and southern earthquake swarms of Changdao area |
为保证双差波速比值计算精度,地震事件选取遵循以下限定条件:
1) 震中距选取范围为50~130 km,至少有4个相同地震台站清晰记录到P波和S波震相的地震事件。如果震中距小于50 km,当扣除同一地震台站记录的一组地震的相同射线路径时,误差会较大;而震中距大于130 km,在山东地区会出现Pn、Sn等复杂震相,对Pg、Sg波到时的拾取有较大影响。长岛震群发生在海域,最近的3个台BHC、CHD、LYTA都位于海岛上,海浪噪声较大,且LYTA台是震后临时架设的流动台,台基未作处理,如果一次事件仅有这3个台记录到,其震级水平不高,震相到时可能有较大误差。
2) 在双差波速比计算中,震中集中区的直径也是影响计算结果的一个关键参数。直径越大,理论上产生的双差范围就越大,对误差的包容性也越强,但需要的可靠震例也越多;直径太小,影响波速比计算范围。考虑到长岛震群的真实情况,长岛北震群选取地震集中区的直径限定在8 km左右,长岛南震群限定在4 km左右,如图 2(b)圆圈所示。
经过筛选,北、南震群符合条件的地震事件分别为202个、14个,触发地震台站有龙口(LOK)、北隍城(BHC)、烟台(YTA)、莱州栖霞(LZH)、大连(DL2)、莱阳(LAY)、招远(ZHY)、牟平(MUP)、莱州(LAIZ)、威海(WEH)。经过震例选取及预处理后,长岛地区两个震群的参数如表 1所示。
|
|
表 1 长岛地区南北震群ML2.0以上地震参数 Tab. 1 Parameters of earthquakes with magnitude ML≥2.0 within northern and southern earthquake swarms of Changdao area |
在后续波速比值计算中,为减小到时误差,增强可信度,需要作数据预处理。首先利用和达直线进行检验,对一些偏离直线的台站震相进行震相重新标注;然后重新进行地震定位,对残差较大且无法校正的震相进行删除。
3 误差分析及处理计算长岛震群波速比值前,对双差波速比方法进行到时敏感性分析,从而更好地理解计算误差范围。选取长岛北震群中202个震例数据进行误差检测,震例震源深度为5~15 km,均处于康拉德界面以上。设计Pg波速度为6 km/s,波速比为1.73,根据设计参数,模拟计算得到Pg、Sg波到时;然后加入随机误差,验证到时敏感性。具体结果如图 4和表 2所示。
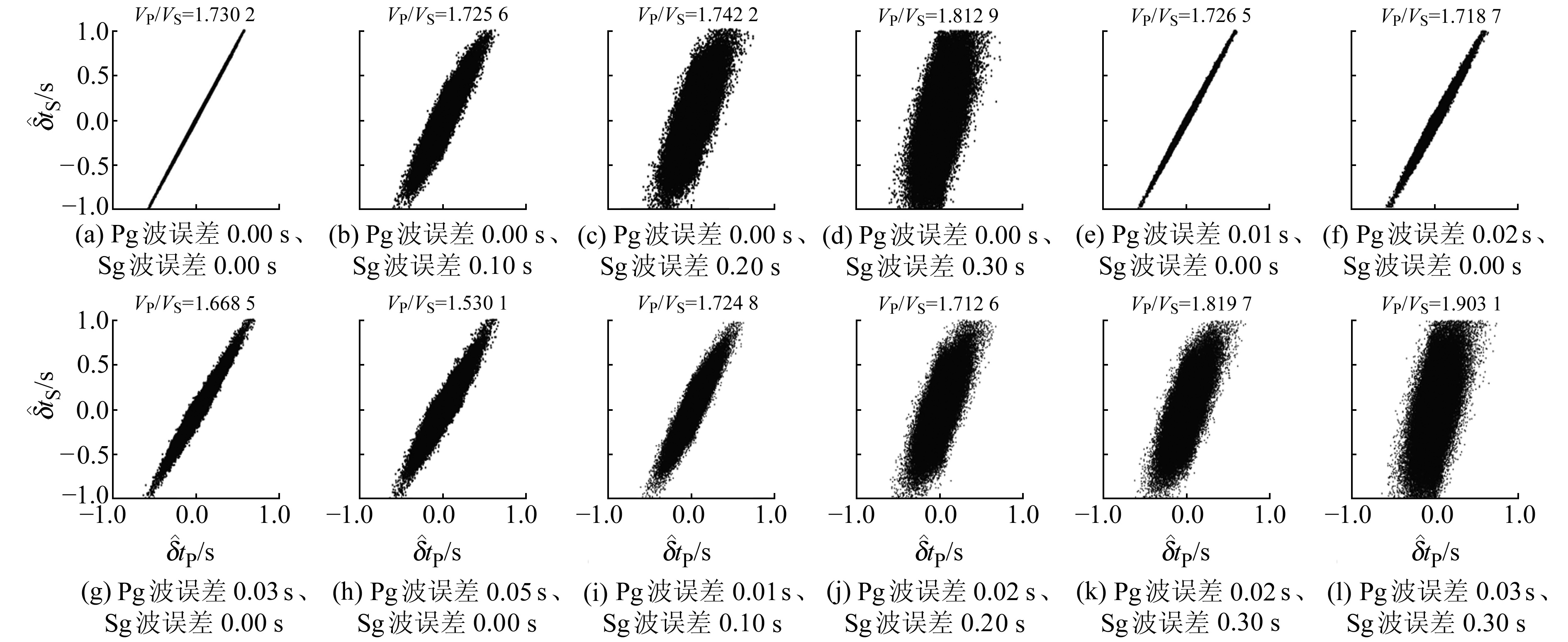
|
图 4 双差波速比误差 Fig. 4 Errors of double-differential wave velocity ratio |
|
|
表 2 双差波速比误差 Tab. 2 Error analysis table of double-differential wave velocity ratio |
当没有设定随机值误差时,拟合直线斜率(波速比值)为1.730 2,约等于设定值1.73,可以认为回归了设定的波速比值,验证了程序的正确性(图 4(a))。当Pg波到时无误差,Sg波到时以0.10 s的间距增大随机误差时(图 4(b)~4(d)),拟合结果与设定值之间误差百分比逐渐增大;当Sg波加入一个较大误差0.30 s时,波速比误差百分比达到4.57%,可见影响较大。当Pg波到时以0.01 s的间距增大随机误差,Sg波到时无误差时(图 4(e)~4(h)),误差百分比逐渐增大;当Pg波到时加入0.03 s的随机误差时,波速比误差百分比达到3.69%。可见Pg波误差对结果的敏感性要高于Sg波误差。
为验证最大可接受的误差范围,图 4(i)~4(l)分别增加Pg波、Sg波的随机误差,图 4(i)模拟Pg波、Sg波的误差分别设定为0.01 s和0.10 s的情况,图 4(j)模拟Pg波、Sg波的误差分别为0.02 s和0.20 s的情况,当Pg波误差范围在0.02 s以内、Sg波误差范围在0.20 s以内时,误差百分比约为1%;当加入更大的误差,图 4(k)模拟Pg波、Sg波的随机误差分别为0.02 s和0.30 s,图 4(l)模拟Pg波、Sg波的随机误差分别为0.03 s和0.30 s时,对波速比值影响较大。由此可见,双差法计算波速比值产生的误差与震群集中区的直径有关,观测震相误差、触发台站的间距不等、台网布局不合理,也是误差的来源。
4 计算结果及分析 4.1 时差数据对对长岛地区北、南震群的数据进行双差波速比计算,北、南震群地震事件分别有202个和14个,最终组成Pg波、Sg波到时差数据对分别有17 363对、377对(图 5)。
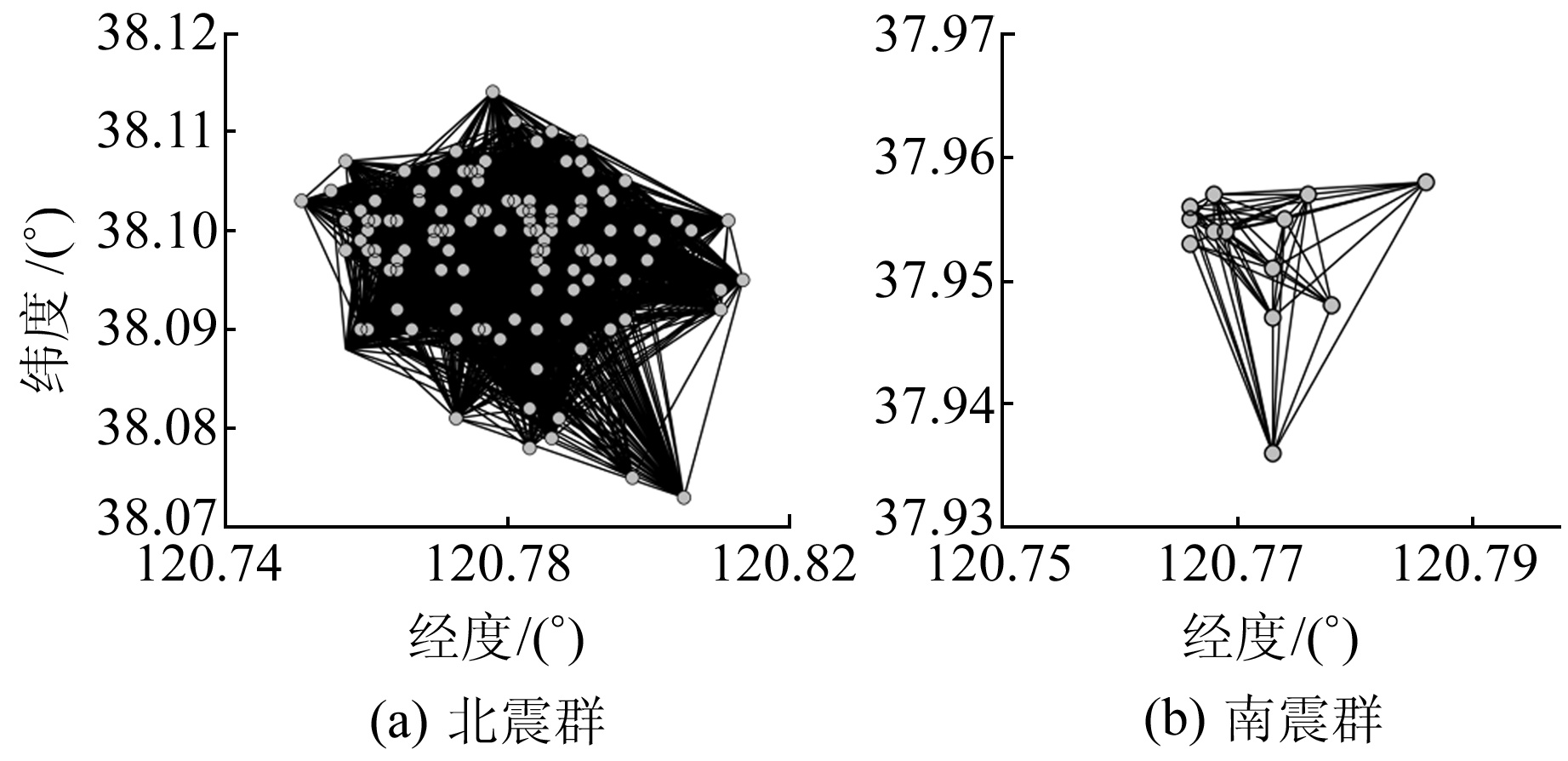
|
图 5 长岛北震群、南震群地震事件对 Fig. 5 The pairs of seismic events within the northern and the southern earthquake swarms |
因长岛地区2个震群的数据量有很大差别,所以采用不同的方式进行窗口扫描,开展双差波速比值的计算。在长岛北震群以步长1周、窗长1个月、窗内至少5个以上震例为条件进行滑动,以时间扫描的形式开展实验;长岛南震群数据量较小,故采用2个震例为步长、窗长为8个震例的条件进行滑动,计算结果分别如图 6和图 7所示,图中给出扫描的中心时间。波速比值随时间的变化如图 8所示,并以误差棒的形式给出每个点的计算误差。
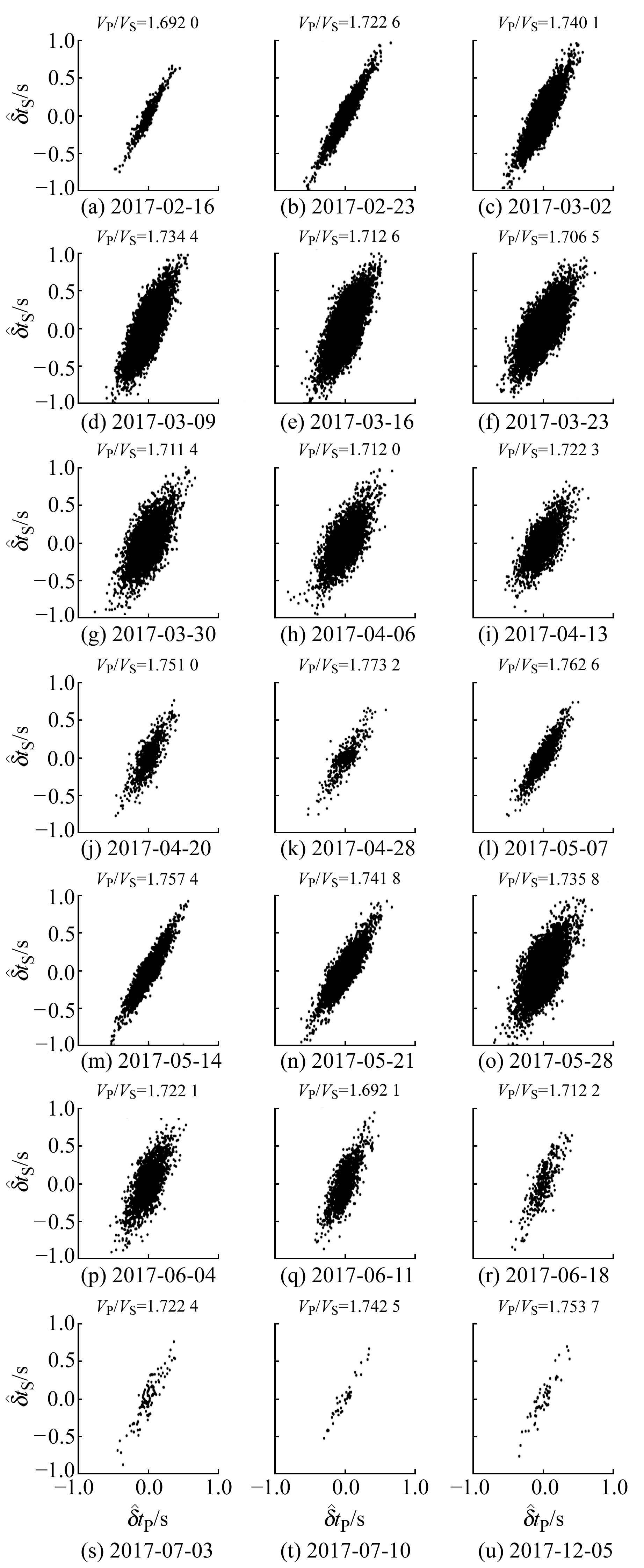
|
图 6 长岛北震群时间扫描双差波速比计算结果 Fig. 6 Calculation results of double-difference wave velocity ratio in time scanning of the Changdao northern earthquake swarm |
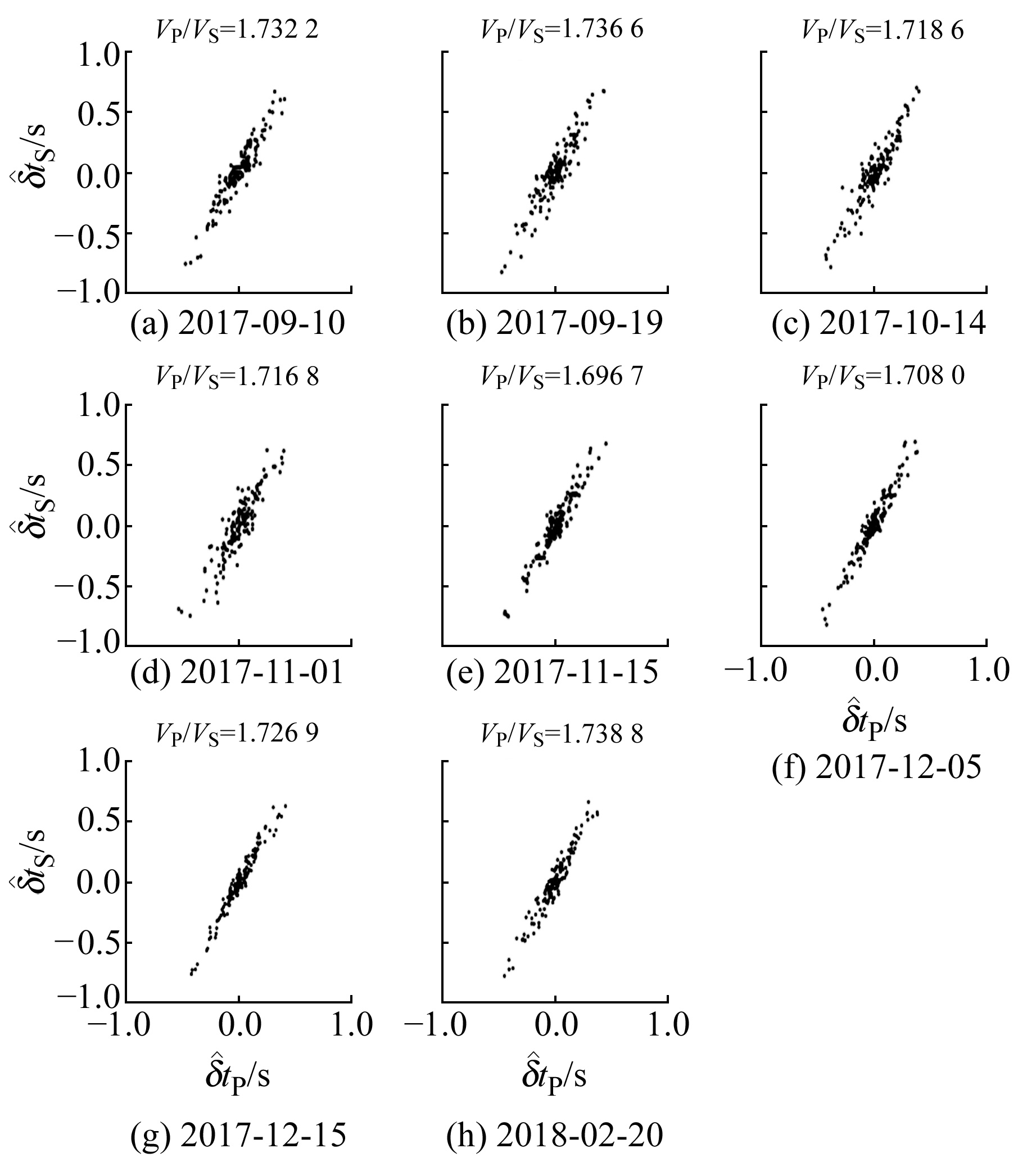
|
图 7 长岛南震群扫描双差波速比计算结果 Fig. 7 Calculation results of double-difference wave velocity ratio in time scanning of the Changdao southern earthquake swarm |
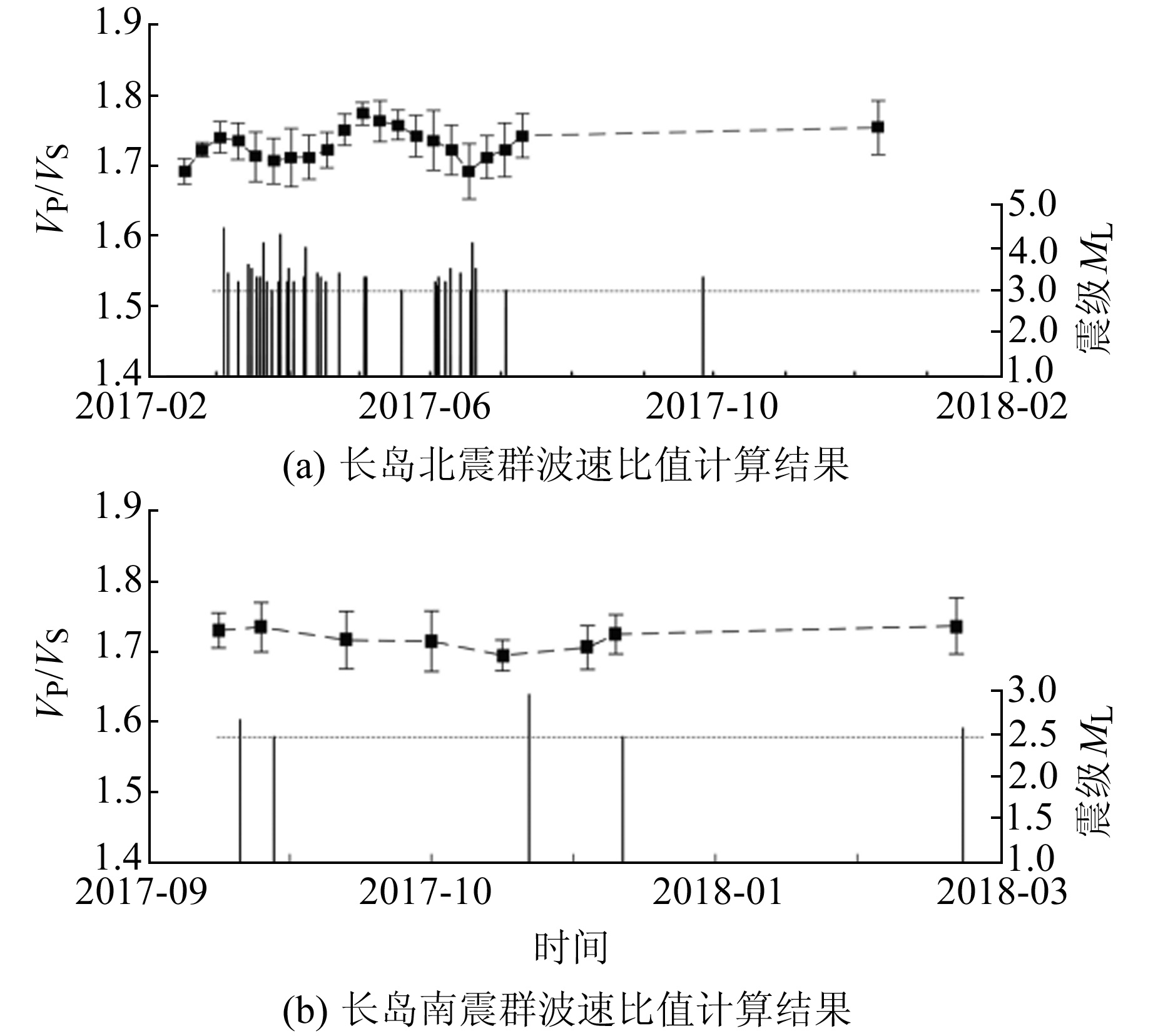
|
图 8 长岛震群波速比值计算结果 Fig. 8 Calculation results of wave velocity ratio of Changdao earthquake swarm |
从计算结果来看,波速比的时空分布具有如下特征:
1) 2017~2018年长岛震群波速比值范围为1.69~1.78,大部分时段都高于该地区2002~2012年间平均波速比值1.708[13-14]。
2) 长岛北震群中小地震活动较强,波速比值随时间呈现较大起伏;南震群波速比值的波动变化幅度不大,与北震群相比,波速比值稍低,可能与2组震群的活动强弱有关。
3) 2017-03、04、06正是长岛北震群活跃且3.0~4.0级地震多发时期,特别是2017-03-21的4.1级、03-27的4.3级、04-08的4.0级、06-18的4.1级地震发震前,波速比相应呈低值状态。2017-11-20长岛南震群发生3.0级地震时,波速比值也呈现低值状态,较大余震前波速比值的变化应当与震群活动过程中震源区应力的扰动变化有关。
4) 2017-03-03长岛4.5级主震前的波速比值处于较高状态,分析可能有2个方面的原因:一是计算的时间窗内包含了本次4.5级地震后短时间的余震;二是在震群爆发活动前,震源处的岩石处于受压初期,波速比随着压力的增大而增大,震群爆发后,随着大量小震的密集活动,岩石裂隙增加,导致波速比下降。
5) 2018年中小地震活动减弱时,2个震群波速比值呈现回升,没有出现低值异常。
分析认为,2017~2018年长岛震群波速比的变化过程与震群活动过程密切相关,表明波速比变化与震源区岩石介质的物性变化之间具有较好的关联性。
4.3 误差分析图 9给出计算波速比时的标准误差,误差集中分布在0.01~0.05。图 9(a)给出在长岛北震群以时间窗口滑动时震例个数与标准误差之间的关系,可以看出,随着符合条件的震例数据的增多,标准误差变小。因长岛南震群震例数少,所以图 9(b)给出了Pg波、Sg波到时差数据对与标准误差之间的关系,可以看出,随着数据对的增多,标准误差值变小。此规律与蔡静观[6]和李霞等[14]的统计结果相同,说明波速比值计算精度与记录台站数据密切相关,触发台站数目越多,数据的线性相关度越高,波速比计算误差就越小。从数据精度来看,长岛地区位于近海地区,由于台网布局包围性不好,得到的标准误差也会较内陆地区的大。
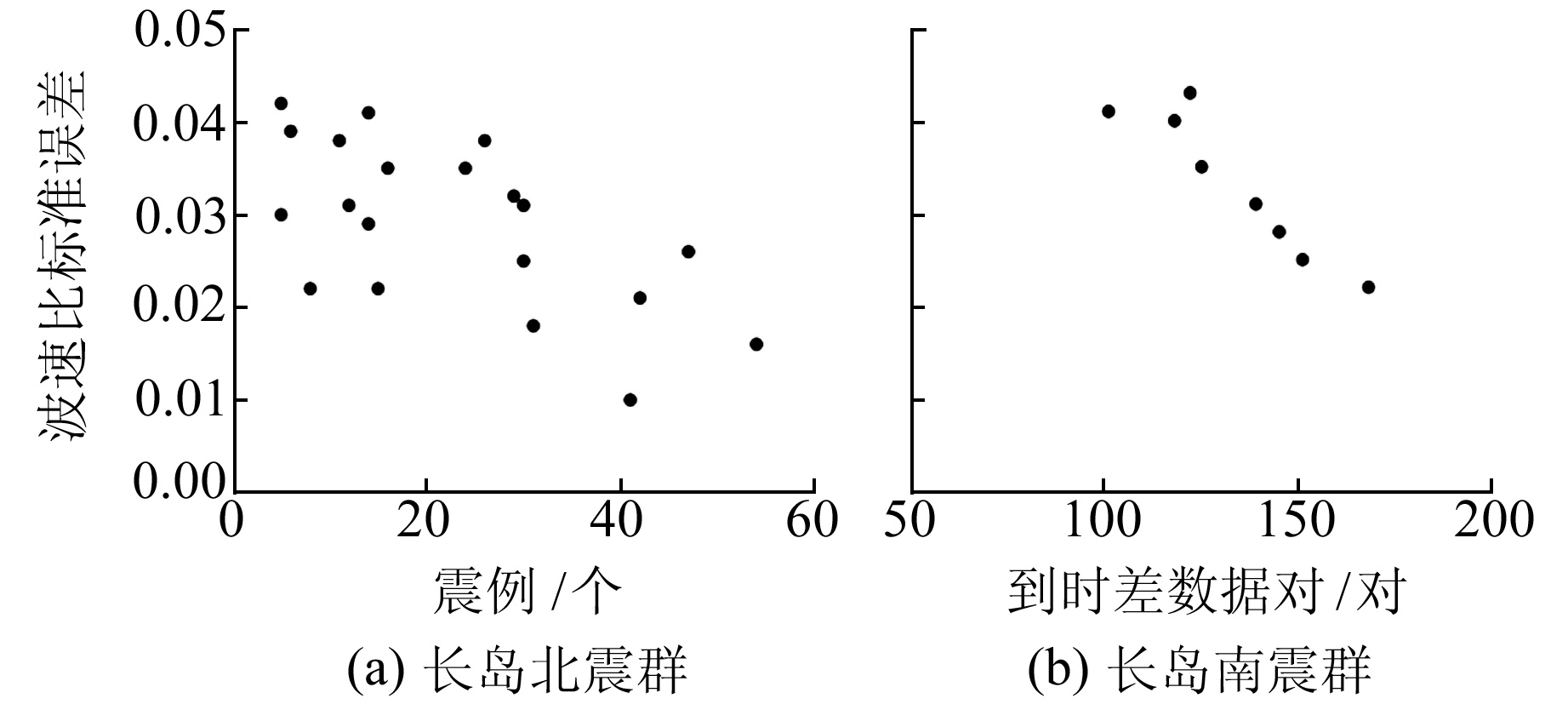
|
图 9 长岛震群波速比值标准误差 Fig. 9 Standard error by the double-difference wave velocity ratio method within the Changdao earthquake swarms |
本文以2017~2018年长岛震群为研究对象,采用双差波速比方法对该区域波速比值进行计算,测算震相数据误差影响,并开展波速比值变化特征分析,得到如下认识:
1) 双差波速比方法对震相到时,特别是Pg波到时较敏感,需要在资料处理时将Pg波、Sg波拾取误差控制在0.02 s及0.20 s以内。
2) 长岛震群波速比值波动范围为1.69~1.78,波速比的波动变化与震群活动过程密切相关。
3) 长岛震群4.0级以上余震发生前,波速比都处于低值状态。2017-03-03的4.5级主震和后续4.0级以上余震前的波速比变化差异,可能反映震群主震与余震发震机理有所不同。
致谢: 感谢陈时军研究员在论文修改过程中给予指导和帮助。
| [1] |
何应文, 杨晓琳, 王建芳, 等. 滇西至滇西南地区近期中强地震前单台波速比变化特征研究[J]. 大地测量与地球动力学, 2019, 39(8): 798-803 (He Yingwen, Yang Xiaolin, Wang Jianfang, et al. Temporary Variation of VP/VS at Single Seismic Station before Recent Moderate and Strong Earthquakes in West to Southwest Yunnan[J]. Journal of Geodesy and Geodynamics, 2019, 39(8): 798-803)
(  0) 0) |
| [2] |
王亚茹, 宋昭, 刘晓丹, 等. 唐山地区波速比变化特征研究[J]. 大地测量与地球动力学, 2019, 39(7): 686-690 (Wang Yaru, Song Zhao, Liu Xiaodan, et al. Change Characteristics of Wave Velocity Ratio in Tangshan Area[J]. Journal of Geodesy and Geodynamics, 2019, 39(7): 686-690)
(  0) 0) |
| [3] |
李艳娥, 王林瑛, 宋美卿, 等. 从波速比变化看汶川与芦山地震的孕震过程[J]. 大地测量与地球动力学, 2016, 36(11): 991-997 (Li Yan'e, Wang Linying, Song Meiqing, et al. Study of the Seismogenic Process from Wenchuan to the Lushan Earthquake Based on Wave Velocity Ratio Temporal Variation[J]. Journal of Geodesy and Geodynamics, 2016, 36(11): 991-997)
(  0) 0) |
| [4] |
王林瑛, 李艳娥, 李芳, 等. 汶川地震前后地震波速比和视速度变化特征的研究[J]. 地震学报, 2011, 33(1): 1-14 (Wang Linying, Li Yan'e, Li Fang, et al. Temporal Variation of VP/VS, VP and VS before and after 2008 Wenchuan Earthquake[J]. Acta Seismologica Sinica, 2011, 33(1): 1-14 DOI:10.3969/j.issn.0253-3782.2011.01.001)
(  0) 0) |
| [5] |
陈俊华, 甘家思, 李普丽, 等. 三峡水库蓄水后巴东地区波速比(VP/VS)研究[J]. 大地测量与地球动力学, 2007, 27(增1): 12-14 (Chen Junhua, Gan Jiasi, Li Puli, et al. On Wave Velocity Ratio(VP/VS) in Badong Area after Impoundment of Three Gorges Reservoir[J]. Journal of Geodesy and Geodynamics, 2007, 27(S1): 12-14)
(  0) 0) |
| [6] |
蔡静观. 波速比计算中的不确定因素和在地震预报中的应用[J]. 地震研究, 2000, 23(1): 51-56 (Cai Jingguan. Nondeterministic Factors in Calculation of VP/VS Ratio and Their Application to Earthquake Prediction[J]. Journal of Seismological Research, 2000, 23(1): 51-56)
(  0) 0) |
| [7] |
Lin G, Shearer P. Estimating Local VP/VS Ratios within Similar Earthquake Clusters[J]. Bulletin of the Seismological Society of America, 2007, 97(2): 379-388
(  0) 0) |
| [8] |
贾漯昭, 王志铄, 张亚琳, 等. 用双差波速比方法分析2014~2015年安徽金寨震群[J]. 地震, 2017, 37(1): 112-120 (Jia Luozhao, Wang Zhishuo, Zhang Yalin, et al. Analysis of the 2014-2015 Jinzhai Earthquake Swarm by Double-Difference VP/VS Ratio Method[J]. Earthquake, 2017, 37(1): 112-120)
(  0) 0) |
| [9] |
Gritto R, Jarpe S P. Temporal Variations of VP/VS-Ratio at the Geysers Geothermal Field, USA[J]. Geothermics, 2014, 52(4): 112-119
(  0) 0) |
| [10] |
刘春成, 戴福贵, 杨津, 等. 渤海湾盆地海域古近系-新近系地质结构和构造样式地震解释[J]. 中国地质, 2010, 37(6): 1545-1558 (Liu Chuncheng, Dai Fugui, Yang Jin, et al. Seismic Interpretation of Eogene-Neogene Geological Structures and Tectonic Styles in the Sea Area of Bohai Gulf Basin[J]. Geology in China, 2010, 37(6): 1545-1558)
(  0) 0) |
| [11] |
应绍奋, 沈永坚, 郭良迁. 渤海沿岸地区的现代构造运动[J]. 中国地震, 1986, 2(1): 35-41 (Ying Shaofen, Shen Yongjian, Guo Liangqian. Recent Tectonic Movements in the Coastal Area of the Bohai Sea[J]. Earthquake Research in China, 1986, 2(1): 35-41)
(  0) 0) |
| [12] |
王椿镛, 段永红, 吴庆举, 等. 华北强烈地震深部构造环境的探测与研究[J]. 地震学报, 2016, 38(4): 511-549 (Wang Chunyong, Duan Yonghong, Wu Qingju, et al. Exploration on the Deep Tectonic Environment of Strong Earthquakes in North China and Relevant Research Findings[J]. Acta Seismologica Sinica, 2016, 38(4): 511-549)
(  0) 0) |
| [13] |
李霞, 刘希强, 李亚军, 等. 山东及邻区地震的重新定位及其与活动构造的关系[J]. 中国地震, 2012, 28(4): 381-392 (Li Xia, Liu Xiqiang, Li Yajun, et al. Relocation of Earthquakes in Shandong and Its Neighboring Areas in China and Relationship between Their Tectonics[J]. Earthquake Research in China, 2012, 28(4): 381-392)
(  0) 0) |
| [14] |
李霞, 周彦文, 赵瑞, 等. 沂沭断裂带及附近地区分段平均波速比研究[J]. 地震研究, 2013, 36(2): 148-154 (Li Xia, Zhou Yanwen, Zhao Rui, et al. Research on Average Wave Velocity Ration of Segmentation in Yishu Fault and Its Adjacent Area[J]. Journal of Seismological Research, 2013, 36(2): 148-154)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

