2. 中冶成都勘察研究总院有限公司,成都市三色路199号,610023
地震活动目录是地震台网运行产生的综合数据库,主要包括地震位置、震源时间和震级信息。这些数据是分析地震活动的空间、时间和规模分布、地震活动变化以及危险评估的基础。随着地方、国家和全球地震监测网络逐步改善,全世界在发震地区记录到的地震事件越来越多,使得地震目录得以完善,基于地震目录的研究在地震学研究中具有重要意义。研究地震目录的目的是调查特定研究区域内地震的时间、空间和规模分布特征,进而估算一些基本地震目录相关参数,如古登堡-里克特(G-R)b值和完整性震级(MC)等,是地震学常用的分析方法[1-2]。在研究局部地震活动时,通常需要将地震进行分区。聚类分析是一种多变量方法,通过将观测值分组,在数据集中搜索相关模式。该方法的目标是找到一个最佳分组,每个组内的观测值或对象相似(同质)。然而,这些集群彼此不同(异构),数据之间的距离决定了数据的相似程度。数据之间的距离小表示数据的高相似性水平,相反,数据之间的距离大表示数据的低相似性水平[3]。常规的地震区划方法是通过对构造特征、地壳特征等进行主观分析,来了解地震特征,这种分析容易出现主观判断错误[4]。Zamani等[5]提出一种利用层次聚类分析进行地震区划的替代方法。这种方法是地震区划的起点,有可能改进和重新定义新的数据集。该方法也可用于研究新构造、地震构造、地震分区和发震区的危险性评估。地震资料是识别地震构造区最重要的信息来源之一,历史和仪器地震数据的模式识别为从大量数据中提取有用信息提供了一种更稳健、更合适的工具。Ansari等[6]提出基于最大似然估计模糊修正的聚类方法,聚类分析结果与地震构造模型之间的比较表明,如果将地震事件的空间分布(震中)划分为不同的区域,主要事件的聚类将取得最佳结果。
为探索聚类分析方法在地震空间上快速扫描地震群的实用性,本文使用K-means和高斯混合模型(Gaussian mixture model, GMM)两种方法分别对甘东南及邻近地区的原始目录以及精定位目录进行聚类分析,结果发现,结合精定位分析能让地震聚类更好地将地震划分成地震丛集,为研究地震群识别、区域地震危险性判断提供参考。
1 数据介绍甘肃东南及邻近地区(32°~36°N,102°~106°E)处于青藏高原东北缘与东缘,构造活动强烈,主要有祁连山地震带和南北地震带北段。研究区构造上主要受印度板块北推碰撞欧亚大陆的主动力控制,在往东北向挤压过程中受到相对稳定的阿拉善地块及鄂尔多斯地块的阻挡,使得该区域成为构造活动与应力场变化的敏感地区。研究区发育多条活动断裂,地震活动率较高,历史上曾发生过多次中强以上破坏性地震,近10 a来主要发生2013年岷县MS6.6地震与2017年九寨沟MS7.0地震,造成重大的人员伤亡与财产损失,因此长期以来该地区一直是地学工作者研究的热点区域之一。本文从中国地震台网中心下载了研究区范围内2013-01-01~2021-11-01的地震台网观测报告,为保证地震震中位置的可靠性,选取最小台站记录数为6,按照如上挑选条件共下载地震事件15 590次。另外,由于研究区属于甘肃、四川、陕西交界处,地震目录中掺杂重复地震事件,因此首先去除不同台网间记录的边界重复地震事件,在处理上以地震位置所在省份为准,只保留各台网给出的自己省份地震事件,最终得到一共11 659次地震事件,地震震中分布以及时间分布如图 1(a)所示。地震台网给出的地震目录震源位置存在一定误差,通常用地震精定位方法来减小该定位误差。为提高地震定位精度,使用Waldhauser等[7]提出的双差定位方法(HypoDD)对原始地震目录进行精定位处理,进而对比精定位前后地震聚类分析结果的变化。在地震对分配过程中,以20 km作为两个地震对之间的最大距离,超过20 km的不予考虑。由于事件震中分布比较集中,因此设定单一地震最多可以和20个地震组成地震对,速度模型选取甘青一维速度走时模型[2, 8]。震中距范围选取500 km作为阈值,震相走时经过筛选后如图 1(b)所示。数据预处理完成后,使用HypoDD精定位方法进行重定位,得到地震目录6 654条,精定位结果地震分布见图 1(c)所示。
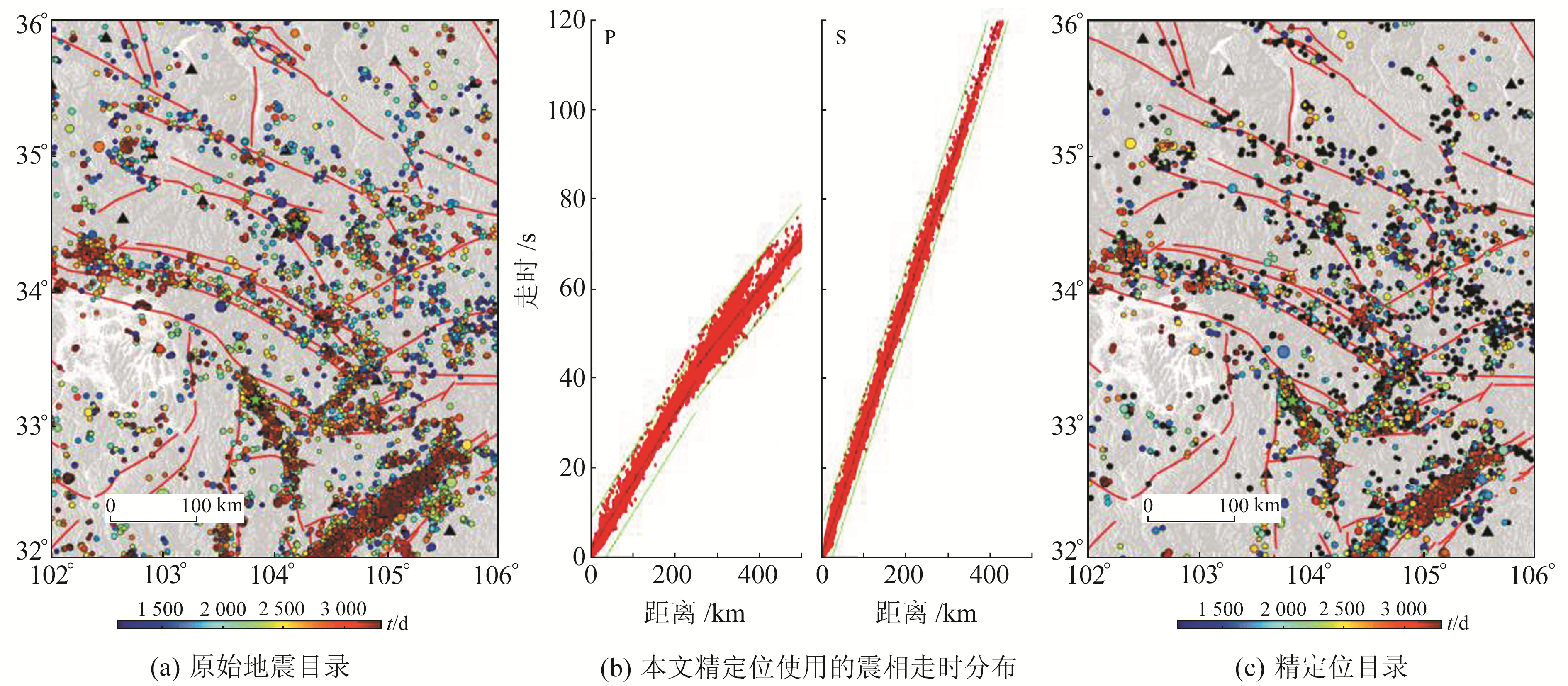
|
图 1 本文所使用地震震中时空分布 Fig. 1 Temporal and spatial distribution of earthquake epicenter used in this paper |
聚类技术是检查数据、基于检查进行预测以及消除其中差异的重要方法。聚类用于识别和分组每天生成的不断增长的数据,并生成可以进一步利用的模式和知识。K-means算法是数据挖掘中最常用的聚类方法之一。该算法以一个聚类的平均值作为聚类的质心,通常根据数据之间的欧氏距离对数据进行分组。K-means聚类分析是一个迭代过程,因为它是一种硬划分算法,试图将一组多元数据中的n个个体划分为k个聚类,其中数据集中的每个个体分配给一个特定的聚类[9]。
高斯混合模型(GMM)是一种使用广泛的聚类算法,该方法将高斯分布作为参数模型,并利用期望最大(expectation maximization,简称EM)算法进行训练。K-means算法在特定约束条件下可以被看作是GMM的一种特殊形式。GMM是一种软分类方法,只给出项目是某个类的概率值。利用概率密度函数表示类别的信息量比一个直接的分类结果要多。每个GMM由K个高斯分布组成,每个高斯分布称为一个“component”,这些component线性加成在一起就组成了GMM的概率密度函数:
| $ \begin{array}{c} p(x) = \sum\limits_{k = 1}^K p (k)p(x\mid k) = \\ \sum\limits_{k = 1}^K {{\pi _k}} Np\left( {x\mid \mu k, {\mathit{\Sigma }_k}} \right) \end{array} $ | (1) |
式中,p(x)=πk是第k个高斯模型的权重,称作选择第k个模型的先验概率,且满足
根据式(1),若要从GMM的分布中随机抽取一个点,可以通过2步来进行:首先随机在这K个component之中选取一个,每个component被选中的概率实际上就是其系数π(k);选中component之后,再单独考虑从这个component的分布中选取一个点就可以了——这里已经回到了普通的Gaussian分布,转化成已知的问题。接下来就是聚类步骤,根据样本数据,假定这些数据是由GMM产生的,那么可以根据数据推算出GMM的概率分布,而GMM的K个component实际上就对应了K个cluster。根据数据来推算概率密度通常被称作概率密度估计。特别地,当我们在已知(或假定)了概率密度函数的形式,而要估计其中的参数的过程被称作参数估计。
2.2 最佳聚类个数的确定根据对先验信息的使用情况,分类技术可以分为监督、半监督和无监督[10],高斯混合模型GMM和K-means属于无监督技术,经典的线性和二次辨别分析属于监督技术。无监督学习最大的优点是不需要先验信息即可完成数据的分类。为选择最佳聚类个数,学者们提出许多信息准则,通常通过加入模型复杂度的惩罚项来避免出现过拟合问题,本文选择了常用的两种模型选择方法——赤池信息准则(Akaike information criterion,AIC)和贝叶斯信息准则(Bayesian information criterion,BIC)。在节点选择上,使用了拐点法,如图 2所示,原始地震目录和精定位目录数据的最佳聚类个数分别为6和14。AIC和BIC的计算公式如下:
| $ \mathrm{AIC}=-2 \ln (L)+2 k $ | (2) |
| $ \mathrm{BIC}=-2 \ln (L)+k \ln (n) $ | (3) |

|
图 2 原始地震目录和地震精定位目录的AIC和BIC判别 Fig. 2 AIC and BIC discrimination of original seismic catalogue and seismic fine positioning catalogue |
式中,L为该模型下的最大似然,n为数据数量,k为模型变量个数。
2.3 聚类结果根据AIC和BIC确定的最佳聚类数结果,分别对本文研究数据原始地震目录和精定位目录进行聚类分析,在聚类个数选择上分别选取6个和14个,具体分布见图 3和4。从结果上看,K-means聚类的地震群主要呈圆形或块状分布,而GMM聚类的地震群主要呈条带状分布,与地震主要沿断层分布的特征相对应。相对原始地震目录,地震精定位结果对地震的分组更精确,更符合区域断层几何分布特征。研究范围内2次6级以上强震分别是2013年岷县MS6.6地震与2017年九寨沟MS7.0地震,根据GMM方法聚类结果,只有精定位目录将这两次地震序列进行了区分,原始目录的聚类中岷县MS6.6地震序列因为与周围地震连接紧密以及最佳聚类数限制,没有聚类成单独的地震群。精定位后九寨沟地震序列空间分布更为收缩,与周边零散地震邻近距离拉长,聚类精度更高(图 3(b)、图 4(b)绿色框处)。为了确定本文聚类方法对震群识别的准确性,对比前人的地震精定位结果[11-13],本文得到的两次地震序列震群空间展布形状均与前人的结果相一致,这也验证了本文方法的可靠性。
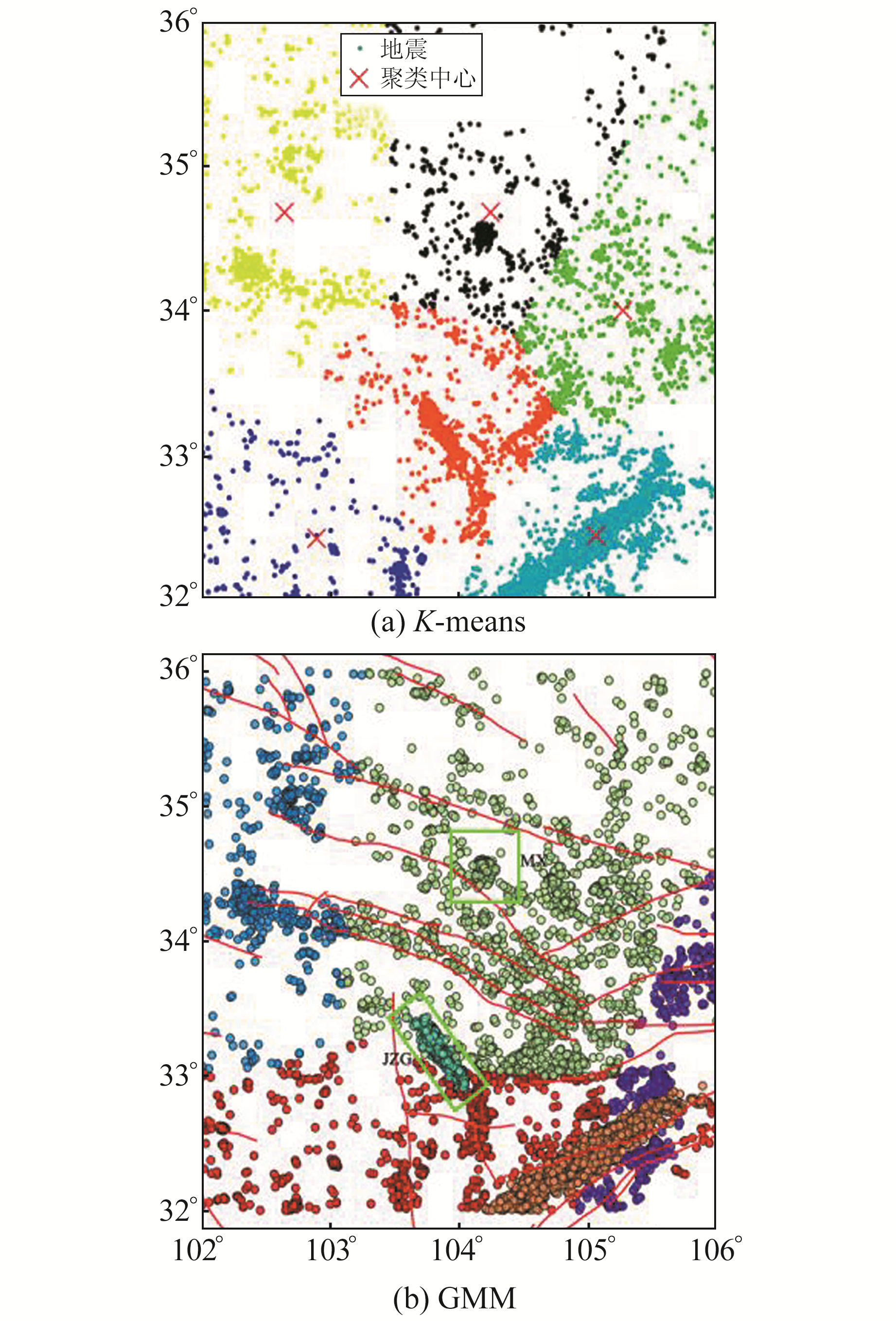
|
图 3 原始地震目录地震两种方法聚类结果 Fig. 3 Clustering results of two methods of original earthquake catalogue |

|
图 4 地震精定位目录地震两种方法聚类结果 Fig. 4 Clustering results of two methods of earthquake fine positioning catalogue |
从两种聚类方法的原理上看,K-means聚类主要是计算聚类中心到各点的欧氏距离,适合于圆形分布的数据集群。地震主要是断层活动产生,而从已有的断层数据来看,多数断层呈条带状分布,因此K-means聚类在地震聚类中未能取得理想的结果。而GMM聚类方法基于概率密度判断相似性,假设数据点是呈高斯分布(椭圆形)的,这与现实地震条带状分布更接近,因此该方法相对于K-means方法来说更适用于地震聚类分析。地震精定位处理通常会将地震的空间位置更好地聚集起来,从而更容易发现断层的几何展布形态。另外,对相对孤立的地震事件,按照设定的地震配对标准不符合条件者会予以去除,这些孤立事件散布在各地震群之间,增加了地震空间数据模型的复杂度,使得对最佳聚类数的选择存在精定位前后不一致的结果,进而对地震聚类分析产生一定干扰。因此结合地震精定位和GMM聚类方法能够提高地震震群识别,这也解释了形状更接近圆形的岷县地震序列在没有进行精定位处理前GMM聚类也无法将其识别区分的原因。
3 结语从本文结果来看,地震空间数据的聚类结果与现实相吻合,并且可以通过使用聚类算法对地震数据进行建模来确定区域内地震活动特征。随着计算机性能的逐步提高,大数据高效分析也得到全方位的普及,而聚类分析是一个历史悠久且易于理解的过程,适用于从大型不相干数据集中提取有意义的特征。为了将地震目录的空间分布划分地震群,本文使用了K-means和GMM两种聚类方法,分别对2013~2021年研究区的11 659条地震目录及6 654次精定位结果进行聚类分析,获得如下认识:
1) 将地震分组为不同的集群可用于改进区域内地震活动的机制识别和模式识别。本文展示了地震空间聚类流程,可作为分析地震数据集的工具以及用于解释结果的可视化。
2) 在地震群个数的选择中,可以通过计算AIC和BIC来确定最佳聚类数,其中,本文所用数据中原始地震目录和精定位目录的最佳聚类数分别为6和14,结合区域断层分布和数量来看,地震精定位对聚类分析有较好的促进作用。
3) GMM聚类的地震群主要呈条带状分布,更符合实际地震主要沿断层分布的普遍情况。根据本文结果,精定位地震目录和GMM聚类方法可以从众多地震分布中突出强震(如九寨沟MS7.0和岷县MS6.6地震)地震序列的震群分布。
此外,与其他无监督算法(如自组织映射)相比,K-means和GMM两种无监督技术较为直接和高效。另外,这两种聚类方法并不是分类不同地震事件的最佳方法,而是可能方法,也适用于其他具有更复杂数据集的地震活动地区。额外的判别器会导致更多维度的问题,而本研究只处理二维问题,计算简单、效率高。根据本文研究结果,可以在没有先验信息的地区使用无监督聚类算法来对地震群进行快速识别分析。
随着地震台网的进一步密集化以及地震预警台网的建立,长期连续观测的地震目录与日俱增,本文使用的聚类分析方法在大数据处理时具有明显优势,可以第一时间提取地震的空间分布特征,为实时地震趋势判断提供参考。另外,本文提出的地震最佳聚类方法给地震集群以及活动性分析提供了新思路。
致谢: 甘肃、四川测震台网提供地震目录数据,本文作图使用了Python和GMT软件,在此一并表示感谢。
| [1] |
Gutenberg B, Richter C F. Frequency of Earthquakes in California[J]. Bulletin of the Seismological Society of America, 1944, 34(4): 185-188 DOI:10.1785/BSSA0340040185
(  0) 0) |
| [2] |
尹欣欣, 曾文浩, 李少华, 等. 青海祁连MS5.2地震微震检测与目录完备性研究[J]. 地震工程学报, 2019, 41(1): 183-188 (Yin Xinxin, Zeng Wenhao, Li Shaohua, et al. Missing Earthquakes Detection and Completeness of Earthquake Catalogs of the 2015 Qilian, Qinghai MS5.2 Earthquake[J]. China Earthquake Engineering Journal, 2019, 41(1): 183-188)
(  0) 0) |
| [3] |
Irwansyah E, Winarko E. Spatial Data Clustering and Zonation of Earthquake Building Damage Hazard Area[J]. EPJ Web of Conferences, 2014, 68
(  0) 0) |
| [4] |
Novianti P, Setyorini D, Rafflesia U. K-Means Cluster Analysis in Earthquake Epicenter Clustering[J]. International Journal of Advances in Intelligent Informatics, 2017, 3(2): 81-89 DOI:10.26555/ijain.v3i2.100
(  0) 0) |
| [5] |
Zamani A, Hashemi N. Computer-Based Self-Organized Tectonic Zoning: A Tentative Pattern Recognition for Iran[J]. Computers and Geosciences, 2004, 30(7): 705-718 DOI:10.1016/j.cageo.2004.04.002
(  0) 0) |
| [6] |
Ansari A, Noorzad A, Zafarani H. Clustering Analysis of the Seismic Catalog of Iran[J]. Computers and Geosciences, 2009, 35(3): 475-486 DOI:10.1016/j.cageo.2008.01.010
(  0) 0) |
| [7] |
Waldhauser F. Fault Structure and Mechanics of the Hayward Fault, California, from Double-Difference Earthquake Locations[J]. Journal of Geophysical Research Atmospheres, 2002, 107(B3): 2054 DOI:10.1029/2000JB000084
(  0) 0) |
| [8] |
尹欣欣, 杨立明, 陈继锋, 等. 甘肃地区一维速度模型计算研究[J]. 地震工程学报, 2017, 39(1): 154-159 (Yin Xinxin, Yang Liming, Chen Jifeng, et al. Study on the one Dimensional Velocity Model in Gansu Area[J]. China Earthquake Engineering Journal, 2017, 39(1): 154-159)
(  0) 0) |
| [9] |
Likas A, Vlassis N, J Verbeek J. The Global K-Means Clustering Algorithm[J]. Pattern Recognition, 2003, 36(2): 451-461 DOI:10.1016/S0031-3203(02)00060-2
(  0) 0) |
| [10] |
Duda R O, Hart P E, Stork D G. Pattern Classification[M]. US: Wiley-Interscience, 2000
(  0) 0) |
| [11] |
梁姗姗, 徐志国, 杜广宝, 等. 2013年甘肃岷县-漳县M6.6地震序列精定位研究[J]. 地震地磁观测与研究, 2017, 38(2): 12-16 (Liang Shanshan, Xu Zhiguo, Du Guangbao, et al. Precise Relocation of Minxian-Zhangxian M6.6 Earthquake Sequence in Gansu Province, 2013[J]. Seismological and Geomagnetic Observation and Research, 2017, 38(2): 12-16)
(  0) 0) |
| [12] |
房立华, 吴建平, 苏金蓉, 等. 四川九寨沟MS7.0地震主震及其余震序列精定位[J]. 科学通报, 2018, 63(7): 649-662 (Fang Lihua, Wu Jianping, Su Jinrong, et al. Relocation of Mainshock and Aftershock Sequence of the MS7.0 Sichuan Jiuzhaigou Earthquake[J]. Chinese Science Bulletin, 2018, 63(7): 649-662)
(  0) 0) |
| [13] |
尹欣欣, 杨立明, 赵林林, 等. 九寨沟M7.0级地震余震目录完备性研究[J]. 地球物理学进展, 2020, 35(2): 475-479 (Yin Xinxin, Yang Liming, Zhao Linlin, et al. Missing Earthquakes Detection and Completeness of Earthquake Catalogues of the 2017 Jiuzhaigou M7.0 Earthquake[J]. Progress in Geophysics, 2020, 35(2): 475-479)
(  0) 0) |
2. Chengdu Surveying Geotechnical Research Institute Co Ltd, MCC, 199 Sanse Road, Chengdu 610023, China
 2022, Vol. 42
2022, Vol. 42


