2. 中国科学院上海天文台,上海市南丹路80号,200030
精密单点定位技术(precise point positioning,PPP)仅利用一台GNSS接收机即可实现cm级甚至mm级的定位精度,其发展对于变形监测[1]、精密导航[2]、大气探测[3]、时钟同步[4]等诸多领域意义重大。然而PPP的收敛时间较长,传统的GNSS PPP通常需要20 min左右甚至更长时间才能收敛至cm级。为解决上述问题,Pan等[5]提出利用GPS和GLONASS多系统进行联合PPP解算,增加历元可见卫星数量、改善几何分布,从而提升PPP收敛时间以及定位精度。但同为中高轨的GNSS系统难以解决GNSS接收信号弱、几何构型变化慢的劣势,于是有学者提出利用低轨卫星增强GNSS系统[6]。低轨卫星的高度较低,通常为400~1 500 km,相较于GNSS系统,其轨道更低、信号播发强度更高[7]。较低的卫星高度使得低轨卫星速度较快,通常100 min左右就可以环绕地球一周,这使得历元间观测数据的相关性大为减小,极大改善了几何精度因子,有利于快速解算GNSS载波相位的模糊度[8],实现快速高精确定位。
随着低轨卫星导航性能增强技术的出现,许多国家开始部署低轨卫星增强系统,如美国的Iridium系统[9]、中国的“鸿雁”[10]、“虹云”[11]等。赵兴隆等[12]在GPS系统的基础上加入Iridium系统,成功利用LEO星座增强了PPP性能;Li等[13]通过加入60、96、192和288颗星的低轨星座增强PPP,使收敛时间达到10 min以内。但以上低轨卫星轨道模型都过于理想,忽略了真实卫星轨道可能存在的日月摄动等因素,而在实测数据中这些因素引起的低轨卫星轨道误差不可忽略。
基于上述分析,本文通过在LEO星座中加入轨道误差,利用实测GPS观测数据以及仿真得到的低轨观测数据进行联合PPP解算,从PDOP值、可视卫星数量、PPP定位精度和收敛时间等方面评估LEO星座对GPS精密单点定位性能的增强作用。
1 LEO地面观测值仿真仿真观测值的基本原理是定位的逆向处理[14],利用单个历元下可观测到的卫星伪距和载波相位观测数据,通过最小二乘法或卡尔曼滤波法估计接收机的位置和钟差,所有的误差(包括与接收机和测站有关的误差、与卫星有关的误差、与信号传播路径有关的误差等)都通过已有模型进行改正。已知测站位置、卫星轨道和卫星钟差,可以计算出测站与卫星间的几何距离。由已有的模型计算从信号发射到接收过程中的所有误差,并考虑观测噪声,最后将这些误差和噪声加入到几何距离上以模拟伪距和载波观测数据。
伪距观测数据仿真公式和相位观测数据仿真公式分别为:
| $ \begin{gathered} P_{\mathrm{r}, j}^{\mathrm{s}}=\boldsymbol{u}_{\mathrm{r}}^{\mathrm{s}}\left(o^{\mathrm{s}}-r_{\mathrm{r}}\right)+d_{\mathrm{pco}, j}^{\mathrm{s}}+d_{\mathrm{pcv}, j}^{\mathrm{s}}+ \\ d_{\mathrm{r}, \mathrm{pco}, j}^{\mathrm{s}}+d_{\mathrm{r}, \mathrm{scv}, j}^{\mathrm{s}}+d_{\mathrm{r}, \mathrm{disp}}^{\mathrm{s}}-t^{\mathrm{s}}+t_{\mathrm{r}}+I_{\mathrm{r}, j}^{\mathrm{s}}+ \\ T_{\mathrm{r}}^{\mathrm{s}}+b_{\mathrm{r}, j}-b_j^{\mathrm{s}}+e_{\mathrm{r}, j}^{\mathrm{s}} \end{gathered} $ | (1) |
| $ \begin{gathered} \varphi_{\mathrm{r}, j}^{\mathrm{s}}=\boldsymbol{u}_{\mathrm{r}}^{\mathrm{s}}\left(o^{\mathrm{s}}-r_{\mathrm{r}}\right)+d_{\mathrm{pco}, j}^{\mathrm{s}}+d_{\mathrm{pcv}, j}^{\mathrm{s}}+d_{\mathrm{r}, \mathrm{pco}, j}^{\mathrm{s}}+ \\ d_{\mathrm{r}, \mathrm{pcv}, j}^{\mathrm{s}}+d_{\mathrm{r}, \mathrm{disp}}^{\mathrm{s}}-t^{\mathrm{s}}+t_{\mathrm{r}}+I_{\mathrm{r}, j}^{\mathrm{s}}+T_{\mathrm{r}}^{\mathrm{s}}+b_{\mathrm{r}, j}- \\ b_j^{\mathrm{s}}+\varepsilon_{\mathrm{r}, j}^{\mathrm{s}}+\lambda_j N_j^{\mathrm{s}} \end{gathered} $ | (2) |
式中,Pr, js和φr, js分别为伪距观测值和相位观测值,上、下标s、r、j分别为卫星、接收机和频率号,u为接收机至卫星视线方向的单位向量,os为卫星质心坐标,rr为测站接收机参考点坐标,dpco、dpcv分别为卫星端相位中心偏差和相位中心变化,dr, disps为固体潮、海潮等改正,I、T分别为电离层延时与对流层延时,εr, js、er, js分别为相位观测值噪声和伪距观测值噪声,b为码硬件延迟,λj为频率j对应的载波波长,Njs为整周模糊度。
接收机钟差、接收机端天线相位中心偏差PCO、潮汐改正、对流层改正可以通过计算得到,伪距噪声和相位噪声则分别选用服从标准正态分布的1 m和0.002 m随机误差。为简化实验,暂不考虑卫星钟差以及天线数值,低轨卫星PCO、天线相位中心变化PCV均设置为0。选取包含轨道误差的轨道文件进行仿真观测值求取,得到包含轨道误差的观测值文件,同时在观测值仿真的过程中设置截止高度角为7°,选取符合条件的低轨卫星。由于低轨卫星播发信号与GPS卫星播发信号相同,因此需进行无电离层组合静态PPP数据处理。
2 低轨卫星轨道数据仿真GPS的32颗导航卫星分布在6个不同的轨道面上,高度为20 200 km,GPS卫星轨道数据由武汉大学GNSS中心提供。本文使用倾斜轨道的低轨卫星,高度为1 000 km,轨道倾角为50°,运行周期约为90 min,分布在24个不同的轨道面上,每个轨道面的低轨卫星数量分别为5、10、15。上述低轨卫星轨道由STK生成,以30 s的采样间隔输出低轨卫星的三维坐标以及三维速度。
3 实验与分析实验选取CPVG、WUH2、KOUG、IISC、FUNC共5个IGS站进行观测数据仿真,研究时段为2018年doy183的5:00:00~10:00:00,取样间隔为1 s,对9:00:00~10:00:00共3 601个历元进行静态PPP数据处理。对单系统GPS和双系统GPS+LEO进行对比分析,同时设计3种GPS+LEO卫星分布场景:1)GPS+120颗倾斜轨道卫星;2)GPS+240颗倾斜轨道卫星;3)GPS+360颗倾斜轨道卫星。对模拟时段的平均可视卫星数量、PDOP值、PPP收敛时间、E、U、N三个方向上的定位RMS值等数据进行统计分析。
3.1 处理策略单系统GPS以及LEO星座增强GNSS PPP的具体处理策略如表 1所示。
|
|
表 1 GPS/LEO联合PPP解算策略 Tab. 1 GPS/LEO joint PPP solution strategy |
三维位置精度因子PDOP的数值可以反映导航卫星与地面监测站形成的几何图形的优劣,可作为基于空间分布结构的导航性能增强分析手段。随着可观测卫星数量的增加,PDOP值逐渐减小,PDOP值越小,代表其卫星与地面监测站形成的几何构型越好,对精度影响越小。5个观测站单系统GPS与3种低轨卫星分布的平均PDOP值和平均可见卫星数量如表 2、3所示。
|
|
表 2 IGS站GPS与3种低轨卫星分布平均PDOP值 Tab. 2 The average PDOP of GPS and three satellite distributionsof IGS station |
|
|
表 3 IGS站GPS与3种低轨卫星分布平均可见星数量 Tab. 3 The average number of visible stars distributed by GPS and three satellitesof IGS station |
随着低轨卫星的加入,5个IGS站每个历元的PDOP平均值由2.0分别降至1.3、1.1、0.9,平均降低0.7、0.9、1.1;平均可视卫星数量由8.3增加至18.0、27.7、39.6,分别增加了9.7、19.4、31.3。上述数据表明,利用低轨卫星增强GPS可以增加单个历元的可视卫星数量、降低精度因子、提升定位精度、优化导航性能。
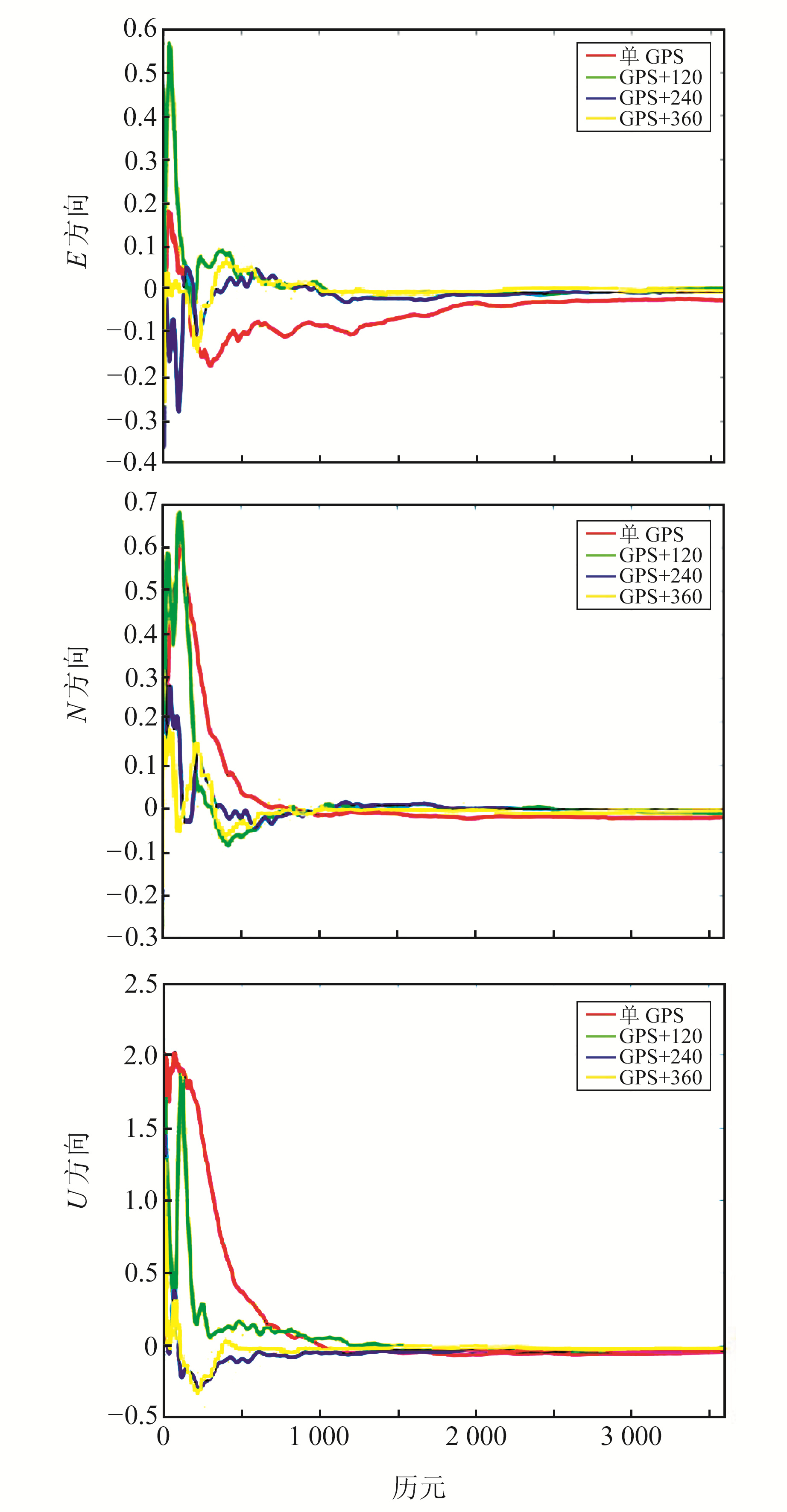
3.3 PPP收敛时间及精度分析接收机钟差、对流层延时、卫星轨道误差与钟差等因素均会影响PPP的收敛时间,而过长的收敛时间则会限制PPP的应用场景。由于轨道积分得到的低轨卫星精密轨道可视为无误差轨道,与真实情况不符,因此加入周期为90 min、径向为±2 cm、法向及切向同为±6 cm、相位为2π倍伪随机误差(该随机误差服从标准正态分布)的周期误差,用于模拟真实轨道误差,最终得到带有卫星轨道误差的伪距观测值以及载波相位观测值。同时本文设定E方向及N方向均为10 cm、U方向为20 cm、连续20个历元不再发散的收敛条件,进行GPS+LEO联合PPP解算。以CPVG站为例,计算结果如图 1所示。
|
图 1 GPS与3种GPS+LEO在E、N、U方向上的定位误差序列 Fig. 1 Sequence of E, N, U direction positioning errors for GPS and three kinds of GPS+LEO |
由图可见,LEO星座对单系统GPS的增强效果极其显著。在加入低轨卫星后,U方向的定位误差改善最显著,E方向的改善效果也十分明显,但N方向的改善程度不大。因此可以认为,低轨卫星系统在U方向上的增强效果最佳。
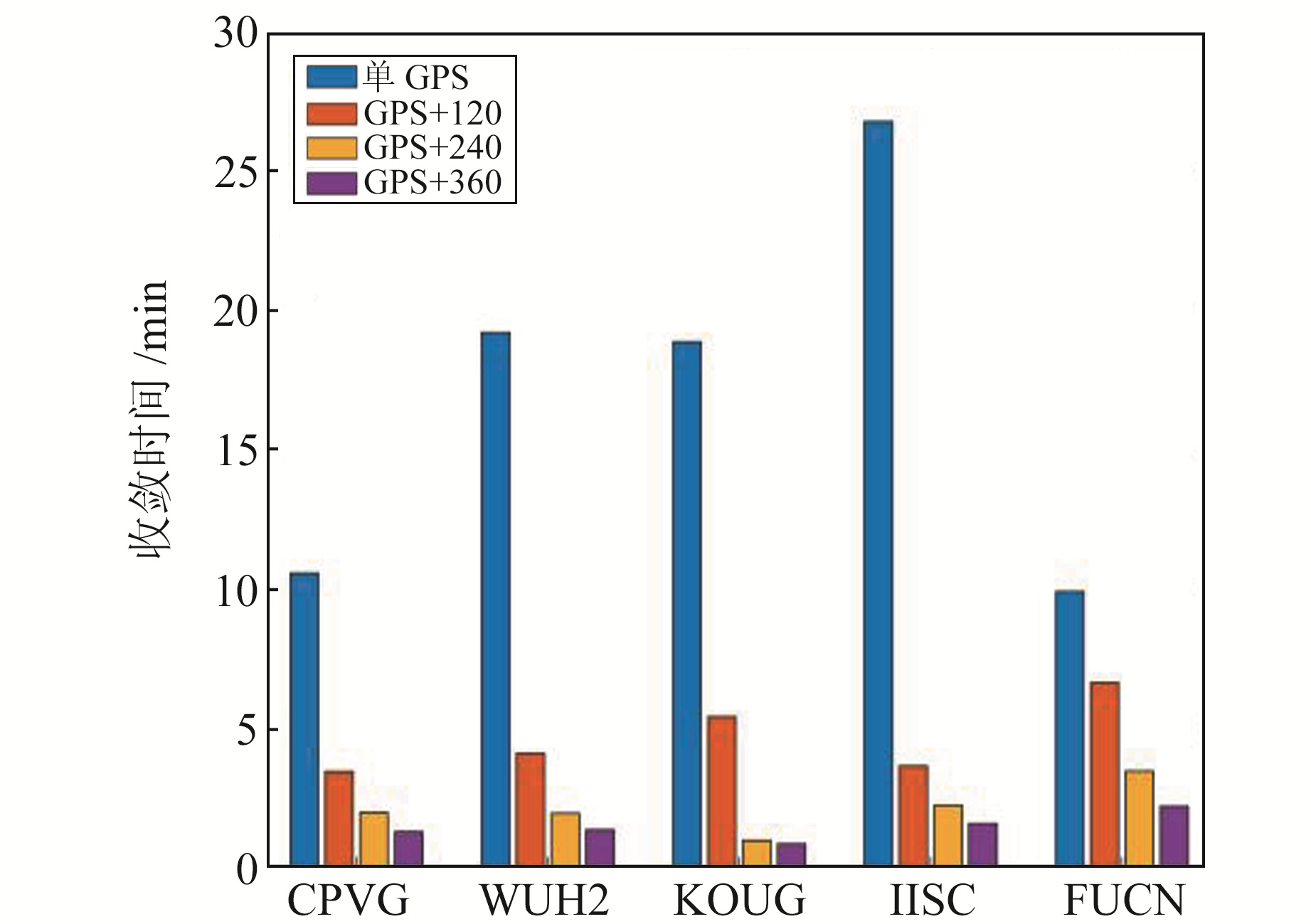
由图 2和表 4可见,加入LEO星座后收敛时间缩短明显。分别引入120、240、360颗LEO卫星后,PPP多站平均收敛时间由17.1 min分别缩短至4.7 min、2.1 min、1.5 min。附加360颗LEO卫星仿真观测数据后,收敛时间降低近90%,观测环境较好的观测站收敛时间甚至可以控制在1 min以内。
|
图 2 不同测站不同星座数量的GPS+LEO收敛时间 Fig. 2 GPS+LEO convergence time for different stations and different constellation numbers |
|
|
表 4 不同测站LEO星座增强PPP收敛时间统计 Tab. 4 Leo constellations enhance PPP convergence time on different stations |
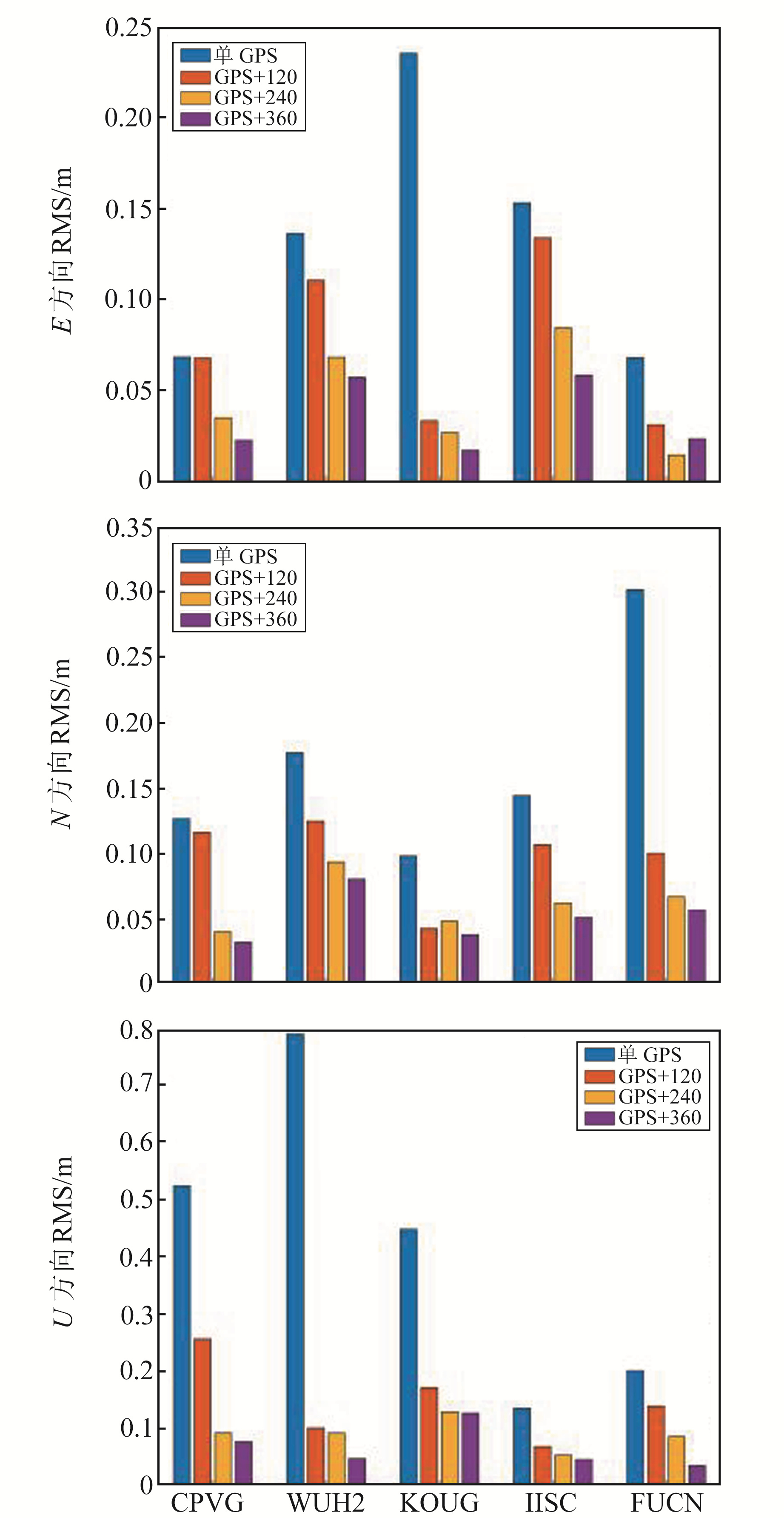
由图 3可见,LEO星座联合GPS解算后其定位误差在E、N、U三个方向上均有明显改善。当加入120颗低轨卫星时N方向上的RMS由0.170 m降至0.098 m,E方向上的RMS由0.132 m降至0.076 m,U方向上的RMS由0.420 m降至0.148 m,3个方向上分别提高约37.4%、34.4%、55.9%;当加入240颗低轨卫星时N方向上的RMS由0.170 m降至0.062 m,E方向上的RMS由0.132 m降至0.046 m,U方向上的RMS由0.420 m降至0.092 m,3个方向上分别提高约60.3%、59.4%、71.7%;当加入360颗低轨卫星时N方向上的RMS由0.170 m降至0.052 m,E方向上的RMS由0.132 m降至0.036 m,U方向上的RMS由0.420 m降至0.068 m,3个方向上分别提高约67.3%、72.9%、79.6%。
|
图 3 各测站在E、N、U方向上定位偏差的RMS值 Fig. 3 RMS of E, N, U direction positioning deviation of each station |
1) 相较于GPS单系统,GPS+LEO系统能有效提高观测历元的平均可见卫星数量,由单系统的8.3增加至18.0(120颗)、27.7(240颗)、39.6(360颗),PDOP平均值由2.0降至1.3(120颗)、1.1(240颗)、0.9(360颗)。
2) 低轨卫星系统可以增强GPS的PPP浮点解,在N、E方向上均有一定程度的改善,在U方向上的精度提升十分显著,最高可达70%以上。
3) 单系统GPS的平均收敛时间为17.1 min,分别加入120颗、240颗、360颗LEO卫星后GPS+LEO联合PPP收敛时间分别为4.7 min、2.1 min、1.5 min。
本文在LEO观测数据仿真过程中未考虑LEO卫星PCO、PCV及钟差的设置及改正,同时LEO轨道误差的函数模型过于简单且在解算过程中仅考虑了静态情况。后续研究中将进一步完善LEO观测数据仿真过程及GPS/LEO联合PPP软件,以获得更细致的分析结论。
| [1] |
赵兴旺, 王胜利, 刘超. GNSS精密单点定位理论与方法[M]. 合肥: 中国科学技术大学出版社, 2015 (Zhao Xingwang, Wang Shengli, Liu Chao. Theory and Method of GNSS Precise Point Positioning[M]. Hefei: University of Science and Technology of China Press, 2015)
(  0) 0) |
| [2] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017 DOI:10.1029/96JB03860
(  0) 0) |
| [3] |
姚宜斌, 张顺, 孔建. GNSS空间环境学研究进展和展望[J]. 测绘学报, 2017, 46(10): 1408-1420 (Yao Yibin, Zhang Shun, Kong Jian. Research Progress and Prospect of GNSS Space Environment Science[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1408-1420)
(  0) 0) |
| [4] |
Pratt J, Axelrad P, Larson K M, et al. Satellite Clock Bias Estimation for iGPS[J]. GPS Solutions, 2013, 17(3): 381-389 DOI:10.1007/s10291-012-0286-4
(  0) 0) |
| [5] |
Li P, Zhang X H. Integrating GPS and GLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J]. GPS Solutions, 2014, 18(3): 461-471 DOI:10.1007/s10291-013-0345-5
(  0) 0) |
| [6] |
张小红, 马福建. 低轨导航增强GNSS发展综述[J]. 测绘学报, 2019, 48(9): 1073-1087 (Zhang Xiaohong, Ma Fujian. Review of the Development of LEO Navigation-Augmented GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1073-1087)
(  0) 0) |
| [7] |
邓琳, 李广侠, 田世伟, 等. 基于LEO增强的COMPASS导航系统抗干扰能力研究[J]. 军事通信技术, 2012, 33(2): 65-69 (Deng Lin, Li Guangxia, Tian Shiwei, et al. Capabilities of LEO Enhanced COMPASS Navigation System for Anti-Jamming[J]. Journal of Communication Technology, 2012, 33(2): 65-69)
(  0) 0) |
| [8] |
Tian S W, Dai W H, Liu R F, et al. System Using HybridLEO-GPS Satellites for Rapid Resolution of Integer Cycle Ambiguities[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 1774-1785 DOI:10.1109/TAES.2014.120662
(  0) 0) |
| [9] |
Joerger M, Gratton L, Pervan B, et al. Analysisof Iridium-Augmented GPS for Floating Carrier Phase Positioning[J]. Navigation, 2010, 57(2): 137-160 DOI:10.1002/j.2161-4296.2010.tb01773.x
(  0) 0) |
| [10] |
蒙艳松, 边朗, 王瑛, 等. 基于"鸿雁"星座的全球导航增强系统[J]. 国际太空, 2018(10): 20-27 (Meng Yansong, Bian Lang, Wang Ying, et al. Global Navigation Augmentation System Based on Hongyan Satellite Constellation[J]. Space International, 2018(10): 20-27)
(  0) 0) |
| [11] |
CNAGA. CASIC Plans to Launch 156 Small Satellites for the Hongyun Program[EB/OL]. http://llen.chinabeidou.org.cn/c/393.html, 2018
(  0) 0) |
| [12] |
赵兴隆, 钟世明, 欧吉坤, 等. LEO星座增强GNSS的精密单点定位初步分析[J]. 大地测量与地球动力学, 2020, 40(6): 624-628 (Zhao Xinglong, Zhong Shiming, Ou Jikun, et al. Precise Point Positioning Primary Analysis of GNSS Enhanced with LEO Constellation[J]. Journal of Geodesy and Geodynamics, 2020, 40(6): 624-628)
(  0) 0) |
| [13] |
Li X X, Ma F J, Li X, et al. LEO Constellation-Augmented Multi-GNSS for Rapid PPP Convergence[J]. Journal of Geodesy, 2019, 93(5): 749-764 DOI:10.1007/s00190-018-1195-2
(  0) 0) |
| [14] |
许承东, 李怀建, 张鹏飞. GNSS数学仿真原理及系统实现[M]. 北京: 中国宇航出版社, 2014 (Xu Chengdong, Li Huaijian, Zhang Pengfei. GNSS Mathematical Simulation Principle and System Implementation[M]. Beijing: China Astronautic Publishing House, 2014)
(  0) 0) |
2. Shanghai Astronomical Observatory, CAS, 80 Nandan Road, Shanghai 200030, China
 2022, Vol. 42
2022, Vol. 42

