2. 湖北省电力勘测设计院有限公司,武汉市新桥四路1号, 430040;
3. 西安测绘研究所,西安市雁塔路中段1号,71005;
4. 黄石市自然资源和规划局,湖北省黄石市广州路22号,435004
2020-06北斗三号系统全球组网全面完成,为全球用户提供全天候导航、定位、授时服务。BDS-3面向全球定位用户发播原有的B1I、B3I和新增的B1C、B2a与B2b信号[1],多GNSS实验(multi-GNSS experiment,MGEX)地面站也在逐步更新可接收BDS-3新频点信号的接收机天线。业内学者针对BDS-3的服务性能进行相关研究表明,BDS-3的信号质量总体上要优于BDS-2[2]。由于BDS-3采用星间链路技术,BDS-3卫星的轨道精度和钟差精度相较于BDS-2有显著提高[3]。BDS-3在亚太地区的标准单点定位精度与BDS-2相比,提高了12.1%~60.2%[4]。施闯等[5]采用B1I和B1C信号进行单频精密单点定位(precise point positioning,PPP)测试表明,BDS-3的PPP精度比BDS-2提高约60%。收敛时间方面,BDS-3 PPP的收敛时间比BDS-2缩短超过50%[6]。张小红等[7]研究表明,BDS在观测条件相同的情况下已经可以实现与其他导航卫星系统基本相当的定位性能。与GPS L1/L5或Galileo E1/E5a的双频消电离层组合相比,BDS-3 B1C/B1I/B2a信号的三频最优线性组合可以提高定位精度约20%[8]。
但现阶段针对BDS新增B1C、B2a频点定位性能的相关研究较少,因此,有必要对当前新增频点的定位性能进行全面分析。基于此,本文采用武汉大学(Wuhan University, WHU)精密轨道和钟差产品,评估了GNSS精密产品的精度,选取18个分布在东半球的MGEX站进行静态和仿动态PPP实验,对BDS、GPS、GLONASS、Galileo四个系统的PPP性能进行对比分析,并采用BDS B1C/B2a、B1I/B3I两组频点的观测值进行测试,对比分析新、旧频点的定位性能。
1 GNSS精密产品精度评估精密轨道和钟差产品的质量直接决定着PPP的服务性能[9],因此在开展定位测试之前,有必要对PPP所选用的精密产品进行精度评定。本文采用德国地学中心(Deutsches GeoForschungs Zentrum, GFZ)和武汉大学(WHU)精密产品进行对比分析,以评估4个系统的产品性能。由于两个分析中心精密产品的解算策略并不相同[10],异常值不可避免,本文取3倍于钟差时间序列或轨道差异中位数为阈值,并在分析计算中剔除这些异常值。本文选用2021-08-15~28(doy 227~240)共14 d的精密钟差与轨道产品进行对比分析。
1.1 GNSS精密轨道产品精度评估评估精密轨道产品的精度通常采用不同产品之间的一致性进行,本文以GFZ事后精密轨道产品作为参考,使用WHU精密轨道产品进行对比,以其均方根误差(RMS)作为精度指标。由于两种轨道采样率不同,在作差之前需要内插为相同的采样率。精密轨道产品以30 s为间隔,对比分析轨道径向(R)、切向(A)、法向(C)3个方向的差异,分别计算其RMS。
图 1给出BDS、Galileo、GPS、GLONASS精密轨道产品在R、A、C三个方向的RMS。由于BDS地球静止轨道(GEO)卫星R、A、C方向RMS均较大,图中略去。

|
图 1 GNSS精密卫星轨道精度统计结果 Fig. 1 The accuracy of GNSS precise orbit products |
统计结果显示,4个系统精密卫星轨道在R、A、C三个方向的精度均值在cm级,其中BDS卫星轨道精度分别为6.32 cm、5.71 cm、6.45 cm,GPS卫星轨道的精度最优,3个方向的精度稳定在2 cm以内。GLONASS卫星和Galileo卫星的轨道精度基本相当,三维精度基本都维持在4 cm以内。总体而言,两个分析中心轨道产品的一致性较好。
1.2 GNSS精密钟差产品精度评估在各产品之间存在时间基准的差异[11],本文采用经典的二次差法,对卫星钟差进行精度评定[12]。同时顾及卫星天线相位中心差异导致的几何距离偏差在径向上对卫星钟差精度的影响,因此在钟差估计时,添加了径向误差改正[13]。根据卫星二次差分序列可以统计得到表征产品精度信息的RMS和标准差(STD),统计结果如图 2所示。
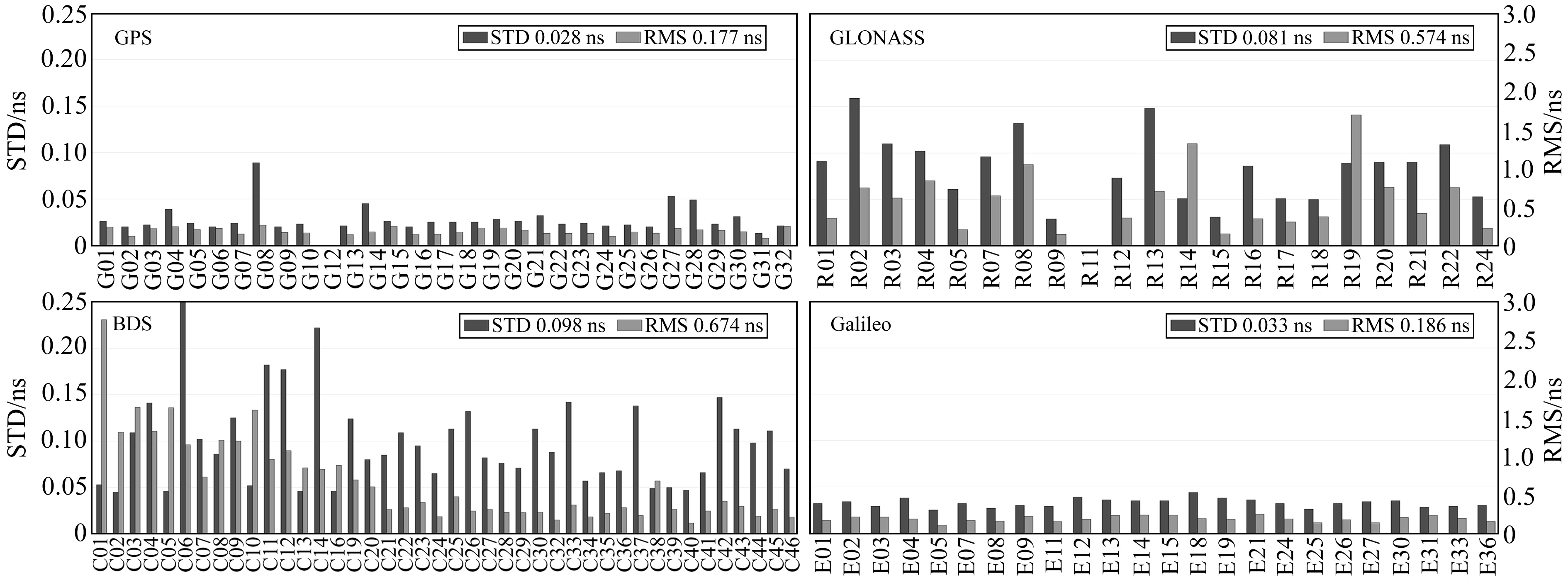
|
图 2 GNSS精密钟差精度统计结果 Fig. 2 The accuracy of GNSS precise clock products |
统计结果表明,GFZ和WHU的卫星钟差产品具有较好的一致性。其中,GPS的产品精度最优,Galileo次之。BDS的GEO卫星的RMS明显大于其他卫星,BDS-3的钟差外符合精度优于BDS-2卫星。GLONASS的钟差内符合精度在0.081 ns(STD),与BDS相当,且略优于BDS。
对比4个系统的产品精度发现,4个系统轨道精度在cm量级,钟差内符合精度都优于0.1 ns。GPS的轨道和钟差精度要优于Galileo和GLONASS,BDS的产品精度略差于其他系统,BDS-3的钟差性能优于BDS-2。
2 PPP精度对比分析本文采用双频消电离层组合模型(IF12),分别进行GNSS各系统静态与动态PPP定位实验,并采用定位精度和收敛时间对各系统PPP性能进行比较。此外,为分析验证BDS新频点B1C/B2a精密单点定位性能,进行BDS实验时分别选用B1C/B2a、B1I/B3I两对观测值进行相应PPP实验:B1I/B3I实验结果与其他系统进行对比分析;B1C/B2a与B1I/B3I进行PPP精度对比。
GNSS原始伪距和载波相位观测方程可以表示为[14]:
| $ \left\{\begin{array}{l} P_{r, f}^s(i)=\rho_r^s(i)+c\left[\mathrm{~d} t_r(i)-\mathrm{d} t^s(i)\right]+m_r^s \cdot \\ \quad T_r(i)+\mu_f I_{r, 1}^s(i)+b_{r, f}-b_f^s+\varepsilon_r^s(i) \\ L_{r, f}^s(i)=\rho_r^s(i)+c\left[\mathrm{~d} t_r(i)-\mathrm{d} t^s(i)\right]+m_r^s \cdot \\ \quad T_r(i)-\mu_f I_{r, 1}^s(i)+\varphi_{r, f}-\varphi_f^s+\lambda_f N_{r, f}^s+\xi_r^s(i) \end{array}\right. $ | (1) |
式中,上标s为卫星号,下标r为接收机号,下标f为频段号,i为对应的历元号,Pr, fs(i)为第i个历元的伪距观测值,Lr, fs(i)为第i个历元的载波相位观测值,ρrs(i)为站星间几何距离,c为真空光速,dtr(i)为接收机钟差,dts(i)为卫星钟差,mrs为对流层投影函数,Tr(i)为天顶对流层延迟,μf=(λf2/λ12)为其他频率电离层与第一频率间的比值,Ir, 1s(i)为第一频率的电离层延迟,br, f为接收机端的伪距硬件延迟,bfs为卫星端的伪距硬件延迟,φr, f为接收机端的相位硬件延迟,φfs为卫星端的相位硬件延迟,λf为载波相位波长,Nr, fs为载波相位整周模糊度,εrs为伪距多路径效应、观测噪声及其他未模型化误差之和,ξrs为载波相位多路径效应、观测噪声及其他未模型化误差之和。
由于伪距硬件延迟与钟差、模糊度参数存在相关性,所以为避免法方程无法求解,也需进行参数重组。因此,B1I/B3I双频消电离层组合的函数模型可表示为:
| $ \left\{\begin{array}{l} P_{r, \mathrm{IF}_{\mathrm{B1IB} 3 \mathrm{I}}}^s=e_r^s \cdot x+m_r^s \cdot T_r+ \\ \quad c \cdot \tilde{\mathrm{d}} t_{r, \mathrm{B1IB} 3 \mathrm{I}}+\varepsilon_r^s \\ L_{r, \mathrm{IF}_{\mathrm{B1IB31}}^s}=e_r^s \cdot x+m_r^s \cdot T_r+ \\ \quad c \cdot \tilde{\mathrm{d}} t_r+\tilde{N}_{r, \mathrm{IF}_{12}}^s+\xi_r^s \end{array}\right. $ | (2) |
| $ \left\{ \begin{array}{l} \widetilde {\rm{d}}{t_{r, {\rm{B}}1{\rm{IB}}3{\rm{I}}}} = {\rm{d}}{t_r} + {d_{r, {\rm{I}}{{\rm{F}}_{{\rm{B1IB3I}}}}}}\\ \widetilde {\rm{d}}{t^s} = {\rm{d}}{t^s} + {d_{{\rm{I}}{{\rm{F}}_{{\rm{B1IB}}3{\rm{I}}}}}}\\ {d_{r, {\rm{I}}{{\rm{F}}_{{\rm{B1IB}}3{\rm{I}}}}}} = {\alpha _{{\rm{B1IB}}3{\rm{I}}}} \cdot {d_{r, {\rm{B1I}}}} + {\beta _{{\rm{B1IB}}3{\rm{I}}}} \cdot {d_{r, {\rm{B}}3{\rm{I}}}}\\ {d_{{\rm{I}}{{\rm{F}}_{{\rm{B}}1{\rm{IB}}3{\rm{I}}}}}} = {\alpha _{{\rm{B}}1{\rm{IB}}3{\rm{I}}}} \cdot d_{_{{\rm{B}}1{\rm{I}}}}^s + {\beta _{{\rm{B}}1{\rm{IB}}3{\rm{I}}}} \cdot d_{_{{,\rm{B}}3{\rm{I}}}}^s\\ \widetilde N_{r, {\rm{I}}{{\rm{F}}_{{\rm{B}}1{\rm{IB}}3{\rm{I}}}}}^s = {\alpha _{{\rm{B}}1{\rm{IB}}3{\rm{I}}}} \cdot \left( {{\lambda _{{\rm{B}}1{\rm{I}}}} \cdot N_{r, {\rm{B}}1{\rm{I}}}^s + } \right.\\ \quad \left. {{b_{r, {\rm{B1I}}}} - b_{, {\rm{B1I}}}^s} \right) + {\beta _{{\rm{B}}1{\rm{IB}}3{\rm{I}}}} \cdot \left( {{\lambda _{{\rm{B}}3{\rm{I}}}} \cdot N_{r, {\rm{B}}3{\rm{I}}}^s + } \right.\\ \quad \left. {{b_{r, {\rm{B}}3{\rm{I}}}} - b_{{\rm{B}}3{\rm{I}}}^s} \right) - {d_{r, {F_{{\rm{B}}1{\rm{IB}}3{\rm{I}}}}}} + d_{, {\rm{I}}{{\rm{F}}_{{\rm{B}}1{\rm{IB}}3{\rm{I}}}}}^s\\ {\alpha _{{\rm{B}}1{\rm{IB}}3{\rm{I}}}} = \frac{{f_{{\rm{B}}1{\rm{I}}}^2}}{{f_{{\rm{B}}1{\rm{I}}}^2 - f_{{\rm{B}}3{\rm{I}}}^2}}, {\beta _{{\rm{B}}1{\rm{IB}}3{\rm{I}}}} = - \frac{{f_{{\rm{B}}3{\rm{I}}}^2}}{{f_{{\rm{B}}1{\rm{I}}}^2 - f_{{\rm{B}}3{\rm{I}}}^2}} \end{array} \right. $ | (3) |
由于卫星钟差中包含B1I/B3I消电离层组合伪距偏差的影响,因此在对应的B1C/B2a组合中,应顾及伪距偏差差异的影响:
| $ \left\{\begin{array}{l} P_{r, \mathrm{IF}_{\mathrm{B} 1 \mathrm{CB} 2 \mathrm{a}}}^s=e_r^s \cdot x+m_r^s \cdot T_r+ \\ \quad c \cdot \tilde{\mathrm{d}} t_{r, \mathrm{B1CB} 2 \mathrm{a}}+\mathrm{DCB}^s+\varepsilon_r^s \\ L_{r, \mathrm{IF}_{\mathrm{B1CB} 2 \mathrm{a}}}=e_r^s \cdot x+m_r^s \cdot T_r+ \\ \quad c \cdot \tilde{\mathrm{d}} t_{r, \mathrm{B1CB} 2 \mathrm{a}}+\widetilde{N}_{r, \mathrm{IF}_{12}}+\xi_r^s \end{array}\right. $ | (4) |
| $ \left\{ \begin{array}{l} {\rm{DC}}{{\rm{B}}^s} = \left( {{\alpha _{{\rm{B1IB}}31}} \cdot d_{, {\rm{B1I}}}^s + {\beta _{{\rm{B1IB}}3{\rm{I}}}} \cdot d_{{\rm{, B3I}}}^s} \right) - \\ \quad \left( {{\alpha _{{\rm{B1CB}}2{\rm{a}}}} \cdot d_{_{{\rm{, B1C}}}}^s + {\beta _{{\rm{B1CB2a}}}} \cdot d_{_{{\rm{, B}}2{\rm{a}}}}^s} \right)\\ \widetilde N_{r, {\mathrm{IF}_{{\rm{B1CB}}2{\rm{a}}}}}^s = {\alpha _{{\rm{B1CB}}2{\rm{a}}}}\left( {{\lambda _{{\rm{B1C}}}} \cdot N_{r, {\rm{B1C}}}^s + {b_{r, {\rm{B1C}}}} - } \right.\\ \quad \left. {b_{, {\rm{B1C}}}^s} \right) + {\beta _{{\rm{B}}1{\rm{CB}}2{\rm{a}}}} \cdot \left( {{\lambda _{{\rm{B}}2{\rm{a}}}} \cdot N_{r, {\rm{B}}2{\rm{a}}}^s + {b_{r, {\rm{B}}2{\rm{a}}}} - } \right.\\ \quad \left. {b_{{\rm{, B}}2a}^s} \right) - {d_{r, {F_{{\rm{B}}1{\rm{CB}}2{\rm{a}}}}}} + d_{{\rm{, I}}{{\rm{F}}_{{\rm{B}}1{\rm{IB}}3{\rm{I}}}}}^s\\ \widetilde {\rm{d}}{t_{r, {\rm{B1CB}}2{\rm{a}}}} = {\rm{d}}{t_r} + {d_{r, {\rm{I}}{{\rm{F}}_{{\rm{B1CB2a}}}}}}\\ {d_{r, {\rm{I}}{{\rm{F}}_{{\rm{B1CB}}2{\rm{a}}}}}} = {\alpha _{{\rm{B1CB}}2{\rm{a}}}} \cdot {d_{r, {\rm{B1C}}}} + {\beta _{{\rm{B1CB}}2{\rm{a}}}} \cdot {d_{r, {\rm{B}}2{\rm{a}}}}\\ {\alpha _{{\rm{B}}1{\rm{CB}}2{\rm{a}}}} = \frac{{f_{{\rm{BIC}}}^2}}{{f_{{\rm{B}}1{\rm{C}}}^2 - f_{{\rm{B}}2{\rm{a}}}^2}}, {\beta _{{\rm{B1CB}}2{\rm{a}}}} = - \frac{{f_{{\rm{B}}2{\rm{a}}}^2}}{{f_{{\rm{BIC}}}^2 - f_{{\rm{B}}2a}^2}} \end{array} \right. $ | (5) |
式(2)~(5)中,fB1I、fB3I、fB1C与fB2a分别为B1I、B3I、B1C与B2a的信号频率,Psr, IFB1IB3I与Psr, IFB1CB2a分别为B1I/B3I与B1C/B2a双频伪距消电离层组合观测值,Lsr, IFB1IB3I与Lsr, IFB1CB2a分别为B1I/B3I与B1C/B2a双频载波相位消电离层组合观测值,ers为方向余弦,x为对应的坐标参数,dr, B1I、dr, B3I、dr, B1C与dr, B2a分别为B1I、B3I、B1C与B2a对应的接收机伪距硬件延迟,d, B1Is、d, B3Is、d, B1Cs与d, B2as分别为B1I、B3I、B1C与B2a对应的卫星伪距硬件延迟。
对比表达式(2)和式(4)可以发现,由于伪距偏差的差异,在B1C/B2a组合中需添加对应的伪距偏差,可以通过中国科学院发布的MGEX多模DCB产品进行改正(ftp://igs.ign.fr//pub//igs/products/mgex/dcb/)。
2.1 PPP实验数据与解算策略本文选取18个能观测到BDS新频点的MGEX站2021-08-25(doy 237)的观测数据(30 s采样间隔)进行静态PPP与动态PPP实验,精密产品使用WHU提供的精密轨道和钟差,采用IGS提供的SNX周解文件作为测站坐标真值,具体解算策略如表 1所示。
|
|
表 1 GNSS PPP解算策略 Tab. 1 The strategy of GNSS PPP |
对选取的18个MGEX测站分别进行静态PPP和动态PPP解算,按测站的地理位置将其分为亚太区域和欧洲与非洲区域,分别统计其定位精度,图 3、图 4分别给出静态PPP和动态PPP的实验结果。
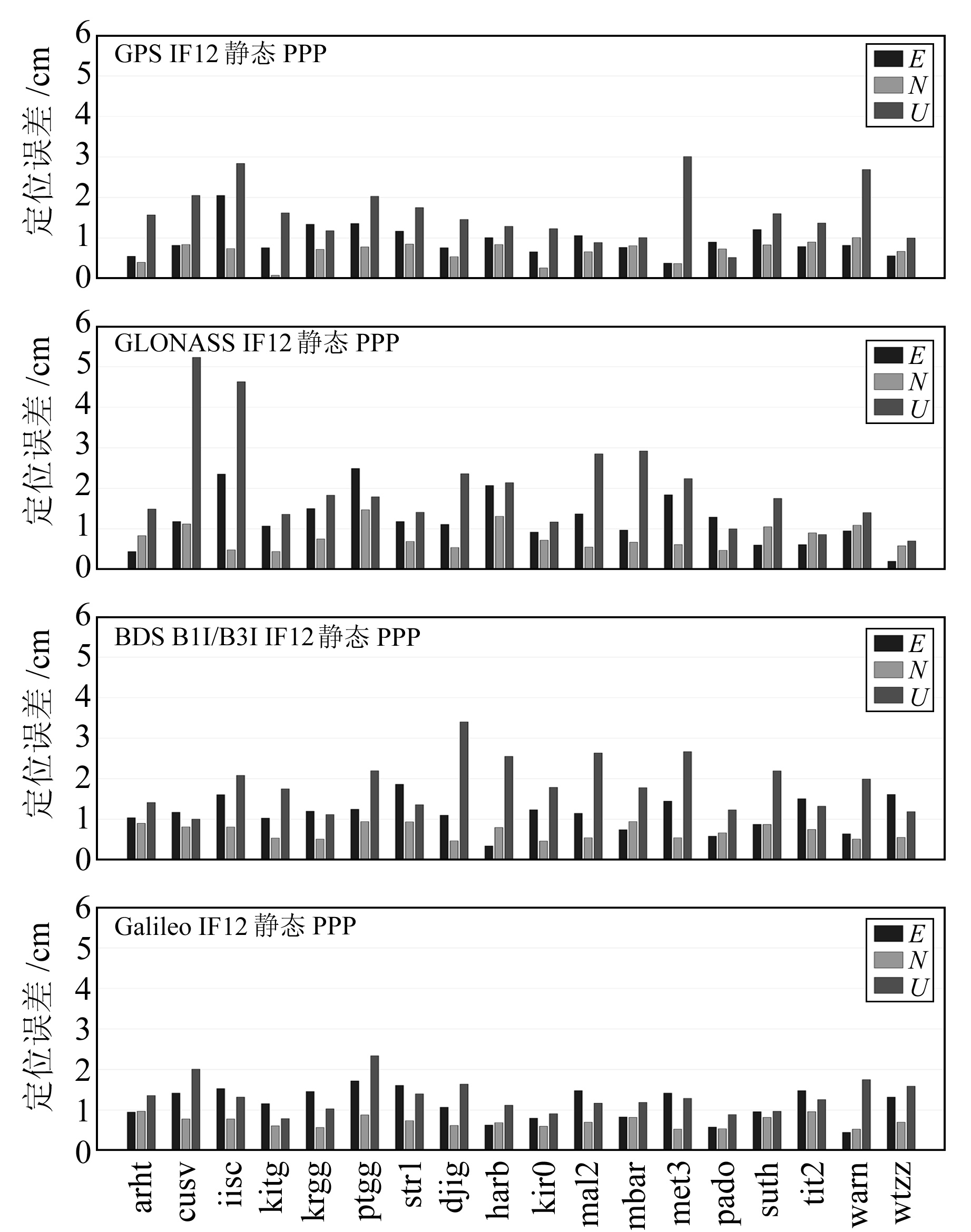
|
图 3 GNSS静态PPP精度统计 Fig. 3 Positioning error of GNSS static PPP |
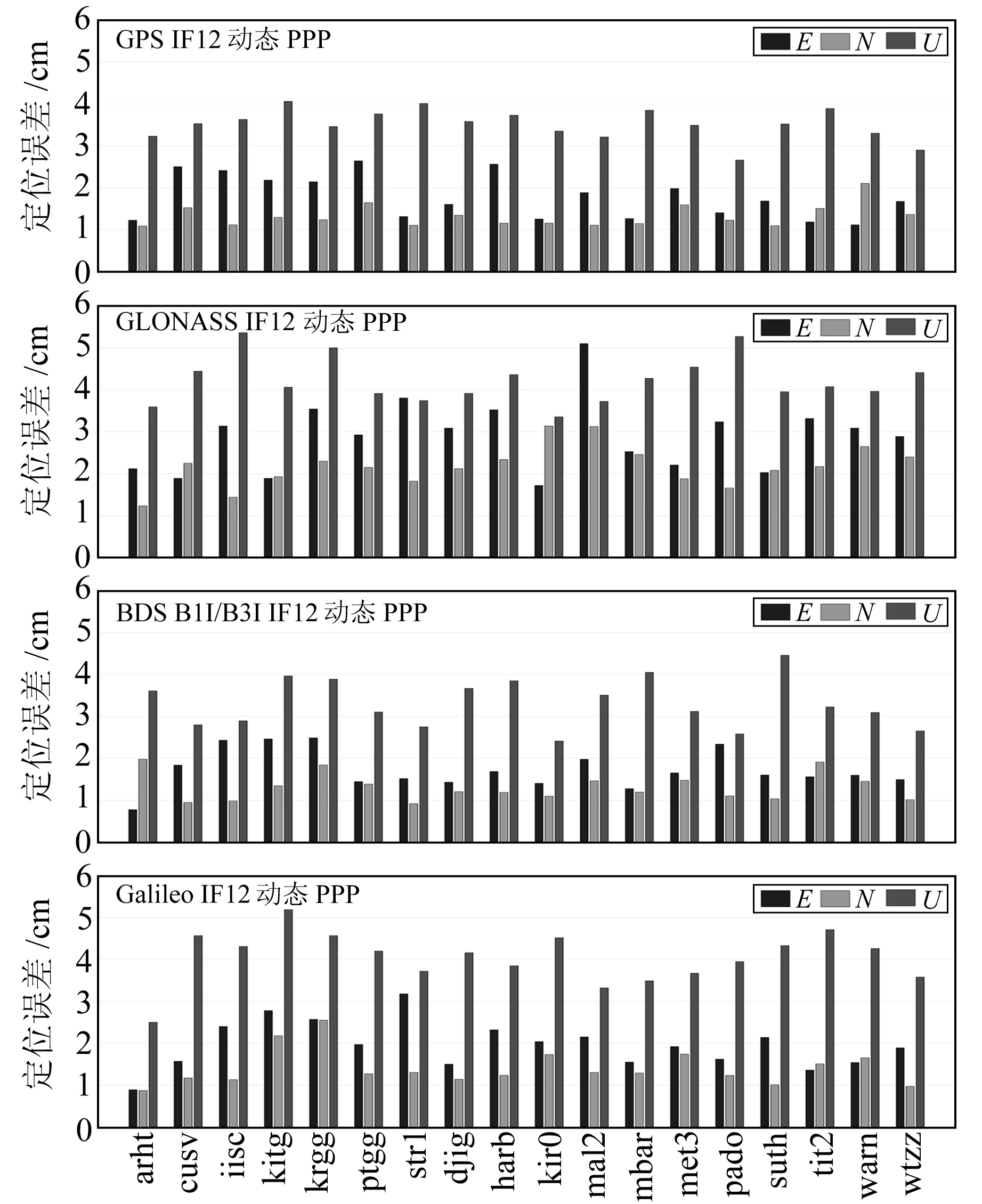
|
图 4 GNSS动态PPP精度统计 Fig. 4 Positioning error of GNSS kinematic PPP |
取两个区域的测站单天定位结果进行统计,统计所有测站E、N、U、3D定位偏差的RMS平均值,统计结果分别在表 2(单位cm)、表 3(单位cm;系统标识中C指代BDS, E指代Galileo, G指代GPS, R指代GLONASS)中列出。
|
|
表 2 静态PPP精度统计 Tab. 2 Positioning error of static PPP |
|
|
表 3 动态PPP精度统计 Tab. 3 Positioning error of kinematic PPP |
PPP实验统计结果表明,在亚太区域,各系统静态PPP三维方向定位精度均优于3.2 cm,动态PPP定位精度在5.5 cm以内。BDS三维方向定位精度最优,静态PPP定位精度约为2.30 cm,动态PPP定位精度约为4.12 cm;GPS定位精度次之,静态与动态PPP定位精度约为2.31 cm和4.43 cm;Galileo静态与动态PPP定位精度约为2.51 cm和4.97 cm;GLONASS定位精度最低,静态与动态PPP定位精度约为3.15 cm和5.50 cm。水平方向上,各系统静态PPP定位精度均优于1.5 cm,动态PPP定位精度均优于2.8 cm;BDS与GPS精度基本相当。高程方向上,BDS静态PPP定位精度约为1.74 cm,动态PPP定位精度约为3.22 cm,精度优于其他3个系统。亚太区域BDS的定位精度最优,主要因为此区域BDS的可见卫星数量更多(亚太区域站点BDS可见卫星数量稳定在15颗以上,GPS卫星在10颗左右),卫星和地面测站构建的几何构型优于其他系统。
在欧洲与非洲区域,各系统静态PPP三维方向定位精度均优于2.5 cm,动态PPP精度均优于6 cm。其中,GPS定位精度最优,静态PPP定位精度优于1.9 cm,动态PPP定位精度优于4.1 cm;BDS定位精度低于GPS与Galileo,静态与动态PPP精度约为2.40 cm和4.54 cm,基本与GLONASS相当。分析其原因,主要是由于BDS产品精度与观测数据的数据质量低于GPS和Galileo。
2.3 PPP收敛性分析本文以连续20个历元E、N、U误差均小于1 dm作为收敛的判定条件,分别统计18个测站静态与动态模式PPP的收敛时间,实验结果在图 5中给出。统计各测站平均收敛时间,结果在表 4(单位min)中给出。结果表明,GPS平均收敛速度最快,静态模式约为26.03 min,动态模式约为52.42 min;Galileo收敛速度次之,静态模式约为35.25 min,动态模式约为74.64 min;BDS平均收敛时间静态模式约为50.33 min,动态模式约为77.83 min,收敛速度略低于GPS、Galileo,优于GLONASS。
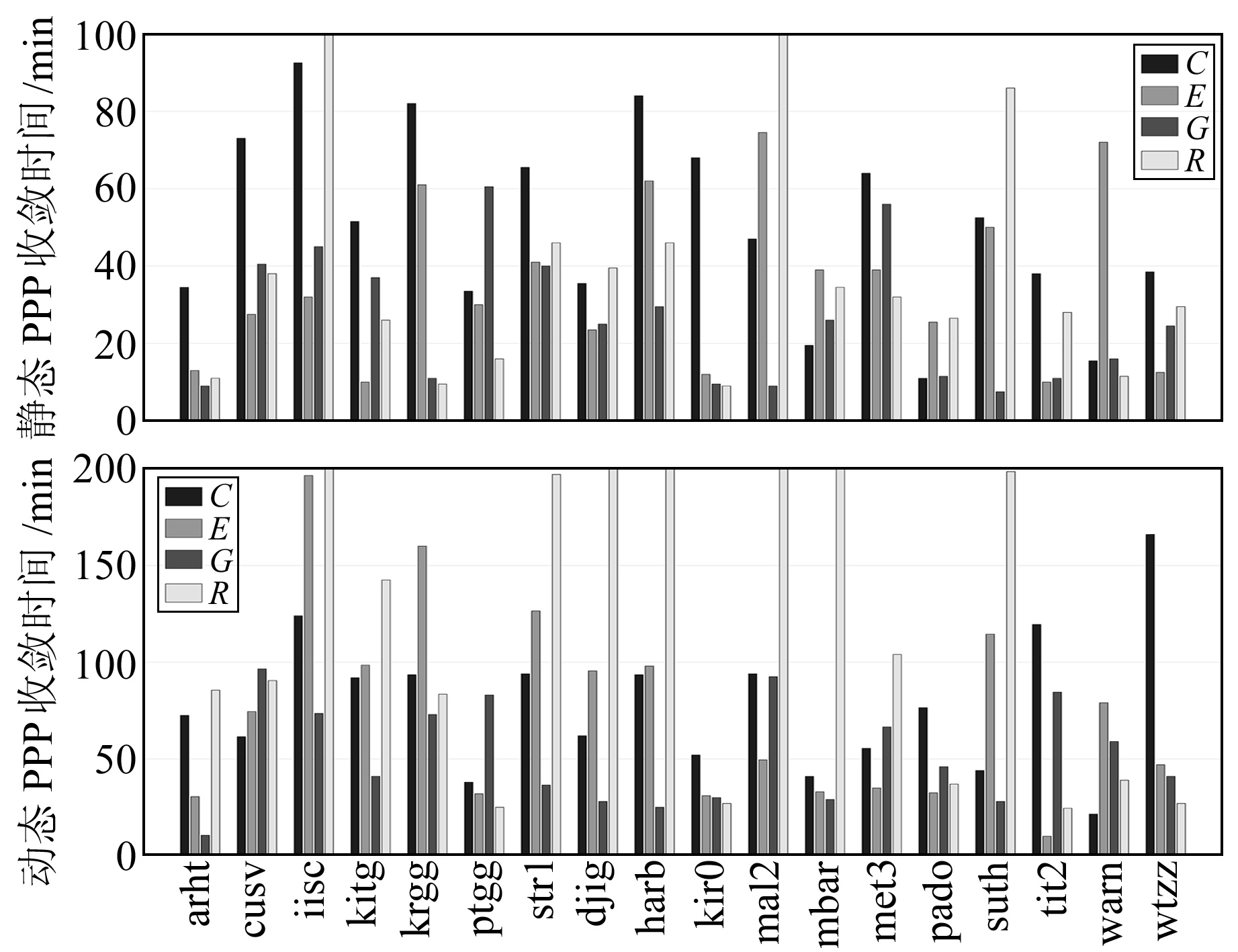
|
图 5 MGEX站PPP收敛时间 Fig. 5 Convergence time of PPP for MGEX stations |
|
|
表 4 PPP收敛时间统计 Tab. 4 Average convergence time of PPP |
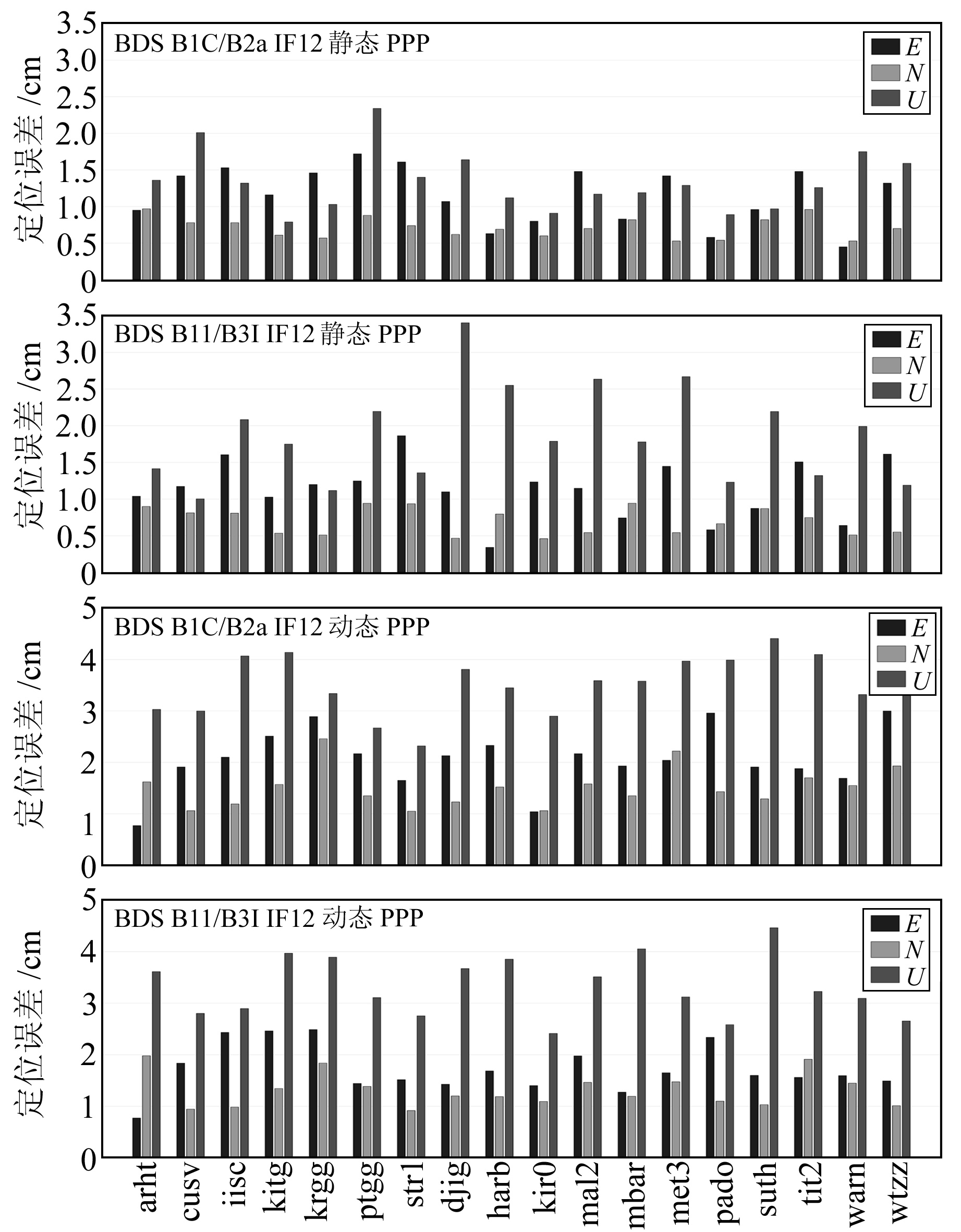
采用与上文相同的解算策略,分别对BDS B1C/B2a、B1I/B3I两对观测值进行IF12模型静态与动态PPP实验,统计其定位精度,图 6给出B1C/B2a、B1I/B3I两对观测值的PPP实验结果。统计所有测站E、N、U、3D定位偏差的RMS平均值,统计结果在表 5(单位cm)中列出;统计两对观测值PPP平均收敛时间,在表 6(单位min)中给出。
|
图 6 BDS新、旧频点PPP精度对比 Fig. 6 Positioning error of BDS B1C/B2a and B1I/B3I PPP |
|
|
表 5 BDS新、旧频点PPP精度统计 Tab. 5 Positioning error of BDS B1C/B2a and B1I/B3I PPP |
|
|
表 6 BDS新、旧频点PPP收敛时间统计 Tab. 6 Average convergence time of BDS B1C/B2a and B1I/B3I PPP |
由图 6和表 5可以看出,B1C/B2a与B1I/B3I两种双频组合的静态PPP水平方向定位精度均优于1.2 cm,高程方向定位精度均优于1.9 cm,三维定位精度均优于2.4 cm;两种双频组合的动态PPP水平方向定位精度均优于2.2 cm,高程方向定位精度均优于3.5 cm,三维定位精度均优于4.5 cm。从表 6的收敛时间统计结果可以看出,两种双频组合PPP平均收敛速度基本相同。
综合对比静态与动态PPP实验结果可知,B1C/B2a与B1I/B3I两种双频组合定位精度基本相当。
3 结语本文选取由WHU与GFZ提供的共14 d的精密钟差与轨道产品,对比分析GNSS精密产品的精度。结果表明,WHU与GFZ精密产品具有很好的一致性;4个系统的轨道精度均在cm级,钟差内符合精度都优于0.1 ns;GPS的轨道产品精度优于Galileo和GLONASS,BDS的轨道产品精度略差于其他3个系统。就钟差产品性能而言,BDS-3的钟差精度优于BDS-2和GLONASS,与Galileo相当,略差于GPS。新一代BDS-3卫星的加入,为BDS系统服务性能的提升提供了重要保障。
选取位于亚太地区及欧洲与非洲地区的18个MGEX地面站,进行静态与动态模糊度浮点解PPP测试。实验表明,亚太区域因为卫星数量多和地面站之间能构建良好的几何构型,BDS定位精度最优,在该区域BDS的定位效果相较于其他系统有明显的优势,静态PPP定位精度优于2.1 cm,动态PPP定位精度优于4.2 cm。在欧洲与非洲区域,GPS定位精度最优,BDS定位精度低于GPS与Galileo,其静态与动态PPP精度约为2.40 cm和4.54 cm,与GLONASS基本相当。
分别对BDS采用B1C/B2a、B1I/B3I两对观测值进行无电离层组合模型静态与动态浮点解PPP测试。结果表明,B1C/B2a与B1I/B3I两种双频组合定位精度基本相当。PPP收敛性分析结果表明,GPS平均收敛速度最快,Galileo收敛速度次之;BDS平均收敛时间静态模式约为42.03 min,动态模式约为85.58 min,收敛速度略低于GPS、Galileo,优于GLONASS。随着支持BDS新频点的观测站数量进一步增加,以及精密轨道与钟差产品的精度进一步提升,BDS的服务性能将会表现出更大的优势。
| [1] |
Yang Y X, Gao W G, Guo S R, et al. Introduction to Beidou-3 Navigation Satellite System[J]. Navigation, 2019, 66(1): 7-18 DOI:10.1002/navi.291
(  0) 0) |
| [2] |
Zhang Z T, Li B F, Nie L W, et al. Initial Assessment of Beidou-3 Global Navigation Satellite System: Signal Quality, RTK and PPP[J]. GPS Solutions, 2019, 23(4): 1-12
(  0) 0) |
| [3] |
Yang Y X, Liu L, Li J L, et al. Featured Services and Performance of BDS-3[J]. Science Bulletin, 2021, 66(20): 2135-2143 DOI:10.1016/j.scib.2021.06.013
(  0) 0) |
| [4] |
Shi J B, Ouyang C H, Huang Y S, et al. Assessment of BDS-3 Global Positioning Service: Ephemeris, SPP, PPP, RTK, and New Signal[J]. GPS Solutions, 2020, 24(3): 1-14
(  0) 0) |
| [5] |
Shi C, Wu X, Zheng F, et al. Modeling of BDS-2/BDS-3 Single-Frequency PPP with B1I and B1C Signals and Positioning Performance Analysis[J]. Measurement, 2021, 178
(  0) 0) |
| [6] |
Chen H, Liu X X, Jiang W P, et al. Preliminary Analysis and Evaluation of BDS-2/BDS-3 Precise Point Positioning[J]. Advances in Space Research, 2021, 68(10): 4113-4128 DOI:10.1016/j.asr.2021.07.044
(  0) 0) |
| [7] |
张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100 (Zhang Xiaohong, Hu Jiahuan, Ren Xiaodong. New Progress of PPP/PPP-RTK and Positioning Performance Comparison of BDS/GNSS PPP[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1084-1100)
(  0) 0) |
| [8] |
Li J L, Yang Y X, He H B, et al. Benefits of BDS-3 B1C/B1I/B2a Triple-Frequency Signals on Precise Positioning and Ambiguity Resolution[J]. GPS Solutions, 2020, 24(4): 1-10
(  0) 0) |
| [9] |
艾青松, 徐天河, 孙大伟, 等. 顾及周期项误差和起点偏差修正的北斗卫星钟差预报[J]. 测绘学报, 2016, 45(增2): 132-138 (Ai Qingsong, Xu Tianhe, Sun Dawei, et al. The Prediction of Beidou Satellite Clock Bias Based on Periodic Term and Starting Point Deviation Correction[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 132-138)
(  0) 0) |
| [10] |
Guo J, Xu X L, Zhao Q L, et al. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143-159 DOI:10.1007/s00190-015-0862-9
(  0) 0) |
| [11] |
宋伟伟. 导航卫星实时精密钟差确定及实时精密单点定位理论方法研究[D]. 武汉: 武汉大学, 2011 (Song Weiwei. Research on Real-Time Clock Offset Determination and Real-Time Precise Point Positioning[D]. Wuhan: Wuhan University, 2011)
(  0) 0) |
| [12] |
于合理, 郝金明, 刘伟平, 等. 一种卫星钟差精度评估方法[J]. 海洋测绘, 2014, 34(2): 11-13 (Yu Heli, Hao Jinming, Liu Weiping, et al. Method of Accuracy Assessment of Satellite Clock Error[J]. Hydrographic Surveying and Charting, 2014, 34(2): 11-13)
(  0) 0) |
| [13] |
张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报, 2014, 43(10): 1099 (Zhang Baocheng. Study on the Theoretical Methodology and Applications of Precise Point Positioning Using Undifferenced and Uncombined GNSS Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1099)
(  0) 0) |
| [14] |
张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100 (Zhang Xiaohong, Hu Jiahuan, Ren Xiaodong. New Progress of PPP/PPP-RTK and Positioning Performance Comparison of BDS/GNSS PPP[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1084-1100)
(  0) 0) |
2. Power China Hubei Electric Engineering Co Ltd, 1 Xinqiaosi Road, Wuhan 430040, China;
3. Xi'an Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China;
4. Huangshi Natural Resources and Planning Bureau, 22 Guangzhou Road, Huangshi 435004, China
 2022, Vol. 42
2022, Vol. 42


