2. 湖北科技学院资源环境科学与工程学院,湖北省咸宁市咸宁大道88号,437100
随着GNSS气象学的发展,Tm作为计算大气中水汽含量的关键因素受到广泛关注。Ross等[1]研究全球53个无线电探空站23 a的探空资料发现,Tm与Ts(地表温度)的相关性随地理位置与季节的变化而变化,且Tm存在一些季节性变化特征。此后,诸多学者对Tm进行深入研究,Tm模型因其具有的普适性、廉价性和实时性等特点已成为最受关注的研究方向,其中构建高精度高时空分辨率的Tm模型更是研究热点[2-6]。
在众多通过无线电探空站数据基于气象参数建立的本地化Tm模型中,其建模方法多为基于最小二乘的线性回归,但Tm与Ts、es(水汽压)等因素存在非线性关系,并且大多数模型没有考虑周期性变化造成的误差。神经网络具有输入-隐层-输出的分层结构,而不是某种特定的非线性激活函数形式,因此拥有几乎能够拟合一切函数的能力[7],已被广泛用于解决多输入的非线性优化问题[8]。考虑到神经网络算法对非线性函数具有强大的拟合能力,本文将水汽压(es)、地表温度(Ts)、纬度(Lat)、高程(H)、年积日(doy)作为Tm模型因子,建立一种顾及水汽压、测站高程、地面温度、纬度及年内周期性变化特征的多层感知器(multi-layer perceptron, MLP)神经网络构建中国西南地区的Tm模型,并对其精度进行验证。
1 数据来源及Tm计算方法 1.1 数据来源本文以中国西南地区为研究区域,该区域共有23个探空站,选取其中17个探空站数据建立模型,其余6个探空站数据用来进行精度验证。数据来源于美国怀俄明州立大学网站(http://weather.uwyo.edu/upperair/sounding.html)免费下载的2015~2018年实测探空站数据,采样间隔为12 h,其中包含气压、温度、水汽压、露点温度等相关气象数据,同时提供地表测站点的经度、纬度及高程信息,使用其中2015~2017年的实测数据作为建模数据,2018年的实测数据作为验证数据。
1.2 Tm计算方法 1.2.1 数值积分法水汽是对流层气体中最活跃多变的部分,其变化与天气和气候的变化息息相关,而Tm是计算水汽含量的关键参数。目前精确求解Tm的方法是利用探空数据通过数值积分来实现,计算公式为:
| $ T_m=\frac{\int_h^{\infty}(e / T) \mathrm{d} z}{\int_h^{\infty}\left(e / T^2\right) \mathrm{d} z} $ | (1) |
式中,e为水汽压(单位hPa),T为气温(单位K),h为高程(单位m)。
由式(1)可知,精确计算Tm需用到水汽压和气温数据,再通过数值积分法进行求解。然而,探空站的气象数据是分层数据,故在计算Tm时需将积分形式转换为离散的表达式,步骤较为繁琐。
1.2.2 Bevis公式对于缺乏探空数据的地区,可根据地面温度Ts采用线性回归方法计算Tm。比较著名的是Bevis等[2]利用美国13个无线电探空站2 a观测资料建立的适合中纬度地区的Tm与Ts的线性回归公式:
| $ T_m=70.2+0.72 \times T_s $ | (2) |
GPT系列模型是目前世界上应用最广、精度最高的对流层经验改正模型,而GPT3模型[9]是GPT系列模型中最新且精度最好的模型,在全球范围内都能提供较高精度的Tm等参数,使用时只需要输入年积日和近似的测站坐标即可获取测站点的Tm值:
| $ \begin{gathered} T_m=T_{m 0}+A_1 \cos \left(2 \pi \frac{\text { doy }}{365.25}\right)+ \\ B_1 \sin \left(2 \pi \frac{\text { doy }}{365.25}\right)+A_2 \cos \left(4 \pi \frac{\text { doy }}{365.25}\right)+ \\ B_2 \sin \left(4 \pi \frac{\text { doy }}{365.25}\right) \end{gathered} $ | (3) |
式中,Tm0为各个格网点上Tm的平均值,A1、B1为年周期变化的参数,A2、B2为半年周期变化的参数,doy为年积日。
2 西南地区MLP大气加权平均温度模型的建立 2.1 多层感知器(MLP)基本原理多层感知器(MLP)由单层感知器拓展而来,是一种前馈式监督学习的神经网络,包括输入层、输出层和至少1个隐藏层,且不同层之间是全连接的,上层的任意神经元与下层的所有神经元都有连接,神经元之间的连接赋予相关的权重,训练学习算法在迭代过程中不断调整这些权重,从而使得预测误差最小化并给出预测精度。MLP具有非常好的非线性映射能力、高并行性、自适应性及高容错性的特点[10],能解决大气平均温度与气象因素及各影响因素之间复杂的非线性关系。
数据预处理采用Z-score标准化:
| $ y=(x-\mu) / \sigma $ | (4) |
式中,μ为均值,σ为标准差。
MLP神经网络隐藏层激活函数为双曲正切函数:
| $ f(y)=\frac{e^y-e^{-y}}{e^y+e^{-y}} $ | (5) |
损失函数为误差平方和函数:
| $ C=\frac{1}{2} \sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2 $ | (6) |
中国西南地区纬度覆盖范围大,自西向东跨越地势第1级和第2级阶梯,气候复杂多变。研究表明,Tm与水汽压[4]、高度[11]、地表温度[2]及纬度[12]都具有一定相关性,且已知Tm具有明显的周期性变化,该变化可直接在Tm模型中加以考虑[6]。然而Tm与Ts、es等气象参数的函数表达式并非呈严格的线性形式,且以往构建的Tm模型未充分顾及非气象参数(如纬度、高程和季节性因素等)对Tm的影响,故本文利用MLP神经网络对非线性函数优秀的拟合能力建立新的Tm模型(下文简称MLP模型)。
以年积日代表年周期性变化特征,将其作为季节性修正因子进行模型构建,因此将es、Ts、Lat、H、doy作为模型因子进行Tm建模。加权平均温度与各气象元素及非气象因素的线性关系不够明确,而MLP神经网络对非线性映射关系具有强大的学习能力,因此采用MLP方法对西南地区17个探空站进行Tm建模。模型的构建步骤如下:
1) 选取与Tm具有一定映射关系的Ts、es、Lat、H、doy作为协变量输入到输入层,Tm作为因变量,因各个协变量量纲不同(各协变量定义标准不同),将其进行Z-core标准化处理,以便于不同量纲的协变量能够进行比较和加权。
2) 将2015~2017年探空站气象数据的70%作为训练集,30%作为验证集,反向优化模型参数,利用2018年的探空站实测Tm评估所建模型的性能。
3) 定义神经网络模型结构,利用试凑法得到模型隐藏层的层数为1、节点数为4。隐藏层激活函数为双曲正切函数,输出层激活函数为恒等函数y=x,损失函数选用误差平方和。
4) 在模型训练中,需设置模型训练类型、优化算法等。以上训练参数都会在一定程度上影响模型的训练准确率和训练速度,属于经验参数,需要通过反复训练模型来逐步确定。本文选取批次训练,优化算法选择标度共轭梯度法。
5) 模型建立完成后将2018年的协变量(即Ts、es、Lat、H、doy)输入到神经网络模型中,得到2018年MLP神经网络Tm模型估计值。
3 Tm模型精度检验为检验本文建立的神经网络模型精度,以2018年中国西南地区23个探空站Tm数据为参考值,采用偏差(bias)和均方根误差(RMSE)作为精度指标对预测结果进行精度评定。具体公式为:
| $ \text { bias }=\frac{\sum\limits_{i=1}^n y_i^{\mathrm{m}}-y_i^{\mathrm{r}}}{n} $ | (7) |
| $ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^n\left(y_i^{\mathrm{m}}-y_i^{\mathrm{r}}\right)^2}{n}} $ | (8) |
式中,n为预测样本数,yir为实测值,yim为模型估计值。
3.1 模型内符合精度检验以中国西南地区17个探空站2018年的探空资料为数据源,利用数值积分方法获得的Tm为参考值,对新建Tm模型进行精度验证,并与Bevis模型及GPT3模型进行比较,结果如表 1所示。
|
|
表 1 2018年3种模型RMSE与bias精度统计 Tab. 1 RMSE and bias accuracy statistics of three models in 2018 |
由表 1可知,GPT3模型在中国西南地区表现出明显的负偏差,其年均值为-1.19 K,而Bevis模型及MLP模型表现为明显的正偏差,其年均值分别为0.85 K和0.15 K。从偏差值可以得出,Bevis模型优于GPT3模型,原因是Bevis模型使用了当地的地表温度这个气象参数进行Tm计算,而GPT3模型是利用全球多年的Tm进行拟合,精度略有不足;新建立的MLP模型比Bevis和GPT3模型表现出更小的偏差。同时,从RMSE误差来看,Bevis模型和GPT3模型的年均RMSE相差不大,分别为3.35 K和3.50 K,Bevis模型精度要略优于GPT3模型。MLP模型的精度最优,年均RMSE为1.99 K,其精度相比于Bevis模型提高了约1.36 K (40.6%),与GPT3模型相比提高了约1.51 K (43.1%),说明MLP模型在中国西南地区相比其他2个模型精度要高、稳定性更好。
为更好地分析模型空间分布精度,以2018年探空站Tm数据为参考值,对各个探空站的年均bias和RMSE进行统计分析,从而检验不同模型在中国西南地区的适用性(图 1)。
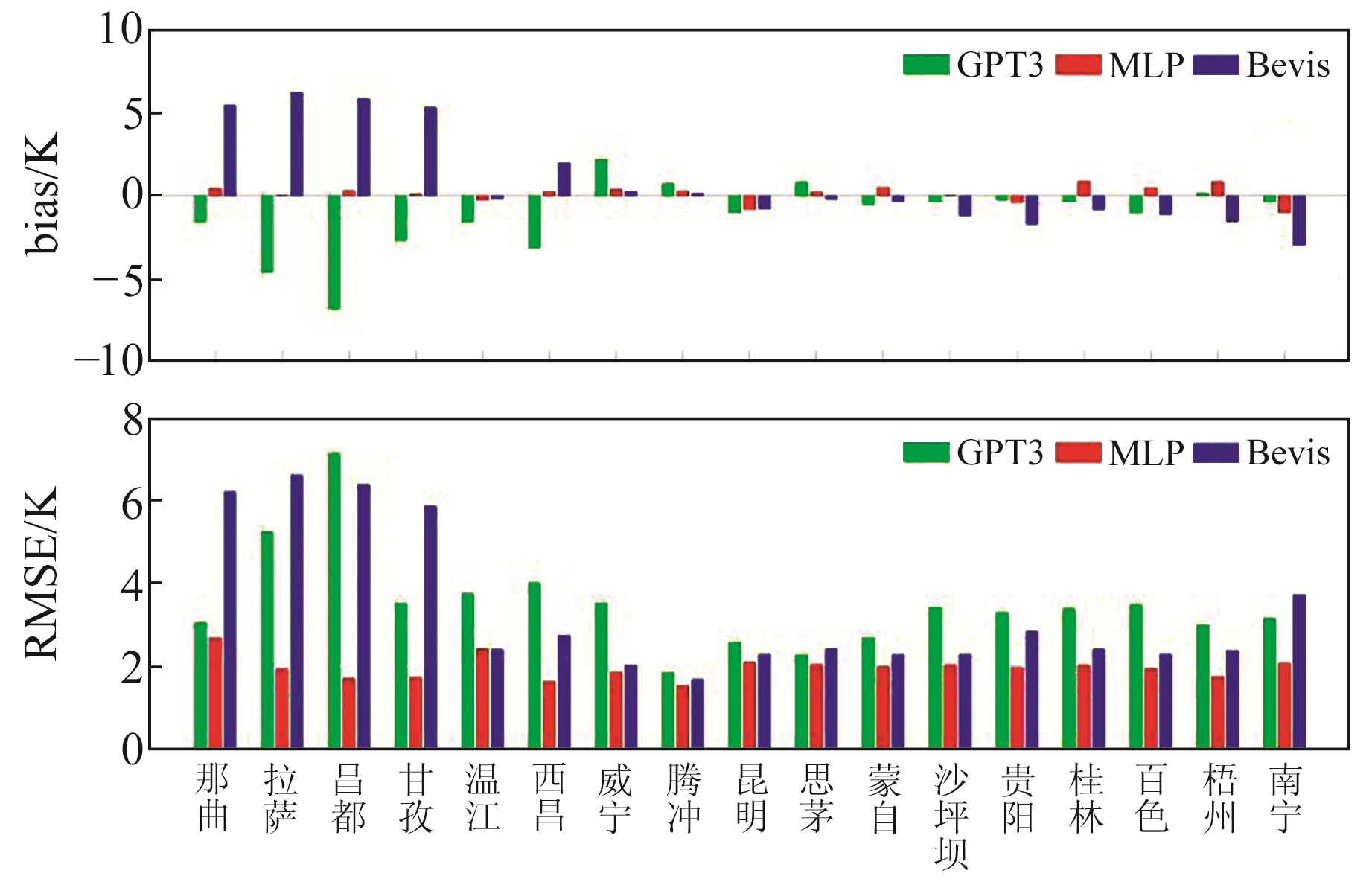
|
图 1 2018年中国西南地区3种模型精度对比 Fig. 1 Accuracy comparison of three models in southwest China in 2018 |
由图 1可知,在那曲、拉萨、昌都、甘孜、西昌、贵阳、南宁等12个探空站,MLP模型相对于Bevis模型和GPT3模型有更好的适用性;在其他几个探空站虽然精度差别不大,但也有所提高。通过直方图可以明显看出,精度得到很好改善的探空站,大多处在低纬度沿海地区和海拔较高地区,这是由于Bevis模型和GPT3模型并未将纬度和海拔作为影响因素进行模型构建。由此说明,在将海拔和纬度2个因子作为模型构建因素后,新建立的MLP模型对Tm的计算精度有了很大改善。对整个研究区域的精度作进一步分析表明,对于年均bias而言,Bevis模型和GPT3模型均在高海拔地区表现出较大偏差,而MLP模型在西南地区bias整体分布在1 K左右,明显比其他2个模型小且稳定;对于RMSE而言,Bevis模型和GPT3模型的RMSE值总体表现出随海拔和纬度的降低而减小的特点,MLP模型将纬度和海拔作为模型构建因子来进行Tm计算,在西南地区每个探空站RMSE基本都分布在2 K左右,而Bevis模型和GPT3模型的RMSE浮动较大,两者的最大RMSE甚至达到了6.59 K和7.1 K,MLP模型精度最优,其精度比Bevis模型提高了40.6%,比GPT3模型提高了43.1%,且RMSE分布范围均比Bevis模型和GPT3模型小,进一步表明MLP模型性能更稳定,更适用于地形复杂、高低起伏大的中国西南地区。综上分析及前人研究结果[13]表明,海拔和纬度对Tm模型精度有重要影响。
为了进一步探究季节变化、纬度、海拔等因素对3种模型Tm的影响,在西南地区综合海拔、纬度分布因素均匀选取6个探空站,利用数值积分获得的2018年Tm作为参考值,对MLP模型、Bevis模型及GPT3模型的Tm模型估计值的时间序列变化进行分析,结果如图 2(括号内表示各个测站的纬度、经度及高程)所示。

|
图 2 3种模型计算的2018年Tm值的时间序列 Fig. 2 Time series of Tm calculated by the three models in 2018 |
由图 2可见,Bevis模型和GPT3模型在高海拔地区(如拉萨站和甘孜站)有明显的系统误差,且2种模型随着探空站海拔的降低,模型精度有所提高。Bevis模型在威宁、蒙自、沙坪坝、百色等测站有良好的吻合性,原因在于Bevis模型是利用美国平原地区的探空站数据所建立的适用于本土中低纬度地区的Tm模型,同样也适用于中国部分中低纬度平原地区。而由MLP模型计算所得的Tm估计值与所有探空站一年四季实测的Tm值均有良好的吻合性,证明MLP模型在整个西南地区所有季节均具有稳定性和通适性。另外,Tm值在一年中呈现出明显的坡度变化,夏秋季高、春冬季低,且在春冬季分布较为离散;Tm值随着纬度的降低,坡度变化幅度也随之减小。
为进一步检验不同模型的季节性表现,以2018年数值积分法计算得到的昌都站(昌都位于西藏东部,处在西藏与四川、青海、云南交界的咽喉部位,为典型的高山峡谷区,对于西南地区复杂的地形、气候来说具有代表性)Tm数据为参考值,对2018年昌都站探空资料计算得到的3种模型Tm估计值进行日偏差检验,统计不同模型的bias和RMSE。统计结果如图 3所示。
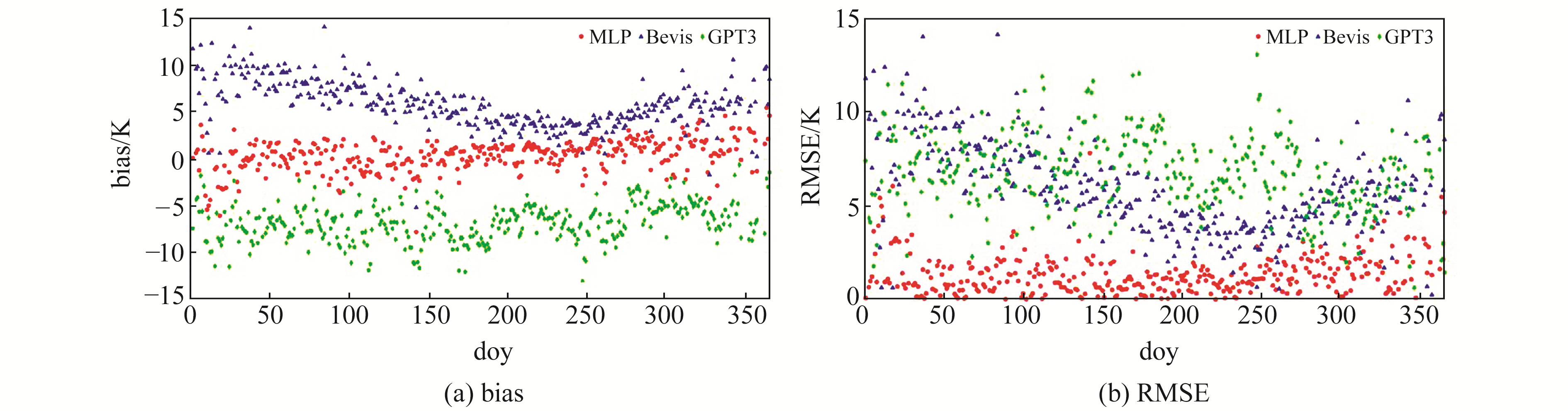
|
图 3 2018年中国西南地区3种模型结果 Fig. 3 The results of three models in southwest China in 2018 |
从图 3(a)可以看出,新建立的MLP模型比Bevis模型和GPT3模型的精度高,Bevis模型及GPT3模型分别表现出较大的正偏差和负偏差,说明这2个模型在西南地区具有显著的系统误差;另外,MLP模型受季节的影响要明显小于GPT3模型和Bevis模型,全年表现较为平稳。GPT3模型和Bevis模型受季节影响较大,有很明显的坡度变化。可以看出,Bevis模型在夏秋两季日均bias分布集中,受季节影响较小,在春冬季节出现明显的坡峰,日均bias分布离散,受季节影响比较大,这是由于Bevis模型未考虑季节变化因素对Tm的影响而产生误差。在全年期间,虽然GPT3模型考虑了Tm的季节变化,但由于系统误差影响,GPT3模型显示出明显的负偏差,并且在春季和夏季期间观察到日均bias分布离散、偏差较大,在秋冬分布略为集中、偏差较小,原因可能与中国西南地区地形复杂、海拔高致使日夜温差大有关。多天的精度检验结果显示,MLP模型的精度要高于Bevis模型和GPT3模型,特别是在春冬季,3种模型的精度对比较为明显,MLP模型要优于Bevis模型和GPT3模型,显示出较小的偏差,且没有明显的季节性变化,稳定性良好。
由图 3(b)可以看出,3个模型均显示出比较明显的季节性变化,主要体现在春季和冬季RMSE值相对较大,而在夏季和秋季的RMSE值较小。这是因为所选取的探空站处于西藏高海拔地区,每年10月至翌年4月,西藏高原上空为西风急流,地面为冷高压控制,干旱多大风,气候复杂,日夜温差变化较大;而夏、秋两季高原近地面层为热低压控制,热低压很少移动故而该时间段温度变化较为稳定,因此在夏季和秋季的Tm值变化较小,而在冬季和春季Tm变化较大。对于RMSE而言,MLP模型与其他模型的RMSE值相比变化更小、更稳定、精度更高,在受到季节影响的条件下显示出更好的适应性。总之,与其他模型相比,顾及了年积日季节变化的MLP模型可明显提高Tm的计算精度。
3.2 模型外符合精度检验为研究本文所建立Tm模型的有效性和适用性,在用来建模的17个探空站之外,均匀选取研究区域外相邻的玉树站、汉中站和清远站等6个站进行空间域上的外符合精度验证,将这6个探空站2018年的探空资料为数据源分别代入3个模型,计算得到Tm模型估计值,并将利用数值积分方法所得6个探空站的Tm作为参考值,统计各站的年均bias和RMSE,结果如表 2(单位K)所示。
|
|
表 2 2018年各个模型在中国西南地区研究区域外的RMSE与bias精度统计 Tab. 2 RMSE and bias accuracy statistics of each model in southwest China outside in 2018 |
由表 2可知,对研究区域外相邻的探空站进行模型精度验证,MLP模型的精度依旧保持着良好的稳定性和适用性。从年均偏差来看,MLP模型依旧在零周围分布均匀且保持较小偏差,尤其是对位于高海拔地区的玉树站和低纬度地区的清远站,精度提升明显。从年均RMSE来看,MLP模型对于GPT3模型和Bevis模型表现更稳定,这是因为MLP模型的构建顾及了海拔、纬度和周期性变化等多种影响因素的缘故。总而言之,本文所建立的MLP模型在研究区域外的空间域上同样有良好的稳定性和适用性,可以为中国西南地区GNSS反演PWV提供高精度的Tm值。
4 结语本文利用多层感知器神经网络回归方法,选用中国西南地区2015~2017年17个探空站数据,建立了适用于中国西南地区的Tm模型(MLP模型),并以2018年探空站获取的Tm作为参考值,计算得到西南地区年均bias和年均RMSE分别为0.15 K和1.99 K,MLP模型相比于Bevis模型的年均bias和年均RMSE分别降低40.6%和82.4%,相比于GPT3模型的年均bias和年均RMSE分别下降43.1%和87.4%,证明本文建立的MLP模型在中国西南地区的精度要优于Bevis模型和GPT3模型,对西南地区有着更好的稳定性和适用性,验证了MLP神经网络在大气加权平均温度建模方面的有效性和可靠性,可为进一步研究Tm提供参考。
| [1] |
Ross R J, Rosenfeld S. Estimating Mean Weighted Temperature of the Atmosphere for Global Positioning System applications[J]. Journal of Geophysical Research: Atmospheres, 1997, 102(D18): 21719-21730 DOI:10.1029/97JD01808
(  0) 0) |
| [2] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15810 DOI:10.1029/92JD01517
(  0) 0) |
| [3] |
姚宜斌, 刘劲宏, 张豹, 等. 地表温度与加权平均温度的非线性关系[J]. 武汉大学学报: 信息科学版, 2015, 40(1): 112-116 (Yao Yibin, Liu Jinhong, Zhang Bao, et al. Nonlinear Relationships between the Surface Temperature and the Weighted Mean Temperature[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 112-116)
(  0) 0) |
| [4] |
李松青, 刘立龙, 容静, 等. 基于支持向量机回归的大气加权平均温度[J]. 桂林理工大学学报, 2019, 39(3): 656-660 (Li Songqing, Liu Lilong, Rong Jing, et al. Atmospheric Weighted Mean Temperature Based on Support Vector Regression[J]. Journal of Guilin University of Technology, 2019, 39(3): 656-660)
(  0) 0) |
| [5] |
杨林, 郑南山, 高淑照, 等. 基于BP神经网络算法构建香港地区加权平均温度模型[J]. 导航定位学报, 2021, 9(4): 92-97 (Yang Lin, Zheng Nanshan, Gao Shuzhao, et al. Establishment of Weighted Average Temperature Model in Hong Kong Based on BP Neural Network Algorithm[J]. Journal of Navigation and Positioning, 2021, 9(4): 92-97)
(  0) 0) |
| [6] |
臧建飞, 彭秀英, 胡卓, 等. 顾及周期性误差修正的加权平均温度模型构建[J]. 测绘科学, 2019, 44(8): 149-153 (Zang Jianfei, Peng Xiuying, Hu Zhuo, et al. Building of Three Improved Weighted Mean Temperature Models Considering the Periodic Error Correction[J]. Science of Surveying and Mapping, 2019, 44(8): 149-153)
(  0) 0) |
| [7] |
Hornik K. Approximation Capabilities of Multilayer Feedforward Networks[J]. Neural Networks, 1991, 4(2): 251-257 DOI:10.1016/0893-6080(91)90009-T
(  0) 0) |
| [8] |
Zheng D Y, Yao Y B, Nie W F, et al. A New Three-Dimensional Computerized Ionospheric Tomography Model Based on a Neural Network[J]. GPS Solutions, 2020, 25(1): 1-17
(  0) 0) |
| [9] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360
(  0) 0) |
| [10] |
韦岗, 贺前华, 欧阳景正. 关于多层感知器的函数逼近能力[J]. 信息与控制, 1996, 25(6): 321-324 (Wei Gang, He Qianhua, Ouyang Jingzheng. On the Function Approximation Ability of Multi Layer Perceptron[J]. Information and Control, 1996, 25(6): 321-324)
(  0) 0) |
| [11] |
Huang L K, Liu LL, Chen H, et al. An Improved Atmospheric Weighted Mean Temperature Model and Its Impact on GNSS Precipitable Water Vapor Estimates for China[J]. GPS Solutions, 2019, 23(2): 1-16
(  0) 0) |
| [12] |
Emardson T R, Derks H J P. On the Relation between the Wet Delay and the Integrated Precipitable Water Vapour in the European Atmosphere[J]. Meteorological Applications, 2000, 7(1): 61-68
(  0) 0) |
| [13] |
莫智翔, 黎杏, 黄良珂, 等. 顾及多因子影响的中国西部地区大气加权平均温度模型精化研究[J]. 大地测量与地球动力学, 2021, 41(2): 145-151 (Mo Zhixiang, Li Xing, Huang Liangke, et al. Refinement of Atmospheric Weighted Mean Temperature Model Considering the Effects of Multiple Factors for Western China[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 145-151)
(  0) 0) |
2. School of Resources and Environment Science and Engineering, Hubei University of Science and Technology, 88 Xianning Road, Xianning 437100, China
 2022, Vol. 42
2022, Vol. 42


