2. 中国科学院大学电子电气与通信工程学院,北京市玉泉路19号甲,100049
为满足GNSS实时精密定位及电离层监测的需要,2017年UPC联合CAS与CNES率先开展全球实时电离层建模研究,并提供全球实时电离层校正服务。截至2021-09,国际GNSS服务组织(IGS)共有5家电离层分析中心(表 1)开展实时电离层建模工作,并以RTCM-SSR及IGS-SSR两种数据格式提供实时电离层改正服务[1]。各分析中心实时电离层建模方法主要包括两类:一是简化的电离层层析建模,以UPC为代表;二是基于电离层单薄层假设的球谐函数建模,以CAS、CNES等为代表[2-6]。
|
|
表 1 RT-GIM产品现状 Tab. 1 Status of RT-GIM products |
为全面了解IGS各分析中心实时电离层产品的精度情况,本文选取CAS、CNES、UPC及NRCan RT-GIM产品2021-01~08的数据进行分析。
1 评估方法由于目前各分析中心采用IGS-SSR或RTCM-SSR格式以球谐系数作为实时电离层产品的播发形式,在数据处理过程中需要基于球谐函数生成IONEX格式的标准电离层文件,以便开展后续的精度分析工作。
1.1 基于IGS-GIM评估将实时电离层SSR恢复至IGS-GIM对应时刻的全球IONEX格网,采用式(1)计算各分析中心的RT-GIM相比于IGS事后GIM的平均偏差(bias)、标准差(STD)及均方根误差(RMS),每天统计1次:
| $ \left\{\begin{array}{l} \text { bias }=\frac{\sum\limits_{t=0}^T \sum\limits_{i=1}^{L \times B}\left(I_{\mathrm{RT}, i, t}-I_{\mathrm{IGS}, i, t}\right)}{N} \\ \mathrm{STD}=\sqrt{\frac{\sum\limits_{t=0}^T \sum\limits_{i=1}^{L \times B}\left(I_{\mathrm{RT}, i, t}-I_{\mathrm{IGS}, i, t}-\mathrm{bias}\right)^2}{N}} \\ \mathrm{RMS}=\sqrt{\frac{\sum\limits_{t=0}^T \sum\limits_{i=1}^{L \times B}\left(I_{\mathrm{RT}, i, t}-I_{\mathrm{IGS}, i, t}\right)^2}{N}} \end{array}\right. $ | (1) |
式中,IRT, i, t、IIGS, i, t分别为t时刻RT-GIM、IGS-GIM格网点i处的电离层VTEC值,T为IGS-GIM天文件包含电离层地图的总个数,L为经线方向格网点总数,B为纬线方向格网点总数,N为IGS-GIM天文件包含的电离层格网点总数。
1.2 基于基准站的dSTEC评估基于基准站实测GNSS数据的GIM评估方法一般包括绝对电离层TEC(STEC)法和相对电离层TEC(dSTEC)法2种。dSTEC法采用未发生周跳的相位连续弧段内的载波相位观测数据提取相位STEC并进行差分得到dSTEC,进而评估电离层GIM产品的精度[7-8]。最大高度角dSTEC法将相位连续弧段中的STEC结果与其最大高度角对应的STEC进行差分,该方法顾及RT-GIM建模误差的同时也考虑了投影函数误差,计算方法如下:
| $ \left\{\begin{array}{l} \mathrm{dSTEC}{ }_m(t)=\operatorname{VTEC}_m\left(t, \varphi_t, \lambda_t\right) M\left(z^{\prime}\right)- \\ \ \ \operatorname{VTEC}_m\left(t_{\max }, \varphi_{t_{\max }}, \lambda_{t_{\max }}\right) M\left(z_{\text {max }}^{\prime}\right) \\ M\left(z^{\prime}\right)=\left[1-R^2 \sin ^2 z^{\prime} /\left(R+H_{\text {ion }}\right)^2\right]^{-1 / 2} \end{array}\right. $ | (2) |
式中,(φt, λt)为t时刻卫星穿刺点的经纬度,VTECm(t, φt, λt)为RT-GIM双线性内插得到的t时刻(φt, λt)处的VTEC,z′为卫星相对于接收机的天顶距,M(z′)为与天顶距相关的投影函数,R为地球平均半径(取6 378 km),Hion为假定的单层薄层高度。
卫星相对于接收机的天顶距计算公式如下:
| $\left\{\begin{array}{l} z^{\prime}={\rm{ \mathsf{ π} }}-\arccos \left(\left(R_1^2+D_s^2-R_2^2\right) / 2 R_1 D_s\right) \\ R_1=\sqrt{X_u^2+Y_u^2+Z_u^2}, R_2=\sqrt{X_s^2+Y_s^2+Z_s^2} \\ D_s=\sqrt{\left(X_s-X_u\right)^2+\left(Y_s-Y_u\right)^2+\left(Z_s-Z_u\right)^2} \end{array}\right. $ | (3) |
式中,R1为接收机坐标矢量的模长,R2为卫星坐标矢量的模长,Ds为接收机卫星坐标差值矢量的模长。基于测站实测dSTEC计算bias、STD与RMS的公式类比式(1)。
1.3 定位增益分析以IGS发布的精密坐标周解文件(snx文件)作为测站坐标参考真值。采用标准单点定位(SPP)单历元解算测站坐标和接收机钟差参数。SPP采用单GPS系统L1频点伪距作为观测输入,观测噪声设置为0.3 m,随机模型采用等权模型,截止高度角设置为15°,观测数据采样间隔与观测值文件采样间隔一致(30 s),卫星轨道和钟差的确定采用广播星历的轨道和钟差参数,对流层误差修正采用Saastamoinen模型,对流层投影函数采用NMF模型。
为评估各分析中心RT-GIM的定位增益效果,使用控制单一变量的原则,以GPS Klobuchar模型修正电离层误差的定位结果为参考,分别统计水平和高程方向残差的95%分位数,分析不同中心RT-GIM的定位增益情况。水平和高程方向定位增益计算公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{H_{{\rm{imp}}}} = - \mathop \sum \limits^N \frac{{H_{{\rm{RT}}}^{95} - H_{{\rm{BRDC}}}^{95}}}{{H_{{\rm{BRDC}}}^{95}}} \times 100\% }\\ {{V_{{\rm{imp}}}} = - \mathop \sum \limits^N \frac{{V_{{\rm{RT}}}^{95} - V_{{\rm{BRDC}}}^{95}}}{{V_{{\rm{BRDC}}}^{95}}} \times 100\% } \end{array}} \right. $ | (4) |
式中,N为测站总数,Himp和Vimp分别为水平和高程方向定位增益百分比,HRT95和VRT95分别为以RT-GIM修正电离层误差的水平和高程方向定位精度,HBRDC95和VBRDC95分别为以GPS Klobuchar模型修正电离层误差的水平和高程方向定位精度。
2 评估结果 2.1 与IGS-GIM对比分析图 1为UTC 2021-08-23 04:00各分析中心RT-GIM与IGS-GIM的TEC残差图。综合4家分析中心的计算结果可以看出,全球残差较大的地方集中在2个区域:一是在太阳活动较强的区域(120°E、20°N附近)RT-GIM的TEC残差较大且为正值;二是在太平洋中部,RT-GIM的TEC残差较大且为负值。UPC和CNES相比CAS和NRCan的TEC残差数值范围更小,与IGS-GIM的一致性更高。电离层中TEC的数值大小与太阳活动程度密切相关,尤其在太阳直射区域和赤道附近,TEC数量会明显增多,并且计算RT-GIM所采用的实时TEC数据实际上存在着十几分钟的时间延迟,因此在太阳活动较强的区域会存在较大的残差;海洋区域GNSS测站稀疏,导致实时观测数据较少,球谐函数和克里金等建模差值方法并不能很好地拟合海洋区域的电离层TEC信息,因此在海洋区域也存在较大的残差。

|
图 1 CAS、CNES、NRCan和UPC的RT-GIM TEC残差分布(UTC 2021-08-23 04:00:00) Fig. 1 TEC residual distribution of CAS, CNES, NRCan and UPC RT-GIM(UTC 2021-08-23 04:00:00) |
图 2给出2021-01-20~08-31各分析中心RT-GIM与IGS-GIM的bias和STD时间序列。从图 2(a)可以看出,各分析中心RT-GIM相比IGS-GIM整体上均存在负值偏差,其中,CNES平均偏差值最大,为-1.63 TECu;CAS偏差的离散程度较其他分析中心略大。从图 2(b)看出,RT-GIM的标准差序列与F10.7走势相似但存在明显的季节异常变化,春季太阳活动弱时RT-GIM误差大、夏季太阳活动强时RT-GIM误差小,证明RT-GIM的精度受太阳活动影响。此外,STD序列中存在个别突跳点,说明RT-GIM并不十分稳定。表 2进一步统计各分析中心RT-GIM的数据完整率(可接收时刻占总时刻的百分比)和RMS等信息。可以发现,UPC的数据缺失较为严重,NRCan SSR数据较为稳定。CAS、CNES和UPC的STD基本一致,在3.6~3.9 TECu范围内,而NRCan的STD为4.49 TECu。

|
图 2 2021-01-20~08-31各分析中心RT-GIM相对于IGS-GIM的bias和STD时间序列 Fig. 2 Bias and STD time series of RT-GIM of all analysis centers compared to IGS-GIM from January 20 to August 31, 2021 |
|
|
表 2 各分析中心RT-GIM与IGS-GIM相比的精度统计 Tab. 2 Analysis results of RT-GIM of all analysis centers compared to IGS-GIM |
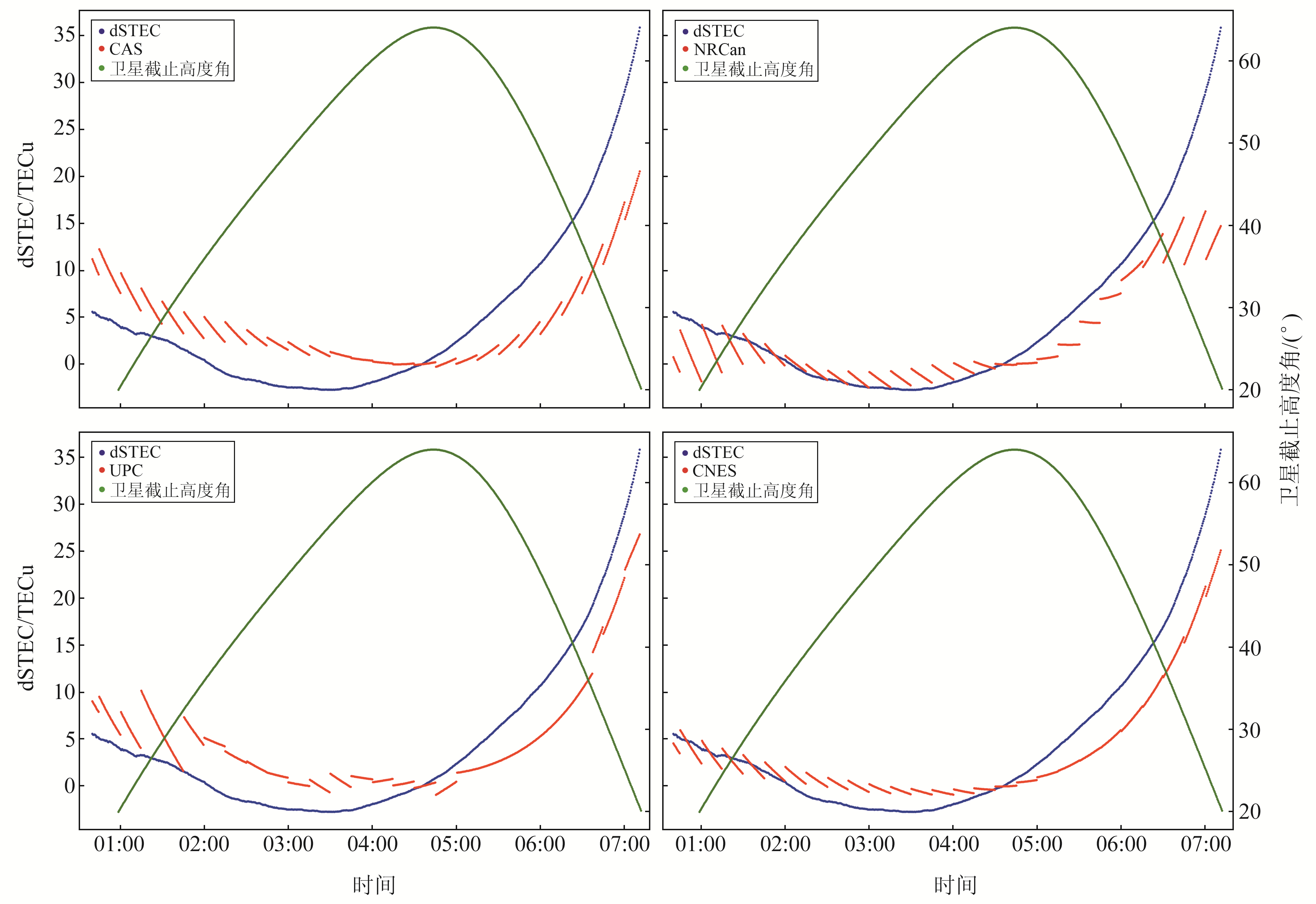
图 3给出2021-08-23 JFNG站G02卫星的实测dSTEC变化序列和各分析中心RT-GIM计算的dSTEC变化序列。可以看出,代表RT-GIM dSTEC变化的红色曲线分段明显,证明相邻时刻的RT-GIM存在微小跳变,其中,UPC和NRCan相邻RT-GIM间的跳变更为显著, 并且NRCan产品在低高度角的精度明显低于其他分析中心产品;虽然CNES仅采用12阶球谐系数建模,但其与测站实测dSTEC吻合度最高。
|
图 3 2021-08-23各分析中心RT-GIM dSTEC时间序列和JFNG站G02卫星实测dSTEC时间序列 Fig. 3 RT-GIM dSTEC time series of all analysis centers and measured dSTEC time series of G02 satellite at JFNG station on August 23, 2021 |
在全球选取150个IGS基准站,采用GPS、BDS、Galileo和GLONASS系统,限定卫星截止高度角大于20°,将提取的基准站dSTEC作为参考真值,分析2021-01-20~08-31不同分析中心RT-GIM dSTEC的精度。相位观测值精度约为2 mm,参考真值dSTEC的精度能达到cm级。计算所有测站所有卫星的RT-GIM dSTEC与基准站dSTEC的残差,每天统计1个偏差和标准差,结果如图 4所示。

|
图 4 2021-01-20~08-31各分析中心RT-GIM dSTEC相比于基准站dSTEC的bias和STD时间序列 Fig. 4 Bias and STD time series of RT-GIM dSTEC of all analysis centers compared to measured dSTEC of reference stations from January 20 to August 31, 2021 |
由图 4(a)可以看出,RT-GIM dSTEC相比于基准站dSTEC的bias较小,CAS和NRCan的平均bias接近0;UPC的平均bias为0.17 TECu;CNES的平均bias稍大,为0.32 TECu。图 4(b)给出了RT-GIM dSTEC相比于基准站dSTEC的STD时间序列。可以看出,CNES、CAS和UPC的STD相近,分别为4.40 TECu、4.42 TECu、4.42 TECu;NRCan的STD较大,为4.96 TECu。
相较于IGS-GIM,各分析中心RT-GIM dSTEC的STD略大,可能原因包括:1)模型构建误差,RT-GIM在构建电离层模型时需要对电离层电子密度分布进行假设(如单薄层假设或双层假设等),电离层函数模型与实际电离层信息分布并不十分匹配会造成RT-GIM产品的精度损失;2)投影转换误差,因为RT-GIM格网的VTEC转到STEC需要进行投影变换,高度角越低造成的精度损失越严重;3)时间延迟误差,RT-GIM的计算一般采用前十几分钟甚至数十分钟的STEC作为输入数据,因此,RT-GIM计算的dSTEC与基准站实测的dSTEC的时刻并不严格对齐。
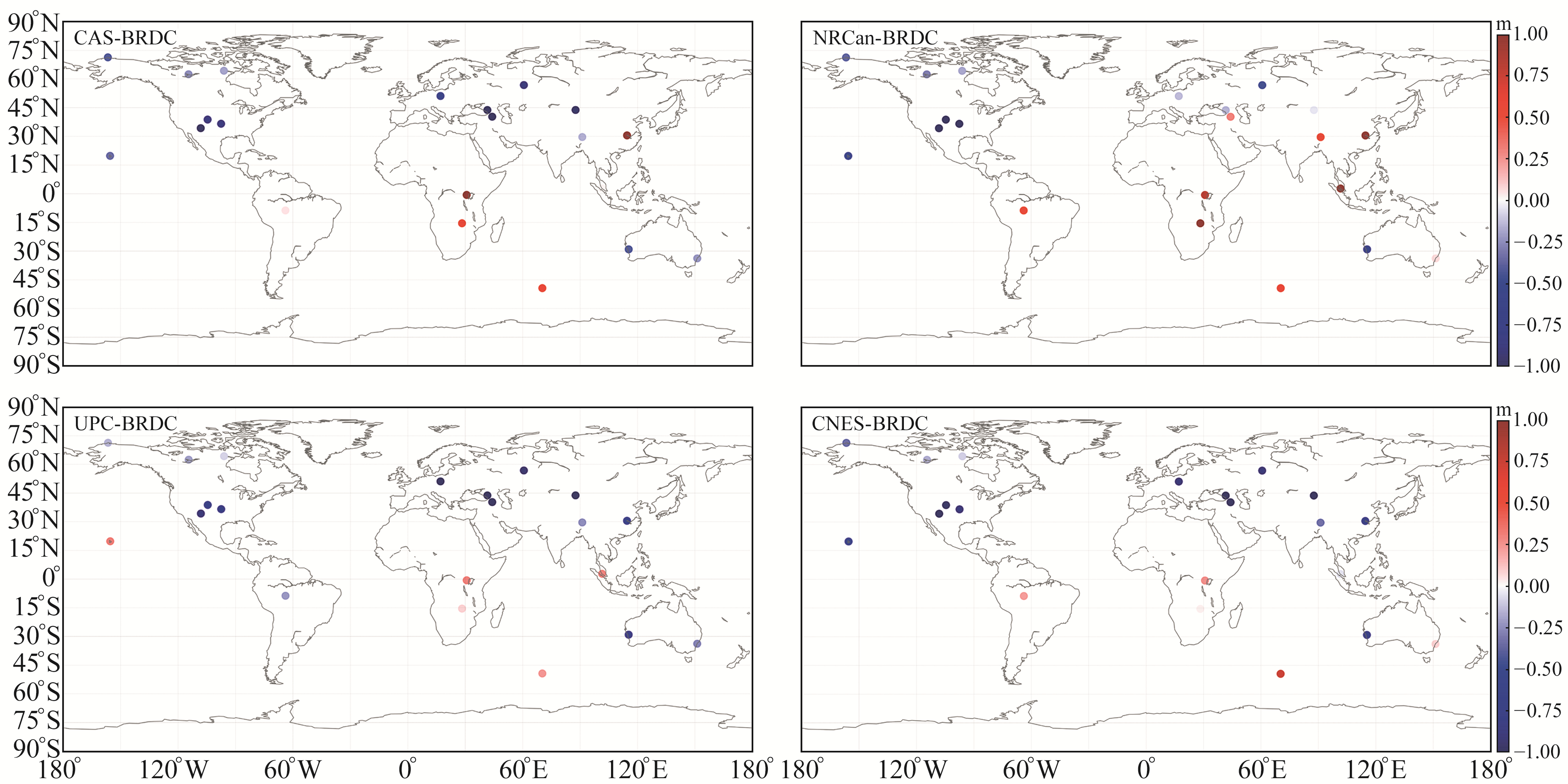
2.3 定位精度增益分析以GPS Klobuchar模型修正电离层误差的定位结果(BRDC)为参考,分别统计水平和高程方向残差的95%分位数,分析不同中心RT-GIM的定位增益情况。采用2021-09-01~07的观测数据对全球均匀分布的21个IGS测站进行定位精度增益统计,结果如图 5所示(图中蓝点表示RT-GIM相对于广播电离层高程方向定位精度提升,红点表示高程方向定位精度下降)。可以看出,UPC与CNES在高程方向定位精度提升的测站数量较多,CAS次之,NRCan在加拿大和美国定位增益明显,在其他区域定位增益不显著。值得注意的是,定位增益效果明显的测站集中分布在北半球,这与RT-GIM建模过程中北半球可用测站数量多,而南半球海洋面积大、可用测站数量较少有关。为此,分别统计全球和北半球定位增益情况,结果如表 3所示。由表可见,各分析中心RT-GIM在北半球定位增益明显,测站定位增益比例相对于全球范围提升10%~24%;CAS、CNES和UPC在全球高程方向定位精度增益5.9%~12.3%,NRCan下降1.1%;CAS、CNES和UPC在北半球高程方向定位增益11.9%~18.3%,NRCan定位增益3.4%。
|
图 5 不同分析中心RT-GIM相对于广播电离层的高程方向定位增益情况 Fig. 5 The positioning gain of RT-GIM of different analysis centers compared to the broadcast ionosphere in the elevation direction |
|
|
表 3 各分析中心RT-GIM相对广播电离层模型的定位增益统计 Tab. 3 Positioning gain statistics of RT-GIM compared to broadcast ionospheric model in all analysis centers |
1) 与IGS-GIM相比,CAS、NRCan和UPC的bias约在-0.7~-0.3 TECu范围,而CNES的bias为-1.63 TECu;CAS、CNES和UPC的STD约在3.6~3.9 TECu范围,而NRCan的STD为4.49 TECu。
2) 与dSTEC相比,各分析中心RT-GIM dSTEC的bias在0.32 TECu以内;CNES、CAS和UPC的STD相近(约4.4 TECu),UPC的STD较高(为4.96 TECu)。
3) 与广播电离层定位结果相比,CAS、CNES和UPC在北半球高程方向定位增益可达11.9%~18.3%,而NRCan定位增益仅为3.4%。
综上,CNES的RT-GIM产品总体定位精度最高,UPC的RT-GIM产品稳定性仍需提升。
| [1] |
Liu Q, Hernández-Pajares M, Yang H, et al. The Cooperative IGS RT-GIMs: A Reliable Estimation of the Global Ionospheric Electron Content Distribution in Real Time[J]. Earth System Science Data, 2021, 13(9): 4 567-4 582 DOI:10.5194/essd-13-4567-2021
(  0) 0) |
| [2] |
Li Z S, Wang N B, Hernández-Pajares M, et al. IGS Real-Time Service for Global Ionospheric Total Electron Content Modeling[J]. Journal of Geodesy, 2020, 94(3): 1-16
(  0) 0) |
| [3] |
Roma-Dollase D, Hernández-Pajares M, García-Rigo A, et al. Real Time Global Ionospheric Maps: A Low Latency Alternative to Traditional GIMs[J]. Radio Science, 2016, 47
(  0) 0) |
| [4] |
Hernández-Pajares M, Juan J M, Sanz J, et al. Application of Ionospheric Tomography to Real-Time GPS Carrier-Phase Ambiguities Resolution, at Scales of 400-1 000 km and with High Geomagnetic Activity[J]. Geophysical Research Letters, 2000, 27(13): 2 009-2 012 DOI:10.1029/1999GL011239
(  0) 0) |
| [5] |
Orús R, Hernández-Pajares M, Juan J M, et al. Improvement of Global Ionospheric VTEC Maps by Using Kriging Interpolation Technique[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2005, 67(16): 1 598-1 609 DOI:10.1016/j.jastp.2005.07.017
(  0) 0) |
| [6] |
García-Rigo A, Roma D, Pajares M H, et al. Towards RT Assessment of Ionospheric Monitoring within IAG's RTIM-WG[C]. EGU General Assembly, Vienna, 2018
(  0) 0) |
| [7] |
Chen P, Liu H, Ma Y C, et al. Accuracy and Consistency of Different Global Ionospheric Maps Released by IGS Ionosphere Associate Analysis Centers[J]. Advances in Space Research, 2020, 65(1): 163-174 DOI:10.1016/j.asr.2019.09.042
(  0) 0) |
| [8] |
陈秀德, 贾小林, 朱永兴, 等. 不同电离层格网产品的精度分析[J]. 大地测量与地球动力学, 2017, 37(8): 849-855 (Chen Xiude, Jia Xiaolin, Zhu Yongxing, et al. Analysis the Accuracy of Different Ionospheric Grid Products[J]. Journal of Geodesy and Geodynamics, 2017, 37(8): 849-855)
(  0) 0) |
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2022, Vol. 42
2022, Vol. 42


