研究地震震源破裂过程可以认识地震的发震机理,了解震源性质。震源过程反演是在时间与空间上对地震断层进行有限离散划分,在空间上将一个震源断层分为多个子断层,在时间上将一个地震事件分为多个子事件,组合全部子断层块的震源时间函数可获得地震事件的时空滑动破裂分布。可以采用先将问题进行预处理再迭代计算的反演方法,该方法计算速度快,但需要选取合适的初始值[1]。此外还有全局搜索方法,如蒙特卡洛随机搜索[2]、模拟退火法[3-4]。热浴算法[5]是模拟退火法的改进,在待解参数数量较大时效率更高[6]。目前较常见的地震震源破裂过程研究方法是采用远震速度数据的波形拟合方法或结合位移数据采用联合反演方法。但这些方法的反演过程始终存在多解性,从同一地震的各个反演结果来看,不确定性较大。
理论上,联合反演时使用的数据越多,对结果的约束力就越强。重力高频观测数据能够很好地反映地震波信息[7],在一定程度上提高反演结果的可靠性,但目前缺乏利用重力数据反演震源破裂过程的相关研究。QSSP软件[8]是基于Fortran语言开发的地震学正演软件,可使用基于球对称、考虑地球自重力影响的地球模型来计算完整的合成地震图,并通过将震源分解为多个源的组合模拟计算地表任意多个位置的速度、位移、应力、应变、重力、重力变化等参数的同震动态变化。本文基于该功能,将其开发为反演震源破裂过程的程序,并对2013-04-20芦山7.0级地震的破裂滑动过程进行反演,以验证该程序的有效性。
1 反演方法对于初始值问题,在有初步震源机制解结果的情况下,对断层模型与地震矩等初始值进行一定限制,根据矩张量、定位结果可以对破裂起始点、最大滑动量的大致区域等进行直接约束。对于大地震,单一的震源机制解不能符合实际的震源破裂过程,需要将地震分为多个子事件分别进行反演并叠加。
可以使用热浴算法[5]提高冷却速率较小情况下模型参数的搜索速度。假设断层模型A有M个模型矢量,即其被划分成M个子断层块,模型矢量
| $ \begin{array}{l} P\left( {\vec A\mid {A_j} = {A_{j, k}}} \right) = \\ \frac{{\exp \left( { - \frac{{G\left( {\vec A\mid {A_j} = {A_{j, k}}} \right)}}{C}} \right)}}{{\sum\limits_{j = 1}^n {\exp } \left( { - \frac{{G\left( {\vec A\mid {A_j} = {A_{j, k}}} \right)}}{C}} \right)}} \end{array} $ | (1) |
| $G=\frac{1}{N} \sum\limits_{l=1}^T\left(1-\frac{\int \mathrm{Cal}_l(t) \mathrm{Obs}_l(t) \mathrm{d} t}{\sqrt{\int\left(\mathrm{Cal}_l(t)\right)^2 \mathrm{~d} t \int\left(\operatorname{Obs}_l(t)\right)^2 \mathrm{~d} t}}\right) $ | (2) |
式中,Call为各台站的理论计算波形,可通过调用QSSP计算获取,Obsl为各台站观测波形,T为最大台站数。计算第j个断层模型参数的接收概率:
| $ H_{j, k}=\sum\limits_{l=1}^j P\left(\vec{A} \mid A_j=A_{j, l}\right) $ | (3) |
随机取ε∈[0, 1],满足Hj, (k-1)<ε<Hj, k时,用Aj, k代替原有的模型参数。不断迭代至曲线的相关性满足要求,迭代一次即对所有模型参数遍历访问一次,同时进行一次降温。降温准则参考Rothman[5]提出的降温法则,在温度较高的开始阶段,所有模型的接收概率相同,随着收敛的进行,温度逐渐降低。在低温阶段,温度低的模型被接收的概率较大,表达式为:
| $ T=\left\{\begin{array}{l} T_{\min }, T \leqslant T_{\min } \\ \beta T_0, T>T_{\min } \end{array}\right. $ | (4) |
式中,β为降温速度,Tmin为最低温度。
热浴算法每次迭代需要计算Q=ΠMn次,虽然相比模拟退火法计算速度更快,但依然需要大量的时间,故仅将其用于全局搜索阶段。在该阶段,收敛标准可相对放低,使模型参数能避开局部最优解进入全局最优解的参数区间即可,如图 1红线中间部分。
|
图 1 全局最优解区间 Fig. 1 Interval of global optimal solution |
为保证断层模型滑动的时空连续性,同时防止计算出现奇异或病态矩阵,需要先对待解参数进行光滑约束。待解参数包括滑动量、滑动破裂方向、滑动起始时间、滑动持续时间等。计算理论波形数据基本原理如下:
| $ \boldsymbol{G} * \boldsymbol{C}=\boldsymbol{W} $ | (5) |
式中,G为格林函数系数矩阵,C为震源参数滑动量(地震矩)、断层块走向、倾向、位置与深度、滑动角、起始破裂时间、破裂持续时间,W为理论计算波形数据,该部分包含于QSSP计算模块中。格林函数系数任一元素可由式(6)计算获得:
| $ \begin{gathered} G_{m, n}=\int g_{u v}\left(T, t_0+x \Delta t ; u v, \theta\right) \cdot \\ \varphi\left[\theta-(\alpha-1) \Delta t_1-t_2\right] \mathrm{d} \theta \end{gathered} $ | (6) |
式中,guv(T, t0+xΔt; uv, θ)为在uv位置的子断层块地震矩引起的台站波形数据格林函数,t0为波形数据起点,Δt为离散时间间隔,α为对应地震矩密度张量时间基本函数数量,Δt1为地震矩基本时间函数间隔,t2为破裂到达uv子断层块的时间。
通过拉普拉斯方程建立平滑约束方程并获取平滑矩阵S,引入光滑因子μ1以平衡各台站权值,引入μ2以控制平滑程度。子断层块以au, v表示,其中u为走向,v为倾向,Du为沿走向相邻子断层块的距离,Dv为沿倾向相邻子断层块的距离,位于边界的子断层块用一阶差分
| $ \begin{aligned} \nabla^2 q=& \gamma \approx \frac{a_{u-1, v}+a_{u+1, v}-2 a_{u, v}}{\left(D_u\right)^2}+\\ & \frac{a_{u, v-1}+a_{u, v+1}-2 a_{u, v}}{\left(D_v\right)^2} \end{aligned} $ | (7) |
联立得:
| $ \left[\begin{array}{ll} \mu_1 & \boldsymbol{G} \\ \mu_2 & \boldsymbol{S} \end{array}\right][\boldsymbol{C}]=\left[\begin{array}{c} \mu_1 \boldsymbol{W} \\ \bf{0} \end{array}\right] $ | (8) |
热浴算法虽然能保证全局性,但其温度越低,收敛速度越慢,导致在全局最优解区间内收敛时间长。故以热浴算法搜索结果为初始值,在此基础上对子断层模型参数进行区间限定。采用拟牛顿法进行快速收敛,使波形趋势拟合程度在得到一定保障的前提下对振幅进行拟合。牛顿法是用泰勒展开保留一阶项和二阶项来近似非线性函数F,利用近似函数的最小值推测非线性函数的极小值,其展开式为:
| $ \begin{gathered} F\left(x_i+\Delta \boldsymbol{x}_i\right) \approx F\left(x_i\right)+\boldsymbol{J}\left(x_i\right)^{\mathrm{T}} \Delta \boldsymbol{x}_i+ \\ \frac{1}{2} \Delta \boldsymbol{x}_i^{\mathrm{T}} \boldsymbol{H}\left(x_i\right) \Delta \boldsymbol{x}_i \end{gathered} $ | (9) |
式中,雅可比矩阵
| $ \frac{\partial\left(F\left(x_i\right)+\boldsymbol{J}\left(x_i\right)^{\mathrm{T}} \Delta \boldsymbol{x}_i+\frac{1}{2} \Delta \boldsymbol{x}_i^{\mathrm{T}} \boldsymbol{H}\left(x_i\right) \Delta \boldsymbol{x}_i\right)}{\partial \Delta \boldsymbol{x}_i}=0 $ | (10) |
得增量方程:
| $ \Delta \boldsymbol{x}_i=-\boldsymbol{H}\left(x_i\right)^{-1} \boldsymbol{J}\left(x_i\right) $ | (11) |
沿此方向一维搜索最优步长β,使F(xi+βΔxi)取最小。
由于海塞矩阵计算量过于庞大,采用构造矩阵替代其进行计算。牛顿法搜索方向式可改写为di=-Hi-1ji,构造矩阵B来近似替代矩阵H。F为二次函数,则H为常数矩阵,任意两点xi、xi+1之间的梯度差为:
| $x_{i+1}-x_i=\boldsymbol{H}^{-1}\left[\nabla F\left(x_{i+1}\right)-\nabla F\left(x_i\right)\right] $ | (12) |
在F为非二次函数时,仿照式(12)构建满足式(13)条件的近似矩阵B来替代矩阵H:
| $ x_{i+1}-x_i=\boldsymbol{B}_{i+1}\left[\nabla F\left(x_{i+1}\right)-\nabla F\left(x_i\right)\right] $ | (13) |
根据式(13)即可按式(14)拟牛顿条件计算增量:
| $ \Delta \boldsymbol{x}_i=\boldsymbol{B}_{i+1} \cdot \Delta \boldsymbol{j}_i $ | (14) |
| $ \Delta \boldsymbol{B}_i=\frac{\Delta \boldsymbol{j}_i \Delta \boldsymbol{j}_i^{\mathrm{T}}}{\Delta \boldsymbol{x}_i^{\mathrm{T}} \Delta \boldsymbol{j}_i}-\frac{\boldsymbol{B}_i \Delta \boldsymbol{x}_i \Delta \boldsymbol{x}_i^{\mathrm{T}} \boldsymbol{B}_i}{\Delta \boldsymbol{x}_i^{\mathrm{T}} \boldsymbol{B}_i \Delta \boldsymbol{x}_i} $ | (15) |
由谢尔曼-莫里森公式可知,任意非奇异方阵A和n维向量r、s,有条件1+sTA-1r≠0,得:
| $\left(\boldsymbol{A}+\boldsymbol{r} \boldsymbol{s}^{\mathrm{T}}\right)^{-1}=\boldsymbol{A}^{-1}-\frac{\left(\boldsymbol{A}^{-1} \boldsymbol{r}\right)\left(\boldsymbol{s}^{\mathrm{T}} \boldsymbol{A}^{-1}\right)}{1+\boldsymbol{s}^{\mathrm{T}} \boldsymbol{A}^{-1} \boldsymbol{r}} $ | (16) |
采用谢尔曼-莫里森公式迭代求得矩阵B的逆的迭代计算式:
| $ \begin{gathered} \left(\boldsymbol{B}_{i+1}\right)^{-1}= \\ \left(\boldsymbol{I}_n-\frac{\Delta \boldsymbol{x}_i \Delta \boldsymbol{j}_i^{\mathrm{T}}}{\Delta \boldsymbol{x}_i^{\mathrm{T}} \Delta \boldsymbol{j}_i}\right) \boldsymbol{B}_i^{-1}\left(\boldsymbol{I}_n-\frac{\Delta \boldsymbol{j}_i \Delta \boldsymbol{x}_i^{\mathrm{T}}}{\Delta \boldsymbol{x}_i^{\mathrm{T}} \Delta \boldsymbol{j}_i}\right)+\frac{\Delta \boldsymbol{x}_i \Delta \boldsymbol{x}_i^{\mathrm{T}}}{\Delta \boldsymbol{x}_i^{\mathrm{T}} \Delta \boldsymbol{j}_i} \end{gathered} $ | (17) |
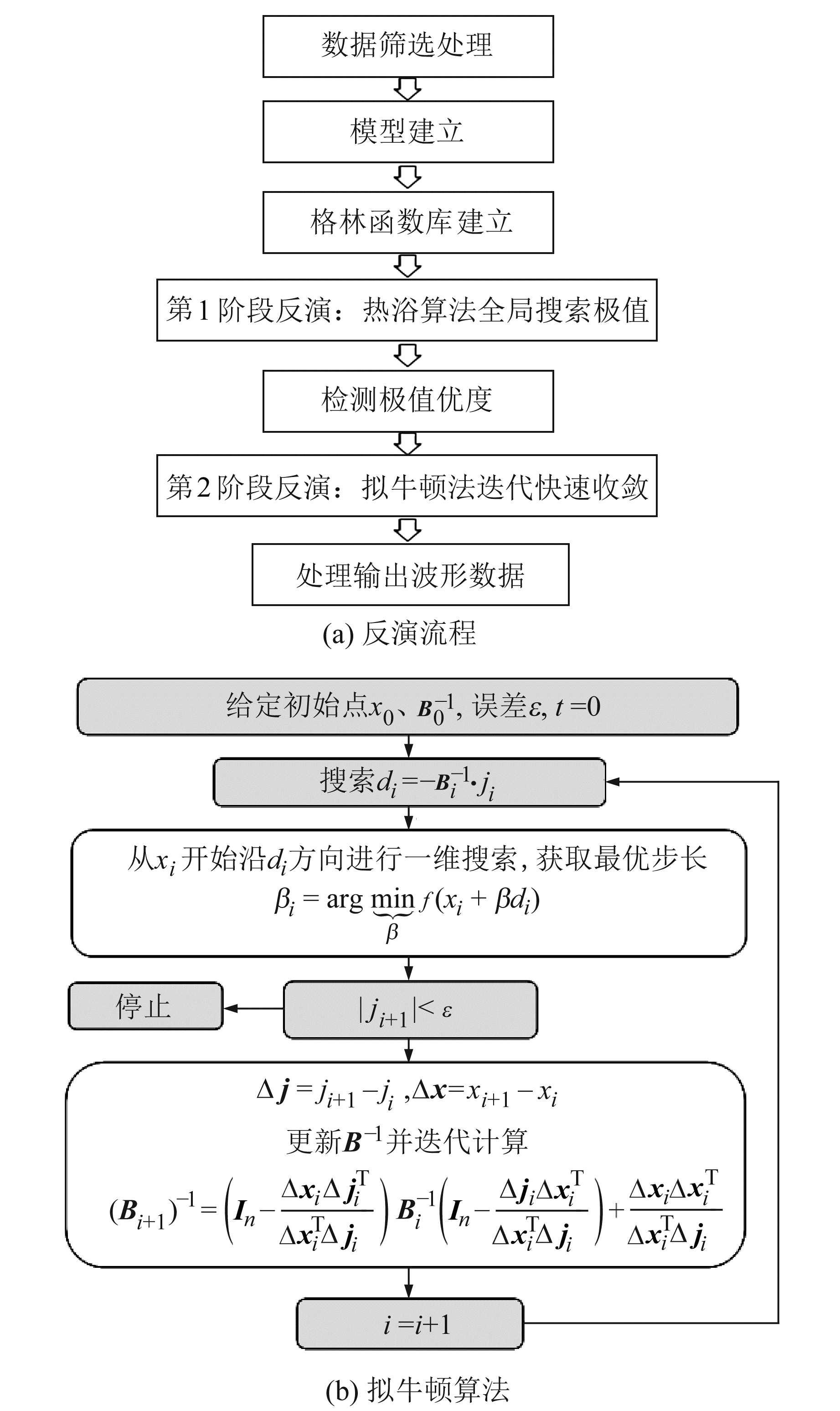
式中,n为x的维数,将矩阵初始值设置为单位矩阵,再根据式(17)迭代逼近海塞矩阵。循环迭代至最小残差项小于设定精度时停止并输出对应待解模型参数。反演过程及拟牛顿算法流程如图 2所示。
|
图 2 算法流程 Fig. 2 Flow chart of algorithm |
为了检验2种算法结合使用的可靠性,采用19×10棋盘模型进行正反演验证。正演模型参数随机给出,设定断层滑动为45°逆冲,滑动量不超过4 m,断层位置为100°E、40°N,断层倾角45°,走向135°,每个子断层块大小为3.5 km×3.5 km,断层起始深度为5 km。主要地震矩释放一次,集中于5~10 s,破裂总持续时间15 s,破裂传播速度3 km/s。反演第1阶段中,用热浴算法进行全局搜索并进行少量迭代收敛,结果如图 3(a)所示。断层滑动模型及最终对子断层块滑动量、滑动角、破裂起始与持续时间的反演结果分别如图 3(b)、3(c)所示。

|
图 3 棋盘滑动分布及滑动量时空分布 Fig. 3 The slip distribution on checkerboard and spatio-temporal distribution of slip |
对比图 3(a)和3(c)可知,2个理论滑动破裂模型在滑动量、主要滑动区域及滑动角方面仍存在差距。从图 3(b)和3(c)可以看出,经第2阶段拟牛顿法在极值附近进行快速收敛后,反演滑动破裂模型与理论值主要破裂区各子断层块间滑动量、滑动角偏差很小,其中滑动量最大偏差不超过18 cm、滑动角偏差不超过5°。由图 3(d)可知,破裂主要集中在4~10 s,持续时间16 s。综上,本文方法稳定可靠,且拟牛顿法可大幅提升后期收敛速度,较单一热浴算法搜索和收敛更迅速,因此可用于地震震源破裂过程反演。下文将使用实际震例进行验证。
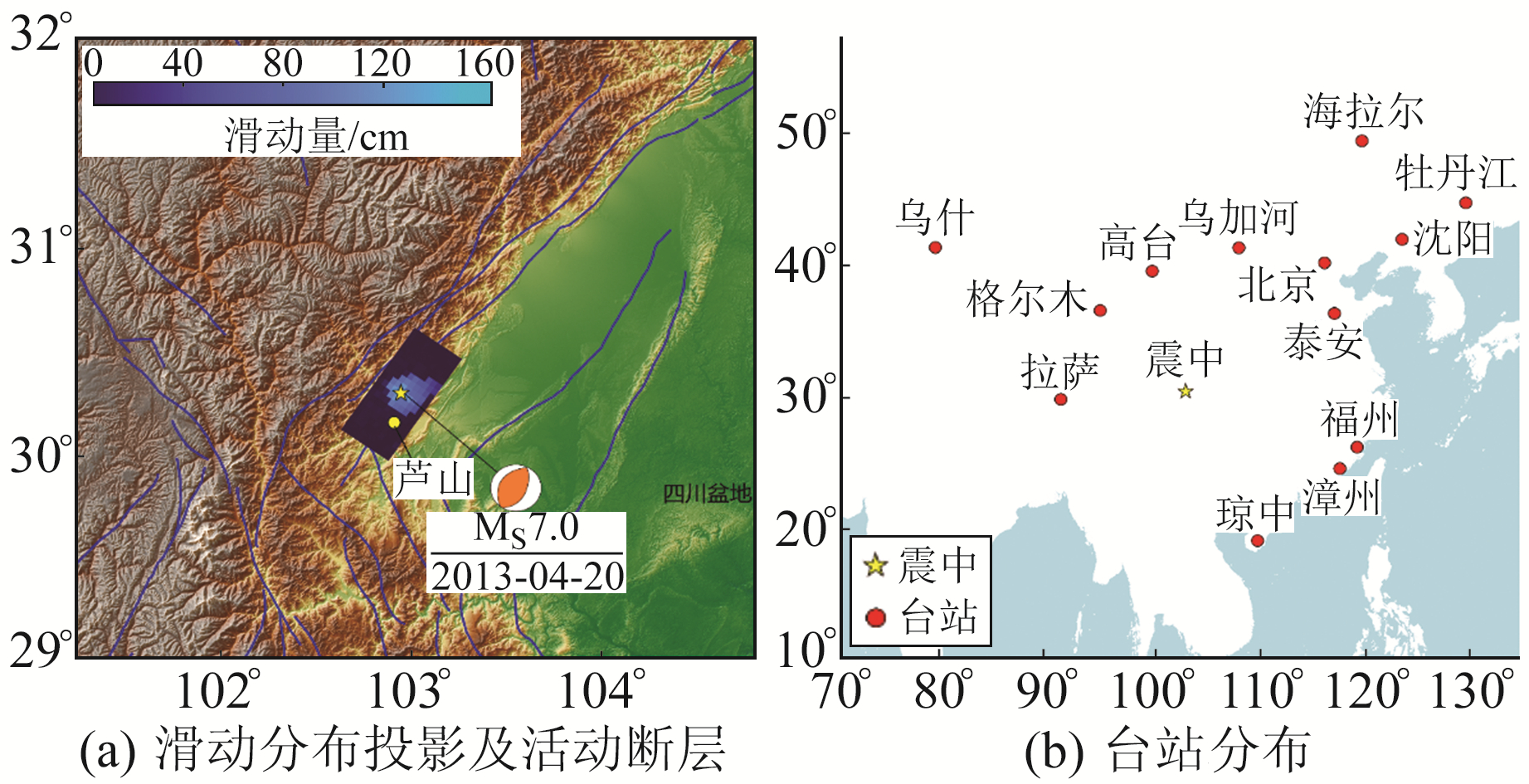
2 断层模型本文采用与刘成利等[9]相同的断层模型,断层走向214°,倾角38°,每个子断层大小为3.5 km×3.5 km,断层面沿走向长66.5 km,沿倾向长35 km,断层起始深度为6.073 km。滑动量不超过3 m,滑动角0~180°,相邻断层破裂起始时间不超过2 s,断层模型投影如图 4(a)所示(图中蓝色矩形块为断层在地表的投影位置,黄色五角星为震中)。可以看出,断层模型走向与龙门山断层在该段投影走向一致,且龙门山断层投影位置基本位于子断层投影面的中央线处。
|
图 4 滑动分布投影及活动断层与台站分布 Fig. 4 The projection of the slip distribution and active fault and distribution of the stations |
2013-04-20芦山7.0级地震前,我国已有18个台站使用秒采样PET重力仪。经过固体潮校正、零漂校正、跳点校正等处理后有13个台站数据可以使用。首先对加速度数据进行积分并去除常数项,使波形更易于分辨和拟合。根据范文华等[7]对重力同震数据与地震仪速度同震数据的对比研究结果,本文对观测数据与格林函数均进行0.01~0.3 Hz滤波。针对观测数据,将QSSP内置滤波器部分源代码重新编译形成单独的滤波软件进行滤波,选取台站仪器接收到地震波后70 s的数据。台站分布如图 4(b)所示。
地球模型包括大气、海洋、地幔、液态外核、固态内核等多层结构,地壳部分采用Crust2.0模型参数,其余深部模型使用Kamamori & Anderson地球模型参数,格林函数库由QSSP直接计算得到,反演时从格林函数库中自动读取。
4 芦山地震震源破裂过程反演图 5为各台站波形拟合情况。可以看出,理论计算波形与观测数据波形拟合较好。

|
图 5 拟合波形 Fig. 5 Fitted waveform |
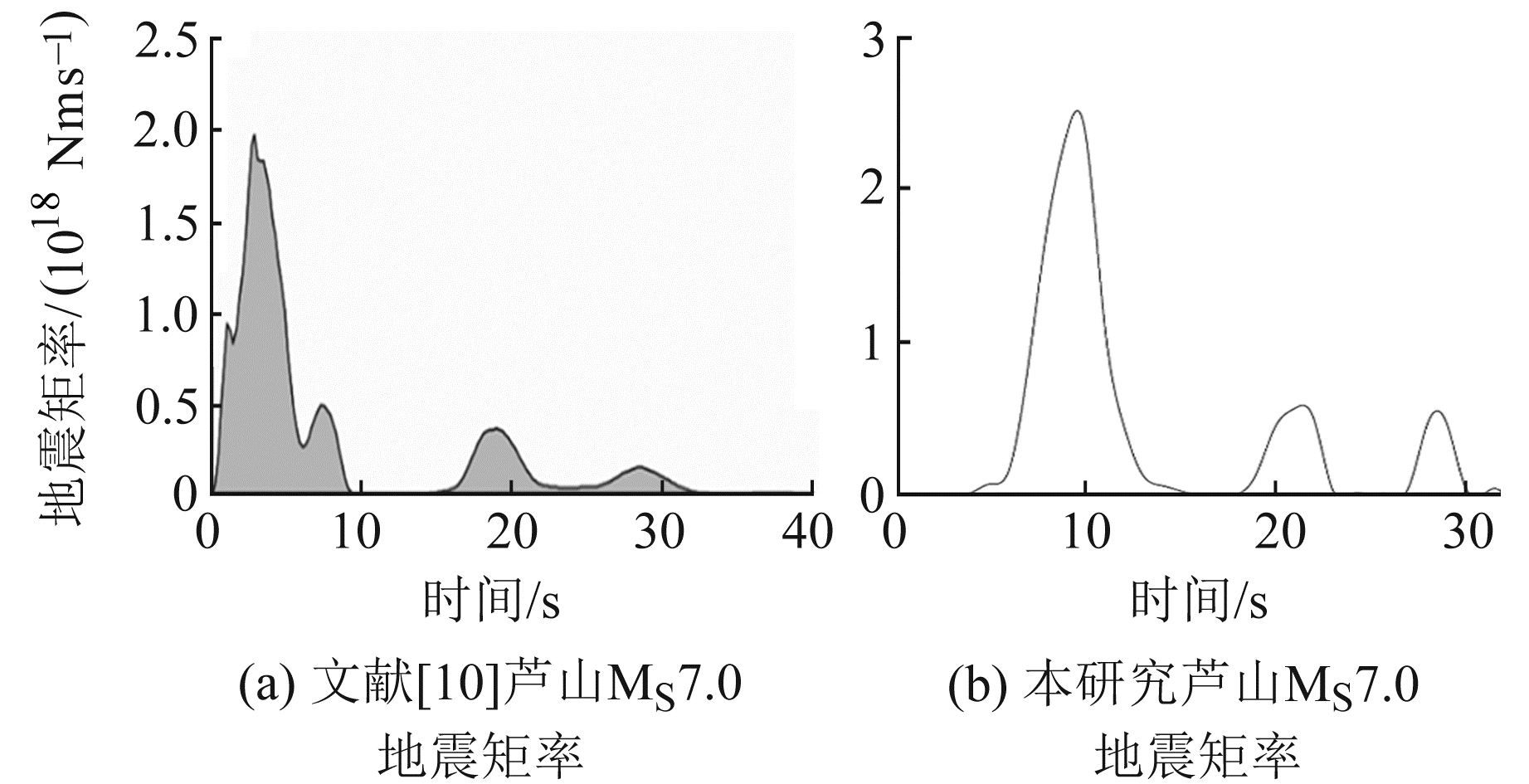
图 6(b)为本文反演得到的断层滑动破裂模型,箭头方向表示滑动方向,箭头长度表示滑移量,图中深色子断层滑动量极小,在实际情况下大概率未发生任何滑动破裂。可以看出,断层滑动方向主要表现为逆冲,最大滑动量位于第6层,沿倾向距离17.5~21 km、沿走向-1.5~1.5 km,滑移量达157 cm。滑移主要发生在最大滑移子断层块周围约7~9 km区域,方向主要为向上发展。图 6(c)为断层滑动量时空分布。可以看出,芦山7.0级地震的破裂持续时间为30 s,地震释放的标量地震矩约1.155×1019 Nm,相当于MW6.64地震,起震深度约16.5 km,与最终标定的17.5 km相比略浅。结合图 6(c)和图 7(b)可以看出,破裂滑动集中发生在10 s、21 s、29 s附近,地震矩释放主要在前12 s,20~22 s和28~29 s发生的破裂地震矩释放和滑动量都相对很小。

|
图 6 芦山MS7.0地震破裂模型 Fig. 6 The rupture model of Lushan MS7.0 earthquake |
|
图 7 芦山MS7.0地震地震矩率 Fig. 7 Seismic moment rate of Lushan MS7.0 earthquake |
本文反演的矩震级为MW6.64,与刘成利等[9]的反演结果MW6.6接近。对于主要破裂滑动区域,刘成利等[9]反演结果(图 6(a))的最大滑移子断层块大约位于15 km,滑动量为141 cm,本文反演结果的最大滑移子断层块位于16.8 km,滑动量为157 cm,滑移主要区域均位于最大滑移子断层块周围7~10 km,本文结果整体相对略深。刘成利等[9]的反演结果中,第1次地震矩释放峰值中心位于3~7 s,本文反演结果的峰值位于6~11 s,发生主要破裂滑动的时间相对较晚。
对比赵翠萍等[10]的反演结果可知,本文反演结果最大滑移区域中心位置接近,区域覆盖相对小;其反演结果最大滑动量为1.8 m,与本文结果相比差异较大;其破裂传播速度约为3 km/s,与本文结果2.89 km/s较为接近;其矩震级约为MW6.8,比本文的MW6.64大,这可能是主要滑移区域面积相对较大导致的。赵翠萍等[10]的3次地震矩释放峰值分别集中于13 s、27 s与39 s附近,本文发生主要破裂滑动的时间与之相比均较早,破裂的整体持续时间也相对较短。郑绪君等[11]的反演结果中,地震矩只释放1次,整个破裂过程约为10 s,释放峰值位于5~7 s附近,本文反演的主要地震矩释放时间与之较为接近;其震中深度为16 km,主要滑动区域位于震中周围约6 km,破裂滑动范围更为集中,本文结果与之相比起震深度较为接近但范围更大;其断层面最大滑动量约为2.2 m,该结果相对其他结果及本文结果均较大。
各反演结果间均存在一定差异。本研究与刘成利等[9]的研究虽采用相同模型,但所得结果存在些许不同,这可能与使用QSSP及采用数据类型不同有关。重力数据与测震仪数据在频率域的P波频谱具有一定的相似度但仍存在差异,QSSP以分层地球模型计算理论波形且考虑海洋的影响,与半无限空间地球模型计算不同,这些因素都会使计算结果出现变化。
5 结语基于QSSP软件,本文利用热浴算法、拟牛顿算法和平滑约束反演震源破裂过程。从棋盘模型验证及实际震例反演结果来看,本文反演方法收敛效率高、稳定可靠。
| [1] |
Tarantola A, Valette B. Generalized Nonlinear Inverse Problems Solved Using the Least Squares Criterion[J]. Reviews of Geophysics, 1982, 20(2): 219-232 DOI:10.1029/RG020i002p00219
(  0) 0) |
| [2] |
Rebbi C. Monte Carlo Calculations in Lattice Gauge Theories[M]. Berlin: Springer, 1987
(  0) 0) |
| [3] |
刘鹏程, 纪晨. 改进的模拟退火——单纯形综合反演方法[J]. 地球物理学报, 1995, 38(2): 199-205 (Liu Pengcheng, Ji Chen. An Improved Simulated Annealing-Downhill Simplex Hybrid Global Inverse Algorithm[J]. Chinese Journal of Geophysics, 1995, 38(2): 199-205)
(  0) 0) |
| [4] |
姚姚. 地球物理非线性反演模拟退火法的改进[J]. 地球物理学报, 1995, 38(5): 643-650 (Yao Yao. Improvement on Nonlinear Geophysical Inversion Simulated Annealing[J]. Chinese Journal of Geophysics, 1995, 38(5): 643-650)
(  0) 0) |
| [5] |
Rothman D H. Automatic Estimation of Large Residual Statics Corrections[J]. Geophysics, 1986, 51(2): 332-346
(  0) 0) |
| [6] |
Sen M K, Stoffa P L. Global Optimization Methods in Geophysical Inversion[M]. Cambridge: Cambridge University Press, 1995
(  0) 0) |
| [7] |
范文华, 申重阳, 谈洪波, 等. 重力仪与地震计记录的地震波信号频谱特征比较: 以芦山7.0地震为例[J]. 大地测量与地球动力学, 2017, 37(4): 411-415 (Fan Wenhua, Shen Chongyang, Tan Hongbo, et al. A Comparison between the Spectral Characteristics of Seismic Signals Recorded by Gravimeter and Seismometer: Taking Lushan 7.0 Earthquake for Example[J]. Journal of Geodesy and Geodynamics, 2017, 37(4): 411-415)
(  0) 0) |
| [8] |
Wang R J, Heimann S, Zhang Y, et al. Complete Synthetic Seismograms Based on a Spherical Self-Gravitating Earth Model with an Atmosphere-Ocean-Mantle-Core Structure[J]. Geophysical Journal International, 2017, 210(3): 1 739-1 764
(  0) 0) |
| [9] |
刘成利, 郑勇, 葛粲, 等. 2013年芦山7.0级地震的动态破裂过程[J]. 中国科学: 地球科学, 2013, 43(6): 1 020-1 026 (Liu Chengli, Zheng Yong, Ge Can, et al. Rupture Process of the MS7.0 Lushan Earthquake, 2013[J]. Science China: Earth Sciences, 2013, 43(6): 1 020-1 026)
(  0) 0) |
| [10] |
赵翠萍, 周连庆, 陈章立. 2013年四川芦山MS7.0级地震震源破裂过程及其构造意义[J]. 科学通报, 2013, 58(20): 1 894-1 900 (Zhao Cuiping, Zhou Lianqing, Chen Zhangli. Source Rupture Process of Lushan MS7.0 Earthquake, Sichuan, China and Its Tectonic Implication[J]. Chinese Science Bulletin, 2013, 58(20): 1 894-1 900)
(  0) 0) |
| [11] |
郑绪君, 张勇, 马强, 等. 基于强震动资料的破裂过程快速反演及其自动化的可行性[J]. 地球物理学报, 2018, 61(10): 4 021-4 036 (Zheng Xujun, Zhang Yong, Ma Qiang, et al. Fast Inversion of Rupture Process Based on Strong Motion Data and the Feasibility of Its Automation[J]. Chinese Journal of Geophysics, 2018, 61(10): 4 021-4 036)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

