2. 水沙科学与水利水电工程国家重点实验室, 北京市清华园1 号, 100089
2017-08-08四川省九寨沟县发生MS7.0地震。关于九寨沟地震强地面运动数值模拟的研究取得了一些成果[1-4],但仍有不足之处,如应用复合震源模型进行模拟及其震源参数敏感性分析的研究较少、随机有限断层法计算地震动分量方向单一、地震峰值加速度拟合精度不高等。为此,本文应用复合震源模型对九寨沟MS7.0地震强地面运动数值模拟展开研究,并探讨不同模型参数对合成地震动的影响规律,为九寨沟地区工程场地地震安全评价提供参考依据。
1 复合震源模型基本理论复合震源模型是用于计算宽频带强地面运动的有限源模型[5]。该模型通过描述震源的运动学特征,结合地震波在层状介质中的传播过程,将广义反射和透射系数法[6]得到的格林函数与震源时间函数进行卷积,计算得到宽频带地震动。模型中,强震震源被认为是大量具有恒定应力降圆形子震的叠加。首先将断层面划分成一系列尺寸相同的正方形子断层网格,之后用一定数量和相应半径大小分布服从Frankel自相似模型[7]的圆形子震填充该断层面,并允许其部分重叠。圆形子震相当于一系列小震,在震源破裂过程中相继被激发,最终释放的能量在断层面上不断被叠加,达到模拟强震的目的。设圆形子震半径为R、数目为N,则有:
| $ \frac{\mathrm{d} N}{\mathrm{~d}(\ln R)}=P R^{-D} $ | (1) |
式中,分形维数D=2,控制断层面上圆形子震数量的分布及圆形子震的上升时间,P为比例常数:
| $ P=\left\{\begin{array}{l} \frac{7 M_0}{16 \Delta \sigma} \frac{3-D}{\left(R_{\max }^{3-D}-R_{\min }^{3-D}\right)}, D \neq 3 \\ \frac{7 M_0}{16 \Delta \sigma} \frac{1}{\ln \left(R_{\max } / R_{\min }\right)}, D=3 \end{array}\right. $ | (2) |
式中,M0为地震矩,Δσ为应力降,Rmax为最大圆形子震半径,Rmin为最小圆形子震半径。对式(1)进行积分,可得半径大于R且小于Rmax圆形子震的分布数量N(R):
| $ N(R)=\frac{P}{D}\left(R^{-D}-R_{\max }^{-D}\right) $ | (3) |
式中,最大圆形子震半径Rmax取断层宽度的一半[8],最小圆形子震半径Rmin取Rmax/20,每个圆形子震的地震矩取决于该圆形子震半径Ri和应力降Δσ。第i个圆形子震的地震矩M0i为:
| $ M_0^i=\frac{16}{7} \Delta \sigma R_i^3 $ | (4) |
震源时间函数由位于断层面上的一系列圆形子震震源时间函数叠加得到,每个圆形子震的破裂时间由其到震源中心的距离和破裂速度决定。在给定地震矩、应力降、破裂速度及子断层尺寸等震源参数的情况下,断层从震源以恒定的速度vr破裂,当破裂经过圆形子震中心时,圆形子震开始辐射能量。其中,第i个圆形子震的震源时间函数
| $ \dot{M}_0^i=\left(2 {\rm{ \mathsf{ π} }} f_c^i\right)^2 M_0^i H(\tau) \tau \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} f_c^i \tau} $ | (5) |
式中,τ=t-ti,t为整个断层的破裂时间,ti为第i个圆形子震的发震时间,ti=X/vr,X为圆形子震圆心到震源的距离,vr为破裂速度,H(τ)为阶梯函数,fci为第i个圆形子震的角频率:
| $ f_c^i=\frac{2.34 \beta}{2 {\rm{ \mathsf{ π} }} R_i} $ | (6) |
式中,β为剪切波的速度。断层面上滑动位移量的空间分布由圆形子震滑动位移量叠加得到,第i个圆形子震的滑动位移量ΔUi为[1]:
| $ \Delta U_i=C \frac{\Delta \sigma}{\mu} R_i $ | (7) |
式中,C为依赖断层类型的常数,μ为介质剪切模量。
2 地震数据与震源参数本文研究区域(103°~105°E,31°~35°N)位于巴颜喀拉块体,该块体近年来地震频发。九寨沟地震后,中国地震台网中心等机构公布了其震源位置、地震矩、震源深度、断层节面的走向、倾角和滑动角等震源参数(表 1),其中,根据美国地质调查局的研究,断层节面Ⅱ为实际断层面[1],因此本文取节面Ⅱ进行研究。
|
|
表 1 九寨沟地震震源参数 Tab. 1 Source parameters of the Jiuzhaigou earthquake |
基于孟令媛等[9]对余震分布情况及断层面上滑动位移的反演结果,建立长30 km、宽20 km的断层模型,并将其划分为150个2 km×2 km的正方形子断层。断层面上圆形子震的分布如图 1所示,其中圆形子震地震矩的总和等于总地震矩。通过式(7)计算得到断层面上滑动位移量的不均匀分布,如图 2所示。九寨沟地震震中距150 km区域范围内台站信息如表 2所示,九寨沟地区介质速度信息(图 3)来自全球地壳模型Crust1.0(https://igppweb.ucsd.edu/~gabi/crust1.html),台站位置分布如图 4所示。对所有台站观测数据进行基线校准和滤波处理,带通滤波范围为0.1~20 Hz。

|
图 1 断层面上圆形子震分布 Fig. 1 Distribution of circular subevents on the fault plane |

|
图 2 断层面上滑移量的不均匀分布 Fig. 2 Non-uniform distribution of slip on the fault plane |
|
|
表 2 台站信息 Tab. 2 Information of the stations |
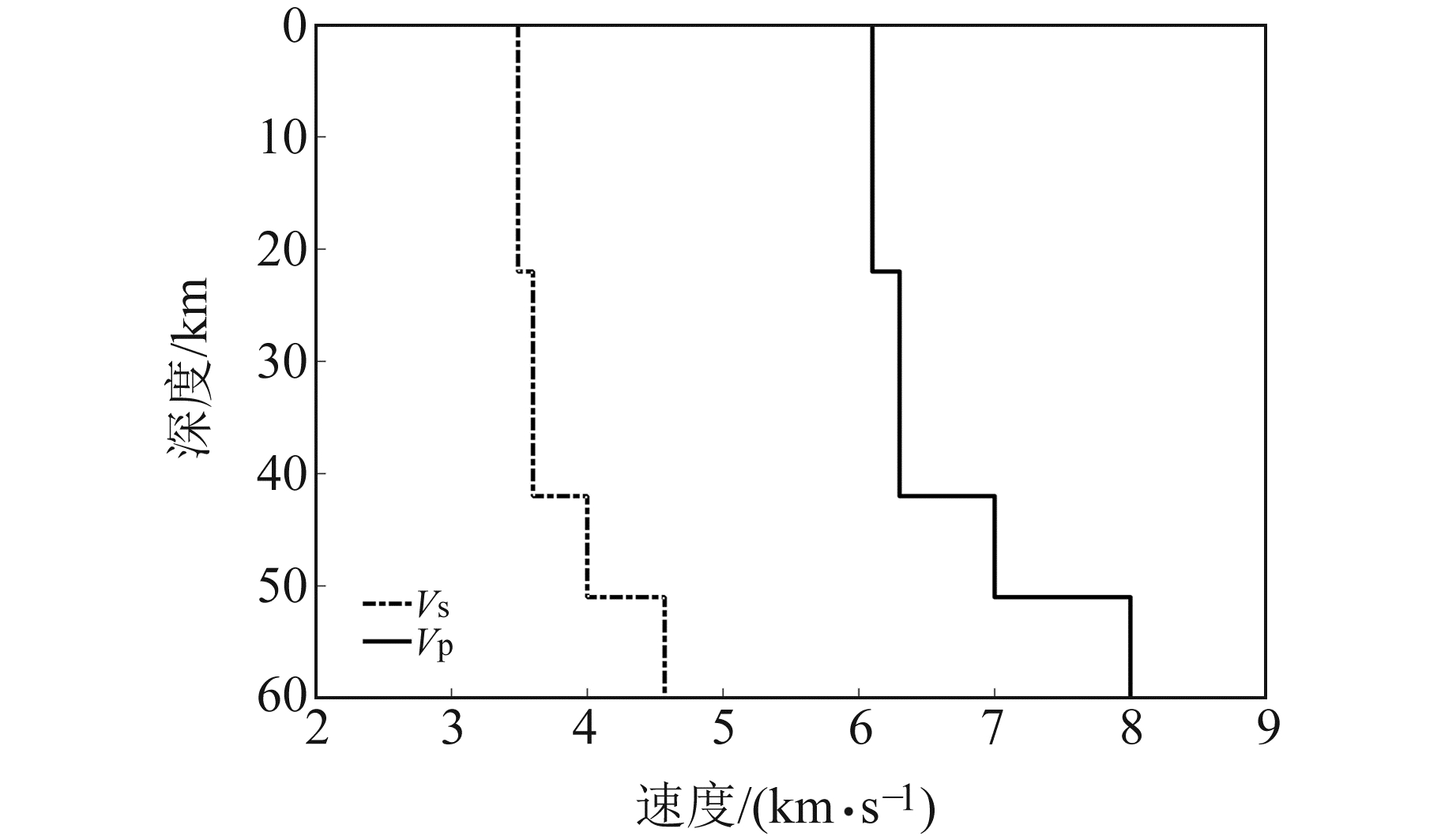
|
图 3 九寨沟地区速度模型 Fig. 3 Velocity model of the Jiuzhaigou region |

|
图 4 台站分布 Fig. 4 Distribution of the stations |
在运动学震源模型中,断层的破裂面积、长度、宽度、埋置深度、走向、倾角和滑移角等是描述断层特征的参数;地震矩、应力降、平均滑动时间、平均破裂速度、破裂方式和初始破裂点位置等是描述平均破裂过程的参数。这些震源参数控制着地震动强度和分布[10],分析这些参数的影响规律可为地震动合成精度提供保证。本文首先以无强震观测记录为前提,研究地震矩、应力降、破裂速度、子断层尺寸、震源深度、断层走向、倾角和滑移角等8个震源参数在所有合理取值范围内对复合震源模型计算结果的影响程度;然后根据九寨沟地震观测数据确定适合的震源参数研究范围,并进行敏感性规律分析,在其他参数保持不变的条件下,仅改变单个参数变量,利用评价指标比较分析计算结果,总结震源参数对地震动计算的影响规律。
3.1 评价参数和评价指标为表征震源参数对台站NS和EW向峰值加速度(peak ground acceleration,PGA)的影响,用误差值E表示计算的PGA相对于观测的PGA的变化:
| $ E=\left|A_{\mathrm{OBS}}-A_{\mathrm{SYN}}\right| / A_{\mathrm{OBS}} \times 100 \% $ | (8) |
式中,AOBS为观测的PGA,ASYN为计算的PGA。
地震动强度主要用PGA、峰值速度或谱加速度等地震动参数表达。本文以PGA为例,根据王德才等[11]的参数敏感性分析模型,通过计算模型偏差和模型标准差讨论不同震源参数对PGA的影响。
用模型偏差B表征计算值和观测值之间的差异,偏差越大,计算值越偏离观测数据:
| $ B=\frac{1}{M} \sum\limits_{j=1}^M \ln \left(\frac{A_{\mathrm{OBS}}}{A_{\mathrm{SYN}}}\right) $ | (9) |
式中,M为总台站数。
用模型标准差S描述数据离散程度,标准差越大,数据波动性越强:
| $ S=\left\{\frac{1}{M} \sum\limits_{j=1}^M\left[\ln \left(\frac{A_{\mathrm{OBS}}}{A_{\mathrm{SYN}}}\right)-B\right]^2\right\}^{1 / 2} $ | (10) |
首先选取地震矩、应力降、破裂速度、子断层尺寸、震源深度、断层走向、倾角和滑移角等8个震源参数的最大合理取值范围,计算得到不同震源参数数值下台站NS和EW向的PGA,然后以模型偏差B和标准差S为衡量标准,分析8个震源参数对复合震源模型计算结果的影响程度。
地震矩根据Hanks等[12]提出的地震矩与矩震级的关系,在强震6~8级范围内取值计算,间隔为1×1018 Nm;应力降参考王振宇等[13]的取值范围10~200 bar,间隔为5 bar;断层的平均破裂速度约为剪切波速的0.6~0.9倍[14],本文选取此区间,并设定区间间隔为0.05;子断层尺寸取值分别为1 km×1 km、2 km×2 km、6 km×6 km、8 km×8 km和10 km×10 km;震源深度范围选定为0~30 km,取值间隔为1 km;断层走向、倾角和滑移角依据理论范围分别取0°~360°、0°~90°和-180°~180°,取值间隔分别为10°、5°和10°。
8个震源参数取值范围和梯度各不相同,本文通过式(9)和式(10)计算出相应PGA的偏差和标准差,然后将每个震源参数下PGA偏差、标准差的最大值及最小值作差,消除AOBS实测数据的影响,得到每个震源参数下PGA偏差和标准差的变化幅度,结果如图 5所示。由图 5可知,地震矩、应力降、破裂速度、子断层尺寸和震源深度对PGA偏差和标准差的影响明显,其中地震矩和应力降影响更突出;断层走向、倾角和滑移角对PGA偏差和标准差的影响极不明显。根据地震学理论,地震矩直接决定地震释放的能量大小,地震矩越大,地震波携带的能量越多,使得整体加速度计算值增加;应力降表示断层上某点破裂前后的应力强度变化,应力降越大,断层上释放的应力越多;破裂速度决定断层面圆形子震的发震时间,间接影响整个断层面的破裂过程;子断层尺寸的划分会对断层面上滑移量分布产生很大的影响;震级相同的地震,震源越浅,造成的破坏越严重。
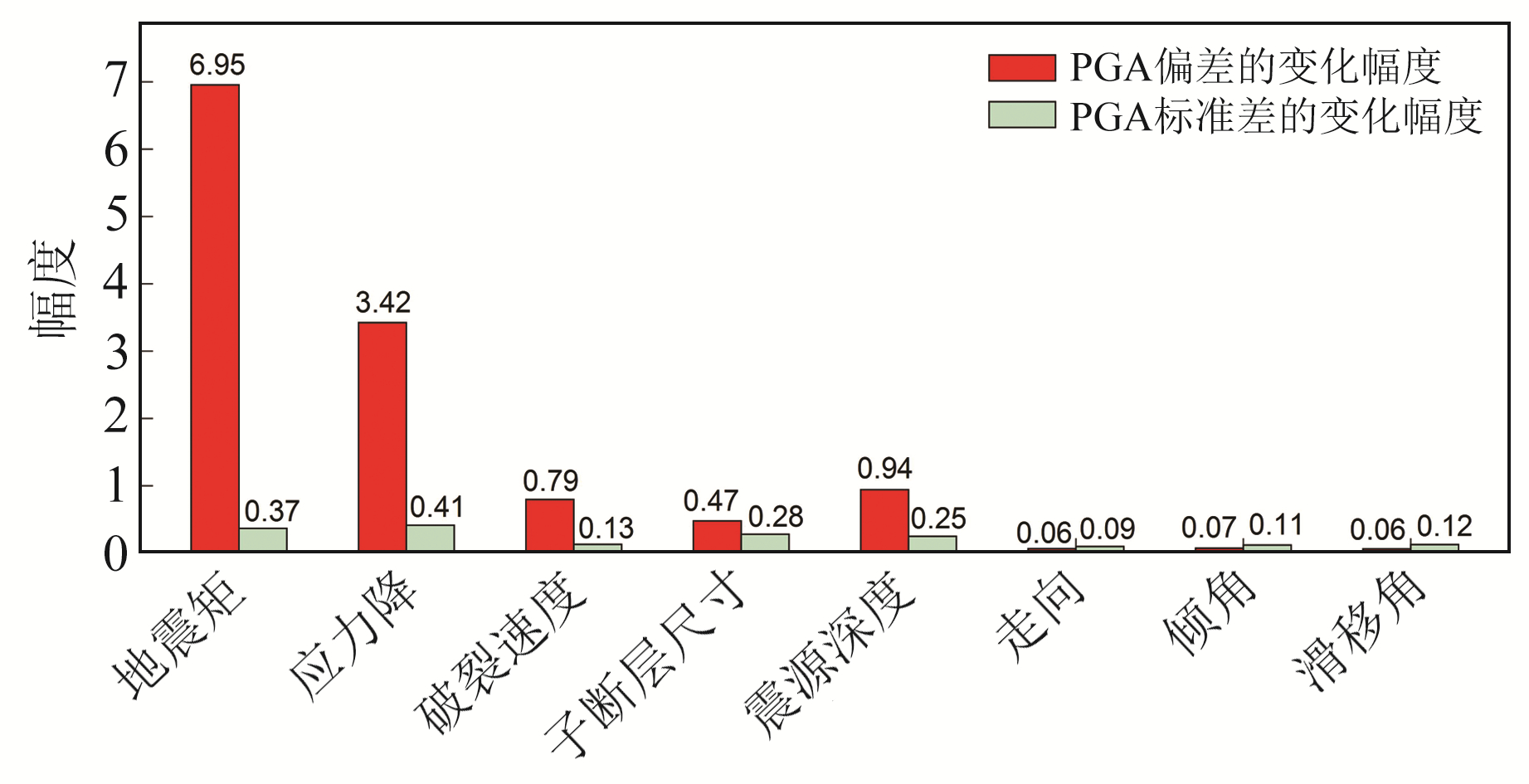
|
图 5 不同震源参数对PGA偏差和标准差的影响幅度 Fig. 5 The influence amplitude of different source parameters on PGA deviation and standard deviation |
基于8个震源参数的影响规律,结合表 1不同研究机构和众多学者[2-4, 8]提供的震源参数,确定九寨沟地震震源参数研究范围,进一步研究8个震源参数对九寨沟11个台站NS和EW向PGA的影响大小和规律,取值间隔如图 6所示。

|
图 6 不同震源参数对台站PGA的影响 Fig. 6 Influence of different source parameters on station PGA |
从图 6看出,地震矩、应力降、破裂速度、子断层尺寸和震源深度对台站PGA的影响大;断层走向、倾角和滑移角对台站PGA的影响小。说明在应用复合震源模型计算九寨沟地震时,即使8个震源参数取值范围有所限制,没有取到理论范围内的所有值,但其对计算结果的影响规律基本与图 5一致。
图 7为地震矩、应力降、破裂速度、子断层尺寸和震源深度等5个震源参数对九寨沟地震地震动模拟的影响规律,其中实心点表示本文取值。由表 3和图 7可知,受地震矩影响,PGA的偏差变化范围超过1,PGA的偏差和标准差随地震矩的增加而减小,其中PGA的偏差下降趋势近似为线性变化,地震矩为7×1018 Nm时,PGA的偏差基本为0,同时PGA的标准差也较小。应力降越大,台站整体PGA越大,PGA的偏差越小,应力降为40 bar时,PGA的偏差接近于0,这与俞瑞芳等[15]应用随机有限断层法得到PGA随着应力降增大而逐渐增加的结论类似。破裂速度越大,PGA的偏差越小,当破裂速度等于剪切速度0.8倍(2.96 km/s)时,偏差接近于0,此时标准差也最小,与傅磊等[16]应用随机有限断层法和李宗超等[4]应用经验格林函数法在地震模拟过程中选取的破裂速度与剪切速度的比例关系一致,PGA的偏差变化范围为0.9。子断层尺寸越小,PGA的偏差越小,最佳尺寸为2 km×2 km,此时标准差也为最小值,与Dang等[1]利用随机有限断层法的研究结论相同。震源深度在20 km处PGA的偏差几乎为0,同时标准差最小,随着震源深度的增加,PGA的偏差增长趋势变缓;而且如图 6所示,震源深度为25 km时,大部分台站的峰值加速度很小,与刘启方等[10]运用震源位错模型得到的研究结果相似。
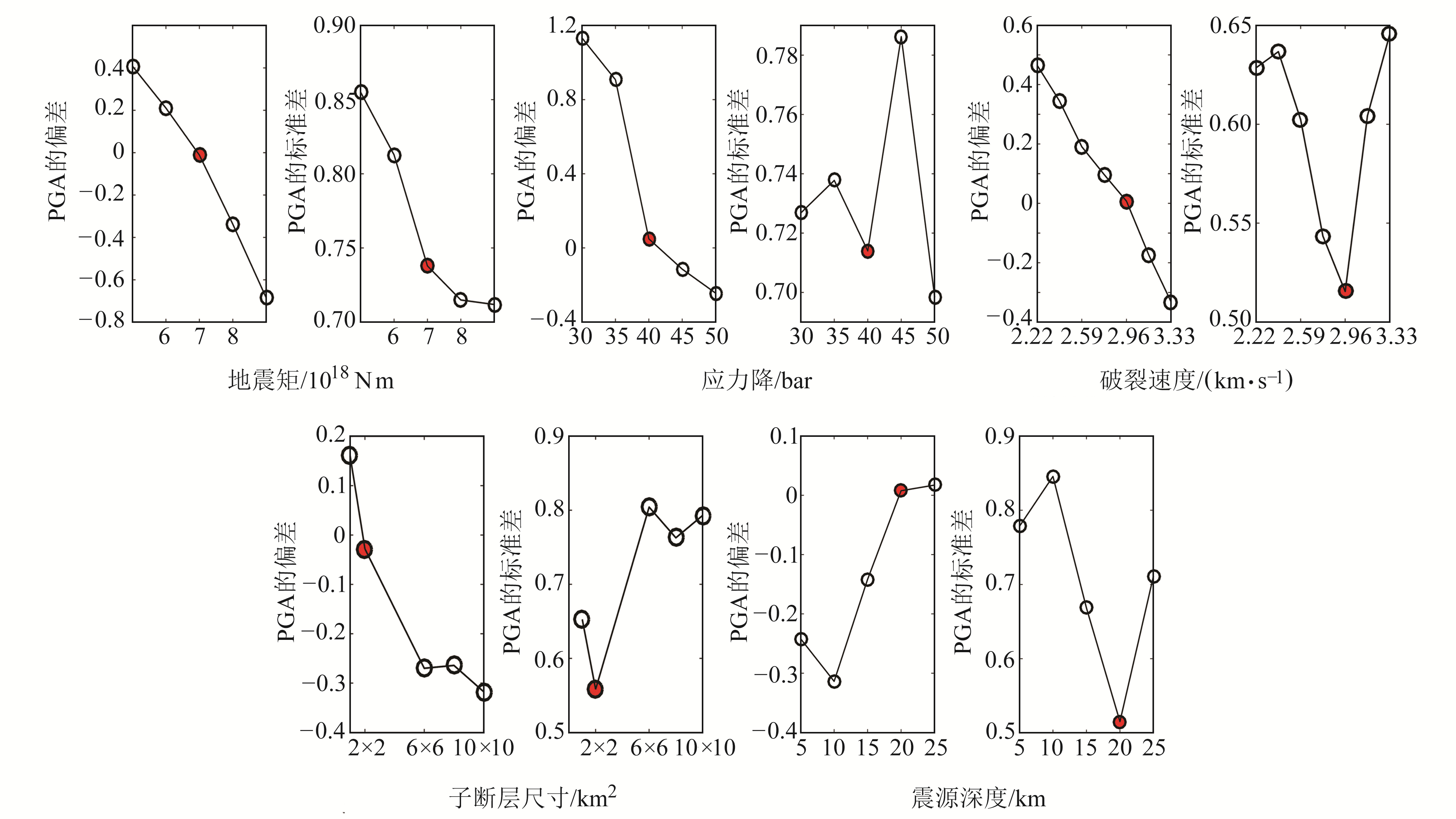
|
图 7 不同震源参数对PGA偏差和标准差的影响 Fig. 7 Influence of different source parameters on PGA deviation and standard deviation |
|
|
表 3 不同震源参数PGA偏差和标准差统计结果 Tab. 3 Statistical results of PGA deviation and standard deviation of different source parameters |
断层走向、倾角和滑移角中,PGA的偏差最大变化幅度为0.08,标准差最大变化幅度仅为0.1,对计算结果影响不明显,与王德才等[11]采用混合方法[17]和随机方法[18]研究的结果一致。
3.3 地震输入参数组合由上文分析结果可知,震源参数整体对PGA偏差影响幅度大,对标准差影响幅度相对较小,因此以PGA的偏差为主要衡量标准,标准差为次要标准,得到一组与观测记录拟合效果较好的震源参数。从表 1各机构提供的数据中选取地震矩、破裂速度、子断层尺寸、震源深度、断层走向、倾角和滑移角;应力降参考Sun等[3]的结果,品质因子Q(f)和高频衰减kappa值参考孟令媛等[9]的结果,具体数值如表 4所示。
|
|
表 4 九寨沟地震复合震源模型输入的震源物理参数 Tab. 4 Focal physical parameters inputted by the composite source model of the Jiuzhaigou earthquake |
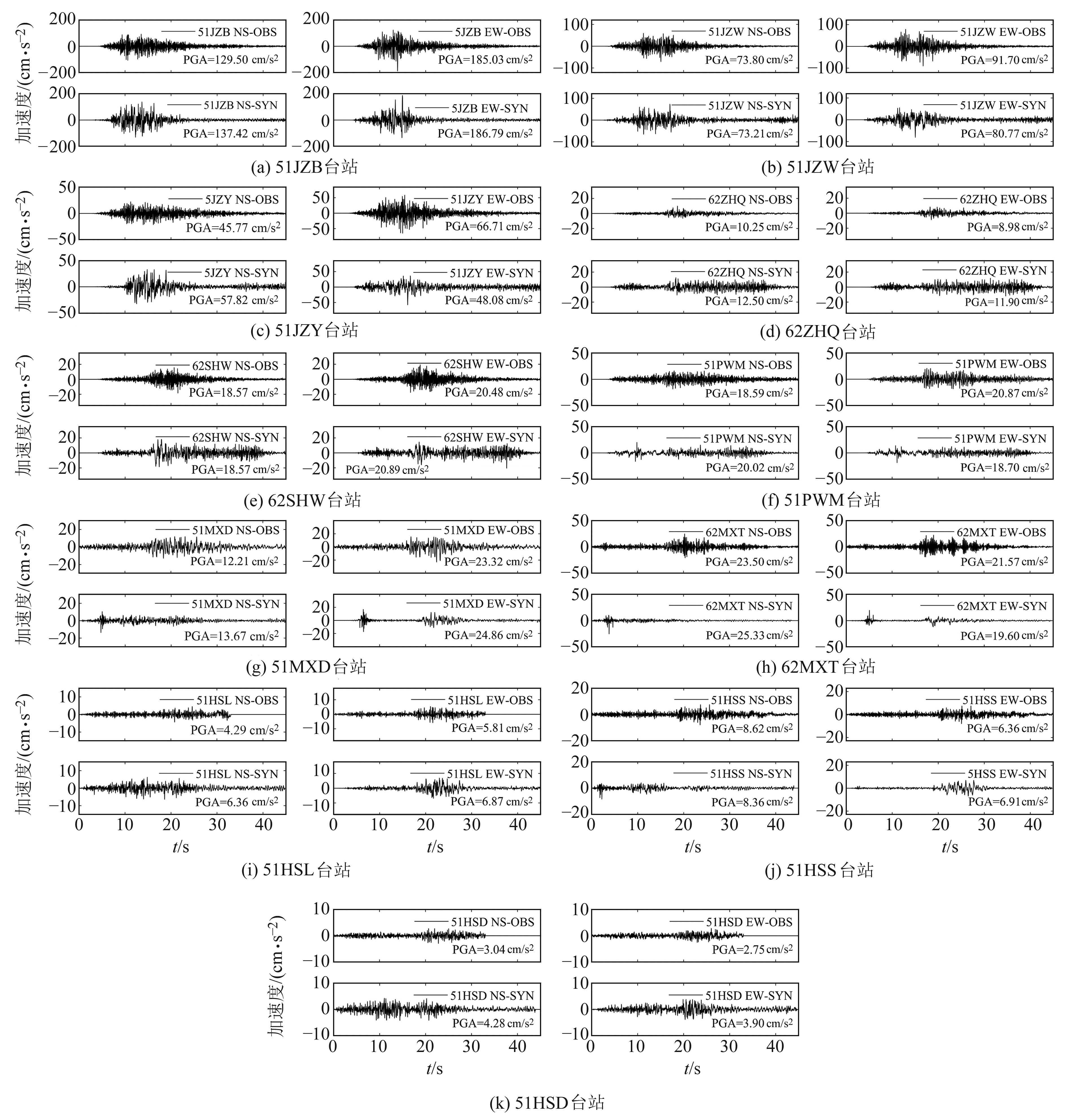
根据式(8)计算11个台站NS和EW向PGA的相对误差,并分别与Dang等[1]和李宗超等[4]的计算结果进行对比(图 8)。可以看出,11个台站NS和EW向PGA相对误差均小于50%。62SHW站NS和EW向PGA相对误差最小,均小于3%;51HSL站NS向、51HSD站NS和EW向PGA误差较大,且计算值均大于观测值,主要原因可能是台站震中距较大,导致传播过程中散射的复杂性增加,同时,台站局部山体地形引起的场地效应也会增加计算误差。11个台站NS和EW向PGA相对误差均在20%以内,说明所有台站PGA与实际数据相比误差小。与Dang等[1]和李宗超等[4]的计算结果相比,除李宗超等[4]51JZY站EW向、62ZHQ站NS向和62MXT站NS向外,本文各台站PGA相对误差均较优。为方便直观地进行地震动持时和波形对比,所有时程均截取45 s时间窗(图 9),台站加速度记录数据中最小PGA为2.75 cm/s2,为避免地震动持时出现零持时这种不合理状态,选取Bolt持时的阈值为0.5倍的PGA作为计算相对Bolt持时的阈值[19]。从图 9看出,个别台站误差较大,但大多数台站地震动持时基本保持一致。如图 10所示,合成反应谱整体变化趋势与观测反应谱一致,说明11个台站的峰值加速度、地震动持时和反应谱整体拟合效果较好,与观测数据较为符合。
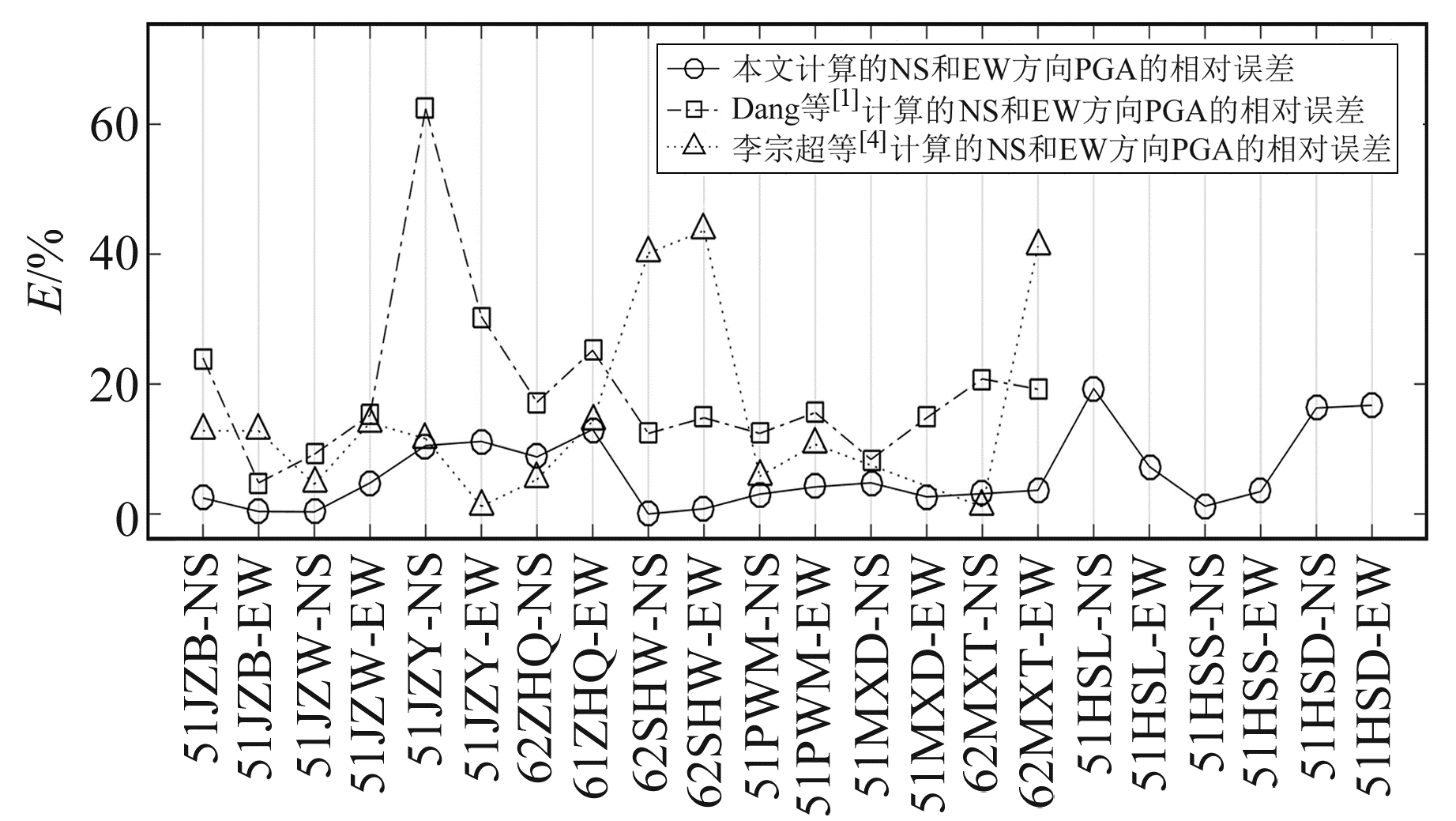
|
图 8 不同台站NS和EW向PGA的相对误差对比 Fig. 8 Comparison of relative errors of PGA in NS and EW directions at different stations |
|
图 9 不同台站NS和EW向加速度时程 Fig. 9 Time history of acceleration in NS and EW directions at different stations |

|
图 10 不同台站合成和观测加速度反应谱 Fig. 10 Synthetic and observed acceleration response spectra at different stations |
部分台站地震动三要素计算结果精度偏低的可能原因是:1)没有充分考虑地形因素对地震动的影响,部分台站如51HSL、51HSS和51HSD等位于山体上,山体地形的高度及底部延展距离对断层动力学破裂过程影响较大,进而影响到相应的地面地震动分布[20],山体的坡角、地震动入射角度会对山体地震动产生抑制作用,导致台站PGA变小[21];2)本文在计算地震动时采用各向同性散射模型,但实际地震波在地壳介质中的传播是各向异性的,而且随着传播路径的增加,散射的影响也会逐渐加强;3)有些震源参数的选取进行了简化,在地震动模拟过程中假定某些参数(如应力降和破裂速度)为常数,忽略了参数与时间和空间的相关性;4)多数台站低频段反应谱模拟结果高于观测值,可能是由于本文模型在破裂过程中没有考虑到圆形子震倾角的可变性,或是在合成格林函数中未纳入小尺度地壳非均匀性的散射效应[22]。
PGA是表征地震能量的重要指标之一,能够为建筑物抗震设防提供合理的参考依据。综合现有11个台站PGA的观测值和计算值可以得到九寨沟地震PGA空间分布特征,如图 11所示。由图 11可知,随着震中距增大,NS和EW向PGA从震源中心呈椭圆形向四周衰减扩散,长轴方向大致呈SW走向,这可能与断层破裂的方向性有关,且2个方向PGA最大值均出现在51JZB站;在51MXD和51PWM站之间有一个PGA值未连通的区域,可能是由于该区域缺少合适的台站记录所致。总体而言,PGA计算值和观测值的空间分布特征较为一致。

|
图 11 九寨沟地震PGA空间分布特征 Fig. 11 PGA spatial distribution characteristics of Jiuzhaigou earthquake |
1) 在最大合理变化范围内,相对于断层走向、倾角和滑移角,地震矩、应力降、破裂速度、子断层尺寸和震源深度对地震动计算结果影响较大。
2) 震源参数敏感性分析规律为九寨沟地震地震动模拟的参数选取提供了依据,进而得到一组合理的震源参数组合,同时能够获得九寨沟地区内任意一点PGA的变化区间。这一结论可以进一步推广到其他缺乏强震观测记录的场地,计算出该区域强度特征的上限值,为建筑物抗震设防提供依据。
3) 复合震源模型强地震动模拟了特定圆形子震在断层上的破裂过程、断层面上滑动位移的不均匀空间分布以及震源时间函数,计算结果可以再现九寨沟地震的地震动特征,模拟区域台站的地震动PGA、地震动持时、反应谱和PGA分布特征与观测值拟合较好,反应谱在高频段拟合精度更高。
| [1] |
Dang P F, Liu Q F, Song J. Simulation of the Jiuzhaigou, China, Earthquake by Stochastic Finite-Fault Method Based on Variable Stress Drop[J]. Natural Hazards, 2020, 103(2): 2 295-2 321 DOI:10.1007/s11069-020-04083-9
(  0) 0) |
| [2] |
周红. 基于NNSIM随机有限断层法的7.0级九寨沟地震强地面运动场重建[J]. 地球物理学报, 2018, 61(5): 2 111-2 121) (Zhou Hong. Reconstruction of Strong Ground Motion of Jiuzhaigou M7.0 Earthquake Based on NNSIM Stochastic Finite Fault Method[J]. Chinese Journal of Geophysics, 2018, 61(5): 2 111-2 121))
(  0) 0) |
| [3] |
Sun J Z, Yu Y X, Li Y Q. Stochastic Finite-Fault Simulation of the 2017 Jiuzhaigou Earthquake in China[J]. Earth, Planets and Space, 2018, 70(1): 128 DOI:10.1186/s40623-018-0897-2
(  0) 0) |
| [4] |
李宗超, 高孟潭, 陈学良, 等. 九寨沟MS7.0地震强地震动模拟及漳扎镇地震动强度预测[J]. 地球物理学报, 2019, 62(7): 2 567-2 581 (Li Zongchao, Gao Mengtan, Chen Xueliang, et al. Simulation of Ground Motion by the 2017 Jiuzhaigou MS7.0 Earthquake and Estimation of Ground Motion Intensity in the Zhangzha Town[J]. Chinese Journal of Geophysics, 2019, 62(7): 2 567-2 581)
(  0) 0) |
| [5] |
Zeng Y H, Anderson J G, Yu G. A Composite Source Model for Computing Realistic Synthetic Strong Ground Motions[J]. Geophysical Research Letters, 1994, 21(8): 725-728 DOI:10.1029/94GL00367
(  0) 0) |
| [6] |
Apsel R J, Luco J E. Apsel R J, Luco J E. On the Green's Functions for a Layered Half-Space. Part Ⅱ[J]. Bulletin of the Seismological Society of America, 1983, 73(4): 931-951 DOI:10.1785/BSSA0730040931
(  0) 0) |
| [7] |
Frankel A. High-Frequency Spectral Falloff of Earthquakes, Fractal Dimension of Complex Rupture, Bvalue, and the Scaling of Strength on Faults[J]. Journal of Geophysical Research: Solid Earth, 1991, 96(B4): 6 291-6 302 DOI:10.1029/91JB00237
(  0) 0) |
| [8] |
Anderson J G. The Composite Source Model for Broadband Simulations of Strong Ground Motions[J]. Seismological Research Letters, 2015, 86(1): 68-74 DOI:10.1785/0220140098
(  0) 0) |
| [9] |
孟令媛, 周龙泉, 臧阳. 九寨沟MS7.0地震震源参数及致灾特征初步分析[J]. 地球物理学进展, 2018, 33(6): 2 251-2 258 (Meng Lingyuan, Zhou Longquan, Zang Yang. Characteristics of Source Parameters, Observed Strong Ground Motion and Intensity of the Jiuzhaigou, Sichuan, MS7.0 Earthquake[J]. Progress in Geophysics, 2018, 33(6): 2 251-2 258)
(  0) 0) |
| [10] |
刘启方, 袁一凡, 金星. 断层附近地面地震动空间分布[J]. 地震学报, 2004, 26(2): 183-192 (Liu Qifang, Yuan Yifan, Jin Xing. Spatial Distribution of Near-Fault Ground Motion[J]. Acta Seismologica Sinica, 2004, 26(2): 183-192)
(  0) 0) |
| [11] |
王德才, 何骁慧. 地震动模拟过程中断层参数的敏感性分析[J]. 地震工程学报, 2016, 38(2): 212-218 (Wang Decai, He Xiaohui. Sensitivity Analysis of Fault Parameters during Ground Motion Simulation[J]. China Earthquake Engineering Journal, 2016, 38(2): 212-218)
(  0) 0) |
| [12] |
Hanks T C, Kanamori H. A Moment Magnitude Scale[J]. Journal of Geophysical Research: Atmospheres, 1979, 84(B5): 2 348-2 350 DOI:10.1029/JB084iB05p02348
(  0) 0) |
| [13] |
王振宇, 赵培培, 薄景山. 地震动随机模拟方法主要影响参数分析[J]. 世界地震工程, 2017, 33(3): 34-41 (Wang Zhenyu, Zhao Peipei, Bo Jingshan. Analysis for the Effects of Main Parameters on Ground Motions by Stochastic Simulation Method[J]. World Earthquake Engineering, 2017, 33(3): 34-41)
(  0) 0) |
| [14] |
Beresnev I A, Atkinson G M. Modelling Finite-Fault Radiation from the ωn Spectrum[J]. Bulletin of the Seismological Society of America, 1997, 87(1): 67-84
(  0) 0) |
| [15] |
俞瑞芳, 时洪涛, 孙吉泽, 等. 基于随机有限断层法的坝址地震动参数综合评价方法[J]. 土木工程学报, 2020, 53(7): 1-11 (Yu Ruifang, Shi Hongtao, Sun Jize, et al. Comprehensive Evaluation of Ground Motion Parameters for Dam Site Based on Stochastic Finite Fault Method[J]. China Civil Engineering Journal, 2020, 53(7): 1-11)
(  0) 0) |
| [16] |
傅磊, 李小军. 龙门山地区的kappa(κ0)模型及汶川MS8.0地震的强地震动模拟[J]. 地球物理学报, 2017, 60(8): 2 935-2 947 (Fu Lei, Li Xiaojun. The kappa(κ0) Model of the Longmenshan Region and Its Application to Simulation of Strong Ground-Motion by the Wenchuan MS8.0 Earthquake[J]. Chinese Journal of Geophysics, 2017, 60(8): 2 935-2 947)
(  0) 0) |
| [17] |
Graves R W, Pitarka A. Broadband Ground-Motion Simulation Using a Hybrid Approach[J]. Bulletin of the Seismological Society of America, 2010, 100(5A): 2 095-2 123
(  0) 0) |
| [18] |
Motazedian D. Stochastic Finite-Fault Modeling Based on a Dynamic Corner Frequency[J]. Bulletin of the Seismological Society of America, 2005, 95(3): 995-1 010
(  0) 0) |
| [19] |
马小燕, 周正华, 黄艳. 汶川地震地震动持时特性分析[J]. 地球科学前沿, 2019, 9(5): 390-397 (Ma Xiaoyan, Zhou Zhenghua, Huang Yan. Analysis of Ground Motion Duration Characteristics of Wenchuan Earthquake[J]. Advances in Geosciences, 2019, 9(5): 390-397)
(  0) 0) |
| [20] |
王铭锋, 郑傲, 于湘伟, 等. 局部山体地形对断层动力学破裂过程的影响研究[J]. 地震学报, 2018, 40(6): 737-752 (Wang Mingfeng, Zheng Ao, Yu Xiangwei, et al. Study on the Influence of Local Mountainous Topography to Fault Dynamic Rupture[J]. Acta Seismologica Sinica, 2018, 40(6): 737-752)
(  0) 0) |
| [21] |
王伟. 地震动的山体地形效应[D]. 哈尔滨: 中国地震局工程力学研究所, 2011 (Wang Wei. Study of Hill Topography Effect on Ground Motion[D]. Harbin: Institute of Engineering Mechanics, CEA, 2011))
(  0) 0) |
| [22] |
Zeng Y H, Anderson J G, Su F. Subevent Rake and Random Scattering Effects in Realistic Strong Ground Motion Simulation[J]. Geophysical Research Letters, 1995, 22(1): 17-20
(  0) 0) |
2. State Key Laboratory of Hydroscience and Engineering, 1 Qinghuayuan, Beijing 100089, China
 2022, Vol. 42
2022, Vol. 42


