EMD[1]和CEEMD[2]在GNSS坐标时间序列降噪过程中发挥着重要作用。但利用EMD、CEEMD进行降噪时,需要确定噪声和真实信号的界限,即需要确定分界IMF函数[3]。多数学者采用相关系数准则[4]和连续均方误差(consecutive mean squared error,CMSE)准则[3]确定分界IMF分量。然而,相关系数准则确定的模态分界点有时并不准确,且无法直接给出分界IMF分量[5];CMSE准则在连续的IMF分量的均方误差比较接近时难以判定信号与噪声的分界点[6]。
GNSS坐标时间序列会表现出明显的非线性变化,特别是垂向的季节性变化更加明显[7]。这种垂向坐标时间序列的季节性变化主要由各类地球物理效应和系统误差造成。对季节性信号的研究不仅有助于建立与维持动态地球参考框架,同时对研究板块构造运动和地球动力学过程也具有重要意义[8-9]。通过计算IMF分量的平均周期,找到符合季节性信号周期的IMF,即可将分解后代表季节信号和噪声的IMF分量进行分离。
因此,顾及到GNSS垂向坐标时间序列中的季节信号,本文采用IMF分量的平均周期作为CEEMD降噪过程中筛选噪声分量的准则,并与以CMSE和相关系数为筛选准则的CEEMD降噪方法进行对比。
1 降噪原理与分界准则 1.1 CEEMD降噪原理CEEMD算法的思路为:将一对互为相反数的正负白噪声作为辅助噪声加入原信号,以消除重构信号中残余的辅助白噪声,同时减少分解时所需的迭代次数,降低计算成本[2]。使用CEEMD将原信号分解为不同频率的IMF分量,可避免EMD模态混叠和端点效应问题,分解得到的IMF分量能更清晰地表达自身特性。根据GNSS信号时间序列噪声频率及周日重复的特点,可以认为噪声主要存在于高频分量中,而由CEEMD分解得到的IMF分量是根据频率从高到低排列的,因此噪声信号大部分出现在靠前的分量中。设
| $\begin{gathered} \hat{x}_k(t)=\sum_{j=k}^m c_j(t)+r_m(t) \\ k=2, \cdots, m-1 \end{gathered} $ | (1) |
式中,m为分解得到的IMF个数,cj为CEEMD分解得到的第j个IMF分量,rm为残差分量。
1.2 平均周期准则将IMF分量平均周期T[6]定义为每一个IMF序列相邻极大值(或极小值)点之间距离的平均值,即
| $ \begin{aligned} \bar{T}_j=& \frac{1}{s} \sum\limits_{i=1}^s\left\{\operatorname{LocalMax}\left[c_j(t)\right]_i-\right.\\ &\left.\operatorname{LocalMax}\left[c_j(t)\right]_{i-1}\right\} \end{aligned} $ | (2) |
式中,LocalMax[cj]0为0,Tj为第j个IMF分量的平均周期,s为该IMF分量的极大或极小值点的个数。
季节性信号表现为周年或半周年形式[9],且IMF分量中的半周年分量周期并不一定为180 d。因此,为顾及周年和半周年信号,本文设定平均周期T的阈值为120 d,即平均周期小于120 d的IMF分量为噪声信号,记第1个满足该条件的IMF分量为分界点。
1.3 降噪效果评价指标引入RMS、半周年振幅、幂律噪声、速度不确定度等4个指标来评价平均周期准则、CMSE准则和相关系数准则的CEEMD方法的降噪效果。
研究表明,白噪声加幂律噪声模型可作为分析GNSS垂向坐标时间序列的最优噪声模型[10]。因此本文在白噪声和幂律噪声组合的噪声模型下,利用极大似然估计方法[11]求解降噪前后GNSS垂向坐标时间序列的模型参数,得到测站的半周年振幅、幂律噪声和速度不确定度。
| $ \begin{gathered} y(t)=a+v\left(t-t_R\right)+\sum\limits_{k=1}^{n_F} s_k \cos \left(\omega_k t+\varphi_k\right)+ \\ \sum\limits_{j=1}^{n_j} b_j H\left(t-t_j\right)+\varepsilon(t) \end{gathered} $ | (3) |
式中,y(t)为测站在t时刻下的位移,tR为参考时间,a为截距,v为测站运动速度,nF为频率个数,通常用来拟合季节性变化,sk和φk分别为频率ωk的振幅和相位,本文只考虑周年项和半周年项(k=1, 2),nJ为出现阶跃的次数,bj为各种原因引起的阶跃,H为Heaviside阶跃函数,ε(t)为随机过程。
2 实验数据与预处理选取中国地壳运动观测网络227个(图 1)GNSS测站的垂向时间序列进行降噪分析,其中,171个测站观测时间为2010.33~2020.99年,25个测站观测时间为2011.01~2020.99年,19个测站观测时间为2012.00~2019.75年,4个测站观测时间为2012.31~2020.99年,其余测站的观测时间见表 1。所有测站观测数据已由GAMIT/GLOCK软件进行基线解算和约束平差处理。
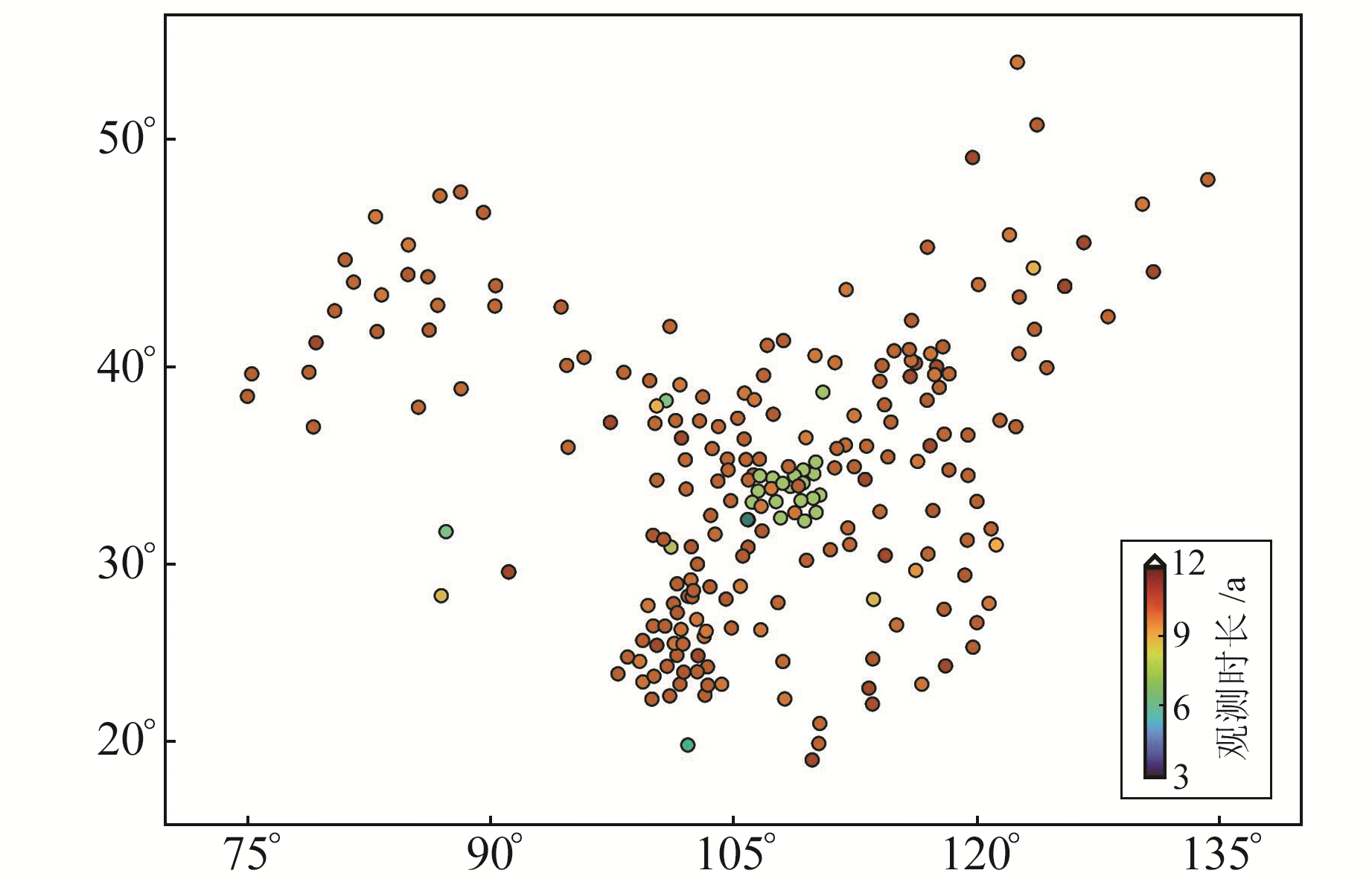
|
图 1 GNSS站分布和观测时长 Fig. 1 Distribution and observation durations of GNSS stations |
|
|
表 1 其余测站的观测时间 Tab. 1 Observation time of other stations |
上述坐标时间序列中仍存在由环境、设备、数据处理策略等因素引起的粗差和数据缺失,在进行降噪前,需要进行数据预处理[11]。首先基于四分位距统计量识别和剔除粗差,然后采用分段三次Hermite插值法进行插值[12],补全序列中缺失的数据。
3 实验与分析以FJWY站为例,图 2为3种方法降噪后的时间序列。图中,raw为降噪前的结果,CEEMD-T、CEEMD-E、CEEMD-R分别为以平均周期、连续均方误差和相关系数为准则的CEEMD降噪方法所得结果。
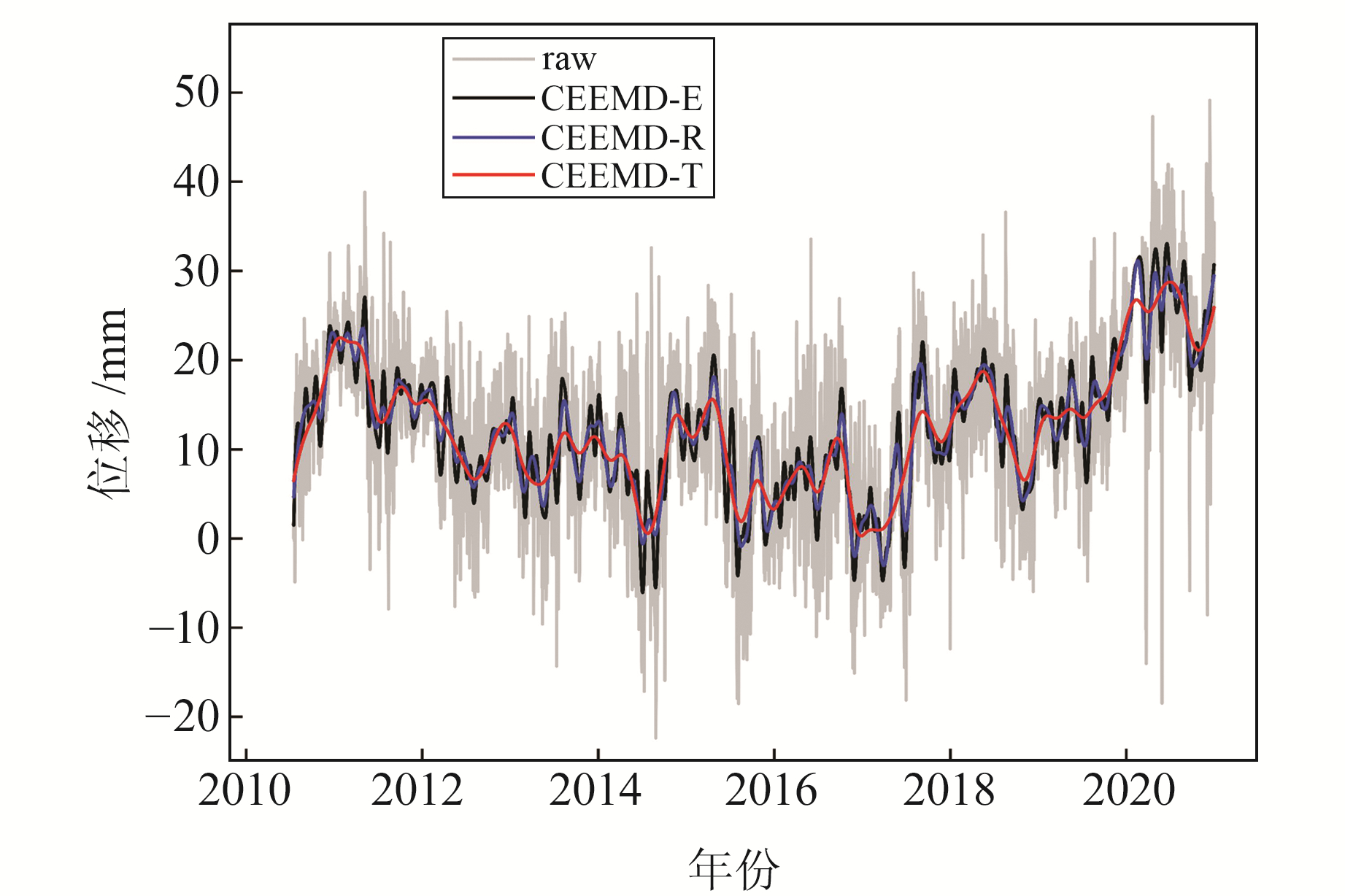
|
图 2 FJWY站降噪后时间序列 Fig. 2 Denoised time sequence at FJWY station |
GNSS垂向坐标时间序列中的季节信号主要包括周年和半周年季节信号,反映地表水文变化、大气等地球物理效应对地表形变监测的影响,因此降噪过程中剔除季节信号的现象,即被认为是过度降噪。本文通过计算降噪前后GNSS垂向坐标时间序列的半周年振幅,判断3种方法是否会造成过度降噪,结果见图 3。由图可见,CEEMD-T方法降噪后的序列与原序列的半周年振幅值较为符合,半周年振幅值损失较小,差值稳定在一定范围,表明CEEMD-T方法对原序列中的半周年信号保留较好,造成半周年振幅损失的部分原因是噪声的扣除提高了其精度。而经CEEMD-E和CEEMD-R方法降噪后,分别存在24个和79个测站的半周年振幅的改正率高于90%,表明这2种方法分别有10.57%和34.80% 的测站出现过度降噪现象。
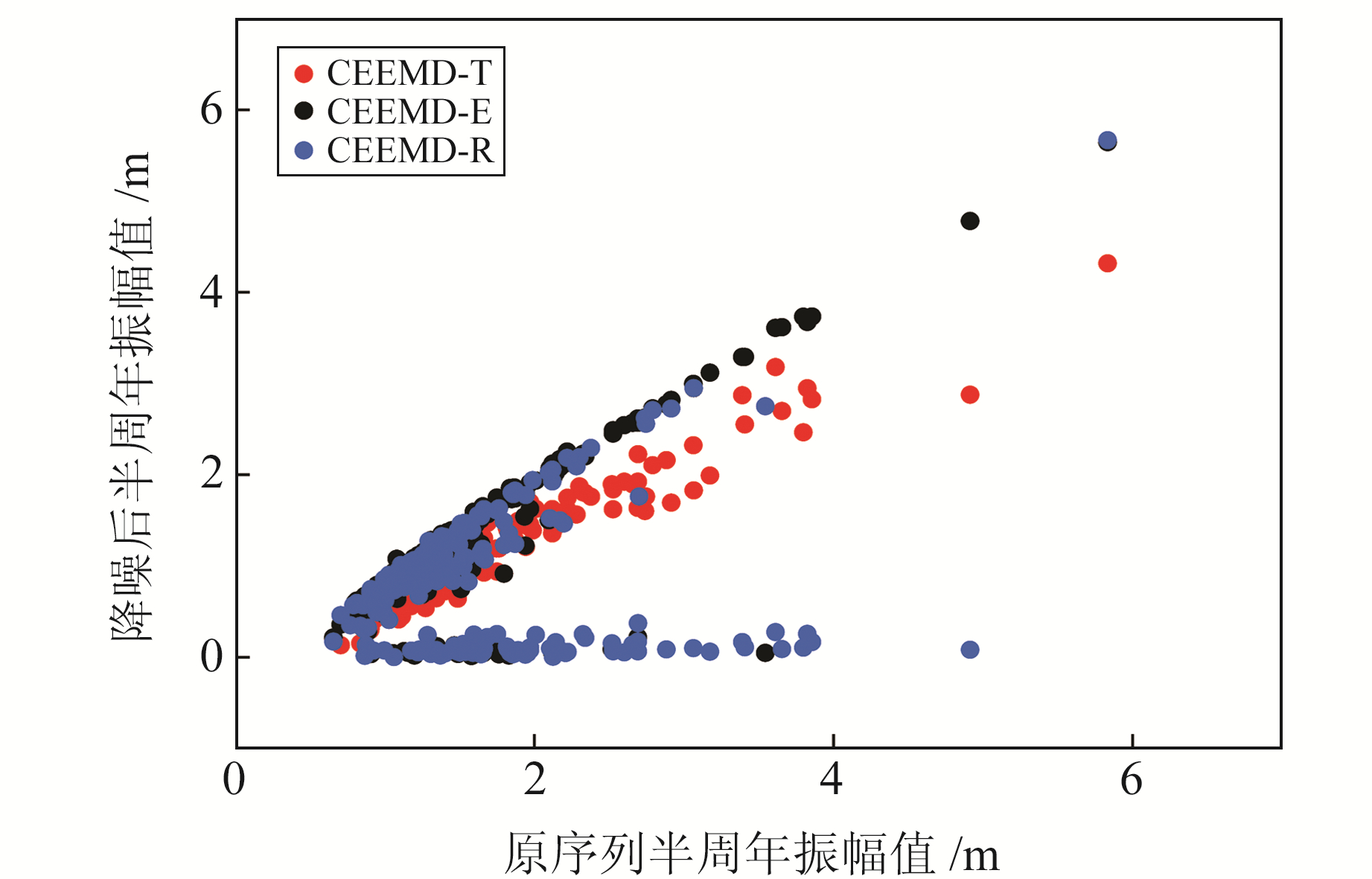
|
图 3 各测站降噪后时间序列 Fig. 3 The time sequence of each station after denoising |
剔除过度降噪的站点,CEEMD-E方法降噪后的时间序列与原序列更为符合,甚至在许多站点上与原序列完全一致。因此,为进一步对比3种方法的降噪效果,剔除过度降噪的100个测站,对剩余127个测站进行分析。
3.2 RMS改正降噪前后127个测站的RMS改正率分布见图 4。由图可得,经CEEMD-T降噪后的127个GNSS测站的平均RMS改正率为19.13%,比CEEMD-E、CEEMD-R的结果分别提高4.72%、3.36%。CEEMD-T、CEEMD-E、CEEMD-R三种方法降噪前后RMS改正率介于0%~20%的比例分别为49.61%、80.32%、64.57%,介于20%~40%的比例分别为49.60%、19.68%、35.43%。CEEMD-T方法的RMS改正率最高可以达到40.42%,而CEEMD-E、CEEMD-R方法的RMS改正率最大值分别为30.82%、27.49%。以上结果表明,CEEMD-T方法对优化RMS的效果最佳。

|
图 4 127个GNSS测站的RMS改正率分布 Fig. 4 Distribution of RMS change rate of 127 GNSS stations |
降噪前后时间序列的幂律噪声值见图 5。由图可见,CEEMD-T方法对幂律噪声的剔除效果优于其他2种方法,能大幅度剔除所有站点序列中的幂律噪声,降噪后幂律噪声值均在5 mm/a0.21以下。CEEMD-R方法效果较差,降噪后大部分幂律噪声值在1~10 mm/a0.21波动,其中,QHTR站降噪后的幂律噪声值高达13.09 mm/a0.21。CEEMD-E方法效果最差,大部分测站降噪后幂律噪声值也在1~10 mm/a0.21波动,其中,SCGU站甚至没有起到剔除效果。CEEM-T、CEEMD-E、CEEMD-R三种方法降噪后幂律噪声平均值由18.91 mm/a0.21分别降至2.21 mm/a0.21、4.27 mm/a0.21、3.55 mm/a0.21,其平均改正率分别为88.29%、77.73%、81.22%。以上结果表明,采用CEEMD-T方法能有效、稳定地剔除GNSS垂向坐标序列中的幂律噪声,改正率较其他2种方法分别提高10.56%、7.07%。
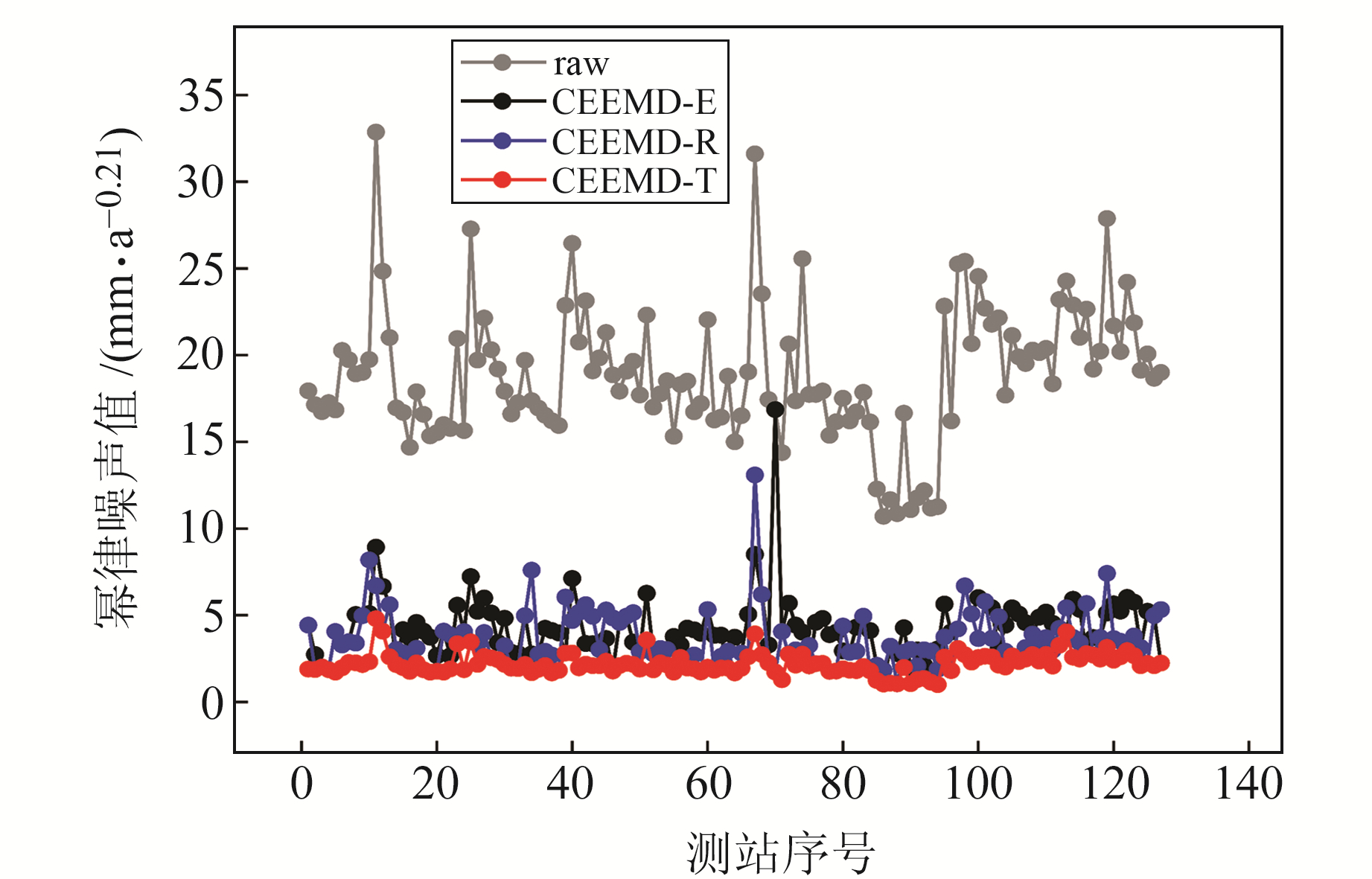
|
图 5 127个GNSS测站降噪前后时间序列的幂律噪声值 Fig. 5 Power law noise values of the time sequence before and after denoising of 127 GNSS stations |
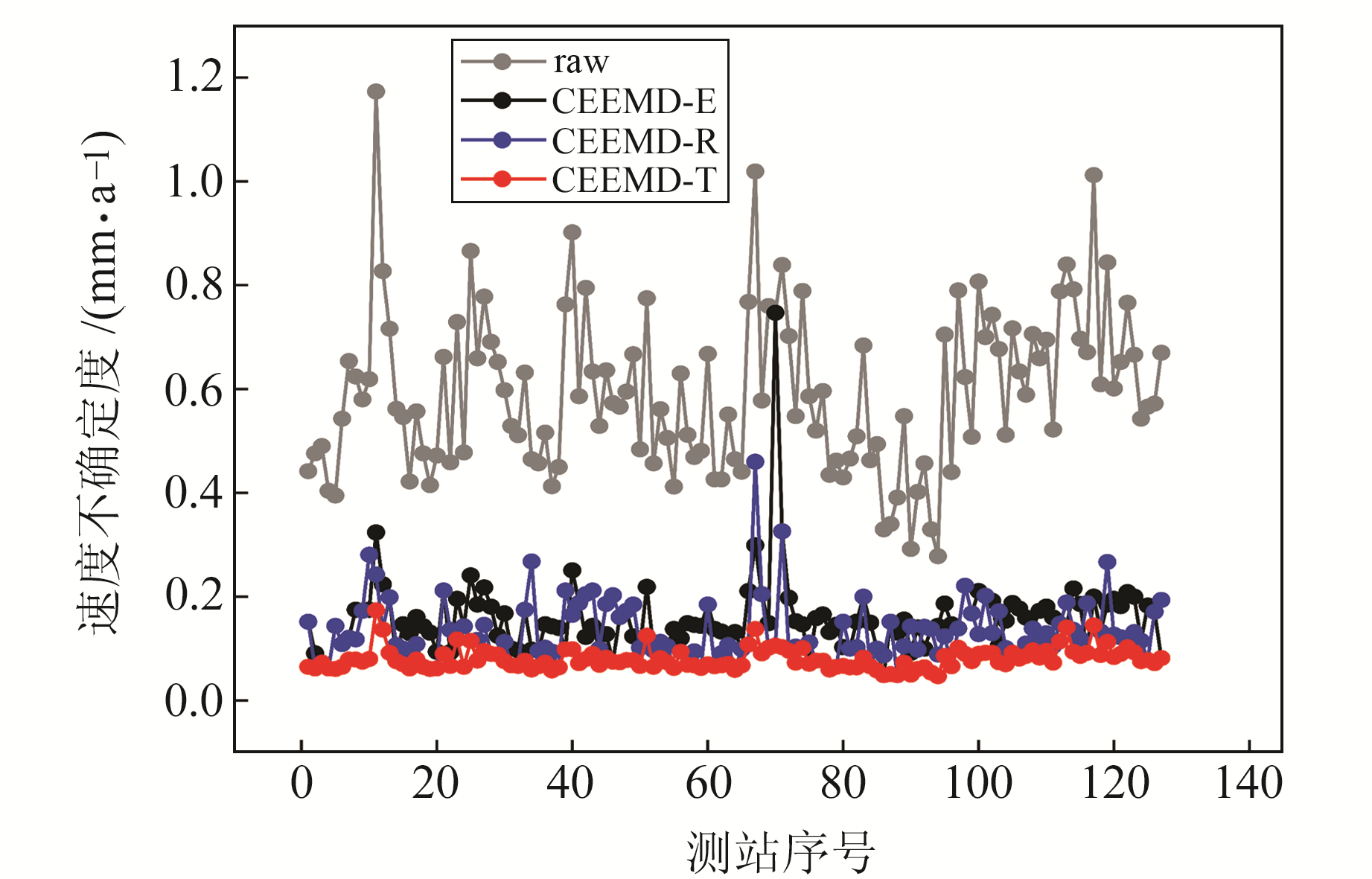
图 6为127个GNSS测站降噪前后时间序列的速度不确定度。由图可见,相比于其他2种方法,CEEMD-T方法能更好地改正所有站点序列的速度不确定度,降噪后速度不确定度均降低至0.2 mm/a以下,平均速度不确定度由0.60 mm/a降至0.08 mm/a,平均改正率为86.46%。CEEMD-R方法除在QHTR站上速度不确定度为0.46 mm/a外,其余测站降噪后速度不确定度在0~0.3 mm/a范围,平均改正率为78.13%。CEEMD-E方法对速度不确定度的改善效果最差,测站降噪后速度不确定度在0~0.3 mm/a波动,但在大多数测站上的改正效果不如其他2种方法,且在SCGU站上同样没有起到改正效果,其速度不确定度平均改正率为73.72%。综上,CEEMD-T方法改正率较其他2种方法分别提高8.33%、12.74%,可以稳定、显著地降低时间序列的速度不确定度。
|
图 6 127个GNSS测站降噪前后序列的速度不确定度 Fig. 6 The velocity uncertainty of the time sequence before and after denoising of 127 GNSS stations |
通过上述分析可知,CEEMD-T方法降噪效果优于CEEMD-E和CEEMD-R方法。CEEMD-E和CEEMD-R方法降噪不完全且不稳定,获得的降噪信号更接近带噪声的原始信号。这能在一定程度上解释去除过度降噪站点后,CEEMD-E方法降噪后的半周年振幅与原序列更吻合、在部分测站上与原序列完全一致的现象。
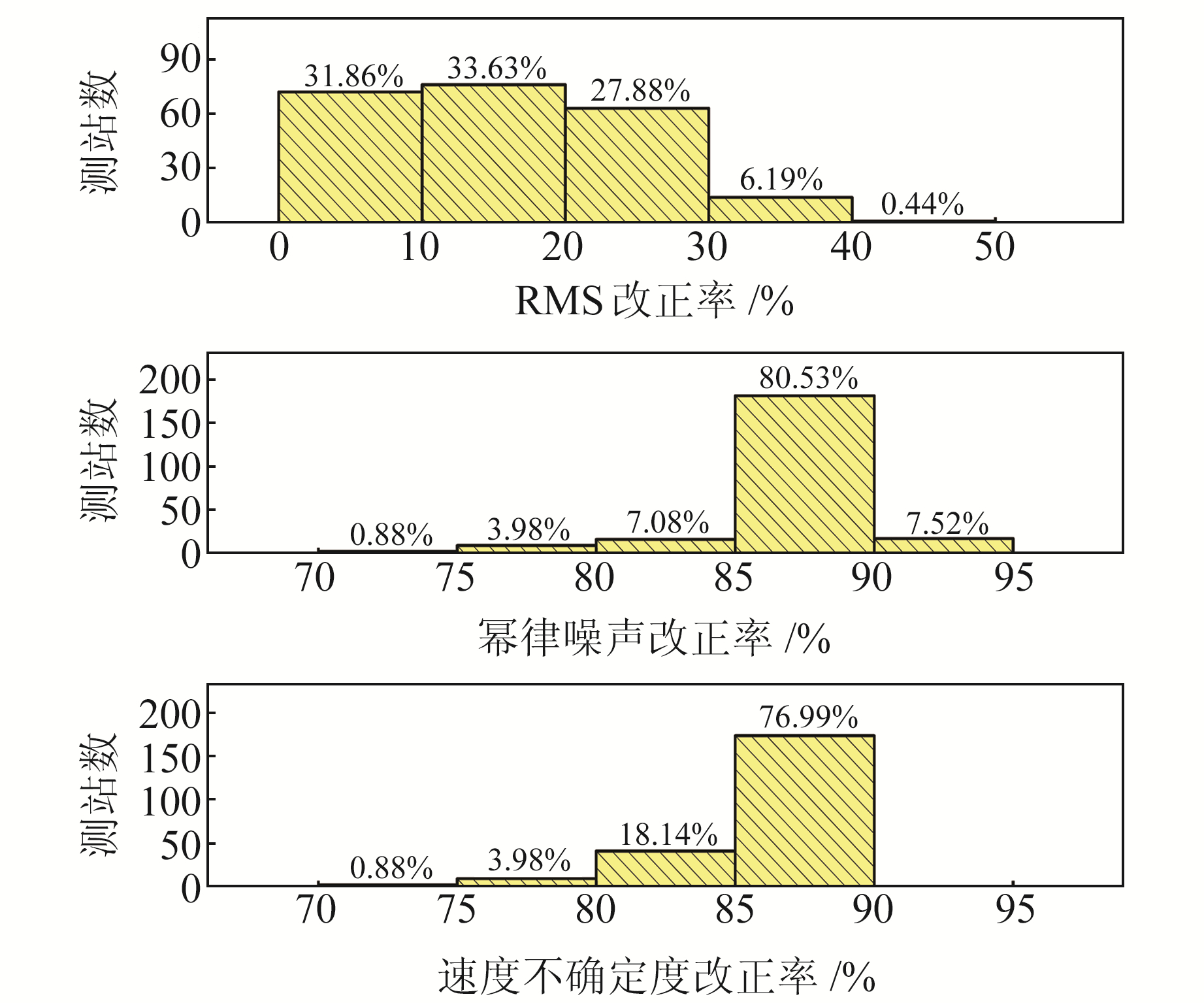
3.4 CEEMD-T结果分析对CEEMD-T方法得到的RMS、幂律噪声、速度不确定度的改正率分布进行分析,结果见图 7。由图可见,在227个测站上,RMS改正率在0%~20%范围的测站比例为65.49%,在20%~40%范围的比例为34.07%,平均改正率为15.63%。87.61%的测站的幂律噪声改正率介于80%~90%之间,同时其平均改正率达到87.41%。速度不确定度的平均改正率为85.57%,且超过95%的测站的速度不确定度改正率高于80%。综上,CEEMD-T方法在所有测站均适用,对GNSS垂向坐标时间序列的RMS、幂律噪声、速度不确定度均有较好的改正效果。
|
图 7 227个GNSS测站降噪前后时间序列各指标改正率分布 Fig. 7 The correction rate distribution of each indicator of time sequence of 227 GNSS stations before and after denoising |
本文提出一种顾及GNSS坐标时间序列中季节信号的CEEMD降噪方法CEEMD-T,并通过降噪前后的RMS值、幂律噪声值、速度不确定度等指标进行降噪效果分析。结果表明,CEEMD-T方法能够很好地保留GNSS测站垂向坐标时间序列中的半周年振幅,不会出现过度降噪的现象,具有良好的稳健性。
| [1] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1 971): 903-995
(  0) 0) |
| [2] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156 DOI:10.1142/S1793536910000422
(  0) 0) |
| [3] |
Boudraa A O, Cexus J C. EMD-Based Signal Filtering[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(6): 2 196-2 202 DOI:10.1109/TIM.2007.907967
(  0) 0) |
| [4] |
张双成, 李振宇, 何月帆, 等. GNSS高程时间序列周期项的经验模态分解提取[J]. 测绘科学, 2018, 43(8): 80-84 (Zhang Shuangcheng, Li Zhenyu, He Yuefan, et al. Extracting of Periodic Component of GNSS Vertical Time Series Using EMD[J]. Science of Surveying and Mapping, 2018, 43(8): 80-84)
(  0) 0) |
| [5] |
鲁铁定, 钱文龙, 贺小星, 等. 一种确定分界IMF分量的改进EMD方法[J]. 大地测量与地球动力学, 2020, 40(7): 720-725 (Lu Tieding, Qian Wenlong, He Xiaoxing, et al. An Improved EMD Method for Determining Boundary IMF[J]. Journal of Geodesy and Geodynamics, 2020, 40(7): 720-725 DOI:10.14075/j.jgg.2020.07.012)
(  0) 0) |
| [6] |
张恒璟, 程鹏飞. 基于EEMD的GPS高程时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2014, 34(2): 79-83 (Zhang Hengjing, Cheng Pengfei. Noise Recognition and Extraction of GPS Height Time Series Based on EEMD[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 79-83)
(  0) 0) |
| [7] |
Dong D, Fang P, Bock Y, et al. Anatomy of Apparent Seasonal Variations from GPS-Derived Site Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B4)
(  0) 0) |
| [8] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报: 信息科学版, 2018, 43(12): 2 112-2 123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 112-2 123)
(  0) 0) |
| [9] |
明锋, 杨元喜, 曾安敏, 等. 中国区域IGS站高程时间序列季节性信号及长期趋势分析[J]. 中国科学: 地球科学, 2016, 46(6): 834-844 (Ming Feng, Yang Yuanxi, Zeng Anmin, et al. Analysis of Seasonal Signals and Long-Term Trends in the Height Time Series of IGS Sites in China[J]. Science China: Earth Sciences, 2016, 46(6): 834-844)
(  0) 0) |
| [10] |
Hao M, Freymueller J T, Wang Q L, et al. Vertical Crustal Movement around the Southeastern Tibetan Plateau Constrained by GPS and GRACE Data[J]. Earth and Planetary Science Letters, 2016, 437: 1-8
(  0) 0) |
| [11] |
Bos M S, Fernandes R M S, Williams S D P, et al. Fast Error Analysis of Continuous GNSS Observations with Missing Data[J]. Journal of Geodesy, 2013, 87(4): 351-360
(  0) 0) |
| [12] |
安云飞. 一种用于BDS-3接收机的分段Hermite插值方法[J]. 全球定位系统, 2020, 45(4): 95-100 (An Yunfei. A Piecewise Hermite Interpolation Method for BDS-3 Receiver[J]. GNSS World of China, 2020, 45(4): 95-100)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


