2. 中国测绘科学研究院, 北京市莲花池西路28 号, 100036
常用的GNSS高程方向去噪方法有Kalman滤波[1]、小波去噪[2-3]、经验模态分解(EMD)及其改进算法[4-7]等。但这几种方法都存在不足:Kalman滤波在处理非线性时间序列时效果不佳;小波去噪在设置阈值时只考虑了高频噪声的影响,对于低频噪声的去噪效果并不理想[8];CEEMDAN算法舍弃高频分量,保留低频分量,容易丢失有用信息且忽略了低频分量中包含的噪声。小波包多阈值分解基于频率高低分段选取合适的阈值,能够高效剔除各频段的噪声,同时保留高频段中的有用信息[9]。
基于以上研究,本文结合CEEMDAN和小波包多阈值去噪的优势,引入一种CEEMDAN+小波包多阈值方法对GNSS高程时间序列进行去噪。
1 算法原理 1.1 CEEMDAN算法原理CEEMDAN算法原理如下[10]:
1) 求出第1阶IMF分量IMF1。假设待分解信号为xt,加入的高斯白噪声为vti,则第i次分解信号为:
| $ X_t^i=x_t+v_t^i $ | (1) |
式中,i=1, 2…N。用EMD算法分解第i次信号Xti得到相应的IMF1i:
| $ \mathrm{IMF}_1=\frac{1}{N} \sum\limits_{i=1}^N \mathrm{IMF}_1^i $ | (2) |
残差为:
| $ r_1^t=x_t-\mathrm{IMF}_1 $ | (3) |
2) 计算IMF2,将残差r1t当作待分解信号,按照步骤1)进行分解,得到IMF2:
| $ \mathrm{IMF}_2=\frac{1}{N} \sum\limits_{i=1}^N \mathrm{IMF}_1^i $ | (4) |
残差为:
| $ r_2^t=r_1^t-\mathrm{IMF}_2 $ | (5) |
3) 按照上述2个步骤进行分解,直到待分解信号只有2个极值点,即为单调函数时停止计算,此时CEEMDAN中原始待分解信号可表示为:
| $ x_t=\sum\limits_{i=1}^N \mathrm{IMF}_i+r_n^t $ | (6) |
小波包多阈值变换包括小波包分解、阈值处理、小波重构等3个步骤[11]。最优小波基、最佳分解层数和小波包去噪阈值的选取是小波包分解的关键因素。本文选择较常用的dbN和symN小波基函数。分解层数的选择对小波包去噪效果尤为重要,任何信号都存在一个去噪效果最好的分解层数,通常分解层数越大,噪声和信号表现的不同特性越明显,越有利于二者的分离;但分解层数越大,重构信号失真越严重,会在一定程度上影响去噪效果。常用信噪比(SNR)和均方根误差(RMSE)综合确定分解层数:
| $ \mathrm{SNR}=10 \lg \left(\sum\limits_{i=1}^m x^{\prime}(i)^2 / \sum\limits_{i=1}^m\left(x(i)-x^{\prime}(i)\right)^2\right) $ | (7) |
| $ \mathrm{RMSE}=\sqrt{\sum\limits_{i=1}^m\left(x(i)-x^{\prime}(i)\right)^2 / m} $ | (8) |
式中,x(i)为原始信号,x′(i)为降噪后的信号,m为信号长度。RMSE反映去噪后信号与原始信号之间的区别,RMSE越小则信号去噪效果越好;SNR反映信号与噪声的比例,重构信号的信噪比越高则信号的重构效果越好。
小波包多阈值去噪方法可根据频率的高低选择阈值,避免了单阈值去噪不能充分考虑信号与噪声分布、极易去掉中高频信号中有用信息、产生过度去噪的缺点。目前小波包分解常用的阈值准则有固定阈值(sqtwolog)准则、自适应阈值(rigrsure)准则与极大极小阈值(minimaxi)准则。sqtwolog准则是将小波包系数全部置0,能够较强地去除噪声,适合处理高频信号;rigrsure准则是基于无偏似然估计原理的自适应阈值准则,仅将部分系数置0,适合处理中低频信号;minimaxi准则是固定形式的阈值准则,是一种较为保守的处理方法,适合处理中低频信号。因此,本文在GNSS高程时间序列去噪时,采用rigrsure准则处理低频段,采用minimaxi准则处理中频段,采用sqtwolog准则处理高频段[12]。对于阈值函数类型,选取最常用的软阈值函数。本文去噪流程见图 1。

|
图 1 本文去噪流程 Fig. 1 Denoising flow chart in this paper |
采用MATLAB开展仿真实验。因高程时间序列季节性变化近似于正弦曲线,且包含周期项、半周期项和趋势项等信息,因此将y=6sin(0.01t)+2cos(0.03t)-0.005t+f(t)+w(t)作为原始信号,其中,f为有色噪声,w为白噪声,信号长度为3 650。根据高程时间序列的噪声特点,将有色噪声振幅设置为白噪声振幅的2倍。利用CEEMDAN对信号进行分解,在添加高斯白噪声时,为削弱添加的白噪声对降噪结果的影响,设置整体平均次数为100,添加的白噪声信噪比为0.2[13]。信号、添加的白噪声和有色噪声分别如图 2(a)~2(c)所示,加入噪声后的混合信号如图 2(d)所示。

|
图 2 仿真实验的模拟信号 Fig. 2 The analog signal used in the simulation experiment |
利用CEEMDAN分解得到10个频率逐渐降低的IMF分量和1个残余项(图 3)。从图 3看出,随着信号分解层数的增加,噪声逐渐减少。

|
图 3 CEEMDAN分解仿真信号 Fig. 3 Decomposition of simulation signal using CEEMDAN |
单独使用CEEMDAN去噪时,利用分界点将IMF分为噪声IMF和信号IMF。然而,在噪声IMF中仍有部分有用信息,在信号IMF中也包含部分噪声。为克服该缺点,本文不进行信号与噪声分界点的判断,而是采用小波包多阈值法对每个IMF分量进行小波包多阈值去噪。首先计算每个IMF分量中的根节点能量占IMF总能量的百分比,根据能量不同将节点分为低、中、高频3个部分,然后分别采用rigrsure、minimaxi和sqtwolog准则进行数据处理。
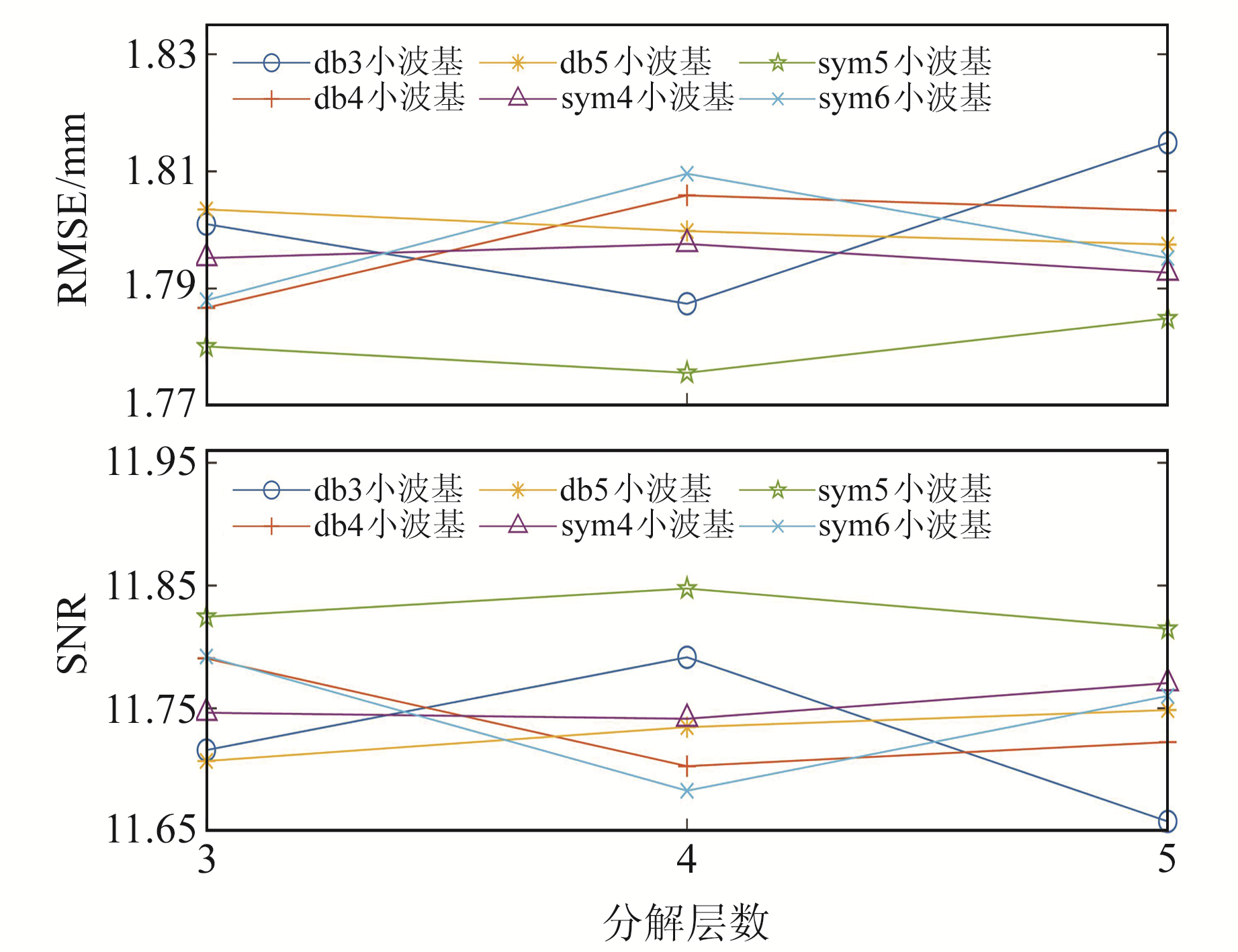
在利用小波包多阈值去噪时,选择对称性与正则性较好的sym小波(sym4、sym5、sym6)和db小波(db3、db4、db5)作为小波基函数,分解层数定为3、4、5层。利用RMSE、SNR评价最终降噪结果。经过多次对比实验(图 4),发现小波基选择sym5、分解层数为4层时得到的RMSE最小,SNR最大,说明此时小波包多阈值去噪效果最优。
|
图 4 利用RMSE和SNR判断最佳小波基与分解层数 Fig. 4 Using RMSE and SNR to determine the best wavelet basis and the number of decomposition layers |
利用小波包多阈值去噪对各IMF分量去噪,将去噪后的IMF分量与残余项进行重构,得到去噪后的信号,结果见图 5。

|
图 5 CEEMDAN+小波包多阈值去噪结果和噪声 Fig. 5 CEEMDAN and wavelet packet multi-threshold denoising results and noise |
为验证本文方法的去噪效果,分别采用本文方法(CEEMDAN+小波包多阈值)、EMD、CEEMDAN、小波去噪和小波包多阈值去噪分析仿真信号,结果见图 6。选择SNR、RMSE评价5种方法的降噪效果,结果见表 1。

|
图 6 5种去噪方法对比 Fig. 6 Comparison of five denoising methods |
|
|
表 1 去噪效果比较 Tab. 1 Comparison of denoising effect |
从图 6可以看出,5种方法均能对模拟信号去噪,但EMD去噪结果过于平缓,丢失了部分信息;与小波包多阈值去噪、小波去噪、CEEMDAN去噪相比,CEEMDAN+小波包多阈值方法去噪后RMSE最小、SNR最大,说明该方法去噪效果最优。
3 实例分析选取JPL发布的拉萨站(LHAZ)2000~2020年单天解高程时间序列进行降噪分析,原始时间序列中已剔除序列初值、地震和非地震跳变的影响,高程时序缺值或者阶跃不影响高程序列降噪效果。利用3倍中误差准则去除时间序列中剩余的粗差,提高数据质量。LHAZ站原始高程时间序列见图 7。

|
图 7 LHAZ站预处理后的高程时间序列 Fig. 7 Height time series after preprocessing at LHAZ station |
利用CEEMDAN算法将时间序列分解成12个IMF分量和1个残余项,将各IMF分量进行小波包多阈值去噪,得到降噪后的各IMF分量,并与残余项重构得到去噪后的信号,结果见图 8。

|
图 8 LHAZ站CEEMDAN+小波包多阈值去噪信号和所剔除的噪声 Fig. 8 CEEMDAN and wavelet packet multi-threshold denoising signal and eliminated noise at LHAZ station |
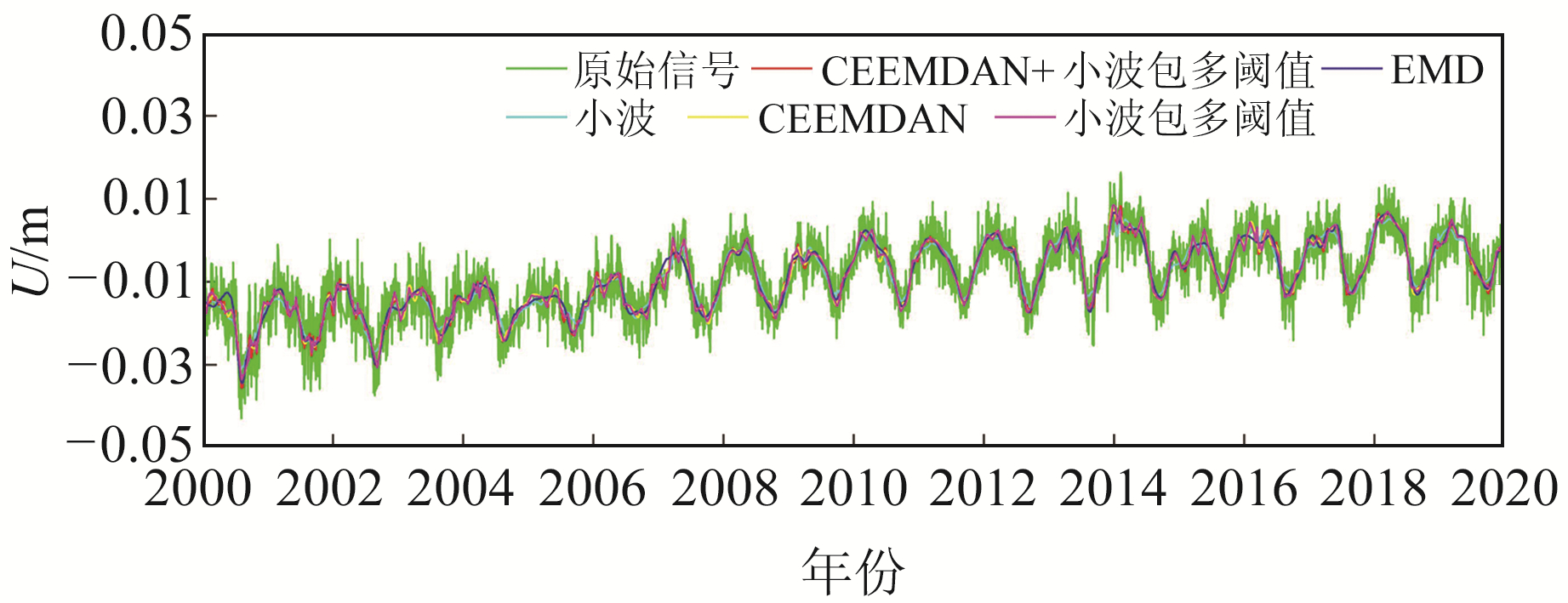
使用上节中5种方法对LHAZ站高程时间序列进行去噪处理,结果见图 9,去噪效果见表 2。结合图 9和表 2可以看出,5种方法均能很好地去除信号中的噪声,其中,CEEMDAN+小波包多阈值去噪法的SNR最大、RMSE最小,表明其去噪效果最好。小波去噪过程中固定了小波阈值,只对低频信号进行分解,没有对高频信号进行分解,导致无法保留高频信号中的有用信息。EMD去噪时在峰值附近会产生过度去噪的现象。
|
图 9 5种去噪方法对比 Fig. 9 Comparison of five denoising methods |
|
|
表 2 5种去噪方法效果比较 Tab. 2 Comparison of five denoising methods |
GNSS高程时间序列中含有大量噪声,本文针对EMD、CEEMDAN、小波、小波包多阈值等传统去噪方法去噪不彻底或去噪过度的缺点,尝试利用CEEMDAN +小波包多阈值的方法对信号进行去噪,并分别利用仿真信号、LHAZ站高程时间序列进行实验。结果表明,5种去噪方法均可以达到去噪效果,但本文方法去噪后各项指标均最优,效果最好。
| [1] |
Su J Z, Xia Y, Xu Y L, et al. Settlement Monitoring of a Supertall Building Using the Kalman Filtering Technique and Forward Construction Stage Analysis[J]. Advances in Structural Engineering, 2014, 17(6): 881-893 DOI:10.1260/1369-4332.17.6.881
(  0) 0) |
| [2] |
戴海亮, 孙付平, 姜卫平, 等. 小波多尺度分解和奇异谱分析在GNSS站坐标时间序列分析中的应用[J]. 武汉大学学报: 信息科学版, 2021, 46(3): 371-380 (Dai Hailiang, Sun Fuping, Jiang Weiping, et al. Application of Wavelet Decomposition and Singular Spectrum Analysis to GNSS Station Coordinate Time Series[J]. Geomatics and Information Science of Wuhan University, 2021, 46(3): 371-380)
(  0) 0) |
| [3] |
邱小梦, 陶国强, 王奉伟, 等. LMD和小波阈值的GNSS坐标时间序列降噪应用[J]. 测绘科学, 2021, 46(8): 28-32 (Qiu Xiaomeng, Tao Guoqiang, Wang Fengwei, et al. Application of LMD and Wavelet Threshold in Noise Reduction of GNSS Coordinate Time Series[J]. Science of Surveying and Mapping, 2021, 46(8): 28-32)
(  0) 0) |
| [4] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156 DOI:10.1142/S1793536910000422
(  0) 0) |
| [5] |
刘豪, 周东旭, 王盼龙, 等. 利用CEEMD分析中国沿海GNSS站高程时序变化[J]. 测绘通报, 2020(3): 39-43 (Liu Hao, Zhou Dongxu, Wang Panlong, et al. Height Time Series Change of China Coastal GNSS Stations Using CEEMD[J]. Bulletin of Surveying and Mapping, 2020(3): 39-43)
(  0) 0) |
| [6] |
Flandrin P, Rilling G, Goncalves P. Empirical Mode Decomposition as a Filter Bank[J]. IEEE Signal Processing Letters, 2004, 11(2): 112-114 DOI:10.1109/LSP.2003.821662
(  0) 0) |
| [7] |
Wu Z H, Huang N E. A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2004, 460(2 046): 1 597-1 611
(  0) 0) |
| [8] |
马俊, 曹成度, 姜卫平, 等. 利用小波包系数信息熵去除GNSS站坐标时间序列有色噪声[J]. 武汉大学学报: 信息科学版, 2021, 46(9): 1 309-1 317) (Ma Jun, Cao Chengdu, Jiang Weiping, et al. Elimination of Colored Noise in GNSS Station Coordinate Time Series by Using Wavelet Packet Coefficient Information Entropy[J]. Geomatics and Information Science of Wuhan University, 2021, 46(9): 1 309-1 317))
(  0) 0) |
| [9] |
章浙涛, 朱建军, 匡翠林, 等. 小波包多阈值去噪法及其在形变分析中的应用[J]. 测绘学报, 2014, 43(1): 13-20 (Zhang Zhetao, Zhu Jianjun, Kuang Cuilin, et al. Multi-Threshold Wavelet Packet De-Noising Method and Its Application in Deformation Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 13-20)
(  0) 0) |
| [10] |
张恒璟, 崔东东, 程鹏飞, 等. 顾及噪声项的连续运行参考站高程建模方法[J]. 测绘科学, 2020, 45(11): 13-19 (Zhang Hengjing, Cui Dongdong, Cheng Pengfei, et al. A Modeling Method for the Height of Reference Station in Continuous Operation Considering the Noise Term[J]. Science of Surveying and Mapping, 2020, 45(11): 13-19)
(  0) 0) |
| [11] |
Daubechies I. Ten Lectures on Wavelets(CBMS-NSF Regional Conference Series in Applied Mathematics)[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1992
(  0) 0) |
| [12] |
葛哲学, 沙威. 小波分析理论与MATLAB R2007实现[M]. 北京: 电子工业出版社, 2007 (Ge Zhexue, Sha Wei. Wavelet Analysis Theory and the Realization of MATLAB R2007[M]. Beijing: Publishing House of Electronics Industry, 2007)
(  0) 0) |
| [13] |
Torres M E, Colominas M A, Schlotthauer G, et al. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise[C]. IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), Prague, 2011
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100036, China
 2022, Vol. 42
2022, Vol. 42

